四边形中的最值问题专题(提纲)
四边形中的最值问题专题

2.三角形任两边之和大 于第三边。
将军饮马视频
P
P
一动两定点 A'B为最小值
两点之间线段最短
例2:如图,菱形ABCD中,AB=2,∠BAD=60°, E是AB的中点,P是对角线AC上的一个动点,则 PE+PB的最小值是______________四边形DMAN是
四边形?
MN=AD
AD⊥BC
利用等面积法求AD BC*AD/2=BA*AC/2
垂线段最短。
例6
垂线段最短。
(D )
C
x 2 勾股定理列方程求边长 x
PQ=2X
例7
垂线段最短。
四边形ABEF的周长: AB+BF+AE+EF
AE=CF
周长转化边长
四边形ABEF的周长最小值由EF决定 当EF⊥AD时,四边形周长最短。
解直角三形求EF
EF 3
四边边ABEF 的周长周 AB + BF + AE + EF 4 3
本节小结
1.将军饮马问题 2.垂线段最短。
P
A
E B
点P在AC上运动,点B、E位置不变
C
2.两定点在AC两侧
做点B(或E)关于AC的对称点D
3.PE+PB=PE+PD
DE为最小值
4.解直角三角形求边长
CC
1.一动两定点
E'
2.两定点在AC两侧 3.E'F为最小值 AP三线合一 E'F=AB=4
例4
() C
CE为最小值
垂线段最短。
例5
() C
专题
四边形中的最值问题
专题02 特殊平行四边形中的四种最值问题(解析版)-2024年常考压轴题攻略(9年级上册人教版)
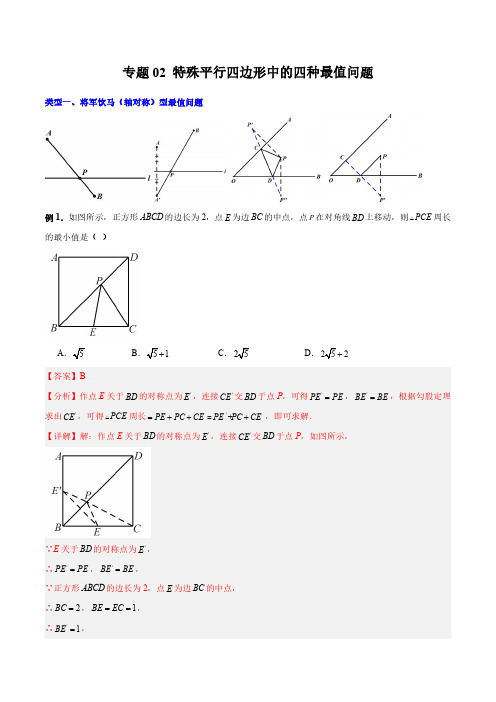
专题02特殊平行四边形中的四种最值问题类型一、将军饮马(轴对称)型最值问题A .5B .【答案】B 【分析】作点E 关于BD 的对称点为∵E 关于BD 的对称点为'E ,∴'PE PE =,'BE BE =,∵正方形ABCD 的边长为2,点A.0B.3【答案】C【分析】要使四边形APQE的周长最小,由于在BC边上确定点P、Q的位置,可在与BC交于一点即为Q点,过A点作后过G点作BC的平行线交DC的延长线于长度.∵四边形ABCD 是矩形,∴8BC AD ==,90D Ð=°,∠QCE =90°,∵2PQ =,∴6DF AD AF =-=,∵点F 点关于BC 的对称点G ,∴FG AD⊥∴90DFG ∠=︒∴四边形FGHD 是矩形,∴GH =DF =6,∠H =90°,∵点E 是CD 中点,∴CE =2,∴EH =2+4=6,∴∠GEH =45°,∴∠CEQ =45°,设BP =x ,则CQ =BC ﹣BP ﹣PQ =8﹣x ﹣2=6﹣x ,在△CQE 中,∵∠QCE =90°,∠CEQ =45°,∴CQ =EC ,∴6﹣x =2,解得x =4.故选:C .【点睛】本题考查了矩形的性质,轴对称﹣最短路线问题的应用,题目具有一定的代表性,是一道难度较大的题目,对学生提出了较高的要求.例3.如图,在矩形ABCD 中,26AB AD ==,,O 为对角线AC 的中点,点P 在AD 边上,且2AP =,点Q【答案】210【分析】①连接PO并延长交BC 明四边形APHB是矩形可得AB②过点O作关于BC的对称点PQ OQ+的最小值为PO'的长度,延长∵GO AD'⊥,点O是AC的中点,∴132AG AD==,【点睛】本题考查矩形的性质、全等三角形的判定与性质、勾股定理及轴对称识是解题的关键.【变式训练1】如图,正方形ABCD的周长为24,P为对角线AC上的一个动点,E是CD的中点,则PE PD+的最小值为()A .35B .32C .6D .5【答案】A 【详解】解:如图,连接BE ,设BE 与AC 交于点P',∵四边形ABCD 是正方形,∴点B 与D 关于AC 对称,∴P'D =P'B ,∴P'D +P'E =P'B +P'E =BE 最小.即P 在AC 与BE 的交点上时,PD +PE 最小,即为BE 的长度.∵正方形ABCD 的周长为24,∴直角△CBE 中,∠BCE =90°,BC =6,CE =12CD =3,∴226335BE =+=故选A.【变式训练2】如图,在矩形ABCD 中,AB =2,AD =3,动点P 满足S △PBC =14S 矩形ABCD ,则点P 到B ,C 两点距离之和PB +PC 的最小值为()A 10B 13C 15D .3【答案】B 【详解】解:设△PBC 中BC 边上的高是h .∵S △PBC =14S 矩形ABCD .∴12BC •h =14AB •AD ,∴h =12AB =1,∴动点P 在与BC 平行且与BC 的距离是1的直线l 上,如图,作B 关于直线l 的对称点E ,连接CE ,则CE 的长就是所求的最短距离.在Rt △BCE 中,∵BC =3,BE =BA =2,∴CE 2213+AB BC 即PB +PC 13故选:B .【变式训练3】如图,在正方形ABCD 中,4AB =,AC 与BD 交于点O ,N 是AO 的中点,点M 在BC 边上,且3BM =,P 为对角线BD 上一点,则PM PN -的最大值为_____________.【答案】1【分析】作N 关于BD 的对称点E ,连接PE ,ME ,过点M 作MQ ⊥AC ,垂足为Q ,可判定当点P ,E ,M 三点共线时,PM -PE 的值最大,为ME 的长,求出CE ,CQ ,得到EQ ,利用垂直平分线的性质得到EM =CM =1即可.【详解】解:如图:作N 关于BD 的对称点E ,连接PE ,ME ,过点M 作MQ ⊥AC ,垂足为Q ,∴PN =PE ,则PM -PN =PM -PE ,【答案】13【分析】连接CF、AF+=+,故当EF MN EF AF类型二、翻折型最值问题例1.如图,在边长为2的菱形ABCD中,∠A=60°,M是AD边的中点,N是AB边上的一动点,将△AMN 沿MN所在直线翻折得到△A'MN,连接A'C,则A'C长度的最小值是()【变式训练1】如图,在矩形ABCD 中,3AB =,4=AD ,E 在AB 上,1BE =,F 是线段BC 上的动点,将EBF △沿EF 所在的直线折叠得到'EB F △,连接'B D ,则'B D 的最小值是()A .6B .4C .2D .1-【答案】D 【详解】解:如图,'B 的运动轨迹是以E 为圆心,以BE 的长为半径的圆.所以,当'B 点落在DE 上时,'B D 取得最小值.根据折叠的性质,△EBF ≌△EB’F ,∴E 'B ⊥'B F ,∴E 'B =EB ,∵1BE =∴E 'B =1,∵3AB =,4=AD ,∴AE =3-1=2,∴DE =D 'B =.故选:D .【变式训练2】如图,在正方形ABCD 中,AB =6,E 是CD 边上的中点,F 是线段BC 上的动点,将△ECF 沿EF 所在的直线折叠得到EC F '△,连接AC ',则的最小值是AC '_______.【答案】3【详解】解:∵四边形ABCD 是正方形,∴6CD AB AD ===,∵E 是CD 边上的中点,∴132EC CD ==∵△ECF 沿EF 所在的直线折叠得到EC F '△,∴3EC EC '==,∴当点A ,C ',E 三点共线时,AC '最小,如图,在Rt ADE △中,由勾股定理得:AE ==3AE EC '-=-,∴AC '的最小值为3.类型三、旋转型最值问题【答案】353-【分析】过点M 作MP CD ⊥,垂足为P ,连接CM ,根据正方形的性质求出CE ,证明EDC DMP △≌△股定理求出CM ,根据CN MN CM +≥即可求出CN 【详解】解:过点M 作MP CD ⊥,垂足为P ,连接由旋转可得:DE DM =,3EF MN ==,90EDM ∠=例2.如图,长方形ABCD 中,6AB =,8BC =,E 为BC 上一点,且2BE =,F 为AB 边上的一个动点,连接EF ,将EF 绕着点E 顺时针旋转30°到EG 的位置,连接FG 和CG ,则CG 的最小值为______.【答案】2+【详解】解:如图,将线段BE 绕点E 顺时针旋转30°得到线段ET ,连接GT ,过E 作EJ CG ⊥,垂足为J ,∵四边形ABCD 是矩形,∴AB =CD =6,∠B =∠BCD =90°,∵∠BET =∠FEG =30°,∴∠BEF =∠TEG ,在△EBF 和△TEG 中,EB ET BEF TEG EF EG =⎧⎪∠=∠⎨⎪=⎩,∴△EBF ≌△ETG (SAS ),∴∠B =∠ETG =90°,∴点G 的在射线TG 上运动,∴当CG ⊥TG 时,CG 的值最小,∵∠EJG =∠ETG =∠JGT =90°,∴四边形ETGJ 是矩形,∴∠JET =90°,GJ =TE =BE =2,∵∠BET =30°,∴∠JEC =180°-∠JET -∠BET =60°,∵8BC =,∴226,3,3EC BC BE EJ CJ EC EJ =-===-=,∴CG =CJ +GJ =332+.∴CG 的最小值为332+.故答案为:332.【变式训练1】如图,已知正方形ABCD 的边长为a ,点E 是AB 边上一动点,连接ED ,将ED 绕点E 顺时针旋转90︒到EF ,连接DF ,CF ,则当DF CF +之和取最小值时,DCF 的周长为______.(用含a 的代数式表示)【答案】()51a +【分析】连接BF ,过点F 作FG AB ⊥交AB 延长线于点G ,先证明AED GFE △≌△,即可得到点F 在CBG ∠的角平分线上运动,作点C 关于BF 的对称点C ',当点D ,F ,C 三点共线时,DF CF DC +='最小,根据勾股定理求出DC DF CF '=+的最小值为35,即可求出此时DCF 的周长为353+.将ED绕点E顺时针旋转90︒到EF,=,∴⊥,EF DEEF DEDEA FEG DEA ADE∴∠+∠=∠+∠=︒,90∴∠=∠,ADE FEG又90,∠=∠=︒DAE FGE(1)试猜想线段BG 和AE 的数量关系,并证明你得到的结论;(2)将正方形DEFG 绕点D 逆时针方向旋转一定角度后(旋转角度大于过观察或测量等方法判断(1)中的结论是否仍然成立?如果成立,请予以证明;如果不成立,请说明理由;(3)若2BC DE ==,在(2)的旋转过程中,①当AE 为最大值时,则AF =___________.ABC 是等腰直角三角形,AD BC ∴⊥,BD CD =,90ADB ADC ∴∠=∠=︒.四边形DEFG 是正方形,DE DG ∴=.在BDG 和ADE V 中,BD AD BDG ADE GD ED =⎧⎪∠=∠⎨⎪=⎩,(SAS)ADE BDG ∴△≌△,BG AE ∴=;(2)(1)中的结论仍然成立,BG AE =,BG AE ⊥.理由如下:如图②,连接AD ,延长EA 交BG 于K ,交DG 于O .在Rt BAC 中,D 为斜边BC 中点,AD BD ∴=,AD BC ⊥,90ADG GDB ∴∠+∠=︒.四边形EFGD 为正方形,DE DG ∴=,且90GDE ∠=︒,90ADG ADE ∴∠+∠=︒,BDG ADE ∴∠=∠.在BDG 和ADE V 中,BD AD BDG ADE GD ED =⎧⎪∠=∠⎨⎪=⎩,(SAS)BDG ADE ∴△≌△,BG AE ∴=,BGD AED ∠=∠,2,==BC DEBG∴=+=.213AE∴=.3在Rt AEF中,由勾股定理,得222=+=+3AF AE EF中,如图②中,在BDGBG∴-≤≤+,2112∴的最小值为1,此时如图④中,AE在Rt AEF中,2=AF EF【点睛】本题属于四边形综合题,考查了旋转的性质的运用,等腰直角三角形的性质的运用,勾股定理的运用,全等三角形的判定及性质的运用,正方形的性质的运用,解答时证明三角形全等是关键.类型四、PA+KPB型最值问题3A.27B.23【答案】C【分析】连接AC与EF相交于∵四边形ABCD是菱形,∠=∠,∴OAE OCFA.3B.22【答案】D【分析】连接AF,利用三角形中位线定理,可知四边形ABCD是菱形,∴==,AB BC23,H分别为AE,EF的中点,GGH∴是AEF△的中位线,【答案】51-【分析】连接BD交EF的中点,求出OB的长,得到AH AM MH>=-–51直线l平分正方形∴O是BD的中点,四边形ABCD是正方形,∴==,BD AB24【答案】26【分析】利用轴对称的性质作出如图的辅助线,在【详解】解:延长DC '''∴E F G H E '''、、、、在同一直线上时,四边形EFCH 作E K AB '⊥交AB 延长于点K ,则23EK BE CD A E AB CD '''=++=+=,E K BC '=+在△ABH中,∠AHB=90°,∠ABH过点D作DE∥AC交BC延长线于点E,作点C【点睛】本题考查了对称的性质,勾股定理,等边三角形的判定和性质,最值问题,直角三角形的性质,多边形的面积,知识点较多,难度较大,解题的关键是作出辅助线,得出当且仅当B,D,F三点共线时,BD+CD取得最小值.。
初中数学 微拓展 特殊平行四边形中的最值问题

微拓展:特殊平行四边形中的最值问题解题策略:线段长度的最值常与图形运动、点运动相关联,需理清定点与动点、常量与变量,动静转化.我们一般根据“对称性+两点之间线段最短或垂线段最短”求最值.几何模型:条件:如图1,A,B是直线l同旁的两个点.问题:在直线l上确定一点P,使PA+PB的值最小.原型:“饮马问题”方法归纳:求线段和最小时,若已知的两点在直线的同侧,则将动点所在的直线为对称轴,作出其中一点的对称点,再将另一点与此对称点连接,则连线与对称轴的交点即为所求动点的位置,再求出所连接的线段长,即为所求的最小值. 作点A关于直线l的对称点A',连接A'B交l于点P,则PA+PB=A'B的值最小(不必证明)模型应用:(出题背景变式很多,有时经常会出现在矩形、菱形、正方形背景下)(1)如图2,已知平面直角坐标系中两定点A(0,−1)和B(2,−1),P为x轴上一动点,则当PA+PB的值最小时,点P的横坐标是______,此时PA+PB=______.(2)如图3,若正方形ABCD的边长为2,E为AB的中点,P是AC上一动点,连接BD,由正方形对称性可知,B与D关于直线AC对称,则PB+PE的最小值是______.(3)如图4,若正方形ABCD的面积为12,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一动点P,则PD+PE的最小值为______.(4)如图5,在菱形ABCD中,AB=8,∠B=60°,点G是边CD边的中点,点E,F分别是AG,AD上的两个动点,则EF+ED的最小值是______.知识迁移:如图,四边形ABCD是正方形,△ABE是等边三角形,M为对角线BD(不含B 点)上任意一点,将B M绕点B逆时针旋转60°得到BN,连接EN、AM、CM,尝试解决:①当M点在何处时,AM+CM的值最小;②当M点在何处时,AM+BM+CM的值最小,并说明理由;③当AM+BM+CM的最小值为√3+1时,求正方形的边长.答案模型应用:解:(1)如答图2,取点A 关于x 轴对称的点A ',连接A'B 交x 轴于P , 则此时PA +PB 最小 ,∵点A 的坐标为(0,-1),点B 的坐标为(2,-1)∴AB //x 轴∴AB =2,过B 作BH ⊥x 轴于H ,则BH =1,△A'OP ≌△BHP ,OP =PH =1∴点P 的横坐标是1,∴PA +PB =A'B =22故答案为:1;22(2) ∵B 与D 关于直线AC 对称∴PB +PE 的最小值是DE 的长∵正方形ABCD 的边长为2,E 为AB 的中点∴AE =1在Rt △ADE 中,DE =5212222=+=+AE AD , 则PB +PE 的最小值是5 故答案为:5;(3)如图4,设BE 与AC 交于点P ′,连接BD .∵点B 与D 关于AC 对称,∴P'D =P'B ,∴P'D +P'E =P'B +P'E =BE 最小.∵正方形ABCD 的面积为12,∴AB =32又∵△ABE 是等边三角形,∴BE =AB =32, 故答案为:32.(3) 如图5,作DH ⊥AC 垂足为H 与AG 交于点E ,∵四边形ABCD 是菱形,∴AB =AD =CD =BC =8,∵∠B =60°∴∠ADC =∠B =60°∴△ADC 是等边三角形,∵AG 是中线,∴∠GAD =∠GAC∴点H 关于AG 的对称点F 在AD 上,此时EF +ED 最小值=DH .在Rt △DHC 中,∵∠DHC =90° DC =8,∠CDH =21∠ADC =30°∴CH =21DC =4,DH =3422=-CH CD ∴EF +DE 的最小值=DH =34故答案为:34知识迁移:解:①当M 点落在BD 的中点时,AM +CM 的值最小.②如图,连接CE ,当M 点位于BD 与CE 的交点处时,AM +BM +CM 的值最理由如下:连接MN ,易知△AMB ≌ △ENB ,∴AM =EN .∵∠MBN =60°,MB =NB ,∴△BMN 是等边三角形.∴BM =MN .∴AM +BM +CM =EN +MN +CM .根据“两点之间线段最短”,得EN +MN +CM =EC 最短∴当M 点位于BD 与CE 的交点处时,AM +BM +CM 的值最小,即等于EC 的长. ⑶过E 点作EF ⊥BC 交CB 的延长线于F ,∴∠EBF =90°-60°=30°,设正方形的边长为x ,则BF =x ,EF =. 在Rt △EFC 中,∵EF 2+FC 2=EC 2,∴()2+(x +x )2=. 解得,x =2±(舍去负值)∴正方形的边长为2.。
2020初中数学中考专题复习——四边形中的线段最值问题专项训练2(附答案详解)

解:∵在△ABC中,AB=6,AC=8,BC=10,
∴AB2+AC2=BC2,
即∠BAC=90°.
又PE⊥AB于E,PF⊥AC于F,
∴四边形AEPF是矩形,
∴EF=AP.
∵M是EF的中点,
∴AM= EF= AP,
因为AP的最小值即为直角三角形ABC斜边上的高
AP= ,
∴AM的最小值是 .
故选C.
②根据对称性:连接ED交BC于点P,此时AP+EP=AD,最小,再过点D作DF垂直AC的延长线于点F,根据勾股定理即可求解.
【详解】
如图所示:
(1)∵BD∥CE,CD∥BE,
∴四边形BDCE是平行四边形,
∵CE⊥AB,
∴∠BEC=90°,
∴四边形BECD是矩形;
(2)①当BE的长为 时,四边形BECD是菱形.理由如下:
6.C
【解析】
【分析】
根据勾股定理的逆定理可以证明∠BAC=90°,根据直角三角形斜边上的中线等于斜边的一半,则AM= EF,要求AM的最小值,即求EF的最小值;根据三个角都是直角的四边形是矩形得四边形AEPF是矩形,根据矩形的对角线相等,得EF=AP,则EF的最小值即为AP的最小值,根据垂线段最短知:AP的最小值即等于直角三角形ABC斜边上的高.
【详解】
设 与AC交于点O,作 ⊥ 于 ,如图所示:
在Rt△ABC中,∠BAC=90 ,∠ACB=45 ,
∴ ,
∵四边形PAQC是平行四边形,
∴ ,
∵ ⊥ ,∠ACB=45 ,
∴ ,
当 与 重合时,OP的值最小,则PQ的值最小,
∴PQ的最小值
故选:A.
【点睛】
本题考查了勾股定理的运用、平行四边形的性质以及垂线段最短的性质,利用垂线段最短求线段的最小值是解题的关键.
高考数学----四边形定值和最值规律方法及典型例题讲解

高考数学----四边形定值和最值规律方法及典型例题讲解【规律方法】正常的四边形我们不去解释,只需多一次余弦定理即可,我们需要注意一些圆内接的四边形,尤其是拥有对角互补的四边形,尤其一些四边形还需要引入托勒密定理.勒密定理:在四边形ABCD 中,有AB CD AD BC AC BD ⋅+⋅≥⋅,当且仅当四边形ABCD 四点共圆时,等号成立.【典型例题】例38.(2022·甘肃·兰州西北中学高三期中(理))在四边形ABCD 中,2,3AB BC CD AD ====,则四边形ABCD 面积的最大值为______.【解析】在ABC 中,由余弦定理知2222cos 44222cos 88cos AC AB BC AB BC B B B =+−⋅=+−⨯⨯=−,在ACD 中,由余弦定理知2222cos 49223cos 1312cos AC AD CD AD CD D D B =+−⋅=+−⨯⨯=−,所以88cos 1312cos B D −=−,即53cos 2cos 4D B −=. 可得11sin sin 2sin 3sin 22ABC ACDABCD S SSAB BC B AD CD D B D =+=⋅+⋅=+四边形, 令53cos 2cos 4M D B =−=,3sin 2sin N D B =+, 则2294232(cos cos sin sin )1312cos()25M N B D B D B D +=+−⨯⨯−=−+≤,等号成立时πB D +=所以2252515251616N ⨯≤−=,所以四边形ABCD .例39.(2022·江苏无锡·高三期中)如图,在平面四边形ABCD 中,cos AB BD ABD =∠.(1)判断ABD △的形状并证明;(2)若AB =,BC =,12BC =,求四边形ABCD 的对角线AC 的最大值.【解析】(1)已知cos AB BD ABD =∠,由正弦定理可得:sin sin cos ADB BAD ABD ∠=∠⋅∠,()sin sin cos BAD ABD BAD ABD ∠+∠=∠∠即sin cos cos sin sin cos BAD ABD BAD ABD BAD ABD ∠∠+∠∠=∠∠ 得cos sin 0BAD ABD ∠∠=,sin 0ABD ∠≠,∴cos 0BAD ∠=,故90BAD ∠=︒,即ABD △为直角三角形.(2)如图,在BC 上方作Rt △BCM 使BM ABCM AD==90BMC ∠=︒,∴BCMBDA ,∴BA BDBM BC=且ABM CBD ∠=∠ ∴ABM BCD ,由BC =,12BC =,得CD =在Rt BCM △中,222BM CM BC +=,由BMCM12BC =,得6CM =.由AM AB CD BD ==,得3AM =, ∴639AC AM CM +=+=≤,当M 在AC 上时等号成立, ∴()max 9AC =.例40.(2022·山西忻州·高三阶段练习)在平面四边形ABCD 中,20AB AD ==,π3BAD ∠=,2π3BCD ∠=.(1)若5π12ABC ∠=,求BC 的长; (2)求四边形ABCD 周长的最大值. 【解析】(1)连接BD ,因为20AB AD ==,π3BAD ∠=,故ABD △为等边三角形,20BD ∴=, 5πππ12312CBD ABC ABD ∴∠=∠−∠=−=,则ππ4BDC BCD CBD ∠=−∠−∠=, 由正弦定理得sin sin BD BC BCD BDC =∠∠,所以,πsin42πsin 3BD BC ==(2)由余弦定理可得222222π4002cos3BD BC CD BC CD BC CD BC CD ==+−⋅=++⋅ ()()()()2222344BC CD BC CD BC CD BC CD BC CD ++=+−⋅≥+−=,所以,BC CD +≤,当且仅当BC CD =. 因此,四边形ABCD周长的最大值为40+例41.(2022·黑龙江·齐齐哈尔市实验中学高三阶段练习)已知函数()((1sin cos 1sin cos f x x x x x ⎡⎤⎡⎤=−⋅−⎣⎦⎣⎦. (1)求()f x 的最小正周期T 和单调递减区间;(2)四边形ABCD 内接于⊙O ,BD =2,锐角A 满足314A f ⎛⎫=− ⎪⎝⎭,求四边形ABCD 面积S 的取值范围.【解析】(1)((1sin cos 1sin cos x x x x ⎡⎤⎡⎤−⋅−⎣⎦⎣⎦()()sin cos sin cos x x x x x x ⎡⎤⎡⎤=−⋅−⎣⎦⎣⎦ ()22sin cos 2sin x x x =−−222sin 2sin cos cos 2sin x x x x x =−+− 212sin sin 2x x =−−cos2sin 2x x =−24x π⎛⎫=+ ⎪⎝⎭,∴()24f x x π⎛⎫=+ ⎪⎝⎭∴T π=. 由()2224k x k k ππππ≤+≤+∈Z ,得()388k x k k ππππ−≤≤+∈Z , 所以()f x 单调递减区间为()3,88k k k ππππ⎡⎤−+∈⎢⎥⎣⎦Z .(2)由于314A f ⎛⎫=− ⎪⎝⎭,根据(132144A π⎛⎫⨯+=− ⎪⎝⎭, ∵02A π<<,∴3A π=,23C π=. 分别设AB =a ,AD =b ,BC =c ,CD =d .因BD =2,分别在ABD △和CBD △中由余弦定理得222cos43a b ab π+−=,2222cos43c d cd π+−=, ∴224a b ab +=+,224c d cd +=−.∵222a b ab +≥,222c d cd +≥,等号在a =b =2,c d ==时成立, ∴42ab ab +≥,42cd cd −≥,解得04ab <≤,403cd <≤.∴1603ab cd <+≤.等号在a =b =2,c d ==∵)11sin sin 22S ab A cd C ab cd =+=+,所以S 的取值范围是⎛ ⎝⎦.例42.(2022·辽宁·朝阳市第一高级中学高三阶段练习)如图,在平面凹四边形ABCD 中,=2AB ,=3BC ,60B ∠=︒.(1)若sin sin AD A CD C =且=1AD ,求凹四边形ABCD 的面积; (2)若120ADC ∠=︒,求凹四边形ABCD 的面积的最小值. 【解析】(1)如图,连接BD ,在ABD △中, 由正弦定理得sin sin AD BD ABD A=∠,所以sin sin AD A BD ABD =∠,同理可得,在CBD △中,有sin sin CD C BD CBD =∠, 因为sin sin AD A CD C =,所以sin sin BD ABD BD CBD ∠=∠, 即sin sin ABD CBD ∠=∠,又ABD ∠,CBD ∠都是锐角,60B ∠=︒ 所以30ABD CBD ∠=∠=︒.(也可由点D 向BA ,BC 作垂线,证明BD 是角平分线)在ABD △中,由余弦定理得2222cos AD AB BD AB BD ABD =+−⋅⋅⋅∠, 即214BD =+−,解得BD 所以凹四边形ABCD 的面积11sin sin 22ABD BCD S S S AB BD ABD CB BD CBD =+=⋅⋅⋅∠+⋅⋅⋅∠=△△.(2)如图,连接AC ,在ABC 中,由余弦定理得2222cos 7AB BC A A A B C BC BC +=−⋅⋅⋅∠=,故AC 在ADC △中,设AD m =,CD n =, 因为120ADC ∠=︒所以,由余弦定理得2222cos AC m n mn ADC =+−∠, 所以2272m n mn mn +=−≥,即73mn ≤,当且仅当m n =时等号成立, 此时显然点D 在ABC 的内部,所以117sin 223ADC S mn ADC =∠≤⨯△(不写取等条件扣1分)又1sin 2ABC S AB BC ABC =⋅⋅⋅∠=△所以凹四边形ABCD 的面积的最小值min S ==例43.(2022·全国·高三阶段练习(理))如图,在平面四边形ABCD 中,AD CD ⊥,()090BAD BCD θθ∠=∠=<<o o ,6AB BC +=.(1)若=2BC AB ,75θ=,求对角线AC 的长;(2)当AD CD =,=3BC 时,求平面四边形ABCD 的面积的最大值及此时θ的值.【解析】(1)因为,75AD CD BAD BCD θ︒⊥∠=∠==所以36027590120ABC ∠=−⨯−=o o o o .又因为2,6BC AB AB BC =+=, 所以4,2BC AB ==.在ABC 中,由余弦定理得2222cos 416224cos120AC AB BC AB BC ABC =+−⋅⋅∠=+−⨯⨯⨯o28=,故AC = 即对角线AC 的长为(2)因为6,3AB BC BC +==, 所以3AB BC ==,连接BD . 又AD CD =, 所以BD 为ADC ∠的平分线, 所以18045135ABD CBD θθ∠=∠=−−=−o o o ,在BCD △中, 由正弦定理sin sin BD BC BDCθ=∠得sin 3sin sin sin 45BC BD BDC θθθ===∠o .所以四边形ABCD 的面积()()122sin 135sin 1352BCD S S BD BC θθθ==⨯⨯⨯−=−o oV29sin cos 9sin θθθθθθ⎫==+⎪⎪⎝⎭()999sin 2(1cos 2)245222θθθ=+−=−+o , 因为090θ<<, 所以45245135θ−<−<o o o .所以当24590θ−=o o , 即67.5θ=o 时,S 例44.(2022·上海·华师大二附中高三开学考试)设()()cos sin f x x x ϕ=−−,其中0,2πϕ⎛⎫∈ ⎪⎝⎭,已知03f π⎛⎫= ⎪⎝⎭.(1)求()f x 的最小值;(2)已知凸四边形ABCD 中,()114,7AB AC AD f A ====,求ABCD 面积的最大值.【解析】(1)依题意,由03f π⎛⎫= ⎪⎝⎭得:cos sin 33ππϕ⎛⎫−== ⎪⎝⎭,而0,2πϕ⎛⎫∈ ⎪⎝⎭,即,363πππϕ⎛⎫−∈− ⎪⎝⎭,于是得36ππϕ−=,解得6πϕ=,()11cos sin sin sin sin cos()6226f x x x x x x x x x ππ⎛⎫=−−=+−=−=+ ⎪⎝⎭,所以当52(Z)6x k k ππ=+∈时,()f x 的最小值为1−. (2)由(1)知,()1cos()67f A A π=+=,在凸四边形ABCD 中,0A π<<,于是得A 为锐角,sin()6A π+,cos cos[()]cos()cos sin()sin 666666A A A A ππππππ=+−=+++=,sin 2A ===, 设()222A A A BAC θθ∠=−−<<,则()222A A ADAC θθ∠=+−<<,令凸四边形ABCD 的面积为S , 11sin sin 98[sin()sin()]2222ABC ADCA AS SSAB AC BAC AD AC DAC θθ=+=⋅∠+⋅∠=−++196sincos 1962A θθ==≤0θ=时取等号, 所以ABCD 面积的最大值为。
特殊的平行四边形中的最值模型-胡不归模型(解析版)

特殊的平行四边形中的最值模型--胡不归模型胡不归模型可看作将军饮马衍生,主要考查转化与化归等的数学思想,近年在中考数学和各地的模拟考中常以压轴题的形式考查,学生不易把握。
本专题就最值模型中的胡不归问题进行梳理及对应试题分析,方便掌握。
在解决胡不归问题主要依据是:点到线的距离垂线段最短。
【模型背景】从前有个少年外出求学,某天不幸得知老父亲病危的消息,便立即赶路回家.根据“两点之间线段最短”,虽然从他此刻位置A 到家B 之间是一片砂石地,但他义无反顾踏上归途,当赶到家时,老人刚咽了气,小伙子追悔莫及失声痛哭.邻居告诉小伙子说,老人弥留之际不断念叨着“胡不归?胡不归?”看到这里很多人都会有一个疑问,少年究竟能不能提前到家呢?假设可以提早到家,那么他该选择怎样的一条路线呢?这就是今天要讲的“胡不归”问题.补充知识:在直角三角形中锐角A 的对边与斜边的比叫做∠A 的正弦,记作sin A ,即sin A =∠A 的对边斜边。
若无法理解正弦,也可考虑特殊直角三角形(含30°,45°,60°)的三边关系。
【模型解读】一动点P 在直线MN 外的运动速度为V 1,在直线MN 上运动的速度为V 2,且V 1<V 2,A 、B 为定点,点C 在直线MN 上,确定点C 的位置使AC V 2+BC V 1的值最小.(注意与阿氏圆模型的区分)1)AC V 2+BC V 1=1V 1BC +V 1V 2AC,记k =V 1V 2,即求BC +kAC 的最小值.2)构造射线AD 使得sin ∠DAN =k ,CH AC=k ,CH =kAC ,将问题转化为求BC +CH 最小值.3)过B 点作BH ⊥AD 交MN 于点C ,交AD 于H 点,此时BC +CH 取到最小值,即BC +kAC 最小.【解题关键】在求形如“PA +kPB ”的式子的最值问题中,关键是构造与kPB 相等的线段,将“PA +kPB ”型问题转化为“PA +PC ”型.(若k >1,则提取系数,转化为小于1的形式解决即可)。
平行四边形最值问题及解决方法

平行四边形最值问题及解决方法一、边长相关的最值问题。
题目1:在平行四边形ABCD中,AB = 5,AD = 3,对角线AC和BD相交于点O,点E 是边AD上的动点,求OE的最大值。
解析:因为平行四边形的对角线互相平分,所以AO=(1)/(2)AC。
在AOD中,OE是AOD的中线,根据三角形中线的性质,OE<(1)/(2)AD。
当E点与D点重合时,OE取得最大值,此时OE=(1)/(2)AD=(3)/(2)。
题目2:已知平行四边形ABCD中,AD = 6,∠ DAB=60^∘,E是AB上的动点,连接DE,求DE的最小值。
解析:过D作DF⊥ AB于F。
在Rt ADF中,∠ DAB = 60^∘,AD=6,则DF =AD×sin60^∘=6×(√(3))/(2)=3√(3)。
因为垂线段最短,所以当E点与F点重合时,DE取得最小值3√(3)。
题目3:平行四边形ABCD中,AB = 8,BC=10,P是平行四边形ABCD内一点,求PA + PC的最小值。
解析:利用平行四边形的对称性,连接AC、BD相交于点O,PA + PC≥slant AC。
根据平行四边形的性质,AC=√(AB^2)+BC^{2- 2AB× BC×cos∠ ABC}。
因为平行四边形ABCD,AB = 8,BC = 10,设∠ ABC=θAC=√(64 + 100-2×8×10×cosθ)根据平行四边形对角线互相平分,PA+PC的最小值就是AC的长。
由平行四边形性质可知cos∠ ABC=cos∠ BAD在ABC中,AC=√(8^2)+10^{2-2×8×10×cos∠ ABC}=√(64 + 100-160×cos∠ ABC)当cos∠ ABC = 1时(∠ ABC = 0^∘,这种极限情况方便计算最小值)AC=√(64+100 - 160)=2实际上,根据平行四边形性质计算AC=√(8^2)+10^{2-2×8×10×cos∠ ABC}=√(164-160cos∠ ABC),AC的最小值为2二、面积相关的最值问题。
专题5.4四边形中的最值问题专项训练(30道)(举一反三)(浙教版)(原卷版)

专题5.4 四边形中的最值问题专项训练(30道)【浙教版】考卷信息:本套训练卷共30题,选择10题,填空10题,解答10题,题型针对性较高,覆盖面广,选题有深度,可强化学生对四边形中最值问题模型的记忆与理解!一.选择题(共10小题)1.(2022春•重庆期末)如图,矩形ABCD中,AB=2√3,BC=6,P为矩形内一点,连接P A,PB,PC,则P A+PB+PC的最小值是()A.4√3+3B.2√21C.2√3+6D.4√52.(2022•灞桥区校级模拟)如图,平面内三点A、B、C,AB=4,AC=3,以BC为对角线作正方形BDCE,连接AD,则AD的最大值是()√2A.5B.7C.7√2D.723.(2022春•中山市期末)如图,在边长为a的正方形ABCD中,E是对角线BD上一点,且BE=BC,点P是CE上一动点,则点P到边BD,BC的距离之和PM+PN的值()aA.有最大值a B.有最小值√22C.是定值a D.是定值√2a24.(2022春•三门峡期末)如图,在矩形ABCD中,AB=2,AD=1,E为AB的中点,F为EC上一动点,P为DF中点,连接PB,则PB的最小值是()A.2B.4C.√2D.2√25.(2022春•滨湖区期末)如图,已知菱形ABCD的面积为20,边长为5,点P、Q分别是边BC、CD上的动点,且PC=CQ,连接PD、AQ,则PD+AQ的最小值为()A.4√5B.√89C.10D.7√26.(2022•泰山区一模)如图,M、N是正方形ABCD的边CD上的两个动点,满足AM=BN,连接AC交BN于点E,连接DE交AM于点F,连接CF,若正方形的边长为2,则线段CF的最小值是()A.2B.1C.√5−1D.√5−27.(2022•龙华区二模)如图,已知四边形ABCD是边长为4的正方形,E为CD上一点,且DE=1,F为射线BC上一动点,过点E作EG⊥AF于点P,交直线AB于点G.则下列结论中:①AF=EG;②若∠BAF=∠PCF,则PC=PE;③当∠CPF=45°时,BF=1;④PC的最小值为√13−2.其中正确的有()A.1个B.2个C.3个D.4个8.(2022•南平校级自主招生)如图,在△ABC中,AB=6,AC=8,BC=10,P为边BC上一动点(且点P不与点B、C重合),PE⊥AB于E,PF⊥AC于F.则EF的最小值为()A.4B.4.8C.5.2D.69.(2022春•崇川区期末)如图,正方形ABCD边长为1,点E,F分别是边BC,CD上的两个动点,且BE=CF,连接BF,DE,则BF+DE的最小值为()A.√2B.√3C.√5D.√610.(2022•泰州)如图,正方形ABCD的边长为2,E为与点D不重合的动点,以DE为一边作正方形DEFG.设DE=d1,点F、G与点C的距离分别为d2、d3,则d1+d2+d3的最小值为()A.√2B.2C.2√2D.4二.填空题(共10小题)11.(2022春•江城区期末)如图,∠MON=90°,矩形ABCD的顶点A、B分别在边OM、ON上,当B在边ON上运动时,A随之在OM上运动,矩形ABCD的形状保持不变,其中AB=6,BC=2.运动过程中点D到点O的最大距离是.12.(2022•东莞市校级一模)如图,在矩形ABCD中,AB=6,AD=5,点P在AD上,点Q在BC上,且AP=CQ,连接CP,QD,则PC+DQ的最小值为.13.(2022•钱塘区一模)如图,在矩形ABCD中,线段EF在AB边上,以EF为边在矩形ABCD内部作正方形EFGH,连结AH,CG.若AB=10,AD=6,EF=4,则AH+CG的最小值为.14.(2022春•东城区期中)在正方形ABCD中,AB=5,点E、F分别为AD、AB上一点,且AE=AF,连接BE、CF,则BE+CF的最小值是.15.(2022春•虎林市期末)如图,在Rt△ABC中,∠BAC=90°,且BA=12,AC=16,点D是斜边BC 上的一个动点,过点D分别作DE⊥AB于点E,DF⊥AC于点F,点G为四边形DEAF对角线交点,则线段GF的最小值为.16.(2022•灞桥区校级三模)在菱形ABCD中,∠D=60°,CD=4,E为菱形内部一点,且AE=2,连接CE,点F为CE中点,连接BF,取BF中点G,连接AG,则AG的最大值为.17.(2022春•靖江市校级期末)如图,线段AB的长为10,点D在AB上,△ACD是边长为3的等边三角形,过点D作与CD垂直的射线DP,过DP上一动点G(不与D重合)作矩形CDGH,记矩形CDGH 的对角线交点为O,连接OB,则线段BO的最小值为.18.(2022春•郫都区期末)如图,在矩形ABCD中,AB=4,AD=8,点E是BC边上一动点,作点B关于AE的对称点F,连接CF,点P为CF中点,则DP的最小值为.19.(2022春•江都区期中)如图,矩形ABCD中,AB=4,AD=2√3,E为AB的中点,F为EC上一动点,P为DF中点,连接PB,则PB的最小值是.20.(2022春•如东县期中)如图,已知AB=2√2,C为线段AB上的一个动点,分别以AC,CB为边在AB的同侧作菱形ACED和菱形CBGF,点C,E,F在一条直线上,∠D=120°.P、Q分别是对角线AE,BF的中点,当点C在线段AB上移动时,点P,Q之间的距离最短为(结果保留根号).三.解答题(共10小题)21.(2022•禹城市二模)(1)如图①,已知正方形ABCD的边长为4,点M和N分别是边BC,CD上两点,且BM=CN,连AM和BN,交于点P.猜想AM与BN的位置关系,并证明你的结论.(2)如图②,已知正方形ABCD的边长为4.点M和N分别从点B、C同时出发,以相同的速度沿BC、CD方向向终点C和D运动,连接AM和BN,交于点P.求△APB周长的最大值.22.(2022春•东坡区校级月考)正方形ABCD中,E、F是AD上的两个点,AE=DF,连CF交BD于点M,连AM交BE于点N,连接DN.如果正方形的边长为2.(1)求证:BE⊥AM;(2)求DN的最小值.23.(2022•黄埔区模拟)如图,在边长为4的菱形ABCD中,BD=4,E、F分别是AD、CD上的动点(包含端点),且AE+CF=4,连接BE、EF、FB.(1)试探究BE与BF的数量关系,并证明你的结论;(2)求EF的最大值与最小值.24.(2022春•洪山区期中)如图1,E,F是正方形ABCD的边上两个动点,满足AE=DF,连接CF交BD于G,连接BE交AG于点H(1)求证:AG⊥BE;(2)如图2,连DH,若正方形的边长为4,则线段DH长度的最小值是.25.(2022•宁德)如图,四边形ABCD是正方形,△ABE是等边三角形,M为对角线BD(不含B点)上任意一点,将BM绕点B逆时针旋转60°得到BN,连接EN、AM、CM.(1)求证:△AMB≌△ENB;(2)①当M点在何处时,AM+CM的值最小;②当M点在何处时,AM+BM+CM的值最小,并说明理由;(3)当AM+BM+CM的最小值为√3+1时,求正方形的边长.26.(2022•南充模拟)如图,M,N是正方形ABCD的边CD上的两个动点,满足CM=DN,AC,BM相交于点E,DE与AN相交于点F,连接CF.(1)求证:DE⊥AN.(2)若正方形ABCD的边长为4,求CF的最小值.27.(2022春•思明区校级期中)已知:在矩形ABCD中,AB=8,BC=12,四边形EFGH的三个顶点E、F、H分别在矩形ABCD的边AB、BC、DA上.(1)如图1,四边形EFGH为正方形,AE=2,求GC的长.x.在(2)如图2,四边形EFGH为菱形,设BF=x,△GFC的面积为S,且S与x满足函数关系S=6−12自变量x的取值范围内,是否存在x,使菱形EFGH的面积最大?若存在,求x的值,若不存在,请说明理由.28.(2022•南岗区校级一模)已知菱形ABCD的对角线相交于O,点E、F分别在边AB、BC上,且BE =BF,射线EO、FO分别交边CD、AD于G、H.(1)求证:四边形EFGH为矩形;(2)若OA=4,OB=3,求EG的最小值.29.(2022春•戚墅堰区校级月考)如图,已知∠MON=90°,线段AB长为6cm,AB两端分别在OM、ON上滑动,以AB为边作正方形ABCD,对角线AC、BD相交于点P,连接OC.(1)求OC的最大值;(2)求证:无论点A、点B怎样运动,点P都在∠AOB的平分线上;(3)若OP=4√2cm,求OA的长.30.(2012秋•吴中区月考)如图①,四边形ABCD是正方形,△ABE是等边三角形,M为对角线BD(不含B点)上任意一点,将BM绕点B逆时针旋转60°得到BN,连接EN、AM、CM.(1)连接MN,△BMN是等边三角形吗?为什么?(2)求证:△AMB≌△ENB;(3)①当M点在何处时,AM+CM的值最小;②如图②,当M点在何处时,AM+BM+CM的值最小,请你画出图形,并说明理由.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
主备(讲)人:八年级10班邓永豪
路在脚下 志在我心 全力以赴 永创辉煌
四边形中的最值问题
例1 如图,菱形ABCD 中,AB=2,∠A=120°,点P ,Q ,K 分别为线段BC ,CD ,BD 上的任意一点,则PK+QK 的最小值为( )
A.1
B. √3 C .2 D .√3+1
试一试 化动为静,先确定K 点位置,从特殊位置切入。
(2012年台州市中考题)
例2 如图,∠MON=90°,矩形ABCD 的顶点A 、B 分别在边OM ,ON 上,当B 在边ON 上运动时,A 随之在边OM 上运动,矩形ABCD 的形状保持不变,其中AB=2,BC=1,运动过程中,点D 到点O 的最大距离为( )
A .
B .
C . 2 D.3
试一试 三角形任两边之和大于第三边。
(2012年济南市中考题)
例3 如图,四边形ABCD 是正方形,△ABE 是等边三角形,M 为对角线BD (不含B 点)上任意一点,将BM 绕点B 逆时针旋转60°得到BN ,连接EN 、AM 、CM ,△AMB ≌△ENB 。
求证:
(1)①当M 点在何处时,AM +CM 的值最小。
②当M 点在何处时,AM +BM +CM 的值最小,并说明理由。
试一试 连接M 、N ,将AM 、BM 、CM 替换。
(2)当AM +BM +CM 的最小值为√3+1时,求正方形的边长。
试一试 ①等腰三角形三线合一 ②构建直角三角形求正方形边长 (2010年宁德市中考题)
①求线段最值常用的方法:
1.两点之间线段最短
例:如图,菱形ABCD 中,AB=2,∠BAD =60°,E 是AB 的中点,P 是对角线AC 上的一个动点,则PE+PB 的最小值是_________________。
2.垂线段最短。
例: (09陕西) 如图,在锐角△ABC 中,AB =4 ,∠BAC =45°,∠BAC 的平分线交BC 于点D ,M 、N 分别是AD 和AB 上的动点,则BM+MN 的最小值是_____________。
3.斜边大于直角边。
4.三角形任两边之和大于第三边。
例:已知菱形ABCD ,点P 是OD 上一点,当AP+CP 值最大时,点P 于何位置?___________________________。
②线段长度最值常与图形运动、点运动相关联,需理清静点与动点、常量与变量,动静转化。
拓展:费马点:
1.若给定一个三角形△ABC 的话,从这个三角形的费马点P 到三角形的三个顶点A 、B 、C 的距离之和比从其它点算起的都要小。
2.这个特殊点对于每个给定的三角形都只有一个。
3.若三角形3个内角均小于120°,那么3条距离连线正好三等分费马点所在的周角,即该点所对三角形三边的张角相等,均为120°。
所以三角形的费马点也称为三角形的等角中心。
D
A
C
E
P。
