常用Fourier变换表
Fourier变换

t
d
2
0
sin
1
sin
2
t
d
所以有
0
sin sint 12
d
2
sin 0
t
| t | | t |
17
例2 求函数 f (t) A et2 旳Fourier变换及其积分体现 式,其中A > 0,β> 0。这个函数叫做钟形脉冲 函 数,也是工程技术中常遇到旳一种函数。
解 根据Fourier变换式,有
2 jsin 12
(cos t
j sin t ) d
1
2
2
sin sin 12
t
d
16
例
求函数
f (t)
sin t
0
|t |t
| |
旳Fourier变换并求:
0
sin
1
sin
2
t
d
.
解: f (t ) F 1[F ( )] 1 F ( )ejtd
2
1
2
2
sin sin 12
2
1
0
cos t 2
sin
2
t
d
所以
0 t0
f (t) 1
0
cos t 2
sint 2
ቤተ መጻሕፍቲ ባይዱ
d
1 / 2 e t
t0 t0
11
例1
求函数
0, f (t ) e t ,
t t
0 0
旳Fourier变换及其积
分体现式,其中β >0。这个f (t) 叫指指数衰减函数,
是工程技术上常遇到旳一种函数。
sin
常用傅立叶变换表完整版

常用傅立叶变换表
Document serial number【NL89WT-NY98YT-NC8CB-NNUUT-NUT108】
18
δ(ω) 代表分布. 这个变换展示了狄拉克δ函数的重要性:该函数是常函数的傅立叶变换
19 变换23的频域对应
20 由变换3和24得到.
21
由变换1和25得到,应用了:
时域信号
弧频率表示的 傅里叶变换
注释
1线性
2 时域平移
3 频域平移, 变换2的频域对应
4
如果
值较大,则
会收缩到
原点附近,而会扩散并变得扁平. 当 | a | 趋向无穷时,成为 Delta 函数。
5 傅里叶变换的二元性性质。
通过交换时域变量 和频域变量 得到. 6 傅里叶变换的微分性质 7 变换6的频域对应 8 表示 和 的卷积 — 这就是 9
和归一化的 10 变换10的频域对应。
矩形函数是理想的低通滤波器,是这类滤波器对冲击的响应。
11
tri 是 12 变换12的频域对应 13 exp( αt 2) 的傅里叶变换是他本身. 只有当 Re(α) > 0时,这是可积的。
14
15
16 a>0
17
变换本身就是一个公式。
常用傅里叶变换表

弧频次表示的时域信号说明傅里叶变换1线性2时域平移3频域平移 ,变换 2 的频域对应假如值较大,则会缩短4到原点邻近,而会扩散并变得扁平 .当 | a | 趋势无量时,成为 Delta函数。
傅里叶变换的二元性性质。
经过5互换时域变量和频域变量获得 .6傅里叶变换的微分性质7变换 6 的频域对应表示和的卷积—这8就是卷积定理9矩形脉冲和归一化的 sinc 函数变换 10 的频域对应。
矩形函数是理10想的低通滤波器, sinc 函数是这种滤波器对反因果冲击的响应。
11tri是三角形函数12变换 12 的频域对应高斯函数 exp(- αt 2) 的傅里叶13变换是他自己 .只有当 Re(α) > 0时,这是可积的。
141516a>017变换自己就是一个公式δ( ω) 代表狄拉克δ函数散布 .18这个变换展现了狄拉克δ 函数的重要性:该函数是常函数的傅立叶变换19变换 23 的频域对应20由变换 3和 24获得 .由变换 1和 25获得,应用了欧拉公21式: cos(at ) = ( e iat + e - iat ) / 2. 22由变换 1和 25获得这里 , n 是一个自然数 .δ ( n)(ω)是狄拉克δ函数散布的 n 阶微分。
23这个变换是依据变换7 和 24 获得的。
将此变换与 1 联合使用,我们能够变换全部多项式。
此处 sgn( ω) 为符号函数;注意此变24换与变换 7 和 24 是一致的 .25 26 27 28 34变换 29 的推行 .变换 29 的频域对应 .此处 u( t ) 是单位阶跃函数 ;此变换依据变换 1 和 31 获得.u( t ) 是单位阶跃函数,且 a > 0.狄拉克梳状函数——有助于解说或理解从连续到失散时间的转变 .。
Fourier变换

1Sec. 7.2 Fourier 变换1 Fourier 变换在Fourier 积分公式中, 令⎰∞∞--=dx e x f w G iwx )()( (1)则⎰∞∞-=dw e w G x f iwx )(21)(π(2)可见函数)(x f 和)(w G 可以通过积分相互表达. 我们称(1)式为函数)(x f 的Fourier 变换, 简称傅氏变换, 记作⎰∞∞--==dx e x f w G x f F iwx )()()]([ (3))(w G 又称为)(x f 的像函数;而称(2)式为函数)(w G 的Fourier 逆变换, 简称傅氏逆变换或傅氏反演, 记作⎰∞∞--==dw e w G x f w G F iwx )(21)()]([1π(4))(x f 又称为)(w G 的像原函数, 因此, 当)(x f 满足傅氏积分定理的条件时, 傅氏积分公式就成为)]}([{)(1x f F F x f -=这是傅氏变换和傅氏逆变换之间的一个重要关系易于看出, 傅氏变换的定义式(3)式和(4)式, 其积分前的系数虽然各书的写法不完全相同, 但只要此二系数的乘积等于π21, (4)式和(5)式仍均是可以互相满足的, 且两积分号内的指数因子iwx e -和iwx e 也可以同时改为iwx e 和iwx e -.由傅氏变换和傅氏逆变换的定义可知, 要求一个函数的傅氏变换(或逆变换), 实际上是求一个含参数的广义积分, 计算含参数的广义积分是一件比较困2难的工作. 但是对于某些函数, 还是比较容易的.如果)(x f 是一个信号, 利用它的像函数分析信号是Fourier 变换的一个很重要的用途, 但是按Fourier 积分定理, 诸如ax E x f cos )(0=的最简单的信号都不满足绝对可积条件. 如果不解决这个困难就不能利用Fourier 变换来研究信号. 下面介绍一个数学工具克服这个困难.2. δ函数定义用数学作为工具来研究物理问题时, 应该有描述研究对象和物理规律的数学概念. 在经典物理中点源是一个很重要的概念, 例如质点和点电荷, 它们的定义很清楚, 但是在经典物理中却没有数学工具来描述它们, 因为处理宏观物理问题时, 点源是一个数学的概念, 仅仅帮助理解物理的概念. 在研究量子力学时, 就需要有描述点源的数学工具了, 否则就无法得到正确的理论. 量子力学的创始人之一Dirac 引进δ函数来描述点源.δ函数是指同时满足下列二式的函数⎩⎨⎧≠=∞=-000 0)(x x x x x x δ 和 ⎰∞∞-=-1)(0dx x x δ可理解)(0x x -δ是放置在0x x =的点源的密度, 它的密度无限大, 但是它的积分值是确定的. 也就是说它的质量并不是无限大. 以质点为例, 质点是几何上的点, 体积为0, 当然密度无限大, 但却有确定的质量m , 而质量就是密度对体积的积分.)(x f 是定义在),(∞-∞的实函数, 计算积分)()()(lim )()()()(000000000x f dx x x f dxx x x f dx x x x f x x x x =-=-=-⎰⎰⎰+-→+-∞∞-εεεεεδξδδ3以上利用了实积分中的中值定理和δ函数的定义, 所以我们知道⎰∞∞-=-)()()(00x f x x x f δ可以验证δ函数是偶函数, 因为⎩⎨⎧≠=∞=-0 00)(x x x δ1)()()()(==---=-⎰⎰⎰∞∞-∞∞-∞∞-dt t x d x dx x δδδ3. δ函数的Fourier 变换根据δ函数的定义.[]0)()(00iw x iw x e dx e x x x x F -∞∞--=-=-⎰δδ如果00=x , []1)(=x F δ而像函数的反演, 也就是δ函数的Fourier 积分[]⎰∞∞----==-dw e eF x x x x iw iw x )(10021)(πδ⎰∞∞-=dw e x iw x πδ21)(例 求x x f 0sin )(ω=的Fourier 变换 解: 利用Fourier 变换的定义式[][])()(2sin )(0000ωωδωωδπωωωω+--=-==⎰⎰∞∞---∞∞--idx e i e e dx xex f F x i x iw x i xi注意:这里面用到了delt 函数为偶函数的性质4. 开关函数⎩⎨⎧<>=0001)(x x x H 也称Heaviside 函数和单位阶跃函数. 它是一个最基本的信号. 此外, 还应该注意它在计算中的作用.4根据δ函数的定义, )(x H 和)(x δ的关系是⎰∞-=xd x H ξξδ)()(例 证明[])(1)(ωπδ+=iwx H F 解: 直接证明要用到一些广义函数的理论, 但是可以证明)()(11x H i F =⎥⎦⎤⎢⎣⎡+-ωπδω 21sin 12121212121212121)(121)(1000001+=++-=++=+=⎥⎦⎤⎢⎣⎡+=⎥⎦⎤⎢⎣⎡+⎰⎰⎰⎰⎰⎰⎰∞∞∞-∞∞-∞∞-∞∞--ωωωπωωπωωπωωπωωπωωπωωπδωπωπδωωωωωωωd x d i e d i e d i e d i e d i e d e i i F x i x i x i x i x i xi因为2s i n 0π=⎰∞dx x x 所以0>x , 2sin 0πωωω=⎰∞d x , 0<x , 2sin 0πωωω-=⎰∞d x . 代入后即可得证.由上例可以得到如下关系式)(1ωπδωω+=⎰∞-i dx e x i 21)(11-=⎥⎦⎤⎢⎣⎡-x H i F ω⎥⎦⎤⎢⎣⎡-=⎰∞∞-21)(2x H i d e xi πωωω Fourier 变换分成两类, 一类是按Fourier 积分定理引进的Fourier 变换, 它要求原函数绝对可积, 这类可以称为经典或者古典Fourier 变换, 另一类是δ函数框架下的Fourier 变换. 虽然两者变换的原函数完全不同, 但是作为计算工具5并无太大差别.例 求xaxx f sin )(=, (0>a )的Fourier 变换 解: 利用定义来求[])()( 2121 2sin sin )()(ωωπωωωω----=-=-==⎥⎦⎤⎢⎣⎡⎰⎰⎰⎰∞∞---∞∞--∞∞---∞∞--a H a H dxxe i dx x e i dx e ix e e dx e x ax x ax F xa i x a i x i iax iax xi 因为⎩⎨⎧><=-a a a H ωωω0 1)(, ⎩⎨⎧->-<=--a a a H ωωω 01)(所以xaxx f sin )(=的像函数如图所示, 因为它的形状, 又被称为门函数.。
Fourier变换.

《积分变换》第一章 Fourier 变换 §.1 Four ier 积设f T (t)以T 为周期,在[-? T"]满足Dirichletf T (t)=亚 + 瓦 I a ^ jbne jn® t2 n =1 L 2变换是数学的灵魂.我们经常利用变换把复杂运算转化为简单运算.例如,解析几何中的坐标变换、复变中的保角变换,四则运算中利用对数变换可将积与商转化为加与减:alg(ab ^lg ^lgb, lg -^lg ^lgb.再取反对数变换复原.b积分变换 T:A T B , T(f) = F(U a f (t)K(t,d )dt ,af(t)壬 A 象原函数,F©)- B ――象函数,K(t,a )——核.它实现了从函数类A 到函数类B 的变换.在一定条件下可逆.积分变换是应用性很强的数学工具,在数学和其它学科中均有应用.主要应用:a .求解线性微分方程(组);b 信号处理.第一类间断点;20只有有限个极值点.则在[- p£]的连续点t 处,有 f T (t)二並+ 2+瓦(a n cosn® t 十 b nn =1sin n ⑷t), 其中2一〒, 21 =T, Ia nb n %T 』巧 f T (t)cos n ⑷ tdt, 2 T /=—f T (t)sin n« tdt,T /2(n =0,1,2,3,…) (n - 1,2,3/ ) 利用Euler 公式,转化成复数形式:cos® =丄(e" + e j) 2 ,sin® -1(e W e j 、 2j (…)收敛条件, 即: 10连续或只有有限个+ a n + jb n -j n « t2V f /T —j n T.b "I j«n t二心f 心d丁-T Tf T (t )=f (t ), tq 〒 2】.1 母-母.,"I ■. t—石J 亠卩亠fC )ej e*, t 匸(-处,+处),(3).称为Fourier 积分公式.它成立的条件如下.Fourier 积分定理.若f (t)在(S +处)上满足:1。
常用fourier变换表

常用fourier变换表傅里叶变换是一种重要的数学工具,常用于信号处理、图像处理、通信等领域。
以下是一些常用的傅里叶变换表:1.Fourier变换对:•时间域函数x(t) 的傅里叶变换X(f):F{ x(t) } = X(f) = ∫[−∞, +∞] x(t) * exp(-j2πft) dt•频率域函数X(f) 的傅里叶逆变换x(t):F^−1{X(f)} = x(t) = ∫[−∞, +∞] X(f) * exp(j2πft) df2.常见信号的傅里叶变换:•常数信号的傅里叶变换:F{1} = δ(f) (其中,δ(f) 表示狄拉克δ函数)•单频正弦信号的傅里叶变换:F{cos(2πf0t)} = 0.5 * [ δ(f - f0) + δ(f + f0) ]•矩形脉冲信号的傅里叶变换:F{rect(t / T)} = T * sin(πfT) / (πfT) (其中,rect(t / T) 表示矩形函数)•高斯函数的傅里叶变换:F{exp(-πt^2)} = exp(-πf^2)3.常见性质和公式:•傅里叶变换的线性性质:F{a * x(t) + b * y(t)} = a * X(f) + b * Y(f)•频率平移性质:F{ x(t - t0) } = X(f) * exp(-j2πft0)•时域和频域的缩放性质:F{ x(a * t) } = (1 / |a|) * X(f / a)•卷积定理:F{ x(t) * y(t) } = X(f) * Y(f) (其中* 表示卷积操作)这些是一些常见的傅里叶变换表中的内容,可以帮助我们理解信号在时域和频域之间的关系,进而应用到实际问题的分析和处理中。
请注意,这里只给出了部分常见的表达式和性质,实际的傅里叶变换表还包含更多的公式和变换对,具体的应用需要根据具体问题进行深入研究和理解。
Fourier变换与Laplace变换

附录F Fourier 变换、Laplace 变换§F.1 一维Fourier 变换在解微分方程的时候经常采用积分变换。
一阶微分方程,用一次积分变换就得到一个代数方程。
然后,求解这个代数方程。
最后,对其解作一次逆变换得到微分方程的解析解。
通常采用的积分变换有Laplace 变换、Fourier 变换。
这里先介绍一维的Fourier 变换: 函数()g t 的Fourier 变换()g ω定义为:()()i t g dt e g t ωω∞-=⎰(F.1-1a )记为()()g g t ω≡⎡⎤⎣⎦F(F.1-1b )这样自变量从原先的t 变成ω。
这是两个对应的自变量。
反过来,已知“象函数”()g ω可以通过逆变换得到“原函数”()g t :()()i tg t d e g ωωω∞-∞=⎰(F.1-2a )记为()()-1g t g ω≡⎡⎤⎣⎦F(F.1-2b )Fourier 变换是一种线性变换,即:()()()()af t bg t af bg ωω+=+⎡⎤⎣⎦F (a 、b 为常数)(F.1-3)性质:(1)若()g t 是实的偶函数,则()g ω也是实的偶函数。
若()g t 是实的奇函数,则()g ω是虚的奇函数。
(2)伸缩:()1g at g a a ω⎛⎫=⎡⎤ ⎪⎣⎦⎝⎭F (F.1-4)(3)翻转:()()g t g ω-=-⎡⎤⎣⎦F (F.1-5) (4)平移:()()00i t g t t g eωω+=⎡⎤⎣⎦F(F.1-6a ) ()()0-10i tg g t eωωω-+=⎡⎤⎣⎦F(F.1-6b )(5)微分:()()()()()()n nn n n d ggt i g gt dtωω⎡⎤=≡⎣⎦F(F.1-7a )()()()()()()()1n nn n nd g g it g t gd ωωωω-⎡⎤=-≡⎣⎦F(F.1-7b ) (6)卷积:()()()()1212g t g t g g ωω*=⋅⎡⎤⎣⎦F(F.1-8)其中()()()()()()ττττττ∞∞*≡⋅--⋅⎰⎰121212g t g t d g g t d g t g(F.1-9)§F.2 三维Fourier 变换任意三维变量r 的函数()V r ,其Fourier 变换()V k 定义为()()3/212i V d eV π⋅Ω⎛⎫≡ ⎪⎝⎭⎰k rk r r(F.2-1a )或记为()()V V ≡⎡⎤⎣⎦k r F(F.2-1b )注意:向量变量r 是在三维空间Ω中的, 体积元2sin d dxdy dz r dr d d θθφ==r(F.2-2)而向量变量k 是在对应的倒易空间Ω-1中的。
常用Fourier变换表
n = -¥
å Fn e
¥
jwnt
, where
1T Fn = ò f (t )e - jw 0 nt dt T 0
Signals & Systems - Reference Tables
3
Some Useful Mathematical Relationships
e jx + e - jx cos( x) = 2 e jx - e - jx sin( x) = 2j cos( x ± y ) = cos( x) cos( y ) m sin( x) sin( y ) sin( x ± y ) = sin( x) cos( y ) ± cos( x) sin( y ) cos(2 x) = cos 2 ( x) - sin 2 ( x) sin( 2 x) = 2 sin( x) cos( x) 2 cos2 ( x) = 1 + cos(2 x) 2 sin 2 ( x) = 1 - cos(2 x) cos 2 ( x) + sin 2 ( x) = 1 2 cos( x) cos( y ) = cos( x - y ) + cos( x + y ) 2 sin( x) sin( y ) = cos( x - y ) - cos( x + y ) 2 sin( x) cos( y ) = sin( x - y ) + sin( x + y )
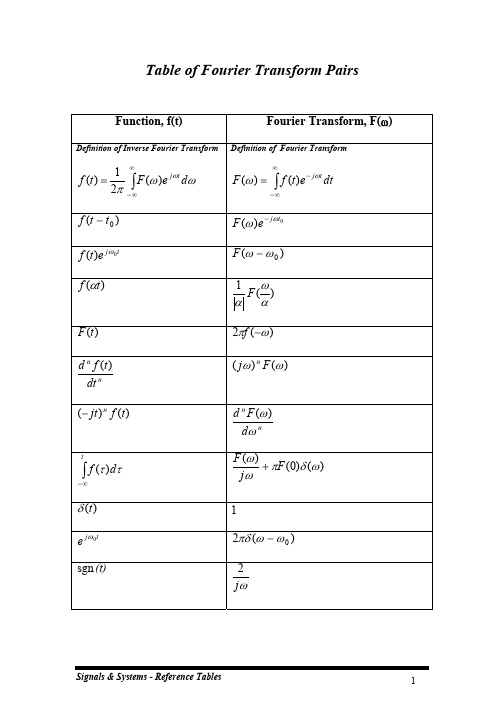
Table of Fourier Transform Pairs
Function, f(t)
Definition of Inverse Fourier Transform
Fourier Transform, F(w)
