用几何画板探究一线三等角相似模型
初中几何 一线三等角模型
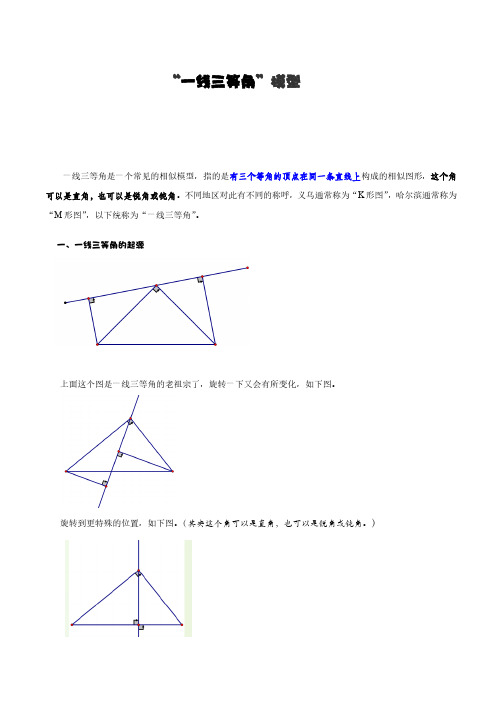
一、一线三等角的起源上面这个图是一线三等角的老祖宗了,旋转一下又会有所变化,如下图。
旋转到更特殊的位置,如下图。
(其实这个角可以是直角,也可以是锐角或钝角。
)“一线三等角”模型一线三等角是一个常见的相似模型,指的是有三个等角的顶点在同一条直线上构成的相似图形,这个角可以是直角,也可以是锐角或钝角。
不同地区对此有不同的称呼,义乌通常称为“K 形图”,哈尔滨通常称为“M 形图”,以下统称为“一线三等角”。
二、一线三等角的两种基本类型1.三等角都在直线的同侧2.三等角分居直线的两侧l三、一线三等角的性质1.一般情况下,由∠1=∠2=∠3,易得△AEC∽△BDE. 2.当等角所对的边相等时,两个三角形全等。
如图,当CE=ED时,易得△AEC≌△BDE.3.“中点型一线三等角”的特殊性质如图,当∠1=∠2=∠3且D 是BC 的中点时,△BDE ∽△CFD ∽△DFE .如图,加画两条垂线......,“一线三等角”就与“四边形中的半角模型”联系在一起了。
半角模型:EF =EM +FN . 4.“中点型一线三等角”的变式 如图,当∠1=∠2且∠AOC =90°+21∠BAC 时,点O 是△ABC 的内心.易证∠4=∠5=∠6,以下就省略了。
四、一线三等角的常用构图下面以等腰三角形为例说明一线三等角的常见构图。
由于角顶点位置的改变,或角绕顶点旋转会产生各种各样的变式,但万变不离其宗:构造相似三角形列比例式解决问题。
当然,特殊情况下也可能是全等。
五、一线三等角的应用1.一线三等角应用的三个层次⑴初级阶段:图形中已经存在“一线三等角”,直接应用模型解题;⑵中级阶段:图形中存在“一线二等角”,补上“一等角”构造此模型;⑶高级阶段:图形中只有直线上的一个角,补上“二等角”构造此模型。
2.在张角问题中,构造“一线三等角”是基本手段之一。
对坐标系中的张角问题,在x轴或y轴(也可以是平行于x轴或y轴的直线)上构造“一线三等角”是解决问题的关键。
中考数学相似三角形重要模型一线三等角模型
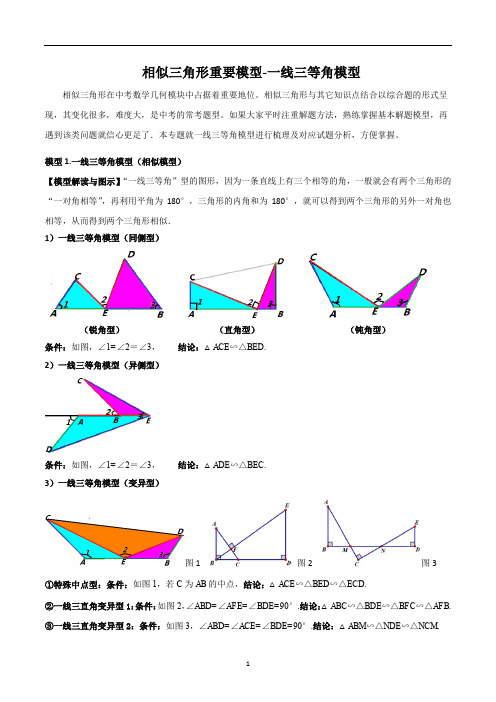
相似三角形重要模型-一线三等角模型相似三角形在中考数学几何模块中占据着重要地位。
相似三角形与其它知识点结合以综合题的形式呈现,其变化很多,难度大,是中考的常考题型。
如果大家平时注重解题方法,熟练掌握基本解题模型,再遇到该类问题就信心更足了.本专题就一线三等角模型进行梳理及对应试题分析,方便掌握。
模型1.一线三等角模型(相似模型)【模型解读与图示】“一线三等角”型的图形,因为一条直线上有三个相等的角,一般就会有两个三角形的“一对角相等”,再利用平角为180°,三角形的内角和为180°,就可以得到两个三角形的另外一对角也相等,从而得到两个三角形相似.1)一线三等角模型(同侧型)(锐角型)(直角型)(钝角型)条件:如图,∠1=∠2=∠3,结论:△ACE∽△BED.2)一线三等角模型(异侧型)条件:如图,∠1=∠2=∠3,结论:△ADE∽△BEC.3)一线三等角模型(变异型)图1 图2 图3①特殊中点型:条件:如图1,若C为AB的中点,结论:△ACE∽△BED∽△ECD.②一线三直角变异型1:条件:如图2,∠ABD=∠AFE=∠BDE=90°.结论:△ABC∽△BDE∽△BFC∽△AFB.③一线三直角变异型2:条件:如图3,∠ABD=∠ACE=∠BDE=90°.结论:△ABM∽△NDE∽△NCM.例1.(2023·山东东营·统考中考真题)如图,A B C为等边三角形,点D,E分别在边B C,A B上,60A D E∠=︒,若4B D D C=, 2.4D E=,则A D的长为()A.1.8B.2.4C.3D.3.2例2.(2023·湖南·统考中考真题)如图,,C A ADE D A D⊥⊥,点B是线段A D上的一点,且C B B E⊥.已知8,6,4A B A C D E===.(1)证明:A B C D E B∽△△.(2)求线段B D的长.例3.(2022·河南新乡·九年级期中)某学习小组在探究三角形相似时,发现了下面这种典型的基本图形.(1)如图1,在ABC中,∠BAC=90°,A BA C=k,直线l经过点A,BD⊥直线I,CE上直线l,垂足分别为D、E.求证:B DA E=k.(2)组员小刘想,如果三个角都不是直角,那么结论是否仍然成立呢?如图2,将(1)中的条件做以下修改:在ABC中,A BA C=k,D、A、E三点都在直线l上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意锐角或钝角.请问(1)中的结论还成立吗?若成立,请你给出证明;若不成立,请说明理由.(3)数学老师赞赏了他们的探索精神,并鼓励他们运用这个知识来解决问题:如图3,在ABC中,沿ABC的边AB、AC向外作矩形ABDE和矩形ACFG,A BA E =A CA G=12,AH是BC边上的高,延长HA交EG于点I.①求证:I是EG的中点.②直接写出线段BC与AI之间的数量关系:.例4.(2022·四川·一模)某学习小组在探究三角形全等时,发现了下面这种典型的基本图形:(1)如图1,已知:在△ABC 中,A B A C=,D 、A 、E 三点都在直线m 上,并且有B D AA E CB AC α∠=∠=∠=.试猜想DE 、BD 、CE 有怎样的数量关系,请证明你的结论;(2)老师鼓励学习小组继续探索相似的情形.于是,学习小组又研究以下问题:如图2,△ABC 中,(060)B C αα∠=∠=<<︒.将一把三角尺中30°角顶点P 放在BC 边上,当P 在BC 边上移动时,三角尺中30°角的一条边始终过点A ,另一条边交AC 边于点Q ,P 、Q 不与三角形顶点重合.设C P Qβ∠=.当β在许可范围内变化时,α取何值总有△ABP ∽△PCQ ?当α在许可范围内变化时,β取何值总有△ABP ∽△QCP ?(3)试探索有无可能使△ABP 、△QPC 、△ABC 两两相似?若可能,写出所有α、β的值(不写过程);若不可能,请说明理由.例5.(2022·山西晋中·一模)阅读材料:我们知道:一条直线经过等腰直角三角形的直角顶点,过另外两个顶点分别向该直线作垂线,即可得三垂直模型”如图①,在A B C中,90A C B ∠=︒,A C B C=,分别过A 、B 向经过点C 直线作垂线,垂足分别为D 、E ,我们很容易发现结论:A D C C E B△≌△.(1)探究问题:如果A CB C≠,其他条件不变,如图②,可得到结论;A D CC E B△∽△.请你说明理由.(2)学以致用:如图③,在平面直角坐标系中,直线12y x=与直线C D 交于点()2,1M ,且两直线夹角为α,且3ta n 2α=,请你求出直线C D 的解析式.(3)拓展应用:如图④,在矩形A B C D 中,3A B=,5B C=,点E为B C 边上—个动点,连接A E ,将线段A E 绕点E 顺时针旋转90︒,点A 落在点P 处,当点P 在矩形A B C D外部时,连接P C ,P D .若D P C △为直角三角形时,请你探究并直接写出B E 的长.Rt ABD中,上一动点,连接折叠得H E F,延长②B E M H E M≅;③当M2B,则正确的有(九年级校考阶段练习)已知A B C是等边三角形,E F和B D F∠,将B C E沿B则A F=P C D△;九年级校考阶段练习)如图,在A B C中,12.(2022·山东济宁·二模)情境观察:将含45°角的三角板的直角顶点R放在直线l上,分别过两锐角的顶点M,N作l的垂线,垂足分别为P,Q,(1)如图1.观察图1可知:与NQ相等的线段是______________,与N R Q∠相等的角是_____(2)问题探究直角A B C中,90B∠=︒,在AB边上任取一点D,连接CD,分别以AC,DC为边作正方形ACEF 和正方形CDGH,如图2,过E,H分别作BC所在直线的垂线,垂足分别为K,L.试探究EK与HL之间的数量关系,并证明你的结论.(3)拓展延伸:直角A B C中,90B∠=︒,在AB边上任取一点D,连接CD,分别以AC,DC为边作矩形ACEF和矩形CDGH,连接EH交BC所在的直线于点T,如图3.如果A C kC E=,试探究TE与TH=,C D kC H之间的数量关系,并证明你的结论.将.A B P沿着这样的点P,使得点问题解决(3)15.(2023春·四川广安·九年级校考阶段练习)如图1和图2,在平面直角坐标系中,点C的坐标为(0,4),A是x轴上的一个动点,M是线段AC的中点.把线段AM以A为旋转中心、按顺时针方向旋转90°得到AB.过B作x轴的垂线、过点C作y轴的垂线,两直线交于点D,直线DB交x轴于点E.设A点的横坐标为m.(1)求证:△AOC∽△BEA;(2)若m=3,则点B的坐标为;若m=﹣3,则点B的坐标为;(3)若m>0,△BCD的面积为S,则m为何值时,S=6?(4)是否存在m,使得以B、C、D为顶点的三角形与△AOC相似?若存在,求此时m的值;若不存在,请说明理由.16.(2020·四川雅安·中考真题)如图,已知边长为10的正方形A B C D E、不重,是B C边上一动点(与B C 合),连结A E G,是B C延长线上的点,过点E作A E的垂线交D C G∠的角平分线于点F,若F G B G⊥.(1)求证:A B E E G FE C=,求C E F△△;(2)若2∽△的△的面积;(3)请直接写出E C为何值时,C E F面积最大.的何位置时有B E H B A E∽?B C。
精品一线三等角相似模型.ppt课件
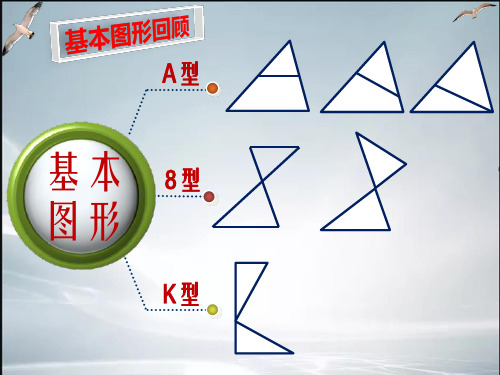
如图,在△ABC中,AB=AC=5cm,BC=8,点P为BC边上一动点(不 与点B、C重合),过点P作射线PM交AC于点M,使∠APM=∠B;
(1)求证:△ABP∽△PCM; (2)设BP=x,CM=y.求 y与x的函数解析式,并写出函数的取值范
A型
基本 8型 图形
K型
一线三等角是一个常见的相似模型,指的是有三 个等角的顶点在同一条直线上构成的相似图形, 这个角可以是直角,也可以是锐角或钝角。
三角形基架
K型 矩形基架
梯形基架
毕达哥拉斯证法
赵爽弦图
K字型的一般形式
你能证明吗?
证明: 在ABC中 1 A ACB 180 又 2 DCE ACB 180
1 2 3 A DCE △ABC∽△CDE
1、如图,等边△ABC的边长为3
,点D是BC上一点,且BD=1,在
AC上取点E,使∠ADE=60度,AE
长为( c )
A. 3 B. 2
2
3
C.
7 3
D. 3
4
2.在矩形ABCD中,AB=4,BC=5,AF平 分∠DAE,EF⊥AE,
1.5 则CF= ______
∴ PM PC 5 PA AB 8
即
8x 5 58
39
∴BP= 8
A M
B
P
C
A
M
BP
CA MBPC5
• ∴BE= 3
【2014德州中考试题】 24.(2)是否存在点P,使得△ACP是以AC为直角边的 直角三角形?若存在,求出所有符合条件的点P的坐标; 若不存在,说明理由.
(2016呼市T9)如图,面积为24的正方形ABCD中,有一
“一线三等角”相似模型
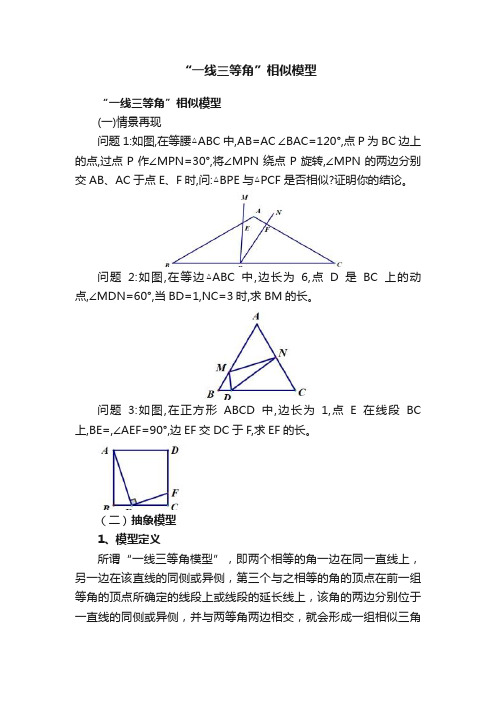
“一线三等角”相似模型“一线三等角”相似模型(一)情景再现问题1:如图,在等腰△ABC中,AB=AC ∠BAC=120°,点P为BC边上的点,过点P作∠MPN=30°,将∠MPN绕点P旋转,∠MPN的两边分别交AB、AC于点E、F时,问:△BPE与△PCF是否相似?证明你的结论。
问题2:如图,在等边△ABC中,边长为6,点D是BC上的动点,∠MDN=60°,当BD=1,NC=3时,求BM的长。
问题3:如图,在正方形ABCD中,边长为1,点E在线段BC 上,BE=,∠AEF=90°,边EF交DC于F,求EF的长。
(二)抽象模型1、模型定义所谓“一线三等角模型”,即两个相等的角一边在同一直线上,另一边在该直线的同侧或异侧,第三个与之相等的角的顶点在前一组等角的顶点所确定的线段上或线段的延长线上,该角的两边分别位于一直线的同侧或异侧,并与两等角两边相交,就会形成一组相似三角形,习惯上把该组相似三角形称为“一线三等角”型相似三角形.(通俗地讲,一条直线上有三个相等的角一般会存在相似三角形)2、基本图形:(1)点P在线段AB上(2)点P在线段AB延长线上三、载体(1)等腰或等边三角形底边上的“一线三等角”模型(2) 矩形或正方形中的“一线三等角”模型(“K”字型)(3)平面直角坐标系中的“一线三等角”模型(三)问题探究问题:如图16,在△ABC中,AB=AC=5,BC=8,点D、E分别在BC、AC上,连接AD、DE,使∠1=∠B 求线段CE的最大值变式1:(2017年无锡中考副卷第28题改编)如图1,在矩形ABCD 中,点P在AD上,AB=2,AP=1,将三角板的直角顶点放于P处,三角板的两直角边分别与AB、BC边相交于点E、F,连接EF。
(1)如图2,当点E与点B重合时,点F恰好与点C重合,求此时PC的长(2)将三角板从图1中点的位置开始,绕点P顺时针旋转,当点E与点A重合时停止,∠PEF的大小是否发生变化?变式2:(1)在平面直角坐标系中,如图,直线l1:y=-2x+4与x 轴、y轴分别交于A、B两点,将△OAB沿l1翻折,求O的对称点P 的坐标(2)直线l2过点P,且与直线l1的夹角是45°,求两直线l1、l2的交点的坐标。
完整版几何模型一线三等角模型

一线三等角模型一 . 一线三等角看法“一线三等角” 是一个常有的相似模型, 指的是有 三个等角的极点在同一条直线上构成的相似图形, 这个角能够是直角, 也能够是锐角或钝角。
不同样地区对此有不同样的称呼, “K 形图”,“三垂直”,“弦图”等,以下称为“一线三等角” 。
二 . 一线三等角的分类全等篇CDDCAPBAPB锐角直角DDDCAPB同侧钝角DAABPPBABPCC相似篇C异侧DCDCAPBA PB锐角直角DDCA PB同侧钝角DDABPABPABPCCC异侧三、“一线三等角”的性质1. 一般情况下,如图 3-1 ,由∠ 1=∠ 2=∠ 3,易得△ AEC ∽△ BDE.2. 当等角所对的边相等时,则两个三角形全等. 如图 3-1 ,若 CE=ED ,则△ AEC ≌△ BDE.3.中点型“一线三等角”如图 3-2,当∠ 1=∠2=∠3,且 D 是 BC 中点时,△ BDE∽△ CFD∽△ DFE.4. “中点型一线三等角“的变式(认识)如图 3-3,当∠ 1=∠2 且BOC 901BAC 时,点O是△ABC的内心.能够考虑构2造“一线三等角”.如图 3- 4“中点型一线三等角”平时与三角形的内心或旁心相关,BOC901BAC 这是内心的性质,反之未必是内心. 2在图 3-4(右图)中,若是延长BE 与 CF,交于点 P ,则点 D 是△ PEF 的旁心 .5.“一线三等角”的各种变式(图 3-5 ,以等腰三角形为例进行说明)图 3-5其实这个第 4 图,延长 DC 反而好理解 . 相当于两侧型的,不延长理解,以为是一种新式的,同侧穿越型?无论怎么变,都是由三等角确定相似三角形来进行解题四、“一线三等角”的应用1.“一线三等角”应用的三种情况 .a.图形中已经存在“一线三等角”,直接应用模型解题;b.图形中存在“一线二等角”,不上“一等角”构造模型解题;c. 图形中只有直线上一个角,不上“二等角”构造模型解题.领悟:感觉最后一种情况出现比很多,特别是压轴题中,经常会有一个特别角或指导该角的三角函数值时,我经常构造“一线三等角”来解题.2.在定边对定角问题中,构造一线三等角是基本手段,特别是直角坐标系中的张角问题,在 x 轴或 y 轴(也能够是平行于 x 轴或 y 轴的直线)上构造一线三等角解决问题更是重要的手段 .3.构造一线三等角的步骤:找角、定线、构相似坐标系中,要讲究“线”的特别性如图 3-6 ,线上有一特别角,就考虑构造同侧型一线三等角自然只加这两条线平时是不够的,为了利用这个特别角导线段的关系,过 C 、D两点作直线 l 的垂线是必不能少的。
相似三角形基本模型一线三等角精品PPT课件

A
D
A
D
F
B
E
C
F
B
E
C
A
△ABE∽ △ECF
F
((2)1)点点E为E为BBCC上上任任意意一一点点若,∠若B= ∠∠CB==α,∠∠CA=E6F0°= ∠, ∠CA,则EF△=A∠BCE,则与△ EC△FA的B关E与系△还成EC立F吗的?关系还成立吗?
说明理由
B
α
α
B
E
α
C
点拨:要善于运用类比、迁移的数学方法 解决问题。
A
A
①
B
F
②
E
C
①
B
③
F
②
E
C
E为中点
D
A
F
①
α
B
α ②α
E
C
A
F
①
α
B
③
α②
α
E
C
1.矩形ABCD中,把DA沿AF对折,使D与CB边上的点E 重合,若AD=10, AB= 8,
则EF=___5___
D
F
C
EE
A
点拨:要善于在复杂图形中寻找基本型。 B
A
E F
B
D
C
变式:已知:△ABC中,AB=AC, ∠BAC= 120°,D为BC的 中点, 且∠EDF =∠C, (1) 若BE·CF=48,则AB=__8___
(2)在(1)的条件下,若EF=m,
则S△DEF =___3__m__
A EH
F
P
B
D
点拨:联想基本模型,寻找 相关结论。
C
初三相似三角形几何模型-一线三等角

相似三角形几何模型——一线三等角【模型讲解】模型一:一线三直角图一 图二90;B ACE D ABC CDE ∠=∠=∠=∆∆如图一、二,已知:结论:(1)∽(2)AB DE=BC CD模型二:一线三等角图三 图四 ;B ACE D ABC CDE ABC CDE ACEα∠=∠=∠=∆∆∆∆∆如图三、四,已知:结论:(1)∽(2)AB DE=BC CD(3)当C 为BD 中点时,∽∽【典型例题】1.△ABC 和△DEF 是两个全等的等腰直角三角形,∠BAC =∠EDF =90°,△EDF 的顶点E 与△ABC 的斜边BC 的中点重合,将△DEF 绕点E 旋转,旋转过程中,线段DE 与线段AB 相交于点P ,线段EF 与射线CA 相交于点Q .(1)如图①,当点Q 在线段AC 上,且AP=AQ 时,求证:△BPE≌△CQE;(2)如图②,当点Q 在线段CA 的延长线上时,求证:△BPE∽△CEQ;(3)在(2)的条件下,BP=2,CQ=9,则BC 的长为_______.2.如图,已知AB BD ⊥,CD BD ⊥.(1)若9AB =,4CD =,10BD =,请问在BD 上是否存在点P ,使以P ,A ,B 三点为顶点的三角形与以P ,C ,D 三点为顶点的三角形相似?若存在,求BP 的长;若不存在,请说明理由;(2)若9AB =,4CD =,12BD =,请问在BD 上存在几个点使以三点为顶点的三角形与以P ,C ,D 三点为顶点的三角形相似?并求BP 的长.3.如图,点P是正方形ABCD边AB上一点(点P不与点A,B重合),连接PD,将线段PD 绕点P顺时针方向旋转90°得到线段PE,PE交边BC于点F,连接BE,DF.(1)求∠PBE的度数;(2)若△PFD∽△BFP,求APAB的值.4.感知:如图①,在四边形ABCD中,AB∥CD,∠B=90°,点P在BC边上,当∠APD=90°时,可知△ABP∽△PCD.(不要求证明)探究:如图②,在四边形ABCD中,点P在BC边上,当∠B=∠C=∠APD时,求证:△ABP∽△PCD.拓展:如图③,在△ABC中,点P是边BC的中点,点D、E分别在边AB、AC上.若∠B=∠C=∠DPE=45°,CE=4,则DE的长为______.5.如图,点B 在线段AC 上,点D 、E 在AC 同侧,90A C ∠=∠=︒,BD BE ⊥,AD BC =.若3AD =,5CE =,点P 为线段AB 上的动点,连结DP ,作PQ DP ⊥,交直线BE 于点Q .(1)当点P 与A ,B 两点不重合时,求DP PQ的值; (2)当点P 从A 点运动到AC 的中点时,求线段DQ 的中点所经过的路径(线段)长.(直接写出结果,不必写出解答过程)6.如图,在ABC △中,点D E 、分别在边BC AC 、上,连接AD DE 、,且B ADE C ∠=∠=∠.(1)证明:BDA CED △∽△;(2)若45,2B BC ∠=︒=,当点D 在BC 上运动时(点D 不与B C 、重合),且ADE △是等腰三角形,求此时BD 的长.。
相似三角形的基本模型[一线三等角]
![相似三角形的基本模型[一线三等角]](https://img.taocdn.com/s3/m/99fa9bcc998fcc22bcd10dfb.png)
模型中的相似三角形(2)【基本模型】CBBC C BAAA1. 如图1,BDEEDFC B ∆⇒∠=∠=∠∽CFD ∆(一线三等角)如图2,ABD ADE C B ∆⇒∠=∠=∠∽DCE ∆(一线三直角) 如图3,特别地,当D 是BC 中点时:BDE ∆∽DFE ∆∽CFD ∆⇒ED 平分BEF ∠,FD 平分EFC ∠。
2. 一线三等角辅助线添加:一般情况下,已知一条直线上有两个等角(直角)或一个直角时,可构造“一线三等角”型相似。
【巩固提高】1. 已知ABC ∆中,120,6︒=∠==BAC AC AB ,D是BC 的中点,AB 边上有一点AC E ,延长线上有一点F ,使.C EDF∠=∠ 已知4=BE ,则=CF427提示:,120,6︒=∠==BAC AC AB ,D 是BC 的中点∴33==CD BD由BDE ∆∽CFD ∆ ∴CF DBDCBE =, 427=CF2. 如图,等边ABC ∆中,D 是边BC 上的一点,且3:1:=DC BD ,把ABC ∆折叠,使点A 落在BC 边上的点D 处.那么ANAM 的值为75 .ABC提示:由翻折可得:A MDN DN AN DM AM ∠=∠==,,设:,3,1==DC BD 则4,4=+=+DN CN DM BM ∵BDM ∆∽CND ∆, ∴753414=++===∆∆CND BDM C C DN DM ANAM3. 在矩形ABCD 中,6=AB ,8=AD ,把矩形ABCD 沿直线MN 翻折,点B 落在边AD 上的E 点处,若AM AE 2=,那么EN 的长等于FE提示:作AD NF ⊥于F ,则6==AB FN∵MAE ∆∽EFN ∆, ∴EFAM FNAE=∵AM AE 2= ∴53,321===EN FN EF4. 在矩形ABCD 中,15=AD ,点E 在边DC 上,联结AE ,△ADE沿直线AE 翻折后点D 落到点F ,过点F 作AD FG ⊥,垂足为点G ,如果3:1:=AD DG ,那么=DENM GGAABEBE提示:作过点F 作MN ∥BC ,分别交AB 、CD 于M 、N 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
用几何画板探究一线三等角相似模型资料编号:202210161100 在学习相似三角形时,我们会遇到一种特殊的相似模型——一线三等角相似模型.这种模型常见于等腰三角形、等边三角形、矩形、正方形等图形中.在处理复杂的几何图形时,如果能从图形中识别出这种模型,将对问题的解决起到至关重要的作用.现在,我们借助于几何画板软件,来探究一线三等角相似模型及其应用.模型制作1. 打开几何画板软件,使用“线工具”任意画一条直线,在该直线上任取两点A、B,再任意画一条线段AD,依次选中点D、A、B(顺时针方向),依次单击“变换”、“标记角度”.如图1所示.2.双击选中点B,单击选中点A,依次单击“变换”、“旋转”,将点A绕点B按标记角度DABBA.如图2、图3所示.旋转到点'A的位置,作直线'3. 在直线AB上任取一点P,连结DP,双击选中点P,单击点D,依次单击“变换”、“旋转”,将点D绕点P按标记角度DABPD,交直旋转到点'D的位置,作直线'线'BA于点C.如图4所示.4.选中点'D、点'A,依次单击“显示”、“隐藏点”.5.依次选中点P、A、D,依次单击“构造”、“三角形的内部”,用同样的方法构造△PBC的内部.如图5所示.6. 单击“标识工具”,单击点A,并向角内拖动鼠标,松开鼠标,标识DAB∠,用同样的方法标识DPC∠.如图6所示.∠、ABC7. 依次选中点P、B、C,依次单击“构造”、“线段”,此时,构造了△PBC.选中直线AB,依次单击“显示”、“线型”、“实线”;选中直线PC、BC,依次单击“显示”、“线型”、“细线”.如图7所示.8. 检查从第1步至第7步作图,完成作图.模型探索当点P在线段AB上时,拖动点D,使DAB∠分别为锐角、直角、钝角,得到图8、图9、图10三种不同类型的图形.其中,点P在线段AB上,PBC=∠,则△DAP∽△PBC.∠DPCDAP∠=模型证明证明:∵BPC=∠∠+DPCDPB∠∠∠=+ADPDAPDPB∠∠=DAPDPC∠∴ADP∠=BPC∠∵ADP∠BPC∠DAP∠=∠,PBC=∴△DAP∽△PBC.当点P在线段BA的延长线上时,如图11所示,由作图可知:=∠DABDPC∠=∠,此时△DAP∽△PBC仍然成立.证明略.ABE当点P在线段AB的延长线上时,如图12所示,由作图可知:=∠DPEDAB=∠∠,此时△DAP∽△PBC仍然成立.证明略.ABF像这样,两个相等的角的一边在同一直线上,另一边在该直线的同侧,如果与这两个角相等的第三个角的顶点在该直线上,角的两边分别与这两个角的非共线边(或该边所在直线)相交所形成的两个三角形相似.我们把包含这种基本图形的一类题目称为一线三等角相似模型.特别地,当点P 是线段AB 的中点时,△DAP ∽△PBC ∽△DPC .如图13所示.图 13证明:易证△DAP ∽△PBC∴BC APCP PD= ∴BCCPAP PD = ∵点P 是线段AB 的中点 ∴BP AP = ∴CBCPBP PD =∵PBC DPC ∠=∠ ∴△DPC ∽△PBC ∴△DAP ∽△PBC ∽△DPC . 模型应用例1.(1)问题:如图(1),在四边形ABCD 中,点P 为AB 上一点,=∠=∠A DPC︒=∠90B .求证:BP AP BC AD ⋅=⋅.(2)探究:如图(2),在四边形ABCD 中,点P 为AB 上一点,当B A DPC ∠=∠=∠θ=时,上述结论是否仍然成立?说明理由.(3)应用:请利用(1)(2)获得的经验解决问题:如图(3),在△ABD 中,6=AB ,5==BD AD ,点P 以每秒1个单位长度的速度,由点A 出发,沿边AB 向点B 运动,且满足A DPC ∠=∠.设点P 的运动时间为t (秒),当以点D 为圆心,以DC 为半径的圆与AB 边相切时,求t 的值.图(1)图 (2)CAB DP图 (3)CDABP(1)证明: ∵︒=∠=∠90A DPC21∠+∠=∠+∠=∠DPC A BPD ∴21∠=∠ ∵B A ∠=∠ ∴△APD ∽△BCP ∴BPADBC AP =∴BC AD BP AP ⋅=⋅. (2)成立.理由如下:∵θ=∠=∠A DPC21∠+∠=∠+∠=∠DPC A BPD ∴∴21∠=∠ ∵B A ∠=∠ ∴△APD ∽△BCP ∴BPADBC AP =∴BC AD BP AP ⋅=⋅. (3)设切点为E ,连结DE . ∴AB DE ⊥∵BD AD =,AB DE ⊥ ∴321==AB AE 在Rt △ADE 中,由勾股定理得:4352222=-=-=AE AD DE∴145,4=-=-==DC BD BC DCE CDABP易证:△APD ∽△BCP ∴BPADBC AP =∴BC AD BP AP ⋅=⋅. 由题意可知:t BP t AP -==6, ∴()156⨯=-t t解之得:5,121==t t经检验,1=t 和5=t 均符合题意.点评 对于第(3)问,我们可以利用几何画板进行动态分析.1. 打开几何画板,单击“点工具”,任意画一点A ,选中点A ,依次单击“变换”、“平移”,在弹出的对话框中选择“直角坐标”,修改水平方向的“固定距离”为6 cm,垂直方向的距离为0 cm,单击“平移”.如图14所示,将平移后的点的标签命名为B .2. 用同样的方法把点A 平移5 cm 得到点'A ,画线段'AA ,分别选中点A 、B ,线段'AA ,依次单击“构造”、“以圆心和半径绘圆(R )”,画出两个圆,在上方的交点命名为D .如图15所示.图 15DA'BA3. 选中线段'AA 、点'A 、两个圆,依次单击“显示”、“隐藏对象”,构造△ABD .4. 依次选中点D 、A 、B ,依次单击“变换”、“标记角度”,标记角度DAB ∠.在线段AB 上任画一点P ,连结DP ,双击点P ,选中点D ,依次单击“变换”、“旋转”,将点D 绕点P 按标记角度DAB ∠旋转到点'D 的位置,作射线'PD ,交BD 边于点C ,隐藏射线'PD 和点'D ,构造线段PC .如图16、图17所示.5. 依次选中点D 、点C ,依次单击“构造”、“以圆心和圆周上的点绘圆(C )”,画出一个圆.如图18所示.图 17图 18拖动点P ,观察⊙D 与AB 边的位置关系,可以发现点P 位于AB 边上两个不同的位置,都能使⊙D 与AB 边相切,如图19、图20所示,所以需要分为两种情况进行讨论.图 19图 20例2.(1)如图(1),在△ABC 中,8,5===BC AC AB ,点P 、Q 分别在射线CB 、AC 上(点P 不与点C 、点B 重合),且保持ABC APQ ∠=∠. ①若点P 在线段CB 上,且6=BP ,求线段CQ 的长;②若y CQ x BP ==,,求y 与x 之间的函数关系式,并写出函数的定义域;QABCP(2)如图(2)所示,正方形ABCD 的边长为5,点P 、Q 分别在直线CB 、DC 上(点P 不与点C 、点B 重合),且保持︒=∠90APQ ,.当1=CQ 时,直接写出线段BP 的长.图 (1)QABCP图 (2)DABC解:(1)①∵6,8==BP BC ∴268=-=-=BP BC CP∵21∠+∠=∠+∠=∠APQ ABC APCABC APQ ∠=∠∴21∠=∠ ∵AC AB = ∴C B ∠=∠∵21∠=∠,C B ∠=∠ ∴△ABP ∽△PCQ ∴CQCQ BP PC AB 625,== ∴512=CQ ; ②分为两种种情况:当点P 在BC 边上时,x BP BC PC -=-=8 由①可知:△ABP ∽△PCQ ∴yxx CQ BP PC AB =-=85, 整理得:x x y 58512+-=(80<<x );当点P 在CB 的延长线上时,如图所示,8+=+=x BP BC PC 易证:△ABP ∽△PCQ∴yx CQ PC =+=8, 整理得:x x y 58512+=(0>x );(2)分为三种情况:①当点P 在BC 边上时,点Q 必在CD 边上.设x BP =,则x PC -=5 易证:△ABP ∽△PCQ ∴155,x x CQ BP PC AB =-=,整理得:0552=+-x x 解之得:255,25521+=-=x x ∴255-=BP 或255+=BP .如图1、图2所示; 图 1POQDABC图 2POQ DABC②当点P 在CB 的延长线上时,点Q 必在DC 的延长线上.如图3所示. 易证:△ABP ∽△PCQ∴15,x CQ PC =+= 整理得:0552=-+x x ,解之得:2535,253521--=+-=x x (舍去) ∴2535+-=BP ; 图 3图 4③当点P 在BC 的延长线上时,点Q 必在DC 的延长线上.如图4所示. 易证:△ABP ∽△PCQ ∴155,xx CQ BP PC AB =-= 整理得:0552=--x x ,解之得:2535,253521-=+=x x (舍去) ∴2535+=BP . 综上所述,线段BP 的长为2535+-或255-或255+或2535+. 点评 对于第(2)问,我们可以利用几何画板进行动态分析.1. 打开几何画板,单击“点工具”,任意画一点A ,选中点A ,依次单击“变换”、“平移”,在弹出的对话框中选择“直角坐标”,修改水平方向的“固定距离”为0 cm, 垂直方向的距离为5-cm,单击“平移”.如图21所示,将平移后的点的标签命名为B .2.选中点A、点B,依次单击“变换”、“平移”,修改水平方向“固定距离”为5 cm,垂直方向“固定距离”为0 cm,单击“平移”,将点A的对应点命名为D,点B的对应点命名为C.如图22所示.3.构造线段AD、直线DC、直线BC,在直线BC上任取一点P,构造线段AP,双击点P,选中点A,依次单击“变换”、“旋转”,修改“固定角度”为0.度,单击“旋90转”,得到点'A,作直线'PA,交直线CD于点Q,如图23、图24所示.4.选中点'A和直线'PA,依次单击“显示”、“隐藏对象”,构造线段PQ.5.依次选中点A、B、P,依次单击“构造”、“三角形的内部”,用同样的方法构造△PCQ的内部.如图25所示.6.选中点C、点Q,依次单击“度量”、“距离”,度量出线段CQ的长度,完成作图.在直线BC上拖动点P,观察CQ长度的变化,可以发现,当1CQ cm时,点P有四个不同的位置,对应四种不同的结果,分别如图26(1)、(2)、(3)、(4)所示.其中,当点P在BC边上时,有两个不同的位置满足条件.(1)(2)(3)图 26模型练习1. 如图所示,在矩形ABCD 中,由8个面积均为1的小正方形组成的L 形模板如图放置,则矩形ABCD 的周长为_________.GFEDCBA提示 设x DF =,则有x BC x CF BE x CD CE AB 3,,2======. 2. 【情景观察】如图(1),将矩形ABCD 纸片沿对角线AC 剪开,得到△ABC 和△D C A ''.将△D C A ''的顶点'A 与点A 重合,并绕点A 按逆时针方向旋转,使点D ,()'A A ,B 在同一条直线上,如图(2)所示.观察图(2)可知:与BC 相等的线段是_________,=∠'CAC _________; 【问题探究】如图27所示,在△ABC 中,BC AG ⊥于点G ,以A 为直角顶点,分别以AB 、AC 为直角边,向△ABC 外作等腰Rt △ABE 和等腰Rt △ACF ,过点E 、F 作射线GA 的垂线,垂足分别为P 、Q ,试探究EP 与FQ 之间的数量关系,并证明你的结论. 【拓展延伸】如图28所示,在△ABC 中,BC AG ⊥于点G ,分别以AB 、AC 为一边向△ABC 外作矩形ABME 和矩形ACNF ,射线GA 交EF 于点H .若kAF AC kAE AB ==,,试探究HE 与HF 之间的数量关系,并说明理由.(2)(1)BCC'A (A')C'A'DCBCABDAD图 27图 28提示 【问题探究】FQ EP =,如右图,只需证明△ABG ≌△EAP (EP AG =),△ACG ≌△F AQ (FQ AG =),就可完成证明.【拓展延伸】作AG FQ AG EP ⊥⊥,,如下页图 所示.易证:△ABG ∽△EAP ,△ACG ∽△F AQ∴k FQAGFA AC k EP AG EA AB ====, ∴kFQ AG kEP AG ==, ∴FQ EP =∴易证:△EHP ≌△FHQ ∴HF HE =.。
