支配集、点独立集和点覆盖集 - Websoft Research Group
图论讲义1图路树

7. 连通性 图中两点的连通:如果在图 G 中 u,v 两点有路相通,则称顶点 u,v 在图 G 中连通。 连通图(connected graph):图 G 中任二顶点都连通。 图的连通分支(connected branch, component):若图 G 的顶点集 V(G)可划分为若干非空子集
这便定义出一个图。
2. 图的图示
通常,图的顶点可用平面上的一个点来表示,边可用平面上的线段来表示(直的或曲的)。 这样画出的平面图形称为图的图示。
例如,例 1.1.1 中图的一个图示为
v1
v2
e1
e6 e5
e2
e4
v5
e7
v3
e3 v4
注:(1)由于表示顶点的平面点的位置的任意性,同一个图可以画出形状迥异的很多图示。
3
(8) 完全图(complete graph)
(9) 图的顶点数(图的阶)ν 、边数 ε
(10) 顶点 v 的度(degree):d(v) = 顶点 v 所关联的边的数目(环边计两次)。
(11) 图 G 的最大度: ∆(G) = max{dG (v) | v ∈V (G)}
图 G 的最小度:δ (G) = min{dG (v) | v ∈V (G)}
证明:按每个顶点的度来计数边,每条边恰数了两次。 推论 1.1.1 任何图中,奇度顶点的个数总是偶数(包括 0)。 4. 子图
子图(subgraph):如果V (H ) ⊆ V (G) 且 E(H ) ⊆ E(G) ,则称图 H 是 G 的子图,记为 H ⊆G。
生成子图(spanning subgraph): 若 H 是 G 的子图且V (H ) = V (G) ,则称 H 是 G 的生成子图。
【国家自然科学基金】_支配集_基金支持热词逐年推荐_【万方软件创新助手】_20140801
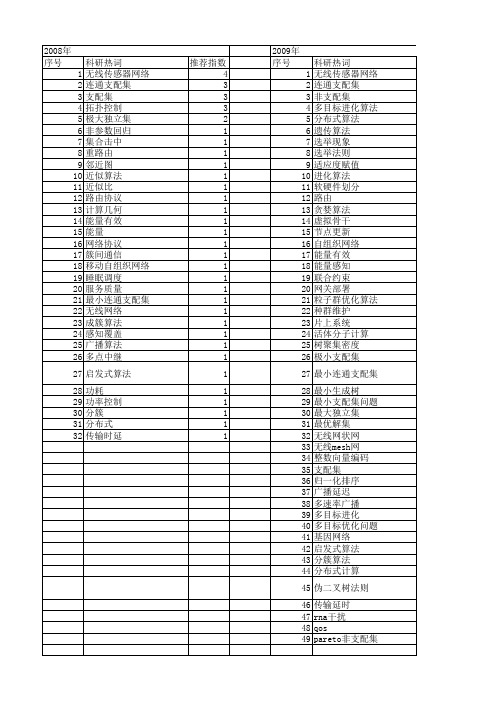
53 54 55 56
2011年 科研热词 推荐指数 无线传感器网络 4 连通支配集 3 连通支配集(cds) 2 极大独立集 2 数据收集 2 支配集 2 顶点集 1 连接图 1 边界解集 1 边支配集 1 车辆路径问题 1 调度 1 训练 1 蚁群算法 1 虚拟骨干网 1 虚拟突发 1 聚类方法 1 网关部署算法 1 网关 1 移动控制 1 移动基站 1 移动代理 1 染色 1 最小连通支配集 1 无线网络 1 无线网 1 无线传感器与执行器网络(wsan) 1 无线mesh网络 1 无线ad hoc网络 1 数据关联 1 擂台赛法则 1 控制数 1 扩展卡尔曼滤波 1 性能指标 1 微分熵 1 弱连通支配集 1 孤立点 1 多粒度 1 多目标遗传算法 1 多目标进化算法 1 多目标优化 1 基数 1 同时定位与地图创建 1 分布式 1 分布广度评价 1 冗余缩减 1 关联支配集 1 关联图 1 光突发交换(obs) 1 信息熵 1 传输功率均衡 1 业务疏导 1
推荐指数 4 3 3 3 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2009年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49
不等式 wsan骨干网 sift qos
1 1 1 1
53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75
2008年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32
支配集的概念

支配集的概念介绍
2015-5-5
1
支配集的定义
我们用G(V,E)表示无权无向的简单图, G(V,E)由V和E构成, 集合V的元素称为顶点,n=|V|称为集合V包含的顶点数量;集 合E的元素称为边,它是一个二元组数对,以(vi,vj)或vivj表示, 其中vi,vj∈V。 开放邻居集合 在G(V,E)所表示的图中,当边e= vivj∈E时,称vi,vj相邻,此 时vi,vj互为邻居节点,边e和vi,vj具有关联关系。 顶点v的开放邻居集合 (记作N(v))由与v相邻的所有顶点集合构 成,即 顶点v开放邻居集合的势|N(v)|,称为顶点v的度,记为deg(v).
11
支配集的性质及求解
通过极大独立集求解连通支配集算法
20
标记阶段
连通阶段
20
20
12
Thank you!
13
10
支配集的性质及求解
定理 极大独立集必为极小支配集,且逆命题不成立。
由上述定理可知,要求极小支配集,一个方法即寻找对应图的 极大独立集,而为了求极大独立集,需要介绍覆盖集的概念。 覆盖集 对集合C∈V,若对于图G中的每一条边,均至少有一端在C中,则 称C为图G的覆盖集。 通过覆盖集求独பைடு நூலகம்集的相关定理: 定理1:I是独立集,当且仅当V-I是覆盖集; 定理2:C是极小覆盖集,当且仅当V-C是极大独立集。
随着图序的增长,计算复杂度将呈现几何级增长,可见此方法仅 适用于极小规模图的支配集求解。 求最小支配集问题被证明属于NP完全问题,即对于给定问题域 的输入规模,目前尚无足够的手段证明该问题能够被判定在多 项式时间内求解。
9
支配集的性质及求解
以独立集解决支配集问题 定义 对于集合I∈V,如果I中任意两个顶点都不相邻,则称I是图G的一 个独立集。 任意取顶点u∈V-I,若I U {u}不是独立集,则称集合I是极大 独立集。 对极大独立集I,若图中不存在独立集I1,|I1|>|I|,则称I是G的 最大独立集.此时,记β (G)=|I|,则β(G)称为图G的独立数.
离散数学sec13 匹配

Hall定理
定理13.11 (Hall定理)设二部图G=<V1,V2,E>中, |V1||V2|. G中存在从V1到V2的完备匹配当且仅当V1中任 意k(k=1,2,…,|V1|)个顶点至少与V2中的k个顶点相邻. 本定理中的条件常称为“相异性条件”. 由Hall定理立刻可 知,上图中(2)为什么没有完备匹配. m个男孩的结婚问题有解 iff 对每个正整数k(1≤k≤m), 任意k个男孩所认识的女孩的总数至少是k个。
证明线索:必要性. 若含可增广交错路径,可生成比M更 大的匹配. 充匹可论分配增为性,广真只 交.. 设 否要 错M则证 路和H明 径M.1|M设分,|=H别此|M=为时1G|不,即[M含H可1中可. M的由增]交必,广错要若路圈性H径=(知的若,匹,存M配M在1=和也)M,最不1其,大含上结 M数与也M相1等的边 (数 因相 为等M与,M且1所均有无交可错增路广径路上径,)M. 与M1中的边
证明见教材.
15
最大匹配与最小边覆盖之间关系(续)
(1)
(2)
图中,红边为匹配M中的边. (1)中匹配是最大匹配. (2)中红 边与绿边组成最小边覆盖W. 反之,由(2)的最小边覆盖W产生(1)中的最大匹配M.
推论 设G是n阶无孤立顶点的图. M为G中的匹配, W是G中的边覆盖,则 |M| |W|,等号成立时,M为 G中完美匹配,W为G中最小边覆盖.
4
点独立集与点独立数
(1)
(2)
在图中,点独立数依次为2, 2
Hale Waihona Puke 5极大独立集与极小支配集
定理13.2 设G=<V,E>中无孤立点,则G的极大顶点 独立集都是极小支配集. 证明线索: (1) 设V*为G的极大顶点独立集,证明它也是支配集.
离散数学第十四章图论基本概念

14.2 通路与回路
定义14.11 给定图G=<V,E>(无向或有向的),G中顶点与
边的交替序列 = v0e1v1e2…elvl,
vi1, vi 是 ei 的端点.
(1) 通路与回路: 为通路;若 v0=vl, 为回路,l 为回路长
度.
(2) 简单通路与回路:所有边各异, 为简单通——v的出度 d(v)——v的入度 d(v)——v的度或度数 (3) (G), (G) (4) +(D), +(D), (D), (D), (D), (D) (5) 奇顶点度与偶度顶点
8
握手定理
定理14.1 设G=<V,E>为任意无向图,V={v1,v2,…,vn}, |E|=m, 则
v的闭邻N 域 D(v)ND(v){v}
9. 标定图与非标定图 10. 基图
6
多重图与简单图
定义14.3 (1) 无向图中的平行边及重数 (2) 有向图中的平行边及重数(注意方向性) (3) 多重图 (4) 简单图 在定义14.3中定义的简单图是极其重要的概念
7
顶点的度数
定义14.4 (1) 设G=<V,E>为无向图, vV, d(v)——v的度数, 简称度 (2) 设D=<V,E>为有向图, vV,
n
d(vi ) 2m
i1
证 G中每条边 (包括环) 均有两个端点,所以在计算G中各顶点 度数之和时,每条边均提供2度,m 条边共提供 2m 度.
定理14.2 设D=<V,E>为任意有向图,V={v1,v2,…,vn}, |E|=m, 则
n
n
n
d (v i)2 m , 且d (v i)d (vi) m
图论讲义第1章-图的概念

图论与网络流理论(Graph Theory and Network Flow Theory)高随祥中科院研究生院专业基础课学时/学分:60/3本课程适合基础数学、应用数学、计算数学、运筹学与控制论、概率论与数理统计各专业的硕士学位研究生作为专业基础课,也可供物理学、化学、天文学、地学、生物科学、计算机科学与技术、计算机软件、管理科学与工程以及通信、信号等学科专业的硕士研究生选修。
主要讲授图论与网络流理论的基本概念、方法和定理,介绍该领域重要的问题以及典型的算法,展示图论与网络流模型及方法的广泛应用。
为学习者将来从事有关方面的理论研究打下基础,也为进行应用性研究提供一种有力的工具。
内容提要第一章 图的基本概念图的基本概念;二部图及其性质;图的同构;关联矩阵与邻接矩阵。
路、圈与连通图;最短路问题。
树及其基本性质;生成树;最小生成树。
第二章 图的连通性割点、割边和块;边连通与点连通;连通度;Whitney定理;可靠通信网络的设计。
第三章 匹配问题匹配与最大匹配;完美匹配;二部图的最大匹配;指派问题与最大权匹配。
第四章 欧拉图与哈密尔顿图欧拉图;中国邮递员问题;哈密尔顿图;旅行商问题。
第五章 支配集、独立集、覆盖集与团支配集、点独立集、点覆盖集、边覆盖集与团的概念及其求法。
第六章图的着色问题点着色;边着色;平面图;四色猜想;色多项式;色数的应用。
第七章网络流理论有向图;网络与网络流的基本概念;最大流最小割定理;求最大流的标号算法;最小费用流问题;最小费用最大流;网络流理论的应用。
主要参考书[1] J.A. Bondy and U.S. Murty, Graph theory with applications, 1976, 有中译本(吴望名等译)。
[2] B.Bollobas, Modern graph theory (现代图论),科学出版社,2001。
[3] 蒋长浩,图论与网络流,中国林业出版社,2001。
《图论》第6章-图的着色

6.1 色数
[定理6-1-1] k-临界图 G=(V, E), =min{deg(vi)|viV}, 则
k-1。
[证明]反证法:设 G 是一个 k-临界图且 <k-1。又设v0V, deg(v0)= 。由 k-临界图的定义,Gv0 是 (k1)可着色的, 在一种 k1着色方案下,Gv0 的顶点可按照颜色划分 成 V1,V2, …, Vk-1 共 k1块,块 Vi 中的顶点被涂以颜色 ci。由于deg(v0)< k1,v0 至少与其中一块 Vj 不邻接即与 Vj 中的任何顶点不邻接。此时可将 v0 涂以颜色 cj,
12
第十二页,编辑于星期六:八点 一分。
6.1 色数
[五色定理] (1890, Heaword) 任何简单平面图都是 5-可着色的。 [证明]设简单平面图 G=(V, E),对 n=|V| 作归纳。
n 5时容易讨论结论成立。
设 n = k1时,结论成立。 当 n = k 时,由[定理5-1-8]简单平面图 G 至少有一个顶点的度 小于6。故可设 v0V,deg(v0) 5。设 G=Gv0,由归纳假设
何顶点的度不小于 k-1。又 G 为 k 色图,其中至少有 k 个顶点。
9
第九页,编辑于ቤተ መጻሕፍቲ ባይዱ期六:八点 一分。
6.1 色数
[推论2] 对 G=(V, E), =max{deg(vi)|viV},有 (G) +1。
[证明] 设 (G)=k,由推论1,有 vV,使得 deg(v) k-1
又: deg(v) 故: k-1 或 (G)-1 即: (G) +1
图所示。
13
第十三页,编辑于星期六:八点 一分。
大学_《离散数学》课后习题答案

《离散数学》课后习题答案《离散数学》简介1、集合论部分:集合及其运算、二元关系与函数、自然数及自然数集、集合的基数2、图论部分:图的基本概念、欧拉图与哈密顿图、树、图的矩阵表示、平面图、图着色、支配集、覆盖集、独立集与匹配、带权图及其应用3、代数结构部分:代数系统的基本概念、半群与独异点、群、环与域、格与布尔代数4、组合数学部分:组合存在性定理、基本的计数公式、组合计数方法、组合计数定理5、数理逻辑部分:命题逻辑、一阶谓词演算、消解原理离散数学被分成三门课程进行教学,即集合论与图论、代数结构与组合数学、数理逻辑。
教学方式以课堂讲授为主,课后有书面作业、通过学校网络教学平台发布课件并进行师生交流。
《离散数学》学科内容随着信息时代的到来,工业革命时代以微积分为代表的连续数学占主流的地位已经发生了变化,离散数学的重要性逐渐被人们认识。
离散数学课程所传授的思想和方法,广泛地体现在计算机科学技术及相关专业的诸领域,从科学计算到信息处理,从理论计算机科学到计算机应用技术,从计算机软件到计算机硬件,从人工智能到认知系统,无不与离散数学密切相关。
由于数字电子计算机是一个离散结构,它只能处理离散的或离散化了的数量关系,因此,无论计算机科学本身,还是与计算机科学及其应用密切相关的现代科学研究领域,都面临着如何对离散结构建立相应的数学模型;又如何将已用连续数量关系建立起来的数学模型离散化,从而可由计算机加以处理。
离散数学是传统的逻辑学,集合论(包括函数),数论基础,算法设计,组合分析,离散概率,关系理论,图论与树,抽象代数(包括代数系统,群、环、域等),布尔代数,计算模型(语言与自动机)等汇集起来的一门综合学科。
离散数学的应用遍及现代科学技术的诸多领域。
离散数学也可以说是计算机科学的基础核心学科,在离散数学中的有一个著名的典型例子-四色定理又称四色猜想,这是世界近代三大数学难题之一,它是在1852年,由英国的一名绘图员弗南西斯格思里提出的,他在进行地图着色时,发现了一个现象,“每幅地图都可以仅用四种颜色着色,并且共同边界的国家都可以被着上不同的颜色”。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1 G G G
D
V(G)\D
13
求最小支配集的算法
• 与集合覆盖问题可以相互转化:NP‐hard
14
求最小支配集的算法
• 与集合覆盖问题可以相互转化:NP‐hard • 贪心算法
– 每一轮迭代总是选取能支配最多剩余顶点的那个顶点 – 近似比:1+logν
26
点独立集与连通度 (续)
• 推论5.1.2 设G是ν (ν≥2)阶简单图。若δ(G)≥ν/2,则α(G)≤κ(G)。 证明: δ(G)≥ν/2 ⇒ 任二不相邻顶点x与y均有d(x)+d(y)≥ν(G) ⇒ α(G)≤κ(G)
27
求最大独立集的算法
• 最大独立集=补图中的最大团:NP‐hard • 不存在近似比显著好于线性的多项式时间算法(除非P=NP)
极小点覆盖集 (minimal vertex cover)
– 顶点数极少(任何一个真子集都不再是点覆盖集)
最小点覆盖集 (minimum vertex cover)
– 顶点数最少
点覆盖数 (vertex cover number)
– β(G):最小点覆盖集的势
31
点覆盖集与支配集
• 点覆盖集与所有边关联 • 支配集与所有剩余点相邻 • 连通图中,点覆盖集必为支配集 • 反之成立吗?
• 不存在近似比好于1.3606的多项式时间算法(除非P=NP) • 目前还没有找到近似比显著小于2的多项式时间算法
– 基于极大匹配的算法已经足够好了
36
作业
• 5.6 //支配集 • 5.11 //点独立集 • 5.15 //点覆盖集
37
D是极小支配集 ⇒ D\{v}不是支配集 ⇒ ∃u∈{v}∪(V(G)\D)与D\{v}中的顶点 均不相邻 ⇒ • u=v ⇒ N(v)∩D=∅ ⇒ (1) • u≠v ⇒ u∈V(G)\D且N(u)∩(D\{v})=∅,而D是支配集 ⇒ (u, v)∈E(G) ⇒ N(u)∩D={v} ⇒ (2) D V(G)\D
17
求最小支配集的算法
• 与集合覆盖问题可以相互转化:NP‐hard • 贪心算法
– 每一轮迭代总是选取能支配最多剩余顶点的那个顶点 – 近似比:1+logν
18
求最小支配集的算法
• 与集合覆盖问题可以相互转化:NP‐hard • 贪心算法
– 每一轮迭代总是选取能支配最多剩余顶点的那个顶点 – 近似比:1+logν
– 顶点数极少(任何一个真子集都不再是支配集)
最小支配集 (minimum dominating set)
– 顶点数最少
支配数 (domination number)
– γ(G):最小支配集的势
4
支配集与匹配
• 支配集与完美匹配之间有什么关系?
– 从完美匹配中的每条边取一个端点构成一个支配集。 – 从最大匹配中的每条边取一个端点构成一个支配集吗?
– 顶点数极多(不是任何一个点独立集的真子集)
最大点独立集 (maximum vertex independent set)
– 顶点数最多
独立数 (independence number)
– α(G):最大点独立集的势
22
点独立集与支配集
• 定理5.1.8 极大点独立集必是极小支配集。 证明: 1. 为什么是支配集?
⇒
– 取x=w,则w与D\{v}中顶点相邻。(#) – D\{v}支配V(G)\D,而w与v相邻 ⇒ D\{v}∪{w}是支配集 |D\{v}∪{w}|=|D| ⇒ D\{v}∪{w}也是最小支配集 ⇒ D\{v}∪{w}的点导出子图的边数≤D的点导出子图 的边数 (**) N(v)∩D=∅ ⇒ v与D\{v}中顶点不相邻 (##) (#)和(##) ⇒ D\{v}∪{w}的点导出子图的边数>D的点导出子图的边数 ⇒ 与(**)矛盾
– I是极大点独立集 ⇒ ∀u∈V(G)\I与I中顶点相邻 ⇒ I是支配集 I是点独立集 ⇒ ∀v∈I与I\{v}中顶点不相邻 ⇒ I\{v}不是支配集
2.
为什么极小?
–
⇒ I是极小支配集 反之成立吗?
v u
23
I
点独立集与支配集 (续)
• 定理5.1.9 若I是点独立集,则它是极大点独立集当且仅当 它是支配集。 证明: • ⇒ 定理5.1.8 • ⇐ 怎么证明? I是支配集 ⇒ ∀u∈V(G)\I与I中顶点相邻 ⇒ I∪{u}不是点独立集 ⇒ I是极大点独立集
34
点覆盖集与独立集 (续)
• 推论5.1.4 α(G)+β(G)=ν(G)。 证明:留作作业。
35
求最小点覆盖集的算法
• 点覆盖集和极大匹配之间有什么关系?
– 极大匹配饱和的所有顶点构成一个点覆盖集 – 极大匹配中的边互不相邻 ⇒ 任何一个点覆盖集至少包含其中每条 边的一个端点 ⇒ 上述点覆盖集的势≤2β,即近似比为2 – 怎么找极大匹配?
28
独立集的应用
• 最大带权独立集:图像分割
– 顶点:所有可能的块 – 边:重叠的块 – 权:块的显著程度
Segmentation as Maximum‐Weight Independent Set
29
30
点覆盖集
• • • • 点覆盖集 (vertex cover)
– F是G的点覆盖集:∀(u, v)∈E(G), {u, v}∩F≠∅
• 不存在近似比好于对数的多项式时间算法(除非P=NP)
– 贪心算法已经足够好了
19
支配集的应用
• 最小连通支配集:自组网络中的虚拟骨干网
20
21
点独立集
• • • • 点独立集 (vertex independent set)
– I是G的点独立集:∀u, v∈I, (u, v)∉E(G)
极大点独立集 (maximal vertex independent set)
支配集、点独立集和点覆盖集
程龚 (gcheng@)
本节课的主要内容
5.1 支配集、点独立集、点覆盖集
2
3
支配集(控制集)
• • • • 支配集 (dominating set)
– D是G的支配集:∀v∈(V(G)\D), ∃u∈D, (u, v)∈E(G)
极小支配集 (minimal dominating set)
5
支配集与其补集
• 定理5.1.1 无孤立顶点的图G中,存在支配集D和V(G)\D。 证明:只讨论连通图。你能想到构造方法吗? 1. ∀u∈V(G)。 2. D={v: d(v, u)是偶数},V(G)\D={v: d(v, u)是奇数}。
6
支配集与其补集 (续)
• 定理5.1.2 无孤立顶点的图G中,极小支配集D的补集 V(G)\D是支配集。 证明: 1. 反证法:V(G)\D不是支配集 ⇒ ∃u∈D与V(G)\D中的顶点均 不相邻 2. 如何推出矛盾(D不是极小支配集)?
4. 5. 6.
D v
V(G)\D w x
11
支配数的估计
• 定理5.1.5 无孤立顶点的图G满足γ(G)≤ν/2。 证明:你能自己证明吗?(很容易) 极小支配集D的补集也是支配集 ⇒ γ(G)≤min{|D|, |V(G)\D|}≤ν/2
12
支配数的估计 (续)
• 定理5.1.7 证明: 1. 右侧显然。 2. 左侧:G有最小支配集D ⇒ V G \ D N v ⇒ |V(G)\D|≤|D|Δ(G) ⇒ ν‐γ(G)≤γ(G)Δ(G) ⇒ 1 G G
– G中无孤立顶点 ⇒ u与D中的顶点相邻 ⇒ D\{u}仍是支配集 ⇒ D不是极小支配集
D V(G)\D
u7支ຫໍສະໝຸດ 集与其补集 (续)• 推论5.1.1 无孤立顶点的图G中,对任意一个极小支配集D1, 必存在另一个极小支配集D2,使得D1∩D2=∅。 证明:你能自己证明吗?(很容易) 定理5.1.2 ⇒ V(G)\D1是支配集且D1∩(V(G)\D1)=∅ ⇒ 在V(G)\D1 的子集中取极小可得D2
D1
V(G)\D1
8
极小支配集的充要条件
• 定理5.1.3 图G的支配集D是一个极小支配集当且仅当D中每 个顶点v满足下列条件之一: (1) N(v)∩D=∅; (2) 存在u∈V(G)\D使得N(u)∩D={v}。 证明:⇐
D v1
V(G)\D
v2
u
9
极小支配集的充要条件 (续)
• 定理5.1.3 图G的支配集D是一个极小支配集当且仅当D中每 个顶点v满足下列条件之一: (1) N(v)∩D=∅; (2) 存在u∈V(G)\D使得N(u)∩D={v}。 证明:⇒
v1
v2
10
一个推论
• 定理5.1.4 无孤立顶点的图G必有最小支配集D满足:∀v∈D,∃u∈V(G)\D, N(u)∩D={v}。 证明: 1. 反证法:D是G中点导出子图的边数最多的最小支配集 ⇒ ∃v∈D, ∀u∈V(G)\D, N(u)∩D≠{v} (*) 2. 定理5.1.3 ⇒ N(v)∩D=∅(条件(1)必成立),而G中无孤立顶点 ⇒ ∃w∈V(G)\D与v相邻 3. ∀x∈V(G)\D: – x与v不相邻:D是支配集 ⇒ x与D\{v}中顶点相邻 – x与v相邻:(*) ⇒ x与D\{v}中顶点相邻
32
点覆盖集与独立集
• 定理5.1.13 F是点覆盖集当且仅当V(G)\F是点独立集。 证明:你能证明吗? F是点覆盖集 ⇔ G的每条边都有至少一个端点在F中 ⇔ 没有 两端点都在V(G)\F中的边 ⇔ V(G)\F是点独立集
33
点覆盖集与独立集 (续)
• 推论5.1.3 F是极小点覆盖集当且仅当V(G)\F是极大点独立 集。 证明:你能证明吗? 1. 定理5.1.13 ⇒ F是点覆盖集当且仅当V(G)\F是点独立集 2. F是极小点覆盖集 ⇔ F中去除任意一些点就会将至少一条 边的两个端点都去除 ⇔ V(G)\F中加入任意一些点就会将 至少一条边的两个端点都加入 ⇔ V(G)\F是极大点独立集
