2010年广州市高二数学学业水平测试题(必修1-5
广州市高二数学学业水平测试题
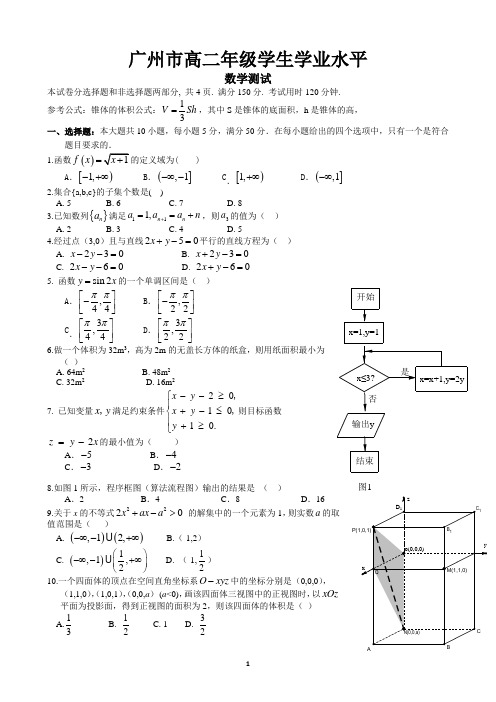
广州市高二年级学生学业水平数学测试本试卷分选择题和非选择题两部分, 共4页. 满分150分. 考试用时120分钟. 参考公式:锥体的体积公式:13V Sh =,其中S 是锥体的底面积,h 是锥体的高, 一、选择题:本大题共10小题,每小题5分,满分50分.在每小题给出的四个选项中,只有一个是符合题目要求的. 1.函数()f x =( )A .[)1,-+∞B .(],1-∞-C .[)1,+∞D .(],1-∞2.集合{a,b,c}的子集个数是( )A. 5B. 6C. 7D. 83.已知数列{}n a 满足111,n n a a a n +==+,则3a 的值为( ) A. 2 B. 3 C. 4 D. 54.经过点(3,0)且与直线250x y +-=平行的直线方程为( ) A. 230x y --= B. 230x y +-= C. 260x y --= D. 260x y +-=5. 函数sin 2y x =的一个单调区间是( )A .,44ππ⎡⎤-⎢⎥⎣⎦ B .,22ππ⎡⎤-⎢⎥⎣⎦C .3,44ππ⎡⎤⎢⎥⎣⎦D .3,22ππ⎡⎤⎢⎥⎣⎦6.做一个体积为32m 3,高为2m 的无盖长方体的纸盒,则用纸面积最小为( )A. 64m 2B. 48m 2C. 32m 2D. 16m 27. 已知变量x y ,满足约束条件201010x y x y y ⎧--≥⎪+-≤⎨⎪+≥⎩,,.则目标函数2z y x =-的最小值为( )A .5-B .4-C .3-D .2-8.如图1所示,程序框图(算法流程图)输出的结果是 ( )A .2B .4C .8D .16 9.关于x 的不等式2220x ax a +-> 的解集中的一个元素为1,则实数a 的取值范围是( ) A. ()(),12,-∞-+∞ B.(-1,2)C. ()1,1,2⎛⎫-∞-+∞ ⎪⎝⎭D. (-1,12) 10.一个四面体的顶点在空间直角坐标系O xyz -中的坐标分别是(0,0,0),(1,1,0),(1,0,1),(0,0,a ) (a <0),画该四面体三视图中的正视图时,以xOz平面为投影面,得到正视图的面积为2,则该四面体的体积是( ) A.13 B. 12 C. 1 D. 32图1二、填空题:本大题共4小题,每小题5分,满分20分.11.在△ABC 中,∠ABC=450,AC=2,BC=1,则sin ∠BAC 的值为 . 12.某赛季甲、乙两名篮球运动员每场比赛得分的原始记录用茎叶图表示(图2),则该赛季发挥更稳定的运动员是 .(填“甲”或“乙”) 13.已知向量(1,2),(3,4),AB AC ==则BC = . 14.已知[x]表示不超过实数x 的最大整数,g(x)=[x],0x 是函数()21log f x x x=-的零点,则g(0x )的值等于 .三、解答题:本大题共6小题,满分80分.解答应写出文字说明、演算步骤和推证过程. 15.(本小题满分12分)某中学高一年级新生有1000名,从这些新生中随机抽取100名学生作为样本测量其身高(单位:cm ),(1)试估计高一年级新生中身高在[)175,180上的学生人数;(2)从样本中身高在区间[)170,180上的女生中任选2名,求恰好有一名身高在区间[)175,180上的概率. 8 0 4 6 3 1 2 5 3 6 8 2 5 43 8 9 3 1 6 1 6 7 94 4 9 15 0乙甲图2已知函数()sin cos ,6f x x x x R π⎛⎫=-+∈ ⎪⎝⎭. (1)求(0)f 的值;(2)若α是第四象限角,且133f πα⎛⎫+= ⎪⎝⎭,求tan α的值.17. (本小题满分14分)如图3,在棱长为1的正方体ABCD-A 1B 1C 1D 1中,E,F 分别是A 1D 1,A 1A 的中点。
2010年广州市高二数学学业水平测试模拟题二天河中学

2010-2011年高中数学必修模块测试试卷天河中学 高二备课组一、选择题(本大题共10小题,共50分) 1、求值:11sin()6π-=( ) A.12-B.12C.-2、已知集合{}{}35,12A x x B x a x a =<<=-≤≤+,若A B ⊆,则实数a 的取值范围是( )A.34a <≤ B.34a ≤≤ C.34a << D.∅3、给出下面4个关系式:①22a a =;②ab a b ⋅=⋅;③a b b a ⋅=⋅;④()()a b c a b c ⋅=⋅;其中正确命题的个数是A.1 B.2 C.3 D.44、如图是容量为100的样本的频率分布直方图, 则样本数据在[6,10)内的频率和频数分别是A.0.32,32 B.0.08,8C.0.24,24 D.0.36,365、某路公共汽车5分钟一班准时到达A 站,则任意一人在A 站 等车时间少于2分钟的概率为A.35 B.12 C.25 D.146、正方体的全面积是24,则它的外接球的体积是B.C.8πD.12π7、运行下列程序:当输入168,72时,输出的结果是 A.168 B.72 C.36 D.248、在ABC ∆中,已知4,1AB AC ==,ABC ∆A.2± B.4± C.2 D.49、函数2sin cos y x x =+的值域是A.41,5⎡⎤-⎢⎥⎣⎦ B.[]1,1- C.41,5⎡⎤⎢⎥⎣⎦D.4(,]5-∞10、若偶函数()f x 在区间[]1,0-上是减函数,,αβ是锐角三角形的两个内角,且αβ≠,则下列不等式中正确的是A.(cos )(cos )f f αβ> B.(sin )(cos )f f αβ<C.(cos )(sin )f f αβ< D.(sin )(sin )f f αβ>二、填空题(本大题共4小题,共20分)11、已知向量(2,1),(,2)a b x ==-,且a b +与2a b -平行,则x = . 12、已知函数()(0,1)x x f x a a a a -=+>≠且,若(1)3f =,则(2)f = .13、已知函数()sin 2cos 2f x x k x =-的图像关于直线8x π=则k 的值是 . 14、计算2222135999++++的程序框图如下:其中空白框①应填入空白框②应填入三、解答题(本大题共6小题,共80分)15、(13分)已知函数2()sin sin2f x x x mπ⎡⎤⎛⎫=+-+⎪⎢⎥⎝⎭⎣⎦.(1)求()f x的最小正周期;(2)若()f x的最大值为3,求m的值.16、(13分)连续掷两次骰子,以先后得到的点数,m n 为点(,)P m n 的坐标,设圆Q 的方程为2217x y +=.(1)求点P 在圆Q 上的概率; (2)求点P 在圆Q 外部的概率.17、(13分)如图:正三角形ABC 与直角三角形BCD 所在平面互相垂直,且090BCD ∠=,030CBD ∠=.(1)求证:AB CD ⊥;(2)求二面角D AB C --的正切值.18、(13分)已知41cos ,(,),tan()522πααππβ=-∈-=,求tan(2)αβ-的值.19、(14分)已知圆22:2610C x y x y ++-+=,直线:3l x my +=. (1)若l 与C 相切,求m 的值;(2)是否存在m 值,使得l 与C 相交于A B 、两点,且0OA OB ⋅=(其中O 为坐标原点),若存在,求出m ,若不存在,请说明理由.20、(14分)已知12x x 、是方程24420x mx m -++=的两个实根.(1)当实数m 为何值时,2212x x +取得最小值?(2)若12x x 、都大于12,求m 的取值范围.数学科参考答案一、选择题(共10小题,每小题5分,共50分,四项选一项)1.答案B解:原式=sin(-2π+6π)=sin 6π=21. 2.答案Ba -1≤3结合数轴 得 ,即3≤a ≤4. a+2≥53.答案B解:①、③正确. 4.答案A解:在[6,10)内频率为0.08×4=0.32, 频数为0.32×100=32.5.答案C解:设乘客到达A 站的时刻为t ,等车时间为x 分钟,则0≤x ≤5,根据几何概型,等车时间少于2分钟的概率为P=52. 6.答案B解:设正方体棱长为a ,外接球半径为R ,则6a 2=24, ∴a=2,又2R=3a ,∴R=3,∴V 球=34πR 3=43π. 7.答案D解:当m ≥n>0时,该程序的作用是求两个正整数的最大公约数, 因为168与72的最大公约数是24,所以输出结果是24. 8.答案A 解:S △ABC =21·|AB|·|AC|·sinA=21×4×1×sinA=3, ∴sinA=23,∴cosA=±A sin 21 =±21,∴AB ·AC=|AB|·|AC|·cosA=4×1×(±21)=±2.9.答案A解:y=sinx+1-sin 2x=-(sinx -21)2+45, ∵sin x ∈[-1,1],∴sinx=21时,y max =45, 又sinx=-1时,y min =-1 ∴值域为[-1,45] 10.答案C解:∵偶函数f(x)在区间[-1,0]上是减函数,∴f(x)在[0,1]上是增函数,又α,β是锐角三角形的两个内角,∴α+β>2π, ∴2π>α>2π-β>0,∴0<cos α<cos(2π-β)<1, 即0<cos α<sin β<1,∴f(cos α)<f(sin β).二、填空题(共4小题,每小题5分,共20分)11.答案-4解:a + b =(2+x ,-1),2a -b =(4-x ,4)∵a + b 与2a -b 平行,∴(2+x)×4=-1×(4-x),∴x=-4. 12.答案7 解:f(1)=a+a 1=3,∴f(2)=a 2+21a =(a+a 1)2-2=32-2=7. 13.答案-1解:依设有f(8π-α)=f(8π+α),令α=8π,得 f(0)=f(4π),∴-k=1,∴k=-114.答案 ①S=S+i 2; ②i=i+2三、解答题:本大题共6个小题,共80分。
2010年广州市普通高中毕业班综合测试(二)数学试题理

试卷类型:A2010年广州市普通高中毕业班综合测试(二)数 学(理科)2010.4本试卷共4页,21小题,满分150分.考试用时120分钟.注意事项:1.答卷前,考生务必用2B 铅笔在“考生号”处填涂考生号.用黑色字迹的钢笔或签字笔将自己所在的市、县/区、学校以及自己的姓名和考生号、试室号、座位号填写在答题卡上.用2B 铅笔将试卷类型 (A) 填涂在答题卡相应位置上.2.选择题每小题选出答案后.用2B 铅笔把答题卡上对应题目选项的答案信息点涂黑;如需改动,用橡皮擦干净后,再选涂其他答案,答案不能答在试卷上.3.非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内的相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液.不按以上要求作答的答案无效.4.作答选做题时,请先用2B 铅笔填涂选做题的题号对应的信息点,再作答.漏涂、错涂、多涂的,答案无效.5.考生必须保持答题卡的整洁.考试结束后,将试卷和答题卡一并交回. 参考公式:如果事件A 、B 互斥,那么()()()P A B P A P B +=+. 如果事件A 、B 相互独立,那么()()()P A B P A P B =.如果事件A 在一次试验中发生的概率是p ,那么n 次独立重复试验中事件A 恰好投生k次的概率()(1)(0,1,2,,)k k n kn n P k C p p k n -=-=.两数立方差公式:3322() ()a b a b a ab b -=-++.一、选择题:本大题共8小题.每小题5分,满分40分.在每小题给出的四个选项中.只有一项是符合题目要求的 l .已知i 为虚数单位,若复数(1)(1)a a -++i 为实数,则实数a 的值为A .-1B .0C . 1D .不确定2.已知全集U A B =中有m 个元素,()()U UA A 中有n 个元索,若A B 非空,则A B 的元素个数为 A .mnB .m n +C .m n -D .n m -3.已知向量()sin ,cos a x x =,向量(b =,则a b +的最大值为A .1BC .3D .94.若m ,n 是互不相同的空问直线,α是平面,则下列命题中正确的是 A .若//m n ,n α⊂,则//m α B .若//m n ,//n α,则//m α C .若//m n ,n α⊥,则m α⊥ D .若m n ⊥,n α⊥,则m α⊥ 5.在如图1所示的算法流程图中,若()2xf x =,()2g x x =,则()2h 的值为(注:框图中的赋值符号“=”也可以写成“←”或“=”) A .9 B .8 C .6 D .46.已知点(),p x y 的坐标满足10,30,2x y x y x -+≥⎧⎪+-≥⎨⎪≤⎩O 为坐标原电,则PO 的最小值为A .22B .322C 5D 137.已知函数()sin f x x x ,若12,[,]22x x ππ∈-且()()12f x f x <,则下列不等式中正确的是 A .12x x >B .12x x <C .120x x +<D .2212x x <8.一个人以6米/秒的匀速度去追赶停在交通灯前的汽车,当他离汽车25米时交通灯由红变绿,汽车开始作变速直线行驶 (汽车与人的前进方向相同),汽车在时刻t 的速度为()v t t =米/秒。
2010年6月高二文科必修1

高二数学必修1质量检测试题(卷)2010.6命题:齐宗锁 审题:张新会本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.第Ⅰ卷1至2页.第Ⅱ卷3至6页.考试结束后. 只将第Ⅱ卷和答题卡一并交回.第Ⅰ卷(选择题 共60分)注意事项:1.答第Ⅰ卷前,考生务必将姓名、准考号、考试科目用铅笔涂写在答题卡上.2.每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案,不能答在试题卷上. 一、选择题:本答题共10小题,每小题6分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.集合{}0,2,A a =,{}21,B a =,若{}0,1,2,4,16A B = ,则a 的值为 A.0 B.1 C.2 D.4 2.下列图像表示的函数能用二分法求零点的是3.某公司为了适应市场需求对产品结构做了重大调整,调整后初期利润增长迅速,后来增长越来越慢,若要建立恰当函数模型来反映该公司调整后利润y 与时间x 的关系,可选用A .一次函数B .二次函数C .指数型函数D .对数型函数 4.具有性质“对任意x ,y R Î,满足()()()f x y f x f y +=+”的函数()f x 是A .()f x x p =B .0.6()log f x x =C .()5xf x = D .()cos f x x = 5.下列各组函数是同一函数的是①()f x =()g x =②f (x )=|x +1|与g (x )=1111x x x x ìïïíïïî³+---<-③0()f x x =与()1g x =;x④2()21f x x x =--与2()21g t t t =--.A. ①③B. ②③C. ②④D.③④6.函数()y f x =是函数1xy a a a =>≠(0,且)的反函数,且1)10(=f ,则()f x =A .lg xB .10xC .110log x D .102-x7.设0.52log 0.5,2,log 3a b c p ===,则A. a b c <<B. a c b <<C. b c a <<D. b a c << 8.已知函数()f x 是(,)-∞+∞上的奇函数,当[0,2)x ∈时,2()log (1f x x =+),则(0)(1)f f +的值为 A .2- B .1- C .1 D .29.要得到函数(24)y ln x =+的图像,只需把函数(2)y ln x =的图像上所有的点A .向左平移4个单位长度,B .向右平移2个单位长度,C .向左平移2个单位长度,D .向右平移4个单位长度,10.如图,全集U =R , 集合P={x|x 2>4},M={x |1<X <3},阴影部分所表示的集合是A .{x |-2≤X <1}B . {x |-2≤X ≤2}C .{x |1<X ≤2}D .{ X ∣X <2}二、填空题:本大题共6小题,每小题5分,共30分.把本大题答案填在第Ⅱ卷题中横线上.11.函数))(1(a x x y ++=在R x ∈上为偶函数,则=a ________;12.定义运算⎩⎨⎧≥=*),(,),(,y x y y x x y x 若32*= ________;13.某品牌文具的标价为132元,若降价以九折出售(即优惠10%),仍可获利10%(相对进货价),则该品牌文具的进货价是________;14.函数2log (4)2()(1)(3),2x x f x f x f x x ì- ïï=íï--->ïî,则(3)f =_____; 15.已知集合{}|24,(,)A x x B a =<?+ 若A B A =⋂,则实数a 的取值范围中的最大值为________;16.已知),10()(≠+=-a a a a x f xx 且 若3)1(=f ,则(2)f =______;高二数学必修1质量检测试题(卷)2010.6二、填空题:本大题共6小题,每小题5分,共30分. 把答案填在题中横线上.11. ;12. ; 13. ;14. ; 15._______________ ;16. __________________.三、解答题:本大题共4小题,共60分.解答应写出文字说明、证明过程或演算步骤.17(本小题满分15分) 已知2()(2)3f x f x x =+,(1)求(2)f 的值; (2)()f x 的解析式; (3)解不等式()0f x ≤.18. (本小题满分15分)已知函数2()22f x x ax =-+, x []3,3-∈. (1)当a =1时,求函数的最大值和最小值;(2)若()y f x =在区间[]3,3-上是单调增函数,求实数a 的取值范围.19.(本小题满分15分)“依法纳税是每个公民应尽的义务”国家征收个人所得税是分段计算,月总收入不超过2000元,免征个人所得税,超过2000元部分需征税. 设全月纳税金额为x,则x=全月总收入-2000元,税率见下表:f x的计算公式;(1)试用分段函数表示1~3级应纳税额()(2)某人2010年5月总收入3000元,试求该人此月份应缴纳个人所得税多少元?(3)某人一月份应缴纳此项税款325元,则他当月工资总收入多少元?20.(本小题满分15分)已知函数22()log (1)log (1)f x x x =--+, (1)求函数()f x 的定义域; (2)判断()f x 的奇偶性;(3)方程()1f x x =+是否有根?如果有根0x ,请求出一个长度为14的区间(,)a b ,使0(,)x a b ∈;如果没有,请说明理由?(注:区间(,)a b 的长度b a =-).高二数学必修1期末考试试题答案 一.选择题:(本大题共10小题,每小题6分,共60分)二、填空题(本大题共6小题,每小题5分,共30分) 11. 1- 12. 3 13. 108元 14. 1- 15. 2 16.7三、解答题:本大题共 4 小题,每题15分,共60分。
广州市高二学业水平测试(数学)含答案

广州市高中二年级水平测试•数学一、选择题:本大题共10小题,每小题5分,满分50分.在每小题给出的四个选项中,只有一个是符合题目要求的.1、已知集合{1,2,4,8}M =,{2,4,6,8}N =,则M N = ( )..A {2,4} .B {2,48}, .C {1,6} .D {12,4,68},,2、下列函数中,与函数1y x=定义域相同的函数为( ). .A 1y x=.B y x =.C 2y x -=.D ln y x =3、设n S 是等差数列{}n a 的前n 项和,已知59a =,24S =,则2a =( )..A 1 .B 2 .C 3.D 5 4、某几何体的三视图及其尺寸如图所示,则这个几何体的体积是( )..A 6.B 9.C 18.D 365、将函数cos y x =的图像向左平移2π个单位,得到函数()y f x = 的图像,则下列说法正确的是( )..A ()y f x =的最小正周期为π.B ()y f x =是偶函数.C ()y f x =的图像关于点(,0)2π对称.D ()y f x =在区间[0,]2π上是减函数6、已知221ab>>,则下列不等关系式中正确的是( )..A sin sin a b >.B 22log log a b <.C 11()()33a b > .D 11()()33a b <7、在ABC △中,已知5AB AC ==,6BC =,则AB BC =( )..A 18 .B 36 .C 18- .D 36-8、设y x ,满足约束条件⎪⎩⎪⎨⎧≥--≤+-≤-+,023,023,06y x y x y x 则y x z 2-=的最小值为( ).A 10- .B 6- .C 1- .D 0 9、设)(x f 为定义在R 上的奇函数,当0≥x 时,3)(1-=+x a x f (a 为常数),则)1(-f 的值为( ).A 6-.B 3-.C 2-.D 610、小李从甲地到乙地的平均速度为a ,从乙地到甲地的平均速度为b )0(>>b a ,他往返甲乙两地的平均速度为v ,则( ).A 2ba v +=.B ab v =.C 2ba v ab +<< .D ab v b <<435俯视图侧视图正视图二、填空题:本大题共4小题,每小题5分,满分20分.11、过点)0,3(-且与直线024=-+y x 平行的直线方程是______12、如图,在半径为1的圆内随机撒100粒豆子,有14粒落在阴影部分, 据此估计阴影部分的面积为______13、执行如图所示的程序框图,则输出的z 的值是______14、在ABC ∆中,已知6=AB ,33cos =C ,C A 2=,则BC 的长为______三、解答题:本大题共6小题,满分80分.解答应写出文字说明、演算步骤和推证过程. 15、(本小题满分12分)实验室某一天的温度(单位:C o)随时间t (单位:h )的变化近似满足函数关系:()[]24,0,312sin 4∈⎪⎭⎫ ⎝⎛-=t t t f ππ.(1)求实验室这一天上午10点的温度;(2)当t 为何值时,这一天中实验室的温度最低.20?z <z 输出开始结束x y =1,2x y ==y z=z x y =+是否16、(本小题满分12分)近年来,某市为了促进生活垃圾的分类处理,将生活垃圾分为“厨余垃圾”、“可回收垃圾”、“有害垃圾”和“其他垃圾”等四类,并分别设置了相应的垃圾箱,为调查居民生活垃圾的正确分类投放情况,现随机抽取了该市四类垃圾箱总计100吨生活垃圾,数据统计如下(单位:吨):“厨余垃圾”箱 “可回收垃圾”箱 “有害垃圾”箱 “其他垃圾”箱厨余垃圾24 4 1 2 可回收垃圾4 19 2 3 有害垃圾2 2 14 1 其他垃圾1 5 3 13 (1)试估计“可回收垃圾”投放正确的概率; (2)试估计生活垃圾投放错误..的概率.17、(本小题满分14分)如图所示,四棱锥ABCD P -中,底面ABCD 为矩形, ABCD PA 平面⊥,AB PA =,点E 为PB 的中点. (1)求证:ACE PD 平面//;(2)求证:PBC ACE 平面平面⊥.EDCBAP18、(本小题满分14分)已知直线05=+-y ax 与圆922=+y x C :相交于不同两点A ,B . (1)求实数a 的取值范围(2)是否存在实数a ,使得过点()12,-P 的直线l 垂直平分弦AB ?若存在,求出a 的值;若不存在,请说明理由.19、(本小题满分14分)已知等差数列{}n a 的公差为2,且1a ,21a a +,()412a a +成等比数列. (1)求数列{}n a 的通项公式; (2)设数列⎭⎬⎫⎩⎨⎧-12n n a 的前n 项和为n S ,求证:6<n S .20、(本小题满分14分)已知R a ∈,函数()a x x x f -=.(1)当2=a 时,求函数()x f y =的单调递增区间; (2)求函数()()1-=x f x g 的零点个数.广州市高中二年级学生学业水平测试数学参考答案一、选择题题号 1 2 3 4 5 6 7 8 9 10 答案BDCCDDCBAD二、填空题11、430x y ++= 12、0.14π 13、21 14、22 三、解答题15、解:(1)依题意()4sin(),[0,24]123f t t t ππ=-∈实验室这一天上午10点,即10t =时,(10)4sin(10)4sin 41232f πππ=⨯-==,所以上午10点时,温度为4C.(2)因为024t ≤≤,所以531233t ππππ-≤-≤, 令123t ππθ=-,即533ππθ-≤≤,所以54sin ,[,]33y ππθθ=∈- 故当32πθ=时,即22t =时,y 取得最小值,min 34sin42y π==- 故当22t =时,这一天中实验室的温度最低。
广东省广州市高二学业水平测试数学试题(含解析) 有答案

广州市高中二年级学生学业水平测试一、选择题:本大题共10小题,每小题5分. 1.已知集合M =-1,0,1{},{}x x x N ==2|,则M ÇN=()A.1{}B.0,1{}C.-1,0{}D.-1,0,1{}2.已知等比数列a n {}的公比为2,则a 4a 2值为()A. 14B.12C. 2D.43.直线l 过点1,-2(),且与直线2x +3y -1=0垂直,则l 的方程是()A. 2x +3y +4=0B.2x +3y -8=0C.3x -2y -7=0D.3x -2y -1=0 4.函数f x ()=12æèçöø÷x-x +2的零点所在的一个区间是()A.-1,0()B.0,1()C.1,2()D.2,3()5.已知非零向量与的方向相同,下列等式成立的是()6.要完成下列两项调查:(1)某社区有100户高收入家庭,210户中等收入家庭,90户低收入家庭,从中抽取100户调查消费购买力的某项指标;(2)从某中学高二年级的10名体育特长生中抽取3人调查学习负担情况,应采取的抽样方法是()A.(1)用系统抽样法,(2)用简单随机抽样法B.(1)用分层抽样法,(2)用系统抽样法C.(1)用分层抽样法,(2)用简单随机抽样法D.(1)(2)都用分层抽样法7.设x ,y 满足约束条件⎪⎩⎪⎨⎧≤-+≥-≥+,03,02,01y x x y x ,则z =x -y 的最大值为()A. 3B.1C.1-D.5- 8.某几何体的三视图及其尺寸图,则该几何体的体积为()A. 6B. 9C. 12D. 18 9.函数f x ()=12-cos 2p 4-x æèçöø÷的单调增区间是() A.2k p -p 2,2k p +p 2éëêùûú,k ÎZ B. 2k p +p 2,2k p +3p 2éëêùûú,k ÎZC.k p +p 4,k p +3p 4éëêùûú,k ÎZ D. k p -p 4,k p +p 4éëêùûú,k ÎZ 10.设a >1,b >2且ab =2a +b 则a +b 的最小值为()A.22B.22+1C.22+2D.22+3二、填空题:本大题共4小题,每小题5分,满分20分。
2010学年度上学期广州市高中二年级学生学业水平测试(必修1-5)
秘密★启用前2010学年度上学期广州市高中二年级学生学业水平测试数 学(必修)本试卷共4页. 满分150分. 考试用时120分钟.注意事项:1.答卷前,考生务必用黑色字迹钢笔或签字笔将自己的姓名和考生号填写在答题卡指定的位置上.2.选择题每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑;如需改动,用橡皮擦干净后,再选涂其它答案,答案不能答在试卷上.3.非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内的相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液. 不按以上要求作答的答案无效.4.本次考试不允许使用计算器.5.考生必须保持答题卡的整洁,考试结束后,将试卷和答题卡一并交回.一、选择题:本大题共10小题,每小题5分,满分50分. 在每小题给出的四个选项中,只有一项是符合题目要求的. 1.函数y =A .(),1-∞B .(],1-∞C .()1,+∞D .[)1,+∞ 20y -=的倾斜角为 A .6π B .3π C .23π D .56π3.已知全集{}1,2,3,4,5,6,7,8U =,集合{}2,4,6,8A =,{}1,2,3,6,7B =,则()U A B = ð A .{}2,4,6,8 B .{}1,3,7 C .{}4,8 D .{}2,64.某赛季,甲、乙两名篮球运动员都参加了7场比赛,他们所有比赛 得分的情况用如图1平均数分别为A .14、12B .13、12C .14、13D .12、145.在边长为1的正方形ABCD 内随机取一点P ,则点P 到点A 的距离小于1的概率为图1A .4πB .14π-C .8πD .18π-6.已知向量a 与b 的夹角为120,且1==a b ,则-a b 等于 A .1 BC .2D .37.有一个几何体的三视图及其尺寸如图2所示 (单位:cm ),则该几何体的表面积...为 A .212cm π B. 215cm πC. 224c m π D. 236cm π8.若23x <<,12xP ⎛⎫= ⎪⎝⎭,2log Q x =,R则P ,Q ,R 的大小关系是A .Q P R <<B .Q R P <<C .P R Q <<D .P Q R << 9.已知函数()2sin()f x x ωϕ=+0,2πωϕ⎛⎫>< ⎪⎝⎭的图像 如图3所示,则函数)(x f 的解析式是A .10()2sin 116f x x π⎛⎫=+⎪⎝⎭B .10()2sin 116f x x π⎛⎫=-⎪⎝⎭C .()2sin 26f x x π⎛⎫=+⎪⎝⎭ D .()2sin 26f x x π⎛⎫=-⎪⎝⎭10.一个三角形同时满足:①三边是连续的三个自然数;②最大角是最小角的2倍,则这个三角形最小角的余弦值为主视图6侧视图图2图3A.8 B .34 C.4D .18二、填空题:本大题共4小题,每小题5分,满分20分. 11.圆心为点()0,2-,且过点()14,的圆的方程为 . 12.如图4,函数()2x f x =,()2g x x =,若输入的x 值为3,则输出的()h x 的值为 .13.若函数()()()2213f x a x a x =-+-+是偶函数,则函数()f x 的单调递减区间为 .14.设不等式组0,02036x y x y x y -+-⎧⎪-+⎨⎪⎩≤≥≥,表示的平面区域为D ,若直线0kx y k -+=上存在区域D 上的点,则k 的取值范围是 .三、解答题:本大题共6小题,满分80分. 解答须写出文字说明、证明过程和演算步骤. 15.(本小题满分12分)在△ABC 中,角A ,B ,C 成等差数列. (1)求角B 的大小;(2)若()sin A B +=sin A 的值. 16.(本小题满分12分)某校在高二年级开设了A ,B ,C 三个兴趣小组,为了对兴趣小组活动的开展情况进行调查,用分层抽样方法从A ,B ,C 三个兴趣小组的人员中,抽取若干人组成调查(1)求x ,y 的值;图4(2)若从A ,B 两个兴趣小组抽取的人中选2人作专题发言,求这2人都来自兴趣小组B 的概率. 17.(本小题满分14分)如图5,在四棱锥P ABCD -中,底面ABCD 为正方形,PA ⊥平面ABCD ,PA AB =,点E 是PD 的中点. (1)求证:PB 平面ACE ; (2)若四面体E ACD -的体积为23,求AB 的长. 18.(本小题满分14分)已知数列{}n a 是首项为1,公比为2的等比数列,数列{}n b 的前n 项和2n S n =. (1)求数列{}n a 与{}n b 的通项公式; (2)求数列n n b a ⎧⎫⎨⎬⎩⎭的前n 项和. 19.(本小题满分14分)直线y kx b =+与圆224x y +=交于A 、B 两点,记△AOB 的面积为S (其中O 为坐标原点).(1)当0k =,02b <<时,求S 的最大值; (2)当2b =,1S =时,求实数k 的值. 20.(本小题满分14分)已知函数()213f x ax x a =+-+()a ∈R 在区间[]1,1-上有零点,求实数a 的取值范围.2010学年度广州市高中二年级学生学业水平测试数学试题参考答案及评分标准5分,满分50分.二、填空题:本大题主要考查基本知识和基本运算.共4小题,每小题5分,满分20分.11.()22225x y ++=(或224210x y y ++-=) 12.913.()0,+∞(或[)0,+∞) 14.122⎡⎤⎢⎥⎣⎦,三、解答题15.本小题主要考查解三角形、三角恒等变换等基础知识,考查运算求解能力.满分12分. 解:(1)在△ABC 中,A B C π++=,由角A ,B ,C 成等差数列,得2B A C =+.解得3B π=.(2)方法1:由()sin 2A B +=()sin 2C π-=,得sin 2C =. 所以4C π=或34C π=. 由(1)知3B π=,所以4C π=,即512A π=. 所以5sin sinsin 1246A πππ⎛⎫==+ ⎪⎝⎭sincoscossin4646ππππ=+12222=⨯+=.方法2:因为A ,B 是△ABC 的内角,且()sin 2A B +=, 所以4A B π+=或34A B π+=.由(1)知3B π=,所以34A B π+=,即512A π=.以下同方法1.方法3:由(1)知3B π=,所以sin 32A π⎛⎫+= ⎪⎝⎭即sin coscos sin332A A ππ+=.即1sin 2A A +=.sin A A .即223cos 2sin A A A =-+. 因为22cos 1sin A A =-,所以()2231sin 2sin A A A -=-+.即24sin 10A A --=.解得sin 4A =. 因为角A 是△ABC 的内角,所以sin 0A >.故sin A =.16.本小题主要考查统计与概率等基础知识,考查数据处理能力.满分12分. 解:(1)由题意可得,3243648x y==, 解得2x =,4y =.(2)记从兴趣小组A 中抽取的2人为1a ,2a ,从兴趣小组B 中抽取的3人为1b ,2b ,3b ,则从兴趣小组A ,B 抽取的5人中选2人作专题发言的基本事件有()12,a a ,()11,a b ,()12,a b ,()13,a b ,()21,a b ,()22,a b ,()23,a b ,()12,b b ,()13,b b ,()23,b b共10种.设选中的2人都来自兴趣小组B 的事件为X ,则X 包含的基本事件有()12,b b ,()13,b b ,()23,b b 共3种.所以()310P X =. 故选中的2人都来自兴趣小组B 的概率为310.17.本小题主要考查直线与平面的位置关系、体积等基础知识,考查空间想象能力、推理论证能力和运算求解能力.满分14分.(1)证明:连接BD 交AC 于点O ,连接EO ,因为ABCD 是正方形,所以点O 是BD 的中点.因为点E 是PD 的中点,所以EO 是△DPB 的中位线. 所以PB EO .因为EO ⊂平面ACE ,PB ⊄平面ACE , 所以PB 平面ACE .(2)解:取AD 的中点H ,连接EH , 因为点E 是PD 的中点,所以EH PA . 因为PA ⊥平面ABCD ,所以EH ⊥平面ABCD . 设AB x =,则PA AD CD x ===,且1122EH PA x ==. 所以13E ACD ACD V S EH -∆=⨯ 1132AD CD EH =⨯⨯⨯⨯3111262123x x x x === . 解得2x =.故AB 的长为2.18.本小题主要考查等差数列、等比数列等基础知识,考查运算求解能力和推理论证能力.满分14分. 解:(1)因为数列{}n a 是首项为1,公比为2的等比数列,所以数列{}n a 的通项公式为12n n a -=. 因为数列{}n b 的前n 项和2n S n =.所以当2n ≥时,1n n n b S S -=-()22121n n n =--=-,当1n =时,111211b S ===⨯-, 所以数列{}n b 的通项公式为21n b n =-. (2)由(1)可知,1212n n n b n a --=. 设数列n n b a ⎧⎫⎨⎬⎩⎭的前n 项和为n T , 则 213572321124822n n n n n T ----=++++++ , ① 即 111357232122481622n n n n n T ---=++++++ , ② ①-②,得2111112111224822n n nn T --=++++++-11121211212n nn -⎛⎫- ⎪-⎝⎭=+-- 2332nn +=-, 所以12362n n n T -+=-. 故数列n n b a ⎧⎫⎨⎬⎩⎭的前n 项和为12362n n -+-.19.本小题主要考查直线与圆、基本不等式等基础知识,考查运算求解能力.满分14分. 解:(1)当0k =时,直线方程为y b =,设点A 的坐标为1()x b ,,点B 的坐标为2()x b ,,由224x b +=,解得12x =,,所以21AB x x =-=所以12S AB b == 22422b b +-=≤.当且仅当b =b =S 取得最大值2.(2)设圆心O 到直线2y kx =+的距离为d,则d =.因为圆的半径为2R =,所以2AB ===.于是241121k S AB d k =⨯===+,即2410k k -+=,解得2k =故实数k的值为2+22-2-20.本小题主要考查二次函数、函数的零点等基础知识,考查运算求解能力,以及分类讨论的数学思想方法.满分14分. 解法1:当0a =时,()1f x x =-,令()0f x =,得1x =,是区间[]1,1-上的零点.当0a ≠时,函数()f x 在区间[]1,1-上有零点分为三种情况: ①方程()0f x =在区间[]1,1-上有重根, 令()14130a a ∆=--+=,解得16a =-或12a =. 当16a =-时,令()0f x =,得3x =,不是区间[]1,1-上的零点. 当12a =时,令()0f x =,得1x =-,是区间[]1,1-上的零点. ②若函数()y f x =在区间[]1,1-上只有一个零点,但不是()0f x =的重根, 令()()()114420f f a a -=-≤,解得102a <≤. ③若函数()y f x =在区间[]1,1-上有两个零点,则()()⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧≥≥<-<->++-=∆>.01-,01,1211,01412,02f f a a a a 或()()⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧≤≤<-<->++-=∆<.01-,01,1211,01412,02f f a a a a 解得a ∈∅.综上可知,实数a 的取值范围为10,2⎡⎤⎢⎥⎣⎦.解法2:当0a =时,()1f x x =-,令()0f x =,得1x =,是区间[]1,1-上的零点.当0a ≠时,()213f x ax x a =+-+在区间[]1,1-上有零点⇔()231x a x +=-在区间[]1,1-上有解⇔213xa x -=+在区间[]1,1-上有解. 问题转化为求函数213xy x -=+在区间[]1,1-上的值域.设1t x =-,由[]1,1x ∈-,得[]0,2t ∈.且()2013ty t =≥-+.而()214132ty t t t==-++-. 设()4g t t t=+,可以证明当(]0,2t ∈时,()g t 单调递减. 事实上,设1202t t <<≤,则()()()()121212121212444t t t t g t g t t t t t t t --⎛⎫⎛⎫-=+-+= ⎪ ⎪⎝⎭⎝⎭,由1202t t <<≤,得120t t -<,1204t t <<,即()()120g t g t ->. 所以()g t 在(]0,2t ∈上单调递减. 故()()24g t g ≥=. 所以()1122y g t =≤-.故实数a 的取值范围为10,2⎡⎤⎢⎥⎣⎦.。
2010年高中数学必修1至必修5综合试题
2010年高二学业水平测试模拟试题 数 学 2010.12.一.选择题:本大题共10小题, 每小题5分,满分50分.1.求值: =210cos ( ).A 21.B 22- .C 23- .D 23 0222=-y x +的倾斜角是( ).A 45 .B 135 .C 120 .D 150)1,2(),1,1(-=-=b a,则=-a 2( ).A 3 .B 4 .C 5 .D 64.设集合{}31<<-=x x A ,{}022>-+x x x B =,则=B A ( ).A {}11<<-x x .B {}12->-<x x x 或 .C {}31<<x x .D {}32<<x x -{}n a 中,,12=a 834+=S S ,则=6a ( ).A 16 .B 64 .C 32 .D 486.如图,ABC ∆是边长为3的正三角形,现随机向圆所在区域内 投掷一点,则这点恰好落在ABC ∆所在区域内的概率是( ).Aπ433 .B 6π.Cπ233 .D π833 α是第四象限角,且33sin -=α,则=α2tan ( ) .A 22- .B 23- .C 22 .D 248.已知函数xx x f 1log )(2-=的零点所在的区间为( ) .A ()0,1- .B )1,0( .C )21(, .D ()32,是否? 0>x12+=x y输入x开始x y sin = 结束输出y9.设y x ,满足⎪⎩⎪⎨⎧≤-+≤+-≥0632010y x y x x ,则y x +的最大值是( ).A 0 .B 1 .C 2 .D511 10.设,0,0>>b a 直线02=-+y b x a 与圆122=+y x 相切,则ba 1lg 1lg +的最小值是( ).A 0 .B 1 .C 2 .D 3-二.填空题:本大题共10小题, 每小题5分,满分50分. 11.在ABC ∆中,4,3,2===c b a ,则=C cos ; 12.抽样检测后的产品净重(单位:克)数据绘制的频率分布直方图,其中产品净重的范围是[96,106], 样本数据分组为[96,98),[98,100),[100,102),[102,104),[104,106],已知样本中产品净重小于 100克的个数是36,则样本中净重大于或等于98克 并且小于104克的产品的个数是 ;13.某几何体的三视图如右图所示, 那么这个几何体的体积是 ;14.定义在实数集R 上的函数)(x f y =,其对应关系 由程序框图(如图)给出,则=)41(log2f , )(x f 的解析式是 .三.解答题:本大题共6小题,,满分80分.96 98 100 102 104 1060.1500.1250.0750.050克频率/组距2 22正视图2 22俯视图侧视图15.(本小题满分12分) 已知函数x x x f cos sin )(=,R x ∈. (1)求)(x f 的最大值和最小正周期. (2)若31)(=αf ,求α4cos 的值.16.(本小题满分13分) 一个袋中装有3个红球1个黑球,现随机从袋中摸出2球.求: (1) 摸出的2球全是红球的概率; (2) 摸出的2球颜色不同的概率.17. (本小题满分13分) 已知数列{}n a 是等差数列,其前n 项和是n S ,44=a .(1)求7S ; (2)若105=S ,求数列{}n a 的通项公式.18. (本小题满分14分) 如图,ABC ∆是正三角形,CD AE 和都垂直于平面ABC ,42===CD AB AE ,F 是BE 的中点.(1)求证://DF 平面ABC ; (2)求证:DE AF ⊥;(3)求这个几何体的体积.19. (本小题满分14分) 已知函数x x ax x f 21)(2-+=,且23)21(=f . ABCDFE(1)求a 的值并判断)(x f 奇偶性; (2)用定义证明)(x f 在),0(+∞上的单调性;(3)对于任意()+∞∈,1x ,不等式)2(log (2+-<b x x f )恒成立,求b 的取值范围..,(0)3(;,11)2(;)1(.,)2,1()1,1(,06:14.(2022请说明理由的值;若不存在,若存在,求为原点)?,满足是否存在圆的值求若的取值范围求实数两点交于两点且与圆和过直线已知圆分)本小题满分m O OB OA C m AB m B A C N M l m y x y x C =⋅=-=+-++。
2010学年度广东省广州市高中二年级学生学业水平测试及答案
12010学年度广州市高中二年级学生学业水平测试英 语本试卷分四部分,共12页,满分150分。
考试时间120分钟。
注意事项:1.答卷前,考生务必在答题卡上用黑色字迹的钢笔或签字笔填写自己的测试证号和姓名;填写考区考场室号、座位号,再用2B 铅笔把对应的两个号码涂黑。
2.选择题每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑;如需改动,用橡皮擦干净后,再选涂其他答案;不能答在试卷上。
3.非选择题必须用黑色字迹的钢笔或签字笔作答。
答案必须写在答题卡各题目指定区域内的相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔、圆珠笔和涂改液。
不按以上要求作答的答案无效。
4.考生必须保持答题卡的整洁,考试结束时,将试卷和答题卡一并交回。
II 语言知识及应用(共两节,满分 45 分)第一节完形填空(共15小题,每小题 2 分,满分 30 分)阅读下面短文,掌握其大意,然后从 16 一 30 各题所给的 A 、 B 、 C 和 D 项中,选出最佳选项,并在答题卡上将该项涂黑。
Are you good at understanding body language? You're probably ___16____than you think,according to the experts.What is body language exactly? __17___, it's signals made by body movement, gesture andeye movement.Body language can actually __18__ a lot of information, and it can help us ___19___ aperson's attitude and state of mind. In fact, studies have suggested that only 7% of communicationinvolves actual __20___, while 55% is body language and 38% is intonation (语调).Many examples of body language are ___21___ to identify. In most cultures, smiling showshappiness and a(an) ___22___ attitude. So, when someone smiles at you, they're telling you thatthey are open, interested and happy to ___23___. But if someone puts their arms across their chest,they don't want to communicate with you. And if this is combined with a serious facial expression,you should ___24___ because this can mean anger.It's very difficult to ___25__ with your body language. For example, when people pretend to___26___, they only use the muscles around the mouth and the top half of their faceremains__27___. However, a true smile involves the ___28___ face; including the cheeks andeyes. Research shows that most people can see whether a smile is true by looking at the top half ofthe ___29___.One of the great advantages with body language is that you don't have to ___30___ it youalready know it, even if you don't know you do.16. A.stronger B.better C.more interested D.more careful17. A. Basically B. Suddenly C. Truly D. Surprisingly218. A.read B.destroy C.receive municate19. A.hide B.create C.understand D.like20. A.words B.signals C.meaning D.gesture21. A.sure B.impossible C.easy D.hard22. A.surprised B.friendly C.curious D.angry23. A.operate B.stay C.go D.talk24. A.leave out B.watch out C.speak out D.turn out25. A.begin B.move C.answer D.lie26. A.smile B.speak C.look D.reply27. A.untouched B.unnoticed C.unchanged D.uncovered28. A.partial B.whole ual D.happy29. A.mouth B.cheek C.face D.body30. A.like B.do C.mean D.learn第二节 语法填空(共 10 小题,第小题 1.5 分,满分15分)阅读下面短文,按照句子结构的语法性和上下文连贯的要求,在空格处填入一个适当的词或使用括号中词语的正确形式填空,并将答案填写在答题卜标号为 31 一 40 的相应位置上。
2010年广州市普通高中毕业班综合测试(一)理数
2010年广州市普通高中毕业班综合测试(一)数 学(理科)2010.3本试卷共4页,21小题, 满分150分. 考试用时120分钟. 注意事项:1.答卷前,考生务必用2B 铅笔在“考生号”处填涂考生号,用黑色字迹钢笔或签字笔将自己所在的市、县/区、学校,以及自己的姓名和考生号、试室号、座位号填写在答题卡上.用2B 铅笔将试卷类型(A )填涂在答题卡相应位置上.2.选择题每小题选出答案后,用2B 铅笔把答题卡上对应题目选项的答案信息点涂黑,如需改动,用橡皮擦干净后,再选涂其他答案,答案不能答在试卷上. 3.非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内的相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液.不按以上要求作答的答案无效.4.作答选做题时,请先用2B 铅笔填涂选做题的题(或题组号)对应的信息点,再作答.漏涂、错涂、多涂的,答案无效.5.考生必须保持答题卡的整洁.考试结束后,将试卷和答题卡一并交回.参考公式:球的体积公式343V R π=,其中R 是球的半径.一、选择题:本大题共8小题,每小题5分,满分40分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1.复数()3i 1i - 的共轭复数....是 A .3i -+B .3i --C .3i +D .3i -2.设一地球仪的球心为空间直角坐标系的原点O ﹐球面上有两个点A ,B 的坐标分别为()1,2,2A ,()2,2,1B -,则AB =A .18B .12C.D.3.已知集合{}1,1A =-,{}10B x ax =+=,若B A ⊆,则实数a 的所有可能取值的集合为A .{}1-B .{}1C .{}1,1-D .{}1,0,1-4.若关于x 的不等式1x a -<的解集为()1,3,则实数a 的值为A .2B .1C .1-D .2-5.已知p :直线a 与平面α内无数条直线垂直,q :直线a 与平面α垂直.则p 是q 的A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件 6.根据《中华人民共和国道路交通安全法》规定:车辆驾驶员血液酒精浓度在20—80 mg/100ml (不含80)之间,属于酒后驾车,处暂扣一个月以上三个月以下驾驶证,并处200元以上500元以下罚款;血液酒精浓度在80mg/100ml (含80)以上时,属醉酒驾车,处十五日以下拘留和暂扣三个月以上六个月以下驾驶证,并处500元以上2000元以下罚款. 据《法制晚报》报道,2009年8月15日至8月28日,全国查处酒后驾车和醉酒驾车共 28800人,如图1是对这28800人酒后驾车血液中酒精含量进行检测所得结果的频率分布直方图,则属于醉酒驾车的人数约为A .2160B .2880C .4320D .86407.在ABC △中,点P 在BC 上,且2BP PC = ,点Q 是AC 的中点,若()4,3PA = ,()1,5PQ =,则BC =A .()2,7-B .()6,21-C .()2,7-D .()6,21-8.如图2所示的三角形数阵叫“莱布尼兹调和三角形”,它们是由整数的倒数组成的,第n 行有n 个数且两端的数均为1n ()2n ≥,每个数是它下一行左右相邻两数的和,如111122=+,111236=+,1113412=+,…, 则第10行第4个数(从左往右数)为A .11260 B .1840 C .1504D .1360二、填空题:本大题共7小题,考生作答6小题,每小题5分,满分30(一)必做题(9~13题)9.在等比数列{}n a 中,11a =,公比2q =,若{}n a 前n 项和127n S =则n 的值为 .10.某算法的程序框如图3所示,若输出结果为12,则输入的实数x 的值是________.(注:框图中的赋值符号“=”也可以写成 “←”或“:=”)1112 12 13 16 1314 112 112 1415 120 130120 15………………………………………图211.有一个底面半径为1、高为2的圆柱,点O 为这个圆柱底面圆的圆心,在这个圆柱内随机取一点P ,则点P 到点O 的距离大于1的概率为 . 12.已知函数()()21,1,log ,1.a a x x f x x x --⎧⎪=⎨>⎪⎩≤若()f x 在(),-∞+∞上单调递增,则实数a 的取值范围为 . 13.如图4,点O 为正方体ABCD A B C D ''''-的中心,点E 为面B BCC ''的中心,点F 为B C ''的中点,则空间四边形D OEF '在该正方体的面上的正投影可能是 (填出所有可能的序号).(二)选做题(14~15题,考生只能从中选做一题) 14.(几何证明选讲选做题)如图5,AB 是半圆O 的直径,点C 在 半圆上,CD AB ⊥,垂足为D ,且5AD DB =,设COD θ∠=, 则tan θ的值为 . 15.(坐标系与参数方程选做题)在极坐标系中,已知两点A 、B 的极坐标分别为3,3π⎛⎫ ⎪⎝⎭,4,6π⎛⎫⎪⎝⎭,则△AOB (其中O 为极点)的面积 为 .三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤. 16.(本小题满分12分) 已知函数()sin cos cos sin f x x x ϕϕ=+(其中x ∈R ,0ϕπ<<). (1)求函数()f x 的最小正周期; (2)若函数24y f x π⎛⎫=+ ⎪⎝⎭的图像关于直线6x π=对称,求ϕ的值.17.(本小题满分12分)某公司为庆祝元旦举办了一个抽奖活动,现场准备的抽奖箱里放置了分别标有数字1000、800﹑600、0的四个球(球的大小相同).参与者随机从抽奖箱里摸取一球(取后即放回),公司即赠送与此球上所标数字等额的奖金(元),并规定摸到标有数字0的球时可以再摸一次﹐但是所得奖金减半(若再摸到标有数字0的球就没有第三次摸球机会),求一个参与抽奖活动的人可得奖金的期望值是多少元. 18.(本小题满分14分)如图6,正方形ABCD 所在平面与圆O 所在平面相交于CD ,线段CD 为圆O 的弦,AE 垂直于圆O 所在平面,垂足E 是圆O 上异于C 、D 的点,3AE =,圆O 的直径为9. (1)求证:平面ABCD ⊥平面ADE ;(2)求二面角D BC E --的平面角的正切值.图5A CD O ① ② ③ ④ 图4 A BC D E FOA 'B 'C 'D '19.(本小题满分14分)已知a ∈R ,函数()ln 1af x x x=+-,()()ln 1x g x x e x =-+(其中e 为自然对数的底数). (1)求函数()f x 在区间(]0,e 上的最小值;(2)是否存在实数(]00,x e ∈,使曲线()y g x =在点0x x =处的切线与y 轴垂直? 若存在,求出0x 的值;若不存在,请说明理由.20.(本小题满分14分)已知点()0,1F ,直线l :1y =-,P 为平面上的动点,过点P 作直线l 的垂线,垂足为Q ,且QP QF FP FQ =.(1)求动点P 的轨迹C 的方程;(2)已知圆M 过定点()0,2D ,圆心M 在轨迹C 上运动,且圆M 与x 轴交于A 、B 两点,设1DA l =,2DB l =,求1221l l l l +的最大值.21.(本小题满分14分)设数列{}n a 的前n 项和为n S ,且对任意的*n ∈N ,都有0n a >,n S =(1)求1a ,2a 的值;(2)求数列{}n a 的通项公式n a ;(3)证明:21221n n nn n n a a a +-+≥.2010年广州市普通高中毕业班综合测试(一)数学(理科)试题参考答案及评分标准说明:1.参考答案与评分标准指出了每道题要考查的主要知识和能力,并给出了一种或几种解法供参考,如果考生的解法与参考答案不同,可根据试题主要考查的知识点和能力比照评分标准给以相应的分数.2.对解答题中的计算题,当考生的解答在某一步出现错误时,如果后继部分的解答未改变该题的内容和难度,可视影响的程度决定后继部分的得分,但所给分数不得超过该部分正确解答应得分数的一半;如果后继部分的解答有较严重的错误,就不再给分.3.解答右端所注分数,表示考生正确做到这一步应得的累加分数.4.只给整数分数,选择题和填空题不给中间分.二、填空题:30分.其中14~15题是选做题,考生只能选做一题.9.7 1011.2312.(]2,313.①②③1415.3三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤.16.(本小题满分12分)(本小题主要考查三角函数性质和三角函数的基本关系等知识,考查化归与转化的数学思想方法,以及运算求解能力)(1)解:∵()()sinf x xϕ=+,∴函数()f x的最小正周期为2π.(2)解:∵函数2sin244y f x xππϕ⎛⎫⎛⎫=+=++⎪ ⎪⎝⎭⎝⎭,又siny x=的图像的对称轴为2x kππ=+(k∈Z),令242x kππϕπ++=+,将6xπ=代入,得12kπϕπ=-(k∈Z).∵0ϕπ<<,∴1112πϕ=.17.(本小题满分12分)(本小题主要考查随机变量的分布列、数学期望等知识,考查或然与必然的数学思想方法,以及数据处理能力、运算求解能力和应用意识)解:设ξ表示摸球后所得的奖金数,由于参与者摸取的球上标有数字1000,800,600,0,当摸到球上标有数字0时,可以再摸一次,但奖金数减半,即分别为500,400,300,0.则ξ的所有可能取值为1000,800,600,500,400,300,0.依题意得:()()()110008006004P P Pξξξ======,()()()()1500400300016P P P Pξξξξ========,则ξ的分布列为所以所求期望值为()()1110008006005004003000416Eξ=++++++675=元.答:一个参与抽奖活动的人可得奖金的期望值是675元.18.(本小题满分14分)(本小题主要考查空间线面关系、空间向量及坐标运算等知识,考查数形结合、化归与转化的数学思想方法,以及空间想象能力、推理论证能力和运算求解能力)(1)证明:∵AE垂直于圆O所在平面,CD在圆O所在平面上,∴AE⊥CD.在正方形ABCD中,CD AD⊥,∵AD AE A=,∴CD⊥平面ADE.∵CD⊂平面ABCD,∴平面ABCD⊥平面ADE.(2)解法1:∵CD⊥平面ADE,DE⊂平面ADE,∴CD DE⊥.∴CE为圆O的直径,即9CE=.设正方形ABCD的边长为a,在Rt△CDE中,222281DE CE CD a=-=-,在Rt△ADE中,22229DE AD AE a=-=-,由22819a a-=-,解得,a=∴6DE==.过点E 作EF AD ⊥于点F ,作FG AB 交BC 于点G ,连结GE , 由于AB ⊥平面ADE ,EF ⊂平面ADE , ∴EF AB ⊥. ∵AD AB A = ,∴EF ⊥平面ABCD . ∵BC ⊂平面ABCD , ∴BC EF ⊥.∵BC FG ⊥,EF FG F = ,∴BC ⊥平面EFG . ∵EG ⊂平面EFG , ∴BC EG ⊥.∴FGE ∠是二面角D BC E --的平面角.在Rt △ADE中,AD =3AE =,6DE =, ∵AD EF AE DE ⋅=⋅,∴5AE DE EF AD ⋅===. 在Rt △EFG中,FG AB ==∴2tan 5EF EGF FG ∠==. 故二面角D BC E --的平面角的正切值为25. 解法2:∵CD ⊥平面ADE ,DE ⊂平面ADE , ∴CD DE ⊥.∴CE 为圆O 的直径,即9CE =. 设正方形ABCD 的边长为a ,在Rt △CDE 中,222281DE CE CD a =-=-, 在Rt △ADE 中,22229DE AD AE a =-=-, 由22819a a -=-,解得,a =∴6DE ==.以D 为坐标原点,分别以ED 、CD 所在的直线为x 轴、y 轴建立如图所示的空间直角坐标系,则()0,0,0D ,()6,0,0E -,()0,C -,()6,0,3A -,()6,B --.设平面ABCD 的法向量为()1111,,x y z =n ,则110,0.DA DC ⎧=⎪⎨=⎪⎩ n n即111630,0.x z -+=⎧⎪⎨-=⎪⎩ 取11x =,则()11,0,2=n 是平面ABCD 的一个法向量. 设平面BCE 的法向量为()2222,,x y z =n ,则220,0.EB EC ⎧=⎪⎨=⎪⎩n n即222230,60.z x ⎧-+=⎪⎨-=⎪⎩ 取22y =,则22,=n 是平面ABCD 的一个法向量.∵()1212121,0,2cos ,===⋅ n n n n n n ,∴12sin ,=n n . ∴122tan ,5=n n . 故二面角D BC E --的平面角的正切值为25.GFxyz19.(本小题满分14分)(本小题主要考查函数与导数等知识,考查分类讨论,化归与转化的数学思想方法,以及推理论证能力和运算求解能力)(1)解:∵()ln 1a f x x x =+-,∴221()a x af x x x x-'=-+=. 令()0f x '=,得x a =.①若a ≤0,则()0f x '>,()f x 在区间(]0,e 上单调递增,此时函数()f x 无最小值. ②若0a e <<,当()0,x a ∈时,()0f x '<,函数()f x 在区间()0,a 上单调递减, 当(],x a e ∈时,()0f x '>,函数()f x 在区间(],a e 上单调递增, 所以当x a =时,函数()f x 取得最小值ln a .③若a e ≥,则()0f x '≤,函数()f x 在区间(]0,e 上单调递减, 所以当x e =时,函数()f x 取得最小值ae. 综上可知,当a ≤0时,函数()f x 在区间(]0,e 上无最小值;当0a e <<时,函数()f x 在区间(]0,e 上的最小值为ln a ; 当a e ≥时,函数()f x 在区间(]0,e 上的最小值为a e. (2)解:∵()()ln 1xg x x e x =-+,(]0,x e ∈,∴ ()()()()ln 1ln 11x xg x x e x e '''=-+-+()1ln 11ln 11x x x e x e x e x x ⎛⎫=+-+=+-+ ⎪⎝⎭. 由(1)可知,当1a =时,1()ln 1f x x x=+-. 此时()f x 在区间(]0,e 上的最小值为ln10=,即1ln 10x x+-≥. 当(]00,x e ∈,00x e >,001ln 10x x +-≥, ∴00001()ln 1110x g x x e x ⎛⎫'=+-+> ⎪⎝⎭≥.曲线()y g x =在点0x x =处的切线与y 轴垂直等价于方程0()0g x '=有实数解.而()00g x '>,即方程0()0g x '=无实数解.故不存在(]00,x e ∈,使曲线()y g x =在点0x x =处的切线与y 轴垂直.20.(本小题满分14分)(本小题主要考查圆、抛物线、基本不等式等知识,考查数形结合、化归与转化、函数与方程的数学思想方法,以及推理论证能力和运算求解能力) (1)解:设(),P x y ,则(),1Q x -,∵QP QF FP FQ =,∴()()()()0,1,2,1,2y x x y x +-=-- . 即()()22121y x y +=--,即24x y =,所以动点P 的轨迹C 的方程24x y =.(2)解:设圆M 的圆心坐标为(),M a b ,则24a b =. ①圆M 的半径为MD =.圆M 的方程为()()()22222x a y b a b -+-=+-. 令0y =,则()()22222x a b a b -+=+-,整理得,22440x ax b -+-=. ② 由①、②解得,2x a =±. 不妨设()2,0A a -,()2,0B a +, ∴1l =2l =.∴22212122112l l l l l l l l ++==== ③ 当0a ≠时,由③得,1221l l l l +=.当且仅当a =±当0a =时,由③得,12212l ll l +=.故当a =±1221l l l l +的最大值为 21.(本小题满分14分)(本小题主要考查数列、不等式、二项式定理等知识,考查化归与转化的数学思想方法,以及抽象概括能力、运算求解能力和创新意识) (1)解:当1n =时,有11a S ==由于0n a >,所以11a =. 当2n =时,有2S =12a a +=,将11a =代入上式,由于0n a >,所以22a =. (2)解:由n S =得()23331212n n a a a a a a +++=+++ , ① 则有()23333121121n n n n a a a a a a a a ++++++=++++ . ② ②-①,得()()223112112n n n n a a a a a a a a ++=++++-+++ ,由于0n a >,所以()211212n n n a a a a a ++=++++ . ③同样有()21212n n n a a a a a -=++++ ()2n ≥, ④③-④,得2211n n n n a a a a ++-=+. 所以11n n a a +-=.由于211a a -=,即当n ≥1时都有11n n a a +-=,所以数列{}n a 是首项为1,公差为1的等差数列. 故n a n =.(3)证明1:由于()0122331C C C C nn n n n x x x x +=++++ ,()0122331C C C C nn n n n x x x x -=-+-+ ,所以()()13355112C 2C 2C nnn n n x x x x x +--=+++ .即()()33551122C 2C n nn n x x nx x x +---=++ .令12x n =,则有11111022n nn n ⎛⎫⎛⎫+--- ⎪ ⎪⎝⎭⎝⎭≥.即1111122n nn n ⎛⎫⎛⎫++- ⎪ ⎪⎝⎭⎝⎭≥, 即()()()21221nnnn n n ++-≥故21221n n n n n n a a a +-+≥.证明2:要证21221n n n n n n a a a +-+≥,只需证()()()21221n n nn n n ++-≥,只需证1111122n nn n ⎛⎫⎛⎫++- ⎪ ⎪⎝⎭⎝⎭≥,只需证1111122n nn n ⎛⎫⎛⎫+-- ⎪ ⎪⎝⎭⎝⎭≥.由于111122n nn n ⎛⎫⎛⎫+-- ⎪ ⎪⎝⎭⎝⎭232301230123111111C C C C C C C C 222222n n n n n n n n n n n n n n ⎡⎤⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫=++++-++⎢⎥⎢⎥ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎢⎥⎢⎥⎣⎦⎣⎦ --351351112C C C 222n n n n n n ⎡⎤⎛⎫⎛⎫⎛⎫=+++⎢⎥ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎢⎥⎣⎦35351112C C 122n n n n ⎡⎤⎛⎫⎛⎫=+++⎢⎥ ⎪ ⎪⎝⎭⎝⎭⎢⎥⎣⎦≥.因此原不等式成立.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
秘密★启用前2010学年度上学期广州市高中二年级学生学业水平测试数 学(必修)本试卷共4页. 满分150分. 考试用时120分钟.注意事项:1.答卷前,考生务必用黑色字迹钢笔或签字笔将自己的姓名和考生号填写在答题卡指定的位置上.2.选择题每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑;如需改动,用橡皮擦干净后,再选涂其它答案,答案不能答在试卷上.3.非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内的相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液. 不按以上要求作答的答案无效.4.本次考试不允许使用计算器.5.考生必须保持答题卡的整洁,考试结束后,将试卷和答题卡一并交回.一、选择题:本大题共10小题,每小题5分,满分50分. 在每小题给出的四个选项中,只有一项是符合题目要求的. 1.函数y =A .(),1-∞B .(],1-∞C .()1,+∞D .[)1,+∞ 20y -=的倾斜角为 A .6π B .3π C .23π D .56π3.已知全集{}1,2,3,4,5,6,7,8U =,集合{}2,4,6,8A =,{}1,2,3,6,7B =,则()UA B =ðA .{}2,4,6,8B .{}1,3,7C .{}4,8D .{}2,64.某赛季,甲、乙两名篮球运动员都参加了7场比赛,他们所有比赛 得分的情况用如图1平均数分别为A .14、12B .13、12C .14、13D .12、145.在边长为1的正方形ABCD 内随机取一点P ,则点P 到点A 的距离小于1的概率为 A .4π B .14π- C .8π D .18π-图16.已知向量a 与b 的夹角为120,且1==a b ,则-a b 等于 A .1 BC .2D .37.有一个几何体的三视图及其尺寸如图2所示 (单位:cm ),则该几何体的表面积...为 A .212cm π B. 215cm πC. 224c m π D. 236cm π8.若23x <<,12xP ⎛⎫= ⎪⎝⎭,2log Q x =,R则P ,Q ,R 的大小关系是A .Q P R <<B .Q R P <<C .P R Q <<D .P Q R << 9.已知函数()2sin()f x x ωϕ=+0,2πωϕ⎛⎫>< ⎪⎝⎭的图像 如图3所示,则函数)(x f 的解析式是A .10()2sin 116f x x π⎛⎫=+⎪⎝⎭B .10()2sin 116f x x π⎛⎫=-⎪⎝⎭C .()2sin 26f x x π⎛⎫=+⎪⎝⎭ D .()2sin 26f x x π⎛⎫=-⎪⎝⎭10.一个三角形同时满足:①三边是连续的三个自然数;②最大角是最小角的2倍,则这个三角形最小角的余弦值为AB .34 CD .18主视图侧视图图2图3二、填空题:本大题共4小题,每小题5分,满分20分. 11.圆心为点()0,2-,且过点()14,的圆的方程为 . 12.如图4,函数()2x f x =,()2g x x =,若输入的x 值为3,则输出的()h x 的值为 .13.若函数()()()2213f x a x a x =-+-+是偶函数,则函数()f x 的单调递减区间为 .14.设不等式组0,02036x y x y x y -+-⎧⎪-+⎨⎪⎩≤≥≥,表示的平面区域为D ,若直线0kx y k -+=上存在区域D 上的点,则k 的取值范围是 .三、解答题:本大题共6小题,满分80分. 解答须写出文字说明、证明过程和演算步骤. 15.(本小题满分12分)在△ABC 中,角A ,B ,C 成等差数列. (1)求角B 的大小;(2)若()sin 2A B +=,求sin A 的值. 16.(本小题满分12分)某校在高二年级开设了A ,B ,C 三个兴趣小组,为了对兴趣小组活动的开展情况进行调查,用分层抽样方法从A ,B ,C 三个兴趣小组的人员中,抽取若干人组成调查小组,有关数据见下表(单位:人)(1)求x ,y 的值;(2)若从A ,B 两个兴趣小组抽取的人中选2人作专题发言,求这2人都来自兴趣小组B 的概率.图4平面ACE E ACD -的体积为 18.(本小题满分14分)已知数列{}n a 是首项为1,公比为2的等比数列,数列{}n b 的前n 项和2n S n =. (1)求数列{}n a 与{}n b 的通项公式; (2)求数列n n b a ⎧⎫⎨⎬⎩⎭的前n 项和.19.(本小题满分14分)直线y kx b =+与圆224x y +=交于A 、B 两点,记△AOB 的面积为S (其中O 为坐标原点).(1)当0k =,02b <<时,求S 的最大值; (2)当2b =,1S =时,求实数k 的值. 20.(本小题满分14分)已知函数()213f x ax x a =+-+()a ∈R 在区间[]1,1-上有零点,求实数a 的取值范围.2010学年度广州市高中二年级学生学业水平测试数学试题参考答案及评分标准5分,满分50分.二、填空题:本大题主要考查基本知识和基本运算.共4小题,每小题5分,满分20分.11.()22225x y ++=(或224210x y y ++-=) 12.913.()0,+∞(或[)0,+∞) 14.122⎡⎤⎢⎥⎣⎦,三、解答题15.本小题主要考查解三角形、三角恒等变换等基础知识,考查运算求解能力.满分12分. 解:(1)在△ABC 中,A B C π++=,由角A ,B ,C 成等差数列,得2B A C =+.解得3B π=.(2)方法1:由()sin 2A B +=()sin 2C π-=,得sin 2C =. 所以4C π=或34C π=. 由(1)知3B π=,所以4C π=,即512A π=. 所以5sin sinsin 1246A πππ⎛⎫==+ ⎪⎝⎭sincoscossin4646ππππ=+12222=⨯+=.方法2:因为A ,B 是△ABC 的内角,且()sin 2A B +=, 所以4A B π+=或34A B π+=.由(1)知3B π=,所以34A B π+=,即512A π=. 以下同方法1.方法3:由(1)知3B π=,所以sin 32A π⎛⎫+= ⎪⎝⎭即sin coscos sin332A A ππ+=.即1sin 2A A +=.sin A A .即223cos 2sin A A A =-+. 因为22cos 1sin A A =-,所以()2231sin 2sin A A A -=-+.即24sin 10A A --=.解得sin 4A =. 因为角A 是△ABC 的内角,所以sin 0A >.故sin A =.16.本小题主要考查统计与概率等基础知识,考查数据处理能力.满分12分. 解:(1)由题意可得,3243648x y==, 解得2x =,4y =.(2)记从兴趣小组A 中抽取的2人为1a ,2a ,从兴趣小组B 中抽取的3人为1b ,2b ,3b ,则从兴趣小组A ,B 抽取的5人中选2人作专题发言的基本事件有()12,a a ,()11,a b ,()12,a b ,()13,a b ,()21,a b ,()22,a b ,()23,a b ,()12,b b ,()13,b b ,()23,b b 共10种.设选中的2人都来自兴趣小组B 的事件为X ,则X 包含的基本事件有()12,b b ,()13,b b ,()23,b b 共3种.所以()310P X =. 故选中的2人都来自兴趣小组B 的概率为310.17.本小题主要考查直线与平面的位置关系、体积等基础知识,考查空间想象能力、推理论证能力和运算求解能力.满分14分.(1)证明:连接BD 交AC 于点O ,连接EO ,因为ABCD 是正方形,所以点O 是BD 的中点.因为点E 是PD 的中点,所以EO 是△DPB 的中位线. 所以PBEO .因为EO ⊂平面ACE ,PB ⊄平面ACE , 所以PB平面ACE .(2)解:取AD 的中点H ,连接EH , 因为点E 是PD 的中点,所以EHPA .因为PA ⊥平面ABCD ,所以EH ⊥平面ABCD . 设AB x =,则PA AD CD x ===,且1122EH PA x ==. 所以13E ACD ACD V S EH -∆=⨯ 1132AD CD EH =⨯⨯⨯⨯3111262123x x x x ===. 解得2x =.故AB 的长为2.18.本小题主要考查等差数列、等比数列等基础知识,考查运算求解能力和推理论证能力.满分14分. 解:(1)因为数列{}n a 是首项为1,公比为2的等比数列,所以数列{}n a 的通项公式为12n n a -=. 因为数列{}n b 的前n 项和2n S n =.所以当2n ≥时,1n n n b S S -=-()22121n n n =--=-,当1n =时,111211b S ===⨯-, 所以数列{}n b 的通项公式为21n b n =-.(2)由(1)可知,1212n n n b n a --=. 设数列n n b a ⎧⎫⎨⎬⎩⎭的前n 项和为n T , 则 213572321124822n n n n n T ----=++++++, ① 即 111357232122481622n n n n n T ---=++++++, ② ①-②,得2111112111224822n n nn T --=++++++- 11121211212n nn -⎛⎫- ⎪-⎝⎭=+-- 2332nn +=-, 所以12362n n n T -+=-. 故数列n n b a ⎧⎫⎨⎬⎩⎭的前n 项和为12362n n -+-.19.本小题主要考查直线与圆、基本不等式等基础知识,考查运算求解能力.满分14分. 解:(1)当0k =时,直线方程为y b =,设点A 的坐标为1()x b ,,点B 的坐标为2()x b ,,由224x b +=,解得12x =,,所以21AB x x =-= 所以12S AB b== 22422b b +-=≤.当且仅当b=b =S 取得最大值2.(2)设圆心O 到直线2y kx =+的距离为d,则d=.因为圆的半径为2R =, 所以2AB ===.于是241121k S AB d k =⨯===+,即2410k k -+=,解得2k =故实数k的值为2+22-2-20.本小题主要考查二次函数、函数的零点等基础知识,考查运算求解能力,以及分类讨论的数学思想方法.满分14分. 解法1:当0a =时,()1f x x =-,令()0f x =,得1x =,是区间[]1,1-上的零点.当0a ≠时,函数()f x 在区间[]1,1-上有零点分为三种情况: ①方程()0f x =在区间[]1,1-上有重根, 令()14130a a ∆=--+=,解得16a =-或12a =. 当16a =-时,令()0f x =,得3x =,不是区间[]1,1-上的零点. 当12a =时,令()0f x =,得1x =-,是区间[]1,1-上的零点. ②若函数()y f x =在区间[]1,1-上只有一个零点,但不是()0f x =的重根, 令()()()114420f f a a -=-≤,解得102a <≤. ③若函数()y f x =在区间[]1,1-上有两个零点,则()()⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧≥≥<-<->++-=∆>.01-,01,1211,01412,02f f a a a a 或()()⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧≤≤<-<->++-=∆<.01-,01,1211,01412,02f f a a a a 解得a ∈∅.综上可知,实数a 的取值范围为10,2⎡⎤⎢⎥⎣⎦.解法2:当0a =时,()1f x x =-,令()0f x =,得1x =,是区间[]1,1-上的零点.当0a ≠时,()213f x ax x a =+-+在区间[]1,1-上有零点⇔()231x a x +=-在区间[]1,1-上有解⇔213xa x -=+在区间[]1,1-上有解.问题转化为求函数213xy x -=+在区间[]1,1-上的值域. 设1t x =-,由[]1,1x ∈-,得[]0,2t ∈.且()2013ty t =≥-+.而()214132ty t t t==-++-. 设()4g t t t=+,可以证明当(]0,2t ∈时,()g t 单调递减. 事实上,设1202t t <<≤, 则()()()()121212121212444t t t t g t g t t t t t t t --⎛⎫⎛⎫-=+-+= ⎪ ⎪⎝⎭⎝⎭, 由1202t t <<≤,得120t t -<,1204t t <<,即()()120g t g t ->. 所以()g t 在(]0,2t ∈上单调递减. 故()()24g t g ≥=. 所以()1122y g t =≤-.故实数a 的取值范围为10,2⎡⎤⎢⎥⎣⎦.。
