数学:3.5.2 切线的判定 学习课件(北师大版九年级下册)
合集下载
【北师大版】初三九年级数学下册《3.6.2 切线的性质》课件

1 知识小结
圆的切线垂直于过切点的半径. 已知直线满足: (1)过圆心; (2)过切点; (3)垂直于直线任意两个,就可得到第三个.
2 易错小结
【中考·嘉兴】如图,△ABC中,AB=5,BC=3,AC=4,
以点C为圆心的圆与AB相切,则⊙C的半径为( B )
A.2.3
B.2.4
C.2.5
D.2.6
OA 2
总结
知2-讲
当圆中有切线和切点时,通常连接过切点的半径, 则这条半径必与切线垂直,本例中作辅助线的方法, 适用于同类条件下与圆有关的求值或证明题.
(来自《点拨》)
知2-练
1 如图,一枚直径为d的硬币沿着直线滚动一圈, 圆心经过的距离是多少?
解:πd.
(来自《教材》)
知2-练
2 如图,以点O为圆心的两个圆中,大圆的弦AB
第三章 圆
3.6 直线和圆的位置关系
第2课时 切线的性质
1 课堂讲解 切线的性质定理
切线性质定理的应用
2 课时流程
逐点 导讲练
课堂 小结
作业 提升
前一节课已经学到点和圆的位置关系.设⊙O的 半径为r,点P到圆心的距离OP=d,
O dr
P (a)
r O
dP
(b)
r O d
P (c)
则有:点P在圆外⇔ d>r,如图(a)所示;
(来自《点拨》)
知1-讲
导引: 如图,连接OA,根据切线的性质,先求出∠OAC =90°,再根据等腰三角形的性质和∠B=20°, 可以求出∠AOC=40°,最后根据直角三角形中 两锐角互余就可以求出∠C=50°. 答案:D
(来自《点拨》)
总结
知1-讲
北师大版九年级数学下册课件3.6.2 切线的判定

个,并且只能作一个.
B
A
F
E
I
●
┓ C
定义:与三角形三边都相切的圆叫做三角形的内切圆. 内切圆的圆心叫做三角形的内心,是三角形三条角平分线的交点.
新知探究
做一做 :
分别作出锐角三角形,直角三角形,钝角三角形的内切圆 , 并说明它 们内心的位置情况.
A
A
A
●
●
┐
B
CB
内心均
新知探究
D
C
E
F
O
A
B
课堂小测
tan tan tan
∴DE=DC•tan∠DCE=1, Rt
设⊙O的半径为r,则在Rt△COE中,
●O
αd
┓α
l
A
新课导入
探究新知:
过半径外端且垂直于半径的直线是圆的切线.
∵ AB是⊙O的直径,直线CD经过A点,且CD⊥AB,
B
∴ CD是⊙O的切线.
这个定理实际上就是
d=r
直线和圆相切
的另一种说法.
●O
C
A
D
新知探究
例1.如图,AB是⊙O的直径, ∠ABT=45°,AT=BA.
B
求证 : AT是⊙O的切线.
九年级数学北师版·下册
第三章 圆
3.6.2 切线的判定
教学目标
1.通过学习判定一条直线是否为圆的切线,训练学生的推理判断能力. 2.会过圆上一点画圆的切线,训练学生的作图能力. 3.会作三角形的内切圆.
新课导入
情境引入
相交 d<r d=r d>r
相切 直线和圆相交 直线和圆相切 直线和圆相离
相离
那么直线 AB是⊙O的切线吗?
北师大版九年级下数学《3.6.2切线的判定及三角形的内切圆》课件

是圆的切线.
要点归纳
判断一条直线是一个圆的切线有三个方法:
1.定义法:直线和圆只有一个公共
点时,我们说这条直线是圆的切线; 2.数量关系法:圆心到这条直线的 距离等于半径(即d=r)时,直线与 圆相切;
l
dr
l
3.判定定理:经过半径的外端且垂直 于这条半径的直线是圆的切线.
O
A
l
做一做 用三角尺过圆上一点画圆的切线.
应用格式
B
O
A
O
OA为⊙O的半径 BC ⊥ OA于A
BC为⊙O的切线
C
判一判 下列各直线是不是圆的切线?如果不是,请说明为什么?
O.
l
A
(1) (1)不是,因为 没有垂直.
O. O
A
l
B
(2)
A
l
(3)
(2),(3)不是,因为没有
经过半径的外端点A.
注意 在此定理中,“经过半径的外端”和“垂 直于这条半径”,两个条件缺一不可,否则就不
理,要证明AC是⊙O的切
E
F
线,只要证明由点O向AC
所作的垂线段OF是⊙O的 B
O
C
半径就可以了,而OE是
⊙O的半径,因此只需要
证明OF=OE.
证明:连接OE ,OA, 过O 作OF ⊥AC.
∵⊙O 与AB 相切于E , ∴OE ⊥ AB.
又∵在△ABC 中,AB =AC ,
O 是BC 的中点.
∴AO 平分∠BAC,
图形 A
O
性质 1.OA=OB=OC 2.外心不一定在 三角形的内部.
内心: 三角形 内切圆 的圆心
三角形三 条角平分 线的交点
B
A
要点归纳
判断一条直线是一个圆的切线有三个方法:
1.定义法:直线和圆只有一个公共
点时,我们说这条直线是圆的切线; 2.数量关系法:圆心到这条直线的 距离等于半径(即d=r)时,直线与 圆相切;
l
dr
l
3.判定定理:经过半径的外端且垂直 于这条半径的直线是圆的切线.
O
A
l
做一做 用三角尺过圆上一点画圆的切线.
应用格式
B
O
A
O
OA为⊙O的半径 BC ⊥ OA于A
BC为⊙O的切线
C
判一判 下列各直线是不是圆的切线?如果不是,请说明为什么?
O.
l
A
(1) (1)不是,因为 没有垂直.
O. O
A
l
B
(2)
A
l
(3)
(2),(3)不是,因为没有
经过半径的外端点A.
注意 在此定理中,“经过半径的外端”和“垂 直于这条半径”,两个条件缺一不可,否则就不
理,要证明AC是⊙O的切
E
F
线,只要证明由点O向AC
所作的垂线段OF是⊙O的 B
O
C
半径就可以了,而OE是
⊙O的半径,因此只需要
证明OF=OE.
证明:连接OE ,OA, 过O 作OF ⊥AC.
∵⊙O 与AB 相切于E , ∴OE ⊥ AB.
又∵在△ABC 中,AB =AC ,
O 是BC 的中点.
∴AO 平分∠BAC,
图形 A
O
性质 1.OA=OB=OC 2.外心不一定在 三角形的内部.
内心: 三角形 内切圆 的圆心
三角形三 条角平分 线的交点
B
A
北师大版九年级数学下册 第三章《圆》3.6.2 切线的判定【名校课件】

A.h=R+r B.R=2r
C.r=
3 4a
D.R=
3 3a
【点拨】如图,∵△ABC 是等边三角形, ∴△ABC 的内切圆和外接圆是同心圆,圆心为 O. 设 D,E 为切点,连接 OE,OD,OA, 易得点,A,O,D 共线, 则 OE=OD=r,AO=R,AD=h, ∴h=R+r,故 A 正确.
证明:如图,连接 EO 并延长交 BC 于点 H,连接 OB,OC, ∵OB=OC,EB=EC, ∴直线 EO 垂直平分 BC. ∴EH⊥BC.∵EF∥BC,∴EH⊥EF. ∵OE 是⊙O 的半径,∴EF 为⊙O 的切线.
15.(2019·天水)如图,AB,AC 分别是⊙O 的直径和弦,OD⊥ AC 于点 D,过点 A 作⊙O 的切线与 OD 的延长线交于点 P, PC,AB 的延长线交于点 F.
4.如图所示,AB 是⊙O 的直径,BC 交⊙O 于点 D,DE⊥AC 于点 E,要使 DE 是⊙O 的切线,还需补充一个条件,则补 充的条件不正确的是( A ) A.DE=DO B.AB=AC C.CD=DB D.AC∥OD
5.(2019·南充)如图,在△ABC 中,以 AC 为直径的⊙O 交 AB 于点 D,连接 CD,∠BCD=∠A.
∴∠BOD=∠BAC,∠ODB=∠ACB. ∴△OBD∽△ABC. ∴OACD=BBDC,即3552=BDB+D254.∴BD=1270.
14.(2020·威海)如图,△ABC 的外角∠BAM 的平分线与它的外 接圆相交于点 E,连接 BE,CE,过点 E 作 EF∥BC,交 CM 于点 D.求证:
(1)BE=CE;
证明:由题意得四边形 ACBE 是圆内接四边形, ∴∠EBC+∠EAC=180°. 又∵∠EAC+∠EAM=180°,∴∠EAM=∠EBC. ∵AE 平分∠BAM,∴∠BAE=∠EAM. ∵∠BAE=∠BCE,∴∠BCE=∠EAM. ∴∠BCE=∠EBC.∴BE=CE.
初三下数学课件(北师大)-切线长定理
︵ 过劣弧DE (不包括端点 D、E)上任一点作⊙O 的切线 MN 与 AB、BC 分别 交于点 M、N.若⊙O 的半径为 r,则 Rt△MBN 的周长为 2r .
12.如图,已知 AB 为⊙O 的直径,AB=2,AD 和 BE 是圆 O 的两条切线,
A、B 为切点,过圆上一点 C 作⊙O 的切线 CF,分别交 AD、BE 于点 M、 3
解:(1)△ABC 为等腰三角形,∵△ABC 的内切圆⊙O 与 AB、BC、AC 分 别相切于点 D、E、F,∴∠CFO=∠CEO=∠BDO=∠BEO=90°,∵四边
︵︵ 形内角和为 360°,∴∠EOF+∠C=180°,∠DOE+∠B=180°,∵EF=DE, ∴∠EOF=∠DOE,∴∠B=∠C,AB=AC,∴△ABC 为等腰三角形;
切线长定理的综合运用. 【例 2】如图所示,在△ABC 中,∠C=90°,AC=8,AB=10,点 P 在 AC 上,AP=2,若⊙O 的圆心在线段 BP 上,且⊙O 与 AB、AC 都相切,则⊙ O 的半径是( A )
A.1 C.172
B.45 D.94
【思路分析】如图所示,过点 O 作 OD⊥AC,OE⊥AB,OF⊥BC,垂足分 别为 D、E、F,CP=AC-AP=8-2=6,BC= AB2-AC2= 102-82=6. ∴CP=CB,∴∠CPB=∠CBP=45°,设⊙O 的半径为 r,则 OD=OE=DP =r,BF=OF=6-r,AD=AE=r+2,BE=8-r,在 Rt△BOE 中,由勾 股定理,得 BE2+OE2=BO2,而 BO2=BF2+OF2,即(8-r)2+r2=2(6-r)2, ∴r=1.
⊙O 的切线条数为( C )
A.0 条
B.1 条
C.2 条
D.无数条
12.如图,已知 AB 为⊙O 的直径,AB=2,AD 和 BE 是圆 O 的两条切线,
A、B 为切点,过圆上一点 C 作⊙O 的切线 CF,分别交 AD、BE 于点 M、 3
解:(1)△ABC 为等腰三角形,∵△ABC 的内切圆⊙O 与 AB、BC、AC 分 别相切于点 D、E、F,∴∠CFO=∠CEO=∠BDO=∠BEO=90°,∵四边
︵︵ 形内角和为 360°,∴∠EOF+∠C=180°,∠DOE+∠B=180°,∵EF=DE, ∴∠EOF=∠DOE,∴∠B=∠C,AB=AC,∴△ABC 为等腰三角形;
切线长定理的综合运用. 【例 2】如图所示,在△ABC 中,∠C=90°,AC=8,AB=10,点 P 在 AC 上,AP=2,若⊙O 的圆心在线段 BP 上,且⊙O 与 AB、AC 都相切,则⊙ O 的半径是( A )
A.1 C.172
B.45 D.94
【思路分析】如图所示,过点 O 作 OD⊥AC,OE⊥AB,OF⊥BC,垂足分 别为 D、E、F,CP=AC-AP=8-2=6,BC= AB2-AC2= 102-82=6. ∴CP=CB,∴∠CPB=∠CBP=45°,设⊙O 的半径为 r,则 OD=OE=DP =r,BF=OF=6-r,AD=AE=r+2,BE=8-r,在 Rt△BOE 中,由勾 股定理,得 BE2+OE2=BO2,而 BO2=BF2+OF2,即(8-r)2+r2=2(6-r)2, ∴r=1.
⊙O 的切线条数为( C )
A.0 条
B.1 条
C.2 条
D.无数条
切线长定理课件北师大版数学九年级下册

你还有其他 A 的画法吗?
O
P
O
P
B
知识要点
1. 切线长的定义:
经过圆外一点画圆的
A
切线,这点和切点之间的
线段的长叫作切线长.
O
P
2. 切线长与切线的区别在哪里?
① 切线是直线,不能度量.
② 切线长是线段的长,这条线段的两个端点分别是
圆外一点和切点,可以度量.
2 切线长定理
合作探究
如图,PA、PB 是⊙O 的两
EC
∴ AB = BD + AD = BE + AF = 34 – 2r.
而 AB = 26,∴ 34 – 2r = 26. ∴ r = 4,即 ⊙O 的半径为 4.
链接中考
B
A P
O B
2.(天津)如图,已知 AB 为⊙O 的直径,PA,PC 是
⊙O 的切线,A,C 为切点,∠BAC = 30°.
B O
∴∠P = 60°.
(2) 如图,连接 BC,则∠ACB = 90°. P
在 Rt△ACB 中,AB = 2,∠BAC = 30°.
∴ BC = 1,AC = ,∠PAC = 60°.
A
∴ △PAC 为等边三角形.
∴ PA = AC.
∴ PA = .
C B
O
切线长 作 用
提供了证线段和 角相等的新方法
第三章 圆
*3.7 切线长定理
1. 直线和圆有哪些位置关系? 相离、相交、相切.
2. 如何判断直线和圆相切?(常用方法) (1) 数量关系法(证明 d = r); (2) 判定定理:经过半径的外端且 垂直于这条半径的直线是圆的切线.
l
d
r
O
P
O
P
B
知识要点
1. 切线长的定义:
经过圆外一点画圆的
A
切线,这点和切点之间的
线段的长叫作切线长.
O
P
2. 切线长与切线的区别在哪里?
① 切线是直线,不能度量.
② 切线长是线段的长,这条线段的两个端点分别是
圆外一点和切点,可以度量.
2 切线长定理
合作探究
如图,PA、PB 是⊙O 的两
EC
∴ AB = BD + AD = BE + AF = 34 – 2r.
而 AB = 26,∴ 34 – 2r = 26. ∴ r = 4,即 ⊙O 的半径为 4.
链接中考
B
A P
O B
2.(天津)如图,已知 AB 为⊙O 的直径,PA,PC 是
⊙O 的切线,A,C 为切点,∠BAC = 30°.
B O
∴∠P = 60°.
(2) 如图,连接 BC,则∠ACB = 90°. P
在 Rt△ACB 中,AB = 2,∠BAC = 30°.
∴ BC = 1,AC = ,∠PAC = 60°.
A
∴ △PAC 为等边三角形.
∴ PA = AC.
∴ PA = .
C B
O
切线长 作 用
提供了证线段和 角相等的新方法
第三章 圆
*3.7 切线长定理
1. 直线和圆有哪些位置关系? 相离、相交、相切.
2. 如何判断直线和圆相切?(常用方法) (1) 数量关系法(证明 d = r); (2) 判定定理:经过半径的外端且 垂直于这条半径的直线是圆的切线.
l
d
r
北师版九年级数学下册《切线的判定及三角形的内切圆》课件精品(2022年新版)
方法总结:图形中求三角形外接圆的面积时,关键是 确定外接圆的直径(或半径)长度.
当堂练习
1.判断: 〔1〕经过三点一定可以作圆 〔 ×〕 〔2〕三角形的外心就是这个三角形两边垂直平分线的
交点 〔 √ 〕 〔3〕三角形的外心到三边的距离相等 〔×〕 〔4〕等腰三角形的外心一定在这个三角形内 〔 ×〕
O
E
B
PC
3.△ABC的内切圆⊙O与三边分别切于D、E、F三点,如 图,AF=3,BD+CE=12,那么△ABC的周长是 30 .
A
F
E
O
BD
C
第4题
A
拓展提升:
直角三角形的两直角边分别是3cm ,4cm,试问:
〔1〕它的外接圆半径是 5 cm;内切圆半径
D
F O·
是 1 cm?
〔2〕假设移动点O的位置,使⊙O保持与△ABC的 C E
填一填:
三角形三边
中垂线的交
点
B
三角形三条 角平分线的 交点
B
A
1.OA=OB=OC
2.外心不一定
O
在三角形的内 部.
A
1.到三边的距离相 等;
2.OA、OB、OC分
别平分∠BAC、
O
∠ABC、∠ACB; 3.内心在三角形内
C 部.
例3 △ABC的内切圆⊙O与BC、CA、AB分别相切于点D、
E、F,且AB=13cm,BC=14cm,CA=9cm,求AF、BD、CE
A.第①块 C.第③块
B.第②块 D.第④块
二 三角形的外接圆及外心
试一试: △ABC,用直尺与圆规作出过A、B、C
三点的圆.
A
O C
B
当堂练习
1.判断: 〔1〕经过三点一定可以作圆 〔 ×〕 〔2〕三角形的外心就是这个三角形两边垂直平分线的
交点 〔 √ 〕 〔3〕三角形的外心到三边的距离相等 〔×〕 〔4〕等腰三角形的外心一定在这个三角形内 〔 ×〕
O
E
B
PC
3.△ABC的内切圆⊙O与三边分别切于D、E、F三点,如 图,AF=3,BD+CE=12,那么△ABC的周长是 30 .
A
F
E
O
BD
C
第4题
A
拓展提升:
直角三角形的两直角边分别是3cm ,4cm,试问:
〔1〕它的外接圆半径是 5 cm;内切圆半径
D
F O·
是 1 cm?
〔2〕假设移动点O的位置,使⊙O保持与△ABC的 C E
填一填:
三角形三边
中垂线的交
点
B
三角形三条 角平分线的 交点
B
A
1.OA=OB=OC
2.外心不一定
O
在三角形的内 部.
A
1.到三边的距离相 等;
2.OA、OB、OC分
别平分∠BAC、
O
∠ABC、∠ACB; 3.内心在三角形内
C 部.
例3 △ABC的内切圆⊙O与BC、CA、AB分别相切于点D、
E、F,且AB=13cm,BC=14cm,CA=9cm,求AF、BD、CE
A.第①块 C.第③块
B.第②块 D.第④块
二 三角形的外接圆及外心
试一试: △ABC,用直尺与圆规作出过A、B、C
三点的圆.
A
O C
B
初三下数学课件(北师大)-切线的判定
知识点一:切线的判定 切线的判定 (1)过半径外端且 垂直 于半径的直线是圆的切线. (2)若圆心到一条直线的距离等于 半径 ,则这条直线是圆的切线.
1.下列说法中,正确的是( D ) A.AB 垂直于⊙O 的半径,则 AB 是⊙O 的切线 B.经过半径外端的直线是圆的切线 C.经过切点的直线是圆的切线 D.圆心到直线的距离等于半径,那么这条直线是圆的切线
知识点二:三角形的内切圆 三角形的内切圆 (1)和三角形各边都 相切 的圆叫三角形的内切圆,内切圆的圆心是三角形
三内角平分线 的交点,叫三角形的 内心 . (2)三角形的内心到三角形 三边 的距离相等.
5.下列命题正确的是( C ) A.三角形的内心到三角形三个顶点的距离相等 B.三角形的内心不一定在三角形的内部 C.等边三角形的内心、外心重合 D.一个圆一定有唯一的一个外切三角形
6.如图,在△ABC 中,∠A=66°,点 I 是内心,则∠BIC 的大小为( C )
A.114°
B.122°
C.123°
D.132°
7.如图,O 是△ABC 的内心,过点 O 作 EF∥AB,与 AC、BC 分别交于点
E、F,则( C )
A.EF>AE+BF
B.EF<AE+BF
C.EF=AE+BF
D.EF≤AE+BF
8.△ABC 的内切圆分别切 BC、CA、AB 于 D、E、F.如果∠A=70°,则∠
EDF 的度数为( B )
A.35°
B.55°
C.70°
D.110°
︵ 9.如图,已知 AB 是⊙O 的直径,AD 切⊙O 于点 A,点 C 是EB的中点,
则下列结论不成立的是( D )
A.OC∥AE
(2)证明:连接 MC,NC,∵AN 是⊙M 的直径,∴∠ACN=90°,∴∠NCB =90°,在 Rt△NCB 中,D 为 NB 的中点,∴CD=12NB=ND,∴∠CND= ∠NCD,∵MC=MN,∴∠MCN=∠MNC,∵∠MNC+∠CND=90°,∴ ∠MCN+∠NCD=90°,即 MC⊥CD,∴直线 CD 是⊙M 的切线.
北师大版数学九年级下册切线长定理课件
A
O 130°
B
P
50°
如何用圆规和直尺
作出这两条
A
切线呢?
O.
P
B 思考:已画出切线PA,PB,A,B为切点,则∠OAP=90°, 连接OP,可知A,B 除了在⊙O上,还在怎样的圆上?
A
OO ·
P
B
切线长概念
过圆外一点作圆的切线,这点和切点之间的线段长叫 做这点到圆的切线长.
A
O
·
P
B
切线与切线长是一回事吗?它们有什么区分与联系呢?
C
求证:AD+BC=AB+CD.
N
证明:由切线长定理得
D
AL=AP,LB=MB,NC=MC,
M O
DN=DP,
P
∴AP+MB+MC+DP=AL+LB+NCA L
B
+DN,
即AD+BC=AB+CD,
补充:圆的外切四边形的两组对边
【跟踪训练】
1.如果PA=4cm,PD=2cm, 求半径OAB
定理 圆的切线垂直于过切点的半径
●
∵CD与⊙O相切与点A,且OA是半
O
径∴CD⊥OA.
提示:
CAD
“见切点,连圆心”是常用辅助线之一.
你还记得内切圆与内心吗?
A
F
E
I
●●
B
┓
C
定义:与三角形三边都相切的圆叫做三角形的内切圆. 内 切圆的圆心叫做三角形的内心,是三角形三条角平分线的 交点.
1.理解切线长的概念,掌握切线长定理. 2.学会运用切线长定理解有关问题. 3.通过对例题的分析,培养学生分析总结问题的习 惯,提高学生综合运用知识解题的能力,培养数形 结合的思想.
O 130°
B
P
50°
如何用圆规和直尺
作出这两条
A
切线呢?
O.
P
B 思考:已画出切线PA,PB,A,B为切点,则∠OAP=90°, 连接OP,可知A,B 除了在⊙O上,还在怎样的圆上?
A
OO ·
P
B
切线长概念
过圆外一点作圆的切线,这点和切点之间的线段长叫 做这点到圆的切线长.
A
O
·
P
B
切线与切线长是一回事吗?它们有什么区分与联系呢?
C
求证:AD+BC=AB+CD.
N
证明:由切线长定理得
D
AL=AP,LB=MB,NC=MC,
M O
DN=DP,
P
∴AP+MB+MC+DP=AL+LB+NCA L
B
+DN,
即AD+BC=AB+CD,
补充:圆的外切四边形的两组对边
【跟踪训练】
1.如果PA=4cm,PD=2cm, 求半径OAB
定理 圆的切线垂直于过切点的半径
●
∵CD与⊙O相切与点A,且OA是半
O
径∴CD⊥OA.
提示:
CAD
“见切点,连圆心”是常用辅助线之一.
你还记得内切圆与内心吗?
A
F
E
I
●●
B
┓
C
定义:与三角形三边都相切的圆叫做三角形的内切圆. 内 切圆的圆心叫做三角形的内心,是三角形三条角平分线的 交点.
1.理解切线长的概念,掌握切线长定理. 2.学会运用切线长定理解有关问题. 3.通过对例题的分析,培养学生分析总结问题的习 惯,提高学生综合运用知识解题的能力,培养数形 结合的思想.
北师大版九年级数学下册切线长定理课件
∠P= 50 °,点C是⊙O上异于A、B的点,则
∠ACB= 65 °或115 °.
P
O
B
五、当堂达标检测
6.△ABC的内切圆⊙O与BC,CA,AB分别相切于点D,E,F,且
AB=9cm,BC=14cm,CA=13cm,求AF,BD,CE的长.
解:设AF=x,则AE=x
∴CD=CE=AC-AE=13-x,
A
D
P
O
C
E
B
二、自主合作,探究新知
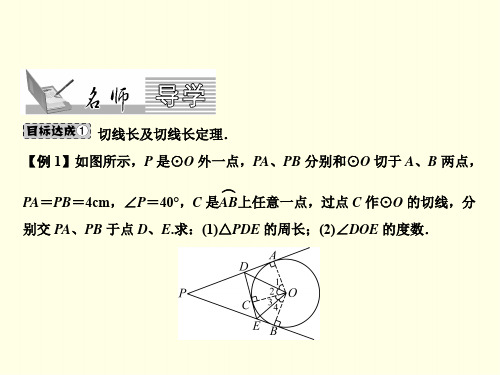
又∵DC、DA是☉O的两条切线,点C、A是切点,
∴DC=DA.同理可得CE=EB.
l△PDE=PD+DE+PE=PD+DC+CE+PE=PA+PB=14.
∵OA=OC,OD=OD,
∴△AOD≌△COD,
∴∠DOC=∠DOA= ∠AOC.
P
同理可得∠COE= ∠COB.
7.如图,在△ABC 中,∠ABC=50º,∠ACB=75º,点O是△ ABC的内心,
求∠BOC的度数.
解:∵点O是△ABC 的内心,
∴∠OBC
∠OCB
= ∠ABC
= ∠ACB
= ×50º=
25º,
= ×75º=37.5º.
在△OBC 中,∠BOC =180º- ∠OBC - ∠OCB
=180º- 25º- 37.5º= 117.5º.
四、课堂小结
切线长
切线长定理
切线长定理
经过圆外一点作圆的切线,这点和切
点之间的线段的长叫作切线长.
过圆外一点画圆的两条切线,它们的
∠ACB= 65 °或115 °.
P
O
B
五、当堂达标检测
6.△ABC的内切圆⊙O与BC,CA,AB分别相切于点D,E,F,且
AB=9cm,BC=14cm,CA=13cm,求AF,BD,CE的长.
解:设AF=x,则AE=x
∴CD=CE=AC-AE=13-x,
A
D
P
O
C
E
B
二、自主合作,探究新知
又∵DC、DA是☉O的两条切线,点C、A是切点,
∴DC=DA.同理可得CE=EB.
l△PDE=PD+DE+PE=PD+DC+CE+PE=PA+PB=14.
∵OA=OC,OD=OD,
∴△AOD≌△COD,
∴∠DOC=∠DOA= ∠AOC.
P
同理可得∠COE= ∠COB.
7.如图,在△ABC 中,∠ABC=50º,∠ACB=75º,点O是△ ABC的内心,
求∠BOC的度数.
解:∵点O是△ABC 的内心,
∴∠OBC
∠OCB
= ∠ABC
= ∠ACB
= ×50º=
25º,
= ×75º=37.5º.
在△OBC 中,∠BOC =180º- ∠OBC - ∠OCB
=180º- 25º- 37.5º= 117.5º.
四、课堂小结
切线长
切线长定理
切线长定理
经过圆外一点作圆的切线,这点和切
点之间的线段的长叫作切线长.
过圆外一点画圆的两条切线,它们的
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第 2 课时 切线的判定
1.切线的判定 切线的判定定理:经过直径的端,并且垂直于这条直径
切线 的直线是圆的______
2.三角形的内切圆和内心 相切 的圆. 三角形的内切圆:和三角形三边都______ 三条角平分线 的交点. 内心:内切圆的圆心,是三角形______________ 相等 . 内心到三角形三边的距离______
图1 答案:略
三角形的内切圆和内心 3.边长为 3,4,5 的三角形的内切圆与外接圆的半径之比为 2∶5 . ________ 4.在△ABC 中,∠A=80°, 130° ; (1)点 I 是内心,则∠BIC=________ (2)点 I 是外心,则∠BIC=________. 160°
1.切线的判定方法有 3 种: (1)直线与圆只有唯一一个公共点,直线和圆相切. (2)当圆心到直线的距离等于半径时,直线与圆相切. (3)经过直径的一端,并且垂直于这条直径的直线是圆的切 线. 2.三角形的内心和外心容易混淆,内心是指内切圆的圆心, 是三条内角平分线的交点,性质是到三角形三边的距离相等; 外心是指外接圆的圆心,是三边垂直平分线的交点,性质是到 三顶点的距离相等.
切线的判定(重点) 1.下列说法正确的是( D ) A.垂直于圆的半径的直线和圆相切 B.经过圆的半径外端的直线和圆相切 C.经过半径的端点和这条半径垂直的直线是圆的切线 D.经过直径的端点和这条直径垂直的直线是圆的切线
2.已知:如图 1,AB 是⊙O 的直径,BC 与⊙O 交于 D, 且 BD=DC,DE⊥AC,求证:ED 是⊙O 的切线.
