【2020年初三数学月考真题】2020-莆田擢英中学-初三下3月月考-试卷-答案
2020年福建省莆田市擢英中学中考数学模拟试题

【解析】
【分析】
找到从正面看所得到的图形即可.
【详解】
解:从正面可看到从左往右2列一个长方形和一个小正方形,
故选A.
【点睛】
本题考查了三视图的知识,主视图是从物体的正面看得到的视图.
3.D
【解析】
试题分析:为了解某市老人的身体健康状况,需要抽取部分老人进行调查,在城市和乡镇各选10个点,每个点任选5位老人,这种抽取老人的方法最合适.故选D.
4.下列命题中,逆命题为真命题的是( )
A.对顶角相等
B.邻补角互补
C.两直线平行,同位角相等
D.互余的两个角都小于90°
5.下列计算正确的是( )
A.a2•a3=a6B.a+a=a2C.(a2)3=a6D.a8÷a2=a4
6.如图,在△ABC中,BE是∠ABC的平分线,CE是外角∠ACM的平分线,BE与CE相交于点E,若∠A=60°,则∠BEC是()
①恰好1名男生和1名女生被抽取参加5G体验活动的概率;
②至少1名女生被抽取参加5G体验活动的概率.
22.如图,点C为线段AB上一点,△ACM与△CBN都是等边三角形,AN与MB交于P.
(1)求证:AN=BM;
(2)连接CP,求证:CP平分∠APB.
23.某农场拟用总长为60m的建筑材料建三间矩形牛饲养室,饲养室的一面靠现有墙(墙长为40m),其中间用建筑材料做的墙隔开(如图).设三间饲养室平行于墙的一边合计用建筑材料xm,总占地面积为ym2.
16.如图,直线y=x+m与双曲线y= 交于A,B两点,作BC∥x轴,AC∥y轴,交BC于点C,则S△ABC的最小值是_____.
评卷人
得分
三、解答题
17.解方程: .
福建省莆田市第三中学2023-2024学年下学期九年级数学第一次月考试卷(含答案)

2023-2024莆田三中九年级下学期第一次月考一.选择题1.下列实数中,比大的数是( )A.1B.2C.0D.﹣22.2022年4月16日09时56分,神舟十三号载人飞船返回舱在东风着陆场成功着陆,载人飞行任务取得圆满成功.三位航天员进驻核心舱,进行了为期约为261000分钟的驻留,创造了中国航天员连续在轨飞行时长新纪录.将数据261000用科学记数法表示,其结果是( )A.0.261×106B.261×103C.2.61×105D.2.61×1033.下列运算结果正确的是( )A.a2+a4=a6B.(a+b)2=a2+b2C.﹣a6÷a2=﹣a3D.(﹣2a2b)3=﹣8a6b34.下列环保标志,既是轴对称图形,也是中心对称图形的是( )A.B.C. D.5.下列事件是必然事件的是( )A.通常温度降到0℃以下,纯净的水结冰B.随意翻到一本书的某页,这页的页码是奇数C.汽车累积行驶10000km,从未出现故障D.购买1张彩票,中奖6.下面四个函数中,图象为双曲线的是( )A.y=5x B.y=2x+3C.y=D.y=x2+2x+17.已知方程x2+2x﹣8=0的解是x1=2,x2=﹣4,那么方程(x+1)2+2(x+1)﹣8=0的解是( )A.x1=﹣1,x2=5B.x1=1,x2=5C.x1=1,x2=﹣5D.x1=﹣1,x2=﹣58.我国古代数学著作《九章算术》卷七有下列问题:“今有共买物,人出八,盈三:人出七,不足四,问人数、物价几何?”意思是:现在有几个人共同出钱去买件物品,如果每人出8钱,则剩余3钱:如果每人出7钱,则差4钱.问有多少人,物品的价格是多少?设有x人,物品的价格为y元,可列方程(组)为( )A.B.C.D.=9.如图,点A、B、C在⊙O上,CD⊥OA,CE⊥OB,垂足分别为D、E,若∠DCE=40°,则∠ACB的度数为( )A.140°B.70°C.110°D.80°10.如图,矩形ABCD中,AB=3,AD=3,将矩形ABCD绕点B顺时针旋转90°得到矩形EBGF,再将矩形EBGF绕点G顺时针旋转90°得到矩形IHGJ,则点D在两次旋转过程中经过的路径的长是( )A.4πB.5πC.πD.π二.填空题(共6小题)11.若在实数范围内有意义,则x的取值范围是 .12.在平面直角坐标系中,与点P(2,﹣3)关于原点对称的点的坐标是 .13.不透明袋子中装有3个白球,5个黑球,这些球除了颜色外无其他差别,从袋子中随机摸出1个球,则摸到黑球的概率为 .14.新能源汽车节能、环保,越来越受消费者喜爱.2020年某款新能源汽车销售量为15万辆,销售量逐年增加,2022年预估当年销售量为21.6万辆,求这款新能源汽车的年平均增长率是多少?可设年平均增长率为x,根据题意可列方程 .15.如图,抛物线y=ax2与直线y=bx+c的两个交点坐标分别为A(﹣4,8),B(2,2),则关于x的方程ax2﹣bx﹣c=0的解为 .16.反比例函数y1=(a>0,a为常数)和y2=在第一象限内的图象如图所示,点M在y2=的图象上,MC⊥x轴于点C,交y1=的图象于点A;MD⊥y轴于点D,交y1=的图象于点B,当点M在y2=的图象上运动时,以下结论:①S△ODB=S△OCA;②四边形OAMB的面积为2﹣a;③当a=1时,点A是MC的中点;④若S四边形OAMB=S△ODB+S△OCA,则四边形OCMD为正方形.其中正确的是 .(把所有正确结论的序号都填在横线上)三.解答题(共9小题)17.计算:(π―1)0―|―8|+(―13)―218.解不等式组:.19.先化简,再求值:÷(1﹣),其中m=﹣1.20.为扩大销售,某乡镇农贸公司在某平台新开了一家网店进行线上销售.在对一种特产(成本为10元/千克)在网店试销售期间发现每天销售量y(千克)与销售单价x(元)大致满足如图所示的函数关系(其中14≤x≤25).(1)写出y关于x的函数解析式,并求x=20时,农贸公司每天销售该特产的利润;(2)设农贸公司每天销售该特产的利润为W元,当销售单价x为多少元时,W最大?最大是多少元?21.如图,在等腰△ABC中,∠A=∠B=30°,过点C作CD⊥AC交AB于点D,(1)尺规作图:作△ACD的外接圆⊙O(保留痕迹,不要求写作法);(2)在(1)所作的图形中,求证:BC是⊙O的切线.22.已知:在⊙O中,AB为直径,P为射线AB上一点,过点P作⊙O的切线,切点为点C,D为上一点,连接BD、BC、DC.(Ⅰ)如图1,若∠D=28°,求∠P的度数.(Ⅱ)如图2,若四边形CDBP为平行四边形,BC=5,求CP的长.23.国家利益高于一切,国家安全人人有责,2023年4月15日是第八个全民国家安全教育日,某校开展了“树牢总体国家安全观,感悟新时代国家安全成就”的国安知识竞赛,现从该校七、八年级中各随机抽取20名学生的竞赛成绩(100分制)进行整理、描述和分析(成绩用x表示,共分成四组:不合格0≤x<60,合格60≤x<80,良好80≤x<100,优秀x=100),下面给出了部分信息:七年级抽取的学生竞赛成绩在良好组的数据是:80,84,85,90,95,98八年级抽取的学生竞赛成绩在良好组的数据是:80,82,84,86,86,90,94,98七、八年级抽取的学生竞赛成绩的统计量:年级平均数众数中位数满分率七年级82100a25%八年级82b8835%根据以上信息,解答下列问题:(1)直接写出a,b的值;(2)根据上述数据,你认为该校七、八年级中哪个年级学生对“国安知识”掌握较好?请说明理由(写出一条理由即可);(3)该校七、八年级各有800人参加此次竞赛活动,估计参加此次竞赛活动成绩优秀的学生人数是多少?24.如图1,四边形ABCD为正方形,点E为AD上的定点,点F是射线BE上的动点,连接AF.将点F 绕点A逆时针旋转90°得到点H,连接AH,过点F,H分别作AF和AH的垂线交于点G,射线DH与射线BE交于点P.(1)求证:四边形AFGH为正方形;(2)点F在运动过程中,判断点P的位置是否发生变化?并说明理由;(3)连接CG,PG,AP,探究线段AB,AP,CG,PG的数量关系,并证明.25.如图1,已知抛物线C1:y=ax2+bx﹣3与x轴交于点A(﹣3,0)和点B(1,0),与y轴交于点C.(1)求抛物线的解析式;(2)点P在抛物线上,若△BCP的内心恰好在y轴上,求出点P的坐标;(3)如图2,将抛物线C1向右平移三个单位长度得到抛物线C2,点M,N都在抛物线C2上,且分别在第四象限和第二象限,连接MN,分别交x轴、y轴于点E、F,若∠NOF=∠MOE,求证:直线MN经过一定点.2023-2024莆田三中九年级下学期第一次月考参考答案与试题解析一.选择题1-5.B.C.D.D.A.6-10.C.C.A.C.D10.【解答】解:如图,第一次旋转时,点D绕点B旋转90°,旋转半径为BD,到达点F处,BD===6,此时,点D运动的路径为:,第二次旋转时,点F绕点G旋转90°,旋转半径为GF=AB=3,到达点J处,点F运动的路径为:,故点D在两次旋转过程中经过的路径的长为:3,故选:D.二.填空题11.x≠3.12.(﹣2,3).13..14.15(1+x)2=21.6.15.x1=﹣4,x2=2.16.【解答】解:①由于A、B在同一反比例函数y=图象上,则△ODB与△OCA的面积相等,都为×2=1,正确;②∵点M在y2=的图象上,MC⊥x轴于点C,交y1=的图象于点A,∴四边形OAMB的面积=S矩形DMCO﹣S△BDO﹣S△AOC=2﹣a﹣a=2﹣a;正确;③连接OM,∵a=1,∴y1==,∵A在函数y1=的图象上,∴S△AOC=OC•AC=,S△MOC=OC•CM=1,∴AC=,CM=,∴AC=CM,∴点A是MC的中点;正确;由①②知,2﹣a=a,解得:a=1,∵点M在y2=的图象上运动,∴OC不一定等于OD,∴四边形OCMD不一定为正方形,与a的取值无关,故④错误;故答案为:①②③.三.解答题(共9小题)17.【解答】解:原式=1-8+9=218.【解答】解:由x+4>﹣2x+1,得:x>﹣1,由≤1,得:x≤4,则不等式组的解集为﹣1<x≤4.19.【解答】解:原式=÷(﹣)=•=,当m=﹣1时,原式==.20.【解答】解:(1)设y关于x的函数解析式y=kx+b(k≠0),将(14,320),(25,210)代入得,解得,∴y与x之间的函数关系式为y=﹣10x+460;当x=20时,y=﹣10×20+460=260,农贸公司每天销售该特产的利润为(20﹣10)×260=2600(元),∴当x=20时,农贸公司每天销售该特产的利润为2600元;(2)由题意得:W=(x﹣10)(﹣10x+460)=﹣10x2+560x﹣4600=﹣10(x﹣28)2+3240,∵﹣10<0,∴当x<28时,W随x的增大而增大,∵14≤x≤25,∴当x=25时,W最大,最大值为3150,∴当销售单价x为25元时,W最大,最大是3150元.21.【解答】(1)解:作AD的垂直平分线MN交AD于点O,以点O为圆心,OA的长为半径作圆,如图:⊙O即为所作的;(2)证明:连接OC,∵CD⊥AC,∴∠ACD=90°,∴AD是⊙O的直径;∴OC是⊙O的半径;∵∠A=∠B=30°,∴∠ACB=120°,∵OA=OC,∴∠ACO=∠A=30°,∴∠BCO=∠ACB﹣∠ACO=120°﹣30°=90°,∴BC⊥OC,∵OC是半径,∴BC是⊙O的切线.22.【解答】(Ⅰ)证明:如图1,连接OC,∵∠D=28°,∴∠COP=2×28°=56°,∵过点P作⊙O的切线,切点为点C,∴∠OCP=90°,∴∠P=90°﹣56°=34°;(Ⅱ)解:如图2,连接AC,OC,∵四边形CDBP为平行四边形,∴∠D=∠CPB,∵AB为直径,∴∠ACB=90°,由(1)得∠OCP=90°,∴∠ACB=∠OCP,∵∠D=∠A=∠CPB,∴∠D=∠A=∠CPB=∠PCB,在△ACP中,∠A+∠ACB+∠BCP+∠CPB=180°,∴∠A+∠BCP+∠CPB=90°,∴∠A=∠CPB=∠PCB=30°,∴∠OBC=60°,∵OB=OC,∴△OBC是等边三角形,∴OB=BC=5,∴PC=OB=5.23.【解答】解:(1)七年级学生竞赛成绩从小到大排列后,处在中间位置的两个数的平均数为(80+84)÷2=82(分),因此中位数是82分,即a=82,八年级学生竞赛成绩的中位数是88,因此在88分以上的应有10人,可得100分的有10﹣3=7(人),因此竞赛成绩的众数为100,即b=100;∴a=82,b=100;(2)八年级学生对“国安知识”掌握的比较好,理由如下:虽然七年级和八年级学生的平均分和众数相同,但是八年级学生的中位数和满分率都高于七年级;(3)七年级抽取的学生成绩优秀的人数为800×=200(人),八年级抽取的学生成绩优秀的人数为800×=280(人),则优秀人数为200+280=480(人),答:估计参加此次竞赛活动成绩优秀的学生人数是480人.24.【解答】(1)证明:由旋转可知:AF=AH,∠FAH=90°,∵FG⊥AF,GH⊥AH,∴∠AFG=90°,∠GHA=90°,∴四边形AFGH为矩形,又AF=AH,∴四边形AFGH正方形;(2)解:点F在运动过程中,点P的位置不发生变化,理由如下:如图1,∵四边形ABCD是正方形,∴AB=AD,∠BAD=∠FAH=90°,∴∠BAD﹣∠DAF=∠FAH﹣∠DAF,即∠BAF=∠DAH,在△BAF和△DAH中,,∴△BAF≌△DAH(SAS),∴∠ABE=∠ADP,∵点E为AD上的定点,∴∠ABE为定角,∠ADP为定角,∴点P为定点,F在运动过程中,点P的位置不发生变化;(3)解:AP2+(CG+PG)2=2AB2,理由如下:如图,连接AP、AC、BD、PC、AG和FH,∵四边形ABCD是正方形,∴∠ABC=∠BCD=∠BAD=90°,AB=BC,∠CBD=∠BDC=45°,∴AC2=AB2+BC2=2AB2,∵∠BAD=90°,∴∠ABE+∠AEB=90°,∵∠ABE=∠ADP,∠AEB=∠PED,∴∠ADP+∠PED=90°,∴∠BPD=90°,∵∠BCD=90°,∴B、C、D、P在以BD为直径的圆上,∴∠CPD=∠CBD=45°,∠BPC=∠BDC=45°,∵四边形AFGH正方形,∴∠FGH=∠AFG=90°,∠FHG=∠FAG=45°,∴∠FGH=∠BPD=90°,∴F、G、H、P在以FH为直径的圆上,∴∠FPG=∠FHG=45°,∴∠FPG=∠BPC=45°,∴点G在CP上,∴PC=CG+PG,∵∠FPG=∠FAG=45°,∴F、G、P、A在同一个圆上,∴∠APG=180°﹣∠AFG=90°,∴AP2+PC2=AC2,∴AP2+(CG+PG)2=2AB2.25.【解答】(1)解:把点A(﹣3,0)和点B(1,0)分别代入解析式,得:,解得:,故抛物线的解析式为y=x2+2x﹣3;(2)解:作点B关于y轴的对称点B',连接CA'并延长交抛物线于点P,点P为所求的点,如图1,∴∠ACO=∠A′CO,B'(﹣1,0),∴△BCP的内心在y轴上,在y=x2+2x﹣3中,令x=0,则y=﹣3,故点C的坐标为(0,﹣3),设直线CB'的解析式为y=kx+b,把点C、B'的坐标分别代入解析式,得:,解得:,∴直线CB'的解析式为y=﹣3x﹣3,联立得:,解得:或,∴点P的坐标为(﹣5,12);(3)证明:如图2:过点M作MQ⊥x于点Q,过点N作NP⊥y轴,∵将抛物线C1:y=x2+2x﹣3=(x+1)2﹣4向右平移3个单位长度得到抛物线C2,∴抛物线C2的解析式为:y=(x﹣2)2﹣4=x2﹣4x,∵点M,N都在抛物线C2上,且分别在第四象限和第二象限,∴设点M的坐标为(x1,﹣4x1)(﹣4x_1<0),点N的坐标为(x2,﹣4x2)(x2<0),∴PN=﹣x,OP=﹣4x2,OQ=x1,QM=﹣(﹣4x1),设直线MN的解析式为y=mx+n,代入得:,得x2﹣(4+m)x﹣n=0,则x1+x2=4+m,x1•x2=﹣n,∵∠NOP=∠MOQ,∠OPN=∠OQM=90°,∴△OPN∽△OQM,∴=,∴,得:x1x2=,得:(﹣n)2﹣4×(﹣n)×(4+m)+15×(﹣n)=0,整理得:n2+n+4mn=0,得n(n+1+4m)=0,由图象可知n≠0,∴n+1+4m=0,∴m=﹣,∴y=﹣,当x=4 时,y=﹣1,∴直线MN经过一定点(4,﹣1).。
福建省莆田市九年级下学期数学3月月考试卷

福建省莆田市九年级下学期数学3月月考试卷姓名:________ 班级:________ 成绩:________一、选择题(共10小题,每小题3分,共30分) (共10题;共29分)1. (3分)下列各组有理数比较大小正确的是()A . -10>-1B . -0.1<-100C . 1>-1000D . 0<-102. (3分)使式子有意义的x取值范围是()A . x>﹣1B . x≥﹣1C . x<﹣1D . x≤﹣13. (3分) (2017八下·洛阳期末) 甲、乙、丙、丁四名射击队员考核赛的平均成绩(环)及方差统计如表,现要根据这些数据,从中选出一人参加比赛,如果你是教练员,你的选择是()队员平均成绩方差甲9.7 2.12乙9.60.56丙9.70.56丁9.6 1.34A . 甲B . 乙C . 丙D . 丁4. (3分) (2018八下·灵石期中) 下列图形中,既是轴对称图形又是中心对称图形的是A .B .C .D .5. (3分)如下图,下列四个几何体中,它们各自的三视图(主视图、左视图、俯视图)有两个相同,而另一个不同的几何体是()A . ①②B . ②③C . ②④D . ③④6. (3分)如图,长方形ABCD恰好可分成7个形状大小相同的小长方形,如果小长方形的面积是3,则长方形ABCD的周长是()A . 17B . 18C . 19D .7. (3分) (2017九上·拱墅期中) 现有A,B两枚均匀的小立方体(立方体的每个面上分别标有数字1,2,3,4,5,6).用小莉掷A立方体朝上的数字为、小明掷B立方体朝上的数字为来确定点P(),那么它们各掷一次所确定的点P落在已知抛物线上的概率为()A .B .C .D .8. (2分) (2017八下·丰台期末) 矩形ABCD中,对角线AC , BD相交于点O ,如果∠ABO=70°,那么∠AOB的度数是()A . 40°B . 55°C . 60°D . 70°9. (3分)已知,如上右图,动点P在函数y=(x>0)的图象上运动,PM⊥x轴于点M,PN⊥y轴于点N,线段PM、PN分别与直线AB:y=﹣x+1相交于点E,F,则AF•BE的值是()A . 4B . 2C . 1D .10. (3分) (2017七下·大冶期末) 下列依次给出的点的坐标(0,3),(1,1),(2,﹣1),(3,﹣3),…,依此规律,则第2017个点的坐标为()A . (2017,﹣2015)B . (2016,﹣2014)C . (2016,﹣4029)D . (2016,﹣4031)二、多项选择题(6小题,每小题3分,共18分)说明:下列各题的结 (共6题;共18分)11. (3分)(2016·凉山) 下列计算正确的是()A . 2a+3b=5abB . (﹣2a2b)3=﹣6a6b3C . + =3D . (a+b)2=a2+b212. (3分) (2019八上·盘龙镇月考) 化简: =()A . 1B . 0C . xD . -x13. (3分) (2020九下·青山月考) 定义:等腰三角形的顶角与其一个底角的度数的比值 k 称为这个等腰三角形的特征值等腰ABC 中,∠A=80°,则等腰△ABC 的特征值 k=()A .B .C .D . 414. (3分)如图,DE与的边AB,AC分别相交于D,E两点,且DE//BC.若AD:BD=3:1, DE=6,则BC 等于().A . 8B .C .D . 215. (3分) (2020九下·青山月考) 抛物线 y=x2+bx+3 的对称轴为直线 x=1.若关于 x 的一元二次方程 x2+bx+3-t=0(t为实数)在-1<x<4 的范围内有且只有一个实数根(两个相等的实数根视为一个实数根),则 t 的取值范围是 B,()A . 2≤t<11B . t=2C . 6≤t<11D . 6<t≤1116. (3分) (2020九下·青山月考) 如图,A,B,C,D 为一直线上 4 个点,BC=3,△BCE为等边三角形,⊙O过 A,D, E 三点,且∠AOD=120°.设 AB=x,CD=y,则y与 x的函数关系式().A .B .C . y=3x+3D .三、解答题(共8题,共72分) (共8题;共72分)17. (8分)计算(1)(2a+1)2-(2a+1)(-1+2a)(2)(x-y)3(x-y)2(y-x)(3)(3mn+1)(3mn-1)-8m2n218. (8分)(2018·梧州) 如图,在▱ABCD 中,对角线 AC,BD 相交于点 O,过点 O 的一条直线分别交 AD,BC 于点 E,F.求证:AE=CF.19. (8分) (2019九上·泗阳期末) 某篮球队在一次联赛中共进行了10场比赛,已知这10场比赛的平均得分为48分,且前9场比赛的得分依次为:57,51,45,51,44,46,45,42,48.(1)求第10场比赛的得分;(2)直接写出这10场比赛的中位数,众数和方差.方差公式:s2= [(x1﹣)2+(x2﹣)2+…+(xn﹣)2]20. (8分) (2016九上·济宁期中) 如图,正方形网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点.△ABC的三个顶点A,B,C都在格点上,将△ABC绕点A按顺时针方向旋转90°得到△AB′C′.(1)在正方形网格中,画出△AB′C′;(2)计算线段AB在变换到AB′的过程中扫过区域的面积.21. (8分)(2016·南平模拟) 如图,CD为⊙O的直径,点B在⊙O上,连接BC、BD,过点B的切线AE与CD的延长线交于点A,OE∥BD,交BC于点F,交AE于点E.(1)求证:△BEF∽△DBC.;(2)若⊙O的半径为3,∠C=32°,求BE的长.(精确到0.01)22. (10.0分)(2018·抚顺) 俄罗斯世界杯足球赛期间,某商店销售一批足球纪念册,每本进价40元,规定销售单价不低于44元,且获利不高于30%.试销售期间发现,当销售单价定为44元时,每天可售出300本,销售单价每上涨1元,每天销售量减少10本,现商店决定提价销售.设每天销售量为y本,销售单价为x元.(1)请直接写出y与x之间的函数关系式和自变量x的取值范围;(2)当每本足球纪念册销售单价是多少元时,商店每天获利2400元?(3)将足球纪念册销售单价定为多少元时,商店每天销售纪念册获得的利润w元最大?最大利润是多少元?23. (10分)(2017·大理模拟) 如图,抛物线y=﹣ x2+bx+c与x轴交于A(﹣1,0)、B两点,与y轴交于点C(0,2),抛物线的对称轴交x轴于点D.(1)求抛物线的解析式;(2)求sin∠ABC的值;(3)在抛物线的对称轴上是否存在点P,使△PCD是以CD为腰的等腰三角形?如果存在,直接写出点P的坐标;如果不存在,请说明理由;(4)点E是线段BC上的一个动点,过点E作x轴的垂线与抛物线相交于点F,当点E运动到什么位置时线段EF最长?求出此时E点的坐标.24. (12分)(2018·宜宾模拟) 如图,在平面直角坐标系中,矩形OABC的顶点A,C分别在x轴,y轴的正半轴上,且OA=4,OC=3,若抛物线经过O,A两点,且顶点在BC边上,对称轴交BE于点F,点D,E的坐标分别为(3,0),(0,1).(1)求抛物线的解析式;(2)猜想△EDB的形状并加以证明;(3)点M在对称轴右侧的抛物线上,点N在x轴上,请问是否存在以点A,F,M,N为顶点的四边形是平行四边形?若存在,请求出所有符合条件的点M的坐标;若不存在,请说明理由.参考答案一、选择题(共10小题,每小题3分,共30分) (共10题;共29分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、二、多项选择题(6小题,每小题3分,共18分)说明:下列各题的结 (共6题;共18分) 11-1、12-1、13-1、14-1、15-1、16-1、三、解答题(共8题,共72分) (共8题;共72分)17-1、18-1、19-1、19-2、20-1、20-2、21-1、21-2、22-1、22-2、22-3、23-1、23-2、23-3、23-4、24-1、24-2、。
2020年福建省莆田市擢英中学中考数学模拟试卷(3月份)(含答案解析)

2020年福建省莆田市擢英中学中考数学模拟试卷(3月份)一、选择题(本大题共10小题,共39.0分)1.−2018的绝对值是()D. ±2018A. 2018B. −2018C. 120182.如图是由5个完全相同的小正方体组成的几何体,则该几何体的主视图是()A.B.C.D.3.某课外兴趣小组为了解所在地区老年人的身体健康状况,分别作出了四种不同的抽样调查,你认为抽样比较合理的是()A. 在公园选择1000名老年人了解身体健康状况B. 随意调查10名老年人的健康状况C. 利用所辖派出所的户籍网随机调查10%老年人的健康状况D. 在各医院、卫生院调查100名老年人的健康状况4.有四个命题:(1)两直线平行,同旁内角相等;(2)对顶角相等;(3)如果a2>0,那么a>0;(4)同角的补角相等。
其中真命题有()个A. 1B. 2C. 3D. 45.下列计算正确的是()A. a⋅a2=a3B. (a3)2=a5C. a+a2=a3D. a6÷a2=a36.如下图,在△ABC中,AD平分外角∠CAE,∠B=30°,∠CAD=65°,则∠ACD等于()A. 50°B. 65°C. 80°D. 95°7.下列关于函数y=−2x+3的说法正确的是()A. 函数图象经过一、二、三象限B. 函数图象与y轴的交点坐标为(0,3)C. y的值随着x值的增大而增大D. 点(1,2)在函数图象上8.如图,AB是半圆的直径,点D是弧AC的中点,,则∠DAB等于()A.B.C.D.9.若ab<0,则函数y=ax2和y=ax+b在同一坐标系中的图象大致为()A. B.C. D.10.如图,四边形ACDF是正方形,∠CEA和∠ABF都是直角,且点E,A,B三点共线,AB=4,则阴影部分的面积是()A. 4B. 8C. 12D. 16二、填空题(本大题共6小题,共24.0分)11.函数y=√1−2x的自变量x的取值范围是______.1+x12.在平面直角坐标系中,已知点O(0,0),A(1,3),将线段OA向右平移3个单位,得到线段O1A1,则点O1的坐标是______ ,A1的坐标是______ .x2+bx+c经过点A(−2,0)、C(0,−3),则该抛物线的解析式为______.13.已知抛物线y=3814.如图,点A,B,C在⊙O上,∠A=60°,∠C=70°,OB=9,则AB⏜的长为_____.15.如图,在△ABC中,AD⊥BC,CE⊥AB,垂足分别为D,E,AD,CE交于一点H,已知EH=EB=9,AE=12,则CH的长是____.(k≠0,且x>0)交于点A,点A的16.如图,直线y=3x与双曲线y=kx横坐标是1,点B是双曲线上另一点,且点B的纵坐标是1,连接OB、AB,则△AOB的面积为______.三、解答题(本大题共9小题,共78.0分)17.解方程:2m2m−5−22m+5=1.18.已知:如图,点E、A、C在一条直线上,AB//CD,∠B=∠E,AC=CD.求证:BC=ED.19.先化简,再求值:x2−6x+9x2+3x ÷(1−6x+3),其中x=2.20.如图,在△ABC中,AB=AC,点D是边AB的中点.(1)尺规作图:过点D作AB的垂线DE,交BC于点E;(2)求证:4BD2=BE⋅BC21.某市将开展演讲比赛活动,某校对参加选拔的学生的成绩按A、B、C、D四个等级进行统计,绘制了如下不完整的统计表和扇形统计图,成绩等级频数频率A4nB m0.51CD15(1)求m、n的值;(2)求“C等级”所对应的扇形圆心角的度数;(3)已知成绩等级为A的4名学生中有1名男生和3名女生,现从中随机挑选2名学生代表学校参加全市比赛,求出恰好选中一男生和一女生的概率.22.如图,点E是等边△ABC内一点,且EA=EB,△ABC外一点D满足BD=AC,且BE平分∠DBC,求∠BDE的度数.23.某农场拟建两间矩形饲养室,一面靠现有墙(墙足够长),中间用一道墙隔开,并在如图所示的三处各留1m宽的门.已知计划中的材料可建墙体(不包括门)总长为27m,求饲养室占地的最大面积是多少?24.如图,在Rt△ABC中,∠C=90°,AD是角平分线,DE⊥AD交AB于E,△ADE的外接圆⊙O与边AC相交于点F,过F作AB的垂线交AD于P,交AB于M,交⊙O于G,连接GE.(1)求证:BC是⊙O的切线;(2)若tan∠G=4,BE=4,求⊙O的半径;3(3)在(2)的条件下,求AP的长.25.如图,已知抛物线y=ax2+bx+3经过点A(−1,0)和点B(3,0),点C为抛物线与y轴的交点.(1)求抛物线的解析式;(2)若点E为直线BC上方抛物线上的一点,请求出△BCE面积的最大值.(3)在(2)条件下,是否存在这样的点D(0,m),使得△BDE为等腰三角形?如果有,请直接写出点D的坐标;如果没有,请说明理由.【答案与解析】1.答案:A解析:解:−2018的绝对值是:2018.故选:A.直接利用绝对值的定义进而分析得出答案.此题主要考查了绝对值,正确把握绝对值的定义是解题关键.2.答案:A解析:解:从正面看第一层是三个小正方形,第二层左边一个小正方形,故选:A.根据从正面看得到的视图是主视图,可得答案.本题考查了简单组合体的三视图,从正面看得到的视图是主视图.3.答案:C解析:本题考查了抽样调查的可靠性,样本具有代表性是指抽取的样本必须是随机的,即各个方面,各个层次的对象都要有所体现.抽取样本注意事项就是要考虑样本具有广泛性与代表性,所谓代表性,就是抽取的样本必须是随机的,即各个方面,各个层次的对象都要有所体现.解:A.在公园调查了1000名老年人的健康状况调查不具代表性,故A错误;B.调查不具代表性、广泛性,故B错误;C.利用派出所的户籍网随机调查了该地区10%的老年人健康状况调查具有代表性、广泛性,故C正确;D.在各医院,卫生院调查了100名老年人的健康状况调查不具代表性,故D错误.故选C.4.答案:B解析:本题考查的是命题与定理有关知识,利用平行线的性质,对顶角对所给的命题进行判断即可.解:(1)两直线平行,同旁内角互补,故错误,是假命题;(2)对顶角相等,正确,是真命题(3)当a=−2时,a<0,故错误,(4)同角的补角相等,真命题.真命题的有2个,故选B.5.答案:A解析:本题考查同底数幂的乘法,幂的乘方的性质,同底数幂的除法,熟练掌握运算性质是解题的关键,合并同类项时,不是同类项的一定不能合并.根据同底数幂相乘,底数不变指数相加;幂的乘方,底数不变指数相乘;同底数相除,底数不变指数相减,对各选项分析判断后利用排除法求解.解:A、a⋅a2=a3,正确;B、应为(a3)2=a3×2=a6,故本选项错误;C、a与a2不是同类项,不能合并,故本选项错误;D、应为a6÷a2=a6−2=a4,故本选项错误.故选:A.6.答案:C解析:解:由题意可得,∠CAE=130°,∴∠BAC=50°,∴∠ACD=∠B+∠BAC=30°+50°=80°.故选C.利用角平分线的定义以及外角的性质计算.此题主要考查角平分线的定义以及外角的性质.7.答案:B解析:。
2020年春莆田砺志国际学校九下第一次月考数学卷

莆田砺志国际学校2019-2020学年下学期3月份线上考试九年级数学试卷(满分150分,考试时间120分钟)一、选择题(本大题共10个小题,每小题4分,共40分)1.实数a,b,c,d在数轴上的对应点的位置如图所示,在这四个数中,绝对值最小的数是()A. aB. bC. cD. d2.下列运算结果为2x3的是()A. x3·x3B. x3+x3C. 2x·2x·2xD. 2x6÷x23.福建的地理特点是“依山傍海”,海岸线长度居全国第二位,海岸曲折,陆地海岸线长达37515000米.数据37515000用科学记数法表示为()A.3.7515×103B. 3.7515×107C. 0.37515×108D. 37515×1034.如图,AE∥DB,∠1=84°,∠2=29°,则∠C的度数为()A.55°B.56°C.57°D.58°5.下列不等式组的解集中,能用如图所示的数轴表示的是()A.21xx<-⎧⎨>⎩B.21xx≥-⎧⎨<⎩C.21xx>-⎧⎨<⎩D.21xx>-⎧⎨≤⎩6.图①,图②分别是某厂六台机床十月份第一天和第二天生产零件数的统计图,与第一天相比,第二天六台机床生产零件数的平均数与方差的变化情况是()A. 平均数变大,方差不变B. 平均数变小,方差不变C. 平均数不变,方差变小D. 平均数不变,方差变大7.李强同学借了一本书,共480页,要在一周借期内读完,当他读了一半时,发现平时每天要多读21页才能在借期内读完,他读了前一半时,平均每天读多少页?如果设读前一半时,平均每天读x 页,则下列方程中,正确的是()A.240240721x x+=+B.480480721x x+=+C.240240721x x+=-D.480480721x x+=-(第4题图)(第1题图)(第5题图)(第6题图)8.平面直角坐标系中,将直线1:21l y x =--平移后,得到直线2:25l y x =-+,则下列平移作法正确的是( )A. 将1l 向右平移3个单位B. 将1l 向右平移6个单位C. 将1l 向左平移3个单位D. 将1l 向左平移6个单位9.给出一种运算:对于函数n y x =,规定1n y n x -'=⨯.若函数4y x =,则有34y x '=⨯,已知函数3y x =,则方程9y x '=的解是( )A .3x =B .3x =-C .120,3x x ==D .120,3x x ==- 10.已知函数2y x =与2y x c =-(c 为常数,12x -≤≤)的图象有且只有一个公共点, 则常数c 的值为( )A. 031c c <≤=-或B.103c c -≤<=或C. 13c -≤≤D. 130c c -<≤≠且 二、填空题(本大题共6个小题,每小题4分,共24分) 11.点()2,3P --到x 轴的距离是 . 12.因式分解:a 3-4a = . 13.函数13x y x -=+中,自变量x 的取值范围是 . 14.一个游戏转盘上有红、黄、蓝三种颜色,其中红、黄、蓝所在区域的扇形圆心角度数分别为60°,90°,210°.则指针落在黄色区域的概率是 .15.一次函数1y mx n =+与2y x a =-+的图象如图所示,则0mx n x a ≤+<-+的解集为 .16.如图,反比例函数y =kx (k ≠0)的图象经过△ABD 的顶点A ,B ,交BD 于点C ,AB 经过原点,点D 在y 轴上,若BD =4CD ,△OBD 的面积为15,则k 的值为 .三、解答题(本大题共9小题,共86分)17.(本小题8分)计算:()27323202053--+- (第16题图)(第15题图)18.(本小题8分)解方程组47213x y x y -=⎧⎨+=⎩19.(本小题8分)如图,点B 、E 、C 、F 在同一条直线上,AB =DE ,AC =DF ,BE =CF ,求证:AB ∥DE .20.(本小题8分)先化简,再求值:2211(1)m m m m+--÷,其中m =3+1.21.(本小题8分)点P 是平面直角坐标系中的一点且不在坐标轴上,过点P 向x 轴、y 轴作垂线段,若垂线段的长度的和为4,则点P 叫做“垂距点”,例如:如图中的点()1,3P 是“垂距点”.(1)在点()2,2A -,15,22B ⎛⎫- ⎪⎝⎭,()1,5C -是“垂距点”是 ; (2)若35,22D m m ⎛⎫⎪⎝⎭是“垂距点”,求m 的值.22.(本小题10分)某工厂生产一种产品,该产品根据质量划分为10个等级(第10等级最高),第1等级的产品每天能生产95件,每件产品可获利润6元,已知每提高一个等级,每件利润可增加2元,但每天产量减少5件,且工厂每天只能生产同一等级的产品.设生产第x 等级的产品每天的产量为y 件. (1)求y 关于x 的函数关系式;(2)该工厂当天生产产品等级为多少时,可使获得的利润最大,最大利润为多少元?23.(本小题10分)为积极响应“弘扬传统文化”的号召,某学校倡导全校学生进行经典诗词诵背活动,并在活动之后举办经典诗词大赛.为了解本次系列活动的持续效果,学校团委在活动启动之初,随机抽取部分学生调查“一周诗词诵背数量”.根据调查结果绘制成的统计图(部分)如图所示:大赛结束后一个月,再次抽查这部分学生“一周诗词诵背数量”,绘制成统计表:一周诗词诵背数量3首4首5首6首7首8首人数10 10 15 40 25 20 请根据调查的信息分析:(1)以抽查的这部分学生为样本,求“在大赛启动之初,一周诗词诵背数量不超过5首”的概率;(2)以这部分学生经典诗词大赛启动之初和结束一个月后,一周诗词诵背数量的平均数作为决策依据,说明平均每名学生一周诗词诵背数量的增长率接近16%还是22%?24.(本小题12分)如图①,已知△ABC内接于⊙O,BC交直径AD于点E,过点C作AD的垂线交AB的延长线于点G,垂足为F,连接O C.(1)求证:∠ACB=∠G;(2)如图②,连接OB,若AB=AE,1tan2CAF∠=,求AOBACFSS△△的值.图①图②25.(本小题14分)已知抛物线C :()()2210y a a x x a =-+++≠(1)无论a 为何值,抛物线C 总是经过一个定点,该定点的坐标为 . (2)无论a 为何值,该抛物线的顶点总在一条固定的直线上运动,求出该直线的解析式. (3)当02x <≤时,0y >恒成立,求a 的取值范围.。
2020年福建省莆田市擢英中学中考数学模拟试卷(3月份)(解析版)

2020年福建省莆田市擢英中学中考数学模拟试卷(3月份)一.选择题(共10小题)1.﹣3的绝对值是()A.﹣3B.3C.D.2.如图所示的几何体的主视图是()A.B.C.D.3.为了解某市老人的身体健康状况,需要抽取部分老人进行调查,下列抽取老人的方法最合适的是()A.随机抽取100位女性老人B.随机抽取100位男性老人C.随机抽取公园内100位老人D.在城市和乡镇各选10个点,每个点任选5位老人4.下列命题中,逆命题为真命题的是()A.对顶角相等B.邻补角互补C.两直线平行,同位角相等D.互余的两个角都小于90°5.下列计算正确的是()A.a2•a3=a6B.a+a=a2C.(a2)3=a6D.a8÷a2=a4 6.如图,在△ABC中,BE是∠ABC的平分线,CE是外角∠ACM的平分线,BE与CE相交于点E,若∠A=60°,则∠BEC是()A.15°B.30°C.45°D.60°7.下列关于一次函数y=kx+b(k<0,b>0)的说法,错误的是()A.图象经过第一、二、四象限B.y随x的增大而减小C.图象与y轴交于点(0,b)D.当x>﹣时,y>08.如图,AB是半圆⊙O的直径,△ABC的两边AC,BC分别交半圆于D,E,且E为BC 的中点,已知∠BAC=50°,则∠C=()A.55°B.60°C.65°D.70°9.二次函数y=ax2与一次函数y=ax+a在同一坐标系中的大致图象可能是()A.B.C.D.10.如图,已知∠ACB=90°,AC>BC,分别以△ABC的边AB,BC,CA为一边向△ABC 外作正方形ABDE,正方形BCMN,正方形CAFG,连接EF,GM,设△AEF,△CGM 的面积分别为S1,S2,则下列结论正确的是()A.S1=S2B.S1<S2C.S1>S2D.S1≤S2二.填空题(共6小题)11.函数y=的自变量x的取值范围.12.如图,在平面直角坐标系中,已知点A(2,1),点B(3,﹣1),平移线段AB,使点A 落在点A1(﹣2,2)处,则点B对应点B1的坐标为.13.若二次函数y=ax2+bx+c图象的顶点是A(2,1),且经过点B(1,0),则此函数的解析式为.14.如图,在扇形AOB中,AC为弦,∠AOB=130°,∠CAO=60°,OA=6,则的长为.15.如图,BP平分∠ABC,AP⊥BP,垂足为P,连接CP,若三角形△ABC内有一点M,则点M落在△BPC内(包括边界)的概率为.16.如图,直线y=x+m与双曲线y=交于A,B两点,作BC∥x轴,AC∥y轴,交BC于点C,则S△ABC的最小值是.三.解答题(共9小题)17.解方程:﹣=0.18.如图,点B、F、C、E在一条直线上,FB=CE,AB∥ED,AC∥FD,求证:AC=DF.19.先化简,再求值:,其中x=﹣3.20.如图,在△ABC中,∠C=90°,点D在线段AC上,且CD=2AD.求作DE⊥AC于点D,且DE交AB于点E;并求出的值.(要求:尺规作图保留作图痕迹,不写作法)21.在第二届数字中国建设峰会召开之际,某校举行了第二届“掌握新技术,走进数时代”信息技术应用大赛,将该校八年级参加竞赛的学生成绩统计后,绘制成如下统计图表(不完整):成绩频数分布统计表组别A B C D 成绩x(分)60≤x<7070≤x<8080≤x<9090≤x<100人数10m164请观察上面的图表,解答下列问题:(1)统计表中m=,D组的圆心角为°;(2)D组的4名学生中,有2名男生和2名女生.从D组随机抽取2名学生参加5G体验活动,请你画出树状图或用列表法求:①恰好1名男生和1名女生被抽取参加5G体验活动的概率;②至少1名女生被抽取参加5G体验活动的概率.22.如图,点C为线段AB上一点,△ACM与△CBN都是等边三角形,AN与MB交于P.(1)求证:AN=BM;(2)连接CP,求证:CP平分∠APB.23.某农场拟用总长为60m的建筑材料建三间矩形牛饲养室,饲养室的一面靠现有墙(墙长为40m),其中间用建筑材料做的墙隔开(如图).设三间饲养室平行于墙的一边合计用建筑材料xm,总占地面积为ym2.(1)求y关于x的函数解析式和自变量的取值范围;(2)当x为何值时,三间饲养室占地总面积最大?最大面积为多少?24.如图,在Rt△ABC中,∠ACB=90°,O是线段BC上一点,以O为圆心,OC为半径作⊙O,AB与⊙O相切于点F,直线AO交⊙O于点E,D.(1)求证:AO是△ABC的角平分线;(2)若tan∠D=,求的值;(3)如图2,在(2)条件下,连接CF交AD于点G,⊙O的半径为3,求CF的长.25.已知抛物线y=x2﹣2mx+m2﹣3(m是常数)(1)证明:无论m取什么实数,该抛物线与x轴都有两个交点.(2)设抛物线的顶点为A,与x轴的两个交点分别为B、D,点B在点D的右侧,与y 轴的交点为C.①若点P为△ABD的外心,求点P的坐标(用含m的式子表示);②当|m|≤,m≠0时,△ABC的面积是否有最大值?如果有,请求出最大值;如果没有,请说明理由.参考答案与试题解析一.选择题(共10小题)1.﹣3的绝对值是()A.﹣3B.3C.D.【分析】直接利用绝对值的定义分析得出答案.【解答】解:﹣3的绝对值是:3.故选:B.2.如图所示的几何体的主视图是()A.B.C.D.【分析】根据从正面看得到的视图是主视图,可得答案.【解答】解:主视图为:,故选:A.3.为了解某市老人的身体健康状况,需要抽取部分老人进行调查,下列抽取老人的方法最合适的是()A.随机抽取100位女性老人B.随机抽取100位男性老人C.随机抽取公园内100位老人D.在城市和乡镇各选10个点,每个点任选5位老人【分析】利用抽取的样本得当,能很好地反映总体的情况可对各选项进行判断.【解答】解:为了解某市老人的身体健康状况,需要抽取部分老人进行调查,在城市和乡镇各选10个点,每个点任选5位老人,这种抽取老人的方法最合适.故选:D.4.下列命题中,逆命题为真命题的是()A.对顶角相等B.邻补角互补C.两直线平行,同位角相等D.互余的两个角都小于90°【分析】首先写出各个命题的逆命题,再进一步判断真假.【解答】解:A、对顶角相等的逆命题是相等的角是对顶角,逆命题是假命题;B、邻补角互补的逆命题是互补的角是邻补角,逆命题是假命题;C、两直线平行,同位角相等逆命题是同位角相等,两直线平行,逆命题是真命题;D、互余的两个角都小于90°的逆命题是都小于90°的角互余,逆命题是假命题;故选:C.5.下列计算正确的是()A.a2•a3=a6B.a+a=a2C.(a2)3=a6D.a8÷a2=a4【分析】根据同底数幂相乘,底数不变指数相加;合并同类项法则;幂的乘方,底数不变指数相乘;同底数幂相乘,底数不变指数相减;对各选项分析判断后利用排除法求解.【解答】解:A、a2•a3=a2+3=a5,故本选项错误;B、a+a=2a,故本选项错误;C、(a2)3=a2×3=a6,故本选项正确;D、a8÷a2=a8﹣2=a6,故本选项错误.故选:C.6.如图,在△ABC中,BE是∠ABC的平分线,CE是外角∠ACM的平分线,BE与CE相交于点E,若∠A=60°,则∠BEC是()A.15°B.30°C.45°D.60°【分析】根据角平分线的定义得到∠EBM=∠ABC、∠ECM=∠ACM,根据三角形的外角性质计算即可.【解答】解:∵BE是∠ABC的平分线,∴∠EBM=∠ABC,∵CE是外角∠ACM的平分线,∴∠ECM=∠ACM,则∠BEC=∠ECM﹣∠EBM=×(∠ACM﹣∠ABC)=∠A=30°,故选:B.7.下列关于一次函数y=kx+b(k<0,b>0)的说法,错误的是()A.图象经过第一、二、四象限B.y随x的增大而减小C.图象与y轴交于点(0,b)D.当x>﹣时,y>0【分析】由k<0,b>0可知图象经过第一、二、四象限;由k<0,可得y随x的增大而减小;图象与y轴的交点为(0,b);当x>﹣时,y<0;【解答】解:∵y=kx+b(k<0,b>0),∴图象经过第一、二、四象限,A正确;∵k<0,∴y随x的增大而减小,B正确;令x=0时,y=b,∴图象与y轴的交点为(0,b),∴C正确;令y=0时,x=﹣,当x>﹣时,y<0;D不正确;故选:D.8.如图,AB是半圆⊙O的直径,△ABC的两边AC,BC分别交半圆于D,E,且E为BC 的中点,已知∠BAC=50°,则∠C=()A.55°B.60°C.65°D.70°【分析】连接AE,只要证明△ABC是等腰三角形,AC=AB即可解决问题;【解答】解:如图,连接AE,∵AB是直径,∴∠AEB=90°,即AE⊥BC,∵EB=EC,∴AB=AC,∴∠C=∠B,∵∠BAC=50°,∴∠C=(180°﹣50°)=65°,故选:C.9.二次函数y=ax2与一次函数y=ax+a在同一坐标系中的大致图象可能是()A.B.C.D.【分析】由一次函数y=ax+a可知,一次函数的图象与x轴交于点(﹣1,0),即可排除A、B,然后根据二次函数的开口方向,与y轴的交点;一次函数经过的象限,与y轴的交点可得相关图象进行判断.【解答】解:由一次函数y=ax+a可知,一次函数的图象与x轴交于点(﹣1,0),排除A、B;当a>0时,二次函数y=ax2开口向上,一次函数y=ax+a经过一、二、三象限,当a<0时,二次函数开口向下,一次函数经过二、三、四象限,排除C;故选:D.10.如图,已知∠ACB=90°,AC>BC,分别以△ABC的边AB,BC,CA为一边向△ABC 外作正方形ABDE,正方形BCMN,正方形CAFG,连接EF,GM,设△AEF,△CGM 的面积分别为S1,S2,则下列结论正确的是()A.S1=S2B.S1<S2C.S1>S2D.S1≤S2【分析】设直角三角形的三边分别为a、b、c,作辅助线构造全等三角形,分别表示出△AEF,△CGM的面积,进行比较即可.【解答】解:过E作ER⊥AF,交F A的延长线于R,设△ABC的三边BC,AC,AB的长分别为a、b、c,∵分别以△ABC的边AB、BC、CA为一边向△ABC外作正方形ABDE、BCMN、CAFG,∵AE=AB,∠ARE=∠ACB=90°,∠EAR=∠CAB,∴△AER≌△ABC,∴ER=BC=a,而F A=b,∴S1=ab,∵CG=b,CM=a,∴S2=ab,∴S1=S2,故选:A.二.填空题(共6小题)11.函数y=的自变量x的取值范围x≥1,且x≠3.【分析】本题主要考查自变量的取值范围,函数关系中主要有二次根式和分式两部分.根据二次根式的意义,被开方数x﹣1≥0;根据分式有意义的条件,x﹣3≠0,则函数的自变量x取值范围就可以求出.【解答】解:根据题意得:解得x≥1,且x≠3,即:自变量x取值范围是x≥1,且x≠3.12.如图,在平面直角坐标系中,已知点A(2,1),点B(3,﹣1),平移线段AB,使点A 落在点A1(﹣2,2)处,则点B对应点B1的坐标为(﹣1,0).【分析】由点A(2,1)平移后A1(﹣2,2)可得坐标的变化规律,由此可得点B的对应点B1的坐标.【解答】解:由点A(2,1)平移后A1(﹣2,2)可得坐标的变化规律是:横坐标减4,纵坐标加1,∴点B的对应点B1的坐标(﹣1,0).故答案为(﹣1,0).13.若二次函数y=ax2+bx+c图象的顶点是A(2,1),且经过点B(1,0),则此函数的解析式为y=﹣x2+4x﹣3.【分析】设抛物线的解析式为y=a(x﹣2)2+1,将点B(1,0)代入解析式即可求出a 的值,从而得到二次函数解析式.【解答】解:设抛物线的解析式为y=a(x﹣2)2+1,将B(1,0)代入y=a(x﹣2)2+1得,0=a+1∴a=﹣1,∴函数解析式为y=﹣(x﹣2)2+1,所以该抛物线的函数解析式为y=﹣x2+4x﹣3,故答案为y=﹣x2+4x﹣3.14.如图,在扇形AOB中,AC为弦,∠AOB=130°,∠CAO=60°,OA=6,则的长为π.【分析】连接OC,如图,利用等腰三角形的性质和三角形内角和可计算出∠AOC=60°,则∠BOC=70°,然后根据弧长公式计算的长.【解答】解:连接OC,如图,∵OA=OC,∴∠OCA=∠CAO=60°,∴∠AOC=60°,∴∠BOC=130°﹣60°=70°,∴的长==π.故答案为π.15.如图,BP平分∠ABC,AP⊥BP,垂足为P,连接CP,若三角形△ABC内有一点M,则点M落在△BPC内(包括边界)的概率为.【分析】据已知条件证得△ABP≌△EBP,根据全等三角形的性质得到AP=PE,得出S=S△EBP,S△ACP=S△ECP,推出S△PBC=S△ABC,根据概率公式可得的答案.△ABP【解答】解:延长AP交BC于E,∵BP平分∠ABC,∴∠ABP=∠EBP,∵AP⊥BP,∴∠APB=∠EPB=90°,在△ABP和△EBP中,,∴△ABP≌△EBP(ASA),∴AP=PE,∴S△ABP=S△EBP,S△ACP=S△ECP,∴S△PBC=S△ABC,则点M落在△BPC内(包括边界)的概率=.故答案为.16.如图,直线y=x+m与双曲线y=交于A,B两点,作BC∥x轴,AC∥y轴,交BC于点C,则S△ABC的最小值是12.【分析】设A(a,),B(b,),则C(a,).将y=x+m代入y=得x+m=,得到a+b=﹣m,ab=﹣6,求得S△ABC=m2+12,当m=0时,△ABC的面积有最小值12【解答】解:设A(a,),B(b,),则C(a,).将y=x+m代入y=得x+m=,整理,得x2+mx﹣6=0,则a+b=﹣m,ab=﹣6,∴(a﹣b)2=(a+b)2﹣4ab=m2+24.∵S△ABC=AC•BC=(﹣)(a﹣b)=••(a﹣b)=(a﹣b)2=(m2+24)=m2+12,∴当m=0时,△ABC的面积有最小值12.故答案为12.三.解答题(共9小题)17.解方程:﹣=0.【分析】分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.【解答】解:去分母得:x+1﹣2x=0,解得:x=1,经检验x=1是分式方程的解.18.如图,点B、F、C、E在一条直线上,FB=CE,AB∥ED,AC∥FD,求证:AC=DF.【分析】求出BC=EF,根据平行线性质求出∠B=∠E,∠ACB=∠DFE,根据ASA推出△ABC≌△DEF即可.【解答】证明:∵FB=CE,∴FB+FC=CE+FC,∴BC=EF,∵AB∥ED,AC∥FD,∴∠B=∠E,∠ACB=∠DFE,∵在△ABC和△DEF中,,∴△ABC≌△DEF(ASA),∴AC=DF.19.先化简,再求值:,其中x=﹣3.【分析】先根据分式混合运算的法则把原式进行化简,再x的值代入原式进行计算即可.【解答】解:原式=•=,当x=﹣3时,原式==.20.如图,在△ABC中,∠C=90°,点D在线段AC上,且CD=2AD.求作DE⊥AC于点D,且DE交AB于点E;并求出的值.(要求:尺规作图保留作图痕迹,不写作法)【分析】根据垂直平分线垂线的作法作出AC的垂线,再证明△ADE∽△ACB,可得=,由此即可解决问题.【解答】解:AC的垂线如图所示.∵∠ADE=∠C=90°,∠A=∠A,∴△ADE∽△ACB,∴=,∵CD=2AD,∴AC=3AD,即=,∴=.21.在第二届数字中国建设峰会召开之际,某校举行了第二届“掌握新技术,走进数时代”信息技术应用大赛,将该校八年级参加竞赛的学生成绩统计后,绘制成如下统计图表(不完整):成绩频数分布统计表组别A B C D 成绩x(分)60≤x<7070≤x<8080≤x<9090≤x<100人数10m164请观察上面的图表,解答下列问题:(1)统计表中m=20,D组的圆心角为28.8°;(2)D组的4名学生中,有2名男生和2名女生.从D组随机抽取2名学生参加5G体验活动,请你画出树状图或用列表法求:①恰好1名男生和1名女生被抽取参加5G体验活动的概率;②至少1名女生被抽取参加5G体验活动的概率.【分析】(1)先根据A组人数及其所占百分比求出总人数,由各组人数之和等于总人数求出B组人数m的值,用360°乘以D组人数所占比例可得;(2)列表得出所有等可能结果,从中找到符合条件的结果数,再根据概率公式计算可得.【解答】解:(1)被调查的总人数为10÷20%=50,则m=50﹣(10+16+4)=20,D组的圆心角是360°×=28.8°,故答案为:20、28.8;(2)①设男同学标记为A、B;女学生标记为1、2,可能出现的所有结果列表如下:A B12A/(B,A)(1,A)(2,A)B(A,B)/(1,B)(2,B)1(A,1)(B,1)/(2,1)2(A,2)(B,2)(1,2)/共有12 种可能的结果,且每种的可能性相同,其中刚好抽到一男一女的结果有8种,∴恰好1名男生和1名女生被抽取参加5G体验活动的概率为=;②∵至少1名女生被抽取参加5G体验活动的有10种结果,∴至少1名女生被抽取参加5G体验活动的概率为=.22.如图,点C为线段AB上一点,△ACM与△CBN都是等边三角形,AN与MB交于P.(1)求证:AN=BM;(2)连接CP,求证:CP平分∠APB.【分析】(1)由“SAS”可证△ACN≌△MCB,可得AN=BM;(2)由全等三角形的性质可得S△ACN=S△MCB,由三角形的面积可得CE=CF,由角平分线的性质可得结论.【解答】证明:(1)∵△ACM与△CBN都是等边三角形,∴AC=CM,CN=CB,∠ACM=∠BCN=60°,∴∠ACN=∠BCM=120°,且AC=CM,CN=CB,∴△ACN≌△MCB(SAS)∴AN=BM;(2)如图,过点C作CE⊥AN于点E,作CF⊥BM于点F,∵△ACN≌△MCB,∴S△ACN=S△MCB,∴×AN×CE=×BM×CF,且AN=BM,∴CE=CF,且CE⊥AN于,CF⊥BM,∴CP平分∠APB.23.某农场拟用总长为60m的建筑材料建三间矩形牛饲养室,饲养室的一面靠现有墙(墙长为40m),其中间用建筑材料做的墙隔开(如图).设三间饲养室平行于墙的一边合计用建筑材料xm,总占地面积为ym2.(1)求y关于x的函数解析式和自变量的取值范围;(2)当x为何值时,三间饲养室占地总面积最大?最大面积为多少?【分析】(1)设饲养室长为x(m),则宽为(60﹣x)m,根据长方形面积公式即可得,由墙可用长≤40m可得x的范围;(2)把函数关系式化成顶点式,然后根据二次函数的性质即可得到结论.【解答】解:(1)根据题意得,y=x•(60﹣x)=﹣x2+15x,自变量的取值范围为:0<x≤40;(2)∵y=﹣x2+15x=﹣(x﹣30)2+225,∴当x=30时,三间饲养室占地总面积最大,最大为225(m2).24.如图,在Rt△ABC中,∠ACB=90°,O是线段BC上一点,以O为圆心,OC为半径作⊙O,AB与⊙O相切于点F,直线AO交⊙O于点E,D.(1)求证:AO是△ABC的角平分线;(2)若tan∠D=,求的值;(3)如图2,在(2)条件下,连接CF交AD于点G,⊙O的半径为3,求CF的长.【分析】(1)连接OF,可得OF⊥AB,由∠ACB=90°,OC=OF,可得出结论;(2)连接CE,先求证∠ACE=∠ODC,然后可知△ACE∽△ADC,所以,而tan ∠D==;于是得到结论;(3)连接CF交AD于点M,由(2)可知,AC2=AE•AD,先求出AE,AC的长,则AO可求出,证△CMO∽△ACO,可得OC2=OM•OA,求出OM,CM,则CF=2CM可求解.【解答】(1)证明:连接OF,∵AB与⊙O相切于点F,∴OF⊥AB,∵∠ACB=90°,OC=OF,∴∠OAF=∠OAC,即AO是△ABC的角平分线;(2)如图2,连接CE,∵ED是⊙O的直径,∴∠ECD=90°,∴∠ECO+∠OCD=90°,∵∠ACB=90°,∴∠ACE+∠ECO=90°,∴∠ACE=∠OCD,∵OC=OD,∴∠OCD=∠ODC,∴∠ACE=∠ODC,∵∠CAE=∠CAE,∴△ACE∽△ADC,∴,∵tan∠D=,∴,∴;(3)由(2)可知:=,∴设AE=x,AC=2x,∵△ACE∽△ADC,∴,∴AC2=AE•AD,∴(2x)2=x(x+6),解得:x=2或x=0(不合题意,舍去),∴AE=2,AC=4,∴AO=AE+OE=2+3=5,如图3,连接CF交AD于点M,∵AC,AF是⊙O的切线,∴AC=AF,∠CAO=∠OAF,∴CF⊥AO,∴∠ACO=∠CMO=90°,∵∠COM=∠AOC,∴△CMO∽△ACO,∴,∴OC2=OM•OA,∴OM=,∴CM===,∴CF=2CM=.25.已知抛物线y=x2﹣2mx+m2﹣3(m是常数)(1)证明:无论m取什么实数,该抛物线与x轴都有两个交点.(2)设抛物线的顶点为A,与x轴的两个交点分别为B、D,点B在点D的右侧,与y 轴的交点为C.①若点P为△ABD的外心,求点P的坐标(用含m的式子表示);②当|m|≤,m≠0时,△ABC的面积是否有最大值?如果有,请求出最大值;如果没有,请说明理由.【分析】(1)令y=0,转化成一元二次方程,计算△,判断出△大于0,即可得出结论;(2)①先求出点A的坐标,再求出BD,进而得出BE,再利用勾股定理求出外接圆的半径,即可得出结论;②先求出点B的坐标,点C的坐标,利用坐标系中求三角形面积的计算方法得出S与m的函数关系式,即可得出结论.【解答】解:(1)针对于抛物线y=x2﹣2mx+m2﹣3,令y=0,则0=x2﹣2mx+m2﹣3,而△=(﹣2m)2﹣4(m2﹣3)=12>0,∴方程x2﹣2mx+m2﹣3=0有两个不相等的实数根,即:无论m取什么实数,该抛物线与x轴都有两个交点;(2)①如图1,∵抛物线y=x2﹣2mx+m2﹣3=(x﹣m)2﹣3,∴A(m,﹣3),设点D(x1,0),B(x2,0),∴x1+x2=2m,x1x2=m2﹣3,∴BD=x2﹣x1===2,过点A作平行于y轴的直线,交x轴于点E,则AE⊥x轴,∴∠AEB=90°,∵点A(m,﹣3)是抛物线的顶点,∴AE=3,BE=BD=,∴P为△ABD的外心,∴点P在AE上,连接BP,设△ABD的外接圆的半径为r,则AP=BP=r,∴PE=AE﹣r=3﹣r,在Rt△BEP中,根据勾股定理得,PE2+BE2=BP2,∴(3﹣r)2+3=r2,∴r=2,∴PE=AE﹣AP=1,∴P(m,1);②如图2,针对于抛物线y=x2﹣2mx+m2﹣3,令y=0,则x2﹣2mx+m2﹣3=0,∴x=,∵点B在点D的右侧,∴B(m+,0),令x=0,则y=m2﹣3,∴C(0,m2﹣3),∴直线BC的解析式为y=(﹣m)x+m2﹣3,过点A作y轴的平行线,交BC于F,则F(m,m﹣3),当m>0时,AF=m﹣3+3=m,∴S△ABC=AF•|x B﹣x C|=×m×(m+)=(m2+m)=[(m+)2﹣]=(m+)2﹣,当m<0时,S△ABC=(m+)2﹣即:S△ABC=(m+)2﹣∵|m|≤,m≠0,∴﹣≤m≤,且m≠0,即:当m=时,S△ABC最大=×(+)2﹣=3.。
福建省莆田市擢英中学2020届数学中考模拟试卷
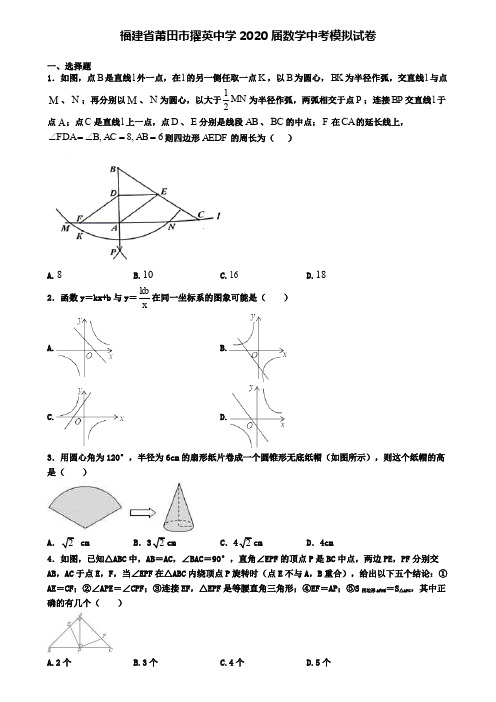
福建省莆田市擢英中学2020届数学中考模拟试卷一、选择题1.如图,点B 是直线l 外一点,在l 的另一侧任取一点K ,以B 为圆心,BK 为半径作弧,交直线l 与点M 、N ;再分别以M 、N 为圆心,以大于12MN 为半径作弧,两弧相交于点P ;连接BP 交直线l 于点A ;点C 是直线l 上一点,点D 、E 分别是线段AB 、BC 的中点;F 在CA 的延长线上,,8,6FDA B AC AB ∠=∠==则四边形AEDF 的周长为( )A.8B.10C.16D.182.函数y =kx+b 与y =kbx在同一坐标系的图象可能是( )A. B.C. D.3.用圆心角为120°,半径为6cm 的扇形纸片卷成一个圆锥形无底纸帽(如图所示),则这个纸帽的高是( )A cmB .cmC .cmD .4cm4.如图,已知△ABC 中,AB =AC ,∠BAC =90°,直角∠EPF 的顶点P 是BC 中点,两边PE ,PF 分别交AB ,AC 于点E ,F ,当∠EPF 在△ABC 内绕顶点P 旋转时(点E 不与A ,B 重合),给出以下五个结论:①AE =CF ;②∠APE =∠CPF ;③连接EF ,△EPF 是等腰直角三角形;④EF =AP ;⑤S 四边形AFPE =S △APC ,其中正确的有几个( )A.2个B.3个C.4个D.5个524a=5===;④=)A.①B.②C.③D.④6.数据2060000000科学记数法表示为()A.206×107B.20.6×108C.2.06×108D.2.06×1097.在平面直角坐标系中,正方形A1B1C1D1,D1E1E2B2,A2D2C2D2,D2E3E4B3,A3B3C3D3,…,按如图所示的方式放置,其中点B1在y轴上,点C1,E1,E2,C2,E3,E4,C3,…,在x轴上已知正方形A1,B1,C1,D1,的边长为1,∠OB1C1=30°,B1C1∥B2C2∥B3C3,…,则正方形A n B n∁n D n的边长是()A.12n⎛⎫⎪⎝⎭B.112n-⎛⎫⎪⎝⎭C.3D.13-8.下列计算正确的是()A.a2⋅a3=a6B.a6÷a3=a2C.(ab)2=ab2D.(﹣a2)3=﹣a69.sin30︒的值等于( )A.12B.1 C.2D.10.如图,△ABC中,BC=2,DE是它的中位线,下面三个结论:(1)DE=1;(2)△ADE∽△ABC;(3)△ADE的面积与△ABC的面积之比为1:4.其中正确的有()A.0个B.1个C.2个D.3个11.正比例函数y=kx(k≠0)的图象上一点A到x轴的距离与到y轴的距离之比为2 : 3,且y随x的增大而减小,则k的值是 ( )A.23B.32C.32-D.23-12.(11·丹东)如图,在Rt△ABC中,∠C=90°, BE平分∠ABC,ED垂直平分AB于D,若AC=9,则AE的值是()A.B.C.6 D.4二、填空题13.将从1开始的连续自然数按以下规律排列:则14.圆内一条弦与直径相交成30°的角,且分直径1cm和5cm两段,则这条弦的长为_____.15.若方程x2+2x-11=0的两根分别为m、n,则mn(m+n)=______.16.若关于x的分式方程7311+=--mx x有增根,则m的值为________。
福建省莆田市擢英中学 九年级中考模拟考试数学试题

O 1((满分:150分,考试时间:120分钟)一、精心选一选(本大题共8小题,每小题4分,共32分) 1、在实数5、37). A 5 B 37CD2、下列运算中正确的是 ( )A.2325a a a +=B.22(2)(2)4a b a b a b +-=- C .23622a a a ⋅= D .222(2)4a b a b +=+ 3、4的算术平方根是A. 2B. -2C. ±2D. 4 4、左下图为主视方向的几何体,它的俯视图是( )5、如图,小红居住的小区内有一条笔直的小路,小路的正中间有一路灯,晚上小红由A 处径直走到B 处,她在灯光照射下的影长l 与行走的路程s 之间的变化关系用图象刻画出来,大致图象是6、如图,在边长为1的小正方形组成的网格中,半径为2的⊙O 1的圆心O 1在格点上,将一个与⊙O 1重合的等圆,向右平移2个单位,再向上平移2个单位得到⊙O 2,则⊙O 2与⊙O 1的位置关系是( ) A .内切 B .外切 C .相交 D .外离 7、下列说法不正确的是 A .某种彩票中奖的概率是11000,买1000张该种彩票一定会中奖 B .了解一批电视机的使用寿命适合用抽样调查C .若甲组数据的标准差S 甲=0.31,乙组数据的标准差S 乙=0.25,则乙组数据比甲组数据稳定D .在一个装有白球和绿球的袋中摸球,摸出黑球是不可能事件8、如图是二次函数y=31x 2—999x+892的图象,对于方程31x 2—999x+892=0的根,下列叙述正确的是( ) A .两根相异,且均为正根 B .两根相异,且只有一个正根 C .两根相同,且为正根 D .两根相同,且为负根 二、细心填一填(本大题共8小题,每小题4分,共32分)9、上海世博会“中国馆”的展馆面积为15800平方米,这个数据用科学记数法可表示为 平方米(保留2个有效数字) 10、不等式组⎩⎨⎧>-<-21312x x 的解集是___________.11、一个多边形的内角和是外角和的2倍,则这个多边形是 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2019~2020莆田擢英中学初三寒假测试卷
一、选择题(每小题4分,共40分)1.-3的绝对值是(
)A.-3
B.3
C.
3
1 D.-
3
12.如图所示的几何体的主视图是(
)
3.为了解某市老人的身体健康状况,需要抽取部分老人进行调查,下列抽取老人的方法最合适的是(
)
A.随机抽取100位女性老人
B.随机抽取100位男性老人
C.随机抽取公园内100位老人
D.在城市和乡镇各选10个点,每个点任选5位老人4.下列命题中,逆命题为真命题的是()A.对顶角相等
B.邻补角互补
C.两直线平行,同位角相等
D.互余的两个角都小于90o
5.下列计算正确的是(
)
A.a 2·a 3=a 6
B.(2a )2=2a 2
C.(a 2)3=a 6
D.a 8÷a 4=a 26.如图,在△ABC 中,BE 是∠ABC 的平分线,CE 是外角∠ACM 的平分线,它们交于点E ,若60A ∠=o ,则∠BEC 度数是()A.15°
B.30°
C.45°
D.60°
7.下列关于一次函数y kx b =+(00k b <>,)的说法,错误的是()
A.图象经过第一、二、四象限
B.y 随x 的增大而减小
C.图象与y 轴交于点(0)
b , D.当b x k
>-时,0
y >8.如图,AB 是半圆O 的直径,△ABC 的两边AC 、BC 分别交半圆于D 、E 两点,且E 为BC 的中点.已知∠BAC=50°,则∠C 的度数为(
)
A.55°
B.60°
C.65°
D.70°
9.二次函数2y ax =和一次函数y ax a =+在同一平面直角坐标系的大致图象可能是(
)
A .
B .
C .
D .
x
y O
1
-x
y
O
1-x
y O
1-x
y
O
1-A
B
C
M
E
10.如图,在Rt △ABC 中,90ACB ∠=o ,分别以△ABC 的边AB 、BC 、CA 为一边向△ABC 外作正方形ABDE 、正方形BCMN 、正方形CAFG ,连接EF 、GM ,
设△AEF 、△CGM 的面积分别为1S 、2S ,则下列结论正确的是()
A.12
S S = B.12
S S < C.12
S S > D.12
S S ≤二、填空题(每小题4分,共24分)11.函数y =的自变量x 的取值范围
.
12.如图,在平面直角坐标系中,已知点(21)A ,,点(31)B -,,平移线段AB ,使点A 落在点1(22)A -,处,则点B 对应点1B 的坐标为
.
13.若二次函数2y ax bx c =++图象的顶点是(21)A ,,且经过点(10)B ,,则此函数的解析式为
.
14.如图,在扇形AOB 中,AC 为弦,∠AOB =130°,∠CAO =60°,OA =6,则BC 的长为______________.
15.如图,BP 平分∠ABC ,AP ⊥BP ,垂足为P ,连接CP ,若三角形△ABC 内有一点M ,则点M 落在△BPC 内(包括边界)的概率为
.
16.如图,直线y x m =+与双曲线6y x
=交于A ,B 两点,作BC //x 轴,AC //y 轴,交BC 于点C ,则S △ABC 的最小值是.
三、解答题(共86分)17.(本小题满分8分)解方程:
01
21
=+-x x .18.如图,点B 、F 、C 、E 在一条直线上,FB CE =,AB ∥ED ,AC ∥FD .求证:AB DE =,AC DF =.
A
B
C
P
F
E
A B
C D
A B C D
E F G
M
N
19.先化简,再求值:
22
144111x x x x -+⎛⎫-÷ ⎪--⎝⎭,其中3x =-.
20.如图,在△ABC 中,∠C=90°,点D 在线段AC 上,且CD=2AD.求作DE ⊥AC 于
点D,且DE 交AB 于点E;并求出BC
DE
的值.(要求:尺规作图保留作图痕迹,不写作
法)
21.在第二届数字中国建设峰会召开之际,某校举行了第二届“掌握新技术,走进数时代”信息技术应用大赛,将该校八年级参加竞赛的学生成绩统计后,绘制成如下统计图表(不完整):
成绩频数分布统计表成绩扇形统计图
组
别
A
B
C
D
成绩x (分)6070
x <≤7080
x <≤8090
x <≤90100
x <≤人
数
10m 164
请观察上面的图表,解答下列问题:(1)统计表中m =
,D 组的圆心角为
o
;
(2)D 组的4名学生中,有2名男生和2名女生.从D 组随机抽取2名学生参加5G 体验活动,请你画出树状图或用列表法求:
①恰好1名男生和1名女生被抽取参加5G 体验活动的概率;②至少1名女生被抽取参加5G 体验活动的概率.
22.如图,点C 为线段AB 上一点,ACM △与CBN △都是等边三角形,AN 与MB 交于P .(1)求证:AN BM =;
(2)连接CP ,求证:CP 平分∠APB.
A 20%B
C
D
23.某农场拟用总长为60m 的建筑材料建三间矩形牛饲养室,饲养室的一面靠现有墙(墙长为40m ),其中间用建筑材料做的墙隔开(如图).设三间饲养室平行于墙的一边合计用建筑材料m x ,总占地面积为2m y .
(1)求y 关于x 的函数解析式和自变量的取值范围;
(2)当x 为何值时,三间饲养室占地总面积最大?最大面积为多少?
24.如图,在Rt ABC △中,ACB ∠=90o ,O 是线段BC 上一点,以O 为圆心,OC 为半径作
O ,AB 与O 相切于点F ,直线AO 交O 于点E ,D .
(1)求证:AO 是ABC △的角平分线;(2)若1tan 2
D ∠=,求A
E AC
的值;
(3)如图2,在(2)条件下,连接CF 交AD 于点G ,O 的半径为3,求CF 的长.
25.(本小题满分14分)已知抛物线y=x 2-2mx+m 2-3(m 是常数)(1)证明:无论m 取什么实数,该抛物线与x 轴都有两个交点.
(2)设抛物线的顶点为A,与x 轴的两个交点分别为B 、D,点B 在点D 的右侧,与y 轴的交点为C.
①若点P 为△ABD 的外心,求点P 的坐标(用含m 的式子表示);
②当|m|≤3,m≠0时,△ABC 的面积是否有最大值?如果有,请求出最大值;如果没有,请说明理由
.
A
B
C
D
E O
一、选择题
1-5BADCC6-10BDCDA 二、填空题
11.
12.
13.
14.
15.
16.
三、解答题
17.
18.19.
20.
莆田擢英中学初三寒假测数学试卷答案
21.
22.23.
24.
25。
