高中数学算法与程序框图训练题
高中数学《算法---程序框图》典型例题练习(含答案)
高中数学《算法---程序框图》典型例题练习（含答案）算法与程序框图在高考中常以小题出现，难度不大，主要考察循环结构。
在处理这类问题时关键在于计算的准确。
一、基础知识：读框图时，要抓住“看头，审尾，记过程”这三点1、看头：观察框图中变量的个数，以及赋予的初始值2、审尾：强调细致的“审查”循环结束时，变量所取到的最后一个值，这也是易错点3、记过程：为了保证计算的准确，在读取框图的过程中，可详细记录循环体中每经过一个步骤，变量取值的变化情况，以便于在跳出循环时能快速准确得到输出变量的值二、典型例题：例1：执行下图所示的程序框图，若输入2x =，则输出y 的值为 .思路：通过框图的判断语句可知y 关于x 的函数为：2321,01,012,1x x y x x x x x −<⎧⎪=+≤<⎨⎪+≥⎩，所以当2x =时，322212y =+⋅=答案：12例2：阅读右边的程序框图，运行相应的程序，则输出的值为（ ）A ．3B ．4C ．5D ．6思路：循环的流程如下：① 1,2i a ==② 2,5i a ==③ 3,16i a ==④ 4,65i a ==i循环终止，所以4i =答案：B例3：某程序框图如图所示，若输出的57S =，则判断框内为（ ）A. 4?k >B. 5?k >C. 6?k >D. 7?k >思路：循环的流程如下：① 2,4k S ==② 3,11k S ==③ 4,26k S ==④ 5,57k S ==所以应该在此时终止，所以填入4?k >答案：A例4：执行右面的程序框图，如果输入的N 是6，那么输出的p 是（ ）A. 120B. 720C. 1440D. 5040思路：循环的流程如下：① 1p =② 2,2k p ==③ 3,6k p ==④ 4,24k p ==⑤ 5,120k p ==⑥ 6,720k p ==答案：B例5：右图是一个算法的流程图，则输出S 的值是______ 第4题思路：循环的流程如下： ① 1123S =+=② 22,327n S ==+=③ 33,7215n S ==+=④ 44,15231n S ==+=⑤ 55,31263n S ==+=循环结束，所以63S =答案：63S =例6：执行如图所示的程序框图，若输出i 的值为2，则输入x 的最大值是( )A ．5B ．6C ．22D ．33思路：因为输出的2i =，说明只经过了一次循环。
高一数学算法和程序框图试题答案及解析
高一数学算法和程序框图试题答案及解析1.如图所示，程序框图（算法流程图）的输出结果是（）A．B．C．D．【答案】A【解析】条件成立，第一次执行循环体，条件成立，第二次执行循环体条件成立，第三次执行循环体；条件不成立，退出循环，输出.【考点】程序框图的识别和应用.2.若某程序图如图所示，则该程序运行后输出的k的值是（）A．4B．5C．6D．7【答案】B【解析】第一次执行循环体，.第二次执行循环体，,.第三次执行循环体，【考点】理解程序框图的逻辑结构.3.如下图所示程序框图，已知集合是程序框图中输出的值}，集合是程序框图中输出的值},全集U=Z，Z为整数集，当时，等于( )A．B．{-3. -1，5，7}C．{-3, -1，7}D．{-3, -1,7，9}【答案】D.【解析】依次执行程序框图中的语句：，；，；，；，；，；，；，；∴，，∴.【考点】读程序框图.4.在如图所示的程序框图中，输入A=192，B=22，则输出的结果是( ).A．0B．2C．4D．6【答案】B.【解析】本题要注意的是C是A除以B所得的余数，按程序框图可知有如下过程：原来：,第一次：C=16,A=22,B=16；第二次：C=6,A=16,B=6；第三次：C=4,A=6,B=4；第四次：C=2,A=4,B=2；第五次：C=0,A=2,B=0，此时B=0，则输出A=2，故选B.【考点】读懂程序框图的流程，赋值语句（如A=B，是把B的值赋值给A）.5.如果执行右边的程序框图，那么输出的（）A．22B．46C．94D．190【答案】C【解析】.运行第1次，=1，=1，=2，=4，=2＞5，否，循环；运行第2次，=3，=10，=3＞5，否，循环；运行第3次，=4，=22，=4＞5，否，循环；运行第4次，=5，=46，=5＞5，否，循环；运行第5次，=6，=94，=6＞5，是，输出S=94，故选C【考点】程序框图6.按右边程序框图运算：若，则运算进行几次才停止？A．B．C．D．【答案】C【解析】第一次循环，第二次循环，第三次循环，第四次循环，第五次循环。
高三数学算法和程序框图试题
高三数学算法和程序框图试题1.执行下图所示的程序框图，若输入A=2014，B=125，输出的A的值是____ ．【答案】1【解析】：第一次循环：,,第二次循环：，,第三次循环：,,第四次循环：,,否，所以输出【考点】程序框图的循环结构2.某流程图如图所示，现输入如下四个函数，则可以输出的函数是（）A．B．C．D．【答案】C【解析】根据程序框图知输出的函数为奇函数，并且此函数存在零点．经验证：不存在零点；不存在零点；为偶函数，且的定义域为全体实数，且，故此函数为奇函数，且令，得，函数存在零点，答案C 【考点】程序框图、函数的奇偶性、函数零点．3.（5分）（2011•陕西）如图框图，当x1=6，x2=9，p=8.5时，x3等于（）A．7B．8C．10D．11【答案】B的值．【解析】从程序框图中得到求p的解析式；列出方程，求出x3解：∵∴=8解得x3故选B点评：本题考查通过程序框图能判断出框图的功能．4.执行如图所描述的算法程序,记输出的一列的值依次为,其中且.(1)若输入,写出全部输出结果.(2)若输入,记,求与的关系().【答案】(1)输出结果共4个,依次是:.(2).【解析】(1)这是一个循环结构，依次写出每次循环的结果即可.（2）由框图中可得当时，.再由可得.将代入即可得与的关系.(1)这是一个循环结构，前4次输出的为：，第5次循环的结果为，与相等，故结束循环.所以输出的为：.（2）当时，..【考点】1、程序框图；2、递推数列.5.已知一个算法的程序框图如图所示，当输出的结果为0时，输入的值为（）A．或B．或C．或D．或【答案】C【解析】当时，，即；当时，，即，所以输入的x的值为1或-2.【考点】程序框图.6.按照下图的程序图计算，若开始输入的值为3，则最后输出的结果是（）A．6B．21C．5050D．231【答案】D【解析】由程序框图，输入，第次进入循环体，，第次进入循环体，，第次进入循环体，，成立，输出结果，故选．【考点】程序框图.7.给出30个数：1，2,4,7，……其规律是：第1个数是1；第2个数比第1个数大1；第3个数比第2个数大2；第4个数比第3个数大3；……以此类推，要计算这30个数的和，现已给出了该问题的程序框图如图所示，那么框图中判断框①处和执行框②处应分别填入（）A．B．C．D．【答案】【解析】由于要计算30个数的和，故循环要执行30次，由于循环变量的初值为1，步长为1，故终值应为30，即①中应填写；又由第1个数是1；第2个数比第1个数大1；第3个数比第2个数大2；第4个数比第3个数大3；…故②中应填写故选【考点】循环结构.8.阅读如下程序框图，如果输出，那么空白的判断框中应填入的条件是A．B．C．D．【答案】B【解析】由程序框图知前3次运算结果：因此终止条件为,故选B.【考点】本题主要考查算法的基本思想、算法的结构和功能，考查抽象思维能力和逻辑推理能力.9.图中，，，为某次考试三个评阅人对同一道题的独立评分，为该题的最终得分，当，，时，等于（）A．11B．10C．8D．7【答案】C【解析】先读懂右图的逻辑顺序，然后进行计算判断，其中判断条件是否成立是解答本题的关键．，,不成立,即为“否”，所以再输入；由绝对值的意义（一个点到另一个点的距离）和不等式知，点到点的距离小于点到的距离，所以当时，成立，即为“是”，此时，所以，即，解得，不合题意；当时，不成立，即为“否”，此时，所以，即，解得，符合题意，故选C．10.如图所示的程序框图，输出的S的值为()A．B．2C．－1D．－【答案】A【解析】k＝1时，S＝2，k＝2时，S＝，k＝3时，S＝－1，k＝4，S＝2，……所以S是以3为周期的循环．故当k＝2 012时，S＝．11.程序框图（即算法流程图）如下图所示，其输出结果是．【答案】127【解析】运行该程序框图如下故填127【考点】程序框图12.右图是计算值的一个程序框图，其中判断框内应填入的条件是A．B．C．D．【答案】A【解析】判断框内应该填循环终止条件，∵要加到，一共加4次∴k＞5.【考点】程序框图.13.执行如图所示的程序框图，输出的S＝________．【答案】【解析】执行第一次循环时S＝，i＝1；第二次循环S＝，i＝2，此时退出循环．故输出S＝.14.定义某种运算S=a⊗b,运算原理如图所示,则式子: +的值是.【答案】4【解析】2tan ="2,ln" e=1,∵2>1,∴⊗ln e==3;lg 100=2,=3,∵2<3,∴lg 100⊗==1.∴+=4.15.程序框图如图所示，该程序运行后输出的的值是（）A．B．C．D．【解析】由程序框图知：…，可知S出现周期为4，当时，结束循环输出S，,即输出的，故选D.【考点】程序框图.16.执行如图所示的程序框图，若输入，则输出的值为 .【答案】.【解析】满足条件，执行第一次循环，，；满足条件，执行第二次循环，，；满足条件，执行第三次循环，，；不满足条件，跳出循环体，输出的值为.【考点】算法与程序框图17.一个算法的程序框图如图，则其输出结果是（）A．0B．C．D．【解析】由题意可知：.【考点】1.程序框图；2.三角函数的周期性.18.阅读下边的程序框图，如果输出的函数值在区间内，则输入的实数的取值范围是．【答案】【解析】本题程序框图所反映的数学问题就是当函数的值域为时，求定义域.，，.【考点】程序框图与函数的定义域.19.阅读如图所示的程序框图，运行相应的程序．若输入某个正整数n后，输出的S∈(31，72)，则n的值为( )A．5B．6C．7D．8【答案】A【解析】由程序框图可知：运行第一次：运行第二次：运行第三次：运行第四次：运行第五次：运行第六次：因为，所以运行第五次后应结束，则判断框中的条件应为，所以答案应选B.【考点】循环结构.20.执行如图所示的框图，若输出结果为3，则可输入的实数值的个数为（）A．1B．2C．3D．4【答案】C【解析】若输入的时，则，当输出结果是，即，解得；若输入的时，则，当输出结果为，即，解得.则可输入的实数值的个数为3.故选C.【考点】1.程序框图的应用；2.指数与对数的运算.21.某算法的程序框图如图所示，如果输出的结果是26，则判断框内应为A．K>1B．K>2C．K>3D．K>4【答案】C【解析】第一次循环，否，；第二次循环，否，；第三次循环，否，；第四次循环，是，输出，运行结束，故判断框内应为K>3，选C.【考点】算法与程序框图22.已知函数f(x)＝ax3＋x2在x＝－1处取得极大值，记g(x)＝。
高中数学高考总复习-----算法与程序框图巩固练习题(含答案解析)
（B）12
i＝3
13
（D）15
S＝S＋i
i＝i＋1
否
i＞5
是
2
输出S
结束
9．如果执行右面的程序框图，那么输出的 S （ ）
Ａ．2450
Ｂ．2500
Ｃ．2550
Ｄ．2652
开始
k 1
S 0
k ≤50? ？是
S S 2k
k k 1
否
输出 S
结束
10．执行右面的程序框图，如果输入的 N 是 6，那么输出的是（ ）
15.【2015 春 宜春期末】x 的取值范围为0,10 ，给出如图所示程序框图，输入一个数 x.
4
(1)请写出程序框图所表示的函数表达式； (2)求输出的 y(y<6)的概率；
(3)求输出的 y( 6 y 8)的概率.
【参考答案】
1．【答案】B； 【解析】赋值语句的左边只能是一个变量。 2．【答案】C
()
A．720
B．360
C．240
D．120
7.如果执行下面的程序框图，那么输出的 S （ ）
开始
k 1
S 0
k 50？
是
S S 2k
否
输出S
k k 1
结束
Ａ ． 2450 开始
Ｂ．2500
Ｃ．2550
Ｄ．2652
8．在如下图 （ A ） 11 （C）
S＝0 所示的算法流程图中，输出 S 的值为（ ）
所以输出的 y 满足 6 y 8的概率为 p 9 5 2 10 5
7
2
2
2
满足条件 i>5，退出循环，输出 S 的值为 0.故选 C.
4．【答案】C 【解析】第一次循环：k＝1＋1＝2，S＝2×0＋2＝2； 第二次循环：k＝2＋1＝3，S＝2×2＋3＝7 第三次循环：k＝3＋1＝4，S＝2×7＋4＝18 第四次循环：k＝4＋1＝5，S＝2×18＋5＝41 第五次循环：k＝5＋1＝6，S＝2×41＋6＝88，满足条件则输出 S 的值，而此时 k＝6，故判断框
(完整版)高考算法程序框图真题练习及答案详解
高中算法程序框图一 •选择题（共18小题）1 •如图给出了一个算法程序框图，该算法程序框图的功能是（ ）A .求输出a , b , c 三数的最大数 C .将a , b , c 按从小到大排列3. （2012?三明模拟）如图给出一个算法的程序框图，该程序框图的功能是（A .找出a 、b 、c 三个数中最大的数 C .找出a 、b 、c 三个数中第二大的数 4. 程序框图表示的算法的运行结果是（B .找出a 、b 、c 三个数中最小的数 D .把c 的值赋给a）A .求a , b , c 三数的最大数 C .将a , b , c 按从小到大排列2. 如图给出一个算法的程序框图，该程序框图的功能是（B .求 a , D .将 a , )b ，c 三数的最小数 b ， c 按从大到小排列CMB .求输出a , b , c 三数的最小数 D .将a , b , c 按从大到小排列）5•程序框图中所表示的算法是（A . 3B . 7C . 157. （2013?合肥二模）如图所示，程序框图（算法流程图）的输出结果是（B . 6B .求x 的相反数C •求x 的平方根 6. （2014?泉州一模）运行图中所示程序框图所表达的算法，输出的结果是（D .求x 的算术平方根）D .31)A .求x 的绝对值 •帕J&阅读如图所示的程序框图，运行相应的程序，输出的结果为（9•阅读如图所示的程序框图，运行相应的程序，输出的结果是（A . 1B . 2C . 310 . （2014?福建）阅读如图所示的程序框图，运行相应的程序，输出的「我］ 启~I/•is/IA . 18B . 20C . 2111. （2014?北京）当m=7, n=3时，执行如图所示的程序框图，输出的S 的值为（D . 40)B . 26S 的值等于（口 w fl 十142 C . 21012.（2013?辽宁）执行如图所示的程序框图，若输入 n=10,则输出的S=（）GE®/输A/i /72 5513.（2012?天津）阅读程序框图，运行相应的程序，当输入 x 的值为-25时，输出x 的值为（）B . 10C. 3&D . _[H 五55A .14. （2012?福建）阅读如图所示的程序框图，运行相应的程序，输出15 . （2012?广东）执行如图所示的程序框图，若输入 n 的值为6,则输出s 的值为（ ）A . 105B . 16C . 15D .116 . （2012?辽宁）执行如图所示的程序框图，则输出的 S 的值是（ ）3^：B . - 10s 值等于（ ）A.4B .::C .::D . - 12 317. （2011?北京）执行如图所示的程序框图，若输入A . 2B . 318.（2011?北京）执行如图所示的程序框图，输出的 s 值为（20 .有如图程序框图，则该程序框图表示的算法功能是 _一A 的值为2,则输入的P 值为（ ）A . — 3.填空题（共9小题）21 •如图所示的程序框图，其算法功能是_____________________24 •某算法的程序框图如图所示，则程序输出y的值是________________26. （2014?惠州模拟）如图所示，程序框图（算法流程图）的输出结果为27 •阅读如图所示的程序框图，运行相应的程序，则输出的三•解答题（共1小题）s值等于________________参考答案与试题解析一•选择题（共18小题）1 •如图给出了一个算法程序框图，该算法程序框图的功能是（）A .求a, b, c三数的最大数B •求a, b，c三数的最小数C.将a, b, c按从小到大排列 D .将a, b, c按从大到小排列考点：设计程序框图解决实际问题.专题：操作型.分析：逐步分析框图中的各框语句的功能，第一个条件结构是比较a, b的大小，并将a, b中的较小值保存在变量a中，第二个条件结构是比较a, c的大小，并将a, c中的较小值保存在变量a中，故变量a的值最终为a, b, c中的最小值.由此不难推断程序的功能.解答：解：逐步分析框图中的各框语句的功能，第一个条件结构是比较a, b的大小，并将a, b中的较小值保存在变量a中，第二个条件结构是比较a, c的大小，并将a, c中的较小值保存在变量a中，故变量a的值最终为a, b, c中的最小值. 由此程序的功能为求a, b, c三个数的最小数.故答案选B点评：算法是新课程中的新增加的内容，也必然是新高考中的一个热点，应高度重视•要判断程序的功能就要对程序的流程图（伪代码）逐步进行分析，分析出各变量值的变化情况，特别是输出变量值的变化情况，就不难得到正确的答案.2 •如图给出一个算法的程序框图，该程序框图的功能是（）c®CiteA •求输出a , b , c 三数的最大数 C •将a , b , c 按从小到大排列B •求输出a , b , c 三数的最小数 D •将a , b , c 按从大到小排列考点：程序框图. 专题：算法和程序框图.分析：根据框图的流程判断，第一个环节的功能是输出的a 是a ,b 之间的最大数，第二个环节功能是输出 a , c之间的最大数，由此可得答案.解答：解：由程序框图知：第一个环节是比较a ,b ,输出的a 是a , b 之间的最大数；第二个环节是比较 a, c ,输出的a 是a , c 之间的最大数. •••算法的功能是输出a , b , c 三数的最大数. 故选：A .点评：本题考查了排序程序框图，根据框图的流程判断算法的功能是关键.3. （2012?三明模拟）如图给出一个算法的程序框图，该程序框图的功能是（ ）考点： 程序框图• 专题： 阅读型•分析： 再输入了三个实数 a 、b 、c 后，首先对其中的两个数 a 、b 的大小加以判断，二者取小的数，然后再比较取 得的数与c 的大小，再取小的数输出•解答： 解：输入框中输入了三个实数a 、b 、c ,然后首先判断a 与b 的大小，若a >b 成立，则用b 替换a ,若a 哉不进仃替换，这样再用两者之间的小的数和c 比较，右a >c ,用c 替换a ,输出a ,否则，直接输出小的数a 所以程序框图的功能是找出a 、b 、c 三个数中最小的数•故选B •点评： 本题考查了程序框图中的条件结构，条件结构有两个路径，满足条件执行一个路径，不满足条件，执行另A .找出a 、b 、c 三个数中最大的数 C .找出a 、b 、c 三个数中第二大的数B .找出a 、b 、c 三个数中最小的数 D .把c 的值赋给a一个路径，解答本题时，一定要注意 =”的意义，是用后者替换前者.考点：程序框图. 专题：计算题.分析：由判断框可知：只要 s€0,则程序就执行 是”，否则就跳出循环程序，执行否”并输出i .据此可得出答案.解答：解：由判断框可知：只要 s €0，则程序就执行 是”否则就跳出循环程序，执行否”并输出i .当s=1+2+3+4+5=15 V 20,应继续执行 是”贝U s=15+6=21 >20，此时i=6+仁7，要跳出循环，输出 7. 故选C .点评：理解循环结构的工作原理并会计算s 与i 是解决问题的关键.5•程序框图中所表示的算法是（ ）考点：选择结构. 专题：图表型.分析：写出经过选择结构得到的结果，得到求的 y 的值的形式，即可判断出框图的功能.解答：解：逐步分析框图中的各框语句的功能，fig该程序框图表示算法的功能是求函数 y= '沁的值，即 y=|x|, 故选A .点评：本题考查解决程序框图中的选择结构时，常采用写出前几次选择的结果，找规律.6. （2014?泉州一模）运行图中所示程序框图所表达的算法，输出的结果是（ ）B .求x 的相反数C •求x 的平方根D •求x 的算术平方根4 •程序框图表示的算法的运行结果是（A .求x 的绝对值考点：循环结构. 专题：图表型.分析：分析程序中各变量、各语句的作用，再根据流程图所示的顺序，可知：该程序的作用是利用循环计算 并输出满足条件 S >20的第一个i 值，模拟程序的运行过程，用表格将程序运行过程中变量 况进行分析，不难给出答案.解答：解：程序在运行过程中各变量的值如下表示：s i 是否继续循环 循环前 1 1/第一圈 1 2 是第二圈23是C . 15D . 31考点：程序框图. 专题：算法和程序框图.分析：由算法的程序框图，计算各次循环的结果，满足条件，结束程序. 解答：解：根据算法的程序框图知，第一次循环得 a=2X1+1=3, 第二次循环得 a=2X 3+1=7,第三次循环得a=2X7+1=15，结束循环， 故选C ,点评：本题考查了应用程序框图进行简单的计算问题，是基础题.7. （2013?合肥二模）如图所示，程序框图（算法流程图）的输出结果是（i 值,k 的值的变化情A . 6第三圈 6 4 是故最后输出的i 值为：5,图（或伪代码），从流程图（或伪代码）中即要分析出计算的类型，又要分析出参与计算的数据（如果参与 择恰当的数学模型 ③解模.&阅读如图所示的程序框图，运行相应的程序，输出的结果为（ ）A . 676考点： 循环结构.专题：图表型.分析： 根据已知中的流程图，我们模拟程序的运行结果，看变量 不满足时执行循环，满足时退出循环，即可得到输出结果.a 的值是否满足判断框的条件，当判断框的条件解答：解：a=1，满足条件a v 15,执行循环， a=2，满足条件a v 15,执行循环， a=5，满足条件a v 15,执行循环， a=26，不满足条件a v 15,退出循环， 执行输出语句，输出 a=26.故选B .点评：本题主要考查的知识点是程序框图，模拟循环的执行过程是解答此类问题常用的办法，属于基础题.9.阅读如图所示的程序框图，运行相应的程序，输出的结果是（ ）第四圈24 5 否 点评:根据流程图（或伪代码）写程序的运行结果，是算法这一模块最重要的题型，其处理方法是: :①分析流程运算的数据比较多，也可使用表格对数据进行分析管理） ?②建立数学模型，根据第一步分析的结果，选 B . 26故选B .A . 1B . 2C . 3D . 4考点：程序框图. 专题：图表型.分析：分析程序中各变量、各语句的作用，再根据流程图所示的顺序，可知：该程序的作用是利用循环计算 重新为2时变量n 的值，并输出，模拟程序的运行过程，即可得到答案.解答： 解：程序在运行过程中各变量的值如下表示：S n 是否继续循环循环前 2 1/ 第一圈-1 2是 第二圈 丄3是 第三圈 2 4否则输出的结果为4故选D点评：本题考查的知识点是程序框图，在写程序的运行结果时，模拟程序的运行过程是解答此类问题最常用的办法.10. （2014?福建）阅读如图所示的程序框图，运行相应的程序，输出的叠—考点：循环结构.S 的值等于（ ）A . 18B . 20C . 21D . 40总三刃十L专题：计算题；算法和程序框图.分析：算法的功能是求 S=21+22+・・+2n +1+2+・・+ n 的值，计算满足条件的 S 值，可得答案.解答：解：由程序框图知：算法的功能是求S=21+22+ ..+2n +1+2+ -+n 的值，12123S =2 +2 +1+2=2+4+1+2=9 V 15, S=2 +2 +2 +1+2+3=2+4+8+1+2+3=20 昌5.•••输出 S=20. 故选：B .点评：本题考查了直到型循环结构的程序框图，根据框图的流程判断算法的功能是解题的关键.11. （2014?北京）当m=7, n=3时，执行如图所示的程序框图，输出的 S 的值为（ ）考点：循环结构.专题：计算题；算法和程序框图.分析：算法的功能是求 S=7>6X ・・・kx 的值，根据条件确定跳出循环的 k 值，计算输出S 的值.解答： 解：由程序框图知：算法的功能是求S=7>6 >•••>的值，当 m=7 , n=3 时，m - n +1=7 - 3+仁5 , •跳出循环的k 值为4, •输出 S=70X5=210 . 故选：C .点评：本题考查了循环结构的程序框图，根据框图的流程判断算法的功能是解答本题的关键.12 . （2013?辽宁）执行如图所示的程序框图，若输入 n=10,则输出的S=（ ）（幵晞J丄/输心/1i=2------ 1 -------青r-l/ S H .'ISS7工i=i+2B . 42C . 210D . 840Iwn * 少 IA . 7B .」11C . _557255考点：循环结构.专题：计算题；图表型.分析：框图首先给累加变量S和循环变量i分别赋值0和2,在输入n的值为10后，对i的值域n的值大小加以判断，满足i韦, 执行二$十一,i=i+2，不满足则跳出循环，输出S.-1解答：解：输入n的值为10,框图首先给累加变量S和循环变量i分别赋值0和2,判断2<10 成立，执行S二。
高中数学-算法与程序框图、基本算法语句分层练习
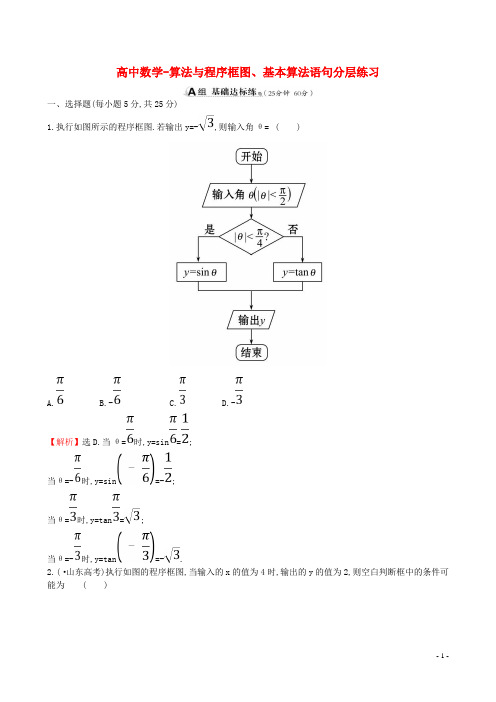
高中数学-算法与程序框图、基本算法语句分层练习一、选择题(每小题5分,共25分)1.执行如图所示的程序框图.若输出y=-,则输入角θ=( )A. B.- C. D.-【解析】选D.当θ=时,y=sin=;当θ=-时,y=sin=-;当θ=时,y=tan=;当θ=-时,y=tan=-.2.(·山东高考)执行如图的程序框图,当输入的x的值为4时,输出的y的值为2,则空白判断框中的条件可能为( )A.x>3B.x>4C.x≤4D.x≤5【解析】选B.输入x为4,要想输出y为2,则程序经过y=log24=2,故判断框填x>4.3.根据下列程序语句,当输入x为60时,输出y的值为 ( )A.25B.30C.31D.61【解析】选C.该语句可转化为分段函数求函数值的问题,y=当x=60时,y=25+0.6×(60-50)=31.4.(·天津高考)阅读如图的程序框图,运行相应的程序,若输入N的值为19,则输出N的值为 ( )A.0B.1C.2D.3【解析】选C.阅读程序框图可得,程序执行过程如下:首先初始化数值为N=19,第一次循环:N=N-1=18,不满足N≤3;第二次循环:N==6,不满足N≤3;第三次循环:N==2,满足N≤3;此时跳出循环体,输出N=2.【变式备选】(2016·天津高考)阅读如图所示的程序框图,运行相应的程序,则输出S的值为( )A.2B.4C.6D.8【解析】选B. 第一次:S=8,n=2,第二次:S=2,n=3,第三次:S=4,n=4,满足n>3,输出S=4.5.执行如图所示的程序框图,则输出的λ是( )A.-4B.-2C.0D.-2或0【解析】选B.依题意,若λa+b与b垂直,则有(λa+b)·b=4(λ+4)-2(-3λ-2)=0,解得λ=-2;若λa+b与b平行,则有-2(λ+4)=4(-3λ-2),解得λ=0.结合题中的程序框图,输出的λ是-2.二、填空题(每小题5分,共15分)6.运行如图所示的程序,若输出y的值为1,则可输入x的个数为________.【解析】模拟程序运行,可得程序的功能是求y=的值,故x≤0时,1=2x,解得x=0,x>0时,1=-x3+3x,x>0时函数f(x)=x3-3x+1的图象与x轴有2个交点,即有2个零点, 综上可得可输入x的个数为3.答案:37.(·宁德模拟)如图是一个程序框图,则输出的k的值是________.【解析】根据程序框图可知,k=1时,12-1×6+5≤0;k=2时,22-2×6+5≤0;k=3时,32-3×6+5≤0;k=4时,42-4×6+5≤0;k=5时,52-5×6+5≤0;k=6时,62-6×6+5>0,故输出的k的值是6.答案:6【一题多解】本题还可以采用如下解法:只需求出不满足k2-6k+5≤0的最小正整数k就行,显然是6.答案:68.阅读如图的程序框图,若输出的y=,则输入的x的值为________.【解析】由程序框图可知是计算分段函数y=的值,当x≤2时,由y=sin=,可得x=+2kπ或x=+2kπ,k∈Z,解得x=1+12k或x=5+12k,k∈Z,此时x的值为1.当x>2时,由y=2x=,解得x=-1(舍去).综上知,输入的x的值为1.答案:1三、解答题(每小题10分,共20分)9.如图所示,运行该程序框图相应的程序,试求输出的x的值.导学号12560765【解析】当x=1时,执行x=x+1后x=2;当x=2时,执行x=x+2后x=4,再执行x=x+1后x=5;当x=5时,执行x=x+1后x=6;当x=6时,执行x=x+2后x=8,再执行x=x+1后x=9;当x=9时,执行x=x+1后x=10;当x=10时,执行x=x+2后x=12,此时12>8,因此输出的x的值为12.10.设计程序框图,求××××…×的值.【解析】程序框图如图所示.1.(5分)执行如图所示的程序框图,若输入的n=5,则输出的结果为( )A.4B.5C.6D.7【解析】选B.由程序框图得,n=5,i=1;n=3×5+1=16,i=2;n==8,i=3;n==4,i=4;n==2,i=5;n=1,结束循环,输出i值,即i=5.2.(5分)运行程序,输入n=4,则输出y的值是 ( )A. B.C. D.【解析】选C.模拟程序的运行,可得程序框图的功能是计算并输出y=的值,由n=4,可得y=sin=sin cos +cos sin =.【变式备选】程序框图如图所示,其输出结果是,则判断框中所填的条件是( )A.n≥5?B.n≥6?C.n≥7?D.n≥8?【解析】选B.由题意可知,第一次运行后S=,n=2;第二次运行后S=,n=3;第三次运行后S=,n=4;第四次运行后S=,n=5;第五次运行后S=,n=6;此时停止运算,故判断框内应填n≥6?.3.(5分)我国古代数学典籍《九章算术》“盈不足”中有一道两鼠穿墙问题:“今有垣厚十尺,两鼠对穿,初日各一尺,大鼠日自倍,小鼠日自半,问几何日相逢?”现用程序框图描述,如图所示,则输出结果n= ( )A.4B.5C.2D.3【解析】选A.第一次循环,得S=2,S≥10?否;第二次循环,得n=2,a=,A=2,S=,S≥10?否;第三次循环,得n=3,a=,A=4,S=,S≥10?否;第四次循环,得n=4,a=,A=8,S=>10,是,所以输出的n=4.4.(12分)如图所示,程序框图输出的各数组成数列{a n}.(1)求{a n}的通项公式及前n项和S n.(2)已知{b n}是等差数列,且b1=a2,b3=a1+a2+a3,求数列{a n·b n}的前n项和T n.【解析】(1)由程序框图知a n=3a n-1,{a n}是a1=3,q=3的等比数列,所以a n=3n,S n==.(2)因为所以d=15,所以b n=15n-6,a n·b n=(15n-6)·3n,所以T n=9×31+24×32+39×33+…+(15n-6)×3n,3T n=9×32+24×33+39×34+…+(15n-21)×3n+(15n-6)×3n+1,两式相减得-2T n=9×3+15×32+15×33+…+15×3n-(15n-6)×3n+1=27+15×-(15n-6)×3n+1=27+15×-(15n-6)×3n+1=27+(3n+1-32)-(15n-6)×3n+1所以-4T n=54+15×3n+1-15×9-(30n-12)×3n+1=-81-(30n-27)×3n+1所以T n=.【变式备选】运行如图所示的程序,如果输入的n是2 016,那么输出的S的值是多少.【解析】模拟程序的运行过程知,该程序运行后输出的是算式S=1×2+2×22+3×23+…+2 016×22 016①, 所以2S=1×22+2×23+3×24+…+2 016×22 017②;②-①得,S=-2-22-23-…-22 016+2 016×22 017=-+2 016×22 017=2+2 015×22 017.所以输出的S是2+2 015×22 017.5.(13分)对任意函数f(x),x∈D,可按如图构造一个数列发生器产生数列{x n}.(1)若定义函数f(x)=,且输入x0=,请利用数列发生器写出数列{x n}的所有项.(2)若定义函数f(x)=2x+3,且输入x0=-1,请利用数列发生器求数列{x n}的通项公式.【解题指南】(1)函数f(x)=的定义域D=(-∞,-1)∪(-1,+∞),由此能推导出数列{x n}只有三项x1=,x2=,x3=-1.(2)f(x)=2x+3的定义域为R,若x0=-1,则x1=1,则x n+1+3=2(x n+3),从而得到数列{x n+3}是首项为4,公比为2的等比数列,由此能求出数列{x n}的通项公式.【解析】(1)函数f(x)=的定义域D=(-∞,-1)∪(-1,+∞),把x0=代入可得x1=,把x1=代入可得x2=,把x2=代入可得x3=-1,因为x3=-1∉D,所以数列{x n}只有三项,x1=,x2=,x3=-1.(2)f(x)=2x+3的定义域为R,若x0=-1,则x1=1,则x n+1=f(x n)=2x n+3,所以x n+1+3=2(x n+3),所以数列{x n+3}是首项为4,公比为2的等比数列,所以x n+3=4·2n-1=2n+1,所以x n=2n+1-3,即数列{x n}的通项公式x n=2n+1-3.。
高中数学必修三习题：第一章1.1-1.1.1算法的概念含答案
第一章 算法初步1.1 算法与程序框图1.1.1 算法的概念A 级 基础巩固一、选择题1．下列四种自然语言叙述中，能称作算法的是( )A ．在家里一般是妈妈做饭B ．做米饭需要刷锅、淘米、添水、加热这些步骤C ．在野外做饭叫野炊D ．做饭必须要有米解析：算法是做一件事情或解决一类问题的程序或步骤，故选B.答案：B2．以下对算法的描述正确的有( )①对一类问题都有效；②算法可执行的步骤必须是有限的；③算法可以一步一步地进行，每一步都有确切的含义；④是一种通法，只要按部就班地做，总能得到结果．A ．1个B ．2个C ．3个D ．4个答案：D3．给出下面一个算法：第一步，给出三个数x ，y ，z .第二步，计算M ＝x ＋y ＋z .第三步，计算N ＝13M .第四步，得出每次计算结果．则上述算法是( )A ．求和B ．求余数C ．求平均数D ．先求和再求平均数解析：由算法过程知，M 为三数之和，N 为这三数的平均数．答案：D4．一个算法步骤如下：S 1，S 取值0，i 取值1；S2，如果i≤10，则执行S3；否则，执行S6；S3，计算S＋i并将结果代替S；S4，用i＋2的值代替i；S5，转去执行S2；S6，输出S.运行以上步骤后输出的结果S＝( )A．16 B．25C．36 D．以上均不对解析：由以上计算可知：S＝1＋3＋5＋7＋9＝25.答案：B5．对于算法：第一步，输入n.第二步，判断n是否等于2，若n＝2，则n满足条件；若n＞2，则执行第三步．第三步，依次从2到(n－1)检验能不能整除n，若不能整除n，则执行第四步；若能整除n，则执行第一步．第四步，输出n.满足条件的n是( )A．质数B．奇数C．偶数D．约数解析：此题首先要理解质数，只能被1和自身整除的大于1的整数叫质数.2是最小的质数，这个算法通过对2到(n－1)一一验证，看是否有其他约数，来判断其是否为质数．答案：A二、填空题6．给出下列算法：第一步，输入x的值．第二步，当x>4时，计算y＝x＋2；否则执行下一步．第三步，计算y＝4－x.第四步，输出y.当输入x＝0时，输出y＝________．解析：因为0<4，执行第三步，所以y＝4－0＝2.答案：27．已知直角三角形两直角边长为a，b，求斜边长c的一个算法分下列三步：(1)计算c＝a2＋b2.(2)输入直角三角形两直角边长a，b的值．(3)输出斜边长c 的值．其中正确的顺序是________________．解析：算法的步骤是有先后顺序的，第一步是输入，最后一步是输出，中间的步骤是赋值、计算．答案：(2)(1)(3)8．如下算法：第一步，输入x 的值；第二步，若x ≥0，则y ＝x ；第三步，否则，y ＝x 2；第四步，输出y 的值．若输出的y 值为9，则x ＝________．解析：根据题意可知，此为求分段函数y ＝⎩⎪⎨⎪⎧x ，x ≥0，x 2，x <0的函数值的算法，当x ≥0时，x＝9；当x <0时，x 2＝9，所以x ＝－3.答案：9或－3三、解答题9．写出求1×2×3×4×5×6的算法．解：第一步，计算1×2得到2.第二步，将第一步的运算结果2乘3，得到6.第三步，将第二步的运算结果6乘4，得到24.第四步，将第三步的运算结果24乘5，得到120.第五步，将第四步的运算结果120乘6，得到720.10．某商场举办优惠促销活动．若购物金额在800 元以上(不含800 元)，打7折；若购物金额在400 元以上(不含400 元)，800 元以下(含800 元)，打8折；否则，不打折．请为商场收银员设计一个算法，要求输入购物金额x ，输出实际交款额y .解：算法步骤如下：第一步，输入购物金额x (x ＞0)．第二步，判断“x ＞800”是否成立，若是，则y ＝0.7x ，转第四步；否则，执行第三步． 第三步，判断“x ＞400”是否成立，若是，则y ＝0.8x ；否则，y ＝x .第四步，输出y ，结束算法．B 级 能力提升1．结合下面的算法：第一步，输入x .第二步，判断x 是否小于0，若是，则输出x ＋2；否则，执行第三步．第三步，输出x －1.当输入的x 的值为－1，0，1时，输出的结果分别为( )A ．－1，0，1B ．－1，1，0C ．1，－1，0D ．0，－1，1解析：根据x 值与0的关系选择执行不同的步骤．答案：C2．求过P (a 1，b 1)，Q (a 2，b 2)两点的直线斜率有如下的算法，请将算法补充完整： S 1 取x 1＝a 1，y 1＝b 1，x 2＝a 2，y 2＝b 2.S 2 若x 1＝x 2，则输出斜率不存在；否则，________．S 3 输出计算结果k 或者无法求解信息．解析：根据直线斜率公式可得此步骤．答案：k ＝y 2－y 1x 2－x 13．鸡兔同笼问题：鸡和兔各若干只，数腿共100条，数头共30只，试设计一个算法，求鸡和兔各有多少只．解：第一步，设有x 只鸡，y 只兔，列方程组⎩⎪⎨⎪⎧x ＋y ＝30，①2x ＋4y ＝100.② 第二步，②÷2－①，得y ＝20.第三步，把y ＝20代入①，得x ＝10.第四步，得到方程组的解⎩⎪⎨⎪⎧x ＝10，y ＝20. 第五步，输出结果，鸡10只，兔20只．。
高一数学算法和程序框图试题答案及解析
高一数学算法和程序框图试题答案及解析1.如图是求样本平均数的程序框图，图中空白框中应填入的内容为（）A．B．C．S=S+n D．S=S+【答案】A【解析】由于，故第次循环为.【考点】程序框图的应用.2.下图为某算法的程序框图，则程序运行后输出的结果是（）A．2B．1C．3D．4【答案】C【解析】这里外是一个循环结构，一共循环了次，而内部是一个选择结构，根据条件确定的值是还是，然后把的值加给，次循环结束后，输出的值，便是正确答案，结果选择C.只要读懂题意，然后把人设想成计算机，按步骤逐步操作，最后就能得到正确答案.【考点】算法中的程序框图和循环结构与选择结构的嵌套.3.如图的程序框图，如果输入三个实数a，b，c，要求输出这三个数中最大的数，那么在空白的判断框中，应该填入下面四个选项中的( ).A．c＞x？B．x＞c？C．c＞b？D．b＞c？【答案】A.【解析】本题是寻找三个数中最大的数，在令a为x后，判断x与b的大小，因此第二个判断框里要判断的是x与c的大小，由于此时判断“是”时，c赋值为x，最后输出x，所以要填的是“c＞x？”.【考点】程序框图的理解与应用，填写判断框处的语句是常考的一个考点.4.按右边程序框图运算：若，则运算进行几次才停止？A．B．C．D．【答案】C【解析】第一次循环，第二次循环，第三次循环，第四次循环，第五次循环。
【考点】直到型循环程序框图。
5.执行如图所示的程序框图，如果输入，那么输出的a值为（）A．B．C．D．【答案】C【解析】根据程序框图的描述，是求使成立的最小a值，故选C．【考点】程序框图．6.执行下图的程序框图,若输入的x=2，则输出的y的值为【答案】23【解析】根据题意，本程序框图为求y的和循环体为“直到型”循环结构，输入x=2，第一次循环：y=2×2+1=5，x=5；第二次循环：y=2×5+1=11，x=11；第三次循环：y=2×11+1=23，∵|x-y|=12＞8，∴结束循环，输出y=23．故答案为：23．【考点】本题为程序框图题，考查对循环结构的理解和认识，按照循环结构运算后得出结果．属于基础题．7.若某程序框图如图所示，则输出的p的值是 ()A．30B．28C．21D．55【答案】A【解析】根据框图的循环结构，依次；；。
(完整word)高中数学算法框图习题及详解.doc
专题复习：算法框图高中数学算法框图习题（含答案详解）一、1． (理 )如所示算法程序框运行，入a＝ tan315 ，°b＝ sin315 ，°c＝ cos315 ，° 出果 ()2 2A. 2 B ．－2 C．－ 1 D ．1[答案 ] C[解析 ] a、 b、 c 三数中的最小，又cos315 °>0， sin315 ＝°－2此程序框是出 2，2tan315 ＝°－ 1<－2，故 C.2．下列程序运行后出果()x＝ 1；for i ＝ 1 10x＝ 2]A.1B.23 C． 113 D．以上都不[答案 ] B[解析 ] 每一次循 x 都重新，与原来 x 的无关，故最后出x 的只与最后一次循 i 的有关，∵i ＝10，∴ x＝23.1( 共 6 个 2)的的算法的程序框，中的判断框中填3． (理 )下面是求 12＋12＋⋯＋ 2A ． i ≤5? B． i <5? C．i ≥5? D． i>5?[答案 ] A[解析 ] 由于所给计算的表达式中共有 6 个2，故只需 5 次循环即可，由此控制循环次数的变量i 应满足 i≤ 5.故选 A.4． (理 )已知数列 { a n} 中， a1＝ 1， a n＋1＝ a n＋ n，利用如图所示的程序框图计算该数列第10 项，则判断框中应填的语句是( )A ． n>10B ． n≤ 10 C． n<9 D． n≤ 9[答案 ] D[解析 ] 本题在算法与数列的交汇处命题，考查了对程序框图的理解能力．数列{ a } 是n一个递推数列，因为递推公式为a1 n ＋1 n 10 9＝ 1， a ＝ a ＋ n，故 a ＝a＋9，因为循环体为m＝m ＋1， n＝ n＋ 1，当 n＝ 10 时结束循环，故判断框内应为n≤ 9.5． (理 )下列程序运行后输出结果为()S＝ 1；n＝ 1；while S<100S ＝ S* n ；n ＝ n ＋ 3；endnA ． 4B ．10C ． 13D ． 16[答案 ]C[解析 ]S ＝ 1<100，进行第一次循环后S ＝ 1， n ＝ 4； S ＝ 1<100再进行第二次循环．循环后 S ＝ 4，n ＝ 7；第三次循环后 S ＝ 28，n ＝ 10；第四次循环后 S ＝ 280，n ＝ 13.因 故不再循环，跳出循环后输出 n ＝ 13. 6． (文 )在如图的程序框图中，若输入 m ＝ 77，n ＝ 33，则输出的 n 的值是( S ＝ 280>100，)A ． 3B ． 7C ． 11D ． 33[答案 ] C[解析 ] 这个程序框图执行的过程是：第一次循环： m ＝ 77，n ＝ 33， r ＝11；第二次循环： m ＝ 33，n ＝ 11， r ＝ 0.因为 r ＝0，则结束循环，输出n ＝ 11.7．下面的程序框图，若输入 a ＝ 0，则输出的结果为 ( )A ． 1022B ． 2046C ． 1024D ． 2048[答案 ] B[解析 ]由程序框图中的循环结构可得到递推公式， a ＝ 2a ＋ 2，且 a ＝ 0，由 ak ＋1k1k ＋1a k ＋1 ＋ 2＝2a k ＋ 2 可得， a k ＋1＋ 2＝ 2(a k ＋ 2)，即 ＝ 2 且 a 1＋ 2＝ 2，∴ { a k ＋ 2} 是以 2 为公比， 2a ＋ 2k为首项的等比数列， ∴ a ＋ 2＝ 2×2 k － 1k，即 ak11＝ 2k ＝ 2 － 2，从而a ＝ 2 － 2＝ 2046，故选k11B.[点评 ]本题的关键是弄清输出的a 的值为数列{ a n } 的第几项，k ＝1 算出的是a 2，k ＝ 2满足条件得a 3，故k ＝10满足条件计算后得到a 11，k ＝ 11不满足，故输出的是a 11 而不是a 10，有不少人在这里搞不清楚，以为判断条件是k ≤ 10，故最后输出的是 a 10，这是没有完整理解算法的典型表现． 因为对同一个判断条件k ≤10，a ＝2a ＋ 2 与 k ＝ k ＋ 1 语句的先后顺序不同输出结果也不同， 还与 k 的初值有关等等， 故应统盘考虑， 解决的一个有效途径就是循环几次把握其规律．【解答题】8．为了让学生更多的了解“数学史”知识，其中学高二年级举办了一次“追寻先哲的足迹， 倾听数学的声音”的数学史知识竞赛活动，共有 800 名学生参加了这次竞赛．为了解本次竞赛的成绩情况，从中抽取了部分学生的成绩(得分均为整数，满分为100 分 )进行统计．请你根据频率分布表，解答下列问题：序号 (i) 分组 (分数 ) 组中值 (G i) 频数 (人数 ) 频率 (F i)1 [60,70) 65 ①0.122 [70,80) 75 20 ②3 [80,90) 85 ③0.244 [90,100] 95 ④⑤合计50 1(1)填充频率分布表中的空格 (在解答中直接写出对应空格序号的答案)；(2)为鼓励更多的学生了解“数学史”知识，成绩不低于85 分的同学能获奖，请估计在参加的 800 名学生中大概有多少同学获奖？(3)在上述统计数据的分析中有一项计算见算法流程图，求输出S 的值．[解析 ] (1)∵样本容量为50，∴①为 6，②为 0.4，③为 12，④为 12，⑤为 0.24.(2)在 [80,90) 之间， 85 分以上约占一半，∴12× 0.24＋ 0.24 × 800＝ 288，即在参加的800 名学生中大概有288 名同学获奖．(3)由流程图知S＝ G1 F1＋ G2F2＋ G3F3＋G4F 4＝65×0.12＋ 75× 0.4＋ 85× 0.24＋ 95× 0.24＝ 81.。
(word完整版)高中数学必修三算法和程序框图练习题
一、选择题1、根据算法的程序框图，当输入n=6时，输出的结果是( )A.35B.84C.49D.252、如图，汉诺塔问题是指有3根杆子A，B，C，杆子上有若干碟子，把所有的碟子从B杆移到A杆上，每次只能移动一个碟子，大的碟子不能叠在小的碟子上面，把B杆上的3个碟子全部移动到A杆上，最少需要移动的次数是( )A.12B.9C.6D.73、一程序框图如图1-1-25所示,它能判断任意输入的数x的奇偶性,其中判断框中的条件是( )A.m=0B.x=0C.x=1D.m=1图1-1-254、阅读下面的程序框图并判断运行结果为…( )A.55B.-55C.5D.-55、给出下面的算法：该算法表示（）S1 m=a；S2 若b＜m，则m=b；S3 若c＜m，则m=c；S4 若d＜m，则m=d；S5 输出m.A.a，b，c，d中最大值B.a，b，c，d中最小值C.将a，b，c，d由小到大排序D.将a，b，c，d由大到小排序6、下列关于算法的说法中，正确的是（）A．求解某一类问题的算法是唯一的B．算法必须在有限步操作之后停止C．算法的每一步操作必须是明确的，不能有歧义或模糊D．算法执行后一定产生确定的结果7、算法共有三种逻辑结构，即顺序结构、条件分支结构和循环结构，下列说法正确的是（）A.一个算法只能含有一种逻辑结构B.一个算法最多可以包含两种逻辑结构C.一个算法必须含有上述三种逻辑结构D.一个算法可以含有上述三种逻辑结构的任意组合8、下面的程序框图中是循环结构的是( )A.①②B.②③C.③④D.②④9、阅读下边的程序框图，若输入的n是100，则输出的变量S和T的值依次是( )A.2 500，2 500B.2 550，2 550C.2 500，2 550D.2 550，2 50010、程序框是程序框图的一个组成部分，下面的对应正确的是（）①终端框（起止框），表示一个算法的起始和结束②输入、输出框，表示一个算法输入和输出的信息③处理框（执行框），功能是赋值、计算④判断框，判断某一条件是否成立，成立时在出口处标明“是”或“Y”，不成立时标明“否”或“N”A．（1）与①，（2）与②，（3）与③，（4）与④B．（1）与④，（2）与②，（3）与①，（4）与③C．（1）与①，（2）与③，（3）与②，（4）与④D．（1）与①，（2）与③，（3）与④，（4）与②。
高中数学算法与框图练习题练习题(含解析)
所以输出的 的最大值为 .
故选：D.
8．C
【分析】根据程序流程图，代入 ，计算出结果即可.
【详解】① ， ， ， ，此时 ；
② ， ， ，此时 ；
③ ， ， ，此时 ；
④ ， ， ，此时 ；
⑤ ， ， ，此时 ；
⑥ ， ， ，此时 ，
结束程序，输出结果为44，
故选：C
第四步：判断 是否成立？若是，则 之间的任意值均为满足条件的近似根；若不是，则返回第二步.
【点睛】本题考查了求方程近似根的算法，意在考查学生对于算法的理解和应用.
【详解】（1） ，所以98的二进制数是 .
（2） ， ，所以 与 的最大公约数为 .
（3） .
【点睛】本题考查二进制，辗转相除法，秦九昭算法等知识，属于基础题.
16．见解析
【分析】根据题目中的条件，找出各要素之间的关系，校长只负责两名副校长和校长办公室，所以校长下只有两名副校长和校长办公室，依次类推，两名副校长又各自管理教务处、教科室和保卫科、政教处、总务处；班级由所有的科室负责.
A．35B．56C．84D．120
二、填空题
11．运行如图所示的伪代码，输出的T的值为________.
12．用秦九韶算法求函数 ，当 时的值时， ___________．
13．执行如图所示的程序框图，若输1455的最大公约数为 ，则 化为三进制为__________.
根据程序框图可知，输出的 ，
又 ， ， ， ， ， ，
所以 .
故选：B.
11．16
【分析】模拟程序的运行过程，即可得出程序运行后的输出结果.
【详解】当 时， ；
当 时， ；
当 时， ；
高中数学 算法初步与程序框图：经典例题和巩固练习(及详解)
高中数学：算法与程序框图（例题、巩固练习、例题和巩固练习详解）【典型例题】 类型一：算法设计例l ．写出解方程2230x x --=的一个算法．例2．设计一个算法，将高一某班56名同学中考试成绩不及格者的分数打印出来．举一反三：【变式1】 写出求过点M(-2，-1)、N(2，3)的直线与坐标轴围成的三角形面积的一个算法．类型二：程序框图及其画法例3．输出1000以内能被3和5整除的所有正整数，画出其程序框图．例4.按下列程序框图来计算：(算法)执行如图所示的程序框图,若输入n 的值为8,则输出s 的值为______.举一反三：【变式1】指出下列程序框图的运行的结果． （1）图1的运行结果是s = ； （2）图2的运行结果是a = ；（3）图3中若输入4-,则输出的结果是 ； （4）图4的运行结果是 ．图2图1【变式3】已知函数()21f x x =-，以下程序框图(图6)表示的是给定x 值，求其相应函数值的算法．请将该程序框图补充完整．其中①处应填 ，②处应填 ．类型三：用基本算法语句编写程序例5．如图所示，在边长为4的正方形ABCD 的边上有一点P ，沿着折线B-C-D-A 由点B(起点)向点A(终点)运动．设点P 运动的路程为x ，△APB 的面积为y ，求y 与x 之间的函数关系式．画出程序框图，并写出程序．图6图3举一反三：【变式1】已知函数1(0)0(0)(0)x xy xx x+>⎧⎪==⎨⎪-<⎩，，，请设计输入x的值，输出y值的算法，画出算法框图，并用基本语句描述算法．例6．某班共有60名同学，在一次考试中，某科的成绩分为三个等级：80～100分为A，60～79分为B，60分以下为C，要求设计输出每个学生相应的成绩等级的算法，并统计各个等级的人数，先画框图，再写程序．举一反三：【变式1】设计算法，求1111112349991000-+-++-…的值，画出程序框图，并写出程序．【巩固练习】1．下列给出的赋值语句中正确的是（）A.4 = MB.M =－MC.B*A=3D.x + y = 02．在如下图所示的算法流程图中，输出S的值为（）A.11B.12C.13D.153．右边程序执行后输出的结果是（ ） A.1- B ．0 C ．1 D ．2 4. 右边程序运行后输出的结果为( ) A. 50 B. 5 C. 25 D. 05．下图给出的是计算201614121+⋅⋅⋅+++的值的一个程序框图，其中判断框内应填入的条件是（ ）A.i>10B.i<10C.i>20D.i<206．下图1是某县参加2007年高考的学生身高条形统计图，从左到右的各条形表示的学生人数依次记为1210A A A ，，，（如2A 表示身高（单位：cm ）在[)150155，内的学生人数）．图2是统计图1中身高在一定范围内学生人数的一个算法流程图．现要统计身高在160～180cm （含160cm ，不含180cm ）的学生人数，那么在流程图中的判断框内应填写的条件是（ ）Ａ．6i < Ｂ．7i <Ｃ．8i <Ｄ．9i <7．如果执行下面的程序框图，那么输出的S =（ ）501图Ａ．2450 Ｂ．2500 Ｃ．2550 Ｄ．26528．阅读下边的程序框图，若输入的n是100，则输出的变量S和T的值依次是（）A．2500，2500 B．2550，2550 C．2500，2550 D．2550，2500` 9．三个数72,120,168的最大公约数是_________________．→内所有奇数的和；10．根据条件把流程图补充完整，求11000（1）处填(2) 处填11．下列各数)9(85 、 )6(210 、 )4(1000 、 )2(111111中最小的数是____________．12．右图给出的是计算201614121++++ 的值的一个流程图，其中判断 框内应填入的条件是____________． 13．用秦九韶算法求多项式x x x x x x x x f ++++++=234567234567)(当3=x 时的值．14．编写一个程序，输入正方形的边长，输出它的对角线长和面积的值．i:=1,S:=015.画出为求1～1000的所有的偶数的和而设计的一个程序框图．数学试题答案【典型例题】 类型一：算法设计例l ．【解析】 算法一：第一步：将方程左边因式分解，得(3)(1)0x x -+=； ① 第二步：由①得x-3＝0， ② 或x+1＝0； ③第三步：解②得x ＝3，解③得x ＝-1． 算法二：第一步：移项，得223x x -=； ①第二步：①式两边同时加1并配方，得2(1)4x -=； ② 第三步：②式两边开方，得12x -=±； ③ 第四步：解③得x ＝3或x ＝-1． 算法三：第一步：计算方程的判别式判断其符号△＝22+4×3＝16＞0；第二步：将1a =，2b =-，3c =-，代入求根公式，得122b x a-±=，，得13x =，21x =-．【总结升华】 比较三种算法，算法三更简单，步骤最少，由此我们只要有公式可以利用，利用公式解决问题是最理想、合算的算法．因此在寻求算法的过程中，首先是利用公式，下面我们设计一个求一般的一元二次方程20(0)ax bx c a ++=≠的根的算法如下：第一步：计算24b ac =-△；第二步：若0<△，方程无实根；第三步：若△≥0，方程的根122b x a-=，．例2．【解析】 算法步骤如下：S1 令n ＝1．S2 如果n ＞56，则转到S7． S3 输入一个学生的成绩G ．S4 将G 和60比较，如果G ＜60，则输出G ． S5 n ＝n+1． S6 转到S2． S7 结束．【总结升华】该题中实际是用到了算法的条件结构和循环结构，条件结构用于判断分数是否小于60；循环结构用于控制输入成绩的次数．举一反三： 【变式1】【解析】算法步骤如下：第一步：取12x =-，11y =-，22x =，23y =； 第二步：得直线方程112121y y x x y y x x --=--；第三步：在第二步的方程中令y ＝0，得y 的值m ，从而得直线与y 轴的交点A(0，m)； 第四步：在第二步的方程中令y ＝0，得x 的值n ，从而得直线与x 轴的交点B(n ，0)；第五步：根据三角形的面积公式求1||||2S m n =； 第六步：输出运算结果．【总结升华】先由M ，N 两点得出直线的方程，再求直线与两坐标轴的交点，求出三角形的两条直角边长，再由面积公式计算．类型二：程序框图及其画法 例3．【解析】 能被3和5整除的正整数一定能被15整除，由于1000＝15×66+10，因此1000以内一共有66个这样的正整数．引入变量a 表示待输出的数，则a ＝15n(n ＝1，2，3，…，66)，n 从1变到66，反复输出a ，就能输出l000以内的所有能被3和5整除的正整数，算法流程图如图所示．【总结升华】像这样的算法结构称为循环结构，其中反复执行的第②部分称为循环体．变量n 控制着循环的开始和结束，称为循环变量，第①部分就是赋予循环变量初始值，预示循环开始．第③部分判断是否继续执行循环体，称为循环的终止条件．循环结构主要用在一些有规律的重复计算的算法中，如累加求和、累乘求积等问题常需要用循环结构来设计算法．在循环结构中，要注意依据条件，设计合理的计数变量、累加变量等，要特别注意循环结构中条件的表述要恰当、精确，以免出现多一次循环或少一次循环的情况．例4.【思路点拨】本题是循环型程序框图，可以依次写出其前面的循环，找到规律，进而解答。
高一数学算法与程序框图试题
高一数学算法与程序框图试题1.算法流程有、、三种控制结构.【答案】顺序结构条件结构循环结构【解析】算法的三种基本结构是顺序结构、条件结构、循环结构。
故选C。
【考点】本题主要考查算法的概念及算法设计中的结构。
点评：关键是对算法的三种基本结构理解并熟练掌握。
2.如图所示的程序框图，输出的结果是S＝7，则输入的A值为________．【答案】3【解析】该程序框图的功能是输入A，计算2A＋1的值．由2A＋1＝7，解得A＝3.3.如图是一个算法的程序框图，该算法所输出的结果是()A．1＋＋＋…＋B．1＋＋＋…＋C．＋＋＋…＋D．＋＋＋…＋【答案】C【解析】第一次循环：s＝，n＝4，i＝2；第二次循环：s＝＋，n＝6，i＝3；第三次循环：s＝＋＋，n＝8，i＝4；由于i＝10时，不满足i>10，所以继续执行循环；此时s＝＋＋…＋，n＝22，i＝11；当i＝11时，满足i>10，输出s.4.下列关于算法的描述正确的是()A．算法与求解一个问题的方法相同B．算法只能解决一个问题，不能重复使用C．算法过程要一步一步执行D．有的算法执行完以后，可能没有结果【答案】C【解析】算法与求解一个问题的方法既有区别又有联系，故A不对．算法能够重复使用，故B不对．每一个算法执行完以后，必须有结果，故D不对．5.计算下列各式中的S值，能设计算法求解的是()①S＝1＋2＋3＋…＋100；②S＝1＋2＋3＋…＋100＋…；③S＝1＋2＋3＋…＋n(n≥1，n∈N)．A．①②B．①③C．②③D．①②③【答案】B【解析】由算法的有限性知②不正确，而①③都可通过有限的步骤操作，输出确定结果．6.下列各式中T的值不能用算法求解的是()A．T＝12＋22＋32＋42＋…＋1002B．T＝＋＋＋＋…＋C．T＝1＋2＋3＋4＋5＋…D．T＝1－2＋3－4＋5－6＋…＋99－100【答案】C【解析】根据算法的有限性知C不能用算法求解．7.关于一元二次方程x2－5x＋6＝0的求根问题，下列说法正确的是()A．只能设计一种算法B．可以设计两种算法C．不能设计算法D．不能根据解题过程设计算法【答案】B【解析】一元二次方程的求解过程可以用公式法和分解因式法进行，可根据不同的解题过程来设计算法，故可以设计两种算法，但两种算法输出的结果是一样的．8.对于解方程x2－2x－3＝0的下列步骤：①设f(x)＝x2－2x－3②计算方程的判别式Δ＝22＋4×3＝16>0③作f(x)的图象④将a＝1，b＝－2，c＝－3代入求根公式x＝，得x1＝3，x2＝－1.其中可作为解方程的算法的有效步骤为()A．①②B．②③C．②④D．③④【答案】C【解析】解一元二次方程可分为两步确定判别式和代入求根公式，故②④是有效的，①③不起作用．9.以下有六个步骤：①拨号；②等拨号音；③提起话筒(或免提功能)；④开始通话或挂机(线路不通)；⑤等复话方信号；⑥结束通话．试写出打一个本地电话的算法________．(只写编号)【答案】③②①⑤④⑥【解析】此题考查算法的思想；此算法应该是：根据常识知道：首先提起话筒（或按免提功能），然后等拨号音后在拨号，然后等复话方信号，然后开始通话或者线路不通挂机，最后结束通话，所以算法是③②①⑤④⑥10.函数y＝，试写出给定自变量x，求函数值y的算法【答案】见解析【解析】解：算法如下：第一步，输入x.第二步，若x>0，则令y＝－x＋1后执行第五步；否则执行第三步．第三步，若x＝0，则令y＝0后执行第五步；否则执行第四步．第四步，令y＝x＋1.第五步，输出y的值．。
(完整版)高考算法程序框图真题练习及答案详解
(完整版)高考算法程序框图真题练习及答案详解1. 该算法程序框图的功能是什么？A. 求a，b，c三数的最大数B. 求a，b，c三数的最小数C. 将a，b，c按从小到大排列2. 该算法程序框图的功能是什么？A. 求输出a，b，c三数的最大数B. 求输出a，b，c三数的最小数C. 将a，b，c按从小到大排列3. 该算法程序框图的功能是什么？A. 找出a、b、c三个数中最大的数B. 找出a、b、c三个数中最小的数C. 找出a、b、c三个数中第二大的数4. 程序框图表示的算法的运行结果是什么？A. 5B. 6C. 75. 程序框图中所表示的算法是什么？A. 求x的绝对值B. 求x的相反数C. 求x的平方根6. 运行图中所示程序框图所表达的算法，输出的结果是什么？A. 3B. 7C. 157. 程序框图（算法流程图）的输出结果是什么？A. 6B. 5C. 48. 运行相应的程序，输出的结果为什么？A. 676B. 26C. 59. 运行相应的程序，输出的结果是什么？A. 1B. 2C. 310. 运行相应的程序，输出的S的值等于什么？A. 18B. 2C. 2111. 当m=7，n=3时，执行如图所示的程序框图，输出的S的值为什么？A. 7B. 42C. 21012. 执行如图所示的程序框图，若输入n=10，则输出的S=什么？A.B.C.13. 运行相应的程序，当输入x的值为-25时，输出x的值为什么？A. -1B. 1C. 314. 运行相应的程序，输出s值等于什么？A. -3B. -10C.15. 执行如图所示的程序框图，若输入n的值为6，则输出s的值为什么？A. 105B.C. 1516. 执行如图所示的程序框图，则输出的S的值是什么？A.B. 16C.D. 1A．9B．10C．11D．12考点：循环结构．专题：程序框图．分析：根据程序框图，计算每次循环后变量a的值，直到不满足循环条件，输出结果．解答：解：根据程序框图，计算每次循环后变量a的值，直到不满足循环条件，输出结果．第一次循环：a=3+2=5第二次循环：a=5+3=8第三次循环：a=8+4=12第四次循环：a=12+5=17第五次循环：a=17+6=23第六次循环：a=23+7=30第七次循环：a=30+8=38第八次循环：a=38+9=47第九次循环：a=47+10=57此时不满足循环条件，输出a的值，为57-9=48，故选A．点评：本题考查了应用程序框图进行简单的计算问题，是基础题．并在满足条件时跳出循环，输出S的值．当k=3时，不满足条件k≥n，跳出循环，输出S=7×6×5×4=840．故选D．点评：本题考查了直到型循环结构的程序框图，根据框图的流程判断算法的功能是解题的关键．同时，需要注意条件的判断和循环变量的变化过程．解：$k=1$，满足判断框，第1次循环，$s=1$，$k=2$；第2次判断后循环，$s=0$，$k=3$；第3次判断并循环$s=-3$，$k=4$，第3次判断退出循环，输出$s=-3$。
高中数学必修3算法初步与框图专项测试题(苏教版)
高中数学必修3算法初步与框图专项测试题（苏教版）1．下面对算法描述正确的一项是（ ）A ．算法只能用伪代码来描述B ．算法只能用流程图来表示C ．同一问题可以有不同的算法D ．同一问题不同的算法会得到不同的结果解析：自然语言、图形和伪代码都可以表示算法，只要是同一问题，不同的算法也应该有相同的结果。
答案：C2．将两个数2,1==b a 交换，使1,2==b a ，下面语句正确的是（ ）A ．a b b a ←←,B ．b a a b ←←,C ．a b b c c a ←←←,,D ．c a a b b c ←←←,, 解析：赋值符号“b a ←”的含义是把b 的值给a 。
选项A 得到的结果是2、2；选项B 得到的结果是1、1；选项C 中的c 的值不明确；选项D 正确。
答案：D3．条件语句表达的算法结构为（ ） A ．顺序结构 B ．选择结构 C ．循环结构 D ．以上都可以 解析：条件语句典型的特点是先判断再执行，对应的是选择结构。
答案：B4．下面的程序执行后的结果是（ ）ba prb a b b a a b a ,int 31-←+←←← A ．3,1 B ．1,4 C ．0,0 D ．0,6解析：由题意得3,1==b a ，故执行到第三步时，把b a +的值给a ，这时4=a ，第四步，把b a -的值给b ，这时1=b 。
答案：B5．关于for 循环说法错误的是（ ）A ．在for 循环中，循环表达式也称为循环体B ．在for 循环中，步长为1，可以省略不写，若为其它值，则不可省略C ．使用for 循环时必须知道终值才可以进行D ．for 循环中end 控制结束一次循环，开始一次新循环解析：for 循环中end 是指整个循环结束，而不是一次循环结束 答案：D6．当3=x 时，下面程序段输出的结果是（ ）ad Re xIF 10<x THEN a y *2← elsea a y *← y pr intA ．9B ．3C ．10D ．6解析：当输入3=x 时，因为103<，所以62==a y .答案：D7．普通高中新课程标准实验教科书（数学必修3）知识结构框图如下，则空白的框内应该填入（ ）A ．分层抽样、相关关系、相关系数B ．分层抽样、相关系数、相关关系C ．相关关系、分层抽样、相关系数D ．相关系数、相关关系、分层抽样 解析：根据知识结构之间的关系，可知选项A 正确。
高一数学算法和程序框图试题
高一数学算法和程序框图试题1.当x=2时，如图所示程序运行后输出的结果为_________ ．【答案】15.【解析】当i=1 s=0*2+1=1当i="2" s=1*2+1=3当i=3 s=3*2+1=7当i="4" s=7*2+1=15故s=15,故应填入:15.【考点】算法程序．2.如图，该程序运行后的输出结果为（）A．B．C．D．【答案】B【解析】第一次运行结果：；第二次运行结果：；第三次运行结果：；此时，条件不满足，跳出循环，输出的值为，故选择B，注意多次给一个量赋值以最后一次的赋值为准.【考点】程序框图中的循环结构.3.如图.程序输出的结果 , 则判断框中应填（）A．B．C．D．【解析】按照程序框图执行如下：，因为输出的结果为，故此时判断条件应为：或.【考点】1、程序框图的运算；2、循环语句.4.执行如图所示的程序框图,若输入的值为,则输出的的值为（）A．B．C．D．【答案】B【解析】由已知初始条件为：n=7,i=1,s=1；第１次运行：判断,是，；第2次运行：判断,是，；第3次运行：判断,是，；第4次运行：判断,是，；第5次运行：判断,是，；第6次运行：判断,是，；第7次运行：判断,否，输出；故选B．【考点】算法与程序框图．5.右图是一个算法的流程图，则输出S的值是 .【答案】7500【解析】根据算法的流程图S=0+3=3,K=1+2=3,S=3+9=12,K=3+2=5,S=12+15=27，以此规律则输出S的值是7500【考点】程序框图6.程序框图符号“”可用于( )A．输出B．赋值C．判断D．输入【解析】在程序框图符号中,矩形方框“”是处理框,平行四边形框才是输出与输入,而判断则是菱形框,故选B.【考点】程序框图.7.若某程序框图如图所示，则输出的p的值是 ()A．30B．28C．21D．55【答案】A【解析】根据框图的循环结构，依次；；。
高一数学算法与程序框图试题
高一数学算法与程序框图试题1.以下说法不正确的是（）A．顺序结构是由若干个依次执行的处理步骤组成的，每一个算法都离不开顺序结构B．循环结构是在一些算法中从某处开始按照一定条件，反复执行某一处理步骤，故循环结构中一定包含选择结构C．循环结构中不一定包含选择结构D．用程序框图表示算法，使之更加直观形象，容易理解【答案】C【解析】根据算法中三种逻辑结构的定义，顺序结构是最基本的结构，每个算法一定包含顺序结构；选择结构是算法中出现分类讨论时使用的逻辑结构，循环结构一定包含一个选择结构；分析四个答案，即可得到结论．解：任何算法都是由若干个顺序结构组成．循环结构中要对是否循环进行判断，所以一定包含选择结构，故选C．点评：本题考查的知识点是算法的概念及算法的特点，是对概念的直接考查，属基础题，熟练掌握相关概念是解答本题的关键．2.执行如图的程序框图，输出的S是（）A．﹣378B．378C．﹣418D．418【答案】D【解析】解答算法框图的问题，要依次执行各个步骤，特别注意循环结构的终止条件，本题中是k≥﹣20就终止循环，因此累加变量累加到值40最后输出S=﹣2﹣0+2+4+…+40，于是计算得到结果．解：据题意输出S=﹣2﹣0+2+4+ (40)其表示一首项为﹣2，公差为2的等差数列前22项之和，故S=×22=418．故选D．点评：本题考查了循环结构、流程图的识别、条件框等算法框图的应用，还考查了对多个变量计数变量、累加变量的理解与应用，属于基础题．3.执行如图的程序框图，如果输入a=10，b=11，则输出的S等于（）A．B．C．D．【答案】C【解析】分析已知中的程序框图，我们易得程序框图中循环结构的功能是计算并输出的值，结合已知中输入a=10，b=11，结合程序中的选择结构，我们计算出进入循环时的a值，即可得到答案．解：∵输入a=10，b=11，不满足分支结构中的条件a≥b，故进行循环时a=b=11，则程序的功能为计算数列的值∵===故选C点评：本题考查的知识点是循环结构，本题易忽略循环结构前条件结构的作用，而错将进入循环的a值定为10，而错选B答案．4.下面的程序框图能判断任意输入的数x的奇偶性．其中判断框内的条件是（）A．m=0B．m=1C．x=0D．x=1【答案】B【解析】本题考查了选择结构，由程序框图所体现的算法可知判断一个数是奇数还是偶数，看这个数除以2的余数是1还是0，从而得到判断框条件．解：由程序框图所体现的算法可知判断一个数是奇数还是偶数，看这个数除以2的余数是1还是0．由图可知应该填m=1．故选B点评：选择结构是考试中常考的知识点，根据流程图计算运行结果是算法这一模块的重要题型，处理的步骤一般为：分析流程图，从流程图中即要分析出计算的类型，又要分析出参与计算的数据建立数学模型，根据第一步分析的结果，选择恰当的数学模型解模．5.看下面的四段话，其中不是解决问题的算法的是（）A．从济南到北京旅游，先坐火车，再坐飞机抵达B．解一元一次方程的步骤是去分母、去括号、移项、合并同类项、系数化为1C．方程x2﹣1=0有两个实根D．求1+2+3+4+5的值，先计算1+2=3，再由3+3=6，6+4=10，10+5=15，最终结果为15【答案】C【解析】A选项B选项D选项均是解决问题的算法，而选项C只是一个真命题，没解决什么问题．解：A选项：从济南到北京旅游，先坐火车，再坐飞机抵达，解决了怎样去的问题，所以A错误；B选项：解一元一次方程的步骤是去分母、去括号、移项、合并同类项、系数化为1，解决了怎样接一元一次方程的问题，所以B错误；D选项：求1+2+3+4+5的值，先计算1+2=3，再由3+3=6，6+4=10，10+5=15，最终结果为15，解决了怎样求数的和的问题，所以D错误；故选C．点评：本题考查了算法的概念和理解，注重算法的用途和意义．6.已知直角三角形两直角边长为a，b，求斜边长c的一个算法分下列三步：①计算；②输入直角三角形两直角边长a，b的值；③输出斜边长c的值；其中正确的顺序是（）A．①②③B．②③①C．①③②D．②①③【答案】D【解析】由算法的概念可知：算法是先后顺序的，结果明确性，每一步操作明确的，根据已知直角三角形两直角边长为a，b，求斜边长c的一个算法的先后顺序，即可判断选项的正误．解：由算法规则得：第一步：输入直角三角形两直角边长a，b的值，第二步：计算，第三步：输出斜边长c的值；这样一来，就是斜边长c的一个算法．故选D．点评：本题考查算法的概念，解题关键是算法的作用，格式．7.若f（x）在区间[a，b]内单调，且f（a）•f（b）＜0，则f（x）在区间[a，b]内（）A．至多有一个根B．至少有一个根C．恰好有一个根D．不确定【答案】C【解析】根据零点存在定理，我们易得到函数f（x）在区间[a，b]上有零点，再根据函数f（x）在区间[a，b]内单调，即可得结论．解：因为f（a）f（b）＜0，所以，f（a）与f（b）异号，即：f（a）＞0，f（b）＜0；或者f（a）＜0，f（b）＞0显然，在[a，b]内，必有一点，使得f（x）=0．又f（x）在区间[a，b]上单调，所以，这样的点只有一个故选C点评：本题考查的知识点是根的存在性及根的个数判断，正确理解零点存在定理是解答本题的关键．8.已知一个学生的语文成绩为89，数学成绩为96，外语成绩为99．求他的总分和平均成绩的一个算法为：第一步：取A=89，B=96，C=99；第二步：；第三步：；第四步：输出计算的结果．【答案】S=A+B+C；．【解析】由题意，第二步，求和，第三步，计算平均成绩．解：由题意，第二步，求和S=A+B+C，第三步，计算平均成绩．故答案为：S=A+B+C；．点评：本题考查算法知识，考查学生分析解决问题的能力，属于基础题．9.写出求1+2+3+4+5+6+…+100的一个算法．可运用公式1+2+3+…+n=直接计算．第一步；第二步；第三步输出计算的结果．【答案】取n=100；计算．【解析】由条件知构成等差数列，再前n项和公式求得其值．解：由条件知构成等差数列，从而前n项和公式求得其值，求1+2+3+4+5+6+…+100，故先取n=100，再代入计算．故答案为：取n=100；计算．点评：本题考查算法知识，考查等差数列的前n项和公式的应用．10.写出按从小到大的顺序重新排列x，y，z三个数值的算法．【答案】见解析【解析】本题主要设计从小到大的顺序重新排列x，y，z的程序，利用赋值语句，采用顺序结构，弄清几个步骤即可写出答案．解：算法如下：（1）输入x，y，z三个数值；（2）从三个数值中挑出最小者并换到x中；（3）从y，z中挑出最小者并换到y中；（4）输出排序的结果．点评：本题主要考查了赋值语句，以及设计程序框图解决实际问题．属于基础题．。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
算法与程序框图训练题1．(2019·湖北八校联考)对任意非零实数a ，b ，定义a *b 的运算原理如图所示，则 (log 222)*⎝ ⎛⎭⎪⎫18-23＝( )A ．1B ．2C ．3D ．4解析：选A 因为log 222＝3，⎝ ⎛⎭⎪⎫18-23＝4,3<4，所以输出4－13＝1，故选A.2．执行如图所示的程序框图，则输出的x ，y 分别为( )A ．90,86B ．94,82C ．98,78D ．102,74解析：选C 第一次执行循环体，y ＝90，s ＝867＋15，不满足退出循环的条件，故x ＝90；第二次执行循环体，y ＝86，s ＝907＋433，不满足退出循环的条件，故x ＝94；第三次执行循环体，y ＝82，s ＝947＋413，不满足退出循环的条件，故x ＝98；第四次执行循环体，y ＝78，s ＝27，满足退出循环的条件，故x ＝98，y ＝78.3．(2018·云南民族大学附属中学二模)执行如图所示的程序框图，若输出的k 的值为6，则判断框内可填入的条件是( )A ．s >12？B ．s >710？C ．s >35？D ．s >45？解析：选B s ＝1，k ＝9，满足条件；s ＝910，k ＝8，满足条件；s ＝45，k ＝7，满足条件；s ＝710，k ＝6，不满足条件．输出的k ＝6，所以判断框内可填入的条件是“s >710？”．故选B. 4．(2019·合肥质检)执行如图所示的程序框图，如果输出的k 的值为3，则输入的a 的值可以是( )A ．20B ．21C ．22D ．23解析：选A 根据程序框图可知，若输出的k ＝3，则此时程序框图中的循环结构执行了3次，执行第1次时，S ＝2×0＋3＝3，执行第2次时，S ＝2×3＋3＝9，执行第3次时，S ＝2×9＋3＝21，因此符合题意的实数a 的取值范围是9≤a <21，故选A.5．(2019·重庆质检)执行如图所示的程序框图，如果输入的x ＝0，y ＝－1，n ＝1，则输出x ，y 的值满足( )A ．y ＝－2xB ．y ＝－3xC ．y ＝－4xD ．y ＝－8x解析：选C 初始值x ＝0，y ＝－1，n ＝1，x ＝0，y ＝－1，x 2＋y 2<36，n ＝2，x ＝12，y ＝－2，x 2＋y 2<36，n ＝3，x ＝32，y ＝－6，x 2＋y 2>36，退出循环，输出x ＝32，y ＝－6，此时x ，y 满足y ＝－4x ，故选C.6．(2018·南宁二中、柳州高中联考)执行如图所示的程序框图，若输出的结果s ＝132，则判断框中可以填( )A ．i ≥10?B ．i ≥11?C ．i ≤11?D ．i ≥12?解析：选B 执行程序框图，i ＝12，s ＝1；s ＝12×1＝12，i ＝11；s ＝12×11＝132，i ＝10.此时输出的s ＝132，则判断框中可以填“i ≥11？”．7．(2019·漳州八校联考)执行如图所示的程序，若输出的y 的值为1，则输入的x 的值为( )INPUT xIF x>＝1 THENy ＝x 2ELSEy ＝－x 2＋1END IF PRINT y ENDA ．0B ．1C．0或1 D．－1,0或1解析：选C 当x≥1时，由x2＝1得x＝1或x＝－1(舍去)；当x<1时，由－x2＋1＝1得x＝0.∴输入的x的值为0或1.8．执行如图所示的程序框图，若输入的n＝4，则输出的s＝( )A．10 B．16C．20 D．35解析：选C 执行程序框图，第一次循环，得s＝4，i＝2；第二次循环，得s＝10，i＝3；第三次循环，得s＝16，i＝4；第四次循环，得s＝20，i＝5.不满足i≤n，退出循环，输出的s＝20.9.(2018·洛阳第一次统考)已知某算法的程序框图如图所示，则该算法的功能是( )A．求首项为1，公差为2的等差数列的前2 018项和B．求首项为1，公差为2的等差数列的前2 019项和C．求首项为1，公差为4的等差数列的前1 009项和D．求首项为1，公差为4的等差数列的前1 010项和解析：选D 由程序框图得，输出的S＝(2×1－1)＋(2×3－1)＋(2×5－1)＋…＋(2×2 019－1)，可看作数列{2n－1}的前2 019项中所有奇数项的和，即首项为1，公差为4的等差数列的前1 010项和．故选D.10．(2018·郑州第一次质量测试)执行如图所示的程序框图，若输出的结果是7，则判断框内m的取值范围是( )A ．(30,42]B ．(30,42)C ．(42,56]D ．(42,56)解析：选A k ＝1，S ＝2，k ＝2；S ＝2＋4＝6，k ＝3；S ＝6＋6＝12，k ＝4；S ＝12＋8＝20，k ＝5；S ＝20＋10＝30，k ＝6；S ＝30＋12＝42，k ＝7，此时不满足S ＝42<m ，退出循环，所以30<m ≤42，故选A.11．(2019·石家庄调研)20世纪70年代，流行一种游戏——角谷猜想，规则如下：任意写出一个自然数n ，按照以下的规律进行变换，如果n 是奇数，则下一步变成3n ＋1；如果n 是偶数，则下一步变成n2.这种游戏的魅力在于无论你写出一个多么庞大的数字，最后必然会落在谷底，更准确地说是落入底部的4－2－1循环，而永远也跳不出这个圈子，下列程序框图就是根据这个游戏而设计的，如果输出的i 值为6，则输入的n 值为( )A ．5或16B ．16C ．5或32D ．4或5或32解析：选C 若n ＝5，执行程序框图，n ＝16，i ＝2；n ＝8，i ＝3；n ＝4，i ＝4；n ＝2，i ＝5；n ＝1，i ＝6，结束循环，输出的i ＝6.若n ＝32，执行程序框图，n ＝16，i ＝2；n ＝8，i ＝3；n ＝4，i ＝4；n ＝2，i ＝5；n ＝1，i ＝6，结束循环，输出的i ＝6.当n ＝4或16时，检验可知不正确，故输入的n ＝5或32，故选C.12．(2018·贵阳第一学期检测)我国明朝数学家程大位著的《算法统宗》里有一道闻名世界的题目：“一百馒头一百僧，大僧三个更无争．小僧三人分一个，大小和尚各几丁？”如图所示的程序框图反映了对此题的一个求解算法，则输出的n 的值为( )A ．20B ．25C ．30D ．35解析：选B 法一：执行程序框图，n ＝20，m ＝80，S ＝60＋803＝8623≠100；n ＝21，m ＝79，S ＝63＋793＝8913≠100； n ＝22，m ＝78，S ＝66＋783＝92≠100； n ＝23，m ＝77，S ＝69＋773＝9423≠100； n ＝24，m ＝76，S ＝72＋763＝9713≠100；n ＝25，m ＝75，S ＝75＋753＝100，退出循环．所以输出的n ＝25.法二：设大和尚有x 个，小和尚有y 个，则⎩⎪⎨⎪⎧x ＋y ＝100，3x ＋13y ＝100，解得⎩⎪⎨⎪⎧x ＝25，y ＝75，根据程序框图可知，n 的值即大和尚的人数，所以n ＝25.13．已知函数y ＝lg|x －3|，如图所示程序框图表示的是给定x 值，求其相应函数值y 的算法．请将该程序框图补充完整．其中①处应填________，②处应填________．解析：由y ＝lg|x －3|＝⎩⎪⎨⎪⎧lgx －3，x >3，lg 3－x ，x <3及程序框图知，①处应填x <3？，②处应填y＝lg(x －3)．答案：x <3？ y ＝lg(x －3)14．执行如图所示的程序框图，若输入的N ＝20，则输出的S ＝________.解析：依题意，结合题中的程序框图知，当输入的N ＝20时，输出S 的值是数列{2k －1}的前19项和，即191＋372＝361. 答案：36115．执行如图所示的程序框图，则输出的λ是________．解析：依题意，若λa ＋b 与b 垂直，则有(λa ＋b )·b ＝4(λ＋4)－2(－3λ－2)＝0，解得λ＝－2；若λa ＋b 与b 平行，则有－2(λ＋4)＝4(－3λ－2)，解得λ＝0.结合题中的程序框图可知，输出的λ是－2.答案：－216．执行如图所示的程序框图，如果输入的x ，y ∈R ，那么输出的S 的最大值为________．解析：当条件x ≥0，y ≥0，x ＋y ≤1不成立时，输出S 的值为1，当条件x ≥0，y ≥0，x ＋y ≤1成立时，输出S ＝2x ＋y ，下面用线性规划的方法求此时S 的最大值．作出不等式组⎩⎪⎨⎪⎧x ≥0，y ≥0，x ＋y ≤1表示的平面区域如图中阴影部分所示，由图可知当直线S ＝2x ＋y 经过点M (1,0)时S 最大，其最大值为2×1＋0＝2，故输出S 的最大值为2.答案：2。