常见的立体图形
《立体图形认识》课件

$number {01}
目录
• 立体图形的基本概念 • 常见立体图形的认识 • 立体图形的性质与计算 • 立体图形的绘制方法 • 立体图形在数学中的应用
01
立体图形的基本概念
定义与分类
定义
立体图形是三维空间中具有大小 和形状的空间几何体。
分类
常见的立体图形包括长方体、正 方体、圆柱体、圆锥体、球体等 。
立体图形的组合与拼接
选择合适的组合方式
考虑实际应用场景
在组合立体图形时,需要选择合适的 组合方式,如叠加、拼接等,以确保 组合后的立体图形整体协调。
在组合与拼接立体图形时,需要考虑 实际应用场景,如室内设计、产品展 示等,以便更好地满足实际需求。
注意图形的对称性
在拼接立体图形时,需要注意图形的 对称性,以确保拼接后的立体图形更 加美观。
圆锥体的认识
总结词
圆锥体的定义、性质和特点
详细描述
圆锥体的定义、性质和特点,包括圆锥体的底面、侧面和高等基本元素,以及圆锥体的侧面展开后为一个扇形、 底面周长等于母线等长、顶点到底面中心的距离等于高等特点。
球体的认识
总结词
球体的定义、性质和特点
详细描述
球体的定义、性质和特点,包括球体的半径、表面积和体积等基本元素,以及球体表面积等于4πr²、 体积等于4/3πr³等特点。
了解立体图形表面积的计算公式 ,如长方体、圆柱体、圆锥体等
。
特殊情况处理
掌握在计算立体图形面积时如何 处理特殊情况,如斜切、打孔等
。
立体图形的体积计算
总结词
掌握计算立体图形体积的基本方法
不规则立体图形体积计算
掌握在计算立体图形体积时如何处理 特殊情况,如空心、叠加等。
认识立体图形

认识立体图形立体图形是我们生活中常见的一种形态,它与平面图形有所不同,拥有立体感和空间感。
我们可以在建筑物、家具、车辆等各个领域中看到立体图形的存在。
本文将介绍一些常见的立体图形,并探讨它们的各个方面。
一、正方体正方体是一种具有六个面的立体图形,每个面都是一个正方形。
正方体的六个面相互平行,并且相邻的两个面之间的边长相等。
正方体具有六个顶点和12条边。
我们可以通过观察正方体的各个面和边来感受它的立体感。
正方体在建筑、设计、游戏等领域中得到广泛应用。
二、长方体长方体是一种具有六个面的立体图形,每个面都是一个长方形。
长方体的六个面相互平行,并且相邻的两个面之间的边长相等。
长方体具有八个顶点和12条边。
它在日常生活中常见于建筑物、电视机、书桌等物体的形状。
三、球体球体是一种具有无限个面的立体图形,它的每个面都称为球面。
球体具有无数个顶点和边。
球体是一种特殊的立体图形,因为它的表面在任何点上都是相等的。
我们可以通过触摸、旋转球体来感受它的特殊性。
四、圆柱体圆柱体是一种具有三个面的立体图形,它由两个平行的圆面和一个侧面组成。
圆柱体的侧面是一个矩形,其长和高分别等于两个圆的周长和两个平行圆的距离。
圆柱体具有两个顶点和三个边。
圆柱体在容器、管道、柱子等物体的形状中得到广泛应用。
五、圆锥体圆锥体是一种具有二个面的立体图形,它由一个圆面和一个侧面组成。
圆锥体的侧面是一个三角形,其底边是一个圆,顶点位于圆的中心。
圆锥体具有一个顶点和两个边。
圆锥体在一些建筑物、灯罩、冰淇淋锥等形状中常见。
六、棱柱棱柱是一种具有多个面的立体图形,它的底面和顶面是相似且平行的多边形。
棱柱的侧面是由底面和顶面的对应边连接而成的一系列矩形或平行四边形。
棱柱具有多个顶点和边,其个数取决于底面的边数。
棱柱在柱子、柜子、建筑物等方面有广泛应用。
通过了解和认识这些常见的立体图形,我们能够更好地理解和感受它们在我们生活中的存在和应用。
立体图形让我们的环境更加多样化和有趣,也给我们带来了更多的创造和发现的机会。
初一认识立体几何图形

认识立体几何图形
考点名称:认识立体几何图形
立体几何图形:
从实物中抽象出来的各种图形,统称为几何图形,几何图形是数学研究的主要对象之一。
有些几何图形(如长方体、正方体、圆柱、圆锥、球等)的各个部分不都在同一平面内,它们是立体图形。
由一个或多个面围成的可以存在于现实生活中的三维图形。
点动成线,线动成面,面动成体。
即由面围成体,看一个体最多看到立体图形实物三个面。
常见立体几何图形及性质:
①正方体:
有8个顶点,6个面。
每个面面积相等(或每个面都有正方形组成)。
有12条棱,每条棱长的长度都相等。
(正方体是特殊的长方体)
②长方体:
有8个顶点,6个面。
每个面都由长方形或相对的一组正方形组成。
有12条棱,相对的4条棱的棱长相等。
③圆柱:
上下两个面为大小相同的圆形。
有一个曲面叫侧面。
展开后
为长方形或正方形或平行四边形。
有无数条高,这些高的长度都相等。
④圆锥:
有1个顶点,1个曲面,一个底面。
展开后为扇形。
只有1条高。
四面体有1个顶点,四面六条棱高。
⑤直三棱柱:
三条侧棱切平行,上表面和下表面是平行且全等的三角形。
⑥球:
球是生活中最常见的图形之一,例如篮球、足球都是球,球是由一个面所围成的几何体。
常见的立体几何图形视图:
几何图形图形
长方体
正方体
圆锥圆柱圆锥球。
生活中常见的立体图形及其特征

生活中常见的立体图形及其特征立体图形是我们日常生活中的常见事物,它们不仅令我们生活更美好,还有很多有趣的特征和用途。
本文将从常见的立体图形入手,探讨它们的特征和应用,让我们了解到立体图形的奥秘。
一、正方体正方体是一种常见的正交多面体,它有六个平面、八个顶点和12条边。
正方体是最稳定的立方体,因为它的6个面都是相等的,也就是说,正方体所承受的压力和重力是相等的。
正方体在我们的日常生活中广泛应用,例如玩具、箱子和建筑等领域。
二、圆柱体圆柱体是一种由一个圆和与其垂直的柱面组成的几何体。
它有两个平面、一个侧面、两个底面和一个轴线,圆柱体也是我们日常生活中的一种常见事物,比如可乐瓶、水管、笔筒等。
三、圆锥体圆锥体是一种由一个圆锥和一个底面组成的几何体,它有一个平面、一个侧面、一个底面和一个轴线。
圆锥体与圆柱体类似,但它的形状更加特殊,因此它有着更广泛的应用,例如圆锥机、储物柜、喇叭等。
四、棱柱棱柱是一个由两个平行的底面和由这些底面到每个底面所垂直的平面面组成的多面体。
棱柱的特征是它的“棱”,也就是说它是由多个长方形组成的,正方形是最常见的。
棱柱在我们的日常生活中也有着广泛的应用,例如铅笔盒、棉花糖、灯罩等。
五、棱锥棱锥是一个由一个多边形和所有连接多边形到一个点的线段组成的几何体。
棱锥的特征是它的“锥”,也就是说它的形状呈尖锐的角度。
棱锥也有广泛的应用,例如灯泡、安全帽等。
六、球体球体是一个由一条半径为r的球面和半径为r的半球组成的三维形体。
球体的特征是它的完美圆形,这种形状在我们的日常生活中也随处可见,例如足球、篮球、地球仪等。
七、金字塔金字塔是一个由一个多边形底面和一个顶点连接底面每个角的三角形组成的几何体。
金字塔的特征是它的形状,它的形状特殊,所以它也有很多特殊的用途,如建筑、博物馆等。
总结立体图形在我们的日常生活中随处可见,它们的特征各不相同,在不同的应用领域也有不同的用途,例如在建筑领域中,我们会用金字塔和棱锥来烘托建筑的氛围;在玩具制作领域中,我们常见到的正方体和球体;在工程制造领域中,我们可以看到的是圆柱体和圆锥体。
生活中立体图形

2、点:地图上的城市, 几何体上的顶点;
线:地图上的公路、铁路、 河流,几何体上的棱;
面:水面,黑板面,球的 表面,水桶的侧面。
生活中立体图形
练一练
图中的棱柱、圆锥分别是由几个面组成的? 它们是平的还是曲的?
生活中立体图形
生活中的立体图形
生活中,哪些物体给你面的形象,哪些 是平的?哪些是曲的?
简单几何体的分类: 议一议:
圆柱
柱体
柱体有何特点?
棱柱
简单的几何体
圆锥 锥体
棱锥
锥体有何特点 ?
球体
生活中立体图形
柱体
圆柱
棱柱
球体
锥体
圆锥
生活中立体图形
棱锥
练习
1. 下面图形中第一行是一些具体的物体,第二行是一些立 体图形,试找出与立体图形对应的实物.
生活中立体图形
圆柱
柱体
三棱柱
四棱柱 棱柱
生活中的立体图形
生活中立体图形
生活中立体图形
生活中你会常见很多实物,由下列实物 能想 象出你熟悉的几何体吗?
(1)文具盒 (2)魔方Βιβλιοθήκη (4)足球(5)漏斗
3)笔筒
生活中立体图形
你是这样想的吗?
文具盒能得到长方体 .
生活中立体图形
你是这样想的吗?
魔方能得到正方体.
生活中立体图形
你是这样想的吗?
圆锥有何特点?
它的底是一个 圆 ;圆锥的顶是 尖 的 侧面 光滑 ,由 曲面 构成。
生活中立体图形
你是这样想的吗?
足球能得到球体.
生活中立体图形
通过对你周边物体的观察、想象,归纳一下 我们常见的几何体有哪些?
一年级数学知识点:立体图形知识点_知识点总结

《一年级数学立体图形知识点总结》在一年级的数学学习中,立体图形是一个重要的知识点。
认识立体图形不仅能够帮助孩子们建立空间观念,还能为他们后续的数学学习打下坚实的基础。
一、立体图形的种类1. 长方体长方体是一种常见的立体图形,它有六个面,每个面都是长方形。
长方体的相对面完全相同,相对的棱长度相等。
例如,我们日常生活中的书本、文具盒等物品的形状就接近长方体。
2. 正方体正方体是一种特殊的长方体,它的六个面都是完全相同的正方形。
正方体的十二条棱长度都相等。
像魔方、骰子等就是正方体。
3. 圆柱圆柱有两个底面和一个侧面。
底面是圆形,侧面是一个曲面。
圆柱的两个底面完全相同且平行。
在生活中,我们常见的易拉罐、柱子等物体的形状就是圆柱。
4. 球球是一个曲面图形,没有平面。
球可以向任意方向滚动。
比如,我们玩的篮球、足球等都是球。
二、立体图形的特征1. 面的特征(1)长方体和正方体都有六个面。
长方体的面可以是长方形,也可能有两个相对的面是正方形。
正方体的六个面都是正方形。
(2)圆柱有两个底面和一个侧面。
底面是圆形,侧面是曲面。
(3)球没有平面,只有一个曲面。
2. 棱的特征(1)长方体有十二条棱,相对的棱长度相等。
(2)正方体的十二条棱长度都相等。
(3)圆柱没有棱。
(4)球没有棱。
3. 顶点的特征(1)长方体有八个顶点。
(2)正方体也有八个顶点。
(3)圆柱没有顶点。
(4)球没有顶点。
三、立体图形的观察与比较1. 观察立体图形让孩子们通过观察实物或模型,了解不同立体图形的形状、大小、颜色等特征。
可以引导孩子们从不同的角度观察立体图形,如从正面、侧面、上面观察,培养他们的空间观察能力。
2. 比较立体图形(1)比较形状:让孩子们比较不同立体图形的形状,说出它们的相同点和不同点。
例如,长方体和正方体都有六个面,但正方体的六个面都是正方形,而长方体的面可能是长方形。
(2)比较大小:可以通过比较立体图形的体积或表面积来比较它们的大小。
生活中的立体图形

圆柱
圆柱特征:侧面是曲面,没有棱,上下底面是圆形。
பைடு நூலகம்
你是这样想的吗?
由漏斗可以想到
圆锥
圆锥特征:侧面是曲面,底面是圆形。
金字塔又可以联想 到什么立体图形呢?
金字塔可以得到
棱锥
棱锥特征:侧面是三角形,有明显的棱,底面是多边形。
你是这样想的吗?
篮球可以想到
球体
球的特征:球面是曲面
小结
圆柱
简 单 几 何 体 的 分 类
柱体
棱柱
球体 棱锥 锥体 圆锥
棱柱和圆柱统称 柱体
议一议:找出棱柱和圆柱的相同点和不同点? 相同点:由两个相同大小的平面图形构成上下两底。
不同点:圆柱侧面为曲面,棱柱都由平面构成。
扩展:棱柱还可以分为:
三棱柱
四棱柱
五棱柱
六棱柱
棱锥还可以分为:
三棱锥
四棱锥
五棱锥
六棱锥
巩固练习
1.下面图形中左面是一些具 体的物体,右面是一些立体图形, 试找出与右面立体图形对应的实 物.
复习回顾
生活中你会常见很多的实物,有下列实物能想象出你熟悉的几何体吗?
1 文具盒, 2蛋糕, 4漏斗, 3笔筒 , 5足球 。
你是这样想的吗?
文具盒能得到 长方体 蛋糕能得到的 三棱柱 像这样的立体图形就是 棱柱
棱柱特征:侧面是平面,且有明显的棱,底面是多边形。
你是这样想的吗?
可乐瓶,笔筒能得到
常见的立体图形
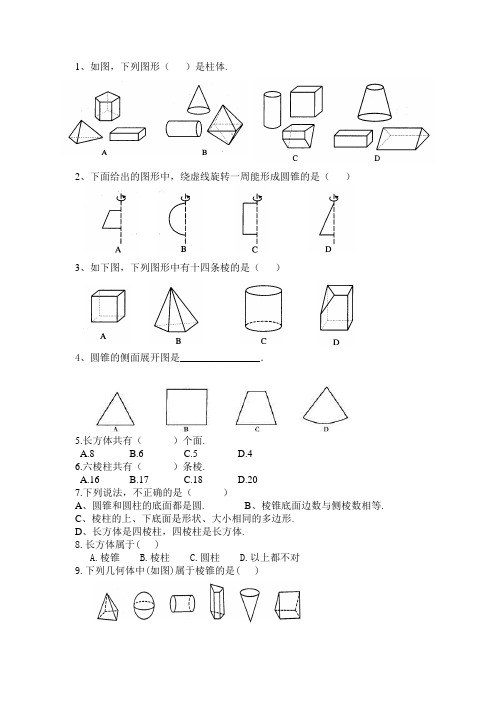
1、如图,下列图形()是柱体.
2、下面给出的图形中,绕虚线旋转一周能形成圆锥的是()
3、如下图,下列图形中有十四条棱的是()
4、圆锥的侧面展开图是________________.
5.长方体共有()个面.
A.8
B.6
C.5
D.4
6.六棱柱共有()条棱.
A.16
B.17
C.18
D.20
7.下列说法,不正确的是()
A、圆锥和圆柱的底面都是圆.
B、棱锥底面边数与侧棱数相等.
C、棱柱的上、下底面是形状、大小相同的多边形.
D、长方体是四棱柱,四棱柱是长方体.
8.长方体属于( )
A.棱锥
B.棱柱
C.圆柱
D.以上都不对
9.下列几何体中(如图)属于棱锥的是( )
(1) (2) (3) (4) (5) (6)
A.(1)(5)
B.(1)
C.(1)(5)(6)
D.(5)(6)
10.下列所讲述的物体,_______与圆锥的形状类似( )
A.香烟盒
B.铅笔
C.西瓜
D.烟囱帽
1C 2D 3D 4D 5B 6C 7D 8B 9A 10D。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
从整体上看,它的形状是长方体。
长方体
正顶点等局部,得到的是线段、点。
长方形
线段
点
生活中你会常见很多实物,由下列实物能 想象出你熟悉的几何体吗?
生活中你会常见很多实物,由下列实物能 想象出你熟悉的几何体吗?
正方体 球 长方体 圆锥 六棱柱 四棱柱
棱柱和棱锥
三棱柱 六棱柱 三棱锥
常见立体图形的归类
立体图形
柱体 球体 锥体
台体
圆柱 棱柱
圆锥 棱锥 圆台 棱台
三棱柱 四棱柱 五棱柱 六棱柱 ……
三棱锥 四棱锥 五棱锥 六棱锥 ……
常见的平面图形
三角形
长方形
五边形
圆形
正方形
六边形
有些几何图形(如线段、角、三角形、长方形、圆等) 的各部分都在同一平面内,它们是平面图形。
从正面看
从正面看
从左面看
从上面看
1 习题4.1 第1、2、4题 2 预习立体图形的展开图
长方体
正方体
球 圆柱体
圆锥体
长方体 正方体 圆柱 球 圆锥 圆台
三角形 长方形 正方形 五边形 六边形 圆形
强调:几何图形是从实物中抽象出来的.
常见的立体图形
有些几何图形的各部分不都在同一平内,这样的几何图 形叫做立体图形.
长方体
正方体
圆柱
球
圆锥
圆台
图中实物的形状对应哪些立体图形?把相应的实物 与图形用线连接起来。
图中的各图中包含哪些简单的平面图形?请再举出一 些平面图形的例子。
简单了解三视图知识
从不同的方向看同一个立体图形,会得到 不同的平面图形.
从正面看
从左面看
从上面看
从上面看
从左边看
长方体
从正面看
从上面看
从左面看
从正面看
从左面看
从上面看 从正面看
从上面看 从左面看
从正面看
从上面看
从左面看
给我最大快乐的, 不是已懂的知识, 而是不断的学习.
----高斯
万里长城—中国
天坛祈年殿—中国
国家体育馆—中国
金字塔—埃及
白宫—美国
大英博物馆—英国
地球—我们的家
4.1.1几何图形
对于各种各样的物体,数学中关注的是它们的形状(如方的、 圆的等)、大小(如长度、面积、体积等)和位置(如相交、垂直、 平行等),而它们的颜色、重量、材料等则是其他学科所关注的。
长方体
生活中你会常见很多实物,由下列实物能 想象出你熟悉的几何体吗?
长方体
正方体
生活中你会常见很多实物,由下列实物能 想象出你熟悉的几何体吗?
长方体
正方体
圆柱体
生活中你会常见很多实物,由下列实物能 想象出你熟悉的几何体吗?
长方体
正方体
球 圆柱体
生活中你会常见很多实物,由下列实物能 想象出你熟悉的几何体吗?
