正弦交流电路中电压与电流的关系

合集下载

在正弦交流电路中,电压与电流的超前滞后关系

在正弦交流电路中,电压与电流的超前滞后关系
在正弦交流电路中，电压与电流的相位关系可以通过超前和滞后这两个概念来描述。

1. 电压与电流的相位差：当电压和电流都是正弦波时，它们之间存在一定的相位差。

相位差可以是0度、90度、180度等，具体取决于电路元件的性
质和连接方式。

2. 超前与滞后的概念：在相位上，如果电压相对于电流是超前的，这意味着电压的峰值比电流的峰值早到达。

相反，如果电压相对于电流是滞后的，则电压的峰值比电流的峰值晚到达。

3. 应用场景：超前和滞后的相位关系取决于电路中元件的种类和连接方式。

例如，纯电阻性负载时，电压和电流同相位；纯电感性负载时，电流滞后于电压90度；纯电容性负载时，电流超前于电压90度。

这些相位关系在分
析交流电路时非常重要，因为它们决定了电路的工作特性和元件之间的相互影响。

综上所述，电压与电流的超前和滞后关系取决于电路的元件性质和连接方式，分析这些关系有助于深入理解交流电路的工作原理。

交流电路中纯电阻电压与电流的关系

交流电路中纯电阻电压与电流的关系下载提示：该文档是本店铺精心编制而成的，希望大家下载后，能够帮助大家解决实际问题。

文档下载后可定制修改，请根据实际需要进行调整和使用，谢谢！本店铺为大家提供各种类型的实用资料，如教育随笔、日记赏析、句子摘抄、古诗大全、经典美文、话题作文、工作总结、词语解析、文案摘录、其他资料等等，想了解不同资料格式和写法，敬请关注！Download tips: This document is carefully compiled by this editor. I hope that after you download it, it can help you solve practical problems. The document can be customized and modified after downloading, please adjust and use it according to actual needs, thank you! In addition, this shop provides you with various types of practical materials, such as educational essays, diary appreciation, sentence excerpts, ancient poems, classic articles, topic composition, work summary, word parsing, copy excerpts, other materials and so on, want to know different data formats and writing methods, please pay attention!1. 引言在电路中，电压和电流是基本的物理量，它们之间的关系在不同类型的电路中可能会有所不同。

正弦交流电路中电压与电流的关系.

（5）
实验和理论均可证明，电容器的电容C越大，交流电频率越高，则1/C越小，也就是对电流的阻碍作用越小，我们把电容对电流的“阻力”称作容抗，用XC代表。
1 1 XC C 2fC
（6）
式（5）中，频率f的单位为Hz，电容C的单位为法拉（F），容抗XC的单位仍是欧姆（），XC与电容C和频率f成反比。当C一定时，电容器具有隔直通交的特性，当f=0时，XC=∞，此时电路可视作开路，即“隔直”作用。
上一页
下一页
返回
解：（1）
XC
1 1 10， I =22 6 C 1000 100 10 m
2A，
Um=ImXc=220 2 V。因为纯电容电路中电压滞后电流90，所以 u=220 2 sin(1000t-60)V （2）
I =2230A
U
=220-60V
d (U m sin t ) du C CU m t I m sin( t 90) dt dt
（ 4）
如图7所示的电容器两端加上正弦电压u=Umsint，则在回路中就有电流
上一页下一页返回
由上式可知：（1）Im=CUm 即
Um U 1 Im I C
表1 正弦交流电路中R、L、C元件的电压与电流关系
上一页
下一页
返回
作业：3-15，3-16，3-17
上一页下一页返回
图6 例3的相量图
上一页下一页返回
三、纯电容电路
加在电容元件两个极板上的电压变化时，极板上贮存的电荷Q=CU就随之而变，电荷量随时间的变化率，就是流过联接于电容导线中的电流，即
i dq du C dt dt
（ 2）（ 3）

正弦交流电中电阻、电感、电容元件电压电流的关系.

与电流瞬时值
最大值、有效值 Um RIm 或
Um U Im I
U m Um
R
00、有效值、最
大值都满足欧姆定律。
2、电压电流的相位关系
u 、i 同相
ui
3、电压电流的相量关系
u i
+
U I
–
R
U m Im
R

I 0 U
相量图
t
二、电感元件
设在电感元件的交流电路中
电阻、电感、电容元件的电压电流关系
一、电阻元件二、电感元件三、电容元件
一、电阻元件
+
设在电阻元件的交流电路中，电压、电流参考方向如图示。
1、电压电流的数值关系
ui R
–
瞬时值设：i Im sin t Im Im 00 电阻的电压
则u Ri RIm sint Um sint
感抗越小，在直流电路中容抗为无限大，可视为开路。
2、电压电流的相位关系
u Um sinω t
U m Um 00
i Im sin(ω t 90 )
Im Im 900
i uC
i 超前u
ui
2
3、电压电流的相量关系 i
u

U m Im
Um
Im
00 900
jXC
当 L一定时,线圈的感抗与频率f 成正比。频率越高，
感抗越大，在直流电路中感抗为零，可视i Im sint
Im Im 00 U m Um
u LIm cost Um sin(t 90 )
u 超前i
ui
e 2u e滞后i

交流电路中的电压和电流关系

交流电路中的电压和电流关系
XX,a click to unlimited possibilities
汇报人：XX
目录
01 交流电路的基本概念
03 电压和电流的测量 05 电压和电流的调节
与控制
02 电压和电流的关系 04 电压和电流的功率
电磁干扰的传播途径
辐射干扰：通过空间电磁场传播，影响电子设备性能传导干扰：通过导电介质传播，影响电子设备正常工作感应耦合：通过磁场变化感应出干扰电压或电流，影响电子设备工作静电放电：瞬间产生高压静电，对电子设备造成干扰或损坏
电磁干扰的抑制方法
屏蔽技术：通过金属材料将电磁干扰隔离在一定区域内
交流电的应用
家电设备：如电冰箱、洗衣机、空调等
工业生产：电动机、电焊机、电动工具等
交通运输：电力机车、电动汽车、飞机等
电力系统：发电、输电、配电等
Part Two
电压和电流的关系
电压和电流的相位关系
电压和电流的相位差：描述电压和电流在时间上的相对位置，影响交流电路的性质
相位差与功率因数：解释相位差对交流电路功率因数的影响，以及如何提高功率因数
电流的测量
电流表：用于测量交流电路中的电流值测量方法：串联在电路中，读取表盘上的数值注意事项：选择合适的量程，避免电流过大烧毁电流表测量单位：安培（A）
相位差的测量
定义：相位差是指交流电信号在任意时刻的瞬时值与其基准值之间的角度差
测量方法：使用相位测量仪表或示波器观察两个信号的相位差
意义：相位差对于交流电路的性能和稳定性具有重要影响
影响因素：电源频率、阻抗和感抗等参数都会影响相位差

正弦稳态交流电路相量的研究实验报告

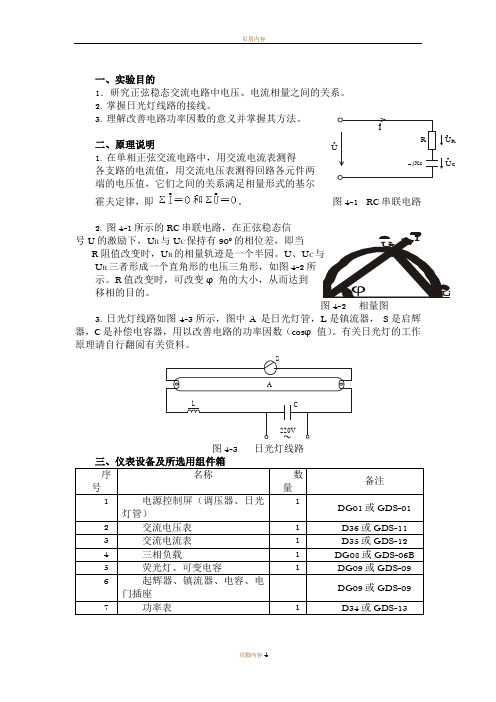
一、实验目的1．研究正弦稳态交流电路中电压、电流相量之间的关系。

2. 掌握日光灯线路的接线。

3. 理解改善电路功率因数的意义并掌握其方法。

二、原理说明 1. 在单相正弦交流电路中，用交流电流表测得各支路的电流值，用交流电压表测得回路各元件两端的电压值，它们之间的关系满足相量形式的基尔霍夫定律，即。

图4-1 RC 串联电路2. 图4-1所示的RC 串联电路，在正弦稳态信号U 的激励下，U R 与U C 保持有90º的相位差，即当 R 阻值改变时，U R 的相量轨迹是一个半园。

U 、U C 与 U R 三者形成一个直角形的电压三角形，如图4-2所示。

R 值改变时，可改变φ角的大小，从而达到移相的目的。

3. 日光灯线路如图4-3所示，图中 A 是日光灯管，L 是镇流器， S 是启辉器，C 是补偿电容器，用以改善电路的功率因数（cos φ值）。

有关日光灯的工作原理请自行翻阅有关资料。

图4-3 日光灯线路序号名称数量备注1 电源控制屏（调压器、日光灯管） 1 DG01或GDS-012 交流电压表 1 D36或GDS-113 交流电流表 1 D35或GDS-124 三相负载 1 DG08或GDS-06B5 荧光灯、可变电容 1 DG09或GDS-096 起辉器、镇流器、电容、电门插座DG09或GDS-097 功率表 1 D34或GDS-13220VL S A CRjXcUcU R IU RU U cI φֹ四、实验内容1. 按图4-1接线。

R为220V、15W的白炽灯泡，电容器为4.7μF/450V。

经指导教师检查后，接通实验台电源，将自耦调压器输出(即U)调至220V。

记录U、U R、U C值，验证电压三角形关系。

2. 日光灯线路接线与测量。

图4-4（1）按图4-4接线。

（2）经指导教师检查后接通实验台电源，调节自耦调压器的输出，使其输出电压缓慢增大，直到日光灯刚刚启辉点亮为止，记下三表的指示值。

正弦交流电路中纯电感元件上电压、电流、电动势关系

论正弦交流纯线性电感电路中电压、电流和自感电动势的相位关系魏培钦 (2008.06.10)摘要：纯线性电感电路中电压、电流和自感电动势的相位关系早已有结论——电压超前电流90，电流超前自感电动势 90。

可是到目前为至，本人所见的教科书在推导上述结论时都以根本不可能存在的电压、电流、自感电动势的正方向关系为推论的基础，也没有完整清楚地分析电流的变化趋势与自感电动势相位的关系，“虛晃一枪”而过，令学生困惑难已。

本文以电压和电动势方向的规定、法拉第电磁感应定律、楞次定律、基尔霍夫电压定律为基础，既完整分析电流的变化趋势对电压、电流、自感电动势之间相位关系的影响，又以真实的电压、电流、自感电动势的正方向关系建立电压方程，论述纯线性电感电路中电压、电流和自感电动势的相位关系，使学生能更好地理解和掌握纯线性电感电路中电压、电流和自感电动势的相位关系。

一、本人所见的教科书对纯线性电感电路中电压、电流和自感电动势的相位关系的推导过程和存在“问题”图1所示电路中，变化的电流经过电感元件L 时，电感元件L 就产生自感电动势来阻碍电流的变化。

设电路中电阻和电容可忽略不计，L 是线性电感元件，并且电压、电流和自感电动势的正方向如图所示，则：L d die L dt dtΦ=-=- （1—1）根据基尔霍夫电压定律得：dtdiL e u L L =-= （1—2）设t I i m ωsin =，则：(sin )cos sin(90)sin(90)(13)m L m m m di d I t u LI L tdt dtI L t U t ωωωωωω====+=+-sin(90)sin(90180)sin(90)(14)L L m m m die u LU t dtU t U t ωωω=-=-=-+=+-=--所以，L u 比i 超前90 ，i 比L e 超前90。

显然，上述的推导过程简洁正确，但存在如下令学生费解的“问题”：1．L u 、i 、L e 之间显然不存在着图1所示的正方向关系，由这一根本不存在的电压、电流、自感电动势之间的正方向关系得出dt di L dt d e L -=Φ-=，并建立方程dtdiL e u L L =-=。

纯电感元件在正弦交流电路中的电压与电流关系

纯电感元件在正弦交流电路中的电压与电流关系
在正弦交流电路中，纯电感元件的电压与电流之间存在一定的关系。

根据电感元件的特性，其电压与电流的关系可以通过以下公式表示：
V = jωLI
其中，V表示电感元件的电压，I表示电感元件的电流，L表示电感元件的电感值，ω表示电路中的角频率。

j是虚数单位，满足j² = -1。

这个公式表明，电压与电流之间存在90度的相位差，且电压与电流之间的关系是线性的，也就是电压与电流成正比。

当电流通过电感元件时，会产生一个由电感元件本身决定的感应电动势，从而引起电压的变化。

需要注意的是，电感元件在交流电路中会引入阻抗，即纯电感元件的阻抗Z可以表示为：
Z = jωL
因此，在交流电路中，纯电感元件的电压和电流之间不仅存在幅值比例关系，还存在相位差。

这个相位差由纯电感元件的阻抗决定，通常为正90度。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

XC
上一页下一页返回
综上所述，综上所述，电容电路中电压与电流的关系可由相量形式的欧姆定律
& U
& 来表达， =-j I XC来表达，
电容不消耗功率，电容不消耗功率，其无功功率是 QC=UI=I2XC=U2/XC。
上一页
下一页
返回
[例4] 在纯电容电路中，已知 i=22 2 sin(1000t+30°)A，电容量C=100µF，求（1）电容器两端电压的瞬时值表达式；（2）用相量表示电压和电流，并作出相量图；（3）求有功功率和无功功率。
& U =220∠120°V
图6 例3的相量图的相量图
上一页下一页返回
三、纯电容电路
加在电容元件两个极板上的电压变化时，极板上贮存的电荷Q=CU就随之而变，电荷量随时间的变化率，就是流过联接于电容导线中的电流，即
i= dq du =C dt dt
（2））（3））（4））
u=
图9 例4的相量图的相量图
上一页下一页返回
表1 正弦交流电路中R、L、C元件的电压与电流关系正弦交流电路中R
上一页
下一页
返回
作业：3-15，3-16，3-17
上一页下一页返回
XL=2πfL=0 =2π
[例3] 在纯电感电路中，已知i=22 2 sin(1000t+30°)A，在纯电感电路中，已知i=22 sin(1000t+30°)A， L=0.01H，求（1）电压的瞬时值表达式；（2 L=0.01H，求（1）电压的瞬时值表达式；（2）用相量表示电流和电压，并作出相量图；（3 电流和电压，并作出相量图；（3）求有功功率和无功功率。
上一页
下一页
返回
解：（1）已知Im=22 2 A，R=10Ω，所以 Um=ImR=220 2 V 因为纯电阻电路电压与电流同相位，所以 u=220 2 sin(1000t+30°)V （2）
& =22∠30°A I
& U =220∠30°V
相量图如图3所示。（3）P=UI=220×22=4840W
• 用相量表示电感元件的电压与电流的关系，则
& U = jX L & I
或
& & & U = jIX L = jIω L
上一页
下一页
返回
2.电感电路中的功率电感电路中的功率
• （1）瞬时功率 p=iLUL=ILMsinωt·ULMsin(ωt+90°)=ULILsinωt • （2）有功功率P=0
上一页
下一页
返回
图3 例1的相量图的相量图
上一页下一页返回
二、纯电感电路
• 电压与电流的关系
u=L d (I m sin ωt ) di =L = ωLI m cos ωt = U m sin(ωt + 90°) dt dt
Um U = = Im I
di e = −L dt
u = −e = L
（5）
实验和理论均可证明，电容器的电容C越大，交流电频率越高，则1/ωC越小，也就是对电流的阻碍作用越小，我们把电容对电流的“阻力”称作容抗，用XC代表。
1 1 XC = = ωC 2πfC
（6）
式（5）中，频率f的单位为Hz，电容C的单位为法拉（F），容抗XC的单位仍是欧姆（Ω），XC与电容C和频率f成反比。当C一定时，电容器具有隔直通交的特性，当f=0时，XC=∞，此时电路可视作开路，即“隔直”作用。
解：（1）XL=ωL=1000×0.01=10Ω，Im=22 2 A，（ Um=ImXL=220 2 V 因为纯电感电电压超前电流90°，故 u=220 2 sin(1000t+120°)V。（2） & =22∠30°A I 相量图见图6。 P=0 Q=UI=220×22=4840var
上一页下一页返回
di dt
（1）
由上式可知：（1）Um=ωLIm，即
=ωL
• 线圈电感L越大，交流电频率越高，则ωL的值越大，也就是对交流电流的阻碍作用越大，我们把这种“阻力”称作感抗，用XL代表。 • XL=ωL=2πfL
上一页下一页返回
L为电感量，单位为亨利（H）, f为为电感量，单位为亨利（）为为电感量流过电感的电流频率，流过电感的电流频率，单位为赫兹）；X （Hz）； L是电感元件两端的电压与流）；过电流的比值，单位显然是Ω 过电流的比值，单位显然是Ω
下一页
返回
电容器两端电压与电流的关系用相量式表示有
& U = − jX C & I
（7）
式（7）不仅表示了电压和电流的大小关系，如表达式（6）所示，同时表示了纯电容电路中电压滞后电流90°的关系，我们也可把式（7）写成
• • & & =−jI X =−jI 1 = I U C ω C jω C
相量图如图3.22所示。（3）P=0，QC=UI=220×22=4840var。
上一页下一页返回
交流电路中的电压与电流的关系（大小和相位）交流电路中的电压与电流的关系（大小和相位）有一定的规律性，是容易掌握的。定的规律性，是容易掌握的。先将上面介绍的三种分立元件在正弦交流电路中的电压与电流的关系列入表1中元件在正弦交流电路中的电压与电流的关系列入表中，以帮助大家总结和记忆。以帮助大家总结和记忆。
上一页
下一页
返回
(a) 瞬时值表示
(b) 相量表示
上一页下一页返回
图4 纯电感电路
（2）由式（1）还可看到电感两端电压超前电流）由式（）相位90° 弧度）相位 °（或π/2弧度）弧度
（a）波形图 (b) 相量图 (c) 瞬时功率图）图5 纯电感电路的波形图与相量图
上一页下一页返回
上一页下一页返回
i
+ u _ R
(a) 瞬时值表示
(b) 有效值表示
图1 纯电阻电路
上一页下一页返回
（a）波形图 (b) 相量图 (c) 瞬时功率图）图2 纯电阻电路的波形图与相量图
上一页下一页返回
2.电路中的功率电路中的功率
• 电路任一瞬时所吸收的功率称为瞬时功率，以 p表示。 p=ui=Umsinωt·Imsinωt =
2 L
U • （3）无功功率 QL = I LU L = I X L = XL 式中，QL——电路的无功功率，单位为乏（var）或千乏（kvar）； UL——线圈两端电压的有效值（V）； IL——流过线圈电流的有效值（A）； XL——线圈的感抗（Ω）。
上一页下一页返回
2 L
[例2] 一线圈的电感量L=0.1H，将其分别接于（1）直流；（2）交流50Hz；（3）交流1000Hz交流电路中，试分别求该电感线圈的感抗XL。解：（1 解：（1）f=0 （2）f=50Hz XL=2πfL=2×3.14×50×0.1=31.4Ω =2πfL=2×3.14×50×0.1=31.4Ω （3）f=1000Hz XL=2πfL=2×3.14×1000×0.1=328Ω =2πfL=2×3.14×1000×0.1=328Ω 由此例可见电感量一定时，频率越高，则电感对电流的阻碍作用越大，即感抗X 电感对电流的阻碍作用越大，即感抗XL越大。
上一页下一页返回
(a) 瞬时值表示图7 纯电容电路
(b) 相量表示
上一页
下一页
返回
（2）式（4）还告诉我们通过电容的电流与它的端电压是同频率的正弦量，电流超前于电压90°（或 π/2弧度）。
（a）波形图）（b）相量图）（c）瞬时功率图）图8 纯电容电路的波形图与相量图
上一页
2
U·
2 Isin
2ωt
=UI(1-cos2ωt)=UI-UIcos2ωt • 通常所说的功率是指一个周期内电路所消耗（吸取）功率的平均值，称为平均功率或有功功率，简称功率，用P表示。
1 T U2 2 UI(1 − cos 2ωt )dt = UI = I R = P= 0 T R
∫
上一页
下一页
上一页
下一页
返回
解：（1）
XC =
1 1 = = 10Ω −6 ，Im=22 ωC 1000 ×100 ×10
2A，
Um=ImXc=220 2 V。因为纯电容电路中电压滞后电流90°，所以 u=220 2 sin(1000t-60°)V （2）
& I =22∠30°A
& U
=220∠-60°V
此式也可以写成
i=C
1 ∫ idt C
d (U m sin ω t ) du =C = ωCU mω t = I m sin(ω t + 90°) dt dt
如图7所示的电容器两端加上正弦电压u=Umsinωt，则在回路中就有电流
上一页下一页返回
由上式可知：（1）Im=ωCUm 即
Um U 1 = = Im I ωC
返回
• 综上所述，电阻电路中的电压与电流的关系可用相量形式的欧姆定律 U = I R 来表示，电阻消耗的功率与直流电路有相似的公式，即
● ●
P = UI = I R = U R
2 2
上一页
下一页
返回
例题：例题：
[例1] 在纯电阻电路中，已知 i=22 2 sin(1000t+30°)A，R=10Ω，求：（1）电阻两端电压的瞬时值表达式；（2）用相量表示电流和电压，并作出相量图；（3）求有功功率。
正弦交流电路中电压与电流的关系