正弦稳态电路的功率要点
合集下载
正弦交流电路的功率因素

提高感性负载功率因数的常用方法之一是在其两端并联电容 器。 感性负载并联电容器后, 它们之间相互补偿, 进行一部分 能量交换, 减少了电源和负载间的能量交换.
3. 感性负载提高功率因数的原理可用图说明。
并联电容
分析:
I
IC
+
R
IL
U
C
_L
1 2 I
U
IC
IL
再从功率这个角度来看 :
则电容电压为 : uc (t)
2I
c
X
c
sin(t
2
)V
其瞬时功率为:
2U C
sin(t
2
)V
pc
(t
)
uc
(t
)ic
(t
)
2U
c
I
c
s
in(t
2
)
sin
t
Uc Ic sin 2t
uc (t)、Ic(t)、pc(t)的波形如图6-12所示。
uiCC
图 6-12 电容元件的瞬时功率
换。
电感消耗的平均功率为:
pL
1 T
T 0
pL
(t)dt
1 T
T
0 U L I L sin 2tdt 0
电感消耗的平均功率为零,说明电感元件 不消耗功率,只是与外界交换能量。
3.电容元件的功率 在电压、电流为关联参考方向下,设流过电 容元件的电流为:
ic (t) 2Ic sintA
S=UI
4、功率因素
式中 cosZ 称为二端电路的功率因素,功率因素
的值取决于电压与电流之间的相位差 Z , Z 也
3. 感性负载提高功率因数的原理可用图说明。
并联电容
分析:
I
IC
+
R
IL
U
C
_L
1 2 I
U
IC
IL
再从功率这个角度来看 :
则电容电压为 : uc (t)
2I
c
X
c
sin(t
2
)V
其瞬时功率为:
2U C
sin(t
2
)V
pc
(t
)
uc
(t
)ic
(t
)
2U
c
I
c
s
in(t
2
)
sin
t
Uc Ic sin 2t
uc (t)、Ic(t)、pc(t)的波形如图6-12所示。
uiCC
图 6-12 电容元件的瞬时功率
换。
电感消耗的平均功率为:
pL
1 T
T 0
pL
(t)dt
1 T
T
0 U L I L sin 2tdt 0
电感消耗的平均功率为零,说明电感元件 不消耗功率,只是与外界交换能量。
3.电容元件的功率 在电压、电流为关联参考方向下,设流过电 容元件的电流为:
ic (t) 2Ic sintA
S=UI
4、功率因素
式中 cosZ 称为二端电路的功率因素,功率因素
的值取决于电压与电流之间的相位差 Z , Z 也
正弦稳态电路的分析功率因数
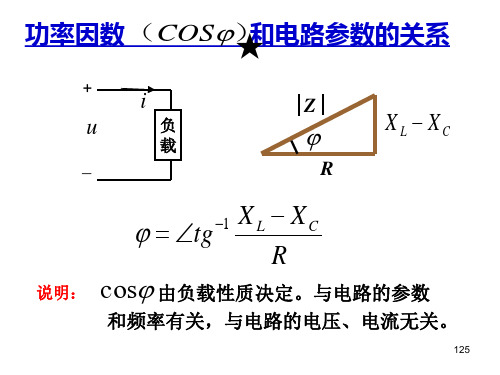
U cos 220 0.5
发电与供电设备 的容量要求功率 因素较大
A
供电局一般要求用户的 COS 0.85 ,
否则受处罚。
126
常用电路的功率因数
纯电阻电路
★
COS 1
( 0)
纯电感电路或 纯电容电路
COS 0 ( 90)
R-L-C串联电路
0 COS 1
(90 90)
电动机 空载 满载
COS 0.2 ~ 0.3
COS 0.7 ~ 0.9
日光灯 (R-L-C串联电路)
COS 0.5 ~ 0.6 127
提高功率因数的原则:
必须保证原负载的工作状态不变。即:加至负 载上的电压和负载的有功功率不变。
提高功率因数的措施:
+
并联电容
U
_
I
R +_UR IRL +
j L UL _
IC
1
j C
128
并联电容值的计算
设原电路的功率因数为 cos L,要求补偿到
cos 须并联多大电容?(设 U、P 为已知)
I
+
R +_UR
U
IRL +
j L UL _
_
IC
1
j C
IC
U
L
I
IRL
129
分析依据:补偿前后 P、U 不变。
由相量图可知:
IC I RL sin L I sin
IC
P UI RL cosL
P UI cos
并联前 并联后
U
L
I
IC
IC U XC U C
UC P U cos L
sin L
发电与供电设备 的容量要求功率 因素较大
A
供电局一般要求用户的 COS 0.85 ,
否则受处罚。
126
常用电路的功率因数
纯电阻电路
★
COS 1
( 0)
纯电感电路或 纯电容电路
COS 0 ( 90)
R-L-C串联电路
0 COS 1
(90 90)
电动机 空载 满载
COS 0.2 ~ 0.3
COS 0.7 ~ 0.9
日光灯 (R-L-C串联电路)
COS 0.5 ~ 0.6 127
提高功率因数的原则:
必须保证原负载的工作状态不变。即:加至负 载上的电压和负载的有功功率不变。
提高功率因数的措施:
+
并联电容
U
_
I
R +_UR IRL +
j L UL _
IC
1
j C
128
并联电容值的计算
设原电路的功率因数为 cos L,要求补偿到
cos 须并联多大电容?(设 U、P 为已知)
I
+
R +_UR
U
IRL +
j L UL _
_
IC
1
j C
IC
U
L
I
IRL
129
分析依据:补偿前后 P、U 不变。
由相量图可知:
IC I RL sin L I sin
IC
P UI RL cosL
P UI cos
并联前 并联后
U
L
I
IC
IC U XC U C
UC P U cos L
sin L
华科电工技术第6章 正弦稳态电路分析 (2)
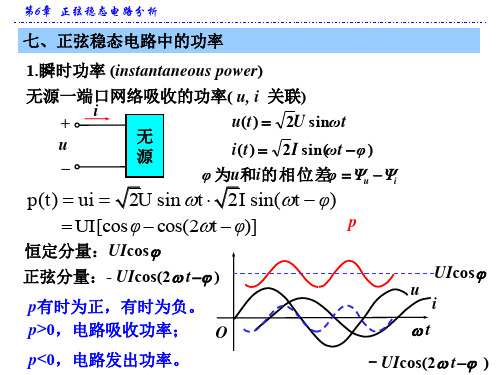
而且与cos 有关,这是交流和直流的很大区别, 主要由于电
压、电流存在相位差。
cos 1,纯电阻
0,纯电抗
一般地,有 0cos1
X>0, >0,感性, 滞后功率因数 X<0, <0,容性, 超前功率因数
例: cos =0.5 (滞后), 则 =60o (电流滞后电压60o)。
u
C 对电容,i 超前 u 90°,QC<0,故电容发出无功
-
功率。
第6章 正弦稳态电路分析
七、正弦稳态电路中的功率
电感、电容的无功补偿作用
iR
L
+
+ uL - +
u -
C
uC -
O
pL pC
i uC
uL t
当L发出功率时,C刚好吸收功率,则与外电路交换功率 为pL+pC。因此,L、C的无功具有互相补偿的作用。
30 12
30(Ω)
|Z| U / I 50(Ω) |Z| R2 (L)2
L 1
| Z |2 R2
1 314
502 302 0.127(H)
第6章 正弦稳态电路分析
七、正弦稳态电路中的功率 3.无功功率 (reactive power) Q
p(t) UI[cos φ cos(2t φ)] UI cos φ(1 cos 2t) UI sin sin 2t
第6章 正弦稳态电路分析
例:如图电路中,已知 is 5 2 sin 2(t A ),求电源提供的P、
Q,并计算电源的视在功率S和功率因素cos 。
2
解法一: 采用定义计算;
·IS
压、电流存在相位差。
cos 1,纯电阻
0,纯电抗
一般地,有 0cos1
X>0, >0,感性, 滞后功率因数 X<0, <0,容性, 超前功率因数
例: cos =0.5 (滞后), 则 =60o (电流滞后电压60o)。
u
C 对电容,i 超前 u 90°,QC<0,故电容发出无功
-
功率。
第6章 正弦稳态电路分析
七、正弦稳态电路中的功率
电感、电容的无功补偿作用
iR
L
+
+ uL - +
u -
C
uC -
O
pL pC
i uC
uL t
当L发出功率时,C刚好吸收功率,则与外电路交换功率 为pL+pC。因此,L、C的无功具有互相补偿的作用。
30 12
30(Ω)
|Z| U / I 50(Ω) |Z| R2 (L)2
L 1
| Z |2 R2
1 314
502 302 0.127(H)
第6章 正弦稳态电路分析
七、正弦稳态电路中的功率 3.无功功率 (reactive power) Q
p(t) UI[cos φ cos(2t φ)] UI cos φ(1 cos 2t) UI sin sin 2t
第6章 正弦稳态电路分析
例:如图电路中,已知 is 5 2 sin 2(t A ),求电源提供的P、
Q,并计算电源的视在功率S和功率因素cos 。
2
解法一: 采用定义计算;
·IS
正弦电路的无功功率及视在功率精

由上两式可以看出,电感或电 容的瞬时功率随时间按正弦规律变 化,正负值交替,一段时间内 p(t) >0,电感或电容吸收功率;另一段 时间内p(t)<0,电感或电容发出 功率。
平均功率为
P = UI cos±90o)= 0
表明:
正弦稳态中,储能元件电感或电容的平均功率等于 零,不消耗能量,但和电源之间存在能量的交换作用, 即在前半个周期吸收电源的功率并储存起来,后半个 周期又将其全部释放,这种能量交换的速率用另外一 种功率——无功功率来描述。
2、功率因数是正弦电路中一个非常重要的物理量。 其大小表征了电气设备功率的利用率。提高负载的功 率因数是电气工程领域一个非常重要的课题。
本讲作业
1、复习本讲内容; 2、预习下一讲内容——三相电路;
3、书面作业:习题9-2,9-5,9-6。
问题:怎样提高电路的功率因数?
方法: 用电容器与感性负载并联,这样可使电感的磁场 能量与电容的电场能量进行部分交换,从而减少了 电源与负载间能量的交换,即减少了电源提供给负 载的无功功率,也就提高了功率因数。
【例18-2】
下图(a)所示电路表示电压源向一个电感性负载供电的电 路模型,试用并联电容的方法来提高负载的功率因数。
Y G j B 1 3 j4 (0 12 j0 16)S 3 j4 32 42
从上式可见,所并联的电容的复导纳应该为YC = jwC = + j0.16 S,才能使二端网络呈现为纯电阻, 这时电路的导纳等于纯电导,即Y = G = 0.12 S。也 就是说,在端口并联电容值为C = (0.16/w)的电 容后,可以使功率因数提高到1,即效率达到100%。
S S~ UI
功率三角形: 下图所示为RLC串联电路的功率三角形:
平均功率为
P = UI cos±90o)= 0
表明:
正弦稳态中,储能元件电感或电容的平均功率等于 零,不消耗能量,但和电源之间存在能量的交换作用, 即在前半个周期吸收电源的功率并储存起来,后半个 周期又将其全部释放,这种能量交换的速率用另外一 种功率——无功功率来描述。
2、功率因数是正弦电路中一个非常重要的物理量。 其大小表征了电气设备功率的利用率。提高负载的功 率因数是电气工程领域一个非常重要的课题。
本讲作业
1、复习本讲内容; 2、预习下一讲内容——三相电路;
3、书面作业:习题9-2,9-5,9-6。
问题:怎样提高电路的功率因数?
方法: 用电容器与感性负载并联,这样可使电感的磁场 能量与电容的电场能量进行部分交换,从而减少了 电源与负载间能量的交换,即减少了电源提供给负 载的无功功率,也就提高了功率因数。
【例18-2】
下图(a)所示电路表示电压源向一个电感性负载供电的电 路模型,试用并联电容的方法来提高负载的功率因数。
Y G j B 1 3 j4 (0 12 j0 16)S 3 j4 32 42
从上式可见,所并联的电容的复导纳应该为YC = jwC = + j0.16 S,才能使二端网络呈现为纯电阻, 这时电路的导纳等于纯电导,即Y = G = 0.12 S。也 就是说,在端口并联电容值为C = (0.16/w)的电 容后,可以使功率因数提高到1,即效率达到100%。
S S~ UI
功率三角形: 下图所示为RLC串联电路的功率三角形:
邱关源—电路—教学大纲—第九章-2

并联电容的作用:减小电流,提高功率因数 *感性负载吸收的无功功率一部分由电源提供,一部分由电容提供。
g g g
g
g
I1 cos ϕ1 I sin ϕ
g
I 1 的有功分量 I cos ϕ = I1 cos ϕ1 I 的有功分量
g
g
I 的无功分量
IC
ϕ ϕ1
IC I IC
g g
U
I 1 的无功分量
给定 P 1 、 cos ϕ1 ,要求将 cos ϕ1 提高 cos ϕ ,求 C=?
: g ∗ g g g ∗ g
则 S = U I = U ∠ψ u ⋅ I ∠ − ψ i = UI ∠(ψ u − ψ i ) = S ∠ϕ Z
= S ⋅ cos ϕ Z + jS ⋅ sin ϕ Z = P + jQ (VA) S = U I = Z I I = ZI 2 = ( R + jX ) I 2 ∴ P = RI 2 = Re [ Z ] ⋅ I 2 Q = XI 2 = Im [ Z ] ⋅ I 2 S = U I = U (U Y ) = Y U U = (G − jB)U 2 P = GU 2 , Q = − BU 2
2. QR = 0, QL = UI , QC = −UI
0o < ϕ < 90o Q > 0 −90o < ϕ < 0o Q < 0
四.视在功率
吸收无功功率 发出无功功率
S @ UI ,反映电源设备的容量(可能输出的最大平均功率) ,量纲:伏安(VA) 。
P、Q 和 S 之间满足下列关系 即有
S 2=P 2+Q 2
g
I1 sin ϕ1
I1
g g g
g
g
I1 cos ϕ1 I sin ϕ
g
I 1 的有功分量 I cos ϕ = I1 cos ϕ1 I 的有功分量
g
g
I 的无功分量
IC
ϕ ϕ1
IC I IC
g g
U
I 1 的无功分量
给定 P 1 、 cos ϕ1 ,要求将 cos ϕ1 提高 cos ϕ ,求 C=?
: g ∗ g g g ∗ g
则 S = U I = U ∠ψ u ⋅ I ∠ − ψ i = UI ∠(ψ u − ψ i ) = S ∠ϕ Z
= S ⋅ cos ϕ Z + jS ⋅ sin ϕ Z = P + jQ (VA) S = U I = Z I I = ZI 2 = ( R + jX ) I 2 ∴ P = RI 2 = Re [ Z ] ⋅ I 2 Q = XI 2 = Im [ Z ] ⋅ I 2 S = U I = U (U Y ) = Y U U = (G − jB)U 2 P = GU 2 , Q = − BU 2
2. QR = 0, QL = UI , QC = −UI
0o < ϕ < 90o Q > 0 −90o < ϕ < 0o Q < 0
四.视在功率
吸收无功功率 发出无功功率
S @ UI ,反映电源设备的容量(可能输出的最大平均功率) ,量纲:伏安(VA) 。
P、Q 和 S 之间满足下列关系 即有
S 2=P 2+Q 2
g
I1 sin ϕ1
I1
第九章 正弦稳态电路的分析

1 1 Y = = −53.13°S = (0.024 − j0.032)S (感 ) 性 eq Zeq 25
9-2
电路的相量图
分析阻抗(导纳) 分析阻抗(导纳)串、并联电路时,可以利用相关的 并联电路时, 电压和电流相量在复平面上组成的电路的相量图。 电压和电流相量在复平面上组成的电路的相量图。 1. 并联电路相量图的画法 并联电路相量图的画法 ① 参考电路并联部分的电压相量。 参考电路并联部分的电压相量。 根据支路的VCR确定各并联支路的电流相量与电压相 ② 根据支路的 确定各并联支路的电流相量与电压相 量之间的夹角。 量之间的夹角。 根据结点上的KCL方程,用相量平移求和法则,画出结点 方程, ③ 根据结点上的 方程 用相量平移求和法则, 上各支路电流相量组成的多边形。 上各支路电流相量组成的多边形。
R = G2GB2 , +
−B X = G2+B2
1 | Y |= , φZ = −φY |Z|
已知:R=15Ω, L=12mH, C=5µF, u =100 2cos(5000t) 例9-1 已知 试求:(1)电路中的电流 i, (瞬时表达式)和各元件的 电路中的电流 瞬时表达式) 试求 电压相量; 电路的等效导纳和并联等效电路 电路的等效导纳和并联等效电路。 电压相量;(2)电路的等效导纳和并联等效电路。 jω L R L R • + • - + UL + + uR - + uL - + + + uS C
第二种分解方法
第一种分解方法: p(t) =UI[cosϕ + cos(2ωt −ϕ)] 第一种分解方法: p UIcosϕ 恒定分量 恒定分量 u i
O
正弦稳态电路的功率公式

正弦稳态电路的功率公式——深入浅出理解正弦稳态电路是电路理论中的基本概念,其功率公式是电学中的热门话题。
本文将深入浅出地介绍正弦稳态电路的功率公式,帮助读者系统地理解和掌握这一重要理论。
首先要明确的是,正弦稳态电路的功率公式是指在周期性交流电源作用下,电路中所传递的功率。
正弦稳态电路中,电流和电压均为正弦波形,其功率公式可以表示为:P=VIcosφ其中,P表示电路的有功功率,V和I分别表示电路中的电压和电流,φ表示电路中电流和电压之间的相位角。
我们可以通过下面的图例来进一步理解这个公式:在图例中,V是电路中的电压,I是电路中的电流,它们的波形均为正弦函数。
在时间t=0时,电流I的相位角为0,电压V的相位角为θ,因此φ的值等于θ。
通过对P=VIcosφ公式的应用,我们可以计算出电路中的有功功率P。
下面举个例子来说明如何求解正弦稳态电路中的功率。
假设我们有一个电路,电压源为220V,电阻为10Ω,交流频率为50Hz,我们需要求解该电路的功率。
首先,我们需要计算电路中的电流,通过欧姆定律可知电流I=V/R,因此I=22A。
接下来,我们需要求解相位角φ。
由于电路中只有电阻,电流和电压之间没有相位差,因此φ=0。
因此,根据功率公式,我们可以计算得到电路中的有功功率P=VIcosφ=22*220*1=4840W。
总之,正弦稳态电路的功率公式是电学中的基本概念,是电路分析和设计中必须掌握的知识点。
本文通过生动的示意图和实例应用,帮助读者深入浅出地理解和掌握正弦稳态电路的功率公式。
无论你是电学专业的学生,还是从事电路设计和调试等工作的工程师,掌握这一知识点都是非常重要的。
正弦稳态电路的功率

电阻分量消耗的平均功率,就是单口 网络吸收的平均功率。
3、视在功率
S UI
表示一个电气设备的容量,是单口网 络所吸收平均功率的最大值,单位: 伏安(VA)。例如我们说某个发电机的 容量为100kVA,而不说其容量为 100kW
4、功率因数
网络吸收的平均功率P与cosZ的大小
密切相关,cosZ表示功率的利用程度
解:电路的相量模型如图(b)所示。先 求出连接电压源单口网络的等效阻抗
Z 0.5 j1.5 (j1)(j1 1 j1) 0.5 j1.5 0.5 j0.5 1 j1 1 j1
用欧姆定律求电流 分流公式求电流
I1
U S Z
20 1 j1
2 45 A
I2
j1 1 j1
I1
,称为功率因数
pf
cos Z
P S
Z=u-i为功率因数角。当二端网络
为无源元件R、L、C组成时:
|Z|<90 ,0< pf <1。
Z<0
,电路呈容性,电流导前电压; Z>0
,电路感呈性,电流滞后电压。
为了提高电能的利用效率,电力部门 采用各种措施力求提高功率因数。例 如使用镇流器的日光灯电路,它等效 于一个电阻和电感的串联,其功率因 数小于1,它要求线路提供更大的电流。 为了提高日光灯电路的功率因数,一 个常用的办法是在它的输入端并联一 个适当数值的电容来抵销电感分量, 使其端口特性接近一个纯电阻以便使 功率因数接近于1。
得最大功率,试设计一个由电抗元件组 成的网络来满足共轭匹配条件。
100 a
+
100∠0o V
-
b
RL=
1000
解:1 若不用匹配网络,将1000Ω负载
3、视在功率
S UI
表示一个电气设备的容量,是单口网 络所吸收平均功率的最大值,单位: 伏安(VA)。例如我们说某个发电机的 容量为100kVA,而不说其容量为 100kW
4、功率因数
网络吸收的平均功率P与cosZ的大小
密切相关,cosZ表示功率的利用程度
解:电路的相量模型如图(b)所示。先 求出连接电压源单口网络的等效阻抗
Z 0.5 j1.5 (j1)(j1 1 j1) 0.5 j1.5 0.5 j0.5 1 j1 1 j1
用欧姆定律求电流 分流公式求电流
I1
U S Z
20 1 j1
2 45 A
I2
j1 1 j1
I1
,称为功率因数
pf
cos Z
P S
Z=u-i为功率因数角。当二端网络
为无源元件R、L、C组成时:
|Z|<90 ,0< pf <1。
Z<0
,电路呈容性,电流导前电压; Z>0
,电路感呈性,电流滞后电压。
为了提高电能的利用效率,电力部门 采用各种措施力求提高功率因数。例 如使用镇流器的日光灯电路,它等效 于一个电阻和电感的串联,其功率因 数小于1,它要求线路提供更大的电流。 为了提高日光灯电路的功率因数,一 个常用的办法是在它的输入端并联一 个适当数值的电容来抵销电感分量, 使其端口特性接近一个纯电阻以便使 功率因数接近于1。
得最大功率,试设计一个由电抗元件组 成的网络来满足共轭匹配条件。
100 a
+
100∠0o V
-
b
RL=
1000
解:1 若不用匹配网络,将1000Ω负载
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
ห้องสมุดไป่ตู้
2
)
是频率为2的正弦量,在一段时间内 p(t)>0,电感或电容吸收功率获得能量 ;另外一段时间内p(t)<0,电感或电容 发出功率释放出它所获得的全部能量。
显然,平均功率为
P0
可见,电感和电容不消耗能量,它们是 无源元件。但要注意,它们的瞬时功率 并不为零。或者说,电感和电容需要电 源(外电路)供给一定的瞬时功率以满足 能量不断的往返交换。
2 2
I U P P G R
2
2
电阻分量消耗的平均功率,就是单口 网络吸收的平均功率。
3、视在功率
S UI
表示一个电气设备的容量,是单口网 络所吸收平均功率的最大值,单位: 伏安(VA)。例如我们说某个发电机的 容量为100kVA,而不说其容量为 100kW
4、功率因数 网络吸收的平均功率P与cosZ的大小密 切相关,cosZ表示功率的利用程度, 称为功率因数 P
pL (t ) UI cos( 2 t 2 u 90 ) pC (t ) UI cos( 2 t 2 u 90 )
若假设电压初相为零,得
pC ( t ) U m cos t I m cos( t U m cos t ( I m sin t )
7-6 正弦稳态电路的功率
本节讨论正弦稳态单口网络的瞬时
功率、平均功率(有功功率)、无功功 率、视在功率、复功率和功率因数。
正弦稳态单口网络向可变负载传输最
大功率的问题。
7-6-1 二端网络的功率
1、瞬时功率
端口电压和电流采用关联参 考方向,它吸收的功率为
p(t ) u(t )i (t )
正弦稳态时 ,端口电压和电流是相同 频率的正弦量,即 u(t ) U m cos( t u ) 2U cos( t u )
上式第二项的最大值为二端网络的无功 功率 Q 。即
Q UI sin Z
可验证L和C时的特殊情况。
无功功率反映电源(或外电路)和单 口网络内储能元件之间的能量交换 情况,单位为乏(var)(无功伏安: volt amper reactive) 与功率计算类似:
Q UI sin Z I X U B
定义:无功功率
把瞬时功率的振幅(最大值)定义为 电感和电容的无功功率,以表明电感和 电容与外电路电流和电压不断往返的程 度。即
Q L UI QC UI
3、任意二端网络的情况
P U I cos Z
设二端网络
Z R j XY G j B P UI cos Z I R U G
Z=u-i是电压与电流的相位差。瞬时功 率由一个恒定分量和一个频率为2ω的正
弦分量组成,周期性变化,当p(t)>0时, 该网络吸收功率;当p(t)<0时,该网络发 出功率。瞬时功率的波形如图所示。
UIcosZ
Z
2、平均功率(有功功率)
简称功率:在一个周期内的平均值:
1 T P p(t )dt T 0 1 T [YI cos Z UI cos( 2 t u i )]dt T 0 UI cos Z
2
)
1 U m I m sin 2 t UI sin 2 t 2 p L ( t ) U m cos t I m cos( t U m cos t ( I m sin t ) 1 U m I m sin 2 t UI sin 2 t 2
i (t ) I m cos( t i ) 2 I cos( t i )
瞬时功率为
p(t ) u(t )i (t ) U m cos( t u ) I m cos( t i ) 1 U m I m [cos( u i ) cos( 2 t u i )] 2 UI cos Z UI cos( 2 t 2 u Z )
5、无功功率 p(t ) U I cos Z U I cos(2 t Z )
U I cos Z U I cos Z cos 2 t U I sin Z sin 2 t U I cos Z (1 cos 2 t ) U I sin Z sin 2 t
2 2
I U Q Q B X
2
2
6、复 功 率
为了便于用相量来计算平均功率,引 入复功率。工作于正弦稳态的网络,其 电压电流采用关联的参考方向,设
此时平均功率:
U P UI I R R
2 2
用电压、电流有效值后,计算电阻消耗 的平均功率公式,与直流电路中相同。 若用电流、电压的振幅值,上述公式为
1 1 2 1 Um P Um Im Im R 2 2 2 R
2
2、网络等效阻抗为一个电抗。 此时单口网络电压与电流相位为正交关 系,即Z=u-i =90, (+电感-电容)
pf cos Z
Z=u-i为功率因数角。当二端网络
为无源元件R、L、C组成时:
S
|Z|<90 ,0< pf <1。 Z<0 ,电路呈容性,电流导前电压; Z>0 ,电路感呈性,电流滞后电压。
为了提高电能的利用效率,电力部门 采用各种措施力求提高功率因数。例 如使用镇流器的日光灯电路,它等效 于一个电阻和电感的串联,其功率因 数小于1,它要求线路提供更大的电流。 为了提高日光灯电路的功率因数,一 个常用的办法是在它的输入端并联一 个适当数值的电容来抵销电感分量, 使其端口特性接近一个纯电阻以便使 功率因数接近于1。
平均功率不仅取决于电压电流有效值乘 积VI,还与阻抗角Z=u-I有关。
几种特殊情况。 1、网络等效阻抗为一个电阻。 此时网络电压与电流相位相同,即 Z=u-i=0, cosZ=1,
p(t ) UI UI cos( 2t 2 u )
波 形 如 图 。 p(t) 在 任何时刻均大于或 等于零,电阻始终 吸收功率和消耗能 量。
2
)
是频率为2的正弦量,在一段时间内 p(t)>0,电感或电容吸收功率获得能量 ;另外一段时间内p(t)<0,电感或电容 发出功率释放出它所获得的全部能量。
显然,平均功率为
P0
可见,电感和电容不消耗能量,它们是 无源元件。但要注意,它们的瞬时功率 并不为零。或者说,电感和电容需要电 源(外电路)供给一定的瞬时功率以满足 能量不断的往返交换。
2 2
I U P P G R
2
2
电阻分量消耗的平均功率,就是单口 网络吸收的平均功率。
3、视在功率
S UI
表示一个电气设备的容量,是单口网 络所吸收平均功率的最大值,单位: 伏安(VA)。例如我们说某个发电机的 容量为100kVA,而不说其容量为 100kW
4、功率因数 网络吸收的平均功率P与cosZ的大小密 切相关,cosZ表示功率的利用程度, 称为功率因数 P
pL (t ) UI cos( 2 t 2 u 90 ) pC (t ) UI cos( 2 t 2 u 90 )
若假设电压初相为零,得
pC ( t ) U m cos t I m cos( t U m cos t ( I m sin t )
7-6 正弦稳态电路的功率
本节讨论正弦稳态单口网络的瞬时
功率、平均功率(有功功率)、无功功 率、视在功率、复功率和功率因数。
正弦稳态单口网络向可变负载传输最
大功率的问题。
7-6-1 二端网络的功率
1、瞬时功率
端口电压和电流采用关联参 考方向,它吸收的功率为
p(t ) u(t )i (t )
正弦稳态时 ,端口电压和电流是相同 频率的正弦量,即 u(t ) U m cos( t u ) 2U cos( t u )
上式第二项的最大值为二端网络的无功 功率 Q 。即
Q UI sin Z
可验证L和C时的特殊情况。
无功功率反映电源(或外电路)和单 口网络内储能元件之间的能量交换 情况,单位为乏(var)(无功伏安: volt amper reactive) 与功率计算类似:
Q UI sin Z I X U B
定义:无功功率
把瞬时功率的振幅(最大值)定义为 电感和电容的无功功率,以表明电感和 电容与外电路电流和电压不断往返的程 度。即
Q L UI QC UI
3、任意二端网络的情况
P U I cos Z
设二端网络
Z R j XY G j B P UI cos Z I R U G
Z=u-i是电压与电流的相位差。瞬时功 率由一个恒定分量和一个频率为2ω的正
弦分量组成,周期性变化,当p(t)>0时, 该网络吸收功率;当p(t)<0时,该网络发 出功率。瞬时功率的波形如图所示。
UIcosZ
Z
2、平均功率(有功功率)
简称功率:在一个周期内的平均值:
1 T P p(t )dt T 0 1 T [YI cos Z UI cos( 2 t u i )]dt T 0 UI cos Z
2
)
1 U m I m sin 2 t UI sin 2 t 2 p L ( t ) U m cos t I m cos( t U m cos t ( I m sin t ) 1 U m I m sin 2 t UI sin 2 t 2
i (t ) I m cos( t i ) 2 I cos( t i )
瞬时功率为
p(t ) u(t )i (t ) U m cos( t u ) I m cos( t i ) 1 U m I m [cos( u i ) cos( 2 t u i )] 2 UI cos Z UI cos( 2 t 2 u Z )
5、无功功率 p(t ) U I cos Z U I cos(2 t Z )
U I cos Z U I cos Z cos 2 t U I sin Z sin 2 t U I cos Z (1 cos 2 t ) U I sin Z sin 2 t
2 2
I U Q Q B X
2
2
6、复 功 率
为了便于用相量来计算平均功率,引 入复功率。工作于正弦稳态的网络,其 电压电流采用关联的参考方向,设
此时平均功率:
U P UI I R R
2 2
用电压、电流有效值后,计算电阻消耗 的平均功率公式,与直流电路中相同。 若用电流、电压的振幅值,上述公式为
1 1 2 1 Um P Um Im Im R 2 2 2 R
2
2、网络等效阻抗为一个电抗。 此时单口网络电压与电流相位为正交关 系,即Z=u-i =90, (+电感-电容)
pf cos Z
Z=u-i为功率因数角。当二端网络
为无源元件R、L、C组成时:
S
|Z|<90 ,0< pf <1。 Z<0 ,电路呈容性,电流导前电压; Z>0 ,电路感呈性,电流滞后电压。
为了提高电能的利用效率,电力部门 采用各种措施力求提高功率因数。例 如使用镇流器的日光灯电路,它等效 于一个电阻和电感的串联,其功率因 数小于1,它要求线路提供更大的电流。 为了提高日光灯电路的功率因数,一 个常用的办法是在它的输入端并联一 个适当数值的电容来抵销电感分量, 使其端口特性接近一个纯电阻以便使 功率因数接近于1。
平均功率不仅取决于电压电流有效值乘 积VI,还与阻抗角Z=u-I有关。
几种特殊情况。 1、网络等效阻抗为一个电阻。 此时网络电压与电流相位相同,即 Z=u-i=0, cosZ=1,
p(t ) UI UI cos( 2t 2 u )
波 形 如 图 。 p(t) 在 任何时刻均大于或 等于零,电阻始终 吸收功率和消耗能 量。
