第九章正弦稳态电路的分析
第9章 正弦稳态电路的分析(答案)

第9章 正弦稳态电路的分析 答案例 如图所示正弦稳态电路,已知I1=I2=10A,电阻R 上电压的初相位为零,求相量•I 和•S U 。
解: 电路中电阻R 和电容C 并联,且两端电压的初相为0。
由电阻和电容傻姑娘的电压与电流的相位关系可知:电阻电流•1I 与电压•R U 同相,电容电流•2I 超前电压•R U 相角90○,故ο0101∠=•I A ο90102∠=•I A由KCL 方程,有 ()101021j I I I +=+=•••A由KVL 方程,有 ︒•••∠==++-=+=9010010010010010010101j j I I j U S V例 如图所示正弦稳态电路,R 1=R 2=1Ω。
(1)当电源频率为f 0时,X C2=1Ω,理想电压表读数V 1=3V ,V 2=6V ,V 3=2V,求I S 。
(2)电路中电阻、电容和电感的值不变,现将电源的频率提高一倍,即为2 f 0,若想维持V 1的读数不变,I S 问应变为多少如果把电源的频率提高一倍,而维持V1的读数不变,即R1上的电压有效值U R1=3V,那么R1上的电流的有效值I也不变,此时仍把•I设置为参考相量,故︒•∠=03I A。
由于L和C1上的电流•I不变,根据电感和电容上电压有效值与频率的关系,电源的频率提高一倍,电感上电压表的读数增大一倍,而电容上电压表的读数降为原来的一半,故电源得频率提高一倍,X C2也降为原来得一半,即所以例如图所示正弦稳态电路,已知I1=10A,I2=20A,R2=5Ω,U=220V,并且总电压•U与总电流•I同相。
求电流I和R,X2,X C的值。
例 如图所示正弦稳态电路,已知有效值U 1=1002V, U=5002V ,I 2=30A ,电阻R=10Ω,求电抗X 1,X 2和X 3的值。
由电路可得两边取模得已知2550=U V ,所以6002=U V ,故有。
最全第九章(正弦稳态电路分析)习题解答打印版.doc
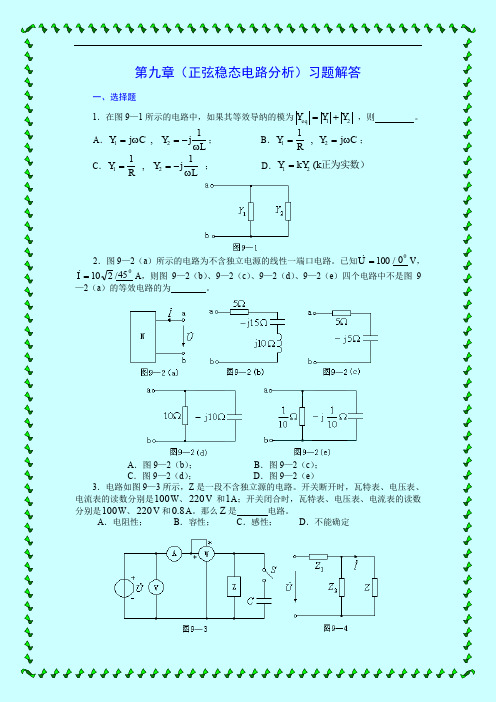
第九章(正弦稳态电路分析)习题解答一、选择题1.在图9—1所示的电路中,如果其等效导纳的模为21Y Y Y eq += ,则 。
A .L Y C Y ω-=ω=1j, j 21; B .C Y RY ω==j , 121;C .L Y R Y ω-==1j , 121 ;D .正为实数)k kY Y ( 21=2.图9—2(a )所示的电路为不含独立电源的线性一端口电路。
已知00 /100=UV ,045 /210=I A ,则图9—2(b )、9—2(c )、9—2(d )、9—2(e )四个电路中不是图9—2(a )的等效电路的为 。
A .图9—2(b );B .图9—2(c );C .图9—2(d );D .图9—2(e )3.电路如图9—3所示,Z 是一段不含独立源的电路。
开关断开时,瓦特表、电压表、电流表的读数分别是100W 、220V 和1A ;开关闭合时,瓦特表、电压表、电流表的读数分别是100W 、220V 和8.0A 。
那么Z 是 电路。
A .电阻性;B .容性;C .感性;D .不能确定4.电路如图9—4所示,U固定不变。
如果 ,则改变Z (Z 不等于无限大)时,I不变。
A .21Z Z =; B .21Z Z -=; C .21Z Z =; D .)Arg()Arg(21Z Z =5.Ω=10R 的电阻,F 1μ=C 的电容与电感L 串联,接到频率1000Hz 的正弦电压源上。
为使电阻两端的电压达到最高,电感应取 。
A .1H ;B .π21H; C .21H ; D .241πH二、填空题1.若Ω=3R ,Ω=ω6L ,Ω=ω2011C ,Ω=ω2012C ,则图9—5所示电路的输入阻抗为 j4)3(-Ω。
.2.线性一端口电路如图9—6所示,A /02 V ,30/5000=-=I U。
则此一端口电路吸收的复功率,有功功率、无功功率分别为V A 30/1000、W 350、50Var 。
第九章正弦稳态电路的分析课本部分习题

第九章正弦稳态电路的分析正弦稳态电路的分析应用相量法。
通过引入相量法,建立了阻抗和导纳的概念,给出了KCL,KVL和欧姆定律的相量形式,由于它们与直流电路的分析中所用的同一公式在形式上完全相同,因此能够把分析直流电路的方法,原理,定律,例如,网孔法(回路法),结点法,叠加定理,戴维宁定理,等效电源原理等等直接应用于分析正弦电路的相量模型,其区别仅在于:(1)不直接引用电压电流的瞬时表达式来表征各种关系,而是用对应的向量形式来表征各种关系;(2)相应的运算不是代数运算,而是复数的运算,因而运算比直流复杂。
但根据复数运算的特点,可画出向量图,利用向量图的几何关系来帮助分析和简化计算,从而扩大了求解问题的思路和方法。
(3)引入了一些新的概念,如平均功率,无功功率,视在功率,复功率,最大功率传输,谐振等。
认识以上区别,对正弦稳态电路的分析是有益的。
9-1试求图示各电路的输入阻抗Z和导纳Y。
解:(a)Z=1+=1+=Y====S(b) Z==Y=(c) Y=SZ=题9-1图设端口电压相量为,根据KVL,得所以输入阻抗为导纳设端口电压,电流相量为,,根据KCL,得且有所以输入阻抗导纳注:本题的求解过程说明,引入阻抗和导纳的概念以后,正弦电路的输入阻抗(或导纳)的定义与计算和直流电路输入电阻(或电导)的定义与计算是相似的。
即输入阻抗若有n个阻抗串联,等效阻抗若有n个导纳并联,等效导纳为只不过Z和Y是复数。
9-2已知图示电路中,。
试求电路中合适的元件值(等效)。
解:把u用余弦函数表示有u和I的相量形式为,根据入端导纳的定义,有既图示的两并联元件为电导和电容,其参数为注:以上计算表明,导纳的模等于电流与电压的模值之比,导纳角等于电流与电压的相位差,若导纳角,表示电流超前电压,导纳为电容性,反之为电感性。
9-3 附图中N为不含独立源的一端口,端口电压u,电流I分别如下列各式所示。
试求没一种情况下的输入阻抗Z和导纳Y,并给出等效电路图(包括元件的参数值)。
《电路》课件:第九章 正弦稳态电路的分析1-3

(4) 当 z 90 ~ 0或Y 0 ~ 90 时为容性
§9-2 阻抗(导纳)的串联和并联
1.串联:
Z Z1Z 2Z n
分压:
U k
Zk Z
U
2.并联:
1 1 1 1
Z Z1 Z2
Zn
Y Y1 Y2 Yn
分流:
Ik
Yk Y
I
例5-4-2 如图RLC串联电路。R= 2105 ,L= 152 mH,C= 150 F,
(2〕当ω =1 rad/s
Zac
1.5
1 2
j(2
1) 2
2
j1.5
(Ω
)
等效相量电路如图
ch9s1-7 例5-4-2 求如图RLC串联电路的阻抗
解:
Zi
R
j(L 1 ) C
X L 1 C
R jX
Zi R2 X2
Zi z
当
z
tg 1
X R
(1)L 1 C
即
=
1 LC
时,Zi
端电压 u=141.4cos(5000t)V。
求:i、元件的电压相量。
解: 用相量法。
U 1000 (V ) 5000(rad / s)
Z R j L 1
1250
j(5000
j
1125
C
10 3
5000
1 15 0
10 6
)
I
U R
1250 U Z
IR
j2505 2558.52 5730.1.03 ()
R
(2)L 1 C
即
1 LC
时,感性Zi
(3)L 1 C
即
1 LC
正弦稳态电路的分析

第九章正弦稳态电路的分析本章内容1.阻抗和导纳的概念2.阻抗的串并联及电路的相量图3.正弦稳态电路的分析4.瞬时功率、有功功率、无功功率、视在功率、复功率及最大输出功率5.串联和并联谐振本章重点:正弦量的向量正表示; 正弦电路中的阻抗和导纳;正弦电路的分析串联谐振的谐振条件及特征; 并联谐振的谐振条件及特征本章重点:正弦电路参数的分析及最大功率输出的分析§9-1 阻抗和导纳阻抗和导纳是正弦电流电路分析的重要内容一、阻抗在无源的线性网络中,端口的电压相量与电流相量的比值定义为该一端口的阻抗(复阻抗),用Z表示。
式中:•U=U∠ϕu•I=I∠ϕI阻抗的模:Z= U/I,阻抗角:ϕZ= ϕu-ϕi 阻抗的代数式: Z=R+jX式中:R—电阻 X—电抗1.若网络N 0内只含单一元件,则单一元件的复阻抗(1)电阻的复阻抗:Z R =R(2)电感的复阻抗:Z L =ωj L=jX L X L =ωL —感抗 (3)电容的复阻抗:Z C =cj ω1=c jω1-=jX C X C =cω1-—容抗 2.若网络N 0内为RLC 串联,则阻抗为(1)阻抗:Z=•U /•I = R+ωj L+cj ω1=R+j(ωL-Cω1)=R+jx=Z ϕ∠Z可见:阻抗Z 的实部为电阻R (R=Z cos ϕZ ),阻抗Z 的虚部为电抗X (X= R=Z sin ϕZ ),三者构成阻抗三角形 (2) 阻抗的模:Z =22)(C L X X R -+=22X R +=U/I (3)阻抗角:ϕZ =arctanR X X C L -=RX=ϕu -ϕi X 〉0 ωL>C ω1电路呈电感性 X<0 ωL<Cω1电路呈电容性X=0 电路呈电阻性一、 导纳:复阻抗的倒数定义为复导纳(电流相量与对应端口的电流相量的比值),用Y 表示 Y=Z 1=••UI =)(u i U Iϕϕ-∠=Y Y ϕ∠导纳的模: Y =U I导纳角: Y ϕ=u i ϕϕ- 导纳的代数式: Y=G+JB式中:G —电导 B —电纳1.若网络N 0内只含单一元件,则单一元件的复阻抗 (1) 电阻的复导纳:Y R =G=1/R (2) 电感的复导纳:Y L =Lj ω1=L jω1- =jB L B L =Lω1-—感纳 (3)电容的复导纳:Z C ==ωj C =jB C B C =ωC —容纳2.若网络N 0内为RLC 并联,则导纳为(1)导纳Y=••UI基尔霍夫电流定律的相量形式:∑•I =0•I =•I R +•I L +•I C =⎥⎦⎤⎢⎣⎡-+)1(1L C j R ωω•U =G+j(B C +B L )•UY=R 1+L j ω1+ωj C=R1+)1(L C j ωω-=G+jB可见:导纳Y 的实部为电导G (G=Y cos ϕY ),导纳Y 的虚部为电纳B (B= Y sin ϕY ),三者构成导纳三角形 (2)导纳的模:Y =22)(L C B B G -+=22B G +=I/U (3)阻抗角:ϕY =arctanG B B L C -=GB=ϕi -ϕu B 〉0 ωC>L ω1电路呈电容性 B<0 ωC<Lω1电路呈电感性B=0 电路呈电阻性二、阻抗和导纳相互转换(自学)§9-2 阻抗(导纳)串联和并联阻抗的串并联与电阻的串并联的计算规则相同,只是要把电阻换成阻抗。
正弦稳态电路的分析

一、阻抗 1. 一端口的阻抗 不含独立电源N0 ,当它在正弦电源激励下处于稳 不含独立电源N 态时,端口的电压、电流都是同频率的正弦量, 态时,端口的电压、电流都是同频率的正弦量,即 u = 2U cos(ωt +ϕ ) U = U∠ϕ →ɺ
u u
9-1 阻抗与导纳
0
i = 2I cos(ωt +ϕi ) I = I∠ϕi →ɺ 则它的端电压相量与端电流相量的比 阻抗Z 值定义为该一端口N 值定义为该一端口N0的(复)阻抗Z,即
ɺ 解: 选择 U'作为参考相量
ɺ IR
ɺ U'
α =45°
ɺ IC
∵ωL = 200×0.25 = 50Ω= R ∴IR = IL 由几何关系得: 由几何关系得:
ɺ IL
ɺ US ɺ UC
ɺ ɺ ɺ IC = I R + I L ɺ ɺ ɺ US = U′ +UC
UC =US =100V, U′ =100 2V U′ ∴IR = IL = = 2 2A , IC = 2IR = 4A , R IC 1 UC ∴ = ,C= = 2×10−4 F = 200µF ωC IC ωUC
def
R jX
|Z|——阻抗 的模; ϕ Z ——阻抗角; 阻抗Z的模 阻抗角; 阻抗 的模; 阻抗角 R——等效电阻;X——等效电抗。 等效电阻; 等效电抗。 等效电阻 等效电抗 为实数, 称为感性阻抗, (R为实数,X>0称为感性阻抗,X<0称 为实数 X>0称为感性阻抗 X<0称
ɺ U U Z === = ∠(ϕu −ϕi ) =| Z | ∠ϕZ = R + jX ɺ I I
第九章 正弦稳态电路的分析
电路第五版课件 第九章正弦稳态电路分析

2017年2月9日星期四
. U
16
9.1.3 阻抗(导纳)的串联和并联
1.阻抗的串联 . . . . U = Z1 I + Z2 I + · · · + Zn I . = (Z1+ Z2 + · · · + Zn) I . = ZI
Z=
n . I Z1 Z2 Zn
+ . U . I
k
∑ Z = ∑ (R + j X )
. I2 Y2
. In Yn
∑ Y = ∑ (G + j B )
k=1
k k
k=1
分流公式
Z1 Z2 两个阻抗Z1、Z2的并联等效阻抗为:Z = Z1 + Z2
2017年2月9日星期四 18
. Yk . Ik = I Y
+ . U -
Y
例:如图所示电路,已知R=10Ω, XL=10 Ω , XC=10 Ω, 求ab两端的等效阻抗Z;电压相量与电流相量相位差
2017年2月9日星期四 7
. . U = R + j X= | Z | j jwL R Z= . Z I . . I + + UR - + UL 1 X = XL - XC = wL. + . wC U UC X jZ = arctan R 讨论: 1 时, ①当 wL> wC 有 X>0 ,jZ>0
. UL
1 jwC
以电流为参考相量的相量图
. . UL + UC
. U
表现为电压超前电流,Z 呈感 性,称电路为感性电路。 满足:U 2 =UR2 + (UL-UC)2
2017年2月9日星期四
电路(第五版)第九章 正弦稳态电路的分析12共52页文档

U . U .R U .L U .C R I . jL I . j1 C I .
[R j( L 1 C )I ] [R j(X L X C )I ]
(RjX)I
j Z R j(L 1 C ) R j( X L X C ) R jX Z
L 1 C
X0, j0
Z2
•
I
Z1 Z2
(分流公式)
并:联 Y Y k,
I•kY k
•
I
Y k
例:已知 Z1=10+j6.28, Z2=20-j31.9 , Z3=15+j15.7 。
a Z3
求 Zab。
Zab
Z2
Z1
b
ZabZ3Z Z 11 Z Z 22Z3Z ZZ 1Z 2 (1 0j6.2)8 2 ( 0j3.9 1 )
•
(Z1 Z2)I
•
Z
U
•
Z1
Z2
I
•
U1
Z1
•
I
Z1 Z
•
U
(分压公式)
串:联 Z Z k,
U •kZ k
•
U
Z k
•
I
•
•
Y
+
•
U
Y1
I1
Y2
I2
-
•
Y
I
•
Y1 Y2
U
•
I1
Y1U• YY1
•
I
•• •
I I1I2
•
•
Y1UY2U
•
(Y1 Y2)U
Z Z1Z 2 Z1 Z2
•
I1
(1)R:
•
•
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第九章 正弦稳态电路的分析本章重点:1.阻抗,导纳及的概念2.正弦电路的分析方法3.正弦电路功率的计算4.谐振的概念及谐振的特点 本章难点:如何求电路的参数 主要内容§9-1阻抗和导纳1.阻抗(1)复阻抗:u i Z UU Z Z R jX II ψψϕ==-=∠=+&&式中22U Z R X I==+为阻抗的模; Z u iX arctg R ϕψψ=-=为阻抗角(辐角); R=Re[Z]cos z Z ϕ=称为电阻; X=Im[Z]=sin z Z ϕ称电抗。
(2)RLC 串联电路的阻抗:1U Z R j L I j cωω==++=&& 1()()L C ZR j L cR j X X R jX Z ωωϕ+-=++=+=∠ 式中L X L ω=称为感抗;1C X c ω=-称为容抗;1L C X X X L c ωω=+=- 可见,当X.>0,即1L c ωω>时,Z 是感性; 当X<0,即1L cωω<时,Z 呈容性。
(3)阻抗三角形: 2.导纳ZϕZRXZ&U&+—I&U&+—CL(1)复导纳:1i u Y II Y Y G jB Z UU ψψϕ===∠-=∠=+&&式中I Y U ==称为导纳的模;arctan Y BGψ=称为导纳角; Re[]cos Y G Y Y ψ==称为电导; Im[]sin Y B Y Y ψ==称为电纳。
(2)RLC 并联电路的导纳:1111()I Y j c j c U R j L R Lωωωω==++=+-=&& ()C L Y G j B B G jB Y ψ++=+=∠式中1L B L ω=-称为感纳;C B C ω=称为容纳;1C L B B B c L ωω=+=-;1G R=。
可见,当0,B >即1c L ωω>时,Y 呈容性;当0,B <即1,c Lωω<Y 呈感性。
(3)导纳三角形:3.阻抗和导纳的等效互换(1)RLC 串联电路的等效导纳: 2222R XY jR X R X =-++ (2) RLC 并联电路的等效阻抗:2222G BZ j G B G B=-++§9-2 阻抗(导纳)的串联和并联1.阻抗串联:(1)等效阻抗:12eq n Z Z Z Z =+++L(2)分压作用:,1,2,,k KeqZ U U k n Z ==&&L 2.导纳并联(1)等效导纳:12eq n Y Y Y Y =++L(2)分流作用:,1,2,,k keqY I I k n Y ==&&L3.两个阻抗并联:YψYGB(1)等效阻抗:1212Z Z Z Z Z =+(2)分流作用:21121212,Z Z I I I I Z Z Z Z ==++&&&&§9-3 电路的相量图相量图可直观地表示相量之间的关系,并可辅助电路的分析和计算,相量图的做法: (1)按比例化出各相量的模(有效值),并确定各相量的相位,相对地确定相量在复平面图上的位置。
(2)若没有给定参考相量时,并联电路以电压相量为参考相量,根据支路的VCR 确定各并联支路的电流相量与电压相量之间的夹角;然后根据结点上的 KCL 方程,用相量平移求和法则,画出结点各支路电流相量组成的多变形。
串联电路以电流相量为参考相量,根据VCR 确定有关电压相量与电流相量的夹角,再根据回路上的KVL 方程,用相量平移求和的法则,画出回路上个电压相量所组成的多边形。
(3)串并联电路往往先设并联电压为参考相量,即先并后串。
§9-4 正弦稳态电路的分析用相量法分析正弦稳态电路时,线性电阻电路的各种分析方法和电路定律可推广用于线性电路的正弦稳态分析,差别仅在于所设电路方程为以相量形式表示的代数方程以及用相量形式描述的电路定律,而计算则为复数运算。
§9-5 正弦稳态电路的功率(1)瞬时功率:设cos()cos()u i u t i t ωψωψ⎧=+⎪⎨=+⎪⎩,u i ϕψψ=-cos cos(22)u P ui UI UI t ϕωψϕ==++- (2)平均功率(有功功率):1cos P pdt UI T ϕ==⎰(W) (3)无功功率:sin defQ UI ϕ= (var)ϕQPS(4)视在功率:defS UI = (VA) (5)P ,Q ,S之间的关系:cos ,sin ,arctanQ P S Q S S Pϕϕϕ==== (6)R ,L ,C 单个元件的功率(7)RLC 串联电路的功率2222cos cos 1sin sin ()L CP UI Z I RI Q UI Z I L I Q Q cϕϕϕϕωω======-=+§9-6复功率(1) 复功率22cos sin defu i SUI UI UI jUI P jQ I Z U Y ψψϕϕ**==∠-=+=+==%&& (2)复功率守恒:电路中有功、无功复功率守恒,但视在功率不守恒,即 cos 0P UI ϕ==∑∑ sin 0Q UI ϕ==∑∑ 0S =∑ 0S ≠∑ (3)感性负载并电容提高功率因数:12()PC tg tg U ϕϕω=-§9-7最大功率传输(1)负载获得最大功率条件:e R eq q eqeqZ Z jX Y Y**====(2) 负载获得最大功率:2maxe 4R ocqU P =§9-8串联电路的谐振1.串联电路的谐振条件:(1) 谐振条件:Im[()]0,Z j ω=即0010L Cωω-= (2)谐振频率:00f ω==2.串联电路谐振的特征:(1)呈电阻性,阻抗最小[(),0];Z j R ωϕ==(2)电流最大(U I R=&&) (3)电压谐振,即L C U U QU ==(001LQ RCR ωω===(4)电路的无功功率为零,即0,cos 0Q ϕ==§9-9并联谐振电路1.并联谐振条件(1) 谐振条件:0Im[()]0,Y j ω=即0010L Cωω-= (2)谐振频率:00f ω==2.并联谐振的特征(1)导纳最小(阻抗最大),呈电阻性00[(),(),0]Y j G Z j R ωωϕ===(2)端电压最大00[()()]S S U Z j I RI ωω==;(3)电流谐振,即L C S I I QI ==(0011C C Q LG G G Lωω===) (4)电路的无功功率为零,即0L C Q Q Q =+=。
典型习题:习题9-11 已知附图电路中,2202(25020)u cos t V =+︒,110R =Ω,120,C F μ=280,C F μ=1L H =。
求电路中各电流表的读数和电路的输入阻抗,画出电路的相量图。
解:解:首先计算L X 和C X 。
161112002502010C X C ω-===Ω⨯⨯ 26211502508010C X C ω-===Ω⨯⨯ 2501250L X L ω==⨯=Ω则LC 串联支路的总阻抗Z 为12()(25020050)0L C C Z j X X X j =--=--= 这条支路相当于短路,所以可得电流表的读数为u+—LA 1A 2C 1C 22C U &LU &1C U &1I &RU U =&&题9-11图题解9-11图RR2102202110A U A A R ==== 各相量为1111212122020220220(200)40070220(50)40070220(250)400110C C C C L LUV IA U I jX j V UI jX j V U I jX j V =∠︒=∠︒=-⨯=∠︒⨯-=∠-︒=-⨯=∠︒⨯-=∠-︒=-⨯=∠︒⨯=∠︒&&&&&&&& 相量图如题解9-11图所示。
注意:LC 串联支路的总电压为零,即发生了串联谐振,但各元件上的电压不为零,甚至可大于输入电压。
习题9-15 已知附图电路中,10S I A =,5000/rad s ω=,1210R R ==Ω,10C F μ=,0.5μ=。
求各支路电流并作出电路的相量图。
解法一:设支路电流如图所示。
另100SI A =∠︒&为参考相量,容抗为 6112050001010C X C ω-===Ω⨯⨯ 根据KCL ,有12100S I I I A =+=∠︒&&& 有KVL 得,有11220C R I R I U μ--=&&&即 1210100.5100(20)0I I j --⨯∠︒⨯-=&& 联立以上求解方程,得1255-4555+45I j A I j A =-=︒=+=︒&&相量图如题解9-15所示。
题解9-15图题9-15图&2R 2I &I&解法二:应用结点法计算,对结点①列方程1121111()()C S C S S U U I jX I I R R R R μμ+=-+=--+&&&&&解得:11120.05201010505050245110.2C S SjX I I R j U j V V R R μ+⨯⨯+===+=∠︒+&&&所以电流为: 11150500.510(20)5510C U U j j I j A R μ+++⨯⨯-===-&&& 12155U I j A R ==+&&习题9-24求图示一端口的戴维宁(或诺顿)等效电路。
解(a):先求开路电压OCU &。
由于开路,0I =&,故受控电流源0I α=&,所以有 SOC12U U Z R R Z=++&&其中 3333111R R j C Z j CR R j Cωωω⨯==+++R 2 R 31j cωI&60V∠︒SU &—R 1ababb10j Ω6Ω6Ω++——15j I &OCU &aIα&题9-24图200V∠︒+—b10j -c10j Ω1I &+-所以3S3S 3OC 3123312123U 1U U ()1R j CR R R R R R j CR R R R R j CR ωωω⨯+==+++++++&&&求短路电流。
