数学七年级上华东师大版4.8平行线同步练习
数学课件 华东师大版七年级上册 同步教学第5章相交线与平行线第二节平行线

12.在写艺术字时,常常运用画“平行线段”这种基本方法,如图 所示写的是字母“M”.
(1)请从正面、上面、右面三个不同方向上各找出一组平行线段, 并用字母表示出来;
解:正面:AB∥EF;上面:A′B′∥AB; 右面:DD′∥HI.(答案不唯一)
(2)EF 与 A′B′有何位置关系? 解:EF∥A′B′.
8 如图,平面内有A,B,C三点,且三点不在同一条直 线上,过这三点画两条平行线,这样的平行线能画几 种?画图说明.
解:能画三种,如图所示.
9 如图,(1)过BC上一点P画AB的平行线交AC于T; (2)过点C画MN∥AB; 解:(1)如图.(2)如图.
(3)直线PT,MN具有何种位置关系?试说明理由. 解:PT∥MN,理由如下:因为PT∥AB,MN∥AB, 所以PT∥MN.
8 如图,P是线段AB的中点,过点P画BC的平行线交AC 于点Q,再过点Q画AB的平行线交BC于点S. 解:所画图形如图所示.
(1)用刻度尺测量后确定AQ与QC,CS与BS的数量关系; 解:经测量得到AQ=QC,CS=BS.
(2)用刻度尺测量后确定PQ与BC,QS与AB的数量关系,你 发现了什么?用简洁的语言把你发现的规律叙述出来. 经测量得到 PQ=12BC,QS=12AB. 经过三角形一边的中点,画另一边的平行线,则这条
3 如图,将一张长方形纸对折三次,则产生的折痕与折 痕间的位置关系是( C )
A.平行 C.平行或垂直
B.垂直 D.无法确定
4 【原创题】如图,能相交的是___②___,平行的是 __③____.
5 在如图所示的方格纸中,经过点C画与线段AB平行的 直线l1. 略
6 读下列语句,并画出图形. P是直线AB外一点,直线CD经过点P且与直线AB平行, 直线EF也经过点P且与直线AB垂直. 解:如图所示.
七年级数学上册第5章相交线与平行线5-2-2平行线的判定同步测试题新版华东师大版

第五章 5.2.2平行线的判定同步测试题一、选择题1.如图是我们学过的用直尺和三角尺画平行线的方法示意图,画图的原理是()A.同位角相等,两直线平行B.内错角相等,两直线平行C.两直线平行,同位角相等D.两直线平行,内错角相等2.如图所示,下列条件:①∠1=∠3;②∠2=∠3;③∠4=∠5;④∠2+∠4=180°.不能判断直线l1∥l2的是()A.①②B.②③ C.④ D.②3.如图,若∠1与∠2互补,∠2与∠3互补,则一定有( )A.l1∥l2 B.l3∥l4C.l1∥l4 D.l2∥l44.如图所示,若∠1=50°,当∠2=()时,AB∥CD.A.50°B.60° C.70° D.80°5.如图,在四边形ABCD中,已知∠B=60°,∠C=2∠B,由这些条件你能判断平行的两条直线是().A.AB∥CD B.AD∥BCC.AC∥BD D.AD∥AB二、填空题6.如图,∠1=50°,∠2=50°,则a,b的位置关系是______.7.如图,要使AC∥BD,则需______=______或______=______.8.如图所示,用两个相同的三角形按照如图方式作平行线,能解释其中道理的定理是______9.如图,已知∠2=∠3,则______.10.如图,一个弯形管道ABCD的拐角∠ABC=120°,∠BCD=60°,这时说管道AB∥CD,是根据______11.已知a,b,c为平面内三条不同直线,若a⊥b,c⊥b,则a与c的位置关系是______.12.如图,在下列条件中:①∠DAC=∠ACB;②∠BAC=∠ACD;③∠BAD+∠ADC=180°;④∠BAD+∠ABC=180°.其中能使直线AB∥CD成立的是______.(填序号)三、解答题13.根据图形填空:(1)∵∠1=∠2(已知),∴______∥______;(2)∵∠3+∠4=180°(已知),∴______∥______;(3)∵∠4+∠5=180°(已知),∴______∥______;(4)∵∠2=∠4(已知),∴______∥______.14.如图,AB⊥AC,EF⊥AC,∠1=∠2,那么AB与CD是否平行?填空注明推理的依据.解:∵AB⊥AC,EF⊥AC(______),∴AB∥EF(______).∵∠1=∠2(______),∴EF∥DC(______).∴AB∥CD(______).15.如图,已知∠B=∠1,∠ECD+∠1=180°,试说明:AB∥CD,BF∥CE.16.如图,直线AB,CD被EF所截,∠3=∠4,∠1=∠2,EG⊥FG.试说明:AB∥CD.17.将一副三角板中的两块直角三角尺的直角顶点C按如图方式叠放在一起(其中∠A=60°,∠D=30°,∠E=∠B=45°):(1)①若∠DCE=45°,则∠ACB的度数为______;②若∠ACB=140°,求∠DCE的度数;(2)由(1)猜想∠ACB与∠DCE的数量关系,并说明理由;(3)当∠ACE<180°且点E在直线AC的上方时,这两块三角尺是否存在一组边互相平行?若存在,请直接写出∠ACE度数所有可能的值(不必说明理由);若不存在,请说明理由.参考答案一、选择题1.如图是我们学过的用直尺和三角尺画平行线的方法示意图,画图的原理是(A)A.同位角相等,两直线平行B.内错角相等,两直线平行C.两直线平行,同位角相等D.两直线平行,内错角相等2.如图所示,下列条件:①∠1=∠3;②∠2=∠3;③∠4=∠5;④∠2+∠4=180°.不能判断直线l1∥l2的是(D)A.①②B.②③ C.④ D.②3.如图,若∠1与∠2互补,∠2与∠3互补,则一定有(B)A.l1∥l2 B.l3∥l4C.l1∥l4 D.l2∥l44.如图所示,若∠1=50°,当∠2=( A )时,AB∥CD.A.50°B.60° C.70° D.80°5.如图,在四边形ABCD中,已知∠B=60°,∠C=2∠B,由这些条件你能判断平行的两条直线是( A).A.AB∥CD B.AD∥BCC.AC∥BD D.AD∥AB二、填空题6.如图,∠1=50°,∠2=50°,则a,b的位置关系是a∥b.7.如图,要使AC∥BD,则需∠A=∠B或∠C=∠D.8.如图所示,用两个相同的三角形按照如图方式作平行线,能解释其中道理的定理是内错角相等,两直线平行.9.如图,已知∠2=∠3,则AD∥BC.10.如图,一个弯形管道ABCD的拐角∠ABC=120°,∠BCD=60°,这时说管道AB∥CD,是根据同旁内角互补,两直线平行.11.已知a,b,c为平面内三条不同直线,若a⊥b,c⊥b,则a与c的位置关系是a∥c.12.如图,在下列条件中:①∠DAC=∠ACB;②∠BAC=∠ACD;③∠BAD+∠ADC=180°;④∠BAD+∠ABC=180°.其中能使直线AB∥CD成立的是②③.(填序号)三、解答题13.根据图形填空:(1)∵∠1=∠2(已知),∴CF∥AD;(2)∵∠3+∠4=180°(已知),∴CF∥AD;(3)∵∠4+∠5=180°(已知),∴BC∥DE;(4)∵∠2=∠4(已知),∴BC∥DE.14.如图,AB⊥AC,EF⊥AC,∠1=∠2,那么AB与CD是否平行?填空注明推理的依据.解:∵AB⊥AC,EF⊥AC(已知),∴AB∥EF(在同一平面内,垂直于同一条直线的两条直线平行).∵∠1=∠2(已知),∴EF∥DC(内错角相等,两直线平行).∴AB∥CD(如果两条直线都和第三条直线平行,那么这两条直线也互相平行).15.如图,已知∠B=∠1,∠ECD+∠1=180°,试说明:AB∥CD,BF∥CE.解:∵∠B=∠1,∴AB∥CD.∵∠1=∠2,且∠ECD+∠1=180°,∴∠ECD+∠2=180°.∴BF∥CE.16.如图,直线AB,CD被EF所截,∠3=∠4,∠1=∠2,EG⊥FG.试说明:AB∥CD.解:∵EG⊥FG,∴∠G=90°.∴∠1+∠3=90°.∵∠1=∠2,∠3=∠4,∴∠1+∠2+∠3+∠4=180°,即∠EFD+∠BEF=180°.∴AB∥CD.17.将一副三角板中的两块直角三角尺的直角顶点C按如图方式叠放在一起(其中∠A=60°,∠D=30°,∠E=∠B=45°):(1)①若∠DCE=45°,则∠ACB的度数为135°;②若∠ACB=140°,求∠DCE的度数;(2)由(1)猜想∠ACB与∠DCE的数量关系,并说明理由;(3)当∠ACE<180°且点E在直线AC的上方时,这两块三角尺是否存在一组边互相平行?若存在,请直接写出∠ACE度数所有可能的值(不必说明理由);若不存在,请说明理由.解:(1)②∵∠ACB=140°,∠ACD=90°,∴∠DCB=140°-90°=50°.∴∠DCE=90°-50°=40°.(2)∠ACB+∠DCE=180°.理由:∵∠ACB=∠ACD+∠DCB=90°+∠DCB,∴∠ACB+∠DCE=90°+∠DCB+∠DCE=90°+90°=180°.(3)存在.当∠ACE=30°时,AD∥BC;当∠ACE=45°时,AC∥BE;当∠ACE=120°时,AD∥CE;当∠ACE=135°时,BE∥CD;当∠ACE=165°时,BE∥AD.。
七上数学每日一练:平行线的性质练习题及答案_2020年综合题版

七上数学每日一练:平行线的性质练习题及答案_2020年综合题版答案解析2020年七上数学:图形的性质_相交线与平行线_平行线的性质练习题1.(2019南关.七上期末)(1) 感知:如图①,若AB ∥CD ,点P 在AB 、CD 内部,则∠P 、∠A 、∠C 满足的数量关系是.(2) 探究:如图②,若AB ∥CD ,点P 在AB 、CD 外部,则∠APC 、∠A 、∠C 满足的数量关系是.请补全以下证明过程:证明:如图③,过点P 作PQ ∥AB∴∠A =∵AB ∥CD ,PQ ∥AB∴∥CD∴∠C =∠∵∠APC =∠﹣∠∴∠APC =(3) 应用:① 如图④,为北斗七星的位置图,如图⑤,将北斗七星分别标为A 、B 、C 、D 、E 、F 、G ,其中B 、C 、D 三点在一条直线上,AB ∥EF ,则∠B 、∠D 、∠E 满足的数量关系是.② 如图⑥,在(1)问的条件下,延长AB 到点M ,延长FE 到点N ,过点B 和点E 分别作射线BP 和EP ,交于点P ,使得B D 平分∠MBP ,EN 平分∠DEP ,若∠MBD =25°,则∠D ﹣∠P =°.考点: 角的平分线;平行线的性质;2.(2019德惠.七上期末) 三角板是学习数学的重要工具,将一副三角板中的两块直角三角板的直角顶点C 按如图方式叠放在一起,当0°<∠ACE <90°且点E 在直线AC 的上方时,解决下列问题:(友情提示:∠A =60°,∠D =30°,∠B =∠E =45°).答案解析答案解析答案解析(1) ①若∠DCE =45°,则∠ACB 的度数为;②若∠ACB =140°,则∠DCE 的度数为;(2) 由(1)猜想∠ACB 与∠DCE 的数量关系,并说明理由.(3) 这两块三角板是否存在一组边互相平行?若存在,请直接写出∠ACE 的角度所有可能的值(不必说明理由);若不存在,请说明理由.考点: 角的运算;平行线的性质;3.(2019宽城.七上期末) (探究)如图①,∠AFH 和∠CHF 的平分线交于点O ,EG 经过点O 且平行于FH ,分别与AB 、C D交于点E 、G .(1) 若∠AFH =60°,∠CHF =50°,求∠EOF 与∠FOH 的度数.(2) 若∠AFH+∠CHF =100°,求∠FOH 的度数.(3) 如图②,∠AFH 和∠CHI 的平分线交于点O ,EG 经过点O 且平行于FH ,分别与AB 、CD 交于点E 、G .若∠AFH +∠CHF =α,直接写出∠FOH 的度数.(用含a 的代数式表示)考点: 角的平分线;平行线的性质;三角形内角和定理;4.(2018平.七上期末) 如图,已知AB ∥CD ,∠B=40°,CN 是∠BCE 的平分线CM ⊥CN .(1) 求∠BCE 的度数;(2) 求∠BCM 的度数.考点: 角的平分线;平行线的性质;5.(2018孟津.七上期末) 如图(1),AB ∥CD ,试求∠BPD 与∠B 、∠D 的数量关系,说明理由.(1) 填空:解:过点P 作EF ∥AB ,答案解析∴∠B+∠BPE=180°∵AB ∥CD ,EF ∥AB∴(如果两条直线都和第三条直线平行,那么这两条直线也互相平行)∠EPD+=180°∴∠B+∠BPE+∠EPD+∠D=360°∴∠B+∠BPD+∠D=360°(2) 依照上面的解题方法,观察图(2),已知AB ∥CD ,猜想图中的∠BPD 与∠B 、∠D 的数量关系,并说明理由.(3) 观察图(3)和(4),已知AB ∥CD ,直接写出图中的∠BPD 与∠B 、∠D 的数量关系,不用说明理由.考点: 平行线的性质;平行公理及推论;2020年七上数学:图形的性质_相交线与平行线_平行线的性质练习题答案1.答案:2.答案:3.答案:4.答案:5.答案:。
4.2.2.平行线的判定+++课件+2024—-2025学年华东师大版数学七年级上册

3.(4分·几何直观、应用意识)已知直线BC,小明和小亮想画出BC的平行线,他们
的方法如下:
下列说法正确的是( C )
A.小明的方法正确,小亮的方法不正确
B.小明的方法不正确,小亮的方法正确
C.小明、小亮的方法都正确
D.小明、小亮的方法都不正确
21
4.(8分·抽象能力、推理能力)如图,∠B=52°,∠ACB=∠A+8°,∠ACD=60°,求
1.描边:描出两个角的两边.
2.定三线:确定截线和被截线,共线的边是截线,另外两边是被截线.
3.定关系:确定两角的位置关系和数量关系.
4.判定:同位角或内错角相等→两直线平行;同旁内角互补→两直线平行.
素养 当堂测评
1.(4分·几何直观、推理能力)如图,直线MN分别与直线AB,CD交于点E和点F,下
证:AB∥CD.
22
【证明】因为∠ACB=180°-∠A-∠B,∠ACB=∠A+8°,∠B=52°,
所以∠A+8°=180°-∠A-52°,
所以∠A=60°,
因为∠ACD=60°,
所以∠A=∠ACD,
所以AB∥CD.
23
本课结束
相等
内错角______,两直线平行
符号
因为∠1=∠2,
所以a∥b.
因为∠2=∠3,
所以a∥b.
互补
的 同旁内角______,两直
因为∠4+∠2=180°,
判 线平行
所以 a∥b.
定
垂直
在同一平面内,______于同
因为CD⊥AB,
一条直线的两条直线平行
EF⊥AB,所以CD∥EF.
图示
5
【对点小练】
四年级认识平行线练习题及答案

四年级认识平行线练习题及答案
一、我会填。
1、在同一个平面内不相交的两条直线的位置关系是( )。
2、长方形的每组对边互相( ),每组邻边互相( )。
3、教室中黑板的长边和短边互相( )。
4、数学书中的两条长边互相( )。
5、五线谱的五条横线互相( )。
二、判断。
1、 不相交的两条直线叫做平行线。
( )
2、长方形相对的两条边是一组平行线。
( )
3、
中两条线没有相交,就可以看作一组平行线。
(
)
4、互相平行的两条直线,无论怎样延长都不会相交。
( ) 三、是平行线的在( )里画“√”。
( ) ( ) ( ) ( ) ( ) ( )
四、
互相平行的有:( ) 互相垂直的有:( )
b c d e f g a
答案:
一、1、平行2、平行垂直3、垂直4、平行5、平行
二、 1.× 2. √ 3. √
三、
四、 d 和e c和f c和a f和a。
【精练精析】2014版七年级数学上册(华师大版)同步练习:5.2.2平行线的判定
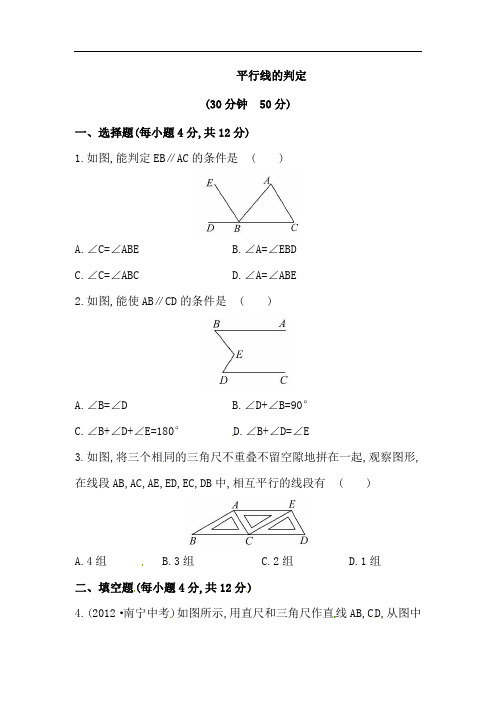
平行线的判定(30分钟50分)一、选择题(每小题4分,共12分)1.如图,能判定EB∥AC的条件是( )A.∠C=∠ABEB.∠A=∠EBDC.∠C=∠ABCD.∠A=∠ABE2.如图,能使AB∥CD的条件是( )A.∠B=∠DB.∠D+∠B=90°C.∠B+∠D+∠E=180°D.∠B+∠D=∠E3.如图,将三个相同的三角尺不重叠不留空隙地拼在一起,观察图形,在线段AB,AC,AE,ED,EC,DB中,相互平行的线段有( )A.4组B.3组C.2组D.1组二、填空题(每小题4分,共12分)4.(2012·南宁中考)如图所示,用直尺和三角尺作直线AB,CD,从图中可知,直线AB与直线CD的位置关系为____________.5.如图,请填写一个你认为恰当的条件____________,使AB∥CD.6.如图,DF平分∠CDE,∠CDF=55°,∠C=70°,则________∥________.三、解答题(共26分)7.(9分)如图所示,已知∠DAB=∠DCB,AF平分∠DAB,CE平分∠DCB,∠FCE=∠CEB.试说明AF∥CE.解:∵AF平分∠DAB,∴________=∠DAB( ).∵CE平分∠DCB,∴∠FCE=________( ).∵∠DAB=∠DCB( ),∴∠FAE=∠FCE.∵∠FCE=∠CEB.∴________=________.∴AF∥CE(__________________).8.(8分)如图,∠BAF=46°,∠ACE=136°,CE⊥CD,问CD∥AB吗?为什么?【拓展延伸】9.(9分)直线AB和CD被直线MN所截.(1)EG平分∠BEF,FH平分∠DFE(平分的是一对同旁内角),则∠1与∠2满足什么条件时,AB∥CD?(2)当EG平分∠MEB,FH平分∠DFE时(平分的是一对同位角),∠1与∠2满足什么条件时,AB∥CD?(3)当EG平分∠AEF,FH平分∠DFE(平分的是一对内错角),∠1与∠2满足什么条件时,AB∥CD?答案解析1.【解析】选D.若∠A=∠ABE,则EB∥AC(内错角相等,两直线平行).2.【解析】选D.如图,过点E作∠BEF=∠B,∴AB∥EF,若∠B+∠D=∠BED,即∠B+∠D=∠BEF+∠DEF,又∵∠BEF=∠B,∴∠DEF=∠D,∴CD∥EF,∴AB∥CD.3.【解析】选 B.由题意可知∠B=∠DCE,∠BCA=∠CAE,∠ACE=∠DEC,于是分别可以得到AB∥EC(同位角相等,两直线平行),A E∥DB(内错角相等,两直线平行),AC∥DE(内错角相等,两直线平行).因此,互相平行的线段有:AE∥DB,AB∥EC,AC∥DE,共三组.4.【解析】根据题意,∠DEF与∠BGF是三角尺的同一个角不同的位置,所以∠DEF=∠BGF,所以AB∥CD(同位角相等,两直线平行).答案:平行5.【解析】根据同位角相等,两直线平行,可以添加∠FCD=∠FAB;根据内错角相等,两直线平行,可以添加∠CDA=∠DAB;根据同旁内角互补,两直线平行,可以添加∠BAC+∠ACD=180°.答案:∠FCD=∠FAB或∠CDA=∠DAB或∠BAC+∠ACD=180°(填一个即可)6.【解析】∵∠CDF=55°,DF平分∠CDE,∴∠EDF=55°,∴∠ADE=70°,∴∠ADE=∠C,∴BC∥DE.答案:BC DE7.答案:∠FAE 角平分线定义∠DCB 角平分线定义已知∠FAE ∠CEB 同位角相等,两直线平行8.【解析】CD∥AB.∵∠BAF+∠BAC=180°,∠BAF=46°(已知),∴∠BAC=180°-∠BAF=180°-46°=134°.∵CE⊥CD(已知),∴∠DCE=90°(垂直的性质).又∵∠FCD+∠DCE+∠ACE=360°,∴∠FCD=360°-∠DCE-∠ACE=360°-90°-136°=134°,∴∠BAC=∠FCD(等量代换),∴CD∥AB(内错角相等,两直线平行).9.【解析】(1)当∠1与∠2互余时,AB∥CD.理由为:∵EG平分∠BEF,FH平分∠DFE,∴∠BEF=2∠1,∠DFE=2∠2,当∠1+∠2=90°时,∠BEF+∠DFE=180°,∴AB∥CD(同旁内角互补,两直线平行).(2)当∠1=∠2时,AB∥CD.理由为:EG平分∠MEB,FH平分∠DFE.∴∠MEB=2∠1,∠DFE=2∠2,当∠1=∠2时,∠MEB=∠DFE,∴AB∥CD(同位角相等,两直线平行).(3)当∠1=∠2时,AB∥CD.理由为:∵EG平分∠AEF,FH平分∠DFE,∴∠AEF=2∠1,∠DFE=2∠2.当∠1=∠2时,∠AEF=∠DFE.∴AB∥CD(内错角相等,两直线平行).【归纳整合】平行线的判定技巧1.两条直线被第三条直线所截,如果同位角相等,或内错角相等,或同旁内角互补,那么两条被截直线互相平行.2.“垂直于同一直线的两条直线互相平行”是由平行线的判定方法推导得来的,利用垂直的特点可以推出同位角相等或内错角相等且都等于90°,或者由同旁内角的和为180°,继而可得两直线平行的位置关系。
数学七年级上华东师大版4.8.1平行线同步练习.doc

5D1C BA FEGH 432华师大版 4.8平行线 同步练习题本试卷时间100分钟,满分100分一 相信你的选择,看清楚了再填(每小题3分,共18分)1.在同一平面内,两条直线可能的位置关系是 ( )(A) 平行. (B) 相交. (C) 相交或平行. (D) 垂直. 2.判定两角相等,不正确的是 ( ) (A ) 对顶角相等.(B ) 两直线平行,同位角相等.(C ) ∵∠1=∠2,∠2=∠3,∴∠1=∠3.(D ) 两条直线被第三条直线所截,内错角相等.3.两个角的两边分别平行,其中一个角是60°,则另一个角是 ( ) (A )60°. (B )120°. (C ) 60°或120°. (D ) 无法确定. 4.下列语句中正确的是( )(A )不相交的两条直线叫做平行线. (B )过一点有且只有一条直线与已知直线平行. (C )两直线平行,同旁内角相等. (D )两条直线被第三条直线所截,同位角相等. 5.下列说法正确的是( )(A )垂直于同一直线的两条直线互相垂直. (B )平行于同一条直线的两条直线互相平行.(C )平面内两个角相等,则他们的两边分别平行.(D )两条直线被第三条直线所截,那么有两对同位角相等.6.已知AB ∥CD ∥EF ,BC ∥AD ,AC 平分∠BAD ,那么图中与∠AGE 相等的角有( ) (A )5个. (B )4个. (C )3个. (D )2个.二.试一试你的身手,想好了再填(每题3分,共12分)7. 如果a ∥b ,b ∥c ,则______∥______,因为________. 8.在同一平面内,如果a ⊥b ,b ⊥c ,则a c ,因为 .9.填注理由:如图,已知:直线AB ,CD 被直线EF ,GH 所截,且∠1=∠2, 试说明:∠3+∠4=180°. 解:∵∠1=∠2 ( ) 又∵∠2=∠5 ( ) ∴∠1=∠5 ( ) ∴AB ∥CD ( )∴∠3+∠4=180° ( )(第6题图)DCBA65D 1CBAF E 43210.如图,直线a 、b 被直线c 所截,且a ∥b , 若∠1=118°,则∠2= 度.三.挑战你的技能,思考好了再做11.如图,从正方形ABCD 中找出互相平行的边.(7分)12.已知:如图,∠1=40°,∠2=65°,AB ∥DC ,求∠ADC 和∠A 的度数.(7分)D1CBA 213.已知:如图AD ∥BE ,∠1=∠2,求证:∠A =∠E .(7分)D1CBAE3214.如图,根据下列条件,可以判定哪两条直线平行?并说明判定的依据.(10分)(1)∠1=∠C(2)∠2=∠4(3)∠2+∠5=180° (4)∠3=∠B (5)∠6=∠2cba1324321l l l l 5143215.已知:如图,∠1=∠4,∠2=∠3,求证:1l // 2l .(7分)16.已知:如图,∠1+∠2=180°,∠3=100°,OK 平分∠DOH , 求∠KOH 的度数.(8分)KD O 1CBAF EG H3217.已知:如图,CD 平分∠ACB ,AC ∥DE ,CD ∥EF ,试说明EF 平分∠DEB .(8分)DCBAFE18.如图,CD ∥BE ,试判断∠1,∠2,∠3之间的关系.(8分)D C BAE13219.已知:如图, AB ∥DF ,BC ∥DE ,求证:∠1=∠2.(8分)答案:一、相信你的选择,看清楚了再填题号 1 2 3 4 5 6 答案C D C B B A二.试一试你的身手,想好了再填7.a ∥c 平行于同一条直线的两条直线平行8.a ∥c 在同一平面内,垂直于同一条直线的两条直线平行9.已知 对顶角相等 等量代换 同位角相等两直线平行 两直线平行同旁内角互补 10. 62°三.挑战你的技能,思考好了再做11.AD ∥BC AB ∥CD 12. ∠ADC =105°, ∠A =75°13.∵∠1=∠2 ∴AC ∥DE ∴∠A +∠ADE =180°∵AD ∥BE ∴∠ADE +∠E =180° ∴∠A =∠E 14.⑴∵∠1=∠C ∴AC ∥DF (同位角相等,两直线平行)⑵∵∠2=∠4 ∴AB ∥DE (内错角相等,两直线平行)⑶∵∠2+∠5=180° ∴AC ∥DF (同旁内角互补,两直线平行) ⑷∵∠3=∠B ∴DE ∥AB (同位角相等,两直线平行) ⑸∵∠6=∠2 ∴FD ∥AC (内错角相等,两直线平行) 15. ∵∠1=∠4 ∴1l ∥3l∵∠2=∠3 ∴2l ∥3l ∴1l ∥2l16. ∠KOH =40°17. ∵AC ∥DE ∴∠ACB =∠DEB ∵EF ∥CD ∴∠FEB=∠DCB∵∠DCB=∠ACD ∴∠FEB=∠DEF ∴EF 平分∠DEB.DCBAF E1218.提示: 过A作AF∥CD∠1=∠2+∠319.提示: 连结BD。
最新华东师大版七年级数学上册全册课时练习(一课一练,附详细解析过程)

华东师大版七年级数学上册全册课时练习数学伴我们成长人类离不开数学 (2)人人都能学会数学 (5)2.1.1正数和负数 (6)2.1.2有理数 (10)2.2 数轴 (14)2.3 相反数 (16)2.4 绝对值 (19)2.5 有理数的大小比较 (21)2.6.1有理数的加法法则 (25)2.6.2有理数加法的运算律 (28)2.7 有理数的减法 (32)2.8 有理数的加减混合运算 (34)2.9.1有理数的乘法法则 (36)2.9.2有理数的乘法运算律 (39)2.10有理数的除法 (43)2.11有理数的乘方 (46)2.12科学记数法 (48)2.13有理数的混合运算 (50)2.14近似数 (55)2.15 用计算器进行运算 (58)3.1列代数式 (60)3.2 代数式的值 (65)3.3 整式 (67)3.4 整式的加减 (69)4.1生活中的立体图形 (73)4.2 立体图形的视图 (77)4.3立体图形的表面展开图 (80)4.4平面图形 (83)4.5.1 点和线 (88)4.5.2 线段的长短比较 (91)4.6 1. 角 (94)4.6 2. 角的比较和运算 (98)4.6 3. 余角和补角 (103)5.1.1对顶角 (109)5.1.2垂线 (113)5.1.3 同位角、内错角、同旁内角 (116)5.2.1 平行线 (119)5.2.2平行线的判定 (122)5.2.3平行线的性质 (126)数学伴我们成长人类离不开数学一、选择题1.李叔叔家客厅长6米,宽4.8米,计划在地面铺上方砖.为了美观,李叔叔想使地面都是整块方砖,请你帮忙选择一种方砖,你的选择是( )A.边长50厘米的B.边长60厘米的C.边长100厘米的D.以上都不选2.如图是老年活动中心门口放着的一个招牌,这个招牌是由三个特大号的骰子摞在一起而成的.每个骰子的六个面的点数分别是1到6,其中可以看见7个面,其余11个面是看不见的,则看不见的面上的点数总和是( )A.41B.40C.39D.383.已知世运会、亚运会、奥运会分别于2009年、2010年、2012年举办过.若这三项运动会均每四年举办一次,则这三项运动会均不举办的年份是( )A.2070年B.2071年C.2072年D.2073年二、填空题4.某种商品每件的进价为180元,按标价的九折销售时,利润率为20%,这种商品每件标价是________元.5.假设2019年8月3日是星期六,则2019年8月18日是星期________.6.如图,甲类纸片是边长为2的正方形,乙类纸片是边长为1的正方形,丙类纸片是长、宽分别为2和1的长方形.现有甲类纸片1张,乙类纸片4张,则应至少取丙类纸片________张才能用它们拼成一个新的正方形.三、解答题7.(8分)为了学生的卫生安全,学校给每个住宿生配一个水杯,每只水杯3元,友谊商城打九折;中百商厦“买8送1”,学校想买180只水杯,请你当“参谋”,算一算:到哪家购买较合算?请写出你的理由.8.(8分)2019年5月1日小明和爸爸一起去旅游,在火车站看到如表所示的列车时刻表:2019年5月1日××次列车时刻表始发点发车时间终点站到站时间A站上午8:20 B站次日12:20小明的爸爸用手机上网找到了以前同一车次的时刻表如下:2006年12月15日××次列车时刻表始发点发车时间终点站到站时间A站[来源:数理化网]下午14:30 B站第三日8:30比较了两张时刻表后,小明的爸爸提出了如下两个问题,请你帮小明解答:(1)现在该次列车的运行时间比以前缩短了多少小时?(2)若该次列车提速后的平均时速为每小时200千米,那么,该次列车原来的平均时速为多少?(结果四舍五入到个位)9.(10分)你玩过火柴吗?如图,用火柴棒搭正方形,所搭正方形个数n与火柴棒根数s之间有一定的关系:将下面表格补充完整并解答后面的问题:正方形个数n 1 2 3 4 5 6 …n火柴棒根数s求搭10个正方形,需要多少根火柴棒?答案1.【解析】选B.6米=600厘米,4.8米=480厘米.选项A:600÷50=12,480÷50=9.6,客厅宽不是方砖边长的整数倍,这种方砖不合适;选项B:600÷60=10,480÷60=8,客厅长和宽都是方砖边长的整数倍,这种方砖可以;选项C:600÷100=6,480÷100=4.8,客厅宽不是方砖边长的整数倍,这种方砖不合适.2.【解析】选C.三个骰子18个面上的数字的总和为:3×(1+2+3+4+5+6)=3×21=63,看得见的7个面上的数字的和为:1+2+3+5+4+6+3=24,所以看不见的面上的点数总和是63-24=39.3.【解析】选B.由于这三项运动会均每四年举办一次,所以只要每个选项与2009,2010,2012的差有一个是4的倍数,则能在这一年举办此项运动会,否则这三项运动会均不在这一年举办.因为选项B中,2071-2009=62,2071-2010=61,2071-2012=59,均不是4的倍数,所以这三项运动会均不在2071年举办.4.【解析】180×(1+20%)÷90%=240(元).答案:2405.【解析】2019年8月3日至2019年8月18日经过了15天,15÷7=2……1,所以2019年8月18日是星期日.答案:日6.【解析】本题可以动手操作,画也行,用纸片拼也行,应该取丙类纸片4张.答案:47.【解析】到中百商厦买合算.因为到友谊商城需花费:180×3×90%=486(元),到中百商厦只需买160只,就送20只,所以需花费:160×3=480(元).因为486元>480元,所以到中百商厦买合算.8.【解析】(1)原来该次列车所用时间=2×24+8.5-14.5=42(小时).现在该次列车的运行时间=24+12-8=28(小时),42-28=14(小时),所以缩短了14小时.(2)28×200÷42≈133(千米).答:(1)现在该次列车的运行时间比以前缩短了14小时,(2)原来的平均时速约为每小时133千米.9.【解析】前三个空可通过直接数得出n=1时,s=4;n=2时,s=7;n=3时,s=10.比较4,7,10,可看出后一个数比前一个数大3,故n=4时,s=13;n=5时,s=16;n=6时,s=19.观察填入的数据可看出正方形个数×3+1即为火柴棒根数,故当正方形个数为n 时,s=3n+1,所以n=10时,s=3×10+1=31.答:需要31根火柴棒.人人都能学会数学1.一件衣服的标价200元,若以6折销售,仍可获利20%,则这件衣服的进价是( )元。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
4.8 平行线同步检测题
一、填空
1.______________________________________,不相交的两条直线叫做平行线.
2.在同一平面内,两条直线(不重合)的位置关系有_____种,它们是_______________.
3.经过已知直线外一点,有且只有______条直线与已知直线平行.
4.平行于同一直线的两条直线(不重合)的位置关系是__________________.
5.如图1,(1)如果∠1=∠2,根据___________________________________,得DE∥BC;
(2)如果∠2+∠BED=180°,根据_______________________________,得DE∥BC;
(3)如果∠EGF=∠GFC,根据____________________________________,得DE∥BC;
(4)如果AB∥GF,根据________________________________________,得∠2=∠GFC;
(5)如果AB∥GF,根据______________________________________,得∠A+∠FGA=180°;
(6)如果AB∥GF,根据_______________________________________,得∠A=∠3.
321(1)E
G D
C F
A
H B
6.如图2,已知CD 平分∠ACB,DE ∥BC,∠AED=80°,则∠EDC=________.
7.不相邻的两个直角,如果它们有一条公共边,那么另两条边相互_______.
8.如图3,已知AB ∥CD,∠1=43°,∠2=47°,则∠B=________,∠ACB=_______.
9.如图4,已知m ∥n,∠1=105°,∠2=140°,则∠α=________.
10.如图5,已知AB ∥CD,AD ∥BC,∠B=60°,∠EDA=50°,则∠CDO=_______.
11.若两条平行线被第三条直线所截,则同旁内角的平分线互相________.
12.如图6,ABC 是直线,∠1=150°,∠D=65°,要证AB ∥DE,请完善证明过程,•并在括号内填上相应依据.∵ABC 是直线(已知),∴∠1+∠2=_______°( ),
∵∠1=•115°(已知),∴∠2=_______°
.
∵∠
D=65
°,∴∠2=∠D( ), ∴AB ∥DE( )
13.如图7,已知∠1=∠A,∠2=∠B,要证MN ∥EF,请完善证明过程,并在括号内填上相应依据:∵∠1=∠A(已知),∴_______∥______( ).
∵∠2=∠B(已知),•∴______∥________( ),
∴MN ∥EF( )
14.如图8,已知AD ∥BC,∠1=∠2,要证∠3+∠4=180°,请完善证明过程,并在括号内填上相应依据:∵AD ∥BC(已知),∴∠1=∠3( ),
∵∠1=∠2(已知),∴∠2=∠3( ),
∴________∥________( ),
∴∠3+∠4=180°(• ).
15. 如图9,已知DF ∥AC,∠C=∠D,要证∠AMB=∠2,请完善证明过程,•并在括号内填上相应依据:∵DF ∥AC(已知),∴∠D=∠1( ),
∵∠C=∠D(已知),∴∠1=∠C( •),
∴DB ∥EC( ),
∴∠AMB=∠2( ).
二、选择
16.下列语句中,不能判定两直线平行的是( ).
A.内错角相等,两直线平行
B.同位角相等,两直线平行
C.同旁内角相等,两直线平行
D.同一平面内,垂直于同一直线的两条直线平行
17.如图10,若∠1是它的补角的3倍,∠2等于它的余角,则AB 和CD 的关系是( )
A.平行
B.相交
C.平行或相交
D.不能确定 43
521(11)D C
F A
E B
18.如图11,已知∠1=∠2,∠3=∠4,求证:AC∥DF,BC∥EF.证明过程如下:
∵∠1=∠2(已知),∴AC∥DF,(A,同位角相等,两直线平行)
∴∠3=∠5.(B.内错角相等,两直线平行)
又∵∠3=∠4(已知),∴∠5=∠4,(C.等量代换)
∴BC∥EF.(D.内错角相等,两直线平行)
理由填错的是( ).
19.如图12,FA⊥MN于A,HC⊥MN于C,指出下列各判断中,错误的是( )
A.由∠CAB=∠NCD,得AB∥CD;
B.由∠DCG=∠BAC,得AB∥CD
C.由∠MAE=∠ACF,∠DCG=∠BAE,得AB∥CD;
D.由∠MAB=∠ACD,得AB∥CD
20.如图13,若AB∥CD,则下列结论正确的是( ).
A.∠3=∠4;
B.∠A=∠C;
C.∠3+∠1+∠4=180°;
D.∠3+∠1+∠A=180°
21.如图14,AB∥CD,若∠2是∠1的2倍,则∠2等于( )
A.60°
B.120°
C.90°
D.150°
22.在同一平面内有三条直线,如果要使其中两条且只有两条平行,那么它们( •)
A.有三个交点;
B.有两个交点;
C.只有一个交点;
D.没有交点
23.写出“对顶角的平分线在一条直线上”的已知、求证,
并画出图形,如图15,已知AB,CD相交于O,OE平分∠AOC,
求证:E,O,F在一条直线上,以上有错误的是( )
A.图形;
B.已知;
C.求证;
D.已知和求证都错.
三、解答.
24.如图,已知∠1=∠2,AB∥CD,求证:CD∥EF.
25.如图,已知AB∥CD,∠3=30°,∠1=70°,求∠A-∠2的度数.
26.如图,已知AB∥CD,∠BAE=40°,∠ECD=70°,EF平分∠AEC,求∠AEF的度数.•
27.如图,已知AB∥CD,∠BAE=30°,∠DCE=60°,EF,EG三等分∠AEC.(1)•求∠AEF的度数;(2)求证:EF∥AB.
28.如图,已知在△ABC中,EF⊥AB,CD⊥AB,G在AC边上,∠1=∠2,求证:∠AGD=∠ACB.
29.如图,已知BD平分∠ABC,∠1=∠2,求证:AB∥CD.
30.如图,已知∠4=∠B,∠1=∠3,求证:AC平分∠BAD.
31.如图,已知AB,CD分别垂直EF于B,D,且∠DCF=60°,∠1=30°,求证:BM=AF.
32.证明:垂直于同一直线的两条直线平行.(要求写出已知、求证,作图,并写出证明过程)
答案:
一、1.在同一平面上; 2.两相交和平行; 3.一 4.平行;
5.(1)同位角相等,两直线平行.(2)同旁内角互补,两直线平行.(3)内错角相等,两直线平行.(4)两直线平行,同位角相等.(5)两直线平行,同旁内角互补.(6)两直线平行,内错角相等
6.40°
7.平行
8.47°90°
9.65° 10.70° 11.垂直 12.180平角的性质65°等量代换内错角相等,两直线平行 13.MN AB 内错角相等,两直线平行 EF AB 同位角相等,两直线平行平行于同一直线的两条直线平行
14.两直线平行,内错角相等等量代换 BE FD 同位角相等,两直线平行• 两直线平行,同旁内角互补
15.两直线平行,内错角相等等量代换同位角相等,两直线平行两直线平行,• 同位角相等
二、16.C 17.A 18.B 19.B 20.D 21.B 22.B 23.B
三、24.证明:∵∠1=∠2,∠1=∠3,
∴∠2=∠3,
∴AB∥EF.
又∵AB∥CD,
∴CD∥EF.
25.∵∠A+∠1+∠3=180°,
∴∠A=180°-∠1-∠3=180°,
又∵AB∥CD,
∴∠2=∠3=30°,
∴∠A-∠2=80°-30°=50°.
26.如答图,过E作EG∥AB,
∴∠A=∠AEG.
又∵∠BAE=40°,
∴∠AEG=40°.
∵AB∥CD,
∴EG∥CD,
∴∠GEC=∠ECD.
∵∠ECD=70°,
∴∠GEC=70°,
∴∠AEC=∠AEG+•∠GEC=40°+70°=110°. 又∵EF平分∠AEC,
∴∠AEF=∠AEC=55°.
27.(1)∠AEF=30°.(2)略.
28-32.(略)。
