六年级数学《立体图形表面积和体积》专题练习
(完整版)六年级总复习之立体图形的表面积与体积练习

人教版小学数学六年级总复习练习卷9、立体图形的表面积与体积一、填空。
1、圆柱的底面半径扩大 3 倍,高不变,底面周长扩大()倍,侧面积扩大()倍,底面积扩大()倍,体积扩大()倍。
2、一个圆柱形容器与一个圆锥形容器等底等高,将圆锥形容器装满水后全部倒入空圆柱形容器内,这时水深 2 厘米,圆锥形容器的高是()厘米。
3、用铁丝焊接成一个长 5 分米,宽 4 分米,高 3 分米的长方体模型,最少需要铁丝();若是用纸糊它的表面,最少需要()纸板;这个长方体模型的体积是()。
4、用 3 个棱长都是 2 厘米的正方体拼成一个长方体,拼成的这个长方体的表面积是()平方厘米,体积是()立方厘米。
5、一个圆锥与和它等底等高的圆柱的体积相差12 立方分米,圆锥的体积是()立方分米。
6、把长、宽、高分别是 6 厘米、 4 厘米、 5 厘米的长方体削成一个最大的圆柱体,圆柱的体积是()立方厘米。
7、把一根直径是20 厘米,长是 2 米的圆柱形木材锯成同样的 3 段,表面积增加了()立方厘米。
8、一个圆柱形的铁皮水桶,从里面量底面直径 4 分米,深 5 分米,做这个无盖水桶最少需要()铁皮;这个水桶最多可以装水()升。
9、圆柱和圆锥的体积比是3﹕ 2,底面积的比是3﹕4,高的比是()。
10、一个正方体的高增加 3 厘米,获取的新长方体的表面积比原来正方体的表面积增加了 60 平方厘米,原来正方体的体积是()立方厘米。
11、两个完满同样的圆柱,能拼成一个高 12 分米的圆柱,但表面积减少了25.12 平方分米。
原来一个圆柱的体积是()。
12、一个圆柱和一个圆锥等底等高,圆柱的底面积 4 m2,高 3 m,圆锥的体积是( )cm 。
的 面张开是( )形。
13、把一个底面直径是 12 cm ,高是 6 cm 的 柱,削成一个与它等底等高的 ,削去部分的体 是()cm 3,节余部分的体 是()cm 3。
14、一个 的体 是 12 立方分米,高是 4 分米,底面 是( )平方分米。
苏教版 数学 六年级上册 长方体、正方体的表面积和体积计算练习

课前预习
请根据预习单思考以下问题,并和同桌说一说。
1.什么是长方体和正方体的表面积?怎样计算? 2.什么是长方体和正方体的体积?怎样计算? 3.什么是容积? 4.表面积和体积、容积有什么区别? 5.常用的面积单位、体积单位、容积单位分别有哪些?
知识梳理
长方体(或正方体)六个面的总面积叫作它的表面积。
基础应用
16.一种长方体的煤气灶包装箱,长8分米,宽4分米,高1.5 分米。 (1)做这个包装箱至少要用多少平方分米硬纸板?是多少 平方米? (2)包装箱的体积是多少立方分米?是多少立方米?
(1)(8×4+8×1.5+4×1.5)×2 (2)8×4×1.5=48(立方分米)
= (32+12+6)×2
常用的面积单位有:平方米、平方分米、平方厘米 常用的体积单位有:立方米、立方分米、立方厘米 常用的容积单位有:升、毫升
基础应用
15.
长方体 正方体
长
宽
高
10 cm 8 cm 6 cm
5 dm 5 cm 4 dm
0.5 m 0.3 m 0.2 m 棱长4 dm
表面积 体积 376cm² 480cm³ 130dm² 100dm³ 0.62m² 0.03m³ 96dm² 64dm³
提高训练
18.一个花坛(如右图),高0.9米,底面 是边长1.2米的正方形,四周用木条围成。 (1)这个花坛占地多少平方米?
1.2×1.2=1.44(平方米) 答:这个水花坛占地1.44平方米。
(2)用泥土填满这个花坛,大约需要泥土 多少立方米?(木条的厚度忽略不计)
1.44×0.9=1.296(立方米) 答:大约需要泥土1.296立方米。
小学数学苏教版六年级上册长方体和正方体表面积和体积练习题

小学数学苏教版六年级上册长方体和正方体表面积和体积练习题小学数学苏教版六年级上册长方体和正方体表面积和体积练题1、有一根长52厘米的铁丝,恰好可以焊接成一个长6厘米,宽4厘米,高多少厘米的长方体?2.一个房间的长6米,宽3.5米,高3米,门窗面积是8平方米。
现在要把这个房间的四壁和顶面粉刷水泥,粉刷水泥的面积是多少平方米?如果每平方米需要水泥4千克,一共要水泥多少千克?3、用96厘米长的铁丝焊接成一个正方体的框架,然后用纸给它的表面包裹起来,至少需要多少平方厘米的纸?4.一盒饼干长20厘米,宽15厘米,高30厘米,现在要在它的四周贴上商标纸,这张商标纸的面积是多少平方厘米?5、用两个棱长为5厘米的正方体拼成一个长方体,这个长方体的表面积是多少平方厘米?6、一个长方体和一个正方体的棱长之和相等,已知长方体的长为5厘米,宽为3厘米,高为4厘米,求正方体的棱长。
7、用两个同样的长、宽、高划分为4厘米、3厘米和2厘米的小长方体,拼成一个外表积最大的长方体,这个大长方体的外表积是多少平方厘米?8.做一个长方体的浴缸(无盖),长8分米,宽4分米,高6分米,至少需要多少平方分米的玻璃?如果每平方分米玻璃4元钱,至少需要多少钱买玻璃?9.一个抽屉,长50厘米,宽30厘米,高10厘米,做2个这样的抽屉,至少需要木板多少平方厘米?1、用一根铁丝恰好焊成一个棱长8厘米的正方体框架,假如用这根铁丝焊成一个长10厘米、宽7厘米的长方体框架,它的高应该是多少厘米?2、一种长方体硬纸盒,长10厘米,宽6厘米,高5厘米,有2平方米的硬纸板210张,可以做这样的硬纸盒多少个?(不计接口)3、一个面的面积是36平方米的正方体,它所有的棱长的和是多少厘米?4、一个长方体的棱长和是72厘米,它的长是9厘米,宽6厘米,它的表面积是多少平方厘米?5、一个长方体的告白箱长是1.2米,宽是5分米,高是2米,做这样一个长方体告白箱需要多少平方米的塑料薄膜?6、一个正方体棱长是1.3米,它的表面积是多少?7、一个长方体铁皮油箱,长8分米,宽6分米,高4.5分米.做10个这样的油箱至少需要多少铁皮?8、一个正方体的棱长总和是24厘米,它的外表积是多少平方厘米?9、用36厘米的铁丝折一个正方体框架,这个正方体棱长是多少?假如用纸糊满框架的外表,最少需要纸多少平方厘米?10、长方体不同的三个面的面积分别为10平方分米,6平方分米,15平方分米,这个长方体的表面积是多少?11、做20个棱长为30厘米的小正方体纸箱,至少需要多少平方米硬纸?12、把一个长方体锯成18块,要锯几次呢?13.用72分米长的铁丝做一个正方体的框架,然后在外面贴上一层纸,至少需要多少平方分米的纸?14、一个正方体的外表积是384平方厘米,它的棱长是多少?15、一个长方体侧面积是360平方厘米,高是9厘米,长是宽的1.5倍,求它的外表积。
六年级立体图形的表面积、体积总复习题

六年级立体图形的表面积、体积总复习题班级______ 姓名__________ 得分__________复习内容:①立体图形的基本概念②立体图形的表面积、体积、容积一、填空1. 长方体有()个面,有()条棱,有()个顶点。
()分别叫做长方体的长、宽、高。
2. ()的长方体叫做正方体。
它的六个面都是()形,六个面的面积都(),它的12条棱都()。
3. 右图是()体的表面展开图,请你测量出有关数据(精确到整厘米数)。
这个形体的底面周长是()厘米。
这个形体的高是()厘米。
这个形体的侧面积是()平方厘米。
这个形体的体积是()立方厘米。
4. 填表:形体名称已知条件表面积体积长方体长3米,宽2米,高1.5米正方体棱长0.6分米底面半径10厘米,高5厘米圆柱体底面直径1.8分米,高12厘米底面周长0.942米,高20厘米圆锥体底面直径和高都是9分米5. 用铁丝焊接成一个长5分米,宽4分米,高3分米的长方体模型,至少需要铁丝();如果用纸糊它的表面,至少需要()纸板;这个长方体模型的体积是()。
6. 用3个棱长都是2厘米的正方体拼成一个长方体,拼成的这个长方体的表面积是()平方厘米,体积是()立方厘米。
7. 一个圆锥与和它等底等高的圆柱的体积相差12立方分米,圆锥的体积是()立方分米。
8. 把长、宽、高分别是6厘米、4厘米、5厘米的长方体削成一个最大的圆柱体,圆柱的体积是()立方厘米。
9. 把一根直径是20厘米,长是2米的圆柱形木材锯成同样的3段,表面积增加了()立方厘米。
10. 一个圆柱形的铁皮水桶,从里面量底面直径4分米,深5分米,做这个无盖水桶至少需要()铁皮;这个水桶最多可以装水()升。
11. 圆柱和圆锥的体积比是3﹕2,底面积的比是3﹕4,高的比是()。
12. 一个正方体的高增加3厘米,得到的新长方体的表面积比原来正方体的表面积增加了60平方厘米,原来正方体的体积是()立方厘米。
二、判断(对的请在括号内打“√”,错的打“×”。
(完整word)六年级奥数表面积和体积计算题

表面积与体积练习和答案专题简析:小学阶段所学的立体图形主要有四种长方体、正方体、圆柱体和圆锥体。
从平面图形到立体图形是认识上的一个飞跃,需要有更高水平的空间想象能力。
因此,要牢固掌握这些几何图形的特征和有关的计算方法,能将公式作适当的变形,养成“数、形”结合的好习惯,解题时要认真细致观察,合理大胆想象,正确灵活地计算。
在解答立体图形的表面积问题时,要注意以下几点:(1)充分利用正方体六个面的面积都相等,每个面都是正方形的特点。
(2)把一个立体图形切成两部分,新增加的表面积等于切面面积的两倍。
反之,把两个立体图形粘合到一起,减少的表面积等于粘合面积的两倍。
(3)若把几个长方体拼成一个表面积最大的长方体,应把它们最小的面拼合起来。
若把几个长方体拼成一个表面积最小的长方体,应把它们最大的面拼合起来。
例1.从一个棱长为10里面的正方体上挖去一个长10厘米、宽2厘米、高2厘米的小长方体,剩下部分的表面积是多少?【思路导航】这是一道开放题,方法有多种:1)沿一条棱挖,剩下部分的表面积为592平方厘米。
2)在某个面挖,剩下部分的表面积为632平方厘米。
3)挖通某两个对面,剩下部分的表面积为672平方厘米。
练习1.1.把一个长为12分米、宽为6分米、高为9分米的长方体木块锯成两个相同的小长方体木块,这两个小长方体的表面积之和比原来长方体的表面积增加了多少平方米?2.在一个棱长是4厘米的立方体上挖一个棱长是1厘米的小正方体后,表面机会发生怎样的变化?例2.把19个棱长为3厘米的正方体重叠起来,拼成一个立体图形,求这个立体图形的表面积。
【思路导航】要求这个复杂形体的表面积,必须从整体入手,从上、左、前三个方向观察,每个方向上的小正方体各面就组合成了如下图形。
练习2:1、用棱长是1厘米的立方体拼成图27-6所示的立体图形。
求这个立体图形的表面积。
2、一堆积木(如图27-7所示),是由16块棱长是2厘米的小正方体堆成的。
图形六年级面积表面积体积专题练习(可编辑修改word版)

测试卷一、填空题。
(每题2 分,共24 分)(1)一个圆柱和一个圆锥的底面积和高分别相等,圆锥的体积是圆柱体积的( ),圆柱的体积是圆锥体积的( ).(2)一个圆柱体和一个圆锥体的底面积和体积分别相等,已知圆柱体的高6 厘米,那么圆锥体的高是 ( )厘米。
(3)一个圆锥体的底面周长是12.56 分米,高是6 分米,它的体积是( )立方分米。
(4)一根长2 米的圆木,截成两同样大小的圆柱后,表面积增加48 平方厘米,这根圆木原来的体积是( )立方厘米。
(5)圆柱的底面半径是3 厘米,体积是6.28 立方厘米,这个圆柱的高是( )厘米。
(6)一个圆柱体高4 分米,体积是40 立方分米,比与它等底的圆锥体的体积多10 立方分米。
这个圆锥体的高是( )分米。
(7)一个圆锥的体积是7.2 立方米,与它等底等高的圆柱的体积是( )立方米.(8)一个圆锥的底面半径是3 厘米,体积是6.28 立方厘米,这个圆锥的高是( )厘米.(9)一个直圆柱底面半径是1 厘米,高是2.5 厘米。
它的侧面积是 ( )平方厘米。
(10)一个圆柱体高4 分米,体积是40 立方分米,比与它等底的圆锥体的体积多10 立方分米。
这个圆锥体的高是( )分米。
(11)一个圆锥体的底面周长是12.56 分米,高是6 分米,它的体积是( )立方分米。
(12)一根长2 米的圆木,截成两段后,表面积增加48 平方厘米,这根圆木原来的体积是( )立方厘米。
二、判断题。
(每题2 分,共10 分)1、圆锥的体积比与它等底等高的圆柱的体积小2 倍。
()2、一个长方体木箱的体积一定大于它的容积。
()13、底面积和高都相等的圆锥体体积是长方体体积的。
()34、一个圆锥的底面半径扩大2 倍,高也扩大2 倍,体积就扩大4 倍。
()5、一个圆柱和一个圆锥的底面半径相等,圆锥的高是圆柱高的3 倍,圆柱体积是15 立方厘米时,圆锥体积是15 立方厘米()6、有一个正方体的底面周长与一个圆柱体底面周长相等,它高也相等,那么它们的体积也必定相等。
立体图形练习题六年级

立体图形练习题六年级立体图形是数学中的一个重要概念,在小学六年级的数学学习中占有一席之地。
通过练习立体图形题目,可以帮助学生深入了解立体图形的性质和特点,从而提升其数学思维和解题能力。
本文将提供一些六年级学生常见的立体图形练习题,通过解答这些题目,帮助学生更好地掌握立体图形的知识。
1. 题目一:计算长方体的表面积和体积小明手里有一块长方体砖块,其边长分别为5厘米、8厘米和10厘米。
请帮助小明计算出这个长方体砖块的表面积和体积。
解析:长方体的表面积可通过公式2lw+2lh+2wh计算,其中l、w、h分别代表长方体的长度、宽度和高度。
带入具体数值,可以得到:表面积 = 2 × 5 × 8 + 2 × 5 × 10 + 2 × 8 × 10 = 176平方厘米长方体的体积可通过公式V = lwh计算。
带入具体数值,可以得到:体积 = 5 × 8 × 10 = 400立方厘米因此,这个长方体砖块的表面积为176平方厘米,体积为400立方厘米。
2. 题目二:判断正方体的性质小红手里有一块正方体磁铁,边长为6厘米。
请判断下列说法是否正确,并给出你的理由。
说法一:正方体的表面积等于6个正方形的面积之和。
说法二:正方体的对角线长度等于边长的平方根乘以立方根。
解析:对于说法一,正方体的表面积确实等于6个正方形的面积之和。
正方体有6个面,每个面都是正方形,所以表面积等于6个正方形的面积之和。
对于说法二,正方体的对角线长度并不等于边长的平方根乘以立方根。
正方体的对角线长度可通过勾股定理计算,即对角线长度d = √(边长的平方 + 边长的平方 + 边长的平方) = √3边长。
所以,正方体的对角线长度等于边长的平方根乘以√3,而不是立方根。
因此,说法一是正确的,而说法二是错误的。
3. 题目三:求解棱柱的面积和体积小华手里有一个棱柱,底面为一个边长为4厘米的正三角形,高度为6厘米。
六年级数学下册典型例题系列之期中专项练习:求不规则或组合立体图形的表面积与体积(原卷版)人教版
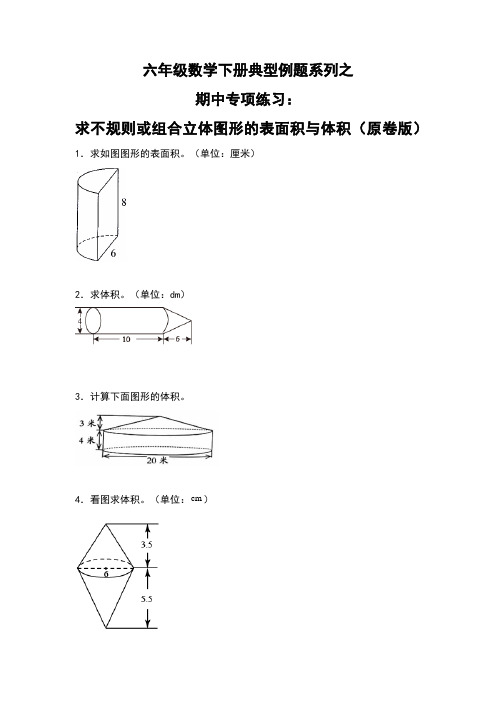
六年级数学下册典型例题系列之期中专项练习:求不规则或组合立体图形的表面积与体积(原卷版)1.求如图图形的表面积。
(单位:厘米)2.求体积。
(单位:dm)3.计算下面图形的体积。
4.看图求体积。
(单位:cm)5.计算下图的表面积与体积。
(单位:厘米)6.计算下面模具(由正方体与圆柱体组成)的表面积与体积。
(单位:厘米)7.下图中圆柱的底面周长是6.28厘米,高是3厘米,求阴影部分的体积。
8.求下面图形的体积。
9.求下面面图形的表面积。
10.如下图,求一个直角梯形以AB为轴旋转一周后形成的立体图形的体积。
(单位:厘米)11.计算下面物体的体积。
(单位:cm)12.求下面图形的表面积和体积。
(单位:cm)13.计算下图(按45°斜切)的体积(单位:厘米)。
14.计算下面图形的体积。
(半圆柱的底面直径是10cm)15.下图是一块长方形铁皮,利用图中的阴影部分,刚好能做成一个圆柱形油桶(接头忽略不计),求这个油桶的体积。
16.右图是一个底面半径为3厘米的圆柱木块被削去一半后的形状,请你计算出它的体积。
17.如图,一个圆柱体零件,高10厘米,底面直径6厘米,零件的一端有一个圆柱形的圆孔,圆孔的直径是4厘米,孔深5厘米。
(1)这个零件的体积是多少立方厘米?(2)如果将这个零件接触空气的部分涂上防锈漆,那么一共要涂多少平方厘米?18.下图ABCD是直角梯形,以AB为轴并将梯形绕这个轴旋转一周,得到一个旋转体,它的体积是多少立方厘米?(除不尽的保留两位小数)19.如图,卫生纸的高度是10cm,中间硬纸轴的直径是4 cm。
制作100个这样的硬纸轴,至少需要多少平方米的硬纸皮?学习与生活的苦,每一个人必须选择一个。
不管你选择了哪一个,都应该尽最大的努力做到最好,只有做到最好,人生才会在不留遗憾。
老一辈教育我们,书山有路勤为径,学海无涯苦作舟;吃得人中苦,方为人上人;吃亏是福,在学习的年龄不要贪图享乐;认认真真听课,勤勤恳恳学习,美好的未来可以值得可期。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
六年级数学《立体图形表面积和体积》专题练习
一、概念辨析:
要在一个长和宽都是30厘米,高是5分米长方体框架的外面糊上一层纸,就是求它的();要在纸盒的四周贴上标签,就是求();这个长方体的纸盒占有多大的空间,就是求()。
A侧面积 B 棱长总和C表面积D体积E 容积
二、求几个面:
①做一个圆柱形的油箱,底面半径3分米,高4分米。
至少需要铁皮多少平方分米?②做一个圆柱形的水桶,底面直径6分米,高4分米。
至少需要铁皮多少平方分米?
③做一节圆柱形的通风管,底面周长分米,长4分米。
至少需要铁皮多少平方分米?(压路机、猪圈、柱子、游泳池、教室墙壁)
切割:
把一个长8厘米、宽4厘米、高6厘米的长方体木块,切削成一个最大的圆柱,圆柱的体积是()立方厘米。
把一个棱长是4分米的立方体钢坯切削成一个最大的圆柱,这个圆柱的体积是( )立方分米。
粘合:
把两个棱长是5厘米的正方体木块粘合成一个长方体,这个长方体的表面积是多少平方厘米?
三、空间思维:
1、把一个圆柱体侧面展开得到一个正方形,已知圆柱体底面周长是10厘米,求圆柱体的侧面积。
2、一个底面直径是27厘米,高9厘米的圆锥体木块,分成形状大小完全相同的两个木块后,表面积比原来增加多少平方厘米?
3、一根长2米的圆木,截成两段后,表面积增加48平方厘米,这根圆木原来的体积是( )立方厘米。
四、锥柱关系1:
1、一个圆柱与一个圆锥等底等高,它们的体积之和是36立方分米,圆锥的体积是( )立方分米。
①12 ②9 ③27 ④24
2、一个圆锥的体积是n立方厘米,和它等底等高的圆柱体的体积是()立方厘米。
①n ②2n ③3n ④
3、把一段圆钢切削成一个最大的圆锥体,切削掉的部分部分重8千克,这段圆钢重()千克。
①24 ②16 ③12 ④8
4、一个圆柱体积比一个与它等底等高的圆锥体的体积大()。
①②1 ③2倍④3倍
5、等底等高的圆柱和圆锥的体积相差16立方米,这个圆柱的体积是()立方米,圆锥的体积是()立方米.
小学六年级全科目课件教案习题汇总语文数学英语
锥柱关系2:
一个圆柱和一个圆锥的底面直径相等,圆锥的高是圆柱的3倍,圆锥的体积是12立方分米,圆柱的体积是()立方分米。
一个圆柱体和一个圆锥体的底面积和体积分别相等,已知圆柱体的高6厘米,那么圆锥体的高是( )厘米。
一个圆锥的底面直径是圆柱底面直径的1/3,如果它们的高相等,那么圆锥体积是圆柱体的( )。
五、等积变换:
一个棱长是4分米正方体容器装满水后,倒入一个底面积是12平方分米的圆锥体容器里正好装满,这个圆锥体的高是多少分米?
一个圆锥形的沙堆,底面积是平方米,高是米,用这堆沙在10米宽的公路上铺2厘米厚的路面,能铺多少米?(用进一法取近似值,得数保留整平方米) 六、条件限制:
有一辆车厢为长方体形状的货车(车厢顶盖封死),长米,宽3米,高米,要装载若干个正方体形状的纸箱,这个正方体的棱长是米。
这辆货车车厢最多可以装多少个纸箱?。
