《二元一次方程组的应用》案例分析
二元一次方程组应用教学案例

二元一次方程组应用教学案例第一篇:二元一次方程组应用教学案例重视知识的形成过程,突出学生的探索精神——消元(2)二元一次方程组的应用教学案例李华本节课来自于人教版七年级数学(下册)书,是学生在学会用代入消元法解二元一次方程组的基础上,探究如何用二元一次方程组解决实际问题。
情景师:解二元一次方程组的基本思路是什么生:消元:二元一元师:请回顾一下代入消元法解二元一次方程组的步骤。
⎧2x+y=0 ⎨⎩4x+3y=4生:变形、代入、消元、解方程、回代、结论师:听民间故事,解数学问题《康熙微服私访记》请一名同学起来朗读,给予适当的评价。
引例:康熙巧算牛马价格康熙皇帝有一年微服私访,在集市上看见两个公差在欺负一个伙计,伙计求两公差:“这位大爷,按我们讲好的价钱,您买1匹马、1头牛,是10两银子;那位大爷,您买2匹马,4头牛,是28两银子。
可是一共只给了我们30两,我们可亏不起这么多啊!”这时,身穿便服的康熙走到公差的面前说:“买卖公平,这是天经地义的事,该多少就多少,怎么能仗势欺人?”甲公差见此人教训他们,大怒:“你知道一匹马,一头牛是什么价?”康熙冷笑道:“马每匹6两,牛每头4两!” 这时,随从亮出康熙的身份,两公差连忙跪下求饶。
同学们,康熙算对了吗?你们能算出一匹马和一头牛的价格吗?师:在这个故事里,我们可以提炼出什么数学信息呢?生:1匹马、1头牛,是10两银子;买2匹马,4头牛,是28两银子。
师:那么我们能用什么样的办法验证出康熙是否算对了呢?四人一小组讨论完成。
讨论结果展示:生1:可以把康熙皇帝计算的回代到问题里验证一下。
师:肯定学生的做法,表扬学生积极思考。
生2:可以用一元一次方程来解,设元,列出方程。
师:黑板板书,请其他同学给予评价。
师:还有其他方法吗?生3:可以用二元一次方程组来解,设两个未知数,列出方程组。
师:黑板板书,要求学生来求解方程组,复习解方程组。
师:对,同学们想到了可以用方程来解决实际问题。
湘教版数学七年级下册_《二元一次方程组的应用》赏析

《二元一次方程组的应用》赏析【知识链接】列二元一次方程组解应用题的一般步骤可概括为“审、找、列、解、答”五步,即:(1)审:通过审题,把实际问题抽象成数学问题,分析已知数和未知数,并用字母表示其中的两个未知数;(2)找:找出能够表示题意两个相等关系;(3)列:根据这两个相等关系列出必需的代数式,从而列出方程组;(4)解:解这个方程组,求出两个未知数的值;(5)答:在对求出的方程的解做出是否合理判断的基础上,写出答案.【典题精析】例1 某停车场的收费标准如下:中型汽车的停车费为6元/辆,小型汽车的停车费为4元/辆.现在停车场有50辆中、小型汽车,这些车共缴纳停车费230元,问中、小型汽车各有多少辆?解析:设中型汽车有x 辆,小型汽车有y 辆.由题意,得解得, 故中型汽车有15辆,小型汽车有35辆.例2 某蔬菜公司收购蔬菜进行销售的获利情况如下表所示: 销售方式直接销售 粗加工后销售 精加工后销售 每吨获利(元) 100 250 450现在该公司收购了140吨蔬菜,已知该公司每天能精加工蔬菜6吨或粗加工蔬菜16吨(两种加工不能同时进行).(1)如果要求在18天内全部销售完这140吨蔬菜,请完成下列表格: 销售方式 全部直接销售全部粗加工后销售 尽量精加工,剩余部分直接销售 获利(元)(2)如果先进行精加工,然后进行粗加工,要求在15天内刚好加工完140吨蔬菜,则应如何分配加工时间?解:(1)全部直接销售获利为:100×140=14000(元);⎩⎨⎧=+=+.23046,50y x y x ⎩⎨⎧==.35,15y x全部粗加工后销售获利为:250×140=35000(元);尽量精加工,剩余部分直接销售获利为:450×(6×18)+100×(140-6×18)=51800(元).(2)设应安排x 天进行精加工, y 天进行粗加工.由题意,得解得, 故应安排10天进行精加工,5天进行粗加工.【跟踪练习】为满足市民对优质教育的需求,某中学决定改变办学条件,计划拆除一部分旧校舍,建造新校舍,拆除旧校舍每平方米需80元,建新校舍每平方米需700元. 计划在年内拆除旧校舍与建造新校舍共7200平方米,在实施中为扩大绿地面积,新建校舍只完成了计划的80%,而拆除旧校舍则超过了计划的10%,结果恰好完成了原计划的拆、建总面积.(1)求:原计划拆、建面积各是多少平方米?(2)若绿化1平方米需200元,那么在实际完成的拆、建工程中节余的资金用来绿化大约是多少平方米?答案:(1)原计划拆、建面积各是4800平方米、2400平方米;(2)可绿化面积为1488平方米.⎩⎨⎧=+=+.140166,15y x y x ⎩⎨⎧==.5,10y x。
题型专题训练:7_2 二元一次方程组的应用——销售、利润问题

7.2 二元一次方程组的应用——销售、利润问题【题型销售、利润问题】【例】2018年某歌手地表最强巡回演唱会于11月17日在贵阳奥林匹克体育中心举行,小颖购买了一张票价为四位数的场地票(动感地带专属),而小明一张购买了票价为三位数的看台票(动感地带专属).小颖说,“在你的票价前面多写个1,都还比我的便宜200元”;小明说,“只需在我的票价后多写个0,就比你的贵3120元”.请问小颖和小明购买的演唱会门票各是多少元?【变式1】(2022·江西吉安·八年级期末)2018年10月,吉州区井冈蜜柚节迎来了四方游客,游客李先生选购了井冈蜜柚和井冈板栗各一箱需要200元.他还准备给4位朋友每人送同样的井冈蜜柚一箱,6位同事每人送同样的井冈板栗一箱,就还需要1040元.(1)求每箱井冈蜜柚和每箱井冈板栗各需要多少元?(2)李先生到收银台才得知井冈蜜柚节期间,井冈蜜柚可以享受6折优惠,井冈板栗可以享受8折优惠,此时李先生比预计的付款少付了多少元?【变式2】(2022·江苏南通·七年级期末)小瑞去花店购买鲜花,若买5支玫瑰和3支百合,则她所带的钱还剩下10元;若买3支玫瑰和5支百合,则她所带的钱还缺4元.(1)若小瑞所带的钱是51元,请分别求出玫瑰和百合单价是多少元?(2)若小瑞所带的钱是m元,且一共只买8支玫瑰,请直接写出小瑞所带的钱还剩下多少元?【变式3】(2022·广西南宁·七年级期中)为响应国家“足球进收园”的号召,满足学校对足求的需求.某商家第一次购进了38个A类足球和20个B类足球进行销售,共花费了5580元,已知商家购进一个B类足球的价格是购进一个A类足球价格的1.2倍.(1)求商家购进一个A类足球和一个B类足球各需多少元?(2)若一个A类足球的售价为110元.两类足球销售完毕,商家要获得1880元的利铜,则B 类足球的总售价为多少元?(3)为了回馈客户,商家决定进行打折销售,若商家第二次又以原进价购进A、B两类足球,购进A类足球的件数不变,而购进B类足球的件数是第一次的2倍,A类足球按原售价销售,而B类足球打折销售,若第二次两类足球全部销售完毕,要使得第二次销售获得利润1688元,则B类足球是打几折销售的?(解析版)【题型 销售、利润问题】【例】2018年某歌手地表最强巡回演唱会于11月17日在贵阳奥林匹克体育中心举行,小颖购买了一张票价为四位数的场地票(动感地带专属),而小明一张购买了票价为三位数的看台票(动感地带专属).小颖说,“在你的票价前面多写个1,都还比我的便宜200元”;小明说,“只需在我的票价后多写个0,就比你的贵3120元”.请问小颖和小明购买的演唱会门票各是多少元? 【答案】1680元,480元.【分析】设小颖的票价为x 元,小明的票价为y 元,根据“小颖说,“在你的票价前面多写个1,都还比我的便宜200元”;小明说,“只需在我的票价后多写个0,就比你的贵3120元”.”找到等量关系,列出方程组,解方程组即可.【详解】设小颖的票价为x 元,小明的票价为y 元,根据题意得:{x −(1000+y )=20010y −x =3120解得:{x =1680y =480答:小颖和小明购买的演唱会门票分别为:1680元,480元.【点睛】本题考查二元一次方程组的应用,正确的找到等量关系是解答关键.【变式1】(2022·江西吉安·八年级期末)2018年10月,吉州区井冈蜜柚节迎来了四方游客,游客李先生选购了井冈蜜柚和井冈板栗各一箱需要200元.他还准备给4位朋友每人送同样的井冈蜜柚一箱,6位同事每人送同样的井冈板栗一箱,就还需要1040元.(1)求每箱井冈蜜柚和每箱井冈板栗各需要多少元?(2)李先生到收银台才得知井冈蜜柚节期间,井冈蜜柚可以享受6折优惠,井冈板栗可以享受8折优惠,此时李先生比预计的付款少付了多少元?【答案】(1)每箱井冈蜜柚需要80元,每箱井冈板栗需要120元;(2)李先生比预计的付款少付了328元【分析】(1)、根据“井冈蜜柚和井冈板栗各一箱需要200元,4箱井冈蜜柚和6箱井冈板栗需要1040元”列二元一次方程组,解之即可得.(2)根据节省的钱数=原价×数量﹣打折后的价格×数量,即可求出结论.【详解】解:(1)设每箱井冈蜜柚需要x 元,每箱井冈板栗需要y 元,依题意,得:{x +y =2004x +6y =1040, 解得:{x =80y =120. 答:每箱井冈蜜柚需要80元,每箱井冈板栗需要120元.(2)200+1040﹣80×0.6×(4+1)﹣120×0.8×(6+1)=328(元).答:李先生比预计的付款少付了328元.【点睛】本题考查了二元一次方程组的应用,找准等量关系,正确列出二元一次方程组是解题的关键.【变式2】(2022·江苏南通·七年级期末)小瑞去花店购买鲜花,若买5支玫瑰和3支百合,则她所带的钱还剩下10元;若买3支玫瑰和5支百合,则她所带的钱还缺4元.(1)若小瑞所带的钱是51元,请分别求出玫瑰和百合单价是多少元?(2)若小瑞所带的钱是m 元,且一共只买8支玫瑰,请直接写出小瑞所带的钱还剩下多少元? 【答案】(1)玫瑰和百合单价分别是每支2.5元和每支9.5元(2)小瑞所带的钱还剩下31元【分析】(1)设每支玫瑰x 元,每支百合y 元,利用总价=单价×数量,结合小瑞带的钱数不变,即可得出关于x ,y 的二元一次方程,化简后可得出;(2)设玫瑰的单价是每支x 元,百合单价是每支y 元,因为小瑞带的钱为m 元,所以列方程{5x +3y =m −10①5x +5y =m +4②,用含m 的代数式解出x 和y ,又因为且一共只买8支玫瑰,所以剩下的钱为:m -8x 即可求解;(1)解:设玫瑰的单价是每支x 元,百合单价是每支y 元.由题意可得{5x +3y =51−10,3x +5y =51+4.解之得{x =2.5,y =9.5.答:玫瑰和百合单价分别是每支2.5元和每支9.5元.(2)解:设玫瑰的单价是每支x 元,百合单价是每支y 元,因为小瑞带的钱为m 元【变式3】(2022·广西南宁·七年级期中)为响应国家“足球进收园”的号召,满足学校对足求的需求.某商家第一次购进了38个A类足球和20个B类足球进行销售,共花费了5580元,已知商家购进一个B类足球的价格是购进一个A类足球价格的1.2倍.(1)求商家购进一个A类足球和一个B类足球各需多少元?(2)若一个A类足球的售价为110元.两类足球销售完毕,商家要获得1880元的利铜,则B 类足球的总售价为多少元?(3)为了回馈客户,商家决定进行打折销售,若商家第二次又以原进价购进A、B两类足球,购进A类足球的件数不变,而购进B类足球的件数是第一次的2倍,A类足球按原售价销售,而B类足球打折销售,若第二次两类足球全部销售完毕,要使得第二次销售获得利润1688元,则B类足球是打几折销售的?【答案】(1)一个A类足球需90元,一个B类足球需108元(2)3280(3)八折【分析】(1)设商家购进一个A类足球需x元,购进一个B类足球需y元,由题意:某商家第一次进了38个A类足球和20个B类足球进行出售,共花费了5580元,已知商家购进一个B类足球的价格是购进一个A类足球价格的1.2倍.列出二元一次方程组,解方程组即可;(2)设B类足球的售价为m元,由题意:一个A类足球的售价为110元,两类足球销售完毕,商家要获得1880元的利润,列出一元一次方程,解方程即可;(3)B类足球是打n折销售的,由题意:购进A类足球的件数不变,而购进B类足球的件数是第一次的2倍,A 类足球按原售价销售,使得第二次销售获得利润1688元,列出一元一次方程,解方程即可.(1)解:设商家购进一个A 类足球需x 元,购进一个B 类足球需y 元,由题意得:{38x +20y =5580y =1.2x, 解得:{x =90y =108, 答:商家购进一个A 类足球需90元,购进一个B 类足球需108元;(2)解∶ 设B 类足球的售价为m 元,由题意得:(110-90)×38+(m -108)×20=1880,解得:m =164,则20×164=3280,答:B 类足球的总售价为3280元;(3)解∶设B 类足球是打n 折销售的,由题意得:(110-90)×38+(164×0.1n -108)×20×2=1688,解得:n =8,答:B 类足球是打八折销售的.【点睛】本题考查了二元一次方程组的应用以及一元一次方程的应用,找准等量关系,正确列出二元一次方程组和一元一次方程是解题的关键.。
二元一次方程组的应用实例及解题技巧

二元一次方程组的应用实例及解题技巧二元一次方程组是数学中常见的一种类型,在日常生活以及工作中也有广泛的应用,比如在车辆的行驶距离、快递员派送的路程、工程施工的时间安排等方面都可以用到二元一次方程组来进行解题。
一、车辆的行驶距离假设小明从A点出发,驾驶汽车前往B点,全程共行驶500公里,其中某段路程小明驾驶时速为70公里/小时,另一段路程行驶时速为80公里/小时。
请问两段路程分别是多长?设小明行驶时速为x公里/小时,则另外一段路程时速为y公里/小时,那么根据题意我们可以列出如下二元一次方程组:x + y = 500(两段路程总和为500公里)0.7x + 0.8y = 450(两段路程共耗时450小时)通过解方程可以得到:x = 200,y = 300因此答案是小明在时速70公里/小时的路程上行驶了200公里,在时速80公里/小时的路程上行驶了300公里。
二、快递员派送的路程假设某快递公司的快递员根据客户的需求,需要前往以下几个地址派送快递:地址A(距离公司5公里)、地址B(距离公司8公里)以及地址C(距离公司15公里)。
公司规定,在前往每个地址的路上,快递员的平均速度为20公里/小时,但是在派送快递时,他的平均速度要降低到15公里/小时。
请问快递员从公司出发到回到公司所需的时间是多少?设快递员从公司出发到地址A、B、C分别需要的时间分别为t1、t2、t3,则根据题意我们可以列出如下二元一次方程组:t1 + t2 + t3 = 2/3(快递员的平均速度为20公里/小时,在前往每个地址的路上所需的时间占总时间的2/3)5t1 + 8t2 + 15t3 = 1(快递员前往每个地址的路程之和为1)通过解方程可以得到:t1 = 0.0588,t2 = 0.3824,t3 = 0.1765因此快递员从公司出发到回到公司所需的时间为:t1 + t2 + t3 + (5 + 8 + 15) / 15 = 1.8235小时三、工程施工的时间安排假设某建筑工程需要从A点开工,分三个工段进行施工,最后在B点结束,其中每个工段的施工时间不同。
二元一次方程组的应用的教学案例分析
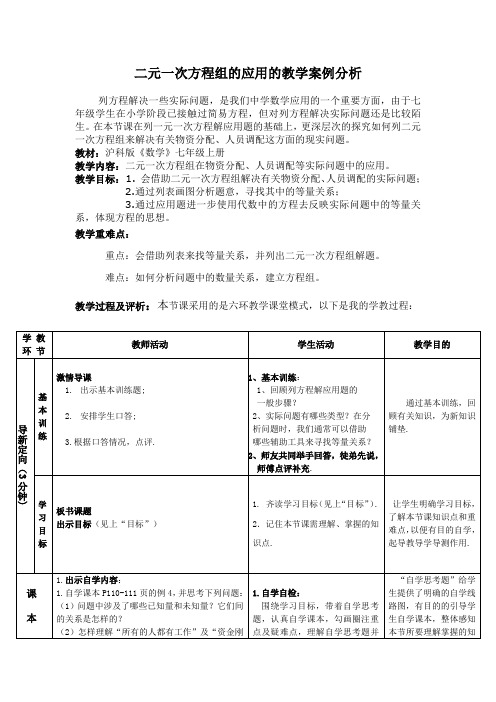
二元一次方程组的应用的教学案例分析列方程解决一些实际问题,是我们中学数学应用的一个重要方面,由于七年级学生在小学阶段已接触过简易方程,但对列方程解决实际问题还是比较陌生。
在本节课在列一元一次方程解应用题的基础上,更深层次的探究如何列二元一次方程组来解决有关物资分配、人员调配这方面的现实问题。
教材:沪科版《数学》七年级上册教学内容:二元一次方程组在物资分配、人员调配等实际问题中的应用。
教学目标:1. 会借助二元一次方程组解决有关物资分配、人员调配的实际问题;2.通过列表画图分析题意,寻找其中的等量关系;3.通过应用题进一步使用代数中的方程去反映实际问题中的等量关系,体现方程的思想。
教学重难点:重点:会借助列表来找等量关系,并列出二元一次方程组解题。
难点:如何分析问题中的数量关系,建立方程组。
教学过程及评析:本节课采用的是六环教学课堂模式,以下是我的学教过程:分钟由于这节是公开课,教学时有点紧张,有些需要重点提的知识点结果给忽略了。
在自学课本环节,由于学生本身对列方程就不是很熟练,总是喜欢直接列式计算,缺乏方程思想,所以自学课本就有点吃力。
通过借助列表格分析题意,将问题的已知量和未知量填入相应的空格中,再根据基本的数量关系列出两个方程联立,形成方程组。
上课时我应该让学生自己列表填空,而不是提前把表格列好让学生填,应该从一开始就让学生自己去思考问题,找到题目中的已知量和未知量,会设未知数,会找题目中的等量关系,然后列出方程组。
解方程组是前面一节的重点内容,所以在这里就没做要求。
在议谈交流环节,学生讨论的也不够激烈,可能题目有点难度,刚接触方程应用题,对分配、调配这类问题不熟悉,所以交流时也比较吃力。
在展示评讲中,应该把课堂交给学生自己,选较多的同学上台演示自己的做题思考过程,还有就是对学生的积极回答予以一定的肯定和激励,小组加分应该要到位。
还有就是我把分配问题作为这节课的子课题不是很好,对应用题进行分门别类的教学,可能会禁固学生的思维,极易使思维稍微迟钝的同学一见到应用题就去分类,一旦遇到综合性问题题,分不出类,就思维受阻,无法对具体问题进行具体分析。
二元一次方程组应用举例
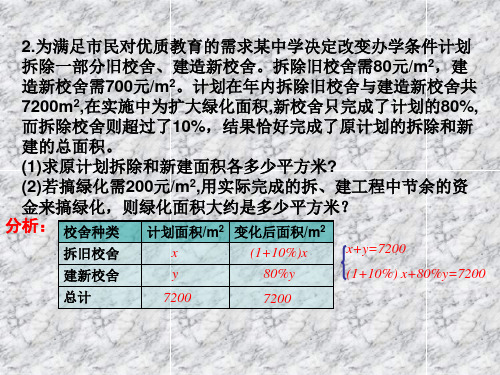
(1)求原计划拆除和新建面积各多少平方米?
(2)若搞绿化需200元/m2,用实际完成的拆、建工程中节余的资
金来搞绿化,则绿化面积大约是多少平方米?
分析: 校舍种类 计划面积/m2 变化后面积/m2
拆旧校舍
x
(1+10%)x
x+y=7200
建新校舍
y
80%y
(1+10%) xƮ
节余资金:(80x+700y)-[ 80×(1+10%)x+ 700×80%y]=(140y-8x)元
3.小明的爸爸骑摩托车带着小明在公路上匀速行驶,小明第 一次注意到路边里程碑上的数时,发现它是一个两位数且它 的两个数字之和为9,刚好过1h,他发现路边里程碑上的数 恰好是第一次看到的个位上的数字和十位上的数字颠倒后得 到的,又过3h,他发现里程碑上的数字比第一次看到的两位 数中间多个0,你知道爸爸骑的摩托车的速度是多少吗?
(1)求原计划拆除和新建面积各多少平方米? (2)若搞绿化需200元/m2,用实际完成的拆、建工程中节余的资 金来搞绿化,则绿化面积大约是多少平方米? 分析: 校舍种类 计划资金/元 变化后资金/元
拆旧校舍
80x
80×(1+10%)x
建新校舍
700y
700×80%y
总计
80x+700y 80×(1+10%)x+ 700×80%y
7200
2.为满足市民对优质教育的需求某中学决定改变办学条件计划 拆除一部分旧校舍、建造新校舍。拆除旧校舍需80元/m2,建 造新校舍需700元/m2。计划在年内拆除旧校舍与建造新校舍共 7200m2,在实施中为扩大绿化面积,新校舍只完成了计划的80%, 而拆除校舍则超过了10%,结果恰好完成了原计划的拆除和新 建的总面积。
《二元一次方程组》案例分析

《二元一次方程组》案例分析情景实录:片段一:创设情境教师:观察右图,你知道笼子里的鸡和兔各有多少只?(学生摇摇头)那么,老师给你们一些提示.(多媒体展示问题)今有鸡兔同笼,上有三十五头,下有九十四足,问鸡兔各几何?教师:请语文课代表把这一题的意思翻译一下.学生:有一群鸡和兔关在同一个笼子里,从上面数鸡头和兔头共35个,从下面看鸡脚和兔脚共94只,问鸡和兔各是多少?教师:根据实际问题列方程的关键是找相等关系,你能找到相等关系吗? 学生(异口同声):能.学生:鸡的只数+兔的只数=35.教师:还有吗?学生(异口同声):鸡的只数×2+兔的只数×4=94.教师:有几个未知数,如何设未知数?学生1:有两个未知数,分别是鸡的只数和兔的只数.可以设鸡x 只、兔y 只.教师:根据题意,可以得到什么方程?可以将相等关系中的未知量,换成x 、y.学生2:x+y=35;2x+4y=94.评析:回顾两个二元一次方程的列出过程,学生按照教师设计好的程序,先找相等关系,再设未知数,最后列方程.整个过程没有停顿,十分流畅,列方程的目的顺利达成,为下一环节引出课题做好准备.反思这个过程,学生被教师“牵”着,完成了列方程的任务,不知学生的收获有多少?是否获取了解决问题的经验?片段二:引出课题,生成概念教师(板书这两个方程):x 、y 表示什么意义?学生(异口同声):x 表示鸡的只数,y 表示兔的只数.教师:鸡的只数x 和兔的只数y 必须同时满足这两个方程,把这两个方程合起来,可以得到方程组.(用大括号把两个方程括起来)像这样,含有两个未知数的两个一次方程组成的方程组叫做二元一次方程组.(板书课题:二元一次方程组并用多媒体展示二元一次方程组的定义.)议一议:1、填空:含有 的 组成的方程组叫做二元一次方程组.2、根据定义,判断下列方程组是不是二元一次方程组.(1) (2) (3) (4) {1n -2m 32m n ==+{62y -x 3z y ==+{1x 52y x ==+{3n m 5n m 2=+=+学生3:含有两个未知数的两个一次方程组成的方程组叫做二元一次方程组.教师:第2题中第一个方程组是二元一次方程组吗?学生(异口同声):是.教师:第二个方程组是二元一次方程组吗?学生(异口同声):不是.教师:二元一次方程组是指含两个未知数且由两个一次方程组成的方程组.第二个方程组中未知数有两个x 、y ,且都是一次方程,所以是二元一次方程组.第三个方程组是二元一次方程组吗?学生(异口同声):不是.教师:第四个方程组是二元一次方程组吗?学生(异口同声):不是.评析:获取概念的主要方式是概念的形成和概念的同化.概念的形成需要对大量的例子进行归纳和概括,得出一类事物的共同本质属性,这是一个发现学习的过程.概念的同化是学生利用原有的知识来理解新概念,是一个接受学习的过程.本节课从具体情境出发,仅仅得到一个二元一次方程组,如果用探究的方式,引导学生归纳二元一次方程组的本质属性,进而得出二元一次方程组的概念,不仅不能帮助学生理解二元一次方程组的概念,反而会冲淡主题,重点不突出.(有一位教师要求学生观察{359442=+=+y x y x ,归纳二元一次方程组的特征.结果学生的回答不得要领,对议一议中的第2题中的第二个方程组作出了错误的判断.)直接抛出这个描述性的定义,同时进行变式训练,帮助学生初步形成二元一次方程组的概念.片段三:例题赏析【例题】 足球的表面由32块黑色的五边形和白色六边形皮块围成,黑、白皮块数的比为3︰5.设黑色的皮块数为x ,白色的皮块数为y. 列出关于x 、y 的二元一次方程组.教师:利用方程解决实际问题,关键在于找相等关系.你能从哪一句话中找到相等关系?学生4:第一句.教师:用等号写成……学生(异口同声):白色的皮块数+黑色的皮块数=32.教师:还有一个呢?学生4:第二句.教师:用等号写成……学生4:……教师:“黑色的皮块数与白色的皮块数的比是3︰5”可以写成 :黑色的皮块数︰白色的皮块数=3︰5 .根据比例的性质“内项之积等于外项之积”可得……学生(异口同声):黑色的皮块数×5=白色的皮块数×3.教师:根据题意,可得……学生(异口同声): . {3253=+=x y yx(教师板书解题过程)评析:教师及时发现学生的不足,帮助学生将比例式转化为等积式,让每个学生都有解决问题的必需的知识.片段四:练习反馈试一试:根据实际问题的意义列出方程组.(1)红圆珠笔每支0.7元,蓝圆珠笔每支1.2元,两种圆珠笔共买了15支,共花了19元,两种圆珠笔各买多少支?(2)在一场篮球比赛中,不计罚球得分,小林共得28分,已知他投中的两分球比三分球多4个,他投中两分球,三分球各多少个?(学生积极练习,教师巡视辅导)评析:问题的难度与例题相当,学生大约用了十分钟左右完成练习.据课后统计发现,全班只有几个学生出现错误.根据实际问题的意义建立方程组模型既是初中数学教学的重点,也是难点,很多学生害怕做这一类问题.从以上四个片段来看,这位教师成功地消除了学生恐惧心理,学生参与学习的积极性较高,教学目标基本达成.究其原因有以下几点:一、本节课设置的情境在学生的身边随时可见,鸡、兔、笔、足球等学生都很熟悉。
《二元一次方程组的应用》案例分析

《二元一次方程组的应用》案例分析答:案例:《二元一次方程组的应用》各环节配题分析分析:1、本课的配题注重从学生亲身经历的活动、学生熟悉的事入手选题,有开放型题、变式题,有数学思想的渗透,从易到难,由浅入深,应该说配题的设置具有一定的挑战性,能够起到激活学生思维的作用。
2、本课的教学容量太大且选题具有一定的难度,对于基础好的学生也很难能够在有限的时间内从容地、完整地完成所有的学习任务;对于基础差的学生来说,由于太多的题不会做,课堂的时间等于空耗。
3、由于时间紧,不能给学生留有充分的思考空间和时间,学生对于习题所传达的知识、方法很难理解透彻。
所以常常出现习题做了很多,但是在遇见题还是有困难,习题的功能没有发挥。
修改:可以结合学生的实际情况,分层次配题。
学生探究的习题,充分发挥习题的功能,使学生在主动学习、探究学习的过程中获得知识,培养能力。
对于“实际问题与二元一次方程组”,不等同于一般例题内容的教学,而是应该以探究学习的方式完成。
从教材设置的“数学活动”及“拓广探索”栏目下的习题等都设置了带有探究性的问题。
对于这些内容的教学,应注意鼓励学生积极探究,当学生在探究过程中遇到困难时,教师应启发诱导,设计必要的铺垫,适时地追问,让学生在经过自己的努力来克服困难的过程中体验如何探究,而不要替代他们思考,不要过早给出答案,应鼓励探究多种不同的分析问题和解决问题的方法,使探究过程活跃起来,在这样的氛围中可以更好地激发学生积极思维,得到更大收获。
所以教学中不能盲目地扩大习题量,而是要充分发挥习题的功能,给学生留有充分的思考时间与空间,引导学生更多的参与数学活动和相互交流,在主动学习、探究学习的过程中获得知识,培养能力,使每一位学生都能获得良好的数学教育,不同的人在数学上得到不同的发展。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
答:
案例:《二元一次方程组的应用》各环节配题分析
分析:
1、本课的配题注重从学生亲身经历的活动、学生熟悉的事入手选题,有开放型题、变式题,有数学思想的渗透,从易到难,由浅入深,应该说配题的设置具有一定的挑战性,能够起到激活学生思维的作用。
2、本课的教学容量太大且选题具有一定的难度,对于基础好的学生也很难能够在有限的时间内从容地、完整地完成所有的学习任务;对于基础差的学生来说,由于太多的题不会做,课堂的时间等于空耗。
3、由于时间紧,不能给学生留有充分的思考空间和时间,学生对于习题所传达的知识、方法很难理解透彻。
所以常常出现习题做了很多,但是在遇见题还是有困难,习题的功能没有发挥。
修改:
可以结合学生的实际情况,分层次配题。
学生探究的习题,充分发挥习题的功能,使学生在主动学习、探究学习的过程中获得知识,培养能力。
对于“实际问题与二元一次方程组”,不等同于一般例题内容的教学,而是应该以探究学习的方式完成。
从教材设置的“数学活动”及“拓广探索”栏目下的习题等都设置了带有探究性的问题。
对于这些内容的教学,应注意鼓励学生积极探究,当学生在探究过程中遇到困难时,教师应启发诱导,设计必要的铺垫,适时地追问,让学生在经过自己的努力来克服困难的过程中体验如何探究,而不要替代他们思考,不要过早给出答案,应鼓励探究多种不同的分析问题和解决问题的方法,使探究过程活跃起来,在这样的氛围中可以更好地激发学生积极思维,得到更大收获。
所以教学中不能盲目地扩大习题量,而是要充分发挥习题的功能,给学生留有充分的思考时间与空间,引导学生更多的参与数学活动和相互交流,在主动学习、探究学习的过程中获得知识,培养能力,使每一位学生都能获得良好的数学教育,不同的人在数学上得到不同的发展。
