2019年高考数学二轮复习试题:专题六 第4讲 用数学归纳法证明数列问题附解析
2019年高考数学二轮复习专题四数列4.2.2数列中的证明及存在性问题课件文

-3-
解 (1)由条件可得 an+1=2(���������+��� 1)an.
将 n=1 代入得,a2=4a1,而 a1=1,所以 a2=4.
将 n=2 代入得,a3=3a2,所以 a3=12.
从而 b1=1,b2=2,b3=4.
(2){bn}是首项为 1,公比为 2 的等比数列.
由条件可得������������+1
(1)求数列{an}的通项公式; (2)证明:������21-������1 + ������31-������2+…+������������+11-������������<1.
(1)解 设等差数列{log2(an-1)}的公差为d.
由a1=3,a3=9,得log22+2d=log28,即d=1.
∴log2(an-1)=1+(n-1)×1=n,即an=2n+1.
(2)证明
∵1
������������+1-������������
=
1 2������+1-2������
=
21������,
∴1
������2-������1
+
������31-������2+…+������������+11-������������
4.2.2 数列中的证明及存
在性问题
-2-
等差(比)数列的判断与证明
设例bn=1(���2���������������0.18全国Ⅰ,文17)已知数列{an}满足a1=1,nan+1=2(n+1)an.
(1)求b1,b2,b3; (2)判断数列{bn}是否为等比数列,并说明理由; (3)求{an}的通项公式.
2019年高考数学二轮复习试题:专题六 第4讲 用数学归纳法证明数列问题(带解析)
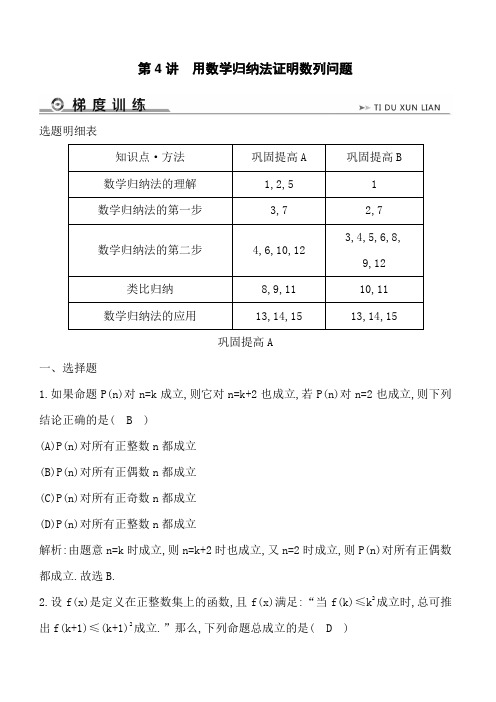
第4讲用数学归纳法证明数列问题选题明细表知识点·方法巩固提高A 巩固提高B数学归纳法的理解1,2,5 1数学归纳法的第一步3,7 2,73,4,5,6,8, 数学归纳法的第二步4,6,10,129,12类比归纳8,9,11 10,11数学归纳法的应用13,14,15 13,14,15巩固提高A一、选择题1.如果命题P(n)对n=k成立,则它对n=k+2也成立,若P(n)对n=2也成立,则下列结论正确的是( B )(A)P(n)对所有正整数n都成立(B)P(n)对所有正偶数n都成立(C)P(n)对所有正奇数n都成立(D)P(n)对所有正整数n都成立解析:由题意n=k时成立,则n=k+2时也成立,又n=2时成立,则P(n)对所有正偶数都成立.故选B.2.设f(x)是定义在正整数集上的函数,且f(x)满足:“当f(k)≤k2成立时,总可推出f(k+1)≤(k+1)2成立.”那么,下列命题总成立的是( D )(A)若f(2)≤4成立,则当k≥1时,均有f(k)≤k2成立(B)若f(4)≤16成立,则当k≤4时,均有f(k)≤k2成立(C)若f(6)>36成立,则当k≥7时,均有f(k)>k2成立(D)若f(7)=50成立,则当k≤7时,均有f(k)>k2成立解析:若f(2)≤4成立,依题意则应有当k≥2时,均有f(k)≤k2成立,故A不成立; 若f(4)≤16成立,依题意则应有当k≥4时,均有f(k)≤k2成立,故B不成立;因命题“当f(k)≤k2成立时,总可推出f(k+1)≤(k+1)2成立”⇔“当f(k+1)>(k+1)2成立时,总可推出f(k)>k2成立”;因而若f(6)>36成立,则当k≤6时,均有f(k)>k2成立 ,故C也不成立;对于D,事实上f(7)=50>49,依题意知当k≤7时,均有f(k)>k2成立,故D成立.3.若f(n)=1+++…+(n∈N*),则f(1)为( C )(A)1 (B)(C)1++++(D)非以上答案解析:注意f(n)的项的构成规律,各项分子都是1,分母是从1到6n-1的正整数, 故f(1)=1++++.故选C.4.用数学归纳法证明(n+1)(n+2)…(n+n)=2n·1·3·…·(2n-1)(n∈N*),从k到k+1时,左端需增乘的代数式为( B )(A)2k+1 (B)2(2k+1)(C)(D)解析:n=k时左边为(k+1)(k+2)…(k+k),n=k+1时左边为(k+2)(k+3)…(k+k+2),所以增加的项为=2(2k+1).故选B.5.利用数学归纳法证明不等式“<n+1”时,由“假设n=k时命题成立”到“当n=k+1时”,正确的步骤是( D )(A)=<=k+2(B)==<k+2(C)===k+2(D)==<=<= k+2解析:由数学归纳法的理解可知D正确.6.用数学归纳法证明“1-+-+…+-=++…+”时,由n=k的假设证明n=k+1时,如果从等式左边证明右边,则必须证得右边为( D )(A)+…++(B)+…+++(C)+…++(D)+…++解析:由n=k时,1-+-+…+-=++…+,则n=k+1时,1-+-+…+-=++…++.故选D.二、填空题7.用数学归纳法证明“2n>n2+1对于n≥n0的正整数n都成立”时,第一步证明中的起始值n0应取.解析:令n0分别取1,2,3,4,5,6,依次验证即得.答案:58.已知f(n)=1+++…+(n∈N*),经计算f(2)=,f(4)>2,f(8)>,f(16)>3,f(32)>,推测当n≥2时,有.解析:括号中的通项公式是2n,右边通分成分母为2,则分子的通项公式是n+2.答案:f(2n)>9.观察下列等式:(1+x+x2)1=1+x+x2,(1+x+x2)2=1+2x+3x2+2x3+x4,(1+x+x2)3=1+3x+6x2+7x3+6x4+3x5+x6,(1+x+x2)4=1+4x+10x2+16x3+19x4+16x5+10x6+4x7+x8, …由以上等式推测:对于n∈N*,若(1+x+x2)n=a0+a1x+a2x2+…+a2n x2n,则a2= .解析:由已知中的式子,我们观察后分析:等式右边展开式中的第三项分别为1,3,6,10,…,即1,1+2,1+2+3,1+2+3+4,…根据已知可以推断:第n个等式中a2为1+2+…+n=.答案:10.平面上有n条直线,它们任何两条不平行,任何三条不共点,设k条这样的直线把平面分成f(k)个区域,则k+1条直线把平面分成的区域数f(k+1)=f(k)+ .解析:当n=k+1时,第k+1条直线被前k条直线分成(k+1)段,而每一段将它们所在区域一分为二,故增加了k+1个区域.答案:k+111.已知a1=,a n+1=,则a2,a3,a4,a5的值分别为,由此猜想a n= .解析:a2====,同理,a3===,a4==,a5==,猜想a n=.答案:,,,12.已知f(n)=1+++…+(n∈N*),用数学归纳法证明f(2n)>时,f(2k+1)-f(2k)= .解析:n=k时,f(2k)=1+++…+,当n=k+1时,f(2k+1)=1+++…+++…+,所以f(2k+1)-f(2k)=1+++…+++…+-(1+++…+)=++…+.答案:++…+三、解答题13.已知数列{a n}满足a n+1=,a1=0,(1)计算a2,a3,a4,a5的值;(2)根据以上计算结果猜想{a n}的通项公式,并用数学归纳法证明你的猜想. 解:(1)由a n+1=和a1=0,得a2==,a3==,a4==,a5==.(2)由以上结果猜测:a n=,用数学归纳法证明如下:①当n=1时,左边=a1 =0,右边=0,等式成立;②假设当n=k(k≥1)时,命题成立,即a k=成立,那么,当n=k+1时,a k+1====,这就是说,当n=k+1时等式成立.由①和②,可知a n=对于任意正整数n都成立.14.已知S n=1++++…+(n>1,n∈N*).求证:>1+(n≥2,n∈N*).证明:(1)当n=2时,=1+++=>1+=2,不等式成立.(2)假设n=k(k≥2)时不等式成立,即=1++++…+>1+,当n=k+1时,=1++++…+++…+>1+++…+>1++=1++=1+.故当n=k+1时不等式也成立.综合(1)(2)知,对任意n∈N*,n≥2,不等式>1+都成立.15.已知数列{a n}(n∈N*),满足a1=1,2a n+1=a n+.(1)求证:<a n+1<a n;(2)设数列{a n}(n∈N*)的前n项和为S n,证明:S n<+.证明:(1)先证明a n+1>.n=1时,2a2=+,所以a2=+>,结论成立,假设n=k时,结论成立,即a k+1>,则n=k+1时,2a k+2=a k+1+>+1=, 所以a k+2>,即n=k+1时,结论成立,所以a n+1>,所以a n+1-a n=-a n+=-(-)2+<-(1-)2+=0.所以<a n+1<a n.(2)问题等价于证明S n-<,即(a i-)<,设b n=a n-,则b1=,2a n+1=a n+可化为2b n+1=b n+-1,所以=+·<,所以b n≤·()n-1,所以S n-<<,所以S n<+.巩固提高B一、选择题1.某个命题与正整数n有关,若n=k(k∈N*)时该命题成立,那么可推得n=k+1时该命题也成立,现在已知当n=5时该命题不成立,那么可推得( C )(A)当n=6时,该命题不成立(B)当n=6时,该命题成立(C)当n=4时,该命题不成立(D)当n=4时,该命题成立解析:对n=4不成立(否则n=5也成立).同理可推得P(n)对n=3,n=2,n=1也不成立.故选C.2.用数学归纳法证明1+a+a2+…+a n+1=(a≠1,n∈N*),在验证n=1时,等式左边是( C )(A)1 (B)1+a(C)1+a+a2 (D)1+a+a2+a3解析:根据数学归纳法的步骤可知,当n=1时,等式的左边应为1+a+a2,故选C. 3.用数学归纳法证明等式1+2+3+…+2n=n(2n+1)时,由n=k到n=k+1时,等式左边应添加的项是( C )(A)2k+1(B)2k+2(C)(2k+1)+(2k+2)(D)(k+1)+(k+2)+ (2)解析:因为要证明等式的左边是连续正整数,所以当由n=k到n=k+1时,等式左边增加了[1+2+3+…+2k+(2k+1)+2(k+1)]-(1+2+3+…+2k)= (2k+1)+(2k+2),故选C. 4.用数学归纳法证明1+2+22+…+2n-1=2n-1(n∈N*)的过程中,第二步假设当n=k时等式成立,则当n=k+1时增加了( A )(A)1个项(B)2个项(C)2k-1个项(D)2k个项解析:增加了1项2k.故选A.5.用数学归纳法证明“1+2+3+…+n3=,n∈N*”,则当n=k+1时,应当在n=k时对应的等式的两边加上( A )(A)(k3+1)+(k3+2)+…+(k+1)3(B)k3+1(C)(k+1)3(D)解析:当n=k时,左边为1+2+3+…+k3,当n=k+1时,左边为1+2+3+…+ k3+(k3+1)+(k3+2)+…+(k+1)3,所以左边增加的项为(k3+1)+(k3+2)+…+ (k+1)3.6.已知f(n)=++…+,则f(k+1)-f(k)等于( C )(A)(B)(C)++-(D)-解析:由f(k+1)=++…+=++…+,f(k)=++…+,所以f(k+1)-f(k)=++-,故选C.二、填空题7.用数学归纳法证明1+++…+<n(n∈N*,n>1)时,第一步应验证不等式.解析:当n=2时,左边=1++=1++,右边=2,故应验证1++<2.答案:1++<28.用数学归纳法证明:1+++…+=时, 由n=k到n=k+1左边需要添加的项是.解析:当n=k时,1+++…+=,则当n=k+1时,1++…+ =+=+.答案:9.若f(n)=12+22+32+…+(2n)2,则f(k+1)与f(k)的递推关系式是.解析:因为f(k)=12+22+…+(2k)2,所以f(k+1)=12+22+…+(2k)2+(2k+1)2+(2k+2)2,所以f(k+1)=f(k)+(2k+1)2+(2k+2)2.答案:f(k+1)=f(k)+(2k+1)2+(2k+2)210.设平面上n个圆周最多把平面分成f(n)片(平面区域),则f(2)= ,f(n)= .(n≥1,n∈N*)解析:易知2个圆周最多把平面分成4片;n个圆周最多把平面分成f(n)片,再放入第n+1个圆周,为使得到尽可能多的平面区域,第n+1个应与前面n个都相交且交点均不同,有n条公共弦,其端点把第n+1个圆周分成2n段,每段都把已知的某一片划分成2片,即f(n+1)=f(n)+2n(n≥1),所以f(n)-f(1)=n(n-1),而f(1)=2,从而f(n)=n2-n+2.答案:4 n2-n+211.观察下面算式:23=3+5;33=7+9+11;43=13+15+17+19;53=21+23+25+27+29;…203=a1+a2+a3+…,其中a1<a2<a3<…,那么a1= .解析:由给出的等式可知,等式的右侧奇数构成以3为首项,2为公差的等差数列,所以前18个等式共有2+3+…+19=189个奇数,所以第19个式子的右侧的第1个数是第190个奇数.所以a1=3+2×(190-1)=381.答案:38112.用数学归纳法证明:当x>-1时,n∈N*,(1+x)n≥1+nx,从n=k到n=k+1时需要证明的不等式是.解析:n=k时,(1+x)k≥1+kx.n=k+1时,(1+x)k+1=(1+x)k(1+x)≥(1+kx)(1+x),只要证右边大于等于1+(k+1)x即可.答案:(1+kx)(1+x)≥1+(k+1)x三、解答题13.在数列{a n}中,a1=6,且a n-a n-1=+n+1(n∈N*,n≥2).(1)求a2,a3,a4的值;(2)猜测数列{a n}的通项公式,并用数学归纳法证明.解:(1)a2=12,a3=20,a4=30.(2)猜测a n=(n+1)(n+2).下面用数学归纳法证明:①当n=1,2,3,4时,显然成立;②假设当n=k(k≥4,k∈N*)时成立,即有a k=(k+1)(k+2),则当n=k+1时,由a n-a n-1=+n+1得a n=a n-1+n+1,故a k+1=a k+k+1+1=(k+1)(k+2)+k+2=(k+2)2+(k+2)=(k+2)(k+3),故n=k+1时等式成立.由①②可知,a n=(n+1)(n+2)对一切n∈N*均成立.14.用数学归纳法证明:对一切大于1的正整数n,不等式(1+)(1+)…(1+)>均成立.证明:(1)当n=2时,左边=1+=,右边=.因为左边>右边,所以不等式成立.(2)假设n=k(k≥2,k∈N*)时不等式成立,即(1+)(1+)…(1+)>.则当n=k+1时,(1+)(1+)…(1+)[1+]>·==>==.所以当n=k+1时,不等式成立.由(1)(2)知,对于一切大于1的正整数n,不等式都成立.15.已知数列{a n}满足a1=3,a n+1=-na n+λ,n∈N*,λ∈R.(1)若a n≥2n恒成立,求λ的取值范围;(2)若λ=-2,求证:++…+<2.(1)解:当n=2时,由a2=6+λ≥2×2得λ≥-2,故a n≥2n时,λ≥-2,下面证λ≥-2时a n≥2n.n=2时,a2≥2×2成立;假设n=k(k≥2)时,a k≥2k,则n=k+1时,a k+1=-ka k+λ=a k(a k-k)+λ≥2k2-2=2(k+1)(k-1)≥2(k+1), 故对任意的n≥2,a n≥2n.n=1时,a1=3≥2×1也成立,故对任意n∈N*,a n≥2n成立.故λ的取值范围为[-2,+∞).(2)证明:λ=-2,由(1)知a n+1-2=-na n-4≥na n-4≥2(a n-2)(n≥2),≤·≤…≤·=(n≥2)从而++…+≤1+++…+=2-<2.。
2019届高考数学二轮复习数列大题课件(31张)(全国通用)

考向一 考向二 考向三 考向四 考向五
解:(1)由已知得
������1 + ������2 + ������3 = 7, (������1 + 3) + (������3 + 4)
专题探究
4.2.1 等差、等比数列与 数列
的通项及求和
专题探究
-9-
考向一 考向二 考向三 考向四 考向五
等差、等比数列的通项及求和
例1(2018全国Ⅱ,理17)记Sn为等差数列{an}的前n项和,已知a1=-
7,S3=-15. (1)求{an}的通项公式; (2)求Sn,并求Sn的最小值. 解:(1)设{an}的公差为d, 由题意得3a1+3d=-15. 由a1=-7得d=2. 所以{an}的通项公式为an=2n-9. (2)由(1)得Sn=n2-8n=(n-4)2-16. 所以当n=4时,Sn取得最小值,最小值为-16. 解题心得对于等差、等比数列,求其通项及前n项和时,只需利用
(2)令Sn=a1+a4+a7+…+a3n-2. 由(1)知a3n-2=-6n+31,故{a3n-2}是首项为25,公差为-6的等差数列. 从而 Sn=���2���(a1+a3n-2)=���2���(-6n+56)=-3n2+28n.
考向一 考向二 考向三 考向四 考向五
专题探究
-11-
可转化为等差、等比数列的问题
bn-b1=(bn-bn-1)+(bn-1-bn-2)+…+(b3-b2)+(b2-b1)
2019年高考数学二轮复习(文科)数列推理与证明 解析几何 系列选讲 ppt课件(打包9套,共414页)

(2017· 全 国 Ⅰ) 在 直 角 坐 标 系 xOy 中 , 曲 线 C 的 参 数 方 程 为
x=a+4t, (θ 为参数),直线 l 的参数方程为 (t 为参数). y=1-t
x=3cos θ, y=sin θ
(1)若a=-1,求C与l的交点坐标;
解答
(2)若C上的点到l的距离的最大值为 17 ,求a.
思维升华
解答
x′=2x, (2)设曲线 C 经过伸缩变换 得到曲线 C′,设曲线 C′上任一 y′=y
点为 M(x,y),求 x+2 3y 的最大值.
思维升华
解决直线、圆和圆锥曲线的有关问题,将极坐标方程化为直
角坐标方程或将参数方程化为普通方程,有助于认识方程所表示的曲线,
从而达到化陌生为熟悉的目的,这是转化与化归思想的应用.
参数,0≤θ≤2π).
3.圆锥曲线的参数方程
x2 y2 x=acos θ, (1)椭圆 2+ 2=1 的参数方程为 (θ 为参数). a b y=bsin θ
2 x = 2 pt , 2 (2)抛物线 y =2px(p>0)的参数方程为 (t 为参数). y=2pt
例 2
C2的极坐标方程为ρ2-2ρcos θ-4ρsin θ+4=0.
解答
π (2)若直线C3的极坐标方程为θ= (ρ∈R),设C2,C3的交点为M,N,求 4
△C2MN的面积.
解
π 将 θ=4代入 ρ2-2ρcos θ-4ρsin θ+4=0,
得 ρ2-3 2ρ+4=0,解得 ρ1=2 2,ρ2= 2, 所以|MN|=ρ1-ρ2= 2.因为 C2 的半径为 1, 1 1 所以△C2MN 的面积为2× 2×1×sin 45° =2.
2019届高考数学总复习4.2.2数列中的证明及存在性问题课件理

解:(1)a1=S1=5,a1+a2=S2= ×22+ ×2=13,解得 a2=8. (2)当 n≥2 时,an=Sn-Sn-1=2[n2-(n-1)2]+2[n-(n-1)] =2(2n-1)+2=3n+2.
又a1=5满足an=3n+2,所以an=3n+2. 因为an+1-an=3(n+1)+2-(3n+2)=3, 所以数列{an}是以5为首项,3为公差的等差数列.
-11-
考向一
考向二
考向三
(2)解:由题设,a1=1,a1a2=λS1-1,可得a2=λ-1. 由(1)知,a3=λ+1. 令2a2=a1+a3,解得λ=4.故an+2-an=4. 由此可得{a2n-1}是首项为1,公差为4的等差数列,a2n-1=4n-3;{a2n} 是首项为3,公差为4的等差数列,a2n=4n-1. 所以an=2n-1,an+1-an=2. 因此存在λ=4,使得数列{an}为等差数列.
= 12������ +1
(������ ������ -1)(������ ������ +1) (2������ -1)(2������ +1) 1 1 1 1 1 2
=
1
=
1
1
2 2������ -1 2������ +1 1 1
-
1
,
< .
解题心得要证明关于一个数列的前n项和的不等式,一般有两种 思路:一是先求和,再对和式放缩;二是先对数列的通项放缩,再求数 列的和,必要时对其和再放缩.
1 3 1 2 1 1 2������
=1+������ .
2019年高考数学试题分项版—数列(解析版)

2019年高考数学试题分项版——数列(解析版)一、选择题1.(2019·全国Ⅲ文,6)已知各项均为正数的等比数列{a n }的前4项和为15,且a 5=3a 3+4a 1,则a 3等于( )A .16B .8C .4D .2 答案 C解析 设等比数列{a n }的公比为q ,由a 5=3a 3+4a 1得q 4=3q 2+4,得q 2=4,因为数列{a n }的各项均为正数,所以q =2,又a 1+a 2+a 3+a 4=a 1(1+q +q 2+q 3)=a 1(1+2+4+8)=15,所以a 1=1,所以a 3=a 1q 2=4.2.(2019·浙江,10)设a ,b ∈R ,数列{a n }满足a 1=a ,a n +1=a n 2+b ,n ∈N *,则( )A .当b =12时,a 10>10 B .当b =14时,a 10>10 C .当b =-2时,a 10>10 D .当b =-4时,a 10>10 答案 A解析 当b =12时,因为a n +1=a n 2+12,所以a 2≥12,又a n +1=a n 2+12≥√2a n ,故a 9≥a 2×(√2)7≥12×(√2)7=4√2,a 10>a 92≥32>10.当b =14时,a n +1-a n =(a n −12)2,故当a 1=a =12时,a 10=12,所以a 10>10不成立.同理b =-2和b =-4时,均存在小于10的数x 0,只需a 1=a =x 0,则a 10=x 0<10,故a 10>10不成立.3.(2019·全国Ⅰ理,9)记S n 为等差数列{a n }的前n 项和.已知S 4=0,a 5=5,则( ) A .a n =2n -5 B .a n =3n -10 C .S n =2n 2-8n D .S n =12n 2-2n答案 A解析 设等差数列{a n }的公差为d ,∵{S 4=0,a 5=5,∴{4a 1+4×32d =0,a 1+4d =5,解得{a 1=−3,d =2, ∴a n =a 1+(n -1)d =-3+2(n -1)=2n -5, S n =na 1+n (n−1)2d =n 2-4n .故选A.4.(2019·全国Ⅲ理,5)已知各项均为正数的等比数列{a n }的前4项和为15,且a 5=3a 3+4a 1,则a 3等于( )A .16B .8C .4D .2 答案 C解析 设等比数列{a n }的公比为q ,由a 5=3a 3+4a 1得q 4=3q 2+4,得q 2=4,因为数列{a n }的各项均为正数,所以q =2,又a 1+a 2+a 3+a 4=a 1(1+q +q 2+q 3)=a 1(1+2+4+8)=15,所以a 1=1,所以a 3=a 1q 2=4. 二、填空题1.(2019·全国Ⅰ文,14)记S n 为等比数列{a n }的前n 项和,若a 1=1,S 3=34,则S 4=________.答案 58解析 设等比数列的公比为q , 则a n =a 1q n -1=q n -1. ∵a 1=1,S 3=34,∴a 1+a 2+a 3=1+q +q 2=34, 即4q 2+4q +1=0,∴q =-12,∴S 4=1×[1−(−12)4]1−(−12)=58.2.(2019·全国Ⅲ文,14)记S n 为等差数列{a n }的前n 项和.若a 3=5,a 7=13,则S 10=________. 答案 100解析 ∵{a n }为等差数列,a 3=5,a 7=13, ∴公差d =a 7−a 37−3=13−54=2,首项a 1=a 3-2d =5-2×2=1, ∴S 10=10a 1+10×92d =100.3.(2019·江苏,8)已知数列{a n }(n ∈N *)是等差数列,S n 是其前n 项和.若a 2a 5+a 8=0,S 9=27,则S 8的值是________. 答案 16解析 方法一 设等差数列{a n }的公差为d ,则a 2a 5+a 8=(a 1+d )(a 1+4d )+a 1+7d =a 12+4d 2+5a 1d +a 1+7d =0,S 9=9a 1+36d =27,解得a 1=-5,d =2,则S 8=8a 1+28d =-40+56=16.方法二 ∵S 9=a 1+a 92×9=27,∴a 1+a 9=6, ∴a 2+a 8=2a 5=6, ∴a 5=3,则a 2a 5+a 8=3a 2+a 8=0, 即2a 2+6=0, ∴a 2=-3,则a 8=9,∴其公差d =a 8−a 58−5=2,∴a 1=-5,∴S 8=8×a 1+a82=16.4.(2019·全国Ⅰ理,14)记S n 为等比数列{a n }的前n 项和.若a 1=13,a 42=a 6,则S 5=________.答案1213解析 设等比数列{a n }的公比为q ,因为a 42=a 6,所以(a 1q 3)2=a 1q 5,所以a 1q =1,又a 1=13,所以q =3,所以S 5=a 1(1−q 5)1−q=13×(1−35)1−3=1213.5.(2019·全国Ⅲ理,14)记S n 为等差数列{a n }的前n 项和.若a 1≠0,a 2=3a 1,则s 10s 5=________.答案 4解析 设等差数列{a n }的公差为d ,由a 2=3a 1, 即a 1+d =3a 1,得d =2a 1,所以s 10s 5=10a1+10×92d 5a1+5×42d=10a1+10×92×2a15a1+5×42×2a1=10025=4.6.(2019·北京理,10)设等差数列{}n a 的前n 项和为n S ,若23a =-,510S =-,则5a = ,n S 的最小值为 .【思路分析】利用等差数列{}n a 的前n 项和公式、通项公式列出方程组,能求出14a =-,1d =,由此能求出5a 的n S 的最小值.【解析】:设等差数列{}n a 的前n 项和为n S ,23a =-,510S =-,∴113545102a d a d +=-⎧⎪⎨⨯+=-⎪⎩,解得14a =-,1d =,5144410a a d ∴=+=-+⨯=, 21(1)(1)19814()22228n n n n n S na d n n --=+=-+=--, 4n ∴=或5n =时,n S 取最小值为4510S S ==-.故答案为:0,10-.【归纳与总结】本题考查等差数列的第5项的求法,考查等差数列的前n 项和的最小值的求法,考查等差数列的性质等基础知识,考查推理能力与计算能力,属于基础题. 三、解答题1.(2019·全国Ⅰ文,18)记S n 为等差数列{a n }的前n 项和.已知S 9=-a 5. (1)若a 3=4,求{a n }的通项公式;(2)若a 1>0,求使得S n ≥a n 的n 的取值范围. 解 (1)设{a n }的公差为d . 由S 9=-a 5,即9a 5=-a 5,所以a5=0,得a1+4d=0.由a3=4得a1+2d=4.于是a1=8,d=-2.因此{a n}的通项公式为a n=10-2n,n∈N*.(2)由(1)得a1=-4d,故a n=(n-5)d,.S n=n(n−9)d2由a1>0知d<0,≥(n-5)d,化简得故S n≥a n等价于n(n−9)d2n2-11n+10≤0,解得1≤n≤10,所以n的取值范围是{n|1≤n≤10,n∈N*}.2.(2019·全国Ⅱ文,18)已知{a n}是各项均为正数的等比数列,a1=2,a3=2a2+16.(1)求{a n}的通项公式;(2)设b n=log2a n,求数列{b n}的前n项和.解(1)设{a n}的公比为q,由题设得2q2=4q+16,即q2-2q-8=0,解得q=-2(舍去)或q=4.因此{a n}的通项公式为a n=2×4n-1=22n-1.(2)由(1)得b n=log222n-1=(2n-1)log22=2n-1,因此数列{b n}的前n项和为1+3+…+2n-1=n2.3.(2019·北京文,16)设{a n}是等差数列,a1=-10,且a2+10,a3+8,a4+6成等比数列.(1)求{a n}的通项公式;(2)记{a n}的前n项和为S n,求S n的最小值.解(1)设{a n}的公差为d.因为a1=-10,所以a2=-10+d,a3=-10+2d,a4=-10+3d.因为a2+10,a3+8,a4+6成等比数列,所以(a3+8)2=(a2+10)(a4+6).即(-2+2d)2=d(-4+3d).解得d=2.所以a n=a1+(n-1)d=2n-12.(2)由(1)知,a n=2n-12.则当n≥7时,a n>0;当n≤6时,a n≤0.所以S n 的最小值为S 5=S 6=-30.4.(2019·天津文,18)设{a n }是等差数列,{b n }是等比数列,公比大于0.已知a 1=b 1=3,b 2=a 3,b 3=4a 2+3.(1)求{a n }和{b n }的通项公式; (2)设数列{c n }满足c n ={1,n 为奇数,b n 2,n 为偶数.求a 1c 1+a 2c 2+…+a 2n c 2n (n ∈N *).解 (1)设等差数列{a n }的公差为d ,等比数列{b n }的公比为q ,q >0. 依题意,得{3q =3+2d ,3q 2=15+4d ,解得{d =3,q =3,故a n =3+3(n -1)=3n ,b n =3×3n -1=3n .所以{a n }的通项公式为a n =3n ,{b n }的通项公式为b n =3n . (2)a 1c 1+a 2c 2+…+a 2n c 2n=(a 1+a 3+a 5+…+a 2n -1)+(a 2b 1+a 4b 2+a 6b 3+…+a 2n b n ) =[n ×3+n(n−1)2×6]+(6×31+12×32+18×33+…+6n ×3n )=3n 2+6(1×31+2×32+…+n ×3n ). 记T n =1×31+2×32+…+n ×3n ,① 则3T n =1×32+2×33+…+n ×3n +1,② ②-①得,2T n =-3-32-33-…-3n +n ×3n +1 =-3(1−3n )1−3+n ×3n +1=(2n−1)3n+1+32.所以a 1c 1+a 2c 2+…+a 2n c 2n =3n 2+6T n =3n 2+3×(2n−1)3n+1+32=3(n−1)3n+2+6n 2+92(n ∈N *).5.(2019·浙江,20)设等差数列{a n }的前n 项和为S n ,a 3=4,a 4=S 3.数列{b n }满足:对每个n ∈N *,S n +b n ,S n +1+b n ,S n +2+b n 成等比数列. (1)求数列{a n },{b n }的通项公式; (2)记c n =√a n 2b n,n ∈N *,证明:c 1+c 2+…+c n <2√n ,n ∈N *.(1)解 设数列{a n }的公差为d ,由题意得 a 1+2d =4,a 1+3d =3a 1+3d , 解得a 1=0,d =2. 从而a n =2n -2,n ∈N *. 所以S n =n 2-n ,n ∈N *.由S n +b n ,S n +1+b n ,S n +2+b n 成等比数列得(S n +1+b n )2=(S n +b n )(S n +2+b n ).解得b n =1a (S n+12-S n S n +2).所以b n =n 2+n ,n ∈N *.(2)证明 c n =√a n 2b n=√2n−22n(n+1)=√n−1n(n+1),n ∈N *.我们用数学归纳法证明.①当n =1时,c 1=0<2,不等式成立; ②假设n =k (k ∈N *,k ≥1)时不等式成立,即 c 1+c 2+…+c k <2√k . 那么,当n =k +1时,c 1+c 2+…+c k +c k +1<2√k +√k(k+1)(k+2)<2√k +√1k+1<2√k +√k+1+√k=2√k +2(√k +1-√k )=2√k +1.即当n =k +1时不等式也成立.根据①和②,不等式c 1+c 2+…+c n <2√n 对任意n ∈N *成立.6.(2019·江苏,20)定义首项为1且公比为正数的等比数列为“M -数列”.(1)已知等比数列{a n }(n ∈N *)满足:a 2a 4=a 5,a 3-4a 2+4a 1=0,求证:数列{a n }为“M -数列”; (2)已知数列{b n }(n ∈N *)满足:b 1=1,1S n=2b n -2b n+1,其中S n 为数列{b n }的前n 项和.①求数列{b n }的通项公式;②设m 为正整数.若存在“M -数列”{c n }(n ∈N *),对任意正整数k ,当k ≤m 时,都有c k ≤b k ≤c k+1成立,求m 的最大值.(1)证明 设等比数列{a n }的公比为q ,所以a 1≠0,q ≠0.由{a 2a 4=a 5,a 3−4a 2+4a 1=0,得{a 12q 4=a 1q 4,a 1q 2−4a 1q +4a 1=0,解得{a 1=1,q =2.因此数列{a n }为“M -数列”. (2)解 ①因为1S n=2b n-2bn+1,所以b n ≠0.由b 1=1,S 1=b 1,得11=21-2b 2,则b 2=2.由2S n=2b n-2bn+1,得S n =b nb n+12(b n+1−b n ),当n ≥2时,由b n =S n -S n -1, 得b n =b nb n+12(b n+1−b n)-b n−1bn2(b n−b n−1), 整理得b n +1+b n -1=2b n .所以数列{b n }是首项和公差均为1的等差数列.因此,数列{b n }的通项公式为b n =n (n ∈N *). ②由①知,b k =k ,k ∈N *.因为数列{c n }为“M -数列”,设公比为q ,所以c 1=1,q >0. 因为c k ≤b k ≤c k +1,所以q k -1≤k ≤q k ,其中k =1,2,3,…,m . 当k =1时,有q ≥1; 当k =2,3,…,m 时,有lnk k≤ln q ≤lnkk−1.设f (x )=lnx x(x >1),则f ′(x )=1−lnx x 2(x >1).令f ′(x )=0,得x =e ,列表如下:因为ln22=ln86<ln96=ln33,所以f (k )max =f (3)=ln33.取q =√33,当k =1,2,3,4,5时,lnk k≤ln q ,即k ≤q k ,经检验知q k -1≤k 也成立.因此所求m 的最大值不小于5.若m ≥6,分别取k =3,6,得3≤q 3,且q 5≤6,从而q 15≥243,且q 15≤216,所以q 不存在.因此所求m 的最大值小于6. 综上,所求m 的最大值为5.7.(2019·全国Ⅱ理,19)已知数列{a n }和{b n }满足a 1=1,b 1=0,4a n +1=3a n -b n +4,4b n +1=3b n -a n -4.(1)证明:{a n +b n }是等比数列,{a n -b n }是等差数列; (2)求{a n }和{b n }的通项公式.(1)证明 由题设得4(a n +1+b n +1)=2(a n +b n ), 即a n +1+b n +1=12(a n +b n ).又因为a 1+b 1=1,所以{a n +b n }是首项为1,公比为12的等比数列.由题设得4(a n +1-b n +1)=4(a n -b n )+8,即a n +1-b n +1=a n -b n +2. 又因为a 1-b 1=1,所以{a n -b n }是首项为1,公差为2的等差数列. (2)解 由(1)知,a n +b n =12n−1,,a n -b n =2n -1.所以a n =12[(a n +b n )+(a n -b n )]=12n +n -12, b n =12[(a n +b n )-(a n -b n )]=12n -n +12.8.(2019·北京理,20)(13分)已知数列{}n a ,从中选取第1i 项、第2i 项、⋯、第m i 项12()m i i i <<⋯<,若12m i i i a a a <<⋯<,则称新数列1i a ,2i a ,⋯,m i a 为{}n a 的长度为m 的递增子列.规定:数列{}n a 的任意一项都是{}n a 的长度为1的递增子列. (Ⅰ)写出数列1,8,3,7,5,6,9的一个长度为4的递增子列;(Ⅱ)已知数列{}n a 的长度为p 的递增子列的末项的最小值为0m a ,长度为q 的递增子列的末项的最小值为0n a .若p q <,求证:00m n a a <;(Ⅲ)设无穷数列{}n a 的各项均为正整数,且任意两项均不相等.若{}n a 的长度为s 的递增子列末项的最小值为21s -,且长度为s 末项为21s -的递增子列恰有12s -个(1s =,2,)⋯,求数列{}n a 的通项公式.【思路分析】()1I ,3,5,6.答案不唯一.()II 考虑长度为q 的递增子列的前p 项可以组成长度为p 的一个递增子列,可得0n a >该数列的第p 项0m a ,即可证明结论.()III 考虑21s -与2s 这一组数在数列中的位置.若{}n a 中有2s ,在2s 在21s -之后,则必然在长度为1s +,且末项为2s 的递增子列,这与长度为s 的递增子列末项的最小值为21s -矛盾,可得2s 必在21s -之前.继续考虑末项为21s +的长度为1s +的递增子列.因此对于数列21n -,2n ,由于2n 在21n -之前,可得研究递增子列时,不可同时取2n 与21n -,即可得出:递增子列最多有2s 个.由题意,这s 组数列对全部存在于原数列中,并且全在21s +之前.可得2,1,4,3,6,5,⋯⋯,是唯一构造. 【解析】:()1I ,3,5,6.()II 证明:考虑长度为q 的递增子列的前p 项可以组成长度为p 的一个递增子列,∴0n a >该数列的第p 项0m a , ∴00m n a a <.()III 解:考虑21s -与2s 这一组数在数列中的位置.若{}n a 中有2s ,在2s 在21s -之后,则必然在长度为1s +,且末项为2s 的递增子列, 这与长度为s 的递增子列末项的最小值为21s -矛盾,2s ∴必在21s -之前. 继续考虑末项为21s +的长度为1s +的递增子列.对于数列21n -,2n ,由于2n 在21n -之前,∴研究递增子列时,不可同时取2n 与21n -, 对于1至2s 的所有整数,研究长度为1s +的递增子列时,第1项是1与2二选1,第2项是3与4二选1,⋯⋯,第s 项是21s -与2s 二选1,故递增子列最多有2s 个.由题意,这s 组数列对全部存在于原数列中,并且全在21s +之前.2∴,1,4,3,6,5,⋯⋯,是唯一构造. 即221k a k =-,212k a k -=,*k N ∈.【归纳与总结】本题考查了数列递推关系、数列的单调性,考查了逻辑推理能力、分析问题与解决问题的能力,属于难题.9.(2019·天津理,19)设{a n }是等差数列,{b n }是等比数列.已知a 1=4,b 1=6,b 2=2a 2-2,b 3=2a 3+4.(1)求{a n }和{b n }的通项公式;(2)设数列{c n }满足c 1=1,c n ={1,2k <n <2k+1,b k ,n =2k,其中k ∈N *. (ⅰ)求数列{a 2n (c 2n -1)}的通项公式;(ⅱ)求(n ∈N *).解 (1)设等差数列{a n }的公差为d ,等比数列{b n }的公比为q . 依题意得{6q =6+2d ,6q 2=12+4d ,解得{d =3,q =2,所以a n =a 1+(n -1)d =4+(n -1)×3=3n +1, b n =b 1·q n -1=6×2n -1=3×2n .所以{a n }的通项公式为a n =3n +1,{b n }的通项公式为b n =3×2n . (2)(ⅰ)a 2n (c 2n -1)=a 2n (b n -1)=(3×2n +1)(3×2n -1)=9×4n -1. 所以数列{a 2n (c 2n -1)}的通项公式为a 2n (c 2n -1)=9×4n -1. (ⅱ)a i c i =[a i +a i (c i -1)] =a i +a 2i (c 2i -1)=[2n ×4+2n (2n −1)2×3]+(9×4i -1) =(3×22n -1+5×2n -1)+9×4(1−4n )1−4-n=27×22n -1+5×2n -1-n -12(n ∈N *).。
2019秋高中数学第四讲数学归纳法证明不等式复习课练习(含解析)新人教A版选修4_5

复习课[整合·网络构建][警示·易错提醒]1.数学归纳法的两个关注点.(1)关注用数学归纳法证题的步骤.第一步称“归纳奠基”,是递推链的起点;第二步称为“归纳递推”,是递推链具有传递性的保证.两步缺一不可,否则不能保证结论成立.(2)关注适用范围,数学归纳法适用于某些与正整数n有关的问题,这里n是任意的正整数,它可取无限多个值,但是,并不能说所有与正整数n有关的问题都可以用数学归纳法.2.数学归纳法的两个易错点.(1)在数学归纳法中,没有应用归纳假设.(2)归纳推理不到位.专题一数学归纳法在使用数学归纳法证明不等式时,一般来说,第一步,验证比较简明,而第二步归纳步骤情况较复杂.因此,熟悉归纳步骤的证明方法是十分重要的,其实归纳步骤可以看作是一个独立的证明问题,归纳假设“P(k)”是问题的条件,而命题P(k+1)成立就是所要证明的结论,因此,合理运用归纳假设这一条件就成了归纳步骤中的关键.[例❶] 设0<a<1,定义a1=1+a,a n+1=1a n+a,求证:对一切正整数n,有1<a n<11-a.证明:(1)当n=1时,a1>1,a1=1+a<11-a,命题成立.(2)假设n=k(k∈N*)时,命题成立.即1<a k<11-a,当n=k+1时,由递推公式,知a k+1=1a k+a>(1-a)+a=1.同时,a k+1=1a k+a<1+a=1-a21-a<11-a,故当n=k+1时,命题也成立,即1<a k+1<11-a,综合(1)(2)可知,对一切正整数n,有1<a n<11-a.归纳升华用数学归纳法证明不等式的题型多种多样,所以不等式的证明是一个难点,在由n=k 成立,推导n=k+1也成立时,其他证明不等式的方法在此都可以使用,如比较法、放缩法、分析法、反证法等,有时还要考虑与原不等式等价的命题.[变式训练] 证明不等式122+132+…+1n2<1(n≥2,n∈N*).证明:先证明122+132+…+1n2<1-1n(n≥2),(*)对(*)运用数学归纳法证明:(1)当n=2时,(*)显然成立.(2)设n=k时,不等式(*)成立,则122+132+…+1k2<1-1k.当n=k+1时,1 22+132+…+1k2+1(k+1)2<1-1k+1(k+1)2<1-1k+1k(k+1)=1-1k+⎝⎛⎭⎪⎫1k-1k+1=1-1k+1.故当n=k+1时,不等式(*)成立.根据(1)和(2)知,对n∈N*且n≥2,不等式(*)成立,故原不等式成立.专题二归纳、猜想、证明思想的应用归纳、猜想、证明属于探索性问题的一种,一般经过计算、观察、归纳,然后猜想出结论,再利用数学归纳法证明,由于“猜想”是“证明”的前提和“对象”,因此务必要保持猜想的正确性,同时要注意数学归纳法步骤的书写.[例2] 数列{a n}满足S n=2n-a n.(1)计算a1,a2,a3,a4,并由此猜想通项公式a n;(2)用数学归纳法证明(1)的猜想.(1)解:当n=1时,a1=S1=2-a1,所以a1=1.当n =2时,a 1+a 2=S 2=2×2-a 2,所以a 2=32. 当n =3时,a 1+a 2+a 3=S 3=2×3-a 3,所以a 3=74. 当n =4时,a 1+a 2+a 3+a 4=S 4=2×4-a 4,所以a 4=158. 由此猜想a n =2n-12n -1(n ∈N *). (2)证明:①当n =1时,a 1=1,结论成立.②假设当n =k (k ≥1且k ∈N +)时,结论成立,即a k =2k -12k -1. 当n =k +1时,a k +1=S k +1-S k =2(k +1)-a k +1-2k +a k =2+a k -a k +1 ,即a k +1=2+a k -a k +1,所以a k +1=2+a k 2=2+2k -12k -12=2k +1-12k , 这表明当n =k +1时,结论成立.由①②知猜想的通项公式a n =2n -12n -1成立.归纳升华归纳—猜想—证明的三步曲(1)计算:根据条件,计算若干项.(2)归纳猜想:通过观察、分析、综合、联想、猜想出一般结论.(3)证明:用数学归纳法证明.[变式训练] “设f (n )=1+12+13+…+1n (n ∈N +),有f (1)=1>12,f (3)>1,f (7)>32,f (15)>2,…”.试问:f (2n -1)与n 2大小关系如何?试猜想并加以证明. 解:数列1,3,7,15,…,通项公式为a n =2n -1,数列12,1,32,2,…,通项公式为a n =n 2, 所以猜想:f (2n -1)>n 2.下面用数学归纳法证明:(1)当n =1时,f (21-1)=f (1)=1>12,不等式成立. (2)假设当n =k (k ≥1,k ∈N +)时不等式成立,即f (2k -1)>k 2. 当n =k +1时, f (2k +1-1)=f (2k -1)+12k +12k+1+…+12k +1-2+12k +1-1> f (2k -1)+12k +1+…+12k +1,2k 个=f (2k -1)+12>k 2+12=k +12. 所以当n =k +1时不等式也成立.据(1)(2)知对任何n ∈N +原不等式均成立.专题三 转化和化归思想把所要证的平面几何问题转化,运用数学归纳法来解决,这体现了转化和化归的思想.一般将待解决的平面几何问题进行转化,使之化为我们熟悉的或容易解决的问题.[例3] 设平面α内有n 条直线,这n 条直线把平面α分成互不垂叠的区域个数的最大值为f (n ),求f (n )的解析式,并用数学归纳法证明.解:设平面α内k (k ≥1)条直线把平面α分成区域个数的最大值为f (k ),则第k +1条直线与前k 条直线最多有k 个交点,因此第k +1条直线最多可以被分成k +1段,每一段可把所在的区域分为两部分,所以比原来的区域增加k +1个,即有f (k +1)=f (k )+k +1,所以f (k +1)-f (k )=k +1.于是f (2)-f (1)=2,f (3)-f (2)=3,…,f (n )-f (n -1)=n .把以上n -1个等式相加得f (n )-f (1)=2+3+…+n .因为f (1)=2,所以f (n )=f (1)+(2+3+…+n )=12(n 2+n +2). 下面用数学归纳法证明:(1)n =1时,一条直线可以把平面分成2个,即f (1)=2,而12(n 2+n +2)=12(1+1+2)=2, 所以命题成立.(2)假设n =k 时,f (k )=12(k 2+k +2)成立, 当n =k +1时,f (k +1)=f (k )+(k +1)=12(k 2+k +2)+(k +1)=12(k 2+2k +1+k +3)=12[(k+1)2+(k+1)+2],所以命题仍成立.由(1)(2)知,当n∈N*时,f(n)=12(n2+n+2)成立.归纳升华有关几何图形的性质、公式等与自然数n有关的命题,主要是抓住递推关系,明确要证明的表达式,然后转化用数学归纳法进行证明.[变式训练] 用数学归纳法证明:对于任意正整数n,整式a n-b n都能被a-b整除.证明:(1)当n=1时,a n-b n=a-b能被a-b整除.(2)假设当n=k(k∈N+,k≥1)时,a k-b k能被a-b整除,那么当n=k+1时,a k+1-b k +1=a k+1-a k b+a k b-b k+1=a k(a-b)+b(a k-b k).因为(a-b)和a k-b k都能被a-b整除,所以上面的和a k(a-b)+b(a k-b k)也能被a-b整除.这也就是说当n=k+1时,a k+1-b k+1能被a-b整除.根据(1)(2)可知对一切正整数n,a n-b n都能被a-b整除.。
2019高考数学(理科)二轮复习(全国通用版):回扣4 数 列Word版含答案
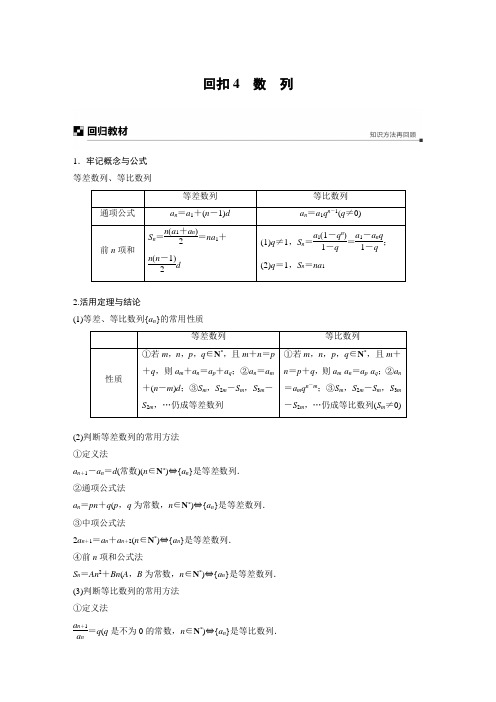
回扣4数列1.牢记概念与公式等差数列、等比数列2.活用定理与结论(1)等差、等比数列{a n}的常用性质(2)判断等差数列的常用方法①定义法a n+1-a n=d(常数)(n∈N*)⇔{a n}是等差数列.②通项公式法a n=pn+q(p,q为常数,n∈N*)⇔{a n}是等差数列.③中项公式法2a n+1=a n+a n+2(n∈N*)⇔{a n}是等差数列.④前n项和公式法S n=An2+Bn(A,B为常数,n∈N*)⇔{a n}是等差数列.(3)判断等比数列的常用方法①定义法a n+1a n=q(q是不为0的常数,n∈N *)⇔{an}是等比数列.②通项公式法a n =cq n (c ,q 均是不为0的常数,n ∈N *)⇔{a n }是等比数列. ③中项公式法a 2n +1=a n ·a n +2(a n ·a n +1·a n +2≠0,n ∈N *)⇔{a n }是等比数列. 3.数列求和的常用方法(1)等差数列或等比数列的求和,直接利用公式求和.(2)形如{a n ·b n }(其中{a n }为等差数列,{b n }为等比数列)的数列,利用错位相减法求和. (3)通项公式形如a n =c (an +b 1)(an +b 2)(其中a ,b 1,b 2,c 为常数)用裂项相消法求和.(4)通项公式形如a n =(-1)n ·n 或a n =a ·(-1)n (其中a 为常数,n ∈N *)等正负项交叉的数列求和一般用并项法.并项时应注意分n 为奇数、偶数两种情况讨论.(5)分组求和法:分组求和法是解决通项公式可以写成c n =a n +b n 形式的数列求和问题的方法,其中{a n }与{b n }是等差(比)数列或一些可以直接求和的数列. (6)并项求和法:先将某些项放在一起求和,然后再求S n .1.已知数列的前n 项和求a n ,易忽视n =1的情形,直接用S n -S n -1表示.事实上,当n =1时,a 1=S 1;当n ≥2时,a n =S n -S n -1.2.易混淆几何平均数与等比中项,正数a ,b 的等比中项是±ab .3.等差数列中不能熟练利用数列的性质转化已知条件,灵活整体代换进行基本运算.如等差数列{a n }与{b n }的前n 项和分别为S n 和T n ,已知S n T n =n +12n +3,求a n b n 时,无法正确赋值求解.4.易忽视等比数列中公比q ≠0导致增解,易忽视等比数列的奇数项或偶数项符号相同造成增解.5.运用等比数列的前n 项和公式时,易忘记分类讨论.一定分q =1和q ≠1两种情况进行讨论.6.利用错位相减法求和时,要注意寻找规律,不要漏掉第一项和最后一项. 7.裂项相消法求和时,裂项前后的值要相等, 如1n (n +2)≠1n -1n +2,而是1n (n +2)=12⎝⎛⎭⎪⎫1n -1n +2.8.通项中含有(-1)n 的数列求和时,要把结果写成n 为奇数和n 为偶数两种情况的分段形式.1.设等差数列{a n }的前n 项和为S n ,已知S 13>0,S 14<0,若a k ·a k +1<0,则k 等于( ) A .6B .7C .13D .14 答案 B解析 因为{a n }为等差数列,S 13=13a 7,S 14=7(a 7+a 8), 所以a 7>0,a 8<0,a 7·a 8<0,所以k =7.2.已知在等比数列{a n }中,a 1+a 2=3,a 3+a 4=12,则a 5+a 6等于( ) A .3B .15C .48D .63 答案 C解析 a 3+a 4a 1+a 2=q 2=4,所以a 5+a 6=(a 3+a 4)·q 2=48.3.设等差数列{a n }的前n 项和为S n ,且a 1>0,a 3+a 10>0,a 6a 7<0,则满足S n >0的最大自然数n 的值为( ) A .6 B .7 C .12 D .13答案 C解析 ∵a 1>0,a 6a 7<0,∴a 6>0,a 7<0,等差数列的公差小于零, 又a 3+a 10=a 1+a 12>0,a 1+a 13=2a 7<0, ∴S 12>0,S 13<0,∴满足S n >0的最大自然数n 的值为12.4.已知数列{a n }满足13n a +=9·3n a(n ∈N *)且a 2+a 4+a 6=9,则15793log ()a a a ++等于( ) A .-13B .3C .-3 D.13答案 C解析 由已知13n a+=9·3n a=23n a +,所以a n +1=a n +2,所以数列{a n }是公差为2的等差数列,a 5+a 7+a 9=(a 2+3d )+(a 4+3d )+(a 6+3d ) =(a 2+a 4+a 6)+9d =9+9×2=27,所以15793log ()a a a ++=13log 27=-3.故选C.5.已知正数组成的等比数列{a n },若a 1·a 20=100,那么a 7+a 14的最小值为( ) A .20 B .25 C .50 D .不存在答案 A解析 在正数组成的等比数列{a n }中,因为a 1·a 20=100,由等比数列的性质可得a 1·a 20=a 7·a 14=100,那么a 7+a 14≥2a 7·a 14=2100=20,当且仅当a 7=a 14=10时取等号,所以a 7+a 14的最小值为20.6.已知数列{a n }的前n 项和为S n ,若S n =2a n -4(n ∈N *),则a n 等于( ) A .2n +1B .2nC .2n -1D .2n -2答案 A解析 a n +1=S n +1-S n =2a n +1-4-(2a n -4)⇒a n +1=2a n ,再令n =1,∴S 1=2a 1-4⇒a 1=4, ∴数列{a n }是以4为首项,2为公比的等比数列, ∴a n =4·2n -1=2n +1,故选A.7.已知等差数列{a n }的公差和首项都不等于0,且a 2,a 4,a 8成等比数列,则a 1+a 5+a 9a 2+a 3等于( )A .2B .3C .5D .7 答案 B解析 ∵在等差数列{a n }中,a 2,a 4,a 8成等比数列,∴a 24=a 2a 8,∴(a 1+3d )2=(a 1+d )(a 1+7d ),∴d 2=a 1d ,∵d ≠0,∴d =a 1,∴a 1+a 5+a 9a 2+a 3=15a 15a 1=3,故选B.8.已知S n 为数列{a n }的前n 项和,若a n (4+cos n π)=n (2-cos n π)(n ∈N *),则S 20等于( ) A .31 B .122 C .324 D .484答案 B解析 由题意可知,因为a n (4+cos n π)=n (2-cos n π), 所以a 1=1,a 2=25,a 3=3,a 4=45,a 5=5,a 6=65,…,所以数列{a n }的奇数项构成首项为1,公差为2的等差数列,偶数项构成首项为25,公差为25的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第4讲用数学归纳法证明数列问题选题明细表知识点·方法巩固提高A 巩固提高B数学归纳法的理解1,2,5 1数学归纳法的第一步3,7 2,73,4,5,6,8,数学归纳法的第二步4,6,10,129,12类比归纳8,9,11 10,11数学归纳法的应用13,14,15 13,14,15巩固提高A一、选择题1.如果命题P(n)对n=k成立,则它对n=k+2也成立,若P(n)对n=2也成立,则下列结论正确的是( B )(A)P(n)对所有正整数n都成立(B)P(n)对所有正偶数n都成立(C)P(n)对所有正奇数n都成立(D)P(n)对所有正整数n都成立解析:由题意n=k时成立,则n=k+2时也成立,又n=2时成立,则P(n)对所有正偶数都成立.故选B.2.设f(x)是定义在正整数集上的函数,且f(x)满足:“当f(k)≤k2成立时,总可推出f(k+1)≤(k+1)2成立.”那么,下列命题总成立的是( D )(A)若f(2)≤4成立,则当k≥1时,均有f(k)≤k2成立(B)若f(4)≤16成立,则当k≤4时,均有f(k)≤k2成立(C)若f(6)>36成立,则当k≥7时,均有f(k)>k2成立(D)若f(7)=50成立,则当k≤7时,均有f(k)>k2成立解析:若f(2)≤4成立,依题意则应有当k≥2时,均有f(k)≤k2成立,故A不成立;若f(4)≤16成立,依题意则应有当k≥4时,均有f(k)≤k2成立,故B不成立;因命题“当f(k)≤k2成立时,总可推出f(k+1)≤(k+1)2成立”⇔“当f(k+1)>(k+1)2成立时,总可推出f(k)>k2成立”;因而若f(6)>36成立,则当k≤6时,均有f(k)>k2成立 ,故C 也不成立;对于D,事实上f(7)=50>49,依题意知当k≤7时,均有f(k)>k2成立,故D成立.3.若f(n)=1+++…+(n∈N*),则f(1)为( C )(A)1 (B)(C)1++++(D)非以上答案解析:注意f(n)的项的构成规律,各项分子都是1,分母是从1到6n-1的正整数,故f(1)=1++++.故选C.4.用数学归纳法证明(n+1)(n+2)…(n+n)=2n·1·3·…·(2n-1)(n∈N*),从k到k+1时,左端需增乘的代数式为( B )(A)2k+1 (B)2(2k+1)(C)(D)解析:n=k时左边为(k+1)(k+2)…(k+k),n=k+1时左边为(k+2)(k+3)…(k+k+2),所以增加的项为=2(2k+1).故选B.5.利用数学归纳法证明不等式“<n+1”时,由“假设n=k时命题成立”到“当n=k+1时”,正确的步骤是( D )(A)=<=k+2(B)==<k+2(C)===k+2(D)==<=<=k+2解析:由数学归纳法的理解可知D正确.6.用数学归纳法证明“1-+-+…+-=++…+”时,由n=k的假设证明n=k+1时,如果从等式左边证明右边,则必须证得右边为( D )(A)+…++(B)+…+++(C)+…++(D)+…++解析:由n=k时,1-+-+…+-=++…+,则n=k+1时,1-+-+…+-=++…++.故选D.二、填空题7.用数学归纳法证明“2n>n2+1对于n≥n0的正整数n都成立”时,第一步证明中的起始值n0应取.解析:令n0分别取1,2,3,4,5,6,依次验证即得.答案:58.已知f(n)=1+++…+(n∈N*),经计算f(2)=,f(4)>2,f(8)>,f(16)>3,f(32)>,推测当n≥2时,有.解析:括号中的通项公式是2n,右边通分成分母为2,则分子的通项公式是n+2.答案:f(2n)>9.观察下列等式:(1+x+x2)1=1+x+x2,(1+x+x2)2=1+2x+3x2+2x3+x4,(1+x+x2)3=1+3x+6x2+7x3+6x4+3x5+x6,(1+x+x2)4=1+4x+10x2+16x3+19x4+16x5+10x6+4x7+x8, …由以上等式推测:对于n∈N*,若(1+x+x2)n=a0+a1x+a2x2+…+a2n x2n,则a2= .解析:由已知中的式子,我们观察后分析:等式右边展开式中的第三项分别为1,3,6,10,…,即1,1+2,1+2+3,1+2+3+4,…根据已知可以推断:第n个等式中a2为1+2+…+n=.答案:10.平面上有n条直线,它们任何两条不平行,任何三条不共点,设k条这样的直线把平面分成f(k)个区域,则k+1条直线把平面分成的区域数f(k+1)=f(k)+ .解析:当n=k+1时,第k+1条直线被前k条直线分成(k+1)段,而每一段将它们所在区域一分为二,故增加了k+1个区域.答案:k+111.已知a1=,a n+1=,则a2,a3,a4,a5的值分别为,由此猜想a n= .解析:a2====,同理,a3===,a4==,a5==,猜想a n=.答案:,,,12.已知f(n)=1+++…+(n∈N*),用数学归纳法证明f(2n)>时,f(2k+1)-f(2k)= .解析:n=k时,f(2k)=1+++…+,当n=k+1时,f(2k+1)=1+++…+++…+,所以f(2k+1)-f(2k)=1+++…+++…+-(1+++…+)=++…+.答案:++…+三、解答题13.已知数列{a n}满足a n+1=,a1=0,(1)计算a2,a3,a4,a5的值;(2)根据以上计算结果猜想{a n}的通项公式,并用数学归纳法证明你的猜想. 解:(1)由a n+1=和a1=0,得a2==,a3==,a4==,a5==.(2)由以上结果猜测:a n=,用数学归纳法证明如下:①当n=1时,左边=a1 =0,右边=0,等式成立;②假设当n=k(k≥1)时,命题成立,即a k=成立,那么,当n=k+1时,a k+1====,这就是说,当n=k+1时等式成立.由①和②,可知a n=对于任意正整数n都成立.14.已知S n=1++++…+(n>1,n∈N*).求证:>1+(n≥2,n∈N*).证明:(1)当n=2时,=1+++=>1+=2,不等式成立.(2)假设n=k(k≥2)时不等式成立,即=1++++…+>1+,当n=k+1时,=1++++…+++…+>1+++…+>1++=1++=1+.故当n=k+1时不等式也成立.综合(1)(2)知,对任意n∈N*,n≥2,不等式>1+都成立.15.已知数列{a n}(n∈N*),满足a1=1,2a n+1=a n+.(1)求证:<a n+1<a n;(2)设数列{a n}(n∈N*)的前n项和为S n,证明:S n<+.证明:(1)先证明a n+1>.n=1时,2a2=+,所以a2=+>,结论成立,假设n=k时,结论成立,即a k+1>,则n=k+1时,2a k+2=a k+1+>+1=, 所以a k+2>,即n=k+1时,结论成立,所以a n+1>,所以a n+1-a n=-a n+=-(-)2+<-(1-)2+=0.所以<a n+1<a n.(2)问题等价于证明S n-<,即(a i-)<,设b n=a n-,则b1=,2a n+1=a n+可化为2b n+1=b n+-1,所以=+·<,所以b n≤·()n-1,所以S n-<<,所以S n<+.巩固提高B一、选择题1.某个命题与正整数n有关,若n=k(k∈N*)时该命题成立,那么可推得n=k+1时该命题也成立,现在已知当n=5时该命题不成立,那么可推得( C )(A)当n=6时,该命题不成立(B)当n=6时,该命题成立(C)当n=4时,该命题不成立(D)当n=4时,该命题成立解析:对n=4不成立(否则n=5也成立).同理可推得P(n)对n=3,n=2,n=1也不成立.故选C.2.用数学归纳法证明1+a+a2+…+a n+1=(a≠1,n∈N*),在验证n=1时,等式左边是( C )(A)1 (B)1+a(C)1+a+a2 (D)1+a+a2+a3解析:根据数学归纳法的步骤可知,当n=1时,等式的左边应为1+a+a2,故选C.3.用数学归纳法证明等式1+2+3+…+2n=n(2n+1)时,由n=k到n=k+1时,等式左边应添加的项是( C )(A)2k+1(B)2k+2(C)(2k+1)+(2k+2)(D)(k+1)+(k+2)+ (2)解析:因为要证明等式的左边是连续正整数,所以当由n=k到n=k+1时,等式左边增加了[1+2+3+…+2k+(2k+1)+2(k+1)]-(1+2+3+…+2k)= (2k+1)+(2k+2),故选C.4.用数学归纳法证明1+2+22+…+2n-1=2n-1(n∈N*)的过程中,第二步假设当n=k时等式成立,则当n=k+1时增加了( A )(A)1个项(B)2个项(C)2k-1个项(D)2k个项解析:增加了1项2k.故选A.5.用数学归纳法证明“1+2+3+…+n3=,n∈N*”,则当n=k+1时,应当在n=k时对应的等式的两边加上( A )(A)(k3+1)+(k3+2)+…+(k+1)3(B)k3+1(C)(k+1)3(D)解析:当n=k时,左边为1+2+3+…+k3,当n=k+1时,左边为1+2+3+…+ k3+(k3+1)+(k3+2)+…+(k+1)3,所以左边增加的项为(k3+1)+(k3+2)+…+ (k+1)3.6.已知f(n)=++…+,则f(k+1)-f(k)等于( C )(A)(B)(C)++-(D)-解析:由f(k+1)=++…+=++…+,f(k)=++…+,所以f(k+1)-f(k)=++-,故选C.二、填空题7.用数学归纳法证明1+++…+<n(n∈N*,n>1)时,第一步应验证不等式. 解析:当n=2时,左边=1++=1++,右边=2,故应验证1++<2.答案:1++<28.用数学归纳法证明:1+++…+=时, 由n=k到n=k+1左边需要添加的项是.解析:当n=k时,1+++…+=,则当n=k+1时,1++…+ =+=+.答案:9.若f(n)=12+22+32+…+(2n)2,则f(k+1)与f(k)的递推关系式是.解析:因为f(k)=12+22+…+(2k)2,所以f(k+1)=12+22+…+(2k)2+(2k+1)2+(2k+2)2,所以f(k+1)=f(k)+(2k+1)2+(2k+2)2.答案:f(k+1)=f(k)+(2k+1)2+(2k+2)210.设平面上n个圆周最多把平面分成f(n)片(平面区域),则f(2)= ,f(n)= .(n≥1,n∈N*)解析:易知2个圆周最多把平面分成4片;n个圆周最多把平面分成f(n)片,再放入第n+1个圆周,为使得到尽可能多的平面区域,第n+1个应与前面n个都相交且交点均不同,有n 条公共弦,其端点把第n+1个圆周分成2n段,每段都把已知的某一片划分成2片,即f(n+1)=f(n)+2n(n≥1),所以f(n)-f(1)=n(n-1),而f(1)=2,从而f(n)=n2-n+2.答案:4 n2-n+211.观察下面算式:23=3+5;33=7+9+11;43=13+15+17+19;53=21+23+25+27+29;…203=a1+a2+a3+…,其中a1<a2<a3<…,那么a1= .解析:由给出的等式可知,等式的右侧奇数构成以3为首项,2为公差的等差数列,所以前18个等式共有2+3+…+19=189个奇数,所以第19个式子的右侧的第1个数是第190个奇数.所以a1=3+2×(190-1)=381.答案:38112.用数学归纳法证明:当x>-1时,n∈N*,(1+x)n≥1+nx,从n=k到n=k+1时需要证明的不等式是.解析:n=k时,(1+x)k≥1+kx.n=k+1时,(1+x)k+1=(1+x)k(1+x)≥(1+kx)(1+x),只要证右边大于等于1+(k+1)x即可.答案:(1+kx)(1+x)≥1+(k+1)x三、解答题13.在数列{a n}中,a1=6,且a n-a n-1=+n+1(n∈N*,n≥2).(1)求a2,a3,a4的值;(2)猜测数列{a n}的通项公式,并用数学归纳法证明.解:(1)a2=12,a3=20,a4=30.(2)猜测a n=(n+1)(n+2).下面用数学归纳法证明:①当n=1,2,3,4时,显然成立;②假设当n=k(k≥4,k∈N*)时成立,即有a k=(k+1)(k+2),则当n=k+1时,由a n-a n-1=+n+1得a n=a n-1+n+1,故a k+1=a k+k+1+1=(k+1)(k+2)+k+2=(k+2)2+(k+2)=(k+2)(k+3),故n=k+1时等式成立.由①②可知,a n=(n+1)(n+2)对一切n∈N*均成立.14.用数学归纳法证明:对一切大于1的正整数n,不等式(1+)(1+)…(1+)>均成立.证明:(1)当n=2时,左边=1+=,右边=.因为左边>右边,所以不等式成立.(2)假设n=k(k≥2,k∈N*)时不等式成立,即(1+)(1+)…(1+)>.则当n=k+1时,(1+)(1+)…(1+)[1+]>·==>==.所以当n=k+1时,不等式成立.由(1)(2)知,对于一切大于1的正整数n,不等式都成立.15.已知数列{a n}满足a1=3,a n+1=-na n+λ,n∈N*,λ∈R.(1)若a n≥2n恒成立,求λ的取值范围;(2)若λ=-2,求证:++…+<2.(1)解:当n=2时,由a2=6+λ≥2×2得λ≥-2,故a n≥2n时,λ≥-2,下面证λ≥-2时a n≥2n.n=2时,a2≥2×2成立;假设n=k(k≥2)时,a k≥2k,则n=k+1时,a k+1=-ka k+λ=a k(a k-k)+λ≥2k2-2=2(k+1)(k-1)≥2(k+1), 故对任意的n≥2,a n≥2n.n=1时,a1=3≥2×1也成立,故对任意n∈N*,a n≥2n成立.故λ的取值范围为[-2,+∞).(2)证明:λ=-2,由(1)知a n+1-2=-na n-4≥na n-4≥2(a n-2)(n≥2),≤·≤…≤·=(n≥2)从而++…+≤1+++…+=2-<2.。
