湖南省长沙市开福区青竹湖湘一外国语学校2019-2020年九年级(上)第三次月考数学试卷 解析版
青竹湖 2019-2020初三第一学期第三次月考

青竹湖2019-2020初三第一学期第三次月考Ⅱ.知识运用(两部分,共20小题,计20分)第一节语法填空从题中所给的A、B、C三个选项中选择最佳答案填空(共10小题,计10分)21. Thanks for staying by my side at the painful times. I see it as memory I’ve ever had.A. valuableB. more valuableC. the most valuable22. —Does the pink toy piggy belong to ?—No. is a purple one.A. hers; HersB. her; HersC. her; Her23. In my eyes, sticking my dreams means not only working hard but also being always ready to clean off everything that gets the way of my victory.A. to; inB. with; inC. to; on24. —Could you tell me more about the movie Frozen II you have watched it.—No problem. But you’d better watch it in person I can’t express its beauty.A. since; soB. unless; asC. since; as25. This is one of my favorite TV dramas that this year.A. has been shownB. have been-shownC. have shown26.—We be allowed computer games for the homework hasn't be done.—I suppose so. You know how strict our parents are!A. must; playingB. might; to playC. can’t: to play27. great fun the noise maker had fear in the neighborhood!A. What creatingB. How; creatingC. What; to create28. the Yangtze River from being polluted, the volunteers prefer the rubbish along it in their spare time rather than stay at home.A. Protect; to pick upB. Protecting; picking upC. To protest: to pick up29. We may forget we started to become good friends, but we will never forget the days we spent together.A. when; whichB. when; whoC. that; which30.—How long do you think ?—It might take 10 years, according to Ren Zhengfei, CEO of Huawei.A. will it take to fully develop 66B.it will take to fully develop 6GC. will take it to fully develop 6G第二节词语填空通读下面的短文,掌握其大意,然后从各题所给的A、B、C 三个选项中选出最佳答案。
湖南省长沙市青竹湖湘一外国语学校2021-2022学年九年级上学期第三次月考数学试卷

青竹湖湘一外国语学校2021-2022学年度九年级上学期第三次练习数学时量:120分钟总分:120分一、单选题(每小题3分,共30分) 1.下列各数中,为负数的是() A .3-B .()3+-C .()3--D .()23-2.下列计算正确的是() A .235a a a +=B .3322a b b a ÷=C .()42828a a =D .()222a b a b -=-3.下列说法正确的是()A .圆既是轴对称图形又是中心对称图形B .0的倒数是0C .“太阳从西边出来”是随机事件D .三角形的内心到三角形三个顶点的距离相等 4.新冠病毒由蛋白质外壳和单链核酸组成,直径大约在60~140纳米(1纳米=0.0000001厘米)某冠状病毒的直径约0.0000135厘米.数据“0.0000135”用科学记数法表示为()A .61.3510-⨯B .613.510-⨯C .51.3510-⨯D .40.13510-⨯ 5.如图,把一个含有45°角的直角三角板放在两条平行线m ,n 上,若∠α=118°,则∠β的度数是() A .63° B .73° C .75° D .83°第5题图第6题图第7题图6.如图,AC 、BD 交于O 点,AD ∥BC ∥EO ,则下列结论一定正确的是() A .AE AD EB BC = B .AO EO OC AD = C .AE EO EB BC = D .AE DOAB OB =7.如图,菱形ABCD 的周长为16,∠A :∠B=1:2,则菱形的面积为()A .B .C .D .8.已知一次函数y kx k =-的图像过点(3-,4),则下列结论正确的是() A .y 随x 增大而增大 B .1k = C .直线过点(1,0) D .直线过原点9.如图,△ABC ∽△ADE ,且BC=2DE ,则S 四边形BEDC :S △ABC 的值为() A .1:4 B .3:4 C .2:3 D .1:210.如图,在平面直角坐标系中,反比例函数ky x=(0x >,0k >)的图象经过矩形ABCD 的顶点C 、D ,∠BAO=60°,且A (1,0),B 点横坐标为1-,则k 的值为()A B . C .D第9题图第10题图第16题图二、填空题(每小题3分,共18分)11.分解因式:2218m-=.12.实数x、y满足关系式2y=,则xy=.13.若圆锥的母线长为6cm,侧面展开图的面积为224cmπ,则底面半径是cm.14.若单项式15n x y-和27mx y是同类项,则m n+的值为.15.在△ABC中,90C∠=︒,若1tan3B=,则cos A=.16.如图,正方形ABCD的边长为12,⊙B的半径为6,点P是⊙B上一个动点,则12PD PC+的最小值为.三、解答题(第17-19题各6分,第20、21题各8分,第22、23题各9分,第24、25题各10分,共72分)172122sin602-⎛⎫+︒+--⎪⎝⎭.18.先化简,再求值:222214244a aa a a a+⎛⎫-÷⎪--++⎝⎭;请在12a-<≤中选择一个合适的整数代入求值.19.平面直角坐标系中,△ABC 的三个顶点坐标分别为A (1,2-),B (1,1-),C (4,3-).(1)画出111A B C △,使它与△ABC 关于x 轴对称;(2)以原点为位似中心,在第一象限....画出111A B C △的位似图形222A B C △,使222A B C △与111A B C △的相似比为2:1;(3)若将222A B C △绕原点顺时针旋转90°得到333A B C △,求点C 2经过的路径长.20.中华文化,源远流长,在古典文学方面,《西游记》《三国演义》《水浒传》《红楼梦》(分别记作A 、B 、C 、D )是我国古代长篇小说中的典型代表,被称为“四大名著”.我校为了了解学生对四大名著的阅读情况,就“四大名著你读完了几部?”的问题在全校学生中进行了抽样调查.根据调查结果绘制成如所示的两个不完整的统计图,请结合图中信息解决下列问题:(1)本次调查一共抽取了_____名学生;扇形统计图中“1部”所在扇形的圆心角为_____度; (2)被抽取的学生四大名著阅读数量的平均数为______本;(3)若没有读过四大名著的两名学生准备从四大名著中各自随机选择一部来阅读,请你用列表法或列树状图法求他们选中同一种名著的概率.21.如图,在菱形ABCD中,对角线AC,BD交于点O,过点A作AE⊥BC于点E,延长BC 到点F,使CF=BE,连接DF.(1)求证:四边形AEFD是矩形;(2)若AD=10,EC=4,求OE的长度.22.2021年10月17日是我国第8个扶贫日,也是第29个国际消除贫困日.为组织开展好扶贫日系列活动,加快脱贫攻坚步伐.我市决定将一批生姜送往外地销售.现有甲、乙两种货车,已知甲种货车比乙种货车每辆车多装20箱生姜,且甲种货车装运1000箱生姜所用车辆与乙种货车装运800箱生姜所用车辆相等.(1)求甲、乙两种货车每辆车可装多少箱生姜?(2)如果这批生姜有1535箱,用甲、乙两种汽车共16辆来装运,甲种车辆刚好装满,乙种车辆最后一辆只装了55箱,其它装满,求甲、乙两种货车各有多少辆?23.如图,⊙O经过△ABC的顶点A、C,并与AB边相交于点D,过点D作DF//BC,交AC 于点E,交⊙O于点F,连接DC,点C为弧DF的中点.(1)求证:BC为⊙O的切线;(2)若⊙O的半径为3,DF=CE CA⋅的值;(3)在(2)的条件下,连接AF,若BD AF=,求AD的长.24.如图1,在平面直角坐标系中,抛物线223y ax ax a =--(0a <)交x 轴于A 、B 两点(A 在B 的左侧),交y 轴于点C ,点D 是抛物线的顶点,对称轴交x 轴于E 点,且OB=OC . (1)求抛物线的解析式;(2)连接BD ,抛物线上是否存在点F ,使FBO BDE ∠=∠?若存在,求出点F 的坐标;若不存在,说明理由;(3)如图2,点P 是直线5y =上的动点(点P 不在抛物线的对称轴上),过点P 的两条直线1l ,2l 与抛物线均只有唯一公共点,且都不与y 轴平行,1l ,2l 分别交抛物线的对称轴于点M 、N ,点G 为抛物线对称轴上点M 、N 下方一点,且总满足2GP GM GN =⋅,求点G 的坐标.25.我们知道,如图1,点P为线段AB上一点,且PA PB>,如果PB PAkPA AB==,那么点P是线段AB的一个黄金分割点,比值k=0.618≈)叫做黄金分割比.(1)如图1,若线段AB的长为2,P是线段AB的黄金分割点(PA PB>),则PB的长为_______;(保留根号)(2)如图2,在△ABC中,D、E分别是边AB、BC的黄金分割点,其中BD AD>,BE CE>,AE与CD相交于点O,若△AOC的面积为2,求△ABC的面积;(3)如图3,直线2y x=-与抛物线222y x mx m m=---++(m为常数)交于M、N两点,若点O为线段MN的黄金分割点(OM ON<),求m的值.青竹湖湘一外国语学校2021-2022学年度九年级上学期第三次练习数学参考答案时间:120分钟总分:120分一、选择题(每小题3分,共30分)二、填空题(每小题3分,共18分) 11.()()233m m +- 12.2-13.414.415 16.15三、解答题(共9小题,第17、18、19题每题6分,第20、21题每题8分,第22、23题每题9分,第24、25题每题10分,共72分) 17.原式=5 18.22a a +-,当1a =时,原式=3- 19.(1)(2)如图所示(3)5π20.(1)本次调查被调查的学生10÷25%=40(人),扇形统计图中“1部”所在扇形的圆心角为126度 (2)2.05(3)将《西游记》、《三国演义》、《水浒传》、《红楼梦》分别记作A ,B ,C ,D , 画树状图可得:共有16种等可能的结果,其中选中同一名著的有4种, 故P (两人选中同一名著)=41164=. 21.(1)证明:∵四边形ABCD 是菱形, ∴AD ∥BC 且AD=BC , ∵BE=CF , ∴BC=EF , ∴AD=EF , ∵AD ∥EF ,∴四边形AEFD 是平行四边形, ∵AE ⊥BC , ∴∠AEF=90°, ∴四边形AEFD 是矩形;(2)∵四边形ABCD 是菱形,AD=10, ∴AD=AB=BC=10, ∵EC=4, ∴BE=10-4=6在Rt △ABE 中,勾股定理得AE=8在Rt △AEC 中,勾股定理得AC=∴12OE AC ==22.解:(1)设乙种货车每辆车可装x 箱生姜,则甲种货车每辆车可装(x+20)箱生姜,依题意,得:100080020x x=+,解得:x=80,经检验,x=80是原方程的解,且符合题意,∴x+20=100.答:甲种货车每辆车可装100箱生姜,乙种货车每辆车可装80箱生姜.(2)设甲种货车有m辆,则乙种货车有(16-m)辆,依题意,得:100m+80(16-m-1)+55=1535,解得:m=14,∴16-m=2.答:甲种货车有14辆,乙种货车有2辆.23.(1)证明:连接CO并延长交⊙O于G,连接DG,如图:∵CG为直径,∴∠GDC=90°,∴∠DCG+∠DGC=90°,∵∠DGC=∠BAC,点C为弧DF的中点∴∠CDF=∠BAC,∴∠DGC=∠CDF,∴∠DCG+∠CDF=90°,∵DF∥BC,∴∠CDF=∠DCB,∴∠DCG+∠DCB=90°,∴OC⊥BC,又∵OC是⊙O的半径∴BC为⊙O的切线;(2)12CE CA⋅=(3)3AD=24.(1)对于抛物线y=ax2-2ax-3a,令y=0,得到ax2-2ax-3a=0,解得x=-1或3,∴A(-1,0),B(3,0),∴OA=1,OB=OC=3,∴C(0,3),∴-3a=3,∴a=-1,∴抛物线的解析式为y=-x2+2x+3.(2)点F的坐标为(32-,94-)或(12-,74)(3)点G的坐标为(1,154)25.(1)3PB=-(2)△ABC的面积为4+(3)14m=。
精品解析:2023年湖南省长沙市开福区青竹湖湘一外国语学校中考三模化学试题(原卷版)

A.AB.BC.CD.D
14.同学们学完初中化学后掌握了很多生活除渍或除垢的方法。下列有关说法或做法正确的是
A.可以用盐酸除金属表面的铁锈
B.水垢的主要成分是碳酸钙和氢氧化镁,可以用烧碱溶液除去水垢
C.稀硫酸可以除去油烟机上的油污
D.洗碗时用洗洁精去油污的原理是洗洁精能溶解油污
(3)将乙的饱和溶液变为不饱和溶液的方法有______(写一种)。
19.世界棉花看中国,中国棉花君新疆1新疆长绒棉,世界顶级,长年供不应求。长绒棉可做衣被,暖和、透气、舒适。长绒棉还可以用来制作纸币,人民币的主要成分就有棉花纤维。
(1)棉花、羊毛和涤纶是常见 服装面料纤维,为了鉴别它们,可以分别点燃闻气味,其中燃烧能产生烧焦羽毛气味的纤维是______。
C.乌头碱属于有机物
D.乌头碱中 、 原子个数比为
5.漂白粉可用于自来水的杀菌消毒,其有效成分是次氯酸钙[化学式为Ca(C1O)2]。次氯酸钙可发生如下反应: ,则X的化学式为
A. Cl2B. CO2C. CaCl2D. O2
6.“归纳与比较”是化学学习的主要方法,下列关于 与 的说法正确的是
A.组成:二氧化碳与一氧化碳都由碳元素和氧元素组成
步骤⑤:取少量“暖宝宝”中的粉末于烧杯中,加入一定量的稀盐酸,观察到产生气泡,再次证明“暖宝宝”中含有铁。
(3)小黄发现上述实验步骤⑤中用到了稀盐酸,如果将反应后的废液直接倒入下水道可能会因为盐酸过量导致严重的水污染。小黄取少量步骤⑤实验后得到的废液滴加两滴稀氢氧化钠溶液,观察到无明显现象,则步骤⑤实验后得到的废液中的溶质为_______(填化学式)。小黄于是将上述废液倒入废液桶后集中处理。
钠
锂
湖南省长沙市青竹湖湘一外国语学校2020年初三中考第三次全真模拟考试数学试卷

青竹湖湘一外国语学校2020年初三中考三模试卷数学注意事项:1.答题前,请考生先将自己的姓名、准考证号填写清楚,并认真核对条形码上的姓名、准考证号、考室和座位号;2.必须在答题卡上答题,在草稿纸、试题卷上答题无效; 3.答题时,请考生注意各大题题号后面的答题提示; 4.请勿折叠答题卡,保持字体工整、笔迹清晰、卡面清洁; 5.答题卡上不得使用涂改液、涂改胶和贴纸;6.本学科试卷共26个小题,考试时量120分钟,满分120分.一、选择题(在下列各题的四个选项中,只有一项是符合题意的。
请在答题卡中填涂符合题意的选项。
本大题共12个小题,每小题3分,共36分) 一、选择题(本大题共12小题、每题3分,共36分) 1.下列运算正确的是( ) A .2a a a -= B .()326aa -=-C .632x x x ÷= D .()222x y x y +=+ 2.下列说法正确的是( )A.a -一定是负数B.73是有理数D.平方根等于它本身的数是0和13.地球上的海洋面积约为361 000 000 2km ,用科学记数法可表示为( )2km .A .90.36110⨯B .93.6110⨯C .83.6110⨯D .736.110⨯4.已知点P (a -,1a -)在平面直角坐标系的第二象限,则a 的取值范围在数轴上可表示为( )A B C DA. B.C. D.5.已知等腰三角形的一个角是80°,则这个三角形的顶角是()A.20°B.80°C.100°D.20°或80°6.如图,在四个几何体中,主视图与其它几何体的主视图的形状不同的是()7.有一圆锥,它的高为8cm,底面半径为6cm,则这个圆锥的侧面积是()A.30πB.48πC.60πD.80π8.如图,AB是O的直径,若∠BAC=35°,那么∠ADC的度数为()A.35°B.45°C.55°D.70°9.为备战奥运会,甲乙两位射击运场员在一次训练中的成绩为(单位,环)甲:9 10 9 8 10 9 8乙:8 9 10 7 10 8 10下列说法正确的是()A.甲的中位数为8B.乙的平均数为9C.甲的众数为9D.乙的极差为210.下列函数,当0x>时,y随x的增大而增大的是()第16题图 第18题图A.2y x =-B.2y x=C.()221y x =+D.21y x =-+ 11.尺规作图作∠AOB 的平分线(如图)方法如下:以O 为圆心,任意长为半径画弧交OA ,OB 于C ,D ,再分别以点C ,D 为圆心,以大于12CD 长为半径画弧,两弧交于点P ,作射线OP .由作法得△COP ≌△DOP 的根据是( )A. SASB. ASAC. AASD. SSS12.若不等式组12x x m<≤⎧⎨>⎩有解,则m 的取值范围是( )A.2m <B.2m ≥C.1m <D.12m ≤< 二、填空题(本大题共6小题,每题3分,共18分)13.计算:2111m m m -=++ . 14.设α,β是一元二次方程2370x x +-=的两个根,则24ααβ++= .15.已知实数x 满足22162x x +=.则1x x+的值是 . 16.如图,为测量某物体AB 的高度,在D 点测得A 点的仰角为30°,朝物体AB 方向前进20米,到达点C ,再次测得点A 的仰角为60°,则物体AB 的高度为 . 17.“水中捞月”是一个 事件.18.如图,在矩形ABCD 中,O 为AC 中点,EF 过O 点且EF ⊥AC 分别交DC 于F ,交AB 于E ,点G 是AE 中点且∠AOG=30°,则下列结论正确的是 . (1)DC=3OG ; (2)OG=12BC ; (3)△OGE 是等边三角形; (4)16AOEABCD S S =.三、解答题(本大题共8个小题,第19、20题每小题6分,第21、22题每小题8分,第23、24题每小题9分,第25、26题每小题10分,共66分。
2020年青竹湖湘一外国语学校初三中考三模考试化学试卷

青竹湖湘一外国语学校2019-2020学年度初三中考第三次模拟考试化学问卷本试卷中g取10N/kg可能用到的相对原子质量:H~1、C~12、N~14、O~16、S~32、Na~23、Ca~40、Zn~65、Fe~56一、选择题(本大题共27个小题,每小题3分,共81分,在每小题提供的四个选项中,只有一项符合题目的要求)1.化学改变世界的途径是使物质发生化学变化。
下列属于化学变化的是()A.冰块制成冰雕B.利用海水淡化膜从海水中获得淡水C.泥土烧成瓷器D.工业上从空气中分离出氧气2.下图所示实验装置或实验操作正确的是()A.除去CO中少量的CO2B.滴加液体C.加热蒸发NaCl溶液D.稀释浓H2SO43.原子、分子、离子等微粒都是构成物质的粒子。
下列叙述错误的是()A.原子是化学变化中的最小粒子B.由分子构成的物质,分子是保持其化学性质的最小粒子C.整个原子的质量主要集中在原子核上D.离子是带电的粒子,带电的粒子一定是离子4.下列关于水的净化过程的描述中,错误的是()A.加入明矾使小颗粒凝聚后沉降B.通入氯气杀菌消毒C.通过沙滤装置除去可溶性杂质D.通过活性炭吸附掉一些溶解的杂质,除去臭味5.在一密闭容器内加入甲、乙、丙、丁四种物质,在一定条件下发生化学反应,反应前后各物质的质量变化见下表。
下列说法中正确的是()A.C.甲一定属于单质D.该反应前后原子种类发生了改变6.小轩同学编写的化学小报中有如下标题,其中某标题下文章中的主角是一氧化碳,该标题可能是()A.PM2.5与雾霾天气B.新装修房屋内空气中的杀手C.形成酸雨的罪魁祸首D.燃气热水器安装在居室内的危险7.调查统计表明,很多火灾伤亡事故是由于缺乏自救常识造成的,下列自救措施中,正确的是()A.家用电器着火时,立即用水扑灭B.炒菜时油锅着火,立即盖上锅盖C.高层住房着火时,立即乘坐电梯逃离D.发现煤气泄漏时,立即打开排油烟机排气8.口罩、84消毒液、医用酒精等是抗击“新冠”疫情的常用物品。
2019-2020-1青一九上 第三次月考-答案

t 2 0
∴
t
2
4
0
t
2Leabharlann ∴ E 2, 4直线 CD : y kx 2k 5 过定点 2,5 E 到 CD 最大距离为: 2 22 4 52 17 ;
26、【解析】(1)∴点 B 坐标为 (2, 0) ,点 E 坐标为 (m, 0)
(2)∵
S
BCE
=
1 2
BC
EO;
1 2
m
2
2
6;
20.【解析】原式
m 1 m2
2m 1 m 12
2 m
2
将m
2 2 代入得:
2 2 22
2
21.【解析】(1) 200
(2)
(3) 60 1000 300 (人) 200 1
(4)
6
22.【解析】(1)过 P 点作 PQ AB 于 Q ,在 RtAPQ 中, PQ 2 AP 40 2 60
2
2
AB : y 1 (m n)x 2
2
;
AB 直线过 (0, 2)
y kx 2k 5
(3)
y
x2
x2 kx 2k 5 0
设 C x1, y1 , D x2, y2 , E t,t2
x1 x2 k , x1 x2 2k 5
∵ CED 90
∴ kCE kDE 1
n2
∵点 P 在第四象限;
∴ n m 2; n m 2;
∴
P
m
2,
2
8 m
;
kCE
y1 t 2 x1 t
x12 t 2 x1 t
x1 t
kDE
y2 t2 x2 t
x22 t 2 x2 t
湖南省长沙市开福区青竹湖湘一外国语学校2019-2020学年九年级(上)期中数学试卷(解析版)
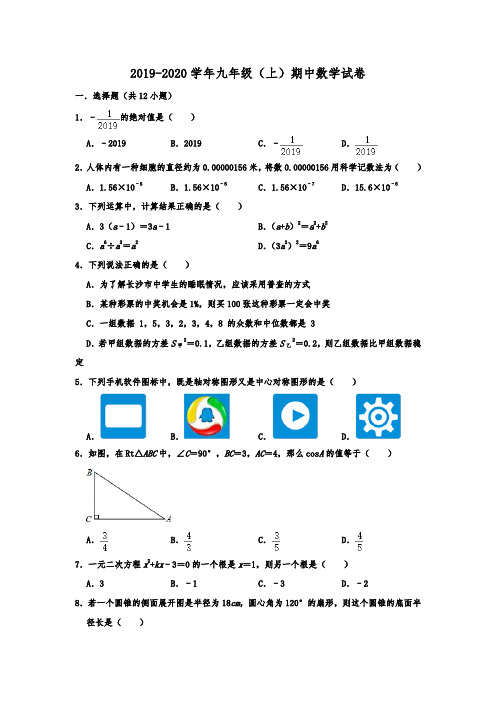
2019-2020学年九年级(上)期中数学试卷一.选择题(共12小题)1.﹣的绝对值是()A.﹣2019 B.2019 C.﹣D.2.人体内有一种细胞的直径约为0.00000156米,将数0.00000156用科学记数法为()A.1.56×10﹣5B.1.56×10﹣6C.1.56×10﹣7D.15.6×10﹣63.下列运算中,计算结果正确的是()A.3(a﹣1)=3a﹣1 B.(a+b)2=a2+b2C.a6÷a3=a2D.(3a3)2=9a64.下列说法正确的是()A.为了解长沙市中学生的睡眠情况,应该采用普查的方式B.某种彩票的中奖机会是1%,则买100张这种彩票一定会中奖C.一组数据 1,5,3,2,3,4,8 的众数和中位数都是 3D.若甲组数据的方差S甲2=0.1,乙组数据的方差S乙2=0.2,则乙组数据比甲组数据稳定5.下列手机软件图标中,既是轴对称图形又是中心对称图形的是()A.B.C.D.6.如图,在Rt△ABC中,∠C=90°,BC=3,AC=4,那么cos A的值等于()A.B.C.D.7.一元二次方程x2+kx﹣3=0的一个根是x=1,则另一个根是()A.3 B.﹣1 C.﹣3 D.﹣28.若一个圆锥的侧面展开图是半径为18cm,圆心角为120°的扇形,则这个圆锥的底面半径长是()A.3cm B.4.5cm C.6cm D.9cm9.如图在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交AC、AB 于点M、N,再分别以M、N为圆心,大于MN的长为半径画弧,两弧交于点P,作射线AP交BC于点D,若CD=2,AB=8,则△ABD的面积是()A.16 B.32 C.8 D.410.如果一个正多边形的内角和为720°,那么这个正多边形的每一个外角是()A.60°B.120°C.135°D.45°11.如图,在平面直角坐标系中,∠AOB=90°,∠OAB=30°,反比例函数y1=的图象经过点A,反比例函数y2=﹣的图象经过点B,则m的值是()A.m=3 B.C.D.12.如图,在正方形ABCD中,E、F分别为BC、CD的中点,连接AE、BF交于点G,将△BCF 沿BF对折,得到△BPF,延长FP交BA的延长线于点Q,则下列结论:①AE=BF;②S四=S△ABG;③△BFQ是等腰三角形;④;其中一定正确的个数是()边形ECFGA.1个B.2个C.3个D.4个二.填空题(共6小题)13.在函数y=中,自变量x的取值范围是.14.分解因式:2m3﹣8m2+8m=.15.如图,点A、B、C都在圆O上,如果∠AOB+∠ACB=90°,那么∠ACB的大小是.16.半径为4的圆内接正六边形的面积是.17.如图,在Rt△ABC中,∠ACB=90°,CD为AB边上的高,若AD=6,BD=18,则AC的长等于.18.二次函数y=ax2+bx+c(a、b、c为常数且a≠0)中的x与y的部分对应值如表:x﹣1 0 1 3y﹣1 3 5 3给出了结论:①二次函数y=ax2+bx+c有最大值,最大值为5;②ac<0;③x>1时,y 的值随x值的增大而减小;④3是方程ax2+(b﹣1)x+c=0的一个根;⑤当﹣1<x<3时,ax2+(b﹣1)x+c>0,则其中正确结论是.三.解答题(共8小题)19.计算:20160+|1﹣|﹣2cos30°﹣(﹣)﹣120.解方程:+=1.21.西宁市教育局自实施新课程改革后,学生的自主学习、合作交流能力有很大提高.张老师为了了解所教班级学生自主学习、合作交流的具体情况,对本班部分学生进行了为期半个月的跟踪调查,将调查结果分成四类,A:特别好;B:好;C:一般;D:较差;并将调查结果绘制成以下不完整的统计图,请你根据统计图解答下列问题:(1)本次调查中,张老师一共调查了名同学;(2)将上面的条形统计图补充完整;(3)为了共同进步,张老师想从被调查的A类和D类学生分别选取一位同学进行“一帮一”互助学习,请用列表法或画树形图的方法列出所有等可能的结果,并求出所选两位同学恰好是一位男同学和一位女同学的概率.22.如图,在平面直角坐标系中,△OAB的顶点坐标分别为O(0,0)、A(2,1)、B(1,﹣2).(1)以原点O为位似中心,在y轴的右侧画出△OAB的一个位似△OA1B1,使它与△OAB 的相似比为2:1,并写出点A的对应点A1的坐标;(2)画出将△OAB向左平移2个单位,再向上平移1个单位后的△O2A2B2,并写出点A2的坐标;(3)判断△OA1B1与△O2A2B2,能否是关于某一点M为位似中心的位似图形?若是,请在图中标出位似中心M,并写出点M的坐标.23.为了落实党的“精准扶贫”政策,A、B两城决定向C、D两乡运送肥料以支持农村生产,已知A、B两城共有肥料500吨,其中A城肥料比B城少100吨,从A城往C、D两乡运肥料的费用分别为20元/吨和25元/吨;从B城往C、D两乡运肥料的费用分别为15元/吨和24元/吨.现C乡需要肥料240吨,D乡需要肥料260吨.(1)A城和B城各有多少吨肥料?(2)设从A城运往C乡肥料x吨,总运费为y元,求出最少总运费.(3)由于更换车型,使A城运往C乡的运费每吨减少a(0<a<6)元,这时怎样调运才能使总运费最少?24.如图,在△ABC中,AB=AC,以AB为直径作圆O,分别交BC于点D,交CA的延长线于点E,过点D作DH⊥AC于点H,连接DE交线段OA于点F.(1)求证:DH是圆O的切线;(2)若A为EH的中点,求的值;(3)若EA=EF=1,求圆O的半径.25.在平面直角坐标系xOy中的点P(x,y)(x≠0),将它的纵坐标y与横坐标x的比称为点P的“湘一比”,记为k p,如点P(﹣3,6),则k p==﹣2.(1)若P(a,2)在直线y=x﹣2上,求点P的“湘一比”k p及直线OP与x轴夹角的正切值;(2)已知点Q(m,n)的“湘一比”k Q为,且Q在y=(x>0),⊙Q的半径为1,若点M在⊙Q上,求M的“湘一比”k M的取值范围;(3)设m、n为正整数,且m≠2,对一切实数t,如果直线y=mtx+3mt与二次函数y=x2+3x交于A(x1,y1),B(x2,y2),且|x1﹣x2|≥|2t+n|,求点N(m,n)的“湘一比”k N的值.26.如图,直线y=x+2与抛物线y=x2﹣2mx+m2+m交于A、B两点(A在B的左侧),与y 轴交于点C,抛物线的顶点为D,抛物线的对称轴与直线AB交于点M.(1)当四边形CODM是菱形时,求点D的坐标;(2)若点P为直线OD上一动点,求△APB的面积;′(3)作点B关于直线MD的对称点B',以点M为圆心,MD为半径作⊙M,点Q是⊙M上一动点,求QB'+QB的最小值.参考答案与试题解析一.选择题(共12小题)1.﹣的绝对值是()A.﹣2019 B.2019 C.﹣D.【分析】根据绝对值的定义,的绝对值是指在数轴上表示的点到原点的距离,即可得到正确答案.【解答】解:||=.故的绝对值是.故选:D.2.人体内有一种细胞的直径约为0.00000156米,将数0.00000156用科学记数法为()A.1.56×10﹣5B.1.56×10﹣6C.1.56×10﹣7D.15.6×10﹣6【分析】根据科学记数法的方法可以表示题目中的数据,从而可以解答本题.【解答】解:0.00000156=1.56×10﹣6,故选:B.3.下列运算中,计算结果正确的是()A.3(a﹣1)=3a﹣1 B.(a+b)2=a2+b2C.a6÷a3=a2D.(3a3)2=9a6【分析】根据去括号法则,完全平方公式,同底数幂的除法,幂的乘方与积的乘方法则作答.【解答】解:A、3(a﹣1)=3a﹣3,故本选项错误;B、(a+b)2=a2+2ab+b2,故本选项错误;C、a6÷a3=a3,故本选项错误;D、(3a3)2=9a6,故本选项正确.故选:D.4.下列说法正确的是()A.为了解长沙市中学生的睡眠情况,应该采用普查的方式B.某种彩票的中奖机会是1%,则买100张这种彩票一定会中奖C.一组数据 1,5,3,2,3,4,8 的众数和中位数都是 3D.若甲组数据的方差S甲2=0.1,乙组数据的方差S乙2=0.2,则乙组数据比甲组数据稳定【分析】利用概率的意义,全面调查与抽样调查,中位数,众数,以及方差的定义判断即可.【解答】解:A、为了解长沙市中学生的睡眠情况,应该采用抽样调查的方式,不符合题意;B、某种彩票的中奖机会是1%,则买100张这种彩票可能会中奖,不符合题意;C、一组数据1,5,3,2,3,4,8,按照从小到大的顺序排列为1,2,3,3,4,5,8,其众数中位数都是3,符合题意;D、若甲组数据的方差S甲2=0.1,乙组数据的方差S乙2=0.2,则甲组数据比乙组数据稳定,不符合题意,故选:C.5.下列手机软件图标中,既是轴对称图形又是中心对称图形的是()A.B.C.D.【分析】根据中心对称图形的定义旋转180°后能够与原图形完全重合即是中心对称图形,以及轴对称图形的定义即可判断出.【解答】解:A、∵此图形旋转180°后不能与原图形重合,∴此图形不是中心对称图形,是轴对称图形,故A选项错误;B、∵此图形旋转180°后不能与原图形重合,∴此图形不是中心对称图形,也不是轴对称图形,故B选项错误;C、∵此图形旋转180°后不能与原图形重合,∴此图形不是中心对称图形,是轴对称图形,故C选项错误;D、∵此图形旋转180°后能与原图形重合,∴此图形是中心对称图形,也是轴对称图形,故D选项正确.故选:D.6.如图,在Rt△ABC中,∠C=90°,BC=3,AC=4,那么cos A的值等于()A.B.C.D.【分析】首先运用勾股定理求出斜边的长度,再利用锐角三角函数的定义求解.【解答】解:∵在Rt△ABC中,∠C=90°,AC=4,BC=3,∴AB=.∴cos A=,故选:D.7.一元二次方程x2+kx﹣3=0的一个根是x=1,则另一个根是()A.3 B.﹣1 C.﹣3 D.﹣2【分析】根据根与系数的关系可得出两根的积,即可求得方程的另一根.【解答】解:设m、n是方程x2+kx﹣3=0的两个实数根,且m=x=1;则有:mn=﹣3,即n=﹣3;故选:C.8.若一个圆锥的侧面展开图是半径为18cm,圆心角为120°的扇形,则这个圆锥的底面半径长是()A.3cm B.4.5cm C.6cm D.9cm【分析】设这个圆锥的底面半径为rcm,根据圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长和弧长公式得到2πr=,然后解方程求出r即可.【解答】解:设这个圆锥的底面半径为rcm,根据题意得2πr=,解得r=6,所以这个圆锥的底面半径长为6cm.故选:C.9.如图在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交AC、AB 于点M、N,再分别以M、N为圆心,大于MN的长为半径画弧,两弧交于点P,作射线AP交BC于点D,若CD=2,AB=8,则△ABD的面积是()A.16 B.32 C.8 D.4【分析】作DH⊥AB于H.利用角平分线的性质定理证明DH=DC=2即可解决问题.【解答】解:作DH⊥AB于H.由作图可知:PA平分∠CAB,∵DC⊥AC,DH⊥AB,∴DH=DC=2,∴S△ABD=•AB•DH=×8×2=8,故选:C.10.如果一个正多边形的内角和为720°,那么这个正多边形的每一个外角是()A.60°B.120°C.135°D.45°【分析】首先设这个正多边形的边数为n,根据多边形的内角和公式可得180(n﹣2)=720,继而可求得答案.【解答】解:设这个正多边形的边数为n,∵一个正多边形的内角和为720°,∴180(n﹣2)=720,解得:n=6,∴这个正多边形的每一个外角是:360°÷6=60°.故选:A.11.如图,在平面直角坐标系中,∠AOB=90°,∠OAB=30°,反比例函数y1=的图象经过点A,反比例函数y2=﹣的图象经过点B,则m的值是()A.m=3 B.C.D.【分析】根据∠AOB=90°,∠OAB=30°,可求出OA与OB的比,设出点B的坐标,再根据相似三角形的性质,求出点A的坐标,进而求出m的值.【解答】解:过A、B分别作AM⊥x轴,BN⊥x轴,垂足为M、N,∵∠AOB=90°,∠OAB=30°,∴tan30°==,由△BON∽△OMA得,===,设ON=a,BN=b,则MA=a,OM=b,∴B(﹣a,b),A(a,b),∵点B在反比例函数y2=﹣的图象上,∴ab=1,∵点A在反比例函数y1=的图象上,∴m=a•b=3ab=3,故选:A.12.如图,在正方形ABCD中,E、F分别为BC、CD的中点,连接AE、BF交于点G,将△BCF 沿BF对折,得到△BPF,延长FP交BA的延长线于点Q,则下列结论:①AE=BF;②S四=S△ABG;③△BFQ是等腰三角形;④;其中一定正确的个数是()边形ECFGA.1个B.2个C.3个D.4个【分析】①根据正方形的性质和已知条件即可证明AE=BF;②根据三角形ABE和三角形BFC面积相等即可证明S四边形ECFG=S△ABG;③根据折叠可得∠CFB=∠PFB,DC∥AB得∠CFB=∠FBA,等量代换后即可证明△BFQ是等腰三角形;④可以设正方形边长为1,AQ=x,AH=y,作FI⊥AB于点I,进而根据对应边成比例用含x的式子表示y,再根据勾股定理即可求出x的值,进而可得.【解答】解:①∵在正方形ABCD中,E、F分别为BC、CD的中点,∴△BFC≌△AEB(SAS),∴AE=BF;所以①正确;②∵△BFC≌△AEB∴S△BFC=S△ABE∴S BFC﹣S△BGE=S△ABE﹣S△BGE∴S四边形ECFG=S△ABG所以②正确;③∵由折叠可知:∠CFB=∠PFB,∵DC∥AB,∴∠CFB=∠FBA∴∠PFB=∠FBA∴QF=QB∴△BFQ是等腰三角形,所以③正确;④如图所示:设PQ与AD交于点H,作FI⊥AB于点I,得矩形DAIF,设正方形边长为1,AQ=x,AH=y,则FI=AD=1,AI=,QI=x+在Rt△AQH和FIQ中,tan∠Q==,即=∴y=在Rt△AHQ中,根据勾股定理,得x2+y2=y2(1+x)2x2+()2=()2(1+x)2等式两边同乘以()2并化简得,4x=1,x=(=6≠0,检验合理)∴sin∠Q====∴;所以④正确.一定正确的是①②③④.故选:D.二.填空题(共6小题)13.在函数y=中,自变量x的取值范围是x≥﹣1 .【分析】根据被开方数大于等于0,分母不等于0解答.【解答】解:由题意得,1+x≥0且x+2≠0,解得x≥﹣1且x≠﹣2,所以,x≥﹣1.故答案为:x≥﹣1.14.分解因式:2m3﹣8m2+8m=2m(m﹣2)2.【分析】先提取公因式2m,再利用完全平方公式分解可得.【解答】解:原式=2m(m2﹣4m+4)=2m(m﹣2)2,故答案为:2m(m﹣2)2.15.如图,点A、B、C都在圆O上,如果∠AOB+∠ACB=90°,那么∠ACB的大小是30°.【分析】根据∠AOB=2∠ACB,再结合条件,列出等式即可解决问题.【解答】解:∵∠AOB=2∠ACB,∠AOB+∠ACB=90°∴3∠ACB=90°,∴∠ACB=30°,故答案为:30°.16.半径为4的圆内接正六边形的面积是.【分析】解题的关键要记住正六边形的特点,它被半径分成六个全等的等边三角形.【解答】解:连接正六边形的中心与各个顶点,得到六个等边三角形,等边三角形的边长是4,因而面积是=4,因而正六边形的面积是24.17.如图,在Rt△ABC中,∠ACB=90°,CD为AB边上的高,若AD=6,BD=18,则AC的长等于12 .【分析】利用射影定理得到:AC2=AD•AB,把相关线段的长度代入进行解答即可.【解答】解:∵AD=6,BD=18,∴AB=AD+BD=24.∵Rt△ABC中,∠ACB=90°,CD是AB边上的高,∴AC2=AD•AB=6×24,∴AC=12.故答案是:12.18.二次函数y=ax2+bx+c(a、b、c为常数且a≠0)中的x与y的部分对应值如表:x﹣1 0 1 3y﹣1 3 5 3给出了结论:①二次函数y=ax2+bx+c有最大值,最大值为5;②ac<0;③x>1时,y 的值随x值的增大而减小;④3是方程ax2+(b﹣1)x+c=0的一个根;⑤当﹣1<x<3时,ax2+(b﹣1)x+c>0,则其中正确结论是②④⑤.【分析】先利用待定系数法求出二次函数y=ax2+bx+c的解析式,再化为顶点式,则可对①②进行判断;根据二次函数的性质可对③进行判断;根据一元二次方程解的定义对④进行判断;先解方程﹣x2+2x+3=0得抛物线y=﹣x2+2x+3与x轴的交点坐标为(﹣1,0),(3,0),然后利用抛物线在x轴上方对应的自变量的范围可对⑤进行判断.【解答】解:把(0,3),(1,5),(﹣1,﹣1)代入y=ax2+bx+c得,解得∴抛物线解析式为y=﹣x2+3x+3,∵y=﹣(x﹣)2+,∴当x=时,y有最大值,所以①错误;∵a=﹣1,b=3,∴ac=﹣3<0,所以②正确;∵抛物线开口向下,对称轴为直线x=,∴当x>时,y的值随x值的增大而减小,所以③错误;当x=3时,ax2+(b﹣1)x+c=﹣1×9+(3﹣1)×3+3=0,即3是方程ax2+(b﹣1)x+c=0的一个根,所以④正确;二次函数y=ax2+(b﹣1)x+c=﹣x2+2x+3,解方程﹣x2+2x+3=0得x1=﹣1,x2=3,∴抛物线y=﹣x2+2x+3与x轴的交点坐标为(﹣1,0),(3,0),∴当﹣1<x<3时,﹣x2+2x+3>0,所以⑤正确.故答案为②④⑤.三.解答题(共8小题)19.计算:20160+|1﹣|﹣2cos30°﹣(﹣)﹣1【分析】直接利用零指数幂的性质以及绝对值的性质和负整数指数幂的性质分别化简得出答案.【解答】解:原式=1+﹣1﹣2×+4=1+﹣1﹣+4=4.20.解方程:+=1.【分析】分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.【解答】解:去分母得:(x+1)(x+1)﹣4=x2﹣1,解得:x=1,经检验x=1是分式方程的增根,∴原分式方程无解.21.西宁市教育局自实施新课程改革后,学生的自主学习、合作交流能力有很大提高.张老师为了了解所教班级学生自主学习、合作交流的具体情况,对本班部分学生进行了为期半个月的跟踪调查,将调查结果分成四类,A:特别好;B:好;C:一般;D:较差;并将调查结果绘制成以下不完整的统计图,请你根据统计图解答下列问题:(1)本次调查中,张老师一共调查了20 名同学;(2)将上面的条形统计图补充完整;(3)为了共同进步,张老师想从被调查的A类和D类学生分别选取一位同学进行“一帮一”互助学习,请用列表法或画树形图的方法列出所有等可能的结果,并求出所选两位同学恰好是一位男同学和一位女同学的概率.【分析】(1)根据A组总人数与所占的百分比进行计算即可得解;(2)求出C组的总人数,然后减去男生人数即可得到女生人数,求出D组人数所占的百分比,再求出D组的总人数,然后减去女生人数得到男生人数,最后补全统计图即可;(3)画出树状图,根据概率公式求解即可.【解答】解:(1)(1+2)÷15%=20人;(2)C组人数为:20×25%=5人,所以,女生人数为5﹣3=2人,D组人数为:20×(1﹣15%﹣50%﹣25%)=20×10%=2人,所以,男生人数为2﹣1=1人,补全统计图如图;(3)画树状图如图:所有等可能结果:男男、男女、女男、女女、女男、女女,P(一男一女)==.22.如图,在平面直角坐标系中,△OAB的顶点坐标分别为O(0,0)、A(2,1)、B(1,﹣2).(1)以原点O为位似中心,在y轴的右侧画出△OAB的一个位似△OA1B1,使它与△OAB 的相似比为2:1,并写出点A的对应点A1的坐标;(2)画出将△OAB向左平移2个单位,再向上平移1个单位后的△O2A2B2,并写出点A2的坐标;(3)判断△OA1B1与△O2A2B2,能否是关于某一点M为位似中心的位似图形?若是,请在图中标出位似中心M,并写出点M的坐标.【分析】(1)利用位似图形的性质得出对应点坐标,进而得出答案;(2)利用平移变换规律得出对应点坐标,进而得出答案;(3)利用位似图形的性质得出位似中心,进而得出答案.【解答】解:(1)如图所示:△OA1B1即为所求,A1(4,2);(2)如图所示:△O2A2B2即为所求,A2(0,2);(3)△OA1B1与△O2A2B2,是关于点M(﹣4,2)为位似中心的位似图形.23.为了落实党的“精准扶贫”政策,A、B两城决定向C、D两乡运送肥料以支持农村生产,已知A、B两城共有肥料500吨,其中A城肥料比B城少100吨,从A城往C、D两乡运肥料的费用分别为20元/吨和25元/吨;从B城往C、D两乡运肥料的费用分别为15元/吨和24元/吨.现C乡需要肥料240吨,D乡需要肥料260吨.(1)A城和B城各有多少吨肥料?(2)设从A城运往C乡肥料x吨,总运费为y元,求出最少总运费.(3)由于更换车型,使A城运往C乡的运费每吨减少a(0<a<6)元,这时怎样调运才能使总运费最少?【分析】(1)根据A、B两城共有肥料500吨,其中A城肥料比B城少100吨,列方程或方程组得答案;(2)设从A城运往C乡肥料x吨,用含x的代数式分别表示出从A运往运往D乡的肥料吨数,从B城运往C乡肥料吨数,及从B城运往D乡肥料吨数,根据:运费=运输吨数×运输费用,得一次函数解析式,利用一次函数的性质得结论;(3)列出当A城运往C乡的运费每吨减少a(0<a<6)元时的一次函数解析式,利用一次函数的性质讨论,并得结论.【解答】解:(1)设A城有化肥a吨,B城有化肥b吨根据题意,得解得答:A城和B城分别有200吨和300吨肥料;(2)设从A城运往C乡肥料x吨,则从A城运往D乡(200﹣x)吨,从B城运往C乡肥料(240﹣x)吨,则从B城运往D乡(60+x)吨.若总运费为y元,根据题意,得:y=20x+25(200﹣x)+15(240﹣x)+24(60+x)=4x+10040由于y=4x+10040是一次函数,k=4>0,y随x的增大而增大.因为x≥0,所以当x=0时,运费最少,最少运费是10040元.(3)从A城运往C乡肥料x吨,由于A城运往C乡的运费每吨减少a(0<a<6)元,所以y=(20﹣a)x+25(200﹣x)+15(240﹣x)+24(60+x)=(4﹣a)x+10040当0<a<4时,∵4﹣a>0∴当x=0时,运费最少是10040元;当a=4时,运费是10040元;当4<a<6时,∵4﹣a<0∴当x最大时,运费最少.即当x=200时,运费最少.所以:当0<a<4时,A城化肥全部运往D乡,B城运往C城240吨,运往D乡60吨,运费最少;当a=4时,不管A城化肥运往D乡多少吨,运费都是10040元.当4<a<6时,A城化肥全部运往C乡,B城运往C城40吨,运往D乡260吨,运费最少.24.如图,在△ABC中,AB=AC,以AB为直径作圆O,分别交BC于点D,交CA的延长线于点E,过点D作DH⊥AC于点H,连接DE交线段OA于点F.(1)求证:DH是圆O的切线;(2)若A为EH的中点,求的值;(3)若EA=EF=1,求圆O的半径.【分析】(1)根据同圆的半径相等和等边对等角证明:∠ODB=∠OBD=∠ACB,则DH⊥OD,DH是圆O的切线;(2)如图2,先证明∠E=∠B=∠C,则H是EC的中点,设AE=x,EC=4x,则AC=3x,由OD是△ABC的中位线,得:OD=AC=,证明△AEF∽△ODF,列比例式可得结论;(3)如图2,设⊙O的半径为r,即OD=OB=r,证明DF=OD=r,则DE=DF+EF=r+1,BD=CD=DE=r+1,证明△BFD∽△EFA,列比例式为:,则=,求出r 的值即可.【解答】证明:(1)连接OD,如图1,∵OB=OD,∴△ODB是等腰三角形,∠OBD=∠ODB①,在△ABC中,∵AB=AC,∴∠ABC=∠ACB②,由①②得:∠ODB=∠OBD=∠ACB,∴OD∥AC,∵DH⊥AC,∴DH⊥OD,∴DH是圆O的切线;(2)如图2,在⊙O中,∵∠E=∠B,∴由(1)可知:∠E=∠B=∠C,∴△EDC是等腰三角形,∵DH⊥AC,且点A是EH中点,设AE=x,EC=4x,则AC=3x,连接AD,则在⊙O中,∠ADB=90°,AD⊥BD,∵AB=AC,∴D是BC的中点,∴OD是△ABC的中位线,∴OD∥AC,OD=AC=×3x=,∵OD∥AC,∴∠E=∠ODF,在△AEF和△ODF中,∵∠E=∠ODF,∠OFD=∠AFE,∴△AEF∽△ODF,∴,∴==,∴=;(3)如图2,设⊙O的半径为r,即OD=OB=r,∵EF=EA,∴∠EFA=∠EAF,∵OD∥EC,∴∠FOD=∠EAF,则∠FOD=∠EAF=∠EFA=∠OFD,∴DF=OD=r,∴DE=DF+EF=r+1,∴BD=CD=DE=r+1,在⊙O中,∵∠BDE=∠EAB,∴∠BFD=∠EFA=∠EAB=∠BDE,∴BF=BD,△BDF是等腰三角形,∴BF=BD=r+1,∴AF=AB﹣BF=2OB﹣BF=2r﹣(1+r)=r﹣1,在△BFD和△EFA中,∵,∴△BFD∽△EFA,∴,∴=,解得:r1=,r2=(舍),综上所述,⊙O的半径为.25.在平面直角坐标系xOy中的点P(x,y)(x≠0),将它的纵坐标y与横坐标x的比称为点P的“湘一比”,记为k p,如点P(﹣3,6),则k p==﹣2.(1)若P(a,2)在直线y=x﹣2上,求点P的“湘一比”k p及直线OP与x轴夹角的正切值;(2)已知点Q(m,n)的“湘一比”k Q为,且Q在y=(x>0),⊙Q的半径为1,若点M在⊙Q上,求M的“湘一比”k M的取值范围;(3)设m、n为正整数,且m≠2,对一切实数t,如果直线y=mtx+3mt与二次函数y=x2+3x交于A(x1,y1),B(x2,y2),且|x1﹣x2|≥|2t+n|,求点N(m,n)的“湘一比”k N的值.【分析】(1)根据“湘一比”的定义求出a的值,即可得出结论;(2)先确定出点Q的坐标,进而判断出直线OM和⊙Q相切时,两种情况即可得出k M的最大值和最小值,就是分界点,即可得出结论;(3)先求出x1=﹣3,x2=mt,进而建立不等式组,得出m>2且(mn﹣6)2≤0,即可得出结论.【解答】解:(1)∵P(a,2)在直线y=x﹣2上,∴2=a﹣2.∴a=4.∴k p==,此时直线OP与x轴夹角的正切值是;(2)由题意知,k Q==,∴n=m.∴Q(m,m).∵Q在y=(x>0)上,∴,∴或m=﹣(舍去),∴,根据点M的“湘一比”知,直线OM和⊙Q相切时,一个是k M的最大值和另一个是最小值,当M(,0)时,k M最小,此时k M=0,当M(,)时,k M最大,此时k M=,∴0≤k≤;(3)由题意知,,∴x2+(3﹣mt)x﹣3mt=0,∴x1=﹣3,x2=mt,∵|x1﹣x2|≥|2t+n|,∴(mt+3)2≥(2t+n)2,∵等于一切实数t不等式恒成立,∴,∵m为正整数,∴m>2且(mn﹣6)2≤0,∵(mn﹣6)2≥0,∴mn=6,∵m,n为正整数,∴m=3,n=2或m=6,n=1,∴k N=或.26.如图,直线y=x+2与抛物线y=x2﹣2mx+m2+m交于A、B两点(A在B的左侧),与y 轴交于点C,抛物线的顶点为D,抛物线的对称轴与直线AB交于点M.(1)当四边形CODM是菱形时,求点D的坐标;(2)若点P为直线OD上一动点,求△APB的面积;′(3)作点B关于直线MD的对称点B',以点M为圆心,MD为半径作⊙M,点Q是⊙M上一动点,求QB'+QB的最小值.【分析】(1)根据菱形的性质可得OD=OC=m,求出m=,则D点坐标可求出;(2)联立直线与抛物线求出交点A、B的坐标,然后求出AB的长,再根据AB∥OC求出两平行线间的距离,最后根据三角形的面积公式列式计算即可得解;(3)根据A、B的坐标求出AM、BM的长,再求出点M的坐标,从而得到⊙M的半径为2,取MB的中点N,连接QB、QN、QB′,然后利用两边对应成比例夹角相等两三角形相似求出△MNQ和△MQB相似,再根据相似三角形对应边成比例求出QN=QB,然后根据三角形任意两边之和大于第三边判断出Q、N、B′三点共线时QB′+QB最小,然后根据勾股定理列式计算即可得解.【解答】解:(1)∵D(m,m),OD=m,四边形CODM为菱形,∴OD=OC=2=m,∴m=,∴D();(2)∵y=x+2与抛物线y=x2﹣2mx+m2+m交于A、B两点,∴联立,解得,,∵点A在点B的左侧,∴A(m﹣1,m+1),B(m+2,m+4),∴AB==3,∵直线OC的解析式为y=x,直线AB的解析式为y=x+2,∴AB∥OC,两直线AB、OC之间距离h=2×=,∴S△APB=AB•h=×3×=3;(3)∵A(m﹣1,m+1),B(m+2,m+4),∴AM=1×=,BM=2×=2,由M点坐标(m,m+2),C点坐标(m,m)可知以MC为半径的圆的半径为(m+2)﹣m=2,取MB的中点N,连接QB、QN、QB′,∴MN=BM=,∵,∠QMN=∠BMQ,∴△MNQ∽△MQB,∴,∴,由三角形三边关系,当Q、N、B′三点共线时QB′+QB最小,∵直线AB的解析式为y=x+2,∴直线AB与对称轴夹角为45°,∵点B、B′关于对称轴对称,∴∠BMB′=90°,由勾股定理得,QB′+QB最小值为B'N===.即QB'+QB的最小值是.。
英语_2020年湖南省长沙市青竹湖湘一外国语学校中考三模英语试题(含答案)

2020年湖南省长沙市青竹湖湘一外国语学校中考三模英语试题一、单选题1. Linda often keeps everything to ________ and seldom shares her stories with others.A herselfB herC she2. Since they believe in you, I think you are the ________ person of the two to solve the problem.A goodB betterC best3. After climbing for nearly three hours, we were glad to take ________ rest.A a few minutesB a few minutes’C a little minutes’4. —I’m waiting for the visitors for quite a while.—Look! Here ________ the visitors.A comeB comesC is coming5. My mom always tells me: when things are a disappointment, ________ be so discouraged. (气馁的)A trying not toB to try not toC try not to6. —Would you like to go to the amusement park with us?—If my twin sister doesn’t go, ________.A neither I wouldB so do IC neither will I7. The next thing to be done is to get the students ________ in small groups.A organizeB organizedC organizing8. — Louis, are you leaving for Guilin for your trip tomorrow?— No. It will be two days ________ I start my trip.A afterB asC before9. He doesn’t like people in the company ________ talk much but do little.A whoseB whichC who10. — Have you decided ________?—Not yet. I don’t want to hurt him.A whether you will tell him the truthB which apartment you would buyC that are you going to spend the summer vacation二、完型填空11. When I was small, I used to visit my grandparents in the countryside, far away from the city. My grandpa was a ______ farmer. Though he passed away many years ago, I still remember a lesson Grandpa taught me one summer.Grandpa looked after the sheep and ______ them from wolves and other wild animals in the forest. One morning, when Grandpa gathered (聚焦) the sheep, we set out. As we were guarding (看护) the sheep, Grandpa sa id to me, “Nick, ______ yourself to be a sheep farmer. What will you do if one of the sheep is lost? Will you go to look for it?”“Of course,” I replied. “As a sheep farmer, I should ______ every sheep. If one sheep is lost, I will do whatever it takes to ______ it back.”Grandpa shook his head and said, “You have a kind heart, ______ I don’t think you are wise enough.”At that time, I didn’t ______. Then, Grandpa continued, “Remember, no matter what happens, you must keep your cool. If you don’t, you won’t be able to make right ______. If one of these sheep is lost and we go to look for it, what will happen to the other sheep? They might get______, too. What’s worse, they might be eaten up by wolves.”The more I thought about Grandpa’s word s, the more I realized how ______ it was!From then on, I always remembered to keep my cool no matter what happened.(1)A chickenB cottonC sheep(2)A avoidedB protectedC borrowed(3)A doubtB imagineC encourage(4)A take awayB take part inC take care of(5)A bringB callC give(6)A soB butC because(7)A hearB understandC wait(8)A wishesB mistakesC decisions(9)A lostB sickC lucky(10)A trueB easyC surprising三、阅读单选(1)The study tour doesn’t include a visit to ________.A a museumB HollywoodC Disneyland(2)Which is NOT mentioned in the table?A The study tour to England will last 15 days.B You have to pay 3000 dollars for the tour.C Miss Lin can provide more information about the tour.13. Spring break is here! Tom and Jack are also on vacation from work all week. They want to plan all kinds of fun things to do, like biking, hiking (远足), fishing, swimming, and tennis. They are hoping for some warm, enjoyable weather. However, they just c an’t decide which day to do each activity. So they decide to check the weaker forecast (预报) in the newspaper before making some final plans.THE FIVE-DAY FORECASTMonday Tuesday Wednesday Thursday Fridaya beautiful day with no clouds, high temperature of 32℃partly cloudywith a 80%chance ofrainstorm; hightemperature of27℃heavy rain untilnoon; thenclearer and coolerwith a hightemperature of21℃partly sunnywith a hightemperature of16 ℃partly cloudywith a hightemperature of18 ℃(1)Which days will be the best for hiking?A Monday and TuesdayB Tuesday and WednesdayC Thursday and Friday(2)Tom and Jack are going out on Tuesday, what will they most probably take?A An umbrella.B Sunglasses.C A sweater.(3)What can we infer from the information above?A They must be very pleased with the weather forecastB They will wear jeans and jackets on Monday.C They can make the final plans according to the weather.14. There can be no doubt about Sherlock Holmes or Indiana Jones. They are surely invented character. But Robin Hood: fact or fiction (虚构)? That question has many answers. It depends on what you mean by a “real person”. If we mean, “W as there a man called Robin Hood, who did all the things we can read about?” then the answer is NO. But if we mean, “Was there a man who lived in the Middle Ages, and is remembered in the legends (传说) of Robin Hood?” then YES.The legend of Robin Hood is a very old one, and it is certainly based on reality.According to one story Robin was really an Anglo-Saxon nobleman (贵族), perhaps called Robin of Huntingdon, or Robin Fitzooth, and he was a rebel against England’s Norman rulers.After William conquered (征服) England in 1066, England was ruled by Norman kings and Norman barons (男爵). Most of the common Anglo-Saxon people accepted their new masters, but some didn’t. Robin was one of them. He took money from the Normans (who were rich compared to common people), and gave it to poor Anglo Saxons. That’s why he became the enemy of the Norman barons.Other stories said that Robin lived in Yorkshire. And later stories had him living in Sherwood Forest, Nottingham. In Nottingham, Robin is now a very popular character. Visitors to the city can learn all about him at the “Legends of Robin Hood” exhibition (展览), where Robin and his experiences are brought to life.Maybe Robin never lived at all in the past, but that would be too bad! His spirit is certainly alive today.(1)According to the passage, which of the following is TRUE?A Someone created a role called Sherlock Holmes in his story.B There was a man called Indiana Jones in people’s real life.C Robin Hood was the real name of a hero in the history of England.(2)What does the underlined word “rebel” mean in Paragraph 4?A 同盟B 造反者C 下属(3)From this passage, we can learn that Robin Hood in different stories ________.A is a real person who conquered England in 1066B is the enemy of the Anglo-Saxon poor peopleC has got different names and different birth places(4)What can we infer from the passage?A Many Norman barons might want to help Robin Hood.B At the “Legends of Robin Hood” exhibition, people can enjoy lifelike pictures of Robin Hood.C Fewer and fewer people are encouraged by Robin's spirit.(5)What’s the best title for this passage?A A Legend of Robin HoodB Robin Hood: Fact or Fiction?C The History of Robin Hood15. Are kids getting too much praise? Too much praise may be doing kids more harm than good.A cover story in Scholastic Instructor magazine asks whether kids today are over-praised. The worry is that while trying to build up kid s’ confidence (自信), parents are paying little attention to kids’ real goals and achievements. In a recent study, eighth graders in Korea and the United States were asked whether they were good at math. Among the American students, 39 percent said they were excellent at math, compared to just 6 percent of the Korean eighth graders. But the reality was kind of different. The Korean kids scored far better than the over-confident American students.The disadvantage of too much praise is that kids may start to focus on the reward (奖励) rather than what they are learning. Worse, when a student fails, whose confidence comes from a blind sense of achievement rather than his or her real abilities, the result can be devastating (毁灭性). This doesn’t mean we shouldn’t praise our kids or that teachersshouldn’t try to build up their students’ self-confidence. But self-confidence should be the result of good grades and real achievements instead of empty praise from others.Last month, Cognitive Daily reported that parents and teachers should be specific rather than general when they offer praise. An example of general praise is telling a child, “You’re smart.” Specific praise would be to say, “You did a good job on reading...”, or “You did great on your math test.” Ki ds who receive general praise about their abilities probably show “helpless” behavior when they meet with problems with learning, compared with kids who receive specific praise about their achievement on a task. The reason: a child who knows she’s a smart girl feel defeated (挫败的) if she has trouble reading a sentence. But a child who has been told she is a good reader will probably have confidence in that specific ability and work a little harder to deal with a more difficult book.(1)The study of the eighth graders in Paragraph 2 shows that ________.A Korean students are over-praised so they got higher scoresB American students are over-confident but they achieve lessC American students are really good at math(2)According to Paragraph 3. kids’ self-confidence should come from ________.A teachers’ love and supportB what they are able to do wellC a blind sense of achievement(3)Which of the following is the best example about specific praise?A Mr. Miller told her daughter “You are a fantastic girl”.B The headmaster wrote to one of his students, saying “I am so proud of you”.C Your English teacher said to you, “Your writing has improved a lot because of practice.”(4)Kids getting general praise will ________ in the face of problems with learning.A probably give up easilyB encourage themselves to try againC work harder than before(5)The writer of the passage means to prove that ________.A too much praise may be doing kids more harm than goodB Korean students are less confident than American studentsC Achievement lies in self-confidence四、补全短文5选416. 根据短文内容,用方框中的单词或其恰当形式填空,每词只用一次。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2019-2020学年九年级(上)第三次月考数学试卷一.选择题(共12小题)1.2019的相反数是()A.2019 B.﹣2019 C.D.﹣2.人体中枢神经系统中约含有1千亿个神经元,某种神经元的直径约为52微米,52微米为0.000052米.将0.000052用科学记数法表示为()A.5.2×10﹣6B.5.2×10﹣5C.52×10﹣6D.52×10﹣53.如图是由一个长方体和一个球组成的几何体,它的主视图是()A.B.C.D.4.下列长度的三条线段,能组成三角形的是()A.3,4,8 B.5,6,10 C.5,5,11 D.5,6,115.下列函数表达式中,y不是x的反比例函数的是()A.y=B.y=C.y=D.xy=6.下表是我市七个区(县)今年某日最高气温(°C)的统计结果:县(区)开福区岳麓去芙蓉区天心区雨花区望城区长沙县气温(℃)26 26 25 25 25 23 22 则该日最高气温(°C)的众数和中位数分别是()A.25,25 B.25,26 C.25,23 D.24,257.如图所示,小明书上的三角形被墨水污染了,他根据所学知识画出了完全一样的一个三角形,他根据的定理是()A.SSS B.SAS C.AAS D.ASA8.已知x1,x2是一元二次方程x2﹣2x=0的两个实数根,下列结论错误的是()A.x1≠x2B.x12﹣2x1=0 C.x1+x2=2 D.x1•x2=29.下列命题是假命题的是()A.抛物线y=x2﹣3x﹣4与x轴有两个交点B.对角线互相垂直且相等的四边形是正方形C.垂直于弦的直径平分这条弦D.函数y=3x+5的图象可以看作由函数y=3x﹣1的图象向上平移6个单位长度而得到10.如图,在△ABC中,∠BAC=90°,AD⊥BC于D,若AB=3,AC=4,则sin∠DAC的值为()A.B.C.D.11.关于x的方程的解为正数,则k的取值范围是()A.k>0 B.k<0 C.k>0且k≠4 D.k<0且k≠﹣4 12.如图,抛物线y=ax2+bx+c的顶点坐标为(1,2),那么下列结论中:①abc>0;②2a+b ═0;③b2﹣4ac>0;④若关于x的一元二次方程ax2+bx+c﹣m=0没有实数根,则m>2;⑤方程|ax2+bx+c|=1有四个根,则这四个根的和为4.正确的个数为()A.2个B.3个C.4个D.5个二.填空题(共6小题)13.因式分解:x2y﹣y=.14.随意的抛一粒豆子,恰好落在图中的方格的每个方格除颜色外完全相同,那么这粒豆子落在黑色方格中的概率是.15.若一个圆锥的底面积为16πcm2,母线长为12cm,则该圆锥的侧面积为.16.如图,AB是⊙O的直径,弦CD⊥AB于点E,AE=1,CD=6,则OC的长为.17.若一次函数y=x+b与两坐标轴围成的三角形面积为3,则b的值为.18.法国数学家费马提出:在△ABC内存在一点P,使它到三角形顶点的距离之和最小.人们称这个点为费马点,此时PA+PB+PC的值为费马距离.经研究发现:在锐角△ABC中,费马点P满足∠APB=∠BPC=∠CPA=120°,如图,点P为锐角△ABC的费马点,且PA =3,PC=4,∠ABC=60°,则费马距离为.三.解答题(共8小题)19.计算:(3﹣π)0﹣2cos30°+|1﹣|+()﹣1.20.先化简,再求值:(1﹣)÷,其中m=﹣2.21.某中学为了提高学生的综合素质,成立了以下社团:A.机器人,B.围棋,C.羽毛球,D.电影配音.每人只能加入一个社团.为了解学生参加社团的情况,从参加社团的学生中随机抽取了部分学生进行调查,并将调查结果绘制成如下两幅不完整的统计图,其中图(1)中A所占扇形的圆心角为36°.根据以上信息,解答下列问题:(1)这次被调查的学生共有人;(2)请你将条形统计图补充完整;(3)若该校共有1000学生加入了社团,请你估计这1000名学生中有多少人参加了羽毛球社团;(4)在机器人社团活动中,由于甲、乙、丙、丁四人平时的表现优秀,现决定从这四人中任选两名参加机器人大赛.用树状图或列表法求恰好选中甲、乙两位同学的概率.22.如图,一艘海轮位于灯塔P的东北方向,距离灯塔80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东30°方向上的B处.(1)若灯塔P周围50海里范围内有暗礁,海轮从A处到B处的途中,是否有触礁危险?(2)若海轮以每小时30海里的速度从A处到B处,试判断海轮能否在5小时内到达B 处,并说明理由.(参考数据:≈1.41,≈1.73,≈2.45)23.现代互联网技术的广泛应用,催生了快递行业的高速发展,据调查,长沙某家小型“大学生自主创业”的快递公司,今年三月份与五月份完成投递总件数分别为10万件和14.4万件,现假定该公司每月投递总件数的增长率相同.(1)求该快递公司投递总件数的月平均增长率;(2)如果平均每人每月最多可投0.5万件,那么该公司现有的29名快递投递员能否完成今年6月份的快递投递任务?如果不能,请问需要至少增加几名业务员?24.如图,AB是⊙C的直径,M、D两点在AB的延长线上,E是⊙C的点,且DE2=DB•DA,延长AE至F,使得AE=EF,设BF=5,cos∠BED=.(1)求证:△DEB∽△DAE;(2)求DA,DE的长;(3)若点F在B、E、M三点确定的圆上,求MD的长.25.函数上的定点是指,一个含参数的函数无论参数取何值,函数的图象都过某一个点,这个点称为定点.例如,在函数y=kx中,当x=0时,无论参数k取何值,函数值y=0,所以这个函数过定点(0,0).(1)分别求函数y=kx+2k和y=kx2﹣kx+2019的定点;(2)若过原点的两条直线OA、OB分别与二次函数y=x2交于点A(m,m2)和点B(n,n2)(mn<0)且OA⊥OB,试求直线AB上的定点;(3)若直线CD:y=kx+2k+5与抛物线y=x2交于C、D两点,试在抛物线y=x2上找一定点E,使∠CED=90°,求点E的坐标,并求出点E到直线CD的最大距离.26.如图1,已知抛物线;C1:y=﹣(x+2)(x﹣m)(m>0)与x轴交于点B、C(点B在点C的左侧),与y轴交于点E.(1)求点B、点C的坐标;(2)当△BCE的面积为6时,若点G的坐标为(0,b),在抛物线C1的对称轴上是否存在点H,使得△BGH的周长最小,若存在,则求点H的坐标(用含b的式子表示);若不存在,则请说明理由;(3)在第四象限内,抛物线C1上是否存在点F,使得以点B、C、F为顶点的三角形与△BCE相似?若存在,求m的值;若不存在,请说明理由.参考答案与试题解析一.选择题(共12小题)1.2019的相反数是()A.2019 B.﹣2019 C.D.﹣【分析】由相反数的定义即可得到答案.【解答】解:2019的相反数是﹣2019.故选:B.2.人体中枢神经系统中约含有1千亿个神经元,某种神经元的直径约为52微米,52微米为0.000052米.将0.000052用科学记数法表示为()A.5.2×10﹣6B.5.2×10﹣5C.52×10﹣6D.52×10﹣5【分析】由科学记数法可知0.000052=5.2×10﹣5;【解答】解:0.000052=5.2×10﹣5;故选:B.3.如图是由一个长方体和一个球组成的几何体,它的主视图是()A.B.C.D.【分析】从正面看几何体,确定出主视图即可.【解答】解:几何体的主视图为:故选:C.4.下列长度的三条线段,能组成三角形的是()A.3,4,8 B.5,6,10 C.5,5,11 D.5,6,11【分析】根据三角形的三边关系即可求【解答】解:A选项,3+4=7<8,两边之和小于第三边,故不能组成三角形B选项,5+6=11>10,10﹣5<6,两边之各大于第三边,两边之差小于第三边,故能组成三角形C选项,5+5=10<11,两边之和小于第三边,故不能组成三角形D选项,5+6=11,两边之和不大于第三边,故不能组成三角形故选:B.5.下列函数表达式中,y不是x的反比例函数的是()A.y=B.y=C.y=D.xy=【分析】根据反比例函数y=(k≠0)转化为y=kx﹣1(k≠0)的形式,可得答案.【解答】解:A、y=是反比例函数,故A不符合题意;B、y=是正比例函数,故B符合题意;C、y=是反比例函数,故C不符合题意;D、xy=是反比例函数,故D不符合题意.故选:B.6.下表是我市七个区(县)今年某日最高气温(°C)的统计结果:县(区)开福区岳麓去芙蓉区天心区雨花区望城区长沙县气温(℃)26 26 25 25 25 23 22 则该日最高气温(°C)的众数和中位数分别是()A.25,25 B.25,26 C.25,23 D.24,25【分析】根据众数和中位数的概念求解可得.【解答】解:该日最高气温的众数是25℃,中位数是25℃,故选:A.7.如图所示,小明书上的三角形被墨水污染了,他根据所学知识画出了完全一样的一个三角形,他根据的定理是()A.SSS B.SAS C.AAS D.ASA【分析】根据图形,未污染的部分两角与这两角的夹边可以测量,然后根据全等三角形的判定方法解答即可.【解答】解:小明书上的三角形被墨水污染了,他根据所学知识画出了完全一样的一个三角形,他根据的定理是:两角及其夹边分别相等的两个三角形全等(ASA).故选:D.8.已知x1,x2是一元二次方程x2﹣2x=0的两个实数根,下列结论错误的是()A.x1≠x2B.x12﹣2x1=0 C.x1+x2=2 D.x1•x2=2【分析】由根的判别式△=4>0,可得出x1≠x2,选项A不符合题意;将x1代入一元二次方程x2﹣2x=0中可得出x12﹣2x1=0,选项B不符合题意;利用根与系数的关系,可得出x1+x2=2,x1•x2=0,进而可得出选项C不符合题意,选项D符合题意.【解答】解:∵△=(﹣2)2﹣4×1×0=4>0,∴x1≠x2,选项A不符合题意;∵x1是一元二次方程x2﹣2x=0的实数根,∴x12﹣2x1=0,选项B不符合题意;∵x1,x2是一元二次方程x2﹣2x=0的两个实数根,∴x1+x2=2,x1•x2=0,选项C不符合题意,选项D符合题意.故选:D.9.下列命题是假命题的是()A.抛物线y=x2﹣3x﹣4与x轴有两个交点B.对角线互相垂直且相等的四边形是正方形C.垂直于弦的直径平分这条弦D.函数y=3x+5的图象可以看作由函数y=3x﹣1的图象向上平移6个单位长度而得到【分析】根据抛物线与x轴的交点的判断方法、正方形的判定定理、垂径定理、一次函数的平移判断.【解答】解:A、△=(﹣3)2﹣4×1×(﹣4)=25,则抛物线y=x2﹣3x﹣4与x轴有两个交点,是真命题;B、对角线互相垂直且相等的平行四边形是正方形,本选项说法是真命题;C、垂直于弦的直径平分这条弦,是真命题;D、函数y=3x+5的图象可以看作由函数y=3x﹣1的图象向上平移6个单位长度而得到,是真命题;故选:B.10.如图,在△ABC中,∠BAC=90°,AD⊥BC于D,若AB=3,AC=4,则sin∠DAC的值为()A.B.C.D.【分析】因为AD⊥BC,所以∠ADC=90°,直接根据锐角三角函数的定义sin∠DAC=求出.【解答】解:在△ABC中,∠BAC=90°,AB=3,AC=4,由勾股定理BC=,由面积公式得AB•AC=AD•BC,∴AD=,∴CD==3.2,∴sin∠DAC==0.8=.故选:C.11.关于x的方程的解为正数,则k的取值范围是()A.k>0 B.k<0 C.k>0且k≠4 D.k<0且k≠﹣4 【分析】解分式方程,用含k的代数式表示出x,根据解为正数,求出k的范围.【解答】解:方程的两边都乘以(2x﹣4),得k=2x∴x=因为解为正数,所以>0,且≠2解得,k>0且k≠4.故选:C.12.如图,抛物线y=ax2+bx+c的顶点坐标为(1,2),那么下列结论中:①abc>0;②2a+b ═0;③b2﹣4ac>0;④若关于x的一元二次方程ax2+bx+c﹣m=0没有实数根,则m>2;⑤方程|ax2+bx+c|=1有四个根,则这四个根的和为4.正确的个数为()A.2个B.3个C.4个D.5个【分析】由抛物线的开口方向判断a与0的关系,由抛物线与y轴的交点判断c与0的关系,然后根据对称轴及抛物线与x轴交点情况和二次函数的最值进行推理即可.【解答】解:∵抛物线开口向下,∴a<0,∵抛物线与y轴交于正半轴,∴c>0,∵对称轴在y轴右侧,∴b>0,∴abc<0,①错误;∵抛物线的对称轴为直线x=1,∴﹣=1,∴2a+b=0,②正确;∵抛物线与x轴有两个交点,∴b2﹣4ac>0,③正确;∵抛物线y=ax2+bx+c的顶点坐标为(1,2),∴当m>2时,ax2+bx+c﹣m<0,∴当m>2时,一元二次方程ax2+bx+c﹣m=0没有实数根,④正确;由图象可知函数y=ax2+bx+c与直线y=1有两个交点,与直线y=﹣1有两个交点,∴方程|ax2+bx+c|=1有四个根,设函数y=ax2+bx+c与直线y=1两个交点的横坐标为x1,x2,函数y=ax2+bx+c与直线y=﹣1两个交点的横坐标为x3,x4∵=1,=1,∴x1+x2=2,x3+x4=2,∴x1+x2+x3+x4=4,∴方程|ax2+bx+c|=1有四个根,则这四个根的和为4,⑤正确;故选:C.二.填空题(共6小题)13.因式分解:x2y﹣y=y(x+1)(x﹣1).【分析】首先提公因式y,再利用平方差进行二次分解即可.【解答】解:原式=y(x2﹣1)=y(x+1)(x﹣1),故答案为:y(x+1)(x﹣1).14.随意的抛一粒豆子,恰好落在图中的方格的每个方格除颜色外完全相同,那么这粒豆子落在黑色方格中的概率是.【分析】根据面积法:求出豆子落在黑色方格的面积与总面积的比即可解答.【解答】解:∵共有15个方格,其中黑色方格占5个,∴这粒豆子停在黑色方格中的概率是=,故答案为:.15.若一个圆锥的底面积为16πcm2,母线长为12cm,则该圆锥的侧面积为48πcm2.【分析】根据圆锥的底面面积,得出圆锥的半径,进而利用圆锥的侧面积的面积公式求解.【解答】解:∵圆锥的底面面积为16πcm2,∴圆锥的半径为4cm,这个圆锥的侧面积=•2π•4•12=48πcm2).故答案为:48πcm2.16.如图,AB是⊙O的直径,弦CD⊥AB于点E,AE=1,CD=6,则OC的长为 5 .【分析】利用垂径定理,勾股定理解决问题即可.【解答】解:设OC=OA=r.∵AB⊥CD,∴EC=DE=3,在Rt△EOC中,∵OC2=EC2+OE2,∴r2=32+(r﹣1)2,解得r=5,故答案为5.17.若一次函数y=x+b与两坐标轴围成的三角形面积为3,则b的值为.【分析】先求出一次函数y=x+b的图象与两坐标轴的交点,再由三角形的面积公式即可得出结论.【解答】解:当x=0时,y=b,当y=0时,x=﹣b,∴S=|b|×|b|=3∴b=±故答案为:±18.法国数学家费马提出:在△ABC内存在一点P,使它到三角形顶点的距离之和最小.人们称这个点为费马点,此时PA+PB+PC的值为费马距离.经研究发现:在锐角△ABC中,费马点P满足∠APB=∠BPC=∠CPA=120°,如图,点P为锐角△ABC的费马点,且PA =3,PC=4,∠ABC=60°,则费马距离为7+2.【分析】根据相似三角形的判定和性质,即可求解.【解答】解:如图:∵∠APB=∠BPC=∠CPA=120,∠ABC=60°,∴∠1+∠3=60°,∠1+∠2=60°,∠2+∠4=60°,∴∠1=∠4,∠2=∠3,∴△BPC∽△APB∴=,即PB2=12∴PB=2.∴PA+PB+PC=7+2故答案为:7+2.三.解答题(共8小题)19.计算:(3﹣π)0﹣2cos30°+|1﹣|+()﹣1.【分析】原式利用零指数幂、负整数指数幂法则,绝对值的代数意义,以及特殊角的三角函数值计算即可求出值.【解答】解:原式=1﹣2×+﹣1+2=2.20.先化简,再求值:(1﹣)÷,其中m=﹣2.【分析】先根据分式的混合运算顺序和运算法则化简原式,再将m的值代入计算可得.【解答】解:原式=(﹣)÷=•=,当m=﹣2时,原式==.21.某中学为了提高学生的综合素质,成立了以下社团:A.机器人,B.围棋,C.羽毛球,D.电影配音.每人只能加入一个社团.为了解学生参加社团的情况,从参加社团的学生中随机抽取了部分学生进行调查,并将调查结果绘制成如下两幅不完整的统计图,其中图(1)中A所占扇形的圆心角为36°.根据以上信息,解答下列问题:(1)这次被调查的学生共有200 人;(2)请你将条形统计图补充完整;(3)若该校共有1000学生加入了社团,请你估计这1000名学生中有多少人参加了羽毛球社团;(4)在机器人社团活动中,由于甲、乙、丙、丁四人平时的表现优秀,现决定从这四人中任选两名参加机器人大赛.用树状图或列表法求恰好选中甲、乙两位同学的概率.【分析】(1)由A类有20人,所占扇形的圆心角为36°,即可求得这次被调查的学生数;(2)首先求得C项目对应人数,即可补全统计图;(3)该校1000学生数×参加了羽毛球社团的人数所占的百分比即可得到结论;(4)首先根据题意画出树状图,然后由树状图求得所有等可能的结果与恰好选中甲、乙两位同学的情况,再利用概率公式即可求得答案.【解答】解:(1)∵A类有20人,所占扇形的圆心角为36°,∴这次被调查的学生共有:20÷=200(人);故答案为:200;(2)C项目对应人数为:200﹣20﹣80﹣40=60(人);补充如图.(3)1000×=300(人)答:这1000名学生中有300人参加了羽毛球社团;(4)画树状图得:∵共有12种等可能的情况,恰好选中甲、乙两位同学的有2种,∴P(选中甲、乙)==.22.如图,一艘海轮位于灯塔P的东北方向,距离灯塔80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东30°方向上的B处.(1)若灯塔P周围50海里范围内有暗礁,海轮从A处到B处的途中,是否有触礁危险?(2)若海轮以每小时30海里的速度从A处到B处,试判断海轮能否在5小时内到达B 处,并说明理由.(参考数据:≈1.41,≈1.73,≈2.45)【分析】(1)作PC⊥AB于C,则∠PCA=∠PCB=90°,由题意得:PA=80,∠APC=45°,∠BPC=60°,得出△APC是等腰直角三角形,∠B=30°,求出AC=PC=40>50,即可得出结论;(2)由直角三角形的性质得出BC=PC=40,得出AB=AC+BC=40+40,求出海轮以每小时30海里的速度从A处到B处所用的时间,即可得出结论.【解答】解:(1)作PC⊥AB于C,如图所示:则∠PCA=∠PCB=90°,由题意得:PA=80,∠APC=45°,∠BPC=90°﹣30°=60°,∴△APC是等腰直角三角形,∠B=30°,∴AC=PC=PA=40≈56.1(海里)>50(海里),∴若灯塔P周围50海里范围内有暗礁,海轮从A处到B处的途中,有触礁危险;(2)海轮以每小时30海里的速度从A处到B处,海轮不能在5小时内到达B处,理由如下:∵∠PCB=90°,∠B=30°,∴BC=PC=40,∴AB=AC+BC=40+40,∴海轮以每小时30海里的速度从A处到B处所用的时间=≈≈5.15(小时)>5小时,∴海轮以每小时30海里的速度从A处到B处,海轮不能在5小时内到达B处.23.现代互联网技术的广泛应用,催生了快递行业的高速发展,据调查,长沙某家小型“大学生自主创业”的快递公司,今年三月份与五月份完成投递总件数分别为10万件和14.4万件,现假定该公司每月投递总件数的增长率相同.(1)求该快递公司投递总件数的月平均增长率;(2)如果平均每人每月最多可投0.5万件,那么该公司现有的29名快递投递员能否完成今年6月份的快递投递任务?如果不能,请问需要至少增加几名业务员?【分析】(1)根据增长率问题运用题的等量关系即可求解;(2)根据(1)所得增长率,即可求出6月份的投递总件数,进而进行比较,再计算得出结果.【解答】解:(1)设该快递公司投递总件数的月平均增长率为x,根据题意,得10(1+x)2=14.4解得x1=0.2,x2=﹣2.2(不符合题意,舍去),答:该快递公司投递总件数的月平均增长率为20%.(2)由(1)得,14.4×1.2=17.28(万件),29×0.5=14.5,14.5<17.28,故不能完成任务.因为(17.28﹣14.5)÷0.5=5.56,所以还需要至少增加6名业务员.答:需要至少增加6名业务员.24.如图,AB是⊙C的直径,M、D两点在AB的延长线上,E是⊙C的点,且DE2=DB•DA,延长AE至F,使得AE=EF,设BF=5,cos∠BED=.(1)求证:△DEB∽△DAE;(2)求DA,DE的长;(3)若点F在B、E、M三点确定的圆上,求MD的长.【分析】(1)利用两边成比例夹角相等两三角形相似证明即可.(2)由==,即:==,即可求解.(3)在△BED中,过点B作HB⊥ED于点H,设HD=x,利用勾股定理构建方程解决问题即可.【解答】解:(1)∵DE2=DB•DA,∴=,又∵∠D=∠D,∴△DEB∽△DAE.(2)∵△DEB∽△DAE,∴∠DEB=∠DAE=α,∵AB是直径,∴∠AEB=90°,又AE=EF,∴AB=BF=5,∴∠BFE=∠BAE=α,则BF⊥ED交于点H,∵cos∠BED=,则BE=3,AE=4∴==,即:==,解得:BD=,DE=,则AD=AB+BD=,ED=.(3)由点F在B、E、M三点确定的圆上,则BF是该圆的直径,连接MF,∵BF⊥ED,∠BMF=90°,∴∠MFB=∠D=β,在△BED中,过点B作HB⊥ED于点H,设HD=x,则EH=﹣x,则9﹣(﹣x)2=()2﹣x2,解得:x=,则cosβ==,则sinβ=,MB=BF sinβ=5×=,DM=BD﹣MB=.25.函数上的定点是指,一个含参数的函数无论参数取何值,函数的图象都过某一个点,这个点称为定点.例如,在函数y=kx中,当x=0时,无论参数k取何值,函数值y=0,所以这个函数过定点(0,0).(1)分别求函数y=kx+2k和y=kx2﹣kx+2019的定点;(2)若过原点的两条直线OA、OB分别与二次函数y=x2交于点A(m,m2)和点B(n,n2)(mn<0)且OA⊥OB,试求直线AB上的定点;(3)若直线CD:y=kx+2k+5与抛物线y=x2交于C、D两点,试在抛物线y=x2上找一定点E,使∠CED=90°,求点E的坐标,并求出点E到直线CD的最大距离.【分析】(1)y=kx+2k=k(x+2),当x=﹣2时,y=0,故过定点(﹣2,0),即可求解;(2)直线AB的表达式为:y=﹣(m+n)x+mn,则tan∠AOM=tan∠OBM,即:,解得:mn=﹣2,故直线AB的表达式为:y=﹣(m+n)x﹣2,当x=0时,y=﹣2,故直线AB过点(0,﹣2);(3)直线CD的表达为:y=(m+n)x﹣mn,则m+n=k,mn=﹣2k﹣5,tan∠CEM=tan ∠EDN,即:t2+(m+n)t+mn=﹣1,即:t2﹣4+(t﹣2)k=0,即可求解.【解答】解:(1)y=kx+2k=k(x+2),当x=﹣2时,y=0,故过定点(﹣2,0);y=kx2﹣kx+2019=k(x2﹣x)+2019,当x=0或1时,y=2019,故过定点(1,2019)、(0,2019);(2)将点A、B的坐标代入一次函数表达式:y=kx+b并解得:直线AB的表达式为:y=(m+n)x﹣mn,分别过点A、B作x轴的垂线于点M、N,则∠AOM=∠OBN,则tan∠AOM=tan∠OBN,即:,解得:mn=﹣2,故直线AB的表达式为:y=(m+n)x+2,当x=0时,y=2,故直线AB过点(0,2);(3)设点C、D的坐标分别为:(m,m2)、(n,n2),同理可得:直线CD的表达为:y=(m+n)x﹣mn,则m+n=k,mn=﹣2k﹣5,设点E(t,t2),同理可得:tan∠CEM=tan∠EDN,即:,化简得:t2+(m+n)t+mn=﹣1,即:t2﹣4+(t﹣2)k=0,当t=2时,上式横成立,故定点为E(2,4);直线CD:y=kx+2k+5过定点H(﹣2,5),∵点到直线的距离≤EH,故点E到直线的最大距离为EH==.26.如图1,已知抛物线;C1:y=﹣(x+2)(x﹣m)(m>0)与x轴交于点B、C(点B在点C的左侧),与y轴交于点E.(1)求点B、点C的坐标;(2)当△BCE的面积为6时,若点G的坐标为(0,b),在抛物线C1的对称轴上是否存在点H,使得△BGH的周长最小,若存在,则求点H的坐标(用含b的式子表示);若不存在,则请说明理由;(3)在第四象限内,抛物线C1上是否存在点F,使得以点B、C、F为顶点的三角形与△BCE相似?若存在,求m的值;若不存在,请说明理由.【分析】(1)y=﹣(x+2)(x﹣m)(m>0),令y=0,则x=﹣2或m,即可求解;(2)点B关于函数对称轴的对称点为点C(m,0),连接CE交对称轴于点H,则点H为所求,即可求解;(3)分△BEC∽△BCF、△BEC∽△FCB两种情况,分别求解即可.【解答】解:(1)y=﹣(x+2)(x﹣m)(m>0),令y=0,则x=﹣2或m,故点B、C的坐标分别为:(﹣2,0)、(m,0);(2)存在,理由:y=﹣(x+2)(x﹣m),令x=0,则y=2,故点E(0,2),△BCE的面积=×BC×OE=(m+2)×2=6,解得:m=4,则抛物线的对称轴为:x=(﹣2+4)=1,点B关于函数对称轴的对称点为点C(m,0),连接CE交对称轴于点H,则点H为所求,将点C、E的坐标代入一次函数表达式并解得:直线CE的表达式为:y=﹣bx+b,当x=1时,y=b,故点H(1,b);(3)∵OE=OB=2,故∠EBO=45°,过点F作FT⊥x轴于点F;①当△BEC∽△BCF时,则BC2=BE•BF,∠FBO=EBO=45°,则直线BF的函数表达式为:y=﹣x﹣2,故点F(x,﹣x﹣2);将点F的坐标代入抛物线表达式得:﹣x﹣2=﹣(x+2)(x﹣m),解得:x=﹣2(舍去)或2m,故点F(2m,﹣2m﹣2),则BF=2(m+1),BE=2,∵BC2=BE•BF,则(m+2)2=22(m+1),解得:m=2±2(舍去负值),故m=2+2;②当△BEC∽△FCB时,则BC2=BF•EC,∠CBF=∠ECO,则△BFT∽△COE,则,则点F[x,﹣(x+2)],将点F的坐标代入抛物线表达式得:﹣(x+2)=﹣(x+2)(x﹣m),解得:x=﹣2(舍去)或m+2;则点F[m+2,﹣(m+4)]BC2=BF•EC,则(m+2)2=,化简得:m3+4m2+4m=m3+4m2+4m+16,此方程无解;综上,m=2.。
