等腰三角形及全等三角形的中难题证明
全等难题——倍长中线法

三角形中线的定义:三角形顶点和对边中点的连线三角形中线的相关定理: 直角三角形斜边的中线等于斜边的一半等腰三角形底边的中线三线合一(底边的中线、顶角的角平分线、底边的高重合)三角形中位线定义:连结三角形两边中点的线段叫做三角形的中位线.三角形中位线定理:三角形的中位线平行于第三边并且等于它的一半.中位线判定定理:经过三角形一边中点且平行于另一边的直线必平分第三边.中线中位线相关问题(涉及中点的问题)见到中线(中点),我们可以联想的内容无非是倍长中线以及中位线定理(以后还要学习中线长公式),尤其是在涉及线段的等量关系时,倍长中线的应用更是较为常见.版块一 倍长中线【例1】 (2002年通化市中考题)在△ABC 中,9,5==AC AB ,则BC 边上的中线AD 的长的取值范围是什重点:主要掌握中线的处理方法,遇见中线考虑中线倍长法难点:全等三角形的综合运用重、难点知识点睛例题精讲中考要求第二讲全等三角形与中点问题么?【补充】已知:ABC ∆中,AM 是中线.求证:1()2AM AB AC <+. 【例2】 (2008年巴中市高中阶段教育学校招生考试)已知:如图,梯形ABCD 中,AD BC ∥,点E 是CD 的中点,BE 的延长线与AD 的延长线相交于点F .求证:BCE FDE ∆∆≌.【例3】 (浙江省2008年初中毕业生学业考试(湖州市)数学试卷)如图,在ABC ∆中,D 是BC 边的中点,F ,E 分别是AD 及其延长线上的点,CF BE ∥.求证:BDE CDF ∆∆≌.【例4】 如图,ABC ∆中,<AB AC ,AD 是中线.求证:<DAC DAB ∠∠.【例5】 如图,已知在ABC ∆中,AD 是BC 边上的中线,E 是AD 上一点,延长BE 交AC 于F ,AF EF =,求证:AC BE =.【例6】 如图所示,在ABC ∆和A B C '''∆中,AD 、A D ''分别是BC 、B C ''上的中线,且AB A B ''=,AC A C ''=,AD A D ''=,求证ABC A B C '''∆∆≌.【例7】 如图,在ABC ∆中,AD 交BC 于点D ,点E 是BC 中点,EF AD ∥交CA 的延长线于点F ,交EF 于点G ,若BG CF =,求证:AD 为ABC ∆的角平分线.【例8】 已知AD 为ABC ∆的中线,ADB ∠,ADC ∠的平分线分别交AB 于E 、交AC 于F .求证:BE CF EF +>. 【例9】 在Rt ABC ∆中,90A ∠=︒,点D 为BC 的中点,点E 、F 分别为AB 、AC 上的点,且ED FD ⊥.以线段BE 、EF 、FC 为边能否构成一个三角形?若能,该三角形是锐角三角形、直角三角形或钝角三角形?【例10】 如图所示,在ABC ∆中,D 是BC 的中点,DM 垂直于DN ,如果2222BM CN DM DN +=+,求证()22214AD AB AC =+. 【例10】 (2008年四川省初中数学联赛复赛·初二组)在Rt ABC ∆中,F 是斜边AB 的中点,D 、E 分别在边CA 、CB 上,满足90DFE ∠=︒.若3AD =,4BE =,则线段DE 的长度为_________.【例11】 如图所示,90BAC DAE ∠=∠=︒,M 是BE 的中点,AB AC =,AD AE =,求证AM CD ⊥. 版块二、中位线的应用【例12】 AD 是ABC ∆的中线,F 是AD 的中点,BF 的延长线交AC 于E .求证:13AE AC =. 【例13】 如图所示,在ABC ∆中,AB AC =,延长AB 到D ,使BD AB =,E 为AB 的中点,连接CE 、CD ,求证2CD EC =.【例14】 已知:ABCD 是凸四边形,且AC <BD . E 、F 分别是AD 、BC 的中点,EF 交AC 于M ;EF 交BD 于N ,AC 和BD 交于G 点. 求证:∠GMN >∠GNM .【例15】 在ABC ∆中,90ACB ∠=︒,12AC BC =,以BC 为底作等腰直角BCD ∆,E 是CD 的中点,求证:AE EB ⊥且AE BE =.【例16】 如图,在五边形ABCDE 中,90ABC AED ∠=∠=︒,BAC EAD ∠=∠,F 为CD 的中点.求证:BF EF =.【例17】 (“祖冲之杯”数学竞赛试题,中国国家集训队试题)如图所示,P 是ABC ∆内的一点,PAC PBC ∠=∠,过P 作PM AC ⊥于M ,PL BC ⊥于L ,D 为AB 的中点,求证DM DL =.【例18】 (全国数学联合竞赛试题) 如图所示,在ABC ∆中,D 为AB 的中点,分别延长CA 、CB 到点E 、F ,使DE DF =.过E 、F 分别作直线CA 、CB 的垂线,相交于点P ,设线段PA 、PB 的中点分别为M 、N .求证:(1) DEM FDN ∆∆≌;(2) PAE PBF ∠=∠.【例19】 已知,如图四边形ABCD 中,AD BC =,E 、F 分别是AB 和CD 的中点,AD 、EF 、BC 的延长线分别交于M 、N 两点. 求证:AME BNE ∠=∠.【例20】 (2009年大兴安岭地区初中毕业学业考试)已知:在ABC ∆中,BC AC >,动点D 绕ABC ∆ 的顶点A 逆时针旋转,且AD BC =,连结DC .过AB 、DC 的中点E 、F 作直线,直线EF 与直线AD 、BC 分别相交于点M 、N .⑴ 如图1,当点D 旋转到BC 的延长线上时,点N 恰好与点F 重合,取AC 的中点H ,连结HE 、HF ,根据三角形中位线定理和平行线的性质,可得结论AMF BNE ∠=∠(不需证明).⑵ 当点D 旋转到图2或图3中的位置时,AMF ∠与BNE ∠有何数量关系?请分别写出猜想,并任选一种情况证明. 【例21】 如图,AE ⊥AB ,BC ⊥CD ,且AE =AB ,BC =CD ,F 为DE 的中点,FM ⊥AC .证明:FM =12AC . 【例22】 (1991年泉州市初二数学双基赛题)已知:在△ABC 中,分别以AB 、AC 为斜边作等腰直角三角形ABM ,和CAN ,P 是边BC 的中点.求证:PM =PN【习题1】 如图,在等腰ABC ∆中,AB AC =,D 是BC 的中点,过A 作AE DE ⊥,AF DF ⊥,且AE AF =.求证:EDB FDC ∠=∠.【习题2】 如图,已知在ABC ∆中,AD 是BC 边上的中线,E 是AD 上一点,且BE AC =,延长BE 交AC 于F ,AF 与EF 相等吗?为什么?【习题3】 如右下图,在ABC ∆中,若2B C ∠=∠,AD BC ⊥,E 为BC 边的中点.求证:2AB DE =.【备选1】如图,已知AB =DC ,AD =BC ,O 是BD 中点,过O 点的直线分别交DA 、BC 的延长线于E ,F .求证:∠E =∠F【备选2】如图,ABC ∆中,AB AC =,90BAC ∠=︒,D 是BC 中点,ED FD ⊥,ED 与AB 交于E ,FD 与AC交于F .求证:BE AF =,AE CF =. 月测备选 家庭作业。
三角形证明难题

三角形证明难题哎呀,一提到三角形证明难题,那可真是让不少同学头疼得直抓脑袋呀!记得我之前教过一个班,有个叫小明的同学,那叫一个聪明机灵,可就是在三角形证明这一块儿老是栽跟头。
有一次上课,我在黑板上出了一道三角形证明的题目,大家都埋头苦思。
小明呢,眼睛瞪得大大的,手里的笔不停地在草稿纸上比划,嘴里还念念有词。
我在教室里溜达着看大家的解题情况,走到小明身边的时候,他抬头一脸苦相地看着我,那表情仿佛在说:“老师,这题咋这么难啊!”三角形证明难题啊,就像是一个个隐藏在数学森林里的小怪兽,让同学们费了不少心思去对付。
比如说,让你证明两个三角形全等,那条件给得是拐弯抹角,你得像个小侦探一样,从那些边边、角角的关系里找出关键线索。
有时候,一个条件藏得可深了,你得把前面学过的知识都翻出来,才能找到它的踪迹。
就像证明三角形相似,这也是个让人头疼的事儿。
相似三角形的判定条件,什么对应边成比例、对应角相等,听起来好像挺简单,可一放到题目里,那比例关系能把你绕得晕头转向。
还有那些需要添加辅助线的题目,更是让人抓狂。
你得有一双“火眼金睛”,才能看出从哪儿添加辅助线能把难题给破解了。
再比如说,等腰三角形和等边三角形的证明。
等腰三角形两腰相等、两底角相等,等边三角形三边相等、三个角都是 60 度,这些性质大家都能背得滚瓜烂熟。
可真到证明题里,怎么运用这些性质,怎么通过已知条件推导出结论,那可就不容易了。
我还记得有一次考试,有一道关于直角三角形的证明题,大部分同学都没做对。
后来我在讲题的时候,发现大家不是把勾股定理用错了,就是忽略了直角这个关键条件。
看着大家那懊恼的表情,我就知道,这三角形证明难题可真是把大家给难住了。
不过呢,同学们也别害怕。
其实解决三角形证明难题就像玩拼图游戏,只要我们把每一块小拼图(也就是条件和定理)都找对位置,就能拼出完整的答案。
比如说,在证明三角形全等的时候,我们先看看题目给了哪些条件,是边相等还是角相等,然后再根据全等三角形的判定定理去一一对应。
全等三角形难题

全等三角形难题引言在初中数学中,学习了许多有关三角形的性质和定理。
其中,全等三角形是一个重要的概念。
全等三角形是指两个三角形的对应边长和对应角度完全相等的情况。
在解决全等三角形难题时,我们需要利用已知条件和全等三角形的性质来推导出未知信息。
本文将探讨一些全等三角形的难题,并提供相应的解题思路和方法。
难题一:求等腰三角形的底边长度已知一个等腰三角形的顶角度数为60°,求其底边的长度。
解题思路1.假设等腰三角形的底边长度为x。
2.根据等腰三角形的性质,顶角的度数等于底角的度数,所以底角的度数也为60°。
3.由三角形的内角和为180°可得,两个底角的度数之和为180°-60°=120°。
4.由于等腰三角形的两条底边相等,可推导出底角为等边三角形,其两个底角的度数相等,即每个底角的度数为120°/2=60°。
5.由三角形的内角和为180°可得,三个底角的度数之和为180°。
6.将三角形的底边长度记为x,则根据正弦定理可得:(x/2)/sin60° = x/sin180°。
7.化简等式可得:1/2 = x/1。
8.通过求解等式可得:x = 2。
解答和验证根据上述解题思路可得,等腰三角形的底边长度为2。
我们可以通过验证来确保解答的正确性。
1. 等腰三角形的顶角度数为60°,底角的度数也为60°。
2. 底边的长度为2。
3. 三角形的两条底边相等,满足等腰三角形的性质。
4. 三个底角的度数之和为180°。
综上所述,等腰三角形的底边长度为2。
Markdown代码# 全等三角形难题## 引言在初中数学中,学习了许多有关三角形的性质和定理。
其中,全等三角形是一个重要的概念。
全等三角形是指两个三角形的对应边长和对应角度完全相等的情况。
在解决全等三角形难题时,我们需要利用已知条件和全等三角形的性质来推导出未知信息。
三角形、等腰三角形以及全等三角形的证明

儒洋教育学科教师辅导讲义1. 三角形的定义:由不在同一条直线上的三条线段首尾顺次相接所组成的图形叫做三角形。
2. 三角形中的几条重要线段:(1)三角形的角平分线(三条角平分线的交点叫做内心) (2)三角形的中线(三条中线的交点叫重心) (3)三角形的高(三条高线的交点叫垂心) 3. 三角形的主要性质(1)三角形的任何两边之和大于第三边,任何两边之差小于第三边; (2)三角形的内角之和等于180°(3)三角形的外角大于任何一个和它不相邻的内角,等于和它不相邻的两个内角的和; (4)三角形中,等角对等边,等边对等角,大角对大边,大边对大角; (5)三角形具有稳定性。
4. S S ABE CDE ∆∆⋅三角形是最常见的几何图形之一,在工农业生产和日常生活中都有广泛的应用。
三角形又是多边形的一种,而且是最简单的多边形,在几何里,常常把多边形分割成若干个三角形,利用三角形的性质去研究多边形。
实际上对于一些曲线,也可以利用一系列的三角形去逼近它,从而利用三角形的性质去研究它们。
因此,学好本章知识,能为以后的学习打下坚实的基础。
5. 三角形边角关系、性质的应用 【分类解析】例1. 锐角三角形ABC 中,∠C =2∠B ,则∠B 的范围是( ) A. 1020︒<<︒∠B B. 2030︒<<︒∠B C. 3045︒<<︒∠B D. 4560︒<<︒∠B分析:因为∆ABC 为锐角三角形,所以090︒<<︒∠B 又∠C =2∠B ,∴︒<<︒0290∠B ∴︒<<︒045∠B又∵∠A 为锐角,()∴=︒-+∠∠∠A B C 180为锐角 ∴+>︒∠∠B C 90∴>︒390∠B ,即∠B >︒30 ∴︒<<︒3045∠B ,故选择C 。
例2. 选择题:已知三角形的一个外角等于160°,另两个外角的比为2:3,则这个三角形的形状是( )A. 锐角三角形B. 直角三角形C. 钝角三角形D. 无法确定分析:由于三角形的外角和等于360°,其中一个角已知,另两个角的比也知道,因此三个外角的度数就可以求出,进而可求出三个内角的度数,从而可判断三角形的形状。
完整版)全等三角形难题题型归类及解析

完整版)全等三角形难题题型归类及解析1.在三角形ABC中,AD是角BAC的平分线,AE=AC,DE=2cm,BD=3cm,求BC的长度。
为了解决这个问题,我们可以利用角平分线的轴对称性,构造全等三角形ADE和ABC。
因为AE=AC,所以三角形ADE和三角形ABC的两边分别相等,因此它们是全等的。
根据全等三角形的性质,∠DAE=∠CAB,∠AED=∠ACB。
又因为AD是角BAC的平分线,所以∠DAE=∠EAC,因此∠CAB=2∠EAC。
设BC=x,则根据正弦定理可得:3/x=sin(2EAC)/sin(EAC),化简后得到x=6.2.在三角形ABC中,BD是角ABC的平分线,AB=BC,P在BD上,PM⊥AD于M,PN⊥CD于N,求解PM与PN 的关系。
首先,我们可以利用角平分线的性质,构造等腰三角形ABD和CBD。
因为AB=BC,所以三角形ABD和三角形CBD的两边分别相等,因此它们是全等的。
根据全等三角形的性质,∠BDA=∠BDC,∠ADB=∠CDB。
又因为BD是角ABC的平分线,所以∠ADB=∠BDC,因此∠BDA=∠CDB。
因此,三角形APM和三角形CPN是全等的。
因为全等三角形的对应边相等,所以PM=PN。
3.在三角形OAB中,P是角OAB的平分线上的一点,PC⊥OA于C,∠OAP+∠OBP=180°,OC=4cm,求解AO+BO的值。
我们可以利用角平分线的轴对称性,构造全等三角形OAC和OBC。
因为∠OAP+∠OBP=180°,所以∠AOP=∠BOP=90°。
因此,三角形OAP和三角形OBP是直角三角形。
设AO=x,BO=y,则根据勾股定理可得:x^2+PC^2=OP^2,y^2+PC^2=OP^2.又因为OC=4cm,所以PC=2cm。
将PC代入上面的两个式子中,得到x^2+y^2=OP^2-4.又因为三角形OAC和三角形OBC是全等的,所以x=y,因此2x^2=OP^2-4,即OP^2=2x^2+4.因此,AO+BO=2x=2√((OP^2-4)/2)=2√(2x^2)=2√(2y^2)=2√(2x^2+4)/2=2√(OP^2)/2=OP√2=2√6.4.在三角形ABC中,E在边AC上,且∠XXX∠ABC。
初二全等三角形难题全等三角形难题及答案

初二全等三角形难题全等三角形难题及答案1、如图,在ABC 中,AB BC, ABC 90 。
F 为AB延长线上一点,点E在BC上,BE BF ,连接AE,EF 和CF。
求证:AE CFo 2、如图,D是ABC的边BC 上的点,且CD AB, ADB BAD,AE是ABD 的中线。
求证:AC…旋转已知,如图,三角形ABC是等腰直角三角形,/ ACB=90 , F是AB的中点,直线I经过点C,分别过点A、B作I的垂线,即AD丄CE , BE丄CE , (1)如图1,当CE 位于点F的右侧时,求证:AADC CEB ; (2)如图2,当CE位于点F的左侧时…全等三角形难题题型归类及解析一、角平分线型角平分线是轴对称图形,所以我们要充分的利用它的轴对称性,常作的辅助线是:一利用截取一条线段构造全等三角形,二是经过平分线上一点作两边的垂线。
另外掌握两个常用的结论:角平分线与平行线构成等腰三角形,角平分线与垂…1、如图,在ABC中,AB BC, ABC 90 。
F为AB 延长线上一点,点E在BC上,BE BF,连接AE,EF和CF。
求证:AE CFo 2、如图,D是ABC的边BC上的点,且CD AB,ADB BAD, AE是ABD 的中线。
求证:AC 2AE。
AB AC PB PC。
3、如图,在ABC 中,AB AC,求证:1 2,P 为AD上任意一点。
4、如图,BD、CE分别是ABC的边AC、AB上的高,F、G分别是线段DE、BC的中点求证:FG DE5、如图所示,MBC是等腰直角三角形,/ ACB = 90° AD是BC边上的中线,过C作AD的垂线,交AB于点E,交AD于点F,求证:/ ADC =Z BDE6、如图,在锐角ABC中,已知ABC 2 C,ABC的平分线BE与AD垂直,垂足为D,若BD 4cm, 求AC的长参考答案1、思路分析:可以利用全等三角形来证明这两条线段相等,关键是要找到这两个三角形。
全等三角形与等腰三角形的应用
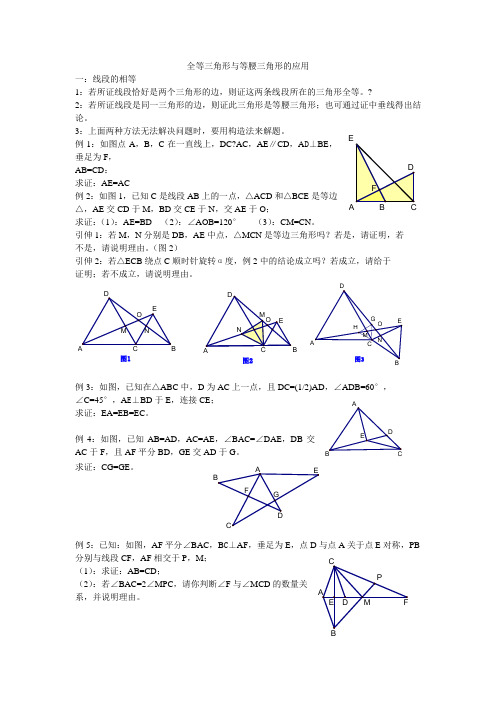
全等三角形与等腰三角形的应用一:线段的相等1:若所证线段恰好是两个三角形的边,则证这两条线段所在的三角形全等。
?2:若所证线段是同一三角形的边,则证此三角形是等腰三角形;也可通过证中垂线得出结论。
3:上面两种方法无法解决问题时,要用构造法来解题。
例1:如图点A ,B ,C 在一直线上,DC?AC ,AE ∥CD ,A D ⊥BE ,垂足为F ,AB=CD :求证:AE=AC例2:如图1,已知C 是线段AB 上的一点,△ACD 和△BCE 是等边△,AE 交CD 于M ,BD 交CE 于N ,交AE 于O ;求证:(1):AE=BD (2):∠AOB=120° (3):CM=CN 。
引伸1:若M ,N 分别是DB ,AE 中点,△MCN 是等边三角形吗?若是,请证明,若 不是,请说明理由。
(图2)引伸2:若△ECB 绕点C 顺时针旋转α度,例2中的结论成立吗?若成立,请给于 证明;若不成立,请说明理由。
例3:如图,已知在△ABC 中,D 为AC 上一点,且DC=(1/2)AD ,∠ADB=60°, ∠C=45°,A E ⊥BD 于E ,连接CE ; 求证:EA=EB=EC 。
例4:如图,已知AB=AD ,AC=AE ,∠BAC=∠DAE ,DB 交AC 于F ,且AF 平分BD ,GE 交AD 于G 。
求证:CG=GE 。
例5:已知:如图,AF 平分∠BAC ,B C ⊥AF ,垂足为E ,点D 与点A 关于点E 对称,PB 分别与线段CF ,AF 相交于P ,M ; (1):求证:AB=CD ;(2):若∠BAC=2∠MPC ,请你判断∠F 与∠MCD 的数量关系,并说明理由。
图2图1例6:如图1,若△ABC 和△ADE 为等边三角形,M ,N 分别为EB ,CD 的中点, 易证CD=BE ,△AMN 是等边三角形; (1):当把△ADE 绕A 点旋转到图2的位置时,CD=BE 是否仍然成立?若成立,请证明,若不成立,请说明理由;? (2):当△ADE 绕点A 旋转到图3的位置时,△AMN 是否还是等边三角形??若是,请给出证明,若不是,请说明理由。
初中数学难点之八:等腰三角形、等边三角形、直角三角形

初中数学难点之八:等腰三角形、等边三角形、直角三角形等腰三角形、等边三角形、直角三角形是初中数学重点考察内容,也是学习的难点。
一、等腰三角形的概念1. 定义有两条边相等的三角形叫做等腰三角形。
两条相等的边叫做腰,所夹的角叫做顶角,另一边叫做底边,底边与腰形成的两个角叫做底角。
2. 性质(1)等腰三角形是轴对称图形,底边中线是对称轴(底边的高、顶角的角的角平分线都是对称轴)(2)等腰三角形两个底角相等,简称等边对等角。
(3)等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合,简称三线合一。
3. 判定(1)两内角相等的三角形叫做等腰三角形(2)两个边相等的三角形叫做等腰三角形二、等边三角形1. 定义三条边都相等的三角形叫做等边三角形。
2. 性质(1)等边三角形有三条对称轴,中线是对称轴(2)等边三角形三个角相等,每个角都为60º(3)等边三角形的顶角平分线、底边上的中线、底边上的高相互重合,简称三线合一。
3. 判定(1)三条边都相等的三角形是等边三角形(2)三个角都相等的三角形叫做等边三角形(3)有一个内角是60º的等腰三角形是等边三角形。
三、直角三角形1. 定义有一个角是直角的三角形叫做直角三角形2. 性质(1)直角三角形两个锐角互余(2)直角三角形斜边上的中线等于斜边的一半(3)直角三角形中,30º角所对的直角边等于斜边的一半(4)勾股定理:a2+b2=c2(a、b为直角边,c为斜边)3. 判定(1)有一个角是直角的三角形,或者两个锐角和为90º的三角形为直角三角形。
(2)一边的中线等于这条边的一半,这个三角形是直角三角形。
(3)勾股定理逆定理:如果有a2+b2=c2(a、b、c为三角形的三个边),则三角行为直角三角形四、基础题型1. 例题1如图,边长为4的等边ΔABC中,D、E分别为AB、BC的中点,EF⊥AC于点F,G为EF的中点,连接DG,则DG的长为?解:连接DE,因为:EF⊥AC,∠C=60º所以∠FEC=30º,因为:ΔABC为等边三角形,DE为中位线所以有:2. 考察知识点(1)等边三角形及内角为60º(2)三角形中位线(3)直角三角形30度内角所对直角边等于斜边的一半(4)直角三角形勾股定理3. 解题思路和技巧DG是非常孤立的,既不是中位线,也不平行某一边,即不是三角形的某一边,也不是规则四边形的边,很难下手,因此必须画辅助线把DG融入某个三角形内,因为D、E分别是所在边的中点,连接起来是三角形的中位线,因此连接DE,尝试解题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1、(1)如图表示长方形纸片ABCD沿对角线BD进行折叠后的情况,图中有没有关于某条直线对称的图形?如图,请作出对称轴;图中是否有相等的线段、相等的角(不含直角)?如有,请写出相等的线段、相等的角;
(2)在(1)中,连接AC,那么AC与BD平行吗?为什么?
2、如图所示,在△ABC中,∠C=90°,AD是∠BAC的平分线,DE⊥AB于E,F在AC 上,BD=DF。
证明:
(1)CF=EB;(2)AB=AF+2EB.
3、在Rt三角形中,∠C=90°,BD平分∠ABC交AC于点D,DE垂直于线段AB。
(1)试找出图中相等的线段,并加以证明;
(2)若DE=1cm,BD=2cm.
4、如图,在Rt△ABC中,AD是∠BAC的平分线,DF⊥AC于点F,且DE=DC.试比较BE 和FC的大小关系并说明理由。
5、已知一个等腰三角形两内角的度数之比为1:4,求这个等腰三角形顶角的度数。
6、如图,已知点D为等腰直角△ABC内一点,∠CAD=∠CBD=15°,E为AD延长线上的一点,且CE=CA。
(1)DE平分∠BDC吗?为什么?
(2)若点M在DE上,且DC=DM,那么ME与BD相等吗?请证明你的结论.
7、如图,在△ABC中,AB=20cm,AC=12cm,点P从点B出发以每秒3cm的速度向点A 运动,点Q从点A同时出发以每秒2cm的速度向点C运动,其中一个动点到达端点时,另一个动点也随之停止运动,当△APQ是等腰三角形时,运动的时间是。
8、如图,在△ABC中,∠ACB=90°,∠B>∠A,点D为边AB的中点,DE∥BC交AC于点E,CF∥AB交DE的延长线于点F.
(1)求证:DE=EF;
(2)连结CD,过点D作DC的垂线交CF的延长线于点G,求证:∠B=∠A+∠DGC.
9、如图,在△ABC中,AE平分∠BAC,BE⊥AE,∠ABE=2∠C.
求证:AC-AB=2BE.
10、如图,D为等边△ABC内一点,且DB=DA,BP=BA,∠DBP=∠DBC,求∠BPD的大小.
11、已知,如图,△ABC中,AB=AC,∠BAC=120°,AD⊥BC,DE⊥AB,垂足分别为D,E.求证:BE=3AE.
12、两个全等的含30°,60°角的三角板ADE和三角板ABC如图所示放置,E,C三点在一条直线上,连结BD,取BD的中点M,连结ME,MC。
试判断△EMC的形状,并说明理由。
13、如图所示,在△ABC中,AC=BC,∠ACB=90°,D是AC上一点,且AE垂直BD的延长线于E,AE=BD,求证:BD是∠ABC的平分线.
14、如图,C 为线段AE 上一动点(不与点A ,E 重合),在AE 同侧分别作等边三角形ABC 和等边三角形CDE ,AD 与BE 交于点O ,AD 与BC 交于点P ,BE 与CD 交于点Q ,连结PQ .以下五个结论:
① AD=BE; ② PQ ∥AE ; ③ AP=BQ ; ④ DE=DP ; ⑤ ∠AOB=60°. 恒成立的结论有______________(把你认为正确的序号都填上).
15、如图,△ABC 中,∠BAC=90°,AD ⊥BC 于点D ,CE 平分∠ACB ,交AD 于G ,GF ∥BC 交AB 于F.
求证:AE=BF.
16、如图①,将一张矩形纸片对折,然后沿虚线剪切,得到两个(不等边)三角形纸片△ABC ,△A 1B 1C 1。
(1)将△ABC ,△A 1B 1C 1如图②摆放,使点A 1与B 重合,点B 1在AC 边的延长线上,连接CC 1交BB 1于点E .求证:∠B 1C 1C=∠B 1BC .
(2)若将△ABC ,△A 1B 1C 1如图③摆放,使点B 1与B 重合,点A 1在AC 边的延长线上,连接CC 1交A 1B 于点F ,试判断∠A 1C 1C 与∠A 1BC 是否相等,并说明理由.
A B C E D O P Q。
