电子科技大学随机信号分析期末考试题1
电子科技大学信号检测与估计2016期末考试

信号检测与估计试题答案三、(15分)现有两个假设00,11,:,1,2,,:,1,2,,j j j j j j H y u z j K H y u z j K=+==+=其中观测样本j y 为复信号,0,1,,j j u u 是复信号样本,j z 是均值为零、方差为2*z j j E z z σ⎡⎤=⎣⎦的复高斯白噪声,代价因子为001101100,1c c c c ====,先验概率010.5ππ==(1)试写出两假设下的似然函数()0p y 和()1p y ,其中12[,,,]T K y y y y =;(4分)(2)采用贝叶斯准则进行检测,给出信号检测的判决规则表达式;(6分) (3)在上题基础上,计算虚警概率。
(5分) 解:(1)观测样本j y 在假设0H 下的概率密度函数为()20,0221exp 1,2,,j jj z z y u p y j K πσσ⎧⎫-⎪⎪=-=⎨⎬⎪⎪⎩⎭……..(2分)由于样本间互相独立,则K 个观测样本的联合概率密度函数为()()()()()20010200,22111exp K K j j Kj z z p y p y p y p y y u σπσ=⎧⎫==--⎨⎬⎩⎭∑…….(1分)同理可得,在假设1H 下的似然函数为()()()()()21111211,22111exp K K j j Kj z z p y p y p y p y y u σπσ=⎧⎫==--⎨⎬⎩⎭∑…….(1分)(2)首先计算似然比:()()(){}{}1**011,0,22221102222exp Re Re K K j j j j j j z z z z p y L y y u y u p y εεσσσσ==⎧⎫==--+⎨⎬⎩⎭∑∑其中∑==K j j u 12,00||21ε,∑==K j j u 12,11||21ε。
……..(2分) 然后,计算贝叶斯准则似然比门限为()()010********B C C C C πτπ-==-………(2分)因此,根据{}{}1**011,0,22221102222exp Re Re 1K K j j j j j j z z z z D y u y u D εεσσσσ==≥⎧⎫--+⎨⎬<⎩⎭∑∑ 化简可得最后的判决表达式:(){}1*1,0,101Re Kj j j j D y u u D εε=≥--<∑ ……..(2分) (3)在假设0H 下,j y 是均值为0,j u 、方差为2z σ的复高斯随机变量,因此,统计决策量(){}*1,0,1Re Kj j j j y u u μ==-∑ 为高斯分布随机变量,其均值和方差分别为:{}002r E H με=- (1分){}()()220101222z r z r Var H σμεεσεε=+-=+- (1分)其中,*0,1,Kj jr i uuJ ρρρ=+=∑ 定义为两信号的相关系数。
电子科技大学随机信号分析期末考试题

电子科技大学20 -20 学年第 学期期 考试 卷课程名称:_________ 考试形式: 考试日期: 20 年 月 日 考试时长:____分钟 课程成绩构成:平时 10 %, 期中 10 %, 实验 %, 期末 80 % 本试卷试题由___2__部分构成,共_____页。
一、填空题(共20分,共 10题,每题2 分) 1. 设随机过程0()cos(),X t A t t ω=+Φ-∞<<∞,其中0ω为常数,A Φ和是相互独立的随机变量,[]01A ∈,且均匀分布,Φ在[]02π,上均匀分布,则()X t 的数学期望为: 02. 已知平稳随机信号()X t 的自相关函数为2()2X R e ττ-=,请写出()X t 和(2)X t +的协方差12-e3. 若随机过程()X t 的相关时间为1τ,()Y t 的相关时间为2τ,12ττ>,则()X t 比()Y t 的相关性要__大___,()X t 的起伏特性比()Y t 的要__小___。
4. 高斯随机过程的严平稳与___宽平稳_____等价。
5. 窄带高斯过程的包络服从___瑞利___分布,相位服从___均匀___分布,且在同一时刻其包络和相位是___互相独立___的随机变量。
6. 实平稳随机过程的自相关函数是___偶____(奇、偶、非奇非偶)函数。
7. 设)(t Y 是一均值为零的窄带平稳随机过程,其单边功率谱密度为)(ωY F ,且0()Y F ωω-为一偶函数,则低频过程)()(t A t A s c 和是___正交___。
二、计算题(共80分)1. (16分)两随机变量X 和Y 的联合概率密度函数为(,)=XY f x y axy ,a 是常数,其中0,1x y ≤≤。
求:1)a ;2)X 特征函数;3)试讨论随机变量X 和Y 是否统计独立。
解:因为联合概率密度函数需要满足归一性,即 (2分)1100111(,)124XY f x y dxdy AxydxdyA xdx ydy A∞∞-∞-∞====⎰⎰⎰⎰⎰⎰(分)所以4A = (1分)X 的边缘概率密度函数:1()4201X f x xydy x x ==≤≤⎰ (2分)所以特征函数1102()2()212212j XX j x X j x j x j x j j E e f x e dxxe dxe xe j j e j e ωωωωωωωφωωωωω∞-∞⎡⎤=⎣⎦==⎡⎤=-⎢⎥⎣⎦⎡⎤=--⎣⎦⎰⎰(分)(分)(分)容易得1()4201Y f y xydx y y ==≤≤⎰则有 (,)()()XY X Y f x y f x f y = (2分) 因此X 和Y 是统计独立。
电子科技大学信号与系统-信号与系统考题
信号与系统1、求积分⎰+∞∞-++dt t t )2()1(2δ 的值。
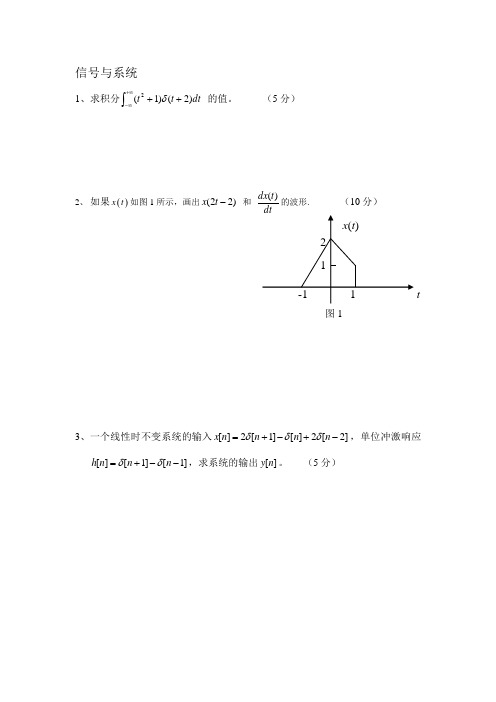
(5分)2、 如果()x t 如图1所示,画出)22(-t x 和t dx )(的波形. (10分)图13、一个线性时不变系统的输入]2[2][]1[2][-+-+=n n n n x δδδ,单位冲激响应]1[]1[][--+=n n n h δδ,求系统的输出][n y 。
(5分)t4、一个线性时不变系统的输入为)(1tx时,输出为)(1ty。
若输出信号为)(2tx,求输出信号)(2ty。
各信号如图2所示。
(5分)图25、已知)1()()(--=tututx,)2/()(txth=,求)(*)()(thtxty=。
(5分)6、一个线性时不变系统的单位冲激响应为 )2sin 8(sin 1)(t t tt h πππ-=, 如果输入信号为 t t t x ππ6sin 4cos 1)(++=, 求输出信号()y t .(10分)7、 设 ()x t 是一个带限信号,()x t 的频谱满足()0 for 100X j ωωπ=>。
现对)()(2t x t y =冲激串采样,得到()()()p n y t y nT t nT δ+∞=-∞=-∑求采样间隔 T 的范围使得 ()t y 能由信号()t y p 恢复。
(10分)8、(15分)一个稳定的线性时不变系统,其微分方程如下)()()(6)(5)(22t x dtt dx t y dtt dy dtt y d +=++1) 求系统函数H(S),决定H(S)的收敛域。
2)求系统的单位冲激响应()h t ,判定系统是否因果。
3)画出系统的模拟方框图。
电子科大17春《随机信号与系统》在线作业1

A. 2t
B. t+2
C. 2
D.以上都不可能
正确答案:
4. N(n)是均值为0,方差为a2的高斯白序列,其功率谱为()。
A. 0
B. a
C. a2
D.以上都不对
正确答案:
5.若N(t)是方差为a的零均值独立高斯过程,则它在不同的两个时刻的相关函数是()。
D. w
正确答案:
10.随机信号X(t)通过一个LTI系统H(jw)=2/(jw+2),已知输出Y(t)的均值为2,则X(t)的均值为()。
A. 2
B. 1
C. 1/2
D. 4
正确答案:
17春《随机信号与系统》在线作业1
二、多选题(共5道试题,共30分。)
1.广义平稳的随机信号具有如下性质()。
A.一阶分布与时间无关
5.只要满足相关函数与两时间参量的绝对值无关的信号都是广义平稳的。
A.错误
B.正确
正确答案:
6.传输数据流时,错误码发生的总数目是个随机信号。
A.错误
B.正确
正确答案:
7.随机信号的每一个样本函数的时间平均等于其统计平均的特性成为各态历经性。
A.错误
B.正确
正确答案:
8.随机信号X(t),其任意n元随机变量{X(t1),X(t2),X(t3)…X(tn)}的联合概率分布为高斯分布则该信号为高斯信号。
C. z=A-B
D. z=Asin(wt)+Bcos(wt)
正确答案:
4.严格平稳信号具有如下特性()。
A.一阶分布与时间无关
B.密度函数与时间无关
C.均值与时间无关
电子科技大学2014-2015 学年第 1 学期信号与系统期 末 考试 A 卷

电子科技大学2014-2015 学年第 1 学期期末考试A 卷课程名称:信号与系统考试形式:一页纸开卷考试日期:20 15年 1 月 15 日考试时长: 120 分钟课程成绩构成:平时 10 %,半期考试 20 %,实验 10 %,期末 60 %本试卷试题由二部分构成,共 5 页。
题号一二合计1234得分得分一、选择填空题(共30分,共 6问,每问5分)1.Consider two signals and , as shown in Figure 1. The Fourier transform of is . Then the Fourier transform ofshould be().(a)(b)(c)(d)Figure 1 The waveforms of and2. The convolution sum ( ).(a) (b) (c) (d) not existed3. Consider a stable discrete-time system, whose system function is a rational function and has only two poles:. The positions of zeros are unknown. The impulse response of the system must be ( ).(a) finite duration (b) right-sided (c) left-sided (d) two sided4.The relation between the input and the output of a causal continuous-time LTI system is described by the differential equation . The system is ().(a) Low-pass filter (b) Band-pass filter (c) High-pass filter (d) Band-stop filter5.The Fourier transform of the signal is shown in Figure 2.The signal may beFigure 2(a) real and even (b) real and odd(c) pure imaginary and odd (d) pure imaginary and even6. The Laplace Transform of is ().(a) , (b) ,(c) , (d) ,二、计算题(共70分)得分1.(15 points)Suppose and are both band-limited signals, where.Impulse-train sampling is performed on to obtain , as shown inFigure 3 where .Deduce the value of so that for .Specify the range ofvalues for the sampling period T which ensures that =.32.( 18 points ) Consider an LTI system with unit impulseresponse .The input signal ,where is the unit stepfunction.得分(a) Sketch. (b) Determine the magnitude and phase responseof this system. (c) Determine the output .3(17分)A causal continuous-time LTI system is given in Figure 4.(a)Determine the range of the constant K toensure that the system is stable.(b)If K=2, determine the unit step response.1/S-31/S-2KFigure 44(20 分)Suppose that we are given the following information about a causal discrete-time LTI system:(1)If the input is ,then the output is .(2)The value of the unit impulse response at n=0 is .Solve the following problems:(a) Determine the system function ,and indicate its ROC.(b) Draw a block diagram representation of this system.(c) Determine the unit impulse response .(d) Suppose. Determine the range of real numberso that is the unit impulse response of a stable system.。
电子科技大学22春“电子信息工程”《数字信号处理》期末考试高频考点版(带答案)试卷号:1

电子科技大学22春“电子信息工程”《数字信号处理》期末考试高频考点版(带答案)一.综合考核(共50题)1.对周期序列的谱分析工具是()。
A.傅里叶变换B.傅里叶级数C.离散傅里叶变换D.离散傅里叶级数参考答案:D2.要处理一个连续时间信号,对其进行采样的频率为6kHz,要无失真的恢复该连续信号,则该连续信号的最高频率可能是()。
A.12kHzB.6kHzC.4kHzD.3kHz参考答案:D3.序列x(n)=u(n)的能量为()。
A.1B.9C.11D.∞参考答案:D4.当输入序列不同时,线性移不变系统的单位抽样响应也不同。
()A.正确B.错误5.离散系统的差分方程为y(n)=x(n)+ay(n-1),则系统的频率响应()。
A.当|a|B.当|a|>1时,系统呈低通特性C.当0D.当-1<a<0时,系统呈低通特性参考答案:C6.两有限长序列的长度分别是12和15,要利用DFT计算两者的线性卷积,则DFT的点数至少应取()。
A.15B.26C.27D.28参考答案:C7.某连续信号的最高频率为5kHz,采样后为了不失真的恢复该连续信号,则采样频率至少为()。
A.5k HzB.10k HzC.2.5k HzD.1.25k Hz参考答案:B8.设y(n)=kx(n)+b,k0,b0为常数,则该系统是线性系统。
()A.正确B.错误参考答案:B9.数字信号的特征是()。
A.时间连续、幅值量化D.时间连续、幅值连续参考答案:B10.任何系统的响应与激励施加于该系统的时刻有关。
()A.正确B.错误参考答案:B11.因果系统一定是稳定系统。
()A.正确B.错误参考答案:B12.与FIR滤波器相似,IIR滤波器的也可以方便地实现线性相位。
()A.正确B.错误参考答案:B13.已知某序列的Z变换收敛域为全Z平面,则该序列为()。
A.有限长序列B.双边序列C.左边序列D.右边序列参考答案:A14.A.M+NB.M+N-1C.M+N+1D.2(M+N)参考答案:B15.计算256点的按时间抽取基-2 FFT,在每一级的蝶形个数是()。
2006随机试卷标准答案(B)

电子科技大学二零零 至二零零 学年第 学期期 考试随机信号分析 课程考试题 B 卷 ( 120 分钟) 考试形式: 一页纸开卷 考试日期 200 年 月 日课程成绩构成:平时 20 分, 期中 10 分, 实验 0 分, 期末 70 分十一道题仍选十道题做。
1. (7分)若随机信号()X t aC =,其中a 为常数,C 是R.V .,且C 的方差2C 0σ≠,讨论(1)X (t )的均值函数和自相关函数; (2) X (t )的各种平稳性; (3) X (t )的均值各态历经性。
解:(1)[][][]() E X t E aC aE C ==常数[]()2222222(,)()()= X c c R t t E X t X t E a C a E C a m ττσ⎡⎤⎡⎤+=+==+⎣⎦⎣⎦常数 (2) 由(1)知X (t )是广义平稳的。
并且X (t )是严格平稳的。
它也是严格周期平稳的和广义周期平稳的。
(3) []1()lim 2TTT A X t aCdt aC T-→∞==⎰,因为2C 0σ≠,所以[]()0Var A X t ⎡⎤≠⎣⎦,故X (t )不是均值各态历经的。
2. (7分)设有随机过程()cos X t A t π=,其中A是均值为零,方差是2的正态随机变量,求:(1) X (t )的均值函数和自相关函数; (2) X (1)和14X ⎛⎫⎪⎝⎭的概率密度函数; (3) X (t )是否为广义平稳随机过程?(4) X (t )是否均值各态历经?解:(1)[()][cos ][]cos 0E X t E A t E A t ππ===2(,)[cos ()cos ][]cos ()cos X R t t EA t A t E A t t τπτππτπ+=+=+2cos ()cos cos (2)cos tt t πτππτπτ=+=++ 与t 有关 (2 ) 由于正态随机变量的线性变换仍然是正态随机变量,所以(1) -X A =, 142X A ⎛⎫= ⎪⎝⎭[(1)]0E X =,[(1)]2Var X =()220224(;1)x x f x e---⋅∴==104E X ⎡⎤⎛⎫= ⎪⎢⎥⎝⎭⎣⎦,21214Var X ⎡⎤⎛⎫=⨯= ⎪⎢⎥⎝⎭⎣⎦⎝⎭22(0)212111(;)4x x f x ee ---⋅∴==(3)因为(,)cos (2)cos X R t t t τπτπτ+=++ 与t 有关,所以X (t )不是广义平稳随机过程。
电子科技大学2009年随机信号分析试题A与标准答案

(1) 试判断 X ( t ) 和 Y ( t ) 在同一时刻和不同时刻的独立性、相关 性及正交性; (2) 试判断 X ( t ) 和 Y ( t ) 是否联合广义平稳。 解: (1) 由于 X ( t ) 和 Y( t ) 包含同一随机变量 θ ,因此非独立。 根据题意有
f (θ ) = 1 2π
π
−π
1 1 = cos[ w0 ( t1 − t2 )] cos( w0τ ) 2 2
同理可得 RY ( t1 ,t2 ) = RX ( t1 ,t2 ) ,因此 X ( t ) 和 Y( t ) 均广义平稳。
,t2 ) C XY ( t1= ,t2 ) 由于 RXY ( t1= 1 1 sin [w0 ( t1 − = t2 )] sin (w0τ ) ,因此 X ( t ) 和 2 2
。
π
−π
E[ X ( t )] E [sin(ω = = 0 t + Θ) ]
E[Y( t )] E [ cos(ω = = 0 t + Θ) ]
π
∫
1 sin( w0= t + θ )dθ 0 , 2π
−π
∫
1 cos( w0= t + θ )dθ 0 2π
C XY ( t1 ,t2 ) = RXY ( t1 ,t2 ) = E[ X ( t1 )Y( t2 )] = E[sin (w0t1 + θ )co s( w0t2 + θ )]
1 1 1 1 − τ 1 −3 τ = P R(0)= += R (τ )= e + e ,所以 4 12 3 4 12
1 ∞ 1 10 20 P S ( ) d 2 d = = = ω ω ω (3) 可以。 2π ∫−∞ 2π ∫−10 π
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
电子科技大学20 -20 学年第 学期期 考试 卷
课程名称:_________ 考试形式: 考试日期: 20 年 月 日 考试时长:____分钟 课程成绩构成:平时 10 %, 期中 10 %, 实验 %, 期末 80 % 本试卷试题由___2__部分构成,共_____页。
一、填空题(共20分,共 10题,每题2
分)
0()cos(),X t A t t ω=+Φ-∞<<∞,其中0ω为常数,A Φ和是相互独立的随机变量,
[]01A ∈,且均匀分布,Φ在[]02π,上均匀分布,则()X t 的数学期望为: 0
2. 已知平稳随机信号()X t 的自相关函数为2()2X R e ττ-=,请写出()X t 和(2)X t +的协方差12-e
3. 若随机过程()X t 的相关时间为1τ,()Y t 的相关时间为2τ,12ττ>,则()X t 比()Y t 的
相关性要__大___,()X t 的起伏特性比()Y t 的要__小___。
4. 高斯随机过程的严平稳与___宽平稳_____等价。
5. 窄带高斯过程的包络服从___瑞利___分布,相位服从___均匀___分布,且在同一时刻其包络
和相位是___互相独立___的随机变量。
6. 实平稳随机过程的自相关函数是___偶____(奇、偶、非奇非偶)函数。
7. 设)(t Y 是一均值为零的窄带平稳随机过程,其单边功率谱密度为)(ωY F ,且0()Y F ωω-为一
偶函数,则低频过程)()(t A t A s c 和是___正交___。
二、计算题(共80分)
两随机变量X 和Y 的联合概率密度函数为(,)=XY f x y axy ,a 是常数,其中0,1x y ≤≤。
求:
1)a ;
2)X 特征函数;
3)试讨论随机变量X 和Y 是否统计独立。
解:因为联合概率密度函数需要满足归一性,即 (2分)
所以4A = (1分)
X 的边缘概率密度函数:
1
()4201X f x xydy x x ==≤≤⎰ (2分)
所以特征函数
容易得1
()4201Y f y xydx y y ==≤≤⎰
则有 (,)()()XY X Y f x y f x f y = (2分) 因此X 和Y 是统计独立。
(2分)
2. (12分)设随机过程()0xt X t e t -=<<∞,其中x 在(]0,2π均匀分布,求: 1) 求均值()X m t 和自相关函数(,)X R t t τ+; 2) 判断是否广义平稳; 解:
因为()X m t 和(,)X R t t τ+均随时间变化,所以不是广义平稳;(2)L L L L 分
3. (12分)设一个积分电路的输入与输出之间满足关系式:()()t t T
Y t X u du -=⎰
其中T 为积分时间常数,
如输入随机过程()X t 是平稳随机过程,且已知其功率谱密度为()X S ω,求()Y t 的功率谱和自相关函数
解:很显然,()Y t 是平稳随机过程,故有:
4. (16分)已知零均值的窄带高斯随机过程00()()cos ()sin X t a t t b t t ωω=-,其中0100ωπ=,且已知
()X t 的功率谱如图所示,求:
1)自相关函数()a R τ和()b R τ; 2)()a t 和()b t 的一维联合概率密度; 解:
因为()X t 是零均值的高斯随机过程,因此有: (2分)
00()()
10()()0
x x a b S S S S ωωωωωπ
ωω⎧-++≤⎪==⎨
⎪⎩其它
(2分)
所以3
10()()0
a b S S ωπ
ωω⎧≤⎪=⎨
⎪⎩=其它
(2分)
因此sin(10)
()()3
a b R R πτττπτ
== (2分)
因为()a t 和()b t 都为零均值的高斯随机过程,且在同一时刻是独立的,所以只要求出其方差,即
可得到其一维联合概率密度: (3分)
显然有和22
30a b σσ== (2分)
所以:
22
60
(,;,)(;)(;)60a b ab a b e
f a b t t f a t f b t π
+-==
(3分)
5. (12分)一数学期望为零的平稳高斯白噪声()N t ,功率谱密度为0/2N ,经过如图所示的系统,输出为()Y t ,求输出过程的相关函数。
解:令1/RC α=,得RC 积分电路的功率传输函数为:
2
2
2
2
()H αωαω=+ (2分) 则()X t 的功率谱密度为:
20
2
2
()2X N S αωαω=+ (2分) 得()X t 的自相关函数为:
()4
X N R e
ατ
αω-=
(2分)
最后得:
6. (12分)证明平稳随机过程()X t 希尔伯特变换^
()X t 的自相关函数^
()()X X R R ττ=。
证明:平稳随机过程进行希尔伯特变换后仍为平稳随机过程,因此有: 证毕。
