物理化学打印完整版要点
物理化学复习要点

dS ≥
δ Qr
T −T 1 T 2
热机将热转换为功时的最高效率,非热机不遵守卡诺定律 -如电池
不可逆过程要设计成始终态相同的可逆过程进行计算,如过冷液体的凝固等 (4)化学反应过程的 ΔS=∑ν B S Bе
F = U − TS G = H − TS 自发变化的方向 ΔGT,p ≤ 0 ΔFT,V ≤ 0
ΔC p = 0, ΔH 与温度无关
1 1 ΔH 和温度的通用关系式: Δ r H m = Δ r H m,0 + ΔaT + ΔbT 2 + ΔcT 3 2 3
第二定律 卡诺定律
η = 2
(可逆过程的热温熵等于熵变,不可逆过程小于熵变) T 熵是系统混乱度的量度,熵是有绝对值的 熵增加原理:孤立系统自发变化的方向是熵增加的方向 ΔSm 计算: (1)ΔS = ΔH m Qr T T (恒温); (2)ΔS = C pln 2 , ΔS = CV ln 2 (变温过程) : (3)ΔS = (可逆相变) T T1 T1 T (5)电池反应: ΔS=zF( ∂E )p ∂T (6)其它
H 2 O(208K,g,100kPa) → H 2 O(298K,l,100kPa)
8. 扩展表面
恒温恒压不做非膨胀功时,自发变化的方向 ΔGT,p < 0 恒温恒压做非膨胀功时, 自发变化的方向 ΔGT,p ≤ −We
ΔGT,p = 0 是平衡
四个基本公式和 ΔG 的计算
中国药科大学物理化学教研室 2008 年 6 月
l A 电解质Λm和c的关系 电导率-
κ = L⋅
摩尔电导率- Λm =
k c
测电导用韦斯电桥,要用交流信号源
∞ ∞ 无限稀释定律 Λ∞ m =ν+ λm,+ +ν−λm,−
物理化学的知识点总结

物理化学的知识点总结一、热力学1. 热力学基本概念热力学是研究能量转化和传递规律的科学。
热力学的基本概念包括系统、环境、热、功、内能、焓、熵等。
2. 热力学第一定律热力学第一定律描述了能量守恒的原理,即能量可以从一个系统转移到另一个系统,但总能量量不变。
3. 热力学第二定律热力学第二定律描述了能量转化的方向性,熵的增加是自然界中不可逆过程的一个重要特征。
4. 热力学第三定律热力学第三定律表明在绝对零度下熵接近零。
此定律是热力学的一个基本原理,也说明了热力学的某些现象在低温下会呈现出独特的特性。
5. 热力学函数热力学函数是描述系统状态和性质的函数,包括内能、焓、自由能、吉布斯自由能等。
二、化学热力学1. 热力学平衡和热力学过程热力学平衡是指系统各个部分之间没有宏观可观察的能量传输,热力学过程是系统状态发生变化的过程。
2. 能量转化和热力学函数能量转化是热力学过程中的一个重要概念,热力学函数则是描述系统各种状态和性质的函数。
3. 热力学理想气体理想气体是热力学研究中的一个重要模型,它通过状态方程和理想气体定律来描述气体的性质和行为。
4. 热力学方程热力学方程是描述系统热力学性质和行为的方程,包括焓-熵图、温度-熵图、压力-体积图等。
5. 反应焓和反应熵反应焓和反应熵是化学热力学研究中的重要参数,可以用来描述化学反应的热力学过程。
三、物质平衡和相平衡1. 物质平衡物质平衡是研究物质在化学反应和物理过程中的转化和分配规律的一个重要概念。
2. 相平衡相平衡是研究不同相之间的平衡状态和转化规律的一个重要概念,包括固相、液相、气相以及其之间的平衡状态。
3. 物质平衡和相平衡的研究方法物质平衡和相平衡的研究方法包括热力学分析、相平衡曲线的绘制和分析、相平衡图的绘制等。
四、电化学1. 电解质和电解电解质是能在水溶液中发生电离的化合物,电解是将电能转化为化学能或反之的过程。
2. 电化学反应和电势电化学反应是在电化学过程中发生的化学反应,电势是描述电化学系统状态的一个重要参数。
物理化学知识点

物理化学知识点物理化学知识点概述1. 热力学定律- 第零定律:如果两个系统分别与第三个系统处于热平衡状态,那么这两个系统之间也处于热平衡状态。
- 第一定律:能量守恒,系统内能量的变化等于热量与功的和。
- 第二定律:熵增原理,自然过程中熵总是倾向于增加。
- 第三定律:当温度趋近于绝对零度时,所有纯净物质的熵趋近于一个常数。
2. 状态方程- 理想气体状态方程:PV = nRT,其中P是压强,V是体积,n是摩尔数,R是理想气体常数,T是温度。
- 范德瓦尔斯方程:(P + a(n/V)^2)(V - nb) = nRT,修正了理想气体状态方程在高压和低温下的不足。
3. 相平衡与相图- 相律:描述不同相态之间平衡关系的数学表达。
- 相图:例如,水的相图展示了水在不同温度和压强下的固态、液态和气态的平衡关系。
4. 化学平衡- 反应速率:化学反应进行的速度,受温度、浓度、催化剂等因素影响。
- 化学平衡常数:在一定温度下,反应物和生成物浓度之比达到平衡时的常数值。
5. 电化学- 电解质:在溶液中能够产生带电粒子(离子)的物质。
- 电池:将化学能转换为电能的装置。
- 电化学系列:金属的还原性或氧化性排序。
6. 表面与胶体化学- 表面张力:液体表面分子间的相互吸引力。
- 胶体:粒子大小在1到1000纳米之间的混合物,具有特殊的表面性质。
7. 量子化学- 量子力学基础:描述微观粒子如原子、分子的行为。
- 分子轨道理论:通过分子轨道来描述分子的结构和性质。
- 电子能级:原子和分子中电子的能量状态。
8. 光谱学- 吸收光谱:分子吸收特定波长的光能,导致电子能级跃迁。
- 发射线谱:原子或分子在电子能级跃迁时发出特定波长的光。
- 核磁共振(NMR):利用核磁共振现象来研究分子结构。
9. 统计热力学- 微观状态与宏观状态:通过系统可能的微观状态数来解释宏观热力学性质。
- 玻尔兹曼分布:描述在给定温度下,粒子在不同能量状态上的分布。
物理化学知识点总结

第一章 热力学第一定律一、基本概念系统与环境,状态与状态函数,广度性质与强度性质,过程与途径,热与功,内能与焓。
二、基本定律热力学第一定律:ΔU =Q +W 。
焦耳实验:ΔU =f (T ) ; ΔH =f (T ) 三、基本关系式1、体积功的计算 δW = -p e d V恒外压过程:W = -p e ΔV可逆过程:1221ln ln p p nRT V V nRT W ==2、热效应、焓等容热:Q V =ΔU (封闭系统不作其他功) 等压热:Q p =ΔH (封闭系统不作其他功) 焓的定义:H =U +pV ; d H =d U +d(pV )焓与温度的关系:ΔH =⎰21d p T T T C3、等压热容与等容热容热容定义:V V )(T U C ∂∂=;p p )(T H C ∂∂=定压热容与定容热容的关系:nR C C =-V p 热容与温度的关系:C p =a +bT +c’T 2 四、第一定律的应用1、理想气体状态变化等温过程:ΔU =0 ; ΔH =0 ; W =-Q =⎰-p e d V 等容过程:W =0 ; Q =ΔU =⎰T C d V ; ΔH =⎰T C d p 等压过程:W =-p e ΔV ; Q =ΔH =⎰T C d p ; ΔU =⎰T C d V 可逆绝热过程:Q =0 ; 利用p 1V 1γ=p 2V 2γ求出T 2,W =ΔU =⎰T C d V ;ΔH =⎰T C d p不可逆绝热过程:Q =0 ; 利用C V (T 2-T 1)=-p e (V 2-V 1)求出T 2,W =ΔU =⎰T C d V ;ΔH =⎰T C d p2、相变化可逆相变化:ΔH =Q =n Δ_H ;W=-p (V 2-V 1)=-pV g =-nRT ; ΔU =Q +W3、热化学物质的标准态;热化学方程式;盖斯定律;标准摩尔生成焓。
摩尔反应热的求算:)298,()298(B H H m f B m r θθν∆=∆∑反应热与温度的关系—基尔霍夫定律:)(])([,p B C T H m p BB m r ∑=∂∆∂ν。
物理化学重要知识点总结及其考点说明

物理化学重要知识点总结及其考点说明
一、化学热力学
1、化学热力学的定义:化学热力学是研究化学反应中物质的热量及能量变化的学科。
2、热力学三定律:第一定律:能量守恒定律;第二定律:热力学第二定律确定有序
能可以被有度能转化;第三定律:热力学第三定律始终指出热力学反应的可能性和温度有关。
3、焓的概念:焓是衡量物质的热力学状态的量,它是物质的热力学特性连续变化的
测量,是物质拥有的热量能量,也可以视为物质拥有的有序能。
4、热力学平衡:热力学平衡是指在不变的温度、压力和其他条件下,恒定的化学反
应发生,直至反应物和生成物的物质形式和化学结构保持不变,热量吸积也变得稳定,这
种状态称为热力学平衡。
二、物理化学
1、物理化学的概念:物理化学是一门融合了物理学和化学的学科,通过应用物理方法,来研究化学性质的变化和分子间的作用及反应,其研究具有多学科的性质。
2、气体的特性:气体的物理性质有很多,如压强、体积、温度、熵、焓等。
质量和
体积的关系为:在一定温度下,气体的质量和体积都成正比。
3、溶质的溶解度:溶解度是衡量溶质溶解在溶剂中的性质,它是指在一定温度、压
力下,溶质在溶剂中的最高溶解量。
溶质的溶解度与温度,压强及溶剂特性有关。
4、化学均衡:化学均衡是指在特定温度和压强下,混合物中物质的各种浓度比例,
产物与原料之间的反应紊乱程度,变化状态的一种稳定平衡状态。
物理化学重点超强总结 doc

物理化学重点超强总结 doc物理化学一、物理性质1、中性:反应物在中性环境下,都呈中性,无味无色;2、不溶解:物质不被水溶解,或是被极性溶剂溶解;3、软硬:反应物可以为软物质,也可以是硬物质。
4、温和性:遇到微弱的酸碱度,反应物仍可稳定存在;5、耐热性:反应物耐温度较高,抗热性较强,热力学性质较好;6、抗寒性:反应物耐冷,能够长时间驻留在这种环境下,抗非温性的腐蚀活动。
二、化学性质1、反应物自身:反应物各自具有一定的化学性质,如碱金属、酸、碱、氧化剂等。
2、反应效应:在不同条件下考虑反应物之间的组成及活性强度,提高反应效率。
3、作用方式:主要是考虑物质凝固、溶解、混合及电离的化学反应和物质的各种性质等。
4、稳定性:考虑反应物的热力学、动力学活性,变成最稳定的化合物,增加反应的稳定性。
5、动力学:动力学说明了反应物之间相互转变时,反应速率随时间变化的规律,以及反应是否会达到较稳定的状态。
6、电化学:电化学研究反应物在电场中的表现,反应物如何受电场作用及其相互作用,表现出的特性。
三、实验方法1、量化:量化是测定反应物的实验方法,主要包括分析法,以量化的方式计算反应物的浓度;2、拉曼光谱:利用拉曼光谱的双光子散射,可以测定反应物的精细化学结构;3、红外光谱:利用红外光谱对反应物的结构和组成进行分析;4、核磁共振:核磁共振光谱是研究反应物基本结构和性质的常用实验方法;5、色谱:利用色谱法可以分析反应物的组成,和控制反应物各自的含量;6、吸收光谱:研究反应物和反应结果对它们吸收特定电子谱讯号之结果所产生的不同响应度。
总之,物理化学包括物理性质、化学性质及实验方法等,反应物的物理性质有:中性、不溶解、软硬、耐热性、抗寒性;反应物的化学性质主要有:反应物自身、反应效应、作用方式、稳定性、动力学和电化学;实验方法有量化、拉曼光谱、红外光谱、核磁共振、色谱和吸收光谱等。
物理化学知识点总结

物理化学每章总结 第1章 热力学第一定律及应用1.系统、环境及性质热力学中把研究的对象(物质和空间)称为系统,与系统密切相关的其余物质和空间称为环境。
根据系统与环境之间是否有能量交换和物质交换系统分为三类:孤立系统、封闭系统和敞开系统。
2.热力学平衡态系统的各种宏观性质不随时间而变化,则称该系统处于热力学平衡态。
必须同时包括四个平衡:力平衡、热平衡、相平衡、化学平衡。
3.热与功 (1) 热与功的定义热的定义:由于系统与环境间温度差的存在而引起的能量传递形式。
以Q 表示,Q>0 表示环境向系统传热。
功的定义:由于系统与环境之间压力差的存在或其它机、电的存在引起的能量传递形式。
以W 表示。
W>0 表示环境对系统做功。
(2) 体积功与非体积功功有多种形式,通常涉及到是体积功,是系统体积变化时的功,其定义为:V p Wd δe -=式中pe 表示环境的压力。
对于等外压过程 )(12e V V p W --=对于可逆过程,因ep p =,p 为系统的压力,则有Vp W V V d 21⎰-=体积功以外的其它功,如电功、表面功等叫非体积功,以W ′表示。
4.热力学能热力学能以符号U 表示,是系统的状态函数。
若系统由状态1变化到状态2,则过程的热力学增量为 12U U U -=∆对于一定量的系统,热力学能是任意两个独立变量的状态函数,即),(V T f U =则其全微分为VV U T T U U TV d d d ⎪⎭⎫ ⎝⎛∂∂+⎪⎭⎫ ⎝⎛∂∂=对一定量的理想气体,则有 0=⎪⎭⎫⎝⎛∂∂TV U 或 U =f (T )即一定量纯态理想气体的热力学能只是温度的单值函数。
5.热力学第一定律及数学表达式 (1) 热力学第一定律的经典描述① 能量可以从一种形式转变为另一种形式,但在转化和传递过程中数量不变 ② “不供给能量而可连续不断做功的机器称为第一类永动机,第一类永动机是不可能存在的。
(2) 数学表达式对于封闭系统,热力学第一定律的数学表达式为W Q U δδd += 或 W Q U +=∆即封闭系统的热力学能的改变量等于过程中环境传给系统的热和功的总和。
物理化学---知识点总结
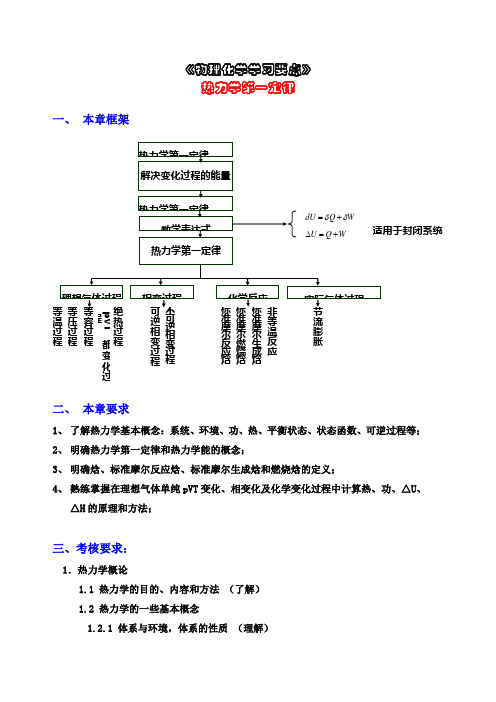
《物理化学学习要点》热力学第一定律一、 本章框架二、 本章要求1、 了解热力学基本概念:系统、环境、功、热、平衡状态、状态函数、可逆过程等;2、 明确热力学第一定律和热力学能的概念;3、 明确焓、标准摩尔反应焓、标准摩尔生成焓和燃烧焓的定义;4、 熟练掌握在理想气体单纯pVT 变化、相变化及化学变化过程中计算热、功、△U 、△H 的原理和方法;三、考核要求:1.热力学概论1.1 热力学的目的、内容和方法 (了解) 1.2 热力学的一些基本概念1.2.1 体系与环境,体系的性质 (理解)温过程 压过程 容过程 pVT 都变化过程热过程逆相变过程 可逆相变过程准摩尔反应焓 准摩尔燃烧焓 准摩尔生成焓等温反应 流膨胀1.2.2 热力学平衡态和状态函数(理解)2.热力学第一定律2.1 热和功(掌握)2.2 热力学能(掌握)2.3 热力学第一定律的表述与数学表达式(应用)3.体积功与可逆过程3.1 等温过程的体积功(应用)3.2 可逆过程与最大功(理解)4.焓与热容4.1 焓的定义(了解)4.2 焓变与等压热的关系(应用)4.3 等压热容和等容热容(理解)5.热力学第一定律对理想气体的应用5.1 理想气体的热力学能和焓(掌握)5.2 理想气体的C p与C v之差(理解)5.3 理想气体的绝热过程(掌握)6.热力学第一定律对实际气体的应用6.1 节流膨胀与焦耳-汤姆逊效应(了解)7.热力学第一定律对相变过程的应用(掌握)8.化学热力学8.1 化学反应热效应8.1.1 等压热效应与等容热效应(掌握)8.1.2 反应进度(了解)8.2 赫斯定律与常温下反应热效应的计算8.2.1 赫斯定律(应用)8.2.2 标准摩尔生成焓与标准摩尔燃烧焓(掌握)8.3 标准反应焓变与温度的关系—基尔霍夫定律(应用)四、重要概念1、系统与环境;2、 隔离系统、封闭系统、敞开系统;注意:隔离系统Q=0,W=03、 广度性质(加和性:V ,U ,H ,S ,A ,G )强度性质(物质的量,T ,p ); 4、 功W 和热Q ;注意W 与Q 的符号;W 与Q 均为途径函数(非状态函数) 5、 热力学能; 6、 焓; 7、 热容;8、 状态与状态函数; 9、 平衡态; 10、可逆过程;11、 节流过程; 12、 真空膨胀过程; 13、 标准态;14、标准摩尔反应焓,标准摩尔生成焓,标准摩尔燃烧焓五、重要公式与适用条件1. 体积功:W = -p 外dV (封闭系统,计算体积功)2. 热力学第一定律:∆ U = Q +W , d U =Q +W (封闭系统) 3.焓的定义: H =U + pV4.热容:定容摩尔热容 C V ,m =Q V /dT =(∂ U m /∂ T )V 定压摩尔热容 C p ,m = Q p /dT =(∂ H m /∂ T )P 理想气体:C p ,m - C V ,m =R ;凝聚态:C p ,m - C V ,m ≈0理想单原子气体C V ,m =3R /2,C p ,m = C V ,m +R =5R /2 5. 标准摩尔反应焓:由标准摩尔生成焓∆f H B (T )或标准摩尔燃烧焓∆c H B (T )计算 ∆ r H m = ∑ v B ∆ f H B (T )= -∑ v B ∆ c H B (T )6. 基希霍夫公式(适用于相变和化学反应过程)∆ r H m(T 2)= ∆ r H m(T 1)+21T r pm T C dT∆⎰7. 等压摩尔反应热与等容摩尔反应热的关系式Q p -Q V = ∆ r H m (T )-∆ r U m (T )=∑ v B (g )RT 8. 理想气体的可逆绝热过程方程:γγ2211V P V P = 122111--=γγV T V T γγγγ/)1(22/)1(11-=-P T P Tγ=Cvm Cpm /六、各种过程Q 、W 、∆ U 、∆ H 的计算1、 理想气体:等温过程dT =0, ∆ U =∆ H =0, Q =W ;非等温过程,∆ U = n C V ,m ∆ T , ∆ H = n C p ,m ∆ T , 单原子气体C V ,m =3R /2,C p ,m = C V ,m +R = 5R /22、对于凝聚相,状态函数通常近似认为与温度有关,而与压力或体积无关,即 ∆ U ≈∆ H = n C p ,m ∆ T3. 等压过程:p 外=p =常数,非体积功为零W '=0 (1) W = -p 外(V 2-V 1), ∆ H = Q p =dTnC T Tm p ⎰2,, ∆ U =∆ H -∆(pV ),Q =∆ U -W(2) 真空膨胀过程p 外=0,W =0,Q =∆ U理想气体结果:d T =0,W =0,Q =∆ U =0,∆ H =0 (3) 等外压过程:W = -p 外(V 2-V 1) 4. 等容过程 :d V =0 W =0,Q V =∆ U =dTnC T Tm v ⎰2,, ∆ H =∆ U +V ∆ p5.绝热过程:Q =0 (1)绝热可逆过程 W =dVp T T ⎰2= ∆ U =dTnC T Tm v ⎰2,,∆ H =∆ U +∆ pV理想气体:γγ2211V P V P = 122111--=γγV T V T γγγγ/)1(22/)1(11-=-P T P T(2)绝热一般过程:由方程WdVp T T外⎰2= ∆ U = dTnC T Tm v ⎰2, 建立方程求解。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
物理化学核心教程P132. 在两个密封、绝热、体积相等的容器中,装有压力相等的某种理想气体。
试问,这两容器中气体的温度是否相等?答:不一定相等。
根据理想气体状态方程,若物质的量相同,则温度才会相等。
3. 两个容积相同的玻璃球内充满氮气,两球中间用一玻管相通,管中间有一汞滴将两边的气体分开。
当左球的温度为273 K ,右球的温度为293 K 时,汞滴处在中间达成平衡。
试问:(1)若将左球温度升高10 K ,中间汞滴向哪边移动?(2)若两球温度同时都升高10 K, 中间汞滴向哪边移动?答:(1)左球温度升高,气体体积膨胀,推动汞滴向右边移动。
(2)两球温度同时都升高10 K ,汞滴仍向右边移动。
因为左边起始温度低,升高10 K 所占比例比右边大,283/273大于303/293,所以膨胀的体积(或保持体积不变时增加的压力)左边比右边大。
P241. 在两个容积均为V 的烧杯中装有氮气,烧瓶之间有细管相通,细管的体积可以忽略不计。
若将两烧杯均浸入373 K 的开水中,测得气体压力为60 kPa 。
若一只烧瓶浸在273 K 的冰水中,另外一只仍然浸在373 K 的开水中,达到平衡后,求这时气体的压力。
设气体可以视为理想气体。
解: 12n n n =+ 根据理想气体状态方程 1221122p V p V p V RT RT RT =+ 化简得: 12112211()p p T T T =+ 221212732260 kPa 50.7 kPa 273373T p p T T =⨯=⨯⨯=++ 5. 有氮气和甲烷(均为气体)的气体混合物100 g ,已知含氮气的质量分数为0.31。
在420 K 和一定压力下,混合气体的体积为9.953dm 。
求混合气体的总压力和各组分的分压。
假定混合气体遵守Dalton 分压定律。
已知氮气和甲烷的摩尔质量分别为281g mol -⋅和161g mol -⋅。
解:()210.31100 g N 1.11 mol 28 g molm n M -⨯===⋅ 41(10.31)100 g (CH ) 4.31 mol 16 g mol n --⨯==⋅ 1133(1.11+4.31) mol 8.314 J mol K 420 K 1902 kPa 9.9510 mnRT p V ---⨯⋅⋅⨯===⨯ 2224(N ) 1.11(N )1902 kPa=389.5 kPa (N )(CH ) 1.11 4.31n p p n n =⨯=⨯++ 4(CH )(1902389.5) kPa=1512.5 kPa p =-P65一、思考题1. 判断下列说法是否正确,并简述判断的依据(1)状态给定后,状态函数就有定值,状态函数固定后,状态也就固定了。
答:是对的。
因为状态函数是状态的单值函数。
(2)状态改变后,状态函数一定都改变。
答:是错的。
因为只要有一个状态函数变了,状态也就变了,但并不是所有的状态函数都得变。
(3)因为ΔU =Q V ,ΔH =Q p ,所以Q V ,Q p 是特定条件下的状态函数? 这种说法对吗?答:是对的。
∆U ,∆H 本身不是状态函数,仅是状态函数的变量,只有在特定条件下与Q V ,Q p 的数值相等,所以Q V ,Q p 不是状态函数。
(4)根据热力学第一定律,因为能量不会无中生有,所以一个系统如要对外做功,必须从外界吸收热量。
答:是错的。
根据热力学第一定律U Q W ∆=+,它不仅说明热力学能(ΔU )、热(Q )和功(W )之间可以转化,有表述了它们转化是的定量关系,即能量守恒定律。
所以功的转化形式不仅有热,也可转化为热力学能系。
(5)在等压下,用机械搅拌某绝热容器中的液体,是液体的温度上升,这时ΔH =Q p =0答:是错的。
这虽然是一个等压过程,而此过程存在机械功,即W f ≠0,所以ΔH ≠Q p 。
(6)某一化学反应在烧杯中进行,热效应为Q 1,焓变为ΔH 1。
如将化学反应安排成反应相同的可逆电池,使化学反应和电池反应的始态和终态形同,这时热效应为Q 2,焓变为ΔH 2,则ΔH1=ΔH2。
答:是对的。
Q是非状态函数,由于经过的途径不同,则Q值不同,焓(H)是状态函数,只要始终态相同,不考虑所经过的过程,则两焓变值∆H1和∆H2相等。
5. 用热力学概念判断下列各过程中功、热、热力学能和焓的变化值。
第一定律数学表示式为ΔU = Q + W。
(1)理想气体自由膨胀(2) van der Waals气体等温自由膨胀(3) Zn(s)+ 2HCl(l)= ZnCl2 + H2 (g)进行非绝热等压反应(4) H2(g)+ Cl2(g)= 2HCl(g)在绝热钢瓶中进行(5)常温、常压下水结成冰(273.15 K,101.325kPa)答:(1)W = 0 因为自由膨胀外压为零。
Q = 0 理想气体分子间没有引力。
体积增大分子间势能不增加,保持温度不变,不必从环境吸热。
∆U = 0 因为温度不变,理想气体的热力学能仅是温度的函数。
∆H = 0 因为温度不变,理想气体的焓也仅是温度的函数。
(2)W = 0 因为自由膨胀外压为零。
Q> 0 范氐气体分子间有引力。
体积增大分子间势能增加,为了保持温度不变,必须从环境吸热。
∆U >0 因为从环境所吸的热使系统的热力学能增加。
∆H >0 根据焓的定义式可判断,系统的热力学能增加,焓值也增加。
(3)W <0 放出的氢气推动活塞,系统克服外压对环境作功。
Q <0 反应是放热反应。
∆U <0 系统既放热又对外作功,热力学能下降。
∆H < 0 因为这是不做非膨胀功的等压反应,∆H = Q p。
(4)W = 0 在刚性容器中是恒容反应,不作膨胀功。
Q = 0 因为用的是绝热钢瓶∆U = 0 根据热力学第一定律,能量守恒,热力学能不变。
∆H >0 因为是在绝热刚瓶中发生的放热反应,气体分子数没有减少,钢瓶内温度升高,压力也增高,根据焓的定义式可判断焓值是增加的。
(5)W <0 常温、常压下水结成冰,体积变大,系统克服外压对环境作功。
Q < 0 水结成冰是放热过程。
∆U < 0 系统既放热又对外作功,热力学能下降。
∆H < 0 因为这是等压相变,∆H = Q p 。
P683. 在373 K 恒温条件下,计算1 mol 理想气体在下列四个过程中所做的膨胀功。
已知始、终态体积分别为25 dm 3和100 dm 3 。
(1)向真空膨胀;(2)等温可逆膨胀;(3)在外压恒定为气体终态压力下膨胀;(4)先外压恒定为体积等于50 dm 3 时气体的平衡压力下膨胀,当膨胀到50 dm 3以后,再在外压等于100 dm 3 时气体的平衡压力下膨胀。
试比较四个过程的功,这说明了什么问题?解:(1)向真空膨胀,外压为零,所以20W =(2)等温可逆膨胀 1111225ln 1 mol 8.314 J mol K 373 K ln 4299 J 100V W nRT V --==⨯⋅⋅⨯⨯=- (3)恒外压膨胀 3e 21221212()()()nRT W p V V p V V V V V =--=--=-- 11331 mol 8.314 J mol K 373 K (0.10.025)m 2326 J 0.1 m--⨯⋅⋅⨯=-⨯-=- (4)分两步恒外压膨胀 4e,121e,232213223()()()()nRT nRT W p V V p V V V V V V V V =----=---- 12232550(11)(2)50100V V nRT nRT nRT V V =-+-=+-=- 111 mol 8.314 J mol K 373 K 3101 J --=-⨯⋅⋅⨯=-说明作功与过程有关,系统与环境压差越小,膨胀次数越多,做的功也越大。
8. 设有300 K 的1 mol 理想气体作等温膨胀,起始压力为1500kPa ,终态体积为10 dm 3。
试计算该过程的Q ,W ,∆U 和 ∆H 。
解:该过程是理想气体等温过程,故 ΔU =ΔH = 0始态体积 V 1为: 113111 1 mol 8.314 J mol K 300 K 1.66 dm 15100 kPanRT V p --⨯⋅⋅⨯===⨯ 1112 1.66 ln 1 mol 8.314 J mol K 300 K ln 4.48 kJ 10V W nRT V --==⨯⋅⋅⨯⨯=- 4.48 kJ Q W =-=11. 有1 m 3的单原子分子的理想气体,始态为273 K ,1000kPa 。
现分别经(1)等温可逆膨胀;(2)绝热可逆膨胀;(3)绝热等外压膨胀,到达相同的终态压力100 kPa 。
请分别计算终态温度T 2、终态体积V 2和所做的功。
解:(1)理想气体的等温可逆膨胀过程,pV =常数,则有: T 2=T 1=273K 32112m 010100011000..p V p V =⨯== mol 584402733148011010003111...RT V p n =⨯⨯⨯== W = -12ln V V nRT = -21ln p p nRT ∴ W = -440.58×8.314×273×1001000ln = -2302.6kJ (2)绝热可逆膨胀, Q =0,则有ΔU = W 。
R C m V 23=,,R C m p 25=,,则35==m V m p C C ,,γ 又 ∵ γγγγ221111T p T p --=,则11212T p p T γγ-⎪⎪⎭⎫ ⎝⎛= ∴ 11212T p p T γγ-⎪⎪⎭⎫ ⎝⎛==273100100035351⨯⎪⎭⎫ ⎝⎛-// = 108.6KW =ΔU = nC V,m ( T 2 -T 1) = 440.58×23×8.314×( 108.6 -273) = -903.3 kJ (3)绝热恒外压膨胀, Q =0,则有ΔU = W 。
即 -p e (V 2-V 1) = nC V,m ( T 2 -T 1)-2p (22p nRT -11p nRT ) = nC V,m ( T 2 -T 1) 则有:- (2T -112p T p ) = 23×( T 2 -T 1) - (2T -1000273100⨯) = 23×( T 2 -273) T 2 =174.7K 33222m 46101007174314858440....p nRT V =⨯⨯⨯== W =ΔU = nC V,m ( T 2 -T 1) = 440.58×23×8.314×( 174.7 -273) = -540.1 kJ 12.在373K 和101.325kPa 时,有1molH 2O (l )可逆蒸发成同温、同压的H 2O (g ),已知H 2O (l )的摩尔气化焓Δvap H m =40.66kJ·mol -1。
