中考复习微专题----辅助圆问题及题例(二)
2020年江苏中考数学复习第6章圆微专题 辅助圆问题

微专题 辅助圆问题
微专题 辅助圆问题
(宿迁 2016.25,淮安 2016.28,盐城 2015.28)
模型一 “辅助圆”解点的存在性
模型分析
“定边、定角”圆上找.具体来说:当边长一定,其所对角度也一定时,该角顶点 在两段弧上.
微专题 辅助圆问题
针对训练 1. 如图,已知线段AB. (1)请你在图①中画出使∠APB=90°的所有满足条件的点P; (2)请你在图②中画出使∠APB=60°的所有满足条件的点P; (3)请你在图③中画出使∠APB=45°的所有满足条件的点P.
第3题图
请你总结,满足条件的P点具有的特点:_点__P_为__A__B_的__中__垂__线__与__直__线__b_的__交__点___.
微专题 辅助圆问题
4. 如图,当直线b与球门AB互相垂直时,球员(边锋)沿直线b带球,在直线b上是否存 在一点P,使得球员在P点射门更易进球?若存在这样的点,请找出;若不存在,请 说明理由.
微专题 辅助圆问题
针对训练 5. 如图,已知正方形ABCD的边长为4.点M和N分别从B、C同时出发,以相同的速 度沿BC、CD方向向终点C和D运动.连接AM和BN,交于点P,则PC长的最小值为 _2___5___2_.(请在图中画出点P的运动路径)
(完整word)九年级数学提升之辅助圆问题
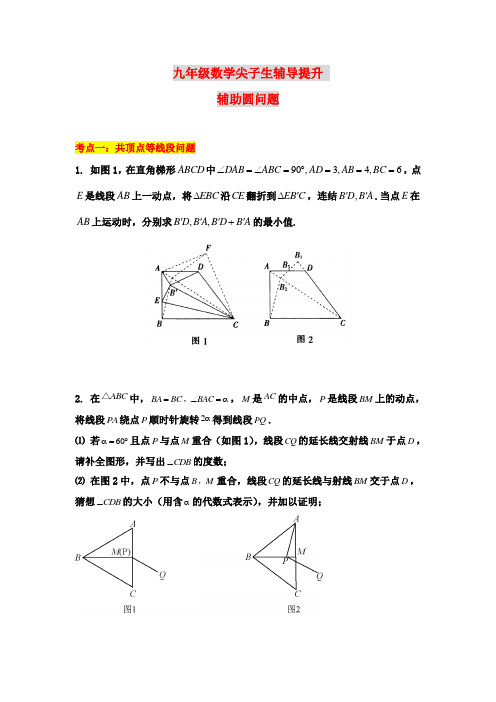
九年级数学尖子生辅导提升辅助圆问题考点一:共顶点等线段问题1. 如图1,在直角梯形ABCD 中90,3,4,6DAB ABC AD AB BC ∠=∠=︒===,点E 是线段AB 上一动点,将EBC ∆沿CE 翻折到EB C '∆,连结,B D B A ''.当点E 在AB 上运动时,分别求,,B D B A B D B A ''''+的最小值.2. 在ABC △中,BA BC BAC =∠=α,,M 是AC 的中点,P 是线段BM 上的动点,将线段PA 绕点P 顺时针旋转2α得到线段PQ .⑴ 若α=60︒且点P 与点M 重合(如图1),线段CQ 的延长线交射线BM 于点D ,请补全图形,并写出CDB ∠的度数;⑵ 在图2中,点P 不与点B M ,重合,线段CQ 的延长线与射线BM 交于点D , 猜想CDB ∠的大小(用含α的代数式表示),并加以证明;3. 已知:AOB △中,2AB OB ==,COD △中,3CD OC ==,ABO DCO =∠∠.连接AD 、BC ,点M 、N 、P 分别为OA 、OD 、BC 的中点.图1NMOPDCBA图2NM OPDCBA⑴ 如图1,若A 、O 、C 三点在同一直线上,且60ABO =∠°,则PMN △的形状是___________,此时ADBC=________; ⑵ 如图2,若A 、O 、C 三点在同一直线上,且2ABO α=∠,证明PMN BAO △∽△,并计算ADBC的值(用含α的式子表示);考点二:定边对定角问题1. 已知90AOB ∠=︒,OM 是AOB ∠的平分线.将一个直角RPS 的直角顶点P 在射线OM 上移动,点P 不与点O 重合.如图,当直角RPS 的两边分别与射线OA 、OB 交于点C 、D 时,请判断PC 与PD 的数量关系,并证明你的结论;RBPCAD OG S M321G N SH ODACMPBR2. 如图,正方形ABCD边长为2,点E是正方形ABCD内一动点,90AEB∠=︒,连结DE,求DE的最小值.3. 如图,四边形ABCD是正方形,M是BC上一点,ME AM⊥交BCD∠的外角平分线于E,求证:AM EM=.AB CDEM4.如图, 45XOY∠=︒,一把直角三角形尺ABC的两个顶点,A B分别在,OX OY 上移动,10AB=,求点O到AB距离的最大值.5. 如图,正三角形ABCAD BC,点E是射线AD上一动点(不∆边长为2,射线//与点A重合),AEC∆外接圆交EB于点F,求AF的最小值.6. 在矩形ABCD中,点P在AD上,AB=2,AP=1,将三角板的直角顶点放在点P 处,三角板的两直角边分别能与AB、BC边相交于点E、F,连接EF.⑴ 如图,当点E与点B重合时,点F恰好与点C重合,求此时PC的长;⑵ 将三角板从⑴中的位置开始,绕点P顺时针旋转,当点E与点A重合时停止,在这个过程中,请你观察、探究并解答:① ∠PEF的大小是否发生变化?请说明理由;② 直接写出从开始到停止,线段EF的中点所经过的路线长.D考点三:四点共圆问题1. 如图,在四边形ABCD 中,AC 是BAD ∠的平分线,若180B D ∠+∠=︒,求证:BC CD =.2. 如图,在正△ABC 中,点D ,E 分别在边AC ,AB 上,且AD=31AC ,AE=32AB ,BD ,CE 相交于点F 。
圆中辅助线应用的典型例题

圆中辅助线应用的典型例题圆是数学中非常重要的一个几何图形,在数学教学中也经常涉及到相关内容。
圆中辅助线的应用也是数学教学中的一个重要内容。
在这里,我将为大家介绍一下圆中辅助线应用的典型例题。
例题一:如图,已知圆的半径OA和圆心角α,求BC 的长度。
解题思路:由于圆心角α是已知的,可以根据圆心角公式计算出弧长AC,即AC = αR,其中R为圆的半径。
又因为BC是弦,所以可以根据弦长公式计算出BC的长度:BC = 2√(R² - AC²/4)。
因此,只需把圆心角α和半径OA 代入公式,就可以得出BC的值。
例题二:如图,已知圆的半径OA和圆心角α,DE与BC平行,求DE的长度。
解题思路:由于DE与BC平行,所以可以构造辅助线EF与BC垂直,如图所示。
则BE = EC = Rcos(α/2),EF = Rsin(α/2),因此BF = 2Rsin(α/2)。
根据正弦定理,在三角形BDF中,有sin(α/2)/BD = sin(γ)/BF,又因为sin(γ) = DE/BD,所以DE = BDsin(α/2)/sin(γ),代入BF的值即可求出DE的长度。
例题三:如图,已知圆上两个点A、B和点P到AB的距离为h,求圆心O到AB的距离d。
解题思路:首先,构造辅助线PC,并延长到圆上的交点D,如图所示。
则OP垂直于AB,所以POD是直角三角形。
由于PO = R - h,OD = √(R² - PD²),所以DP =√(R² - (R - h)²)。
在三角形PBD中,有d/BD = PO/DP,所以d = (R - h)BD/√(R² - (R - h)²),代入数据即可求出d的值。
以上就是三个典型的圆中辅助线应用例题。
这些例题的重点在于如何灵活应用几何知识,构造合适的辅助线,从而得出正确的解答。
在学习数学的过程中,需要不断地训练自己的思维能力,培养解决问题的能力。
初三春季0元课 第22讲 辅助圆(2)(学生版)

PEF第 22 讲 辅助圆(2)1.共端点,等线段 2.两直角三角形共斜边(1)共斜边的两个直角三角形组成的四边形的四个顶点共圆.(两直角顶点位于斜边同侧)(2)共斜边的两个直角三角形组成的四边形的四个顶点共圆.(两直角顶点位于斜边异侧)【例 1】在等腰直角三角形 ABC 中,∠BAC =90°,D 为 BC 边的中点,E 、 F 分别为 AB 、AC 上的点,且满足∠EDF =90°.求证:DE =DF .A BD C【例 2】在△ABC 中,∠ABC = 90 , AB = 6 ,BC = 8 ,O 为 AC 的中点,过O 作OE ⊥ OF ,OE 、OF 分别交射线 AB , BC 于 E 、F ,则 EF 的最小值为多少?A EBFC 【例 3】如图, R t △ABC 中, AB ⊥ BC , AB = 6 , BC = 4 , P 是△ABC 内部的一个动点,且满足∠PAB = ∠PBC ,则线段CP 长的最小值为( )A .3 A2 B . 2 C .8 13 13 D .12 13 13BCO3 【例 4】如图,E 、F 是正方形 ABCD 的边 AD 上两个动点,满足 AE =DF . 连接CF 交 BD 于点G ,连接 BE 交 AG 于点 H .若正方形的边长为2 ,则线段 DH 长度的最小值是多少?A E F DB C【例 5】如图,等边△ABC 中, AB = 6 , P 为 AB 上一动点 PD ⊥ BC ,PE ⊥ AC ,则 DE 的最小值为多少?ABDC 【练习 1】如图,在 ABCD 中, ∠BCD =30︒ , BC =4 ,CD =3 ,M 是 AD 边的中点, N 是 AB 边上一动点,将△AMN 沿 MN 所在直线翻折得到 △PMN ,连接 PC ,则 PC 长度的最小值是多少?DCMPANB【练习 2】如图,在矩形 ABCD 中,AB = 2 ,AD = 3 ,点 E ,F 分别为 AD 、DC 边上的点,且 EF = 2 , G 为 EF 的中点, P 为 BC 边上一动点,则 PA + PG 的最小值为多少?AE D GFEP。
中考数学几何最值模型 专题03 辅助圆模型(学生版+解析版)

辅助圆模型模型讲解一、定点定长1、O为定点,OA=OB,且长度固定,那么O、A、B三点可以确定一个圆,动点P在圆弧AB上运动,如图所示,Q为圆外一定点,当P运动到OQ的连线上时,即:P落到P1处,O、P1、Q三点共线时,PQ最小。
二、定弦定角2、线段AB固定,Q为动点,且∠AQB为定值,那么Q、A、B三点可以确定一个圆,动点Q在圆弧AB上运动,如图所示,R为圆外一定点,当Q运动到OQ的连线上时,即:P落到P1处,O、P1、Q三点共线时,RQ最小。
方法点拨一、题型特征:①动点的运动轨迹为圆②圆外一点到圆上一点的距离最短:即圆外一点与圆心连线与圆的交点③常见确定圆的模型:定点定长、定弦定角。
二、模型本质:两点之间,线段最短。
例题演练1.如图,已知AB=AC=BD=6,AB⊥BD,E为BC的中点,则DE的最小值为()A.3﹣3B.3C.3﹣3D.2【解答】解:取AB的中点O,连接AE,OE,OD.∵AB=AC,BE=EC,∴AE⊥BC,∴∠AEB=90°,∵OA=OB,∴OE=AB=3,∵AB⊥BD,∴∠OBD=90°,∵OB=3,BD=6,∴OD===3,∵DE≥OD﹣OE,∴DE≥3﹣3,∴DE的最小值为3﹣3,故选:C.强化训练1.如图,矩形ABCD中,AB=3,BC=8,点P为矩形内一动点,且满足∠PBC =∠PCD,则线段PD的最小值为()A.5B.1C.2D.3 2.如图,在矩形ABCD中,AB=4,BC=6,E是矩形内部的一个动点,且AE ⊥BE,则线段CE的最小值为.3.如图,△ABC为等边三角形,AB=2.若P为△ABC内一动点,且满足∠P AB =∠ACP,则线段PB长度的最小值为.4.如图,在矩形ABCD中,AB=4,BC=6,E是平面内的一个动点,且满足∠AEB=90°,连接CE,则线段CE长的最大值为.5.如图1,P是⊙O外的一点,直线PO分别交⊙O于点A,B,则P A是点P 到⊙O上的点的最短距离.(1)探究一:如图2,在Rt△ABC中,∠ACB=90°,AC=BC=2,以BC为直径的半圆交AB于D,P是上的一个动点,连接AP,则AP的最小值是.(2)探究二:如图3,在边长为2的菱形ABCD中,∠A=60°,M是AD边的中点,N是AB边上一动点,将△AMN沿MN所在的直线翻折得到△A′MN,连接A′C,请求出A′C长度的最小值.(3)探究三,在正方形ABCD中,点E,F分别从D,C两点同时出发,以相同的速度在直线DC,CB上移动,连接AE和DF交于点P,由于点E,F的移动,使得点P也随之运动,若AD=4,试求出线段CP的最小值.1.如图,在边长为2的菱形ABCD中,∠A=60°,M是AD边的中点,N是AB边上的一动点,将△AMN沿MN所在直线翻折得到△A′MN,连接A′C,则A′C长度的最小值是.辅助圆模型模型讲解一、定点定长1、O为定点,OA=OB,且长度固定,那么O、A、B三点可以确定一个圆,动点P在圆弧AB上运动,如图所示,Q为圆外一定点,当P运动到OQ的连线上时,即:P落到P1处,O、P1、Q三点共线时,PQ最小。
提分专题十 辅助圆问题

距离最大值
+
2
+
过点 作直线 的垂线,其反向延长线与 ⊙ 的交点
此时点 的位置
即为点
点 到直线 的
距离最小值
−
0
过点 作直线 的垂线,与 ⊙ 的
此时点 的位置
交点即为点
0
直线 与 ⊙ 的
交点即为点
针对训练
重合);
(3)如图3,当 ∠ > 90∘ 时,点 的运动轨迹为劣弧 (不与点
, 重合)
针对训练
4.如图, △ 为等边三角形, = 3 .若 为 △ 内一动点,且满足
∠ = ∠ ,则线段 长度的最小值为(
A.1.5
B.
√
3
4 3
C.
4
)
16
D.
5
第8题图
9.如图,在 △ 中, = 9 , = 12 ,
= 15 , 为直线 上方一点,连接 , ,
且 ∠ = 90∘ ,过点 作直线 的垂线,垂足为
12
,则线段 的最大值为____.
第9题图
类型 四 点圆最值
的半径为1,点 是 边上的动点,过点 作 ⊙ 的一条切
线 (点 为切点),则线段 的最小值为(
A. 2
√
2
B. 4 3
C. 2 3
)
D.4
第14题图
提分专题十
辅助圆问题
类型 一 定点定长
已知平面内一定点 和一动点 ,若 长度固定,则点 的运动轨迹是
以点 为圆心, 长为半径的圆(如图1)(依据:圆的定义)
中考数学一轮培优微专题 辅助圆问题

模型一 定点定长作圆
(绵阳:2019.25)
模型分析
平面内,点A为定点,点B为动点,且AB长度固定,则点B的轨迹在以点A为圆心,AB长 为半径的圆上(如图①). 依据的是圆的定义:圆是所有到定点的距离等于定长的点的集合.
拓展:如图②,点E为定点,点F为线段BD上的动 点(不含点B),将△BEF沿EF折叠得到△B′EF,则 点B′的运动轨迹为以点E为圆心,以线段BE为半径 的一段圆弧.
图③
针对演练 5. 如图,在△ABC中,∠ACB=90°,AC=6,BC=8,O为AB的中点,过点O作 OE⊥OF,OE、OF分别交AC、BC于点E、F,则EF的最小值为____5____.
第5题图
模型五 点圆最值 模型分析 平面内一定点D和⊙O上动点E的连线中,当连线过圆心O时,线段DE有最大值和最小 值.具体分以下三种情况讨论(规定:OD=d,⊙O半径为r): 1. 当D点在⊙O外时,d>r,如图①、②:当D、E、O三点共线时,线段DE出现最值, DE的最大值为d+r,DE的最小值为d-r;
图①
分析:本题的关键在于如何确定“k·PB”的大小,(如图②)在线段OB上截取OC使OC= k·r,则可说明△BPO与△PCO相似,即k·PB=PC.所以本题求“PA+k·PB”的最小值转 化为求“PA+PC”的最小值,即A、P、C三点共线时最小(如图③),本题得解.
“阿氏圆”一般解题步骤:
第一步:将系数不为1的线段的两个端点分别与圆心相连接,即连接OP、OB;
2. 如图,⊙O与直线l相离,点P是⊙O上的一个动点,设圆心O到直线l的距离为d,⊙O 的半径为r,则点P到直线l的最小距离是__d_-__r___(如图③),点P到直线l的最大距离是 ___d_+__r__(如图④).
巧作辅助圆解决问题

巧作辅助圆解决问题在近几年中考试卷中,常出现这样一类题目,从表面上看是一个三角形或四边形问题,用三角形或四边形的知识来解决非常困难,甚至根本无法解决,但我们可以从已知条件中发现蛛丝马迹,也就是发现图形中的隐含特征,从而通过构造辅助圆,借助圆的知识来解决问题这样的问题一般具有以下特征一、到定点的距离等于定长例1如图1,在正方形ABCD外侧作直线DE,使45°<∠CDE<90°,点C关于直线DE的对称点为M,连接CM,AM,其中AM交直线DE 于点N,若MN=4,AN=3,则正方形ABCD的边长为( )。
A. B.5C.5D.解析:如图2,连接DM,由于点C、M关于直线DE对称,故直线DE垂直平分线段CM,因而DC=DM.四边形ABCD是正方形,故DA=DC=DM,即点A、C、M到点D的距离相等,根据这一特征,我们可以想到,以点D为圆心,DA的长为半径画圆,则点C、M必在⊙D上.由∠ADC=90°,可得∠AMC=45°.连接CN,则CN=MN=4,故∠MCN=∠AMC=45°,从而∠ANC=90°,连接AC,我们不难求出AC=,选D。
点评:随着直线DE位置的变化,点M的位置也在变化,但它一定在以点D为圆心,DA的长为半径的圆上,这就是运动变化中的不变关系,解决这类问题的关键是抓住“A、C、M三点到点D的距离相等”这一特征,但这个特征比较隐蔽,不容易发现,要综合考虑本题中的所有条件,而且要有一定的洞察力和解题经验.事实上,这类问题中的隐含条件往往都不是一眼就能看出来的。
二、张角为直角例2如图3,在等腰R△ABC中,∠BAC=90º,AB=AC,BC=2,点D 是AC边上一动点,连接BD,以AD为直径的圆交BD于点E,则线段CE长度的最小值为()。
A、2-2B、C、-1D、-1解析:本题中点D在动,直径AD的大小在变,线段BD在动,点E也在动,运动变化中有不变的量吗?有!如图4,连接AE,由于AD为直径,故∠AED的大小保持不变,为直角,从而∠AEB始终为直角,∠AEB的两边经过线段AB的两个端点,我们不妨称∠AEB为线段AB所对的张角。
