(完整版)初中数学_巧添辅助线__解证几何题
巧添辅助线解证几何题
龙源期刊网
巧添辅助线解证几何题
作者：倪小芳
来源：《数理化学习·初中版》2013年第06期
在几何证明或计算问题中，经常需要添加必要的辅助线，它的目的可以归纳为以下三点：一是通过添加辅助线，使图形的性质由隐蔽得以显现，从而利用有关性质去解题；二是通过添加辅助线，使分散的条件得以集中，从而利用它们的相互关系解题；三是把新问题转化为已经解决过的问题加以解决.值得注意的是辅助线的添加目的与已知条件和所求结论有关.下面我们分别举例加以说明.
一、倍角问题
二、中点问题
三、线段的和差问题
四、垂线段问题
五、梯形问题
[江苏省金坛市第五中学（213200）]。
巧添辅助线解几何题(辅导练习题目)
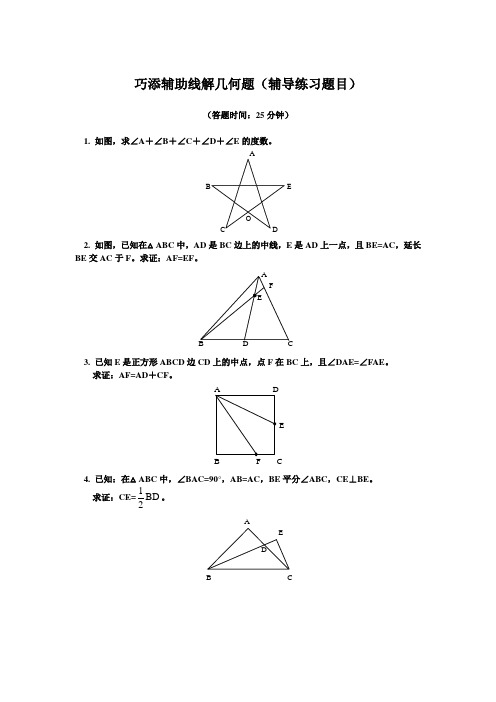
巧添辅助线解几何题（辅导练习题目）（答题时间：25分钟）1. 如图，求∠A ＋∠B ＋∠C ＋∠D ＋∠E 的度数。
AB EOC D2. 如图，已知在△ABC 中，AD 是BC 边上的中线，E 是AD 上一点，且BE=AC ，延长BE 交AC 于F 。
求证：AF=EF 。
AFEB D C3. 已知E 是正方形ABCD 边CD 上的中点，点F 在BC 上，且∠DAE=∠FAE 。
求证：AF=AD ＋CF 。
A DEB F C4. 已知：在△ABC 中，∠BAC=90°，AB=AC ，BE 平分∠ABC ，CE ⊥BE 。
求证：CE=12BD 。
AEB C D【试题答案】1. 解：连结CDAB EOC D∵∠ECD＋∠BDC=∠B＋∠E=180°－∠BOE=180°－∠COD∴∠A＋∠B＋∠ACE＋∠ADB＋∠E=∠A＋∠ECD＋∠BDC＋∠ACE＋∠ADB=∠A＋（∠ECD＋∠ACE）＋（∠BDC＋∠ADB）=∠A＋∠ACD＋∠ADC=180°2. 证明：延长AD至G，使DG=AD，连结BGAFEB D CG∵BD=DC，∠BDG=∠ADC∴△BGD≌△CAD∴BG=AC=BE，∠G=∠CAD∴∠G=∠BEG=∠AEF∴∠AEF=∠CAD ∴AF=EF3. 过E作EG⊥AF于GA DEGB F C∵∠D=90°，∠AGE=90°AE平分∠DAF ∴ED=EG∵ED=EC ∴EG=EC∵∠EGF=∠C=90°EF=EF∴△EGF ≌△ECF （HL ） ∴GF=FC ∵ED=EG ，AE=AE ，∠D=∠AGE=90° ∴△ADE ≌△AGE （HL ） ∴AD=AG ∴AF=AG ＋GF=AD ＋FC即AF=AD ＋FC4. 证明：延长BA 交CE 的延长线于FFD AE B C∵BE 平分∠ABC ，CE ⊥BE∴CE=12CF又∵AB=AC ，∠BAC=∠CAF=90°∠ACF=∠ABD=90°－∠F∴△ACF ≌△ABD ∴CF=BD∴CE=12CF BD。
初中数学中考几何如何巧妙做辅助线大全
人教版北师大初中数学中考几何如何巧妙做辅助线大全人们从来就就是用自己的聪明才智创造条件解决问题的,当问题的条件不够时,添加辅助线构成新图形,形成新关系,使分散的条件集中,建立已知与未知的桥梁,把问题转化为自己能解决的问题,这就是解决问题常用的策略。
一.添辅助线有二种情况:1按定义添辅助线:如证明二直线垂直可延长使它们,相交后证交角为90°;证线段倍半关系可倍线段取中点或半线段加倍;证角的倍半关系也可类似添辅助线。
2按基本图形添辅助线:每个几何定理都有与它相对应的几何图形,我们把它叫做基本图形,添辅助线往往就是具有基本图形的性质而基本图形不完整时补完整基本图形,因此“添线”应该叫做“补图”！这样可防止乱添线,添辅助线也有规律可循。
举例如下:(1)平行线就是个基本图形:当几何中出现平行线时添辅助线的关键就是添与二条平行线都相交的等第三条直线(2)等腰三角形就是个简单的基本图形:当几何问题中出现一点发出的二条相等线段时往往要补完整等腰三角形。
出现角平分线与平行线组合时可延长平行线与角的二边相交得等腰三角形。
(3)等腰三角形中的重要线段就是个重要的基本图形:出现等腰三角形底边上的中点添底边上的中线;出现角平分线与垂线组合时可延长垂线与角的二边相交得等腰三角形中的重要线段的基本图形。
(4)直角三角形斜边上中线基本图形出现直角三角形斜边上的中点往往添斜边上的中线。
出现线段倍半关系且倍线段就是直角三角形的斜边则要添直角三角形斜边上的中线得直角三角形斜边上中线基本图形。
(5)三角形中位线基本图形几何问题中出现多个中点时往往添加三角形中位线基本图形进行证明当有中点没有中位线时则添中位线,当有中位线三角形不完整时则需补完整三角形;当出现线段倍半关系且与倍线段有公共端点的线段带一个中点则可过这中点添倍线段的平行线得三角形中位线基本图形;当出现线段倍半关系且与半线段的端点就是某线段的中点,则可过带中点线段的端点添半线段的平行线得三角形中位线基本图形。
中考数学120分以上必须掌握的几何辅助线技巧
方法4：结论是一条线段与另一条线段之和等于第三条线段这类题目，常采用截长法或补短法，所谓截长法就是把第三条线段分成两部分，证其中的一部分等于第一条线段，而另一部分等于第二条线段。
2平行四边形中常用辅助线的添法
平行四边形(包括矩形、正方形、菱形)的两组对边、对角和对角线都具有某些相同性质，所以在添辅助线方法上也有共同之处，目的都是造就线段的平行、垂直，构成三角形的全等、相似，把平行四边形问题转化成常见的三角形、正方形等问题处理，其常用方法有下列几种，举例简解如下：
1按定义添辅助线：
如证明二直线垂直，可延长使它们相交后证交角为90°；
证线段倍半关系，可倍线段取中点或半线段加倍；
证角的倍半关系，也可类似添辅助线。
2按基本图形添辅助线：
每个几何定理都有与它相对应的几何图形，我们把它叫做基本图形，添辅助线往往是具有基本图形的性质而基本图形不完整时补完整基本图形，因此“添线”应该叫做“补图”!这样可防止乱添线，添辅助线也有规律可循。举例如下：
(1)在梯形内部平移一腰
(2)梯形外平移一腰
(3)梯形内平移两腰
(4)延长两腰
(5)过梯形上底的两端点向下底作高
(6)平移对角线
(7)连接梯形一顶点及一腰的中点
(8)过一腰的中点作另一腰的平行线
(9)作中位线
当然在梯形的有关证明和计算中，添加的辅助线并不一定是固定不变的、单一的。通过辅助线这座桥梁，将梯形问题化归为平行四边形问题或三角形问题来解决，这是解决问题的关键。
(5)两圆相交作公共弦
▌6、全等三角形：
全等三角形有轴对称形，中心对称形，旋转形与平移形等。
初中数学几何辅助线经典100题
初中数学几何辅助线经典100题摘要：初中数学几何辅助线经典100题一、几何辅助线的概念和作用1.几何辅助线的定义2.几何辅助线在解题中的作用二、几何辅助线的常见类型及应用1.角平分线2.线段和差3.中点定理4.倍长中线5.相似三角形6.判定条件7.证明定理三、初中数学几何辅助线经典100题1.题目1-102.题目11-203.题目21-304.题目31-405.题目41-506.题目51-607.题目61-708.题目71-809.题目81-9010.题目91-100正文：初中数学几何辅助线经典100题一、几何辅助线的概念和作用几何辅助线是在解决几何问题时，通过在图形上添加一些特殊的线段，来帮助我们更好地理解和解题的一种工具。
它可以将复杂的几何问题简化为更简单的形式，使问题更容易解决。
几何辅助线在解题中的作用主要体现在以下几个方面：1.揭示图形中隐含的性质：通过添加辅助线，将条件中隐含的有关图形的性质充分揭示出来，以便取得过渡性的推论，达到推导出结论的目的。
2.聚拢集中原则：通过添置适当的辅助线，将图形中分散、远离的元素相对集中、聚拢到有关图形上来，使题设条件与结论建立逻辑关系，从而推导出要求的结论。
3.化繁为简原则：对一类几何命题，其题设条件与结论之间在已知条件所给的图形中，通过添加辅助线，将复杂图形转化为简单图形，从而简化问题，使解题更加顺利。
二、几何辅助线的常见类型及应用几何辅助线有很多种，这里我们列举几种常见的类型及其应用：1.角平分线：角平分线是将一个角平分成两个相等的角的线段。
在解题中，我们常常利用角平分线的性质来证明两个角相等或求解某个角的度数。
2.线段和差：线段和差是指通过两个线段的和与差来求解几何问题。
在解题过程中，我们通常利用线段和差的性质来证明线段相等或求解线段的长度。
3.中点定理：中点定理是指在一个线段上，如果有一个点是线段中点，那么这个点到线段两端的距离相等。
在解题中，我们常常利用中点定理来证明线段相等或求解线段的长度。
常见全等辅助线添加秘籍 解析版-初中数学
常见全等辅助线添加秘籍-精准解读《学习目标分解》1.会添加倍长中线模型、截长补短模型的辅助线构造三角形全等；2.会利用全等三角形的性质和判定进行相关的计算和证明.《重难点精准分析》1.全等辅助线的添加；2.全等三角形的性质和判定的综合应用.《专题精准分析》全等三角形在中考数学几何模块中占据着重要地位，也是学生必须掌握的一块内容，本专题就全等三角形中的重要模型(倍长中线模型、截长补短模型)进行梳理及对应试题分析，方便掌握。
模型1.倍长中线模型【模型解读】中线是三角形中的重要线段之一，在利用中线解决几何问题时，常常采用“倍长中线法”添加辅助线．所谓倍长中线法，就是将三角形的中线延长一倍，以便构造出全等三角形，从而运用全等三角形的有关知识来解决问题的方法．(注：一般都是原题已经有中线时用，不太会有自己画中线的时候)。
【常见模型及证法】1、基本型：如图1，在三角形ABC中，AD为BC边上的中线.证明思路：延长AD至点E，使得AD=DE.若连结BE，则ΔBDE≅ΔCDA；若连结EC，则ΔABD≅ΔECD；2、中点型:如图2，C为AB的中点.证明思路：若延长EC至点F，使得CF=EC，连结AF，则ΔBCE≅ΔACF;若延长DC至点G，使得CG=DC，连结BG，则ΔACD≅ΔBCG.3、中点+平行线型：如图3,AB⎳CD，点E为线段AD的中点.证明思路：延长CE交AB于点F(或交BA延长线于点F)，则ΔEDC≅ΔEAF.倍长中线型辅助线倍长中线型辅助线一般跟中点相关，在初中阶段与中点相关的辅助线大体分成三大类：倍长中线(这里的中线指的是过中点的任意线段)、直角三角形斜边中线、中位线.其中后两种辅助线会在初二下学期的四边形章节中讲到，在此不做过多讲解，本节所讲的中点相关的辅助线主要是倍长中线型辅助线(这里的中线指的是过中点的任意线段)，此种模型的本质都是构造“8字型”全等，主要分成三类处理方法：(1)倍长中线型--这里的中线指的是标准的三角形的中线，具体模型如下：已知：点D为AC边的中点作法：延长BD至E，使得DE=BD，连结AE.（2）倍长过中点的任意线段型--这里只需要出现中点即可构造，具体模型如下：已知：点D为AC边的中点作法：延长FD至E，使得DE=DF，连结AE.（3）平行线构造“8字型”--中点不是三角形的边的中点，具体模型如下：已知：点E为DF的中点作法：过点D作DM⎳AF，交AC于点M.另外，平行线构造“8字型”的模型还可以有以下两种类型：1.如图，AD是△ABC的中线，BE交AC于E，交AD于F，且AE=EF，求证：AC=BF．【答案】证明：∵AD是△ABC的中线，∴BD=CD．方法一：延长AD至点M，使DM=AD，连接BM，在△ADC 和△MDB 中，BD =CD∠BDM =∠CDA DM =DA，∴△ADC ≌△MDB (SAS )，∴∠M =∠MAC ，BM =AC ，∵EA =EF ，∴∠CAM =∠AFE ，而∠AFE =∠BFM ，∴∠M =∠BFM ，∴BM =BF ，∴BF =AC ．方法二：延长AD 至点M ，使MD =FD ，连接MC ，在△BDF 和△CDM 中，BD =CD∠BDF =∠CDM DF =DM，∴△BDF ≌△CDM (SAS )．∴MC =BF ，∠M =∠BFM ．∵EA =EF ，∴∠EAF =∠EFA ，∵∠AFE =∠BFM ，∴∠M =∠MAC ，∴AC =MC ，∴BF =AC .【精准解析】有两种解法：①延长AD 至点M ，使MD =FD ，连接MC ，则可证△BDF ≌△CDM (SAS )，可得MC =BF ，∠M =∠BFM ，再得∠M =∠MAC ，得AC =MC =BF ．②延长AD 至点M ，使DM =AD ，连接BM ，可证△ADC ≌△MDB (SAS )，方法与①相同．2.八年级一班数学兴趣小组在一次活动中进行探究试验活动，请你和他们一起活动吧．【探究与发现】(1)如图1，AD 是△ABC 的中线，延长AD 至点E ，使ED =AD ，连接BE ，写出图中全等的两个三角形【理解与应用】(2)填空：如图2，EP 是△DEF 的中线，若EF =5，DE =3，设EP =x ，则x 的取值范围是．(3)已知：如图3，AD是△ABC 的中线，∠BAC =∠ACB ，点Q 在BC 的延长线上，QC =BC ，求证：AQ=2AD ．【答案】(1)证明：在△ADC与△EDB中，，∴△ADC≌△EDB；故答案为：△ADC≌△EDB；（2）解：如图2，延长EP至点Q，使PQ=PE，连接FQ，在△PDE与△PQF中，，∴△PEP≌△QFP，∴FQ=DE=3，在△EFQ中，EF-FQ<QE<EF+FQ，即5-3<2x<5+3，∴x的取值范围是1<x<4；故答案为：1<x<4；（3）证明：如图3，延长AD到M，使MD=AD，连接BM，∴AM=2AD，∵AD是△ABC的中线，∴BD=CD，在△BMD与△CAD中，，∴△BMD≌△CAD，∴BM=CA，∠M=∠CAD，∴∠BAC=∠BAM+∠CAD=∠BAM+∠M，∵∠ACB=∠Q+∠CAQ，AB=BC，∵∠ACQ=180°-(∠Q+∠CAQ)，∠MBA=180°-(∠BAM+∠M)，∴∠ACQ=∠MBA，∵QC=BC，∴QC=AB，在△ACQ与△MBA中，，∴△ACQ≌△MBA，∴AQ=AM=2AD．【精准解析】(1)根据全等三角形的判定即可得到结论；(2)延长EP至点Q，使PQ=PE，连接FQ，根据全等三角形的性质得到FQ=DE=3，根据三角形的三边关系即可得到结论；(3)延长AD到M，使MD=AD，连接BM，于是得到AM=2AD由已知条件得到BD=CD，根据全等三角形性质得到BM=CA，∠M=∠CAD，得到∠BAC=∠BAM+∠CAD=∠BAM+∠M，推出△ACQ≌△MBA，根据全等三角形的性质即可得到结论．《小结》当题目中出现中线时，常会考利用倍长中线型模型添加辅助线，构造“8字型”的全等.3.如图，在△ABC中，AB>AC，E为BC边的中点，AD为∠BAC的平分线，过E作AD的平行线，交AB于F，交CA的延长线于G．求证：BF=AC+AF．【答案】证明：延长FE至Q，使EQ=EF，连接CQ，∵E为BC边的中点，∴BE=CE，∵在△BEF和△CEQ中，，∴△BEF≌△CEQ，∴BF=CQ，∠BFE=∠Q，∵AD平分∠BAC，∴∠CAD=∠BAD，∵EF∥AD，∴∠CAD=∠G，∠BAD=∠GFA，∴∠G=∠GFA，∴∠GFA=∠BFE，AG=AF，∵∠BFE=∠Q(已证)，∴∠G=∠Q，∴CQ=CG，∵CQ=BF，∴BF=CG=AG+AC=AF+AC．【精准解析】延长FE至Q，使EQ=EF，连接CQ，根据SAS证△BEF≌△CEQ，推出BF=CQ，∠BFE=∠Q，根据平行线性质和角平分线性质推出∠G=∠GFA=∠BFE，推出∠G=∠Q，推出CQ=CG即可．4.已知：如图，△ABC(AB≠AC)中，D、E在BC上，且DE=EC，过D作DF∥BA交AE于点F，DF= AC．求证：AE平分∠BAC．【答案】证明：如图，延长FE到G，使EG=EF，连接CG．在△DEF和△CEG中，∵，∴△DEF≌△CEG．∴DF=GC，∠DFE=∠G．∵DF∥AB，∴∠DFE=∠BAE．∵DF=AC，∴GC=AC．∴∠G=∠CAE．∴∠BAE=∠CAE，即AE平分∠BAC．【解析】延长FE到G，使EG=EF．连接CG，由于已知条件通过SAS证得△DEF≌△CEG得到DF=GC，∠DFE=∠G，由平行线的性质和已知条件得到∠G=∠CAE，故有∠BAE=∠CAE，结论可得．《小结》当题目中出现中点，而没有合适的中线可以倍长时，也可以考虑倍长过中点的任意一条线段，构造“8字型”全等. 5..如图，△ABC中，AB=AC，D在AB上，F在AC的延长线上，且BD=CF，连接DE交BC于E．求证：DE=EF．【答案】证明：过D点作AF的平行线交BC于G点，∴∠ECF=∠DGE，∴∠DGB=∠ACB∵AB=AC，∴∠ABC=∠ACB，∴∠ABC=∠DGB，∴DG=BD，∵BD=CF，∴DG=CF．由∠ECF=∠DGE，∠DEG=∠CEF，DG=CF可得△DGE≌△FCE(AAS)，∴DE=EF．【精准解析】过D点作AF的平行线交BC于G点，利用等腰三角形的性质和平行线的性质，求证△DGE≌△FCE即可.6.如图，已知∠B+∠CDE=180°，AC=CE．求证：AB=DE．【答案】证明：如图，过E点作EH∥AB交BD的延长线于H，故∠A=∠CEH，在△ABC与△EHC中，∴△ABC≌△EHC(ASA)，∴AB=HE，∵∠B+∠CDE=180°，∠HDE+∠CDE=180°∴∠HDE=∠B=∠H，∴DE=HE．∵AB=HE，∴AB=DE．【精准解析】如图，过E点作EH∥AB交BD的延长线于H．构建全等三角形△ABC≌△EHC(ASA)，则由全等三角形的性质得到AB=HE；然后结合已知条件得到DE=HE，所以AB=HE，由等量代换证得AB= DE．《小结》当题目中出现中点，但此中点不是三角形的某条边的中点，只是与三角形某条边有交点时，则可以考虑利用作平行线的方法构造“8字型”的全等.模型2.截长补短模型【模型解读】截长补短的方法适用于求证线段的和差倍分关系。
(完整)八年级数学上册几何添辅助线专题
DCB A全等三角形问题中常见的辅助线的作法(有答案)总论：全等三角形问题最主要的是构造全等三角形，构造二条边之间的相等，构造二个角之间的相等【三角形辅助线做法】图中有角平分线，可向两边作垂线。
也可将图对折看，对称以后关系现。
角平分线平行线，等腰三角形来添。
角平分线加垂线，三线合一试试看。
线段垂直平分线，常向两端把线连。
要证线段倍与半，延长缩短可试验。
三角形中两中点，连接则成中位线。
三角形中有中线，延长中线等中线。
1.等腰三角形“三线合一”法：遇到等腰三角形，可作底边上的高，利用“三线合一”的性质解题2.倍长中线：倍长中线，使延长线段与原中线长相等，构造全等三角形3.角平分线在三种添辅助线4.垂直平分线联结线段两端5.用“截长法”或“补短法”： 遇到有二条线段长之和等于第三条线段的长，6.图形补全法：有一个角为60度或120度的把该角添线后构成等边三角形7.角度数为30、60度的作垂线法：遇到三角形中的一个角为30度或60度，可以从角一边上一点向角的另一边作垂线，目的是构成30-60-90的特殊直角三角形，然后计算边的长度与角的度数，这样可以得到在数值上相等的二条边或二个角。
从而为证明全等三角形创造边、角之间的相等条件。
8.计算数值法：遇到等腰直角三角形，正方形时，或30-60-90的特殊直角三角形，或40-60-80的特殊直角三角形,常计算边的长度与角的度数，这样可以得到在数值上相等的二条边或二个角，从而为证明全等三角形创造边、角之间的相等条件。
常见辅助线的作法有以下几种：最主要的是构造全等三角形，构造二条边之间的相等，二个角之间的相等。
1) 遇到等腰三角形，可作底边上的高，利用“三线合一”的性质解题，思维模式是全等变换中的“对折”法构造全等三角形．2) 遇到三角形的中线，倍长中线，使延长线段与原中线长相等，构造全等三角形，利用的思维模式是全等变换中的“旋转” 法构造全等三角形．3) 遇到角平分线在三种添辅助线的方法，（1）可以自角平分线上的某一点向角的两边作垂线，利用的思维模式是三角形全等变换中的“对折”，所考知识点常常是角平分线的性质定理或逆定理．（2）可以在角平分线上的一点作该角平分线的垂线与角的两边相交，形成一对全等三角形。
2014年中考数学：如何巧妙的添加辅助线
2014年中考数学：如何巧妙的添加辅助线辅助线对于同学们来说都不陌生，解几何题的时候经常用到。
当题目给出的条件不够时，我们通过添加辅助线构成新图形，形成新关系，使分散的条件集中，建立已知与未知的桥梁，把问题转化为自己能解决的问题，这便是辅助线的作用。
一条巧妙的辅助线常常使一道难题迎刃而解。
所以我们要学会巧妙的添加辅助线。
一、添辅助线有二种情况：1.按定义添辅助线：如证明二直线垂直可延长使它们相交后证交角为90°；证线段倍半关系可倍线段取中点或半线段加倍；证角的倍半关系也可类似添辅助线。
2.按基本图形添辅助线：每个几何定理都有与它相对应的几何图形，我们把它叫做基本图形，添辅助线往往是具有基本图形的性质而基本图形不完整时补完整基本图形，因此“添线”应该叫做“补图”！这样可防止乱添线，添辅助线也有规律可循。
举例如下：（1）平行线是个基本图形：当几何中出现平行线时添辅助线的关键是添与二条平行线都相交的等第三条直线（2）等腰三角形是个简单的基本图形：当几何问题中出现一点发出的二条相等线段时往往要补完整等腰三角形。
出现角平分线与平行线组合时可延长平行线与角的二边相交得等腰三角形。
（3）等腰三角形中的重要线段是个重要的基本图形：出现等腰三角形底边上的中点添底边上的中线；出现角平分线与垂线组合时可延长垂线与角的二边相交得等腰三角形中的重要线段的基本图形。
（4）直角三角形斜边上中线基本图形出现直角三角形斜边上的中点往往添斜边上的中线。
出现线段倍半关系且倍线段是直角三角形的斜边则要添直角三角形斜边上的中线得直角三角形斜边上中线基本图形。
（5）三角形中位线基本图形几何问题中出现多个中点时往往添加三角形中位线基本图形进行证明当有中点没有中位线时则添中位线，当有中位线三角形不完整时则需补完整三角形；当出现线段倍半关系且与倍线段有公共端点的线段带一个中点则可过这中点添倍线段的平行线得三角形中位线基本图形；当出现线段倍半关系且与半线段的端点是某线段的中点，则可过带中点线段的端点添半线段的平行线得三角形中位线基本图形。
八年级数学上册几何添辅助线专题
DCB A全等三角形问题中常见的辅助线的作法(有答案)总论：全等三角形问题最主要的是构造全等三角形，构造二条边之间的相等，构造二个角之间的相等【三角形辅助线做法】图中有角平分线，可向两边作垂线。
也可将图对折看，对称以后关系现。
角平分线平行线，等腰三角形来添。
角平分线加垂线，三线合一试试看。
线段垂直平分线，常向两端把线连。
要证线段倍与半，延长缩短可试验。
三角形中两中点，连接则成中位线。
三角形中有中线，延长中线等中线。
1.等腰三角形“三线合一”法：遇到等腰三角形，可作底边上的高，利用“三线合一”的性质解题2.倍长中线：倍长中线，使延长线段与原中线长相等，构造全等三角形3.角平分线在三种添辅助线4.垂直平分线联结线段两端5.用“截长法”或“补短法”： 遇到有二条线段长之和等于第三条线段的长，6.图形补全法：有一个角为60度或120度的把该角添线后构成等边三角形7.角度数为30、60度的作垂线法：遇到三角形中的一个角为30度或60度，可以从角一边上一点向角的另一边作垂线，目的是构成30-60-90的特殊直角三角形，然后计算边的长度与角的度数，这样可以得到在数值上相等的二条边或二个角。
从而为证明全等三角形创造边、角之间的相等条件。
8.计算数值法：遇到等腰直角三角形，正方形时，或30-60-90的特殊直角三角形，或40-60-80的特殊直角三角形,常计算边的长度与角的度数，这样可以得到在数值上相等的二条边或二个角，从而为证明全等三角形创造边、角之间的相等条件。
常见辅助线的作法有以下几种：最主要的是构造全等三角形，构造二条边之间的相等，二个角之间的相等。
1) 遇到等腰三角形，可作底边上的高，利用“三线合一”的性质解题，思维模式是全等变换中的“对折”法构造全等三角形．2) 遇到三角形的中线，倍长中线，使延长线段与原中线长相等，构造全等三角形，利用的思维模式是全等变换中的“旋转” 法构造全等三角形．3) 遇到角平分线在三种添辅助线的方法，（1）可以自角平分线上的某一点向角的两边作垂线，利用的思维模式是三角形全等变换中的“对折”，所考知识点常常是角平分线的性质定理或逆定理．（2）可以在角平分线上的一点作该角平分线的垂线与角的两边相交，形成一对全等三角形。
初中数学】几何题,辅助线的添加方法和典型例题
初中数学】几何题,辅助线的添加方法和典型例题初中数学：几何题型，辅助线的画法和典型例题1.倍长中线法已知在△ABC中，D是BC中点，DE⊥DF，需要判断BE＋CF与EF的大小关系，并证明结论。
思路点拨：利用倍长中线法，倍长过中点的线段DF使DG＝DF，再证明△XXX≌△EDF，△FDC≌△GDB，将BE、CF与EF线段转化到△BEG中，利用两边之和大于第三边证明。
解析：连接BG、EG，因为D是BC中点，所以BD＝CD。
又因为DE⊥DF，在△XXX和△EDF中，ED＝ED，∠XXX∠EDF，DG＝DF，因此△XXX≌△EDF（SAS），所以EG＝EF。
在△XXX与△GDB中，CD＝BD，∠1＝∠2，DF＝DG，因此△FDC≌△GDB（SAS），所以CF＝BG。
因为BG＋BE＞EG，所以BE＋CF＞EF。
结论得证。
总结升华：有中点的时候作辅助线可以考虑倍长中线法（或倍长过中点的线段）。
变式：已知CE、CB分别是△ABC与△ADC的中线，且∠ACB＝∠ABC，需要证明CD＝2CE。
解析：连接BF，延长CE至F使EF＝CE。
因为EC为中线，所以AE＝BE。
在△AEC与△BEF中，AE＝BE，∠AEC ＝∠BEF，CE＝EF，因此△AEC≌△BEF（SAS）。
所以AC ＝BF，∠A＝∠FBE。
又因为∠ACB＝∠ABC，∠XXX∠ACB＋∠A，∠XXX∠ABC＋∠A，所以AC＝AB，∠XXX∠XXX。
因此AB＝BF，BC为△ADC的中线，所以AB＝BD，即BF＝BD。
在△FCB与△DCB中，∠XXX∠DBC，BC＝BC，因此△FCB≌△DCB（SAS），所以CF＝CD。
结论得证。
2.以角平分线为对称轴的翻折变换构造全等三角形已知在△ABC中，∠C＝2∠B，∠1＝∠2，需要证明XXX。
解析：在AB上截取AE＝AC，连接CE，作角ACE的平分线交AB于D，连接CD。
因为∠C＝2∠B，所以∠ACE＝∠XXX∠B，∠XXX∠A＝∠1＝∠2，所以△AED≌△ACD （SAS），因此ED＝CD。
初中数学辅助线添加及例题大全
初中数学辅助线的添加人们从来就是用自己的聪明才智创造条件解决问题的，当问题的条件不够时，添加辅助线构成新图形，形成新关系，使分散的条件集中，建立已知与未知的桥梁，把问题转化为自己能解决的问题，这是解决问题常用的策略。
一．添辅助线有二种情况：（按定义添辅助线：如证明二直线垂直可延长使它们,相交后证交角为90 °；证线段倍半关系可倍线段取中点或半线段加倍；证角的倍半关系也可类似添辅助线。
（按基本图形添辅助线：每个几何定理都有与它相对应的几何图形，我们把它叫做基本图形，添辅助线往往是具有基本图形的性质而基本图形不完整时补完整基本图形，因此“添线”应该叫做“补图”！这样可防止乱添线，添辅助线也有规律可循。
举例如下：（1 ）平行线是个基本图形：当几何中出现平行线时添辅助线的关键是添与二条平行线都相交的等第三条直线（2 ）等腰三角形是个简单的基本图形：当几何问题中出现一点发出的二条相等线段时往往要补完整等腰三角形。
出现角平分线与平行线组合时可延长平行线与角的二边相交得等腰三角形。
（3 ）等腰三角形中的重要线段是个重要的基本图形：出现等腰三角形底边上的中点添底边上的中线；出现角平分线与垂线组合时可延长垂线与角的二边相交得等腰三角形中的重要线段的基本图形。
（4）直角三角形斜边上中线基本图形出现直角三角形斜边上的中点往往添斜边上的中线。
出现线段倍半关系且倍线段是直角三角形的斜边则要添直角三角形斜边上的中线得直角三角形斜边上中线基本图形。
（5 ）三角形中位线基本图形几何问题中出现多个中点时往往添加三角形中位线基本图形进行证明当有中点没有中位线时则添中位线，当有中位线三角形不完整时则需补完整三角形；当出现线段倍半关系且与倍线段有公共端点的线段带一个中点则可过这中点添倍线段的平行线得三角形中位线基本图形；当出现线段倍半关系且与半线段的端点是某线段的中点，则可过带中点线段的端点添半线段的平行线得三角形中位线基本图形。
初中数学关于添加辅助线的方法总结
初中数学关于添加辅助线的方法总结 辅助线对于同学们来说都不陌生，解几何题的时候经常用到。
当题目给出的条件不够时，我们通过添加辅助线构成新图形，形成新关系，使分散的条件集中，建立与未知的桥梁，把问题转化为自己能解决的问题，这便是辅助线的作用。
一条巧妙的辅助线常常使一道难题迎刃而解。
所以我们要学会巧妙的添加辅助线。
添加辅助线的几种方法。
添辅助线有二种情况：▌1、按定义添辅助线：如证明二直线垂直可延长使它们相交后证交角为90°;证线段倍半关系可倍线段取中点或半线段加倍;证角的倍半关系也可类似添辅助线。
▌2、按基本图形添辅助线：每个几何定理都有与它相对应的几何图形，我们把它叫做基本图形，添辅助线往往是具有基本图形的性质而基本图形不完整时补完整基本图形，因此〝添线〞应该叫做〝补图〞!这样可防止乱添线，添辅助线也有规律可循。
举例如下：(1)平行线是个基本图形：当几何中出现平行线时添辅助线的关键是添与二条平行线都相交的等第三条直线(2)等腰三角形是个简单的基本图形：当几何问题中出现一点发出的二条相等线段时往往要补完整等腰三角形。
出现角平分线与平行线组合时可延长平行线与角的二边相交得等腰三角形。
(3)等腰三角形中的重要线段是个重要的基本图形：出现等腰三角形底边上的中点添底边上的中线;出现角平分线与垂线组合时可延长垂线与角的二边相交得等腰三角形中的重要线段的基本图形。
(4)直角三角形斜边上中线基本图形出现直角三角形斜边上的中点往往添斜边上的中线。
出现线段倍半关系且倍线段是直角三角形的斜边那么要添直角三角形斜边上的中线得直角三角形斜边上中线基本图形。
(5)三角形中位线基本图形几何问题中出现多个中点时往往添加三角形中位线基本图形进行证明当有中点没有中位线时那么添中位线，当有中位线三角形不完整时那么需补完整三角形;当出现线段倍半关系且与倍线段有公共端点的线段带一个中点那么可过这中点添倍线段的平行线得三角形中位线基本图形;当出现线段倍半关系且与半线段的端点是某线段的中点，那么可过带中点线段的端点添半线段的平行线得三角形中位线基本图形。
初二几何辅助线添加方法
初中数学辅助线1.三角形问题添加辅助线方法方法1：有关三角形中线的题目,常将中线加倍;含有中点的题目,常常利用三角形的中位线,通过这种方法,把要证的结论恰当的转移,很容易地解决了问题;方法2：含有平分线的题目,常以角平分线为对称轴,利用角平分线的性质和题中的条件,构造出全等三角形,从而利用全等三角形的知识解决问题;方法3：结论是两线段相等的题目常画辅助线构成全等三角形,或利用关于平分线段的一些定理;方法4：结论是一条线段与另一条线段之和等于第三条线段这类题目,常采用截长法或补短法,所谓截长法就是把第三条线段分成两部分,证其中的一部分等于第一条线段,而另一部分等于第二条线段;2.平行四边形中常用辅助线的添法平行四边形包括矩形、正方形、菱形的两组对边、对角和对角线都具有某些相同性质,所以在添辅助线方法上也有共同之处,目的都是造就线段的平行、垂直,构成三角形的全等、相似,把平行四边形问题转化成常见的三角形、正方形等问题处理,其常用方法有下列几种,举例简解如下：1连对角线或平移对角线：2过顶点作对边的垂线构造直角三角形3连接对角线交点与一边中点,或过对角线交点作一边的平行线,构造线段平行或中位线4连接顶点与对边上一点的线段或延长这条线段,构造三角形相似或等积三角形;5过顶点作对角线的垂线,构成线段平行或三角形全等.3.梯形中常用辅助线的添法梯形是一种特殊的四边形;它是平行四边形、三角形知识的综合,通过添加适当的辅助线将梯形问题化归为平行四边形问题或三角形问题来解决;辅助线的添加成为问题解决的桥梁,梯形中常用到的辅助线有：1在梯形内部平移一腰;2梯形外平移一腰3梯形内平移两腰4延长两腰5过梯形上底的两端点向下底作高6平移对角线7连接梯形一顶点及一腰的中点;8过一腰的中点作另一腰的平行线;9作中位线当然在梯形的有关证明和计算中,添加的辅助线并不一定是固定不变的、单一的;通过辅助线这座桥梁,将梯形问题化归为平行四边形问题或三角形问题来解决,这是解决问题的关键;作辅助线的方法一：中点、中位线,延线,平行线;如遇条件中有中点,中线、中位线等,那么过中点,延长中线或中位线作辅助线,使延长的某一段等于中线或中位线；另一种辅助线是过中点作已知边或线段的平行线,以达到应用某个定理或造成全等的目的;二：垂线、分角线,翻转全等连;如遇条件中,有垂线或角的平分线,可以把图形按轴对称的方法,并借助其他条件,而旋转180度,得到全等形,,这时辅助线的做法就会应运而生;其对称轴往往是垂线或角的平分线;三：边边若相等,旋转做实验;如遇条件中有多边形的两边相等或两角相等,有时边角互相配合,然后把图形旋转一定的角度,就可以得到全等形,这时辅助线的做法仍会应运而生;其对称中心,因题而异,有时没有中心;故可分“有心”和“无心”旋转两种;四:造角、平、相似,和、差、积、商见;如遇条件中有多边形的两边相等或两角相等,欲证线段或角的和差积商,往往与相似形有关;在制造两个三角形相似时,一般地,有两种方法：第一,造一个辅助角等于已知角；第二,是把三角形中的某一线段进行平移;故作歌诀：“造角、平、相似,和差积商见;”五：面积找底高,多边变三边;如遇求面积,在条件和结论中出现线段的平方、乘积,仍可视为求面积,往往作底或高为辅助线,而两三角形的等底或等高是思考的关键;如遇多边形,想法割补成三角形；反之,亦成立;另外,我国明清数学家用面积证明勾股定理,其辅助线的做法,即“割补”有二百多种,大多数为“面积找底高,多边变三边”;初中几何常见辅助线口诀人说几何很困难,难点就在辅助线;辅助线,如何添把握定理和概念;还要刻苦加钻研,找出规律凭经验;三角形图中有角平分线,可向两边作垂线;也可将图对折看,对称以后关系现;角平分线平行线,等腰三角形来添;角平分线加垂线,三线合一试试看;线段垂直平分线,常向两端把线连;线段和差及倍半,延长缩短可试验;线段和差不等式,移到同一三角去;三角形中两中点,连接则成中位线;三角形中有中线,延长中线等中线;四边形平行四边形出现,对称中心等分点;梯形问题巧转换,变为△和□;平移腰,移对角,两腰延长作出高;如果出现腰中点,细心连上中位线;上述方法不奏效,过腰中点全等造;证相似,比线段,添线平行成习惯;等积式子比例换,寻找线段很关键;直接证明有困难,等量代换少麻烦;斜边上面作高线,比例中项一大片;三角形中作辅助线的常用方法举例一．倍长中线1：已知△ABC,AD 是BC 边上的中线,分别以AB 边、AC 边为直角边各向形外作等腰直角三角形,如图5-2, 求证EF ＝2AD; 二、截长补短法作辅助线;在△ABC 中,AD 平分∠BAC,∠ACB ＝2∠B,求证：AB ＝AC ＋CD; 三、延长已知边构造三角形：例如：如图7-1：已知AC ＝BD,AD ⊥AC 于A ,BC ⊥BD 于B, 求证：AD ＝BC 分析：欲证 AD ＝BC,先证分别含有AD,BC 的三角形全等,有几种方案：△ADC与△BCD,△AOD 与△BOC,△ABD 与△BAC,但根据现有条件,均无法证全等,差角的相等,因此可设法作出新的角,且让此角作为两个三角形的公共角; 证明：分别延长DA,CB,它们的延长交于E 点,∵AD ⊥AC BC ⊥BD 已知∴∠CAE ＝∠DBE ＝90° 垂直的定义 在△DBE 与△CAE 中∵⎪⎩⎪⎨⎧=∠=∠∠=∠)()()(已知已证公共角AC BD CAE DBE E E∴△DBE ≌△CAE AAS∴ED ＝EC EB ＝EA 全等三角形对应边相等 ∴ED －EA ＝EC －EB 即：AD ＝BC;当条件不足时,可通过添加辅助线得出新的条件,为证题创造条件; 四、连接四边形的对角线,把四边形的问题转化成为三角形来解决; 例如：如图8-1：AB ∥CD,AD ∥BC 求证：AB=CD;分析：图为四边形,我们只学了三角形的有关知识,必须把它转化为三角形来解决; 证明：连接AC 或BD∵AB ∥CD AD ∥BC 已知∴∠1＝∠2,∠3＝∠4 两直线平行,内错角相等 在△ABC 与△CDA 中 ∵⎪⎩⎪⎨⎧∠=∠=∠=∠)(43)()(21已证公共边已证CA AC∴△ABC ≌△CDA ASA∴AB ＝CD 全等三角形对应边相等五、有和角平分线垂直的线段时,通常把这条线段延长;例如：如图9-1：在Rt △ABC 中,AB ＝AC,∠BAC ＝90°,∠1＝∠2,CE ⊥BD 的延长于E ;求证：BD ＝2CE分析：要证BD ＝2CE,想到要构造线段2CE,同时CE 与∠ABC 的平分线垂直,想到要将其延长; 证明：分别延长BA,CE 交于点F;∵BE ⊥CF 已知∴∠BEF ＝∠BEC ＝90° 垂直的定义在△BEF 与△BEC 中,ABC DEF25-图19-图DCBA E F 12A BCD18-图1234ABCD E17-图O∵⎪⎩⎪⎨⎧∠=∠=∠=∠)()()(21已证公共边已知BEC BEF BE BE∴△BEF ≌△BECASA ∴CE=FE=21CF 全等三角形对应边相等∵∠BAC=90° BE ⊥CF 已知∴∠BAC ＝∠CAF ＝90° ∠1＋∠BDA ＝90°∠1＋∠BFC ＝90° ∴∠BDA ＝∠BFC 在△ABD 与△ACF 中∴△ABD ≌△ACF AAS ∴BD ＝CF 全等三角形对应边相等 ∴BD ＝2CE 六、连接已知点,构造全等三角形;例如：已知：如图10-1；AC 、BD 相交于O 点,且AB ＝DC,AC ＝BD,求证：∠A ＝∠D; 分析：要证∠A ＝∠D,可证它们所在的三角形△ABO 和△DCO 全等,而只有AB ＝DC 和对顶角两个条件,差一个条件,,难以证其全等,只有另寻其它的三角形全等,由AB ＝DC,AC ＝BD,若连接BC,则△ABC 和△DCB 全等,所以,证得∠A ＝∠D; 证明：连接BC,在△ABC 和△DCB 中∵⎪⎩⎪⎨⎧===)()()(公共边已知已知CB BC DB AC DC AB∴△ABC ≌△DCB SSS∴∠A ＝∠D 全等三角形对应边相等七、取线段中点构造全等三有形;例如：如图11-1：AB ＝DC,∠A ＝∠D 求证：∠ABC ＝∠DCB; 分析：由AB ＝DC,∠A ＝∠D,想到如取AD 的中点N,连接NB,NC,再由SAS 公理有△ABN ≌△DCN,故BN ＝CN,∠ABN ＝∠DCN;下面只需证∠NBC ＝∠NCB,再取BC 的中点M,连接MN,则由SSS 公理有△NBM ≌△NCM,所以∠NBC ＝∠NCB;问题得证;证明：取AD,BC 的中点N 、M,连接NB,NM,NC;则AN=DN,BM=CM,在△ABN 和△DCN 中 ∵ ⎪⎩⎪⎨⎧=∠=∠=)()()(已知已知辅助线的作法DC AB D A DN AN∴△ABN ≌△DCN SAS∴∠ABN ＝∠DCN NB ＝NC 全等三角形对应边、角相等 在△NBM 与△NCM 中∵⎪⎩⎪⎨⎧)()()(公共边＝辅助线的作法＝已证＝NM NM CM BM NC NB∴△NMB ≌△NCM,SSS ∴∠NBC ＝∠NCB 全等三角形对应角相等∴∠NBC ＋∠ABN ＝∠NCB ＋∠DCN 即∠ABC ＝∠DCB; 二 由角平分线想到的辅助线D BA110-图O 111-图D CBAM N口诀：图中有角平分线,可向两边作垂线;也可将图对折看,对称以后关系现;角平分线平行线,等腰三角形来添;角平分线加垂线,三线合一试试看;角平分线具有两条性质：a 、对称性；b 、角平分线上的点到角两边的距离相等;对于有角平分线的辅助线的作法,一般有两种; ①从角平分线上一点向两边作垂线；②利用角平分线,构造对称图形如作法是在一侧的长边上截取短边;通常情况下,出现了直角或是垂直等条件时,一般考虑作垂线；其它情况下考虑构造对称图形;至于选取哪种方法,要结合题目图形和已知条件; 与角有关的辅助线 一、截取构全等几何的证明在于猜想与尝试,但这种尝试与猜想是在一定的规律基本之上的,希望同学们能掌握相关的几何规律,在解决几何问题中大胆地去猜想,按一定的规律去尝试;下面就几何中常见的定理所涉及到的辅助线作以介绍; 如图1-1,∠AOC=∠BOC,如取OE=OF,并连接DE 、DF,则有△OED ≌△OFD,从而为我们证明线段、角相等创造了条件; 1-2,AB 21如图图1-2ADBCEF图2-1ABCDE F图示3-1ABCD HE如图所示,在直角梯形ABC D 中,∠A ＝90°,AB ∥DC,AD ＝15,AB ＝16,BC ＝17. 求CD 的长. 解：过点D 作DE ∥BC 交AB 于点E.又AB ∥CD,所以四边形BCDE 是平行四边形. 所以DE ＝BC ＝17,CD ＝BE. 在R t △DAE 中,由勾股定理,得AE 2＝DE 2－AD 2,即AE 2＝172－152＝64. 所以AE ＝8.所以BE ＝AB －AE ＝16－8＝8. 即CD ＝8.例2如图,梯形ABCD 的上底AB=3,下底CD=8,腰AD=4,求另一腰BC 的取值范围;解：过点B作BM)(2121CH BGBC GH EF --==512=⨯=BE ED BD DH 6251252DHBC)(AD ABCD =⨯=⨯+=∴梯形S 25252522222100)25()25(AE CE AC ==+=+15cm20cm12cmDCEACD ABD S S S ∆∆∆==DBEABCD S S ∆=梯形2222DH AC DH DE EH -=-=9121522=-=1612202222=-=-=DH BD BH )(15012)169(21212cm DH BE S DBE =⨯+⨯=⋅=∆150cA B DC E Hm 如图所示,四边形ABCD 中,AD 不平行于BC,AC ＝BD,AD ＝BC. 判断四边形ABCD 的形状,并证明你的结论.解：四边形ABCD 是等腰梯形. 证明：延长AD 、BC 相交于点E,如图所示. ∵AC ＝BD,AD ＝BC,AB ＝BA, ∴△DAB ≌△CBA. ∴∠DAB ＝∠CBA. ∴EA ＝EB.又AD ＝BC,∴DE ＝CE,∠EDC ＝∠ECD.而∠E ＋∠EAB ＋∠EBA ＝∠E ＋∠EDC ＋∠ECD ＝180°, ∴∠EDC ＝∠EAB,∴DC ∥AB.又AD 不平行于BC,∴四边形ABCD 是等腰梯形. 三、作对角线即通过作对角线,使梯形转化为三角形;例9如图6,在直角梯形ABCD 中,AD//BC,AB ⊥AD,BC=CD,BE ⊥CD 于点E,求证：AD=DE; 解：连结BD,由AD//BC,得∠ADB=∠DBE ； 由BC=CD,得∠DBC=∠BDC; 所以∠ADB=∠BDE;又∠BAD=∠DEB=90°,BD=BD, 所以Rt △BAD ≌Rt △BED, 得AD=DE;四、作梯形的高 1、作一条高例10如图,在直角梯形ABCD 中,AB//DC,∠ABC=90°,AB=2DC,对角线AC ⊥BD,垂足为F,过点F 作EF//AB,交AD 于点E,求证：四边形ABFE 是等腰梯形;证：过点D 作DG ⊥AB 于点G,则易知四边形DGBC 是矩形,所以DC=BG; 因为AB=2DC,所以AG=GB;从而DA=DB,于是∠DAB=∠DBA;又EF//AB,所以四边形ABFE 是等腰梯形; 2、作两条高例11、在等腰梯形ABCD 中,AD//BC,AB=CD,∠ABC=60°,AD=3cm,BC=5cm, 求：1腰AB 的长；2梯形ABCD 的面积．解：作AE ⊥BC 于E,DF ⊥BC 于F,又∵AD ∥BC, ∴四边形AEFD 是矩形, EF=AD=3cm ∵AB=DC∵在Rt △ABE 中,∠B=60°,BE=1cmA B C D A B C D E A B C D E F∴AB=2BE=2cm,cm BE AE 33==∴2342)(cm AEBC AD S ABCD =⨯+=梯形例12如图,在梯形ABCD 中,AD 为上底,AB>CD,求证：BD>AC;证：作AE ⊥BC 于E,作DF ⊥BC 于F,则易知AE=DF; 在Rt △ABE 和Rt △DCF 中, 因为AB>CD,AE=DF;所以由勾股定理得BE>CF;即BF>CE; 在Rt △BDF 和Rt △CAE 中 由勾股定理得BD>AC 五、作中位线1、已知梯形一腰中点,作梯形的中位线;例13如图,在梯形ABCD 中,AB//DC,O 是BC 的中点,∠AOD=90°,求证：AB ＋CD=AD;证：取AD 的中点E,连接OE,则易知OE 是梯形ABCD 的中位线,从而OE=21AB ＋CD ①在△AOD 中,∠AOD=90°,AE=DE 所以AD OE 21=②由①、②得AB ＋CD=AD;2、已知梯形两条对角线的中点,连接梯形一顶点与一条对角线中点,并延长与底边相交,使问题转化为三角形中位线;例14如图,在梯形ABCD 中,AD//BC,E 、F 分别是BD 、AC 的中点,求证：1EF//AD ；2)(21AD BC EF -=;证：连接DF,并延长交BC 于点G,易证△AFD ≌△CFG则AD=CG,DF=GF由于DE=BE,所以EF 是△BDG 的中位线 从而EF//BG,且BG EF 21=因为AD//BG,AD BC CG BC BG -=-=所以EF//AD,EF )(21AD BC -=3、在梯形中出现一腰上的中点时,过这点构造出两个全等的三角形达到解题的目的;例15、在梯形ABCD 中,AD ∥BC, ∠BAD=900,E 是DC 上的中点,连接AE 和BE,求∠AEB=2∠CBE;解：分别延长AE与BC ,并交于F点∵∠BAD=900且AD∥BC∴∠FBA=1800－∠BAD=900又∵AD∥BC∴∠DAE=∠F两直线平行内错角相等∠AED=∠FEC 对顶角相等DE=EC E点是CD的中点∴△ADE≌△FCE AAS∴ AE=FE在△ABF中∠FBA=900且AE=FE∴ BE=FE直角三角形斜边上的中线等于斜边的一半∴在△FEB中∠EBF=∠FEB∠AEB=∠EBF+ ∠FEB=2∠CBE例16、已知：如图,在梯形ABCD中,AD//BC,AB⊥BC,E是CD中点,试问：线段AE和BE之间有怎样的大小关系解：AE=BE,理由如下：延长AE,与BC延长线交于点F．∵DE=CE,∠AED=∠CEF,∠DAE=∠F∴△ADE≌△FCE∴AE=EF∵AB⊥BC, ∴BE=AE．ABDCEF。
(完整版)初二数学辅助线常用做法及例题(含答案)
DCB A常见的辅助线的作法总论：全等三角形问题最主要的是构造全等三角形，构造二条边之间的相等，构造二个角之间的相等【三角形辅助线做法】图中有角平分线，可向两边作垂线。
也可将图对折看，对称以后关系现。
角平分线平行线，等腰三角形来添。
角平分线加垂线，三线合一试试看。
线段垂直平分线，常向两端把线连。
要证线段倍与半，延长缩短可试验。
三角形中两中点，连接则成中位线。
三角形中有中线，延长中线等中线。
1.等腰三角形“三线合一”法：遇到等腰三角形，可作底边上的高，利用“三线合一”的性质解题2.倍长中线：倍长中线，使延长线段与原中线长相等，构造全等三角形3.角平分线在三种添辅助线4.垂直平分线联结线段两端5.用“截长法”或“补短法”： 遇到有二条线段长之和等于第三条线段的长，6.图形补全法：有一个角为60度或120度的把该角添线后构成等边三角形7.角度数为30、60度的作垂线法：遇到三角形中的一个角为30度或60度，可以从角一边上一点向角的另一边作垂线，目的是构成30-60-90的特殊直角三角形，然后计算边的长度与角的度数，这样可以得到在数值上相等的二条边或二个角。
从而为证明全等三角形创造边、角之间的相等条件。
8.计算数值法：遇到等腰直角三角形，正方形时，或30-60-90的特殊直角三角形，或40-60-80的特殊直角三角形,常计算边的长度与角的度数，这样可以得到在数值上相等的二条边或二个角，从而为证明全等三角形创造边、角之间的相等条件。
常见辅助线的作法有以下几种：最主要的是构造全等三角形，构造二条边之间的相等，二个角之间的相等。
1) 遇到等腰三角形，可作底边上的高，利用“三线合一”的性质解题，思维模式是全等变换中的“对折”法构造全等三角形．2) 遇到三角形的中线，倍长中线，使延长线段与原中线长相等，构造全等三角形，利用的思维模式是全等变换中的“旋转” 法构造全等三角形．3) 遇到角平分线在三种添辅助线的方法，（1）可以自角平分线上的某一点向角的两边作垂线，利用的思维模式是三角形全等变换中的“对折”，所考知识点常常是角平分线的性质定理或逆定理．（2）可以在角平分线上的一点作该角平分线的垂线与角的两边相交，形成一对全等三角形。
(完整版)初二数学辅助线常用做法及例题(含答案)
使 AE = AF，
求证： EF⊥BC
证明：延长 BE到 N，使 AN= AB,连结 CN,则 AB= AN= AC
N
∴∠ B = ∠ ACB, ∠ACN = ∠ ANC ∵∠ B＋∠ ACB＋∠ ACN＋∠ ANC = 180o ∴ 2∠BCA＋ 2∠ ACN = 180o ∴∠ BCA＋∠ ACN = 90o 即∠ BCN = 90o
7. 角度数为 30、 60 度的作垂线法： 遇到三角形中的一个角为 30 度或 60 度，可
以从角一边上一点向角的另一边作垂线，目的是构成
30-60-90 的特殊直角三角形，然后计
算边的长度与角的度数，这样可以得到在数值上相等的二条边或二个角。从而为证明全等三
角形创造边、角之间的相等条件。
8. 计算数值法： 遇到等腰直角三角形，正方形时，或 30-60-90 的特殊直角三角形，或
40-60-80 的特殊直角三角形 , 常计算边的长度与角的度数，这样可以得到在数值上相等的二
条边或二个角，从而为证明全等三角形创造边、角之间的相等条件。
常见辅助线的作法有以下几种：最主要的是构造全等三角形，构造二条边之间的相等，二个
角之间的相等。
1) 遇到等腰三角形，可作底边上的高，利用“三线合一”的性质解题，思维模式是全等变
A
∵ BD⊥AC ∴∠ DBC＋∠ ACB = 90o
DBC （方法二）过 A 作 AE⊥ BC于 E（过程略）
B
E
C
（方法三）取 BC中点 E，连结 AE（过程略）
⑵有底边中点时，常作底边中线
例：已知，如图，△ ABC中， AB = AC，D为 BC中点， DE⊥ AB于 E，DF⊥ AC于 F，
B
初中数学_巧添辅助线__解证几何题
巧添辅助线解证几何题[引出问题] 在几何证明或计算问题中.经常需要添加必要的辅助线.它的目的可以归纳为以下三点：一是通过添加辅助线.使图形的性质由隐蔽得以显现.从而利用有关性质去解题；二是通过添加辅助线.使分散的条件得以集中.从而利用它们的相互关系解题；三是把新问题转化为已经解决过的旧问题加以解决。
值得注意的是辅助线的添加目的与已知条件和所求结论有关。
一、倍角问题研究∠α＝2∠β或∠β=12∠α问题通称为倍角问题。
倍角问题分两种情形：1、∠α与∠β在两个三角形中.常作∠α的平分线.得∠1=12∠α.然后证明∠1=∠β；或把∠β翻折.得∠2=2∠β.然后证明∠2=∠α（如图一）2、∠α与∠β在同一个三角形中.这样的三角形常称为倍角三角形。
倍角三角形问题常用构造等腰三角形的方法添加辅助线（如图二）[例题解析]例1：如图1.在△ABC中.AB=AC,BD⊥AC于D。
求证：∠DBC=12∠BAC.分析：∠DBC、∠BAC所在的两个三角形有公共角∠C.可利用三角形内角和来沟通∠DBC、∠BAC和∠C的关系。
证法一：∵在△ABC中.AB=AC.∴∠ABC=∠C=12（180°-∠BAC）=90°-12∠BAC。
∵BD⊥AC于D ∴∠BDC=90°∴∠DBC=90°-∠C=90°-(90°-12∠BAC)=12∠BAC即∠DBC= 12∠BAC分析二：∠DBC、∠BAC分别在直角三角形和等腰三角形中.由所证的结论“∠DBC= ½∠BAC”中含有角的倍、半关系.因此.可以做∠A的平分线.利用等腰三角形三线合一的性质.把½∠A 放在直角三角形中求解；也可以把∠DBC沿BD翻折构造2∠DBC求解。
证法二：如图2.作AE⊥BC于E.则∠EAC+∠C=90°∵AB=AC ∴∠EAG=12∠BAC∵BD⊥AC于D∴∠DBC+∠C=90°∴∠EAC=∠DBC（同角的余角相等）即∠DBC=12∠BAC。
巧添辅助线解决二倍角问题
因为 Ｄ ／Ａ ， 以 Ｌ５＝ Ｌ ， Ｅ ＝ １， Ｅ／ Ｃ 所 ４
所 以 Ｌ５ ＝ Ｅ， 以 Ａ ＝，Ｅ 所 Ｄ Ａ ．
题， 感觉难度很大， 无从下手 ．其实 ， 这类问题添加辅助线 是有一定技巧和规律的， 可归纳总结为以下四种方法 ：
１做 大 角 的平 分线 ； ． ２ 以小 角 的 顶 点 、 角 的 一 边 为 一 边 ， 小 角 的 外 ． 小 在 部 做 一个 与 小角 相 等 的角 ； ３ 反 向延 长 三 角 形 大 角 的 一 个 边 ， 另 外 一 边 相 ． 与
求证 ：Ｂ Ａ ＋Ｂ ・ Ｂ ：Ａ Ｃ Ａ Ｃ．
Ａ
Ｂ
Ｄ
Ｃ
图３ห้องสมุดไป่ตู้
证明 延长 Ｃ Ｂ到 Ｅ， Ｂ ＝Ｂ 连结 Ａ ， 使 Ｅ Ａ， Ｅ 则 Ｅ
１
＝ Ｌ３＝÷ Ａ ｃ ： Ｃ， Ａ ＝Ａ ． 日 所以 Ｅ Ｃ
图 １
又 ＬＡ ＤＥ ＝ Ｃ＋ Ｌ２， Ａ ＝ Ｌ３＋ １ 所 以 ＬＤ Ｅ ， ＬＡ Ｅ ＝ ＬＤ Ｅ， 以Ａ ＝ＤＥ， 以 Ｂ ：ＤＥ—Ｂ ＝ Ｄ Ａ 所 Ｅ 所 Ｄ Ｅ
巧 添辅 助 线 解 决 二 倍 角 问题
山 东省 即墨 市鳌 山卫 中学
平面 几何 中常 出现 “ 三角 形 的一 个 内角 为另一 个 内 角 的二倍 ”即 “ 二倍 角 ” 件 的 问题 ， 生 遇 到这 样 的 问 条 学
２ ６ ３ ６ ２７
周 义展
又 Ｌ２ ＝ Ｂ Ｄ， 以 ＢＤ ＝Ａ ＝Ａ Ａ 所 Ｄ
ＡＣ Ｄ ＝ ＡＤＣ ．
因 为 １ ：Ｌ２： ３＝１： ２：
４， 以 ＬＡＣ ＝ １ ＋ Ｌ２ ＝ 所 Ｄ
３／ １ ．
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
巧添辅助线 解证几何题[引出问题] 在几何证明或计算问题中，经常需要添加必要的辅助线，它的目的可以归纳为以下三点：一是通过添加辅助线，使图形的性质由隐蔽得以显现，从而利用有关性质去解题；二是通过添加辅助线，使分散的条件得以集中，从而利用它们的相互关系解题；三是把新问题转化为已经解决过的旧问题加以解决。
值得注意的是辅助线的添加目的与已知条件和所求结论有关。
一、倍角问题研究∠α＝2∠β或∠β=12∠α问题通称为倍角问题。
倍角问题分两种情形：1、∠α与∠β在两个三角形中，常作∠α的平分线，得∠1=12∠α，然后证明∠1=∠β；或把∠β翻折，得∠2=2∠β，然后证明∠2=∠α（如图一）2、 ∠α与∠β在同一个三角形中，这样的三角形常称为倍角三角形。
倍角三角形问题常用构造等腰三角形的方法添加辅助线（如图二）[例题解析]例1：如图1，在△ABC 中，AB=AC,BD ⊥AC 于D 。
求证：∠DBC=12∠BAC. 分析：∠DBC 、∠BAC 所在的两个三角形有公共角∠C ，可利用三角形内角和来沟通∠DBC 、∠BAC 和∠C 的关系。
证法一：∵在△ABC 中，AB=AC ，∴∠ABC=∠C=12（180°-∠BAC ）=90°-12∠BAC 。
∵BD ⊥AC 于D ∴∠BDC=90°∴∠DBC=90°-∠C=90°-(90°-12∠BAC)= 12∠BAC 即∠DBC= 12∠BAC分析二：∠DBC 、∠BAC 分别在直角三角形和等腰三角形中，由所证的结论“∠DBC= ½∠BAC ”中含有角的倍、半关系，因此，可以做∠A 的平分线，利用等腰三角形三线合一的性质，把½∠A 放在直角三角形中求解；也可以把∠DBC 沿BD 翻折构造2∠DBC 求解。
证法二：如图2，作AE ⊥BC 于E ，则∠EAC+∠C=90°∵AB=AC ∴∠EAG=12∠BAC ∵BD ⊥AC 于D∴∠DBC+∠C=90°∴∠EAC=∠DBC （同角的余角相等）即∠DBC=12∠BAC 。
证法三：如图3，在AD 上取一点E ，使DE=CD 连接BE ∵BD ⊥AC∴BD 是线段CE 的垂直平分线 ∴BC=BE ∴∠BEC=∠C∴∠EBC=2∠DBC=180°-2∠C ∵AB=AC ∴∠ABC=∠C∴∠BAC=180°-2∠C ∴∠EBC=∠BAC ∴∠DBC=12∠BAC 说明：例1也可以取BC 中点为E ，连接DE ，利用直角三角形斜边的中线等于斜边的一半和等腰三角形的性质求解。
同学们不妨试一试。
例2、如图4，在△ABC 中，∠A=2∠B求证：BC 2=AC 2+AC •AB 分析：由BC 2=AC 2+AC •AB= AC （AC+AB ），启发我们构建两个相似的三角形，且含有边BC 、AC 、AC+AB.又由已知∠A=2∠B 知，构建以AB 为腰的等腰三角形。
证明：延长CA 到D,使AD=AB,则∠D=∠DBA ∵∠BAC 是△ABD 的一个外角 ∴∠BAC=∠DBA+∠D=2∠D ∵∠BAC=2∠ABC ∴∠D=∠ABC又∵∠C=∠C ∴△ABC ∽△BDC ∴AC BCBC CD∴BC 2=AC •CD AD=AB∴BC 2= AC （AC+AB ）=AC 2+AC •AB二、中点问题已知条件中含有线段的中点信息称为中点问题。
这类问题常用三种方法添加辅助线 （1） 延长中线至倍（或者倍长中线），如图一。
若图形中没有明显的三角形的中线，也可以构造中线后，再倍长中线，如图二。
（2） 构造中位线，如图三 （3） 构造直角三角形斜边上的中线，如图四。
ECABDA B C图一 图二 图三 图四[例题解析]例3．已知：如图，△ABC 中，AB=AC,在AB 上取一点D ，在AC 的延长线上取一点E,连接DE 交BC 于点F,若F 是DE 的中点。
求证：BD=CE分析：由于BD 、CE 的形成与D 、E 两点有关， 但它们所在的三角形之间因为不是同类三角形，所以 关系不明显，由于条件F 是DE 的中点，如何利用这个 中点条件，把不同类三角形转化为同类三角形式问题的关键。
由已知AB=AC,联系到当过D 点或E 点作平行线，就可以形成新 的图形关系——构成等腰三角形，也就是相当于先把BD 或CE 移动一下位置，从而使问题得解。
证明：证法一：过点D 作DG ∥AC,交BC 于点G （如上图） ∴∠DGB=∠ACB, ∠DGF=∠FCE ∵AB=AC ∴∠B=∠ACB ∴∠B=∠DGB ∴BD=DG ∵F 是DE 的中点 ∴DF=EF在△DF G 和△DEFC 中，DFG= EFC DGF= FCE DF=EF ∠∠⎧⎪∠∠⎨⎪⎩∴△DF G ≌EFC∴DG=CE ∴BD=CE证法二：如图，在AC 上取一点H,使CH=CE,连接DH ∵F 是DE 的中点∴CF 是△EDH 的中位线 ∴DH ∥BC ∴∠ADH=∠B, ∠AHD=∠BCA ∵AB=AC ∴∠B=∠BCA ∴∠ADH=∠AHD ∴AD=AH ∴AB-AD=AC-AH ∴BD=HC ∴BD=CE说明：本题信息特征是“线段中点”。
也可以过E 作EM ∥BC,交AB 延长线于点G ，仿照证法二求解。
例4．如图，已知AB ∥CD ，AE 平分∠BAD ，且E 是BC 的中点求证：AD=AB+CD证法一：延长AE 交DC 延长线于F ∵AB ∥CD ∴∠BAE=∠F, ∠B=∠ECF ∵E 是BC 的中点 ∴BE=CE 在△ABE 和△CEF 中BAE= FB= ECF BE=CE ∠∠⎧⎪∠∠⎨⎪⎩∴△ABE ≌△CEF ∴AB=CF∵AE 平分∠ABD ∴∠BAE=∠DAE ∴∠DAE=∠F ∴AD=DF ∵DF=DC+CF CF=AB ∴AD=AB+DC证法二：取AD 中点F ，连接EF ∵AB ∥CD ，E 是BC 的中点 ∴EF 是梯形ABCD 的中位线∴EF ∥AB , EF=12（AB+CD ） ∴∠BAE=∠AEF ∵AE 平分∠BAD ∴∠BAE=∠FAE ∴∠AEF=∠FAE ∴AF=EF ∵AF=DF∴EF=AF=FD=12AD ∴12 (AB+CD)= 12AD∴AD=AB+CD三．角平分线问题已知条件中含有角平分线信息称为角平分线问题。
常用的辅助线有两种：1. 以角平分线所在直线为对称轴，构造全等三角形，如图一、二所示。
2. 由角平分线上的点向角的两边做垂线，构造全等三角形，如图二所示。
图一 图二 图三[例题解析]例5．如图（1），OP 是∠MON 的平分线，请你利用图形画一对以OP 所在直线为对称轴的全等三A BCEFDA BCEF角形。
请你参考这个全等三角形的方法，解答下列问题。
（1） 如图（2），在△ABC 中，∠ACB 是直角，∠B=60°,AD 、CE 分别是∠BAC 、∠BCA 的平分线，AD 、CE 相交于点F,请你判断并写出EF 与FD 之间的数量关系。
（2） 如图（3），在△ABC 中，如果∠ACB 不是直角，而（1）中的其他条件不变，请问，你在（1）中所得的结论是否仍然成立？若成立，请证明；若不成立，请说明理由。
分析：本题属于学习性题型。
这类题型的特点是描述一种方法，要求学生按照指定的方法解题。
指定方法是角平分问题的“翻折法”得全等形。
解：（1）EF=FD （2）答：（1）结论EF=FD 仍然成立理由：如图（3），在AC 上截取AG=AE,连接FG 在△AEF 和△AGF 中，AE=AG EAF= FAG AF=AF ⎧⎪∠∠⎨⎪⎩∴△AEF ≌△AGF∴EF=GF, ∠EFA=∠GFA由∠B=60°，AD 、CE 分别是∠BAC ∠BCA 的平分线 可得∠FAG+∠FCA=60° ∴∠EFA=∠GFA=∠DFC=60° ∴∠GFC=60°在△CFG 和△CFD 中GFC= DFC CF=CF DCE= ACE ∠∠⎧⎪⎨⎪∠∠⎩∴△CFG ≌△CFD ∴FG=FD 又因为EF=GF ∴EF=FD说明：学习性问题是新课程下的新型题，意在考查学生现场学习能力和自学能力。
抛开本题要求从角平分线的角度想，本题也可以利用角平分线的性质“角平分线上的点到角的两边的距离相等”达到求解的目的。
解法二：（2）答（1）中的结论EF=FD 仍然成立。
理由：作FG ⊥AB 于G,FH ⊥AC 于H,FM ⊥BC 于M ∵∠EAD=∠DAC ∴FG=FH∵∠ACE=∠BCE ∴FH=FG ∵∠B=60° ∴∠DAC+∠ACE=60° ∴∠EFD=∠AFC=180°- 60°=120°在四边形BEFD 中 ∠BEF+∠BDF=180°∵∠BDF+∠FDC=180° ∴∠FDC =∠BEF 在△EFG 和△DFM 中FDC = BEF EGF= DMF=90FG=FM ∠∠⎧⎪∠∠⎨⎪⎩∴EFG ≌△DFM ∴EF=DF四、线段的和差问题已知条件或所求问题中含有a+b=c 或a=c-b ，称为线段的和差问题，常用的辅助线有两种：1. 短延长：若AB=a,则延长AB 到M,使BM=b,然后证明AM=c ；2. 长截短：若AB=c,则在线段AB 上截取AM=a,然后证明MB=b 。
[例题解析]例6 如图，在△ABC 中，AB=AC,点P 是边BC 上一点，PD ⊥AB 于D,PE ⊥AC 于E,CM ⊥AB 于M,试探究线段PD 、PE 、CM 的数量关系，并说明理由。
分析：判断三条线断的关系，一般是指两较短线段的和与较长线段的大小关系，通过测量猜想PD+PE=CM.分析：在CM 上截取MQ=PD ，得□PQMD,再证明CQ=PE 答：PD+PE=CM证法一：在CM 上截取MQ=PD ，连接PQ. ∵CM ⊥AB 于M, PD ⊥AB 于D ∴∠CMB=∠PDB=90° ∴CM ∥DP∴四边形PQMD 为平行四边形 ∴PQ ∥AB∴∠CQP=∠CMB=90°∠QPC=∠B∵AB=AC ∴∠B=∠ECP ∴∠QPC=∠ECP ∵PE ⊥AC 于E ∴∠PEC=90°在△PQC 和△PEC 中PQC= PEC QPC= ECP PC=PC ∠∠⎧⎪∠∠⎨⎪⎩∴△PQC ≌△PEC ∴QC=PE ∵MQ=PD ∴MQ+QC=PD+PE ∴PD+PE=CM分析2：延长DF 到N 使DN=CM,连接CN,得平行四边形再证明PN=PE 证法2：延长DF 到N ，使DN=CM ，连接CN同证法一得平行四边形DNCM ，及△PNC ≌△PEC ∴PN=PE ∴PD+PE=CM分析3：本题中含有AB=AC 及三条垂线段PD 、DE 、CM ， 且PABPAC ABC SS S +=V V V ，所以可以用面积法求解。