(完整版)初三上专题四点共圆
九年级数学四点共圆例题讲解

九年级数学四点共圆例题讲解知识点、重点、难点四点共圆是圆的基本内容,它广泛应用于解与圆有关的问题.与圆有关的问题变化多,解法灵活,综合性强,题型广泛,因而历来是数学竞赛的热点内容。
在解题中,如果图形中蕴含着某四点在同一个圆上,或根据需要作出辅助圆使四点共圆,利用圆的有关性质定理,则会使复杂问题变得简单,从而使问题得到解决。
因此,掌握四点共圆的方法很重要.判定四点共圆最基本的方法是圆的定义:如果A、B、C、D四个点到定点O的距离相等,即OA=OB=OC=OD,那么A、B、C、D四点共圆.由此,我们立即可以得出1。
如果两个直角三角形具有公共斜边,那么这两个直角三角形的四个顶点共圆。
将上述判定推广到一般情况,得:2。
如果四边形的对角互补,那么这个四边形的四个顶点共圆。
3.如果四边形的外角等于它的内对角,那么这个四边形的四个顶点共圆。
4。
如果两个三角形有公共底边,且在公共底边同侧又有相等的顶角,那么这两个三角形的四个顶点共圆。
运用这些判定四点共圆的方法,立即可以推出:正方形、矩形、等腰梯形的四个顶点共圆。
其实,在与圆有关的定理中,一些定理的逆定理也是成立的,它们为我们提供了另一些证明四点共圆的方法.这就是:1.相交弦定理的逆定理:若两线段AB和CD相交于E,且AE·EB=CE·ED,则A、B、C、D四点共圆。
2.割线定理的逆定理:若相交于点P的两线段PB、PD上各有一点A、C,且PA·PB =PC·PD,则A、B、C、D四点共圆。
3。
托勒密定理的逆定理:若四边形ABCD中,AB·CD+BC·DA=AC·BD,则ABCD是圆内接四边形。
另外,证多点共圆往往是以四点共圆为基础实现的一般可先证其中四点共圆,然后证其余各点均在这个圆上,或者证其中某些点个个共圆,然后判断这些圆实际是同一个圆。
例题精讲例1:如图,P为△ABC内一点,D、E、F分别在BC、CA、AB上。
初三 关于圆 四点共圆
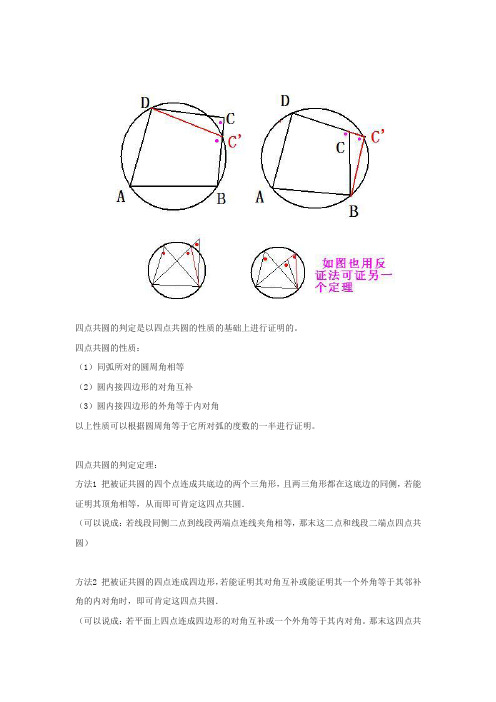
四点共圆的判定是以四点共圆的性质的基础上进行证明的。
四点共圆的性质:
(1)同弧所对的圆周角相等
(2)圆内接四边形的对角互补
(3)圆内接四边形的外角等于内对角
以上性质可以根据圆周角等于它所对弧的度数的一半进行证明。
四点共圆的判定定理:
方法1 把被证共圆的四个点连成共底边的两个三角形,且两三角形都在这底边的同侧,若能证明其顶角相等,从而即可肯定这四点共圆.
(可以说成:若线段同侧二点到线段两端点连线夹角相等,那末这二点和线段二端点四点共圆)
方法2 把被证共圆的四点连成四边形,若能证明其对角互补或能证明其一个外角等于其邻补角的内对角时,即可肯定这四点共圆.
(可以说成:若平面上四点连成四边形的对角互补或一个外角等于其内对角。
那末这四点共
圆)
我们可都可以用数学中的一种方法;反证法开进行证明。
现就“若平面上四点连成四边形的对角互补。
那末这四点共圆”证明如下(其它画个证明图如后)
已知:四边形ABCD中,∠A+∠C=180°
求证:四边形ABCD内接于一个圆(A,B,C,D四点共圆)
证明:用反证法
过A,B,D作圆O,假设C不在圆O上,刚C在圆外或圆内,
若C在圆外,设BC交圆O于C’,连结DC’,根据圆内接四边形的性质得∠A+∠DC’B=180°,∵∠A+∠C=180°∴∠DC’B=∠C
这与三角形外角定理矛盾,故C不可能在圆外。
类似地可证C不可能在圆内。
∴C在圆O上,也即A,B,C,D四点共圆。
24.24专题6:四点共圆问题

24.24专题6:四点共圆一.【知识要点】 四点共圆模型:(1)若四个点到一个定点的距离相等,则这四个点共圆(如图1);(2)共斜边的两个直角三角形,四个顶点共圆(如图2,3);(3)对角互补的四边形四个顶点共圆(如图4);(4)共底边且在同侧的两个三角形顶角相等(如图5)。
二.【经典例题】1.已知OA=OB=OC=2,且∠ACB=45°,则AB 的长为( ) A.2 B.3 C.22 D.322.如图所示,矩形ABCD 的边AB=3,Rt △BEF 的直角顶点E 在对角线AC 上,另一顶点F 在边CD 上,若△BEF 的一个锐角为30°,则BC 的长是( ) A.3 B.33 C.333或 D.63.如图,在Rt△ABC中,∠ACB=90°,AC=BC,点D在AB下方,∠BDC=45°,求证:AD⊥BD.4.如图,四边形ABCD是正方形,E是BC上一点,AE⊥EF交∠BCD的外角平分线于F,求证:AE=EF.5.如图,平面直角坐标系中,将含30°的三角尺的直角顶点C落在第二象限。
其斜边两端点A、B分别落在x轴、y轴上,且AB=12厘米,(1)若OB=6厘米,①求点C的坐标;②若点A向右滑动的距离与点B向上滑动的距离相等,求滑动的距离. (2)点C与点O的距离的最大值是多少厘米?6.(绵阳2015年第25题本题满分14分)如图,在边长为2的正方形ABCD中,G是AD延长线时的一点,且DG = AD,动点M从A点出发,以每秒1个单位的速度沿着A→C→G的路线向G点匀速运动(M不与A,G重合),设运动时间为t秒,连接BM并延长AG于N.(1)是否存在点M,使△ABM为等腰三角形?若存在,分析点M的位置;若不存在,请说明理由;(2)当点N在AD边上时,若BN⊥HN,NH交∠CDG的平分线于H,求证:BN = HN;(3)过点M分别作AB,AD的垂线,垂足分别为E,F,矩形AEMF与△ACG重叠部分的面积为S,求S的最大值.7.如图,菱形ABCD中,两条对角线AC,BD相交于点O,点E和点F分别是BC和CD上一动点,且∠EOF+∠BCD=180°,∠ABC=60°,连接EF.(1)求△OEF是什么特殊的三角形?(2)若AB=2,求CE+CF的长;三.【题库】【A】1.如图,在Rt△ABC中,∠ACB=90°,AC=BC,点D在AB下方,AD⊥BD,求∠BDC的度数.2.如图,在Rt△ABC中,∠ACB=90°,AC=BC,点D在AB上方,AD⊥BD,求∠BDC的度数.3.如图,在Rt△ABC中,∠ACB=90°,AC=BC,点D在AB上方,∠BDC=45°,求证:AD⊥BD.4.如图,在Rt△ABC中,∠ACB=90°,AC=BC,点D在AB上方,∠ADC=135°,求证:AD⊥BD.5.在Rt△ABC中,∠ACB=90°,AC=BC,点E为△ABC外一点,且∠CEA=45°.求证:AE⊥BE.6.如图所示,四边形ABCD中,DC∥AB,BC=1,AB=AC=AD=2.则BD的长为()A.B.C.D.【B】1.如图放置的两个正方形,大正方形ABCD边长为a,小正方形CEFG边长为b(a>b),M 在BC边上,且BM=b,连接AM,MF,MF交CG于点P,将△ABM绕点A旋转至△ADN,将△MEF绕点F旋转至△NGF,给出以下五个结论:①∠MAD=∠AND;②CP=a﹣;③△ABM≌△NGF;=a2+b2;④S四边形AMFN⑤A,M,P,D四点共圆,其中正确的序号为.【C】1.将线段AB绕点A逆时针旋转60°得到线段AC,继续旋转α(0°<α<120°)得到线段AD,连接CD.(1)连接BD,①如图1,若α=80°,则∠BDC的度数为;②在第二次旋转过程中,请探究∠BDC的大小是否改变.若不变,求出∠BDC的度数;若改变,请说明理由.(2)如图2,以AB为斜边作直角三角形ABE,使得∠B=∠ACD,连接CE,DE.若∠CED=90°,求α的值.【D】1.如图,C,D是以AB为直径的半圆上的两点,∠AOC=40°,P在直径AB上,且∠OCP=∠ODP=10°,则∠BOD的度数为().A.20°B.30°C.25°D.15°2.正方形ABCD 的中心为O ,面积为1989cm 2.P 为正方形内一点,且∠OPB =45°,P A :PB =5:14.则PB 的长为( ). A.42cm B.40cm C.35cm D.50cm3.如图,在△ABC 中,∠C =90°,点D 是BC 边上一动点,过点B 作BE ⊥AD 交AD 的延长线于E .若AC =6,BC =8,则的最大值为( )A .B .C. D .4.如图,在菱形ABCD 中,点P 是BC 边上一动点,P 和C 不重合,连接AP ,AP 的垂直平分线交BD 于点G ,交AP 于点E ,在P 点由B 点到C 点的运动过程中,∠APG 的大小变化情况是( )A .变大B .先变大后变小C .先变小后变大D .不变5. 如图,ABC ∆中,45B ∠=︒,75C ∠=︒,4AB =,D 为BC 上一动点,过点D 作DE AC ⊥于点E ,DF AB ⊥于点F ,连接EF ,则EF 的最小值为 ( ) A .3B .2C .5D .6。
数学人教版九年级上册24.探究四点共圆的条件

探究四点共圆阜阳开发区一初王丽 2017/5/1一、内容和内容解析本节内容是探究四点共圆的条件。
四点共圆是在学生学习了经过一个点的圆、经过两个点的圆、经过不在同一直线上三个点的圆、三角形与圆的关系、圆内接四边形后,对经过任意三点都不在同一直线上的四点共圆条件的探究。
圆内接四边形对角互补,相应地,对角互补的四边形的四个顶点共圆。
在四点共圆条件的探究过程中,通过对特殊的四边形(矩形、等腰梯形)、有公共斜边的两个直角三角形的四个顶点组成的四边形等四边形的探究,发现一般的规律(过对角互补的四边形的四个顶点能做一个圆),体现了特殊到一般的思想。
同时在研究过程中类比将四边形转化为三角形来研究,从三点共圆入手探究四点共圆的条件,体现了转化的思想。
另外,学生经历探究四点共圆的条件这一思想活动的全过程,在“做”的过程和“思考”的过程中有利于数学活动经验的积累。
二、学情分析学生在发现问题的阶段可能会受到任意一个三角形的三个顶点做一个圆的影响,去判断第四个顶点是否在这个圆上,解决这一问题的关键是引导学生从特殊的四边形出发,从特殊到一般的探究问题。
通过画图、观察、测量分析矩形、等腰梯形、有公共斜边的两个直角三角形的四个顶点共圆与四边形的边长无关,由此联想圆内接四边形对角互补,获得猜想。
另外,猜想的证明要用到反证法,学生可能不知如何入手,而且猜想的证明对学生来说是难点。
三、教学目标:(1)理解过某个四边形的四个顶点能作一个圆的条件。
(2)通过四点共圆的条件的探究和猜想的证明,体会由特殊到一般转化的数学思想,积累数学活动的经验。
四、教学重难点:重点:四点共圆条件的探究。
难点:对角互补的四边形四个顶点共圆的证明。
五、教学过程:I、创设情境、引入新课同学们,我们的家乡阜阳是有着悠久历史的地方,如果给我们一天的时间参加阜阳一日游活动,你会选择哪里呢?那么,今天老师就带领大家一起参观阜阳生态园。
问题1:某市公园需要经过A、B、C三个旅游景点建一个圆形快车道,如图,假如我们把A、B、C三个旅游景点抽象成点,你能设计出这个圆形轨道吗?设计意图:由学生熟知的参观阜阳生态园入手,让学生去设计不在同一直线上的三点所在的圆,即能复习前面的三点共圆知识,又能为后面的猜想做铺垫。
浙教版九年级上册第三章圆的基本性质 专题:四点共圆

专题:四点共圆一.选择题1.如图,在四边形ABCD中,AC、BD为对角线,点M、E、N、F分别为AD、AB、BC、CD边的中点,下列说法:①当AC=BD时,M、E、N、F四点共圆.②当AC⊥BD时,M、E、N、F四点共圆.③当AC=BD且AC⊥BD时,M、E、N、F四点共圆.其中正确的是()A. ①②B. ①③C. ②③D. ①②③2. 如图,四边形ABCD内接于半圆O,已知∠ADC=140°,则∠AOC的大小是()A. 40°B. 60°C. 70°D. 80°3. 如图,已知四边形ABEC内接于⊙O,点D在AC的延长线上,CE平分∠BCD交⊙O于点E,则下列结论中一定正确的是()A. AB=AEB. AB=BEC. AE=BED. AB=AC4. 如图,以△ABC的一边AB为直径的圆交AC边于D,交BC边于E,连接DE,BD与AE交于点F.则sin∠CAE的值为()A.B.C.D.5. 如图,AB是⊙O的直径,C,D在⊙O上,且BC=CD,过点C作CE⊥AD,交AD延长线于E,交AB延长线于F点.若AB=4ED,则cos∠ABC的值是()A. B. C. D.6. 如图,在△ABC中,∠B=75°,∠C=45°,BC=6-2,点P是BC上一动点,PE⊥AB于E,PD⊥AC于D.无论P的位置如何变化,线段DE的最小值为()A. 3-3B.C. 4-6D. 27. 如图,四边形ABCD是⊙O的内接四边形,AB:BC=2:3,AD=DC,点P在对角线BD上,已知△ABP的面积等于6cm2,则△BCP的面积等于()cm2.A. 8B. 9C. 10D. 128.四边形ABCD内接于圆,且CD=1,AB=√2,BC=2,∠ABC=45°,则四边形ABCD的面积是()A. 3+√33B. √3+2√24C. √3+2√23D. 3+√349. 在圆内接四边形ABCD中,∠BAD、∠ADC的角平分线交于点E,过E作直线MN平行于BC,与AB、CD交于M、N,则总有MN=()A. BM+DNB. AM+CNC. BM+CND. AM+DN10. 如图,已知∠A的平分线分别与边BC、△ABC的外接圆交于点D、M,过D任作一条与直线BC不重合的直线l,直线l分别与直线MB、MC交于点P、Q,下列判断错误的是()A. 无论直线l的位置如何,总有直线PM与△ABD的外接圆相切B. 无论直线l的位置如何,总有∠PAQ>∠BACC. 直线l选取适当的位置,可使A、P、M、Q四点共圆D. 直线l选取适当的位置,可使S△APQ<S△ABC11.如图,一副直角三角板满足∠ACB=∠EDF=90°,AC=BC,AB=DF,∠EFD=30°,将三角板DEF的直角顶点D放置于三角板ABC的斜边AB上,再将三角板DEF绕点D旋转,并使边DE 与边AC交于点M,边DF与边BC于点N.当∠EDF在△ABC内绕顶点D旋转时有以下结论:①点C,M,D,N四点共圆;②连接CD,若AD=DB,则△ADM∽△CDN;③若AD=DB,则DN•CM=BN•DM;④若AD=DB,则CM+CN=AD;⑤若DB=2AD,AB=6,则2≤S△DMN≤4.其中正确结论的个数是()A. 2B. 3C. 4D. 5二.填空题12. 如图,已知等腰三角形ABC,∠ACB=120°且AC=BC=4,在平面内任作∠APB=60°,BP最大值为_____.13. 如图,ABCD是⊙O的内接四边形,AB是⊙O的直径.过点D的切线交BA的延长线于点E.若∠ADE=25°,则∠C= ______ .14. 如图,四边形ABCD中,AB=AC=AD,若∠CAD=76°,则∠CBD=______度.15. 如图,四边形ABCD内接于⊙O,AC平分∠BAD交BD于点E,⊙O的半径为4,∠BAD=60°,∠BCA=15°,则AE=______.16. 如图,ABCD、CEFG是正方形,E在CD上,且BE平分∠DBC,O是BD中点,直线BE、DG交于H.BD,AH交于M,连接OH,则OH=______,BM=______.17. 如图,在⊙O内接四边形ABCD中,∠ABC=60°,AB=BC=6,E、F分别是AD、CD的中点,连接BE、BF、EF.若四边形ABCD的面积为11,则△BEF的面积为____.18. 如图,正方形ABCD的中心为O,面积为1 989 ,P为正方形内一点,且∠OPB=45°,PA:PB=5:14,则PB= ______ .19. 已知△ABC为等腰直角三角形,∠C为直角,延长CA至D,以AD为直径作圆,连BD与圆O交于点E,连CE,CE的延长线交圆O于另一点F,那么的值等于.20. 如图,在等腰△ABC中,∠ABC=90°,点D为BC的中点,点E在AC边上,以DE为腰作等腰Rt△DEF,连接CF,BF.若CE=1,△CDF的面积为7.5,则BF的长为____.三.解答题21. (1)已知:如图1,△ABC为等边三角形,CE平分△ABC的外角∠ACM,点在BC上,连接AD、DE,如果∠ADE=60°,求证:AD=DE.(2)如果△ABC为任意三角形,且∠ACB=60°,其他条件不变,这个结论还成立吗?说明你的理由.22. 如图,已知点P是⊙O外一点,PS,PT是⊙O的两条切线,过点P作⊙O的割线PAB,交⊙O于A,B两点,并交ST于点C.求证:.23. 如图,A、B、C、D四点共圆,AB与DC相交于点E,AD与BC交于点F,∠AED的平分线EX与∠AFB的平分线FX交于点X,M、N分别是AC与BD的中点,求证:(1)FX⊥EX;(2)FX、EX分别平分∠MFN与∠MEN.24. 如图,四边形ABCD是⊙O的内接四边形,AD的延长线与BC的延长线相交于点E,DC=DE.(1) 求证:∠A=∠AEB;(2) 如果DC⊥OE,求证:△ABE是等边三角形.25. 如图,已知四边形ABCD内接于⊙O,∠D=90°,P为上一动点(不与点C,D重合).(1)若∠BPC=30°,BC=3,求⊙O的半径;(2)若∠A=90°,=.求证:PB-PD=PC.26. 如图,BD,CE是△ABC的两条高,F和G分别是DE和BC的中点,O是△ABC的外心.求证:AO∥FG.27. 如图,在锐角三角形ABC中,AB上的高CE与AC上的高BD相交于点H,以DE为直径的圆分别交AB、AC于F、G两点,FG与AH相交于点K,已知BC=25,BD=20,BE=7,求AK 的长.28. 如图,O是Rt△ABC斜边AB的中点,CH⊥AB于H,延长CH至D,使得CH=DH,F为CO上任意一点,过B作BE⊥AF于E,连接DE交BC于G.(1)求证:∠CAF=∠CDE;(2)求证:CF=GF.29. 已知:AB是⊙O的直径,BC是⊙O的切线,AC交⊙O于G,∠ACB的平分线交⊙O于D,E在AC上,BE交AD于F,∠CBD=∠EBD.求证:DF=DG.30. 如图,AB是半圆圆O的直径,C是弧AB的中点,M是弦AC的中点,CH⊥BM,垂足为H.求证:CH2=AH•OH.31. 如图,在△ABC中,已知AD⊥BC,BE⊥AC,AD与BE相交于点H,P为边AB的中点,过点C作CQ⊥PH,垂足为Q,求证:PE2=PH•PQ.参考答案1. C.2. D.3.C.4. D.5.A.6. B.7. B.8. D.9.D.10.C.11.D.12. 8.13. 115°14. 38°.15.2.16. ,AB.17. ;18.42cm.19..20. .21. (1)证明:如图1中,∵△ABC是等边三角形,∴∠ACB=60°,∠ACM=120°,∴CE平分∠ACM,∴∠ACE=∠ECM=60°,∵∠ADE=60°,∠ACE=60°,∴∠ADE=∠ACE,∴A、D、C、E四点共圆,∴∠ECM=∠DAE=60°,∠AED=∠ACB=60°,∴∠DAE=∠DEA,∴AD=DE.(2)结论成立.DA=DE.理由:如图2中,连接AE,∵∠ACB=60°,∴∠ACM=180°-∠ACB=120°,∴CE平分∠ACM,∴∠ACE=∠ECM=60°,∵∠ADE=60°,∠ACE=60°,∴∠ADE=∠ACE,∴A、D、C、E四点共圆,∴∠ECM=∠DAE=60°,∠AED=∠ACB=60°,∴∠DAE=∠DEA,∴AD=DE.22.证明:连PO交ST于点D,则PO⊥ST; 连SO,作OE⊥PB于E,则E为AB中点,于是因为C,E,O,D四点共圆,所以PC•PE=PD•PO又因为Rt△SPD∽Rt△OPS所以即PS 2=PD•PO而由切割线定理知PS 2=PA•PB所以即23. 证明:(1)连接AX.由图知:∠FDC是△ACD的一个外角,则有:∠FDC=∠FAE+∠AED;①同理,得:∠EBC=∠FAE+∠AFB;②∵四边形ABCD是圆的内接四边形,∴∠FDC=∠ABC.又∵∠ABC+∠EBC=180°,即:∠FDC+∠EBC=180°,③①+②,得:∠FDC+∠EBC=2∠FAE+(∠AED+∠AFB),由③,得:2∠FAE+(∠AED+∠AFB)=180°;∵FX、EX分别是∠AFB、∠AED的角平分线,∴∠AFB=2∠AFX,∠AED=2∠AEX,代入上式得:2∠FAE+2(∠AFX+∠AEX)=180°,即∠FAE+∠AFX+∠AEX=180°.由三角形的外角性质知:∠FXE=∠FAE+∠FAX+∠EAX,故FXE=90°,即FX⊥EX.(2)连接MF、FN,ME、NE.∵∠FAC=∠FBD,∠DFB=∠CFA,∴△FCA∽△FDB,∴.∵AC=2AM,BD=2BN,∴.又∵∠FAM=∠FBN,∴△FAM∽△FBNA,得∠AFM=∠BFN.又∵∠AFX=∠BFX,∴∠AFX-∠AFM=∠BFX-∠BFN,即∠MFX=∠NFX.同理可证得∠NEX=∠MEX,故FX、EX分别平分∠MFN与∠MEN.24. (1)证明:∵四边形ABCD是⊙O的内接四边形,∴∠A=∠DCE,∵DC=DE,∴∠DCE=∠DEC,∴∠A=∠AEB(2)证明:∵DC⊥OE,∴DF=CF,∴OE是CD的垂直平分线,∴ED=EC,又DE=DC,∴△DEC为等边三角形,∴∠AEB=60°,又∠A=∠AEB,∴△ABE是等边三角形.25. 解:(1)连接AC.∵∠D=90°,∴AC是⊙O的直径,∴∠ABC=90°.∵∠BAC=∠BPC=30°,∴AC=2BC=6,所以⊙O的半径为3;(2)∵∠BAD=90°,∴∠BCD=90°.∵AC为⊙O直径,∴∠ADC=∠ABC=90°,∴四边形ABCD为矩形.∵=,∴AB=AD,∴矩形ABCD为正方形,∴BC=DC.在BP上截取BE=DP,连接CE,DP.∵BE=DP,∠CBP=∠PDC,BC=DC,∴△BCE≌△DCP,∴∠BCE=∠DCP,PC=CE,又∵∠BCE+∠ECD=∠BCD=90°,∴∠DCP+∠ECD=∠ECP=90°,∴△CPE为等腰直角三角形,∴PE=PC,∴PB-BE=PB-PD=PE=PC.26. 【解答】证明:如图,连接GD和GE.∵∠BDC=∠BEC=90°,BG=GC,∴,又∵DF=EF,∴GF⊥DE,延长OA交DE于H.∵∠BDC=∠BEC=90°∴B,C,E,D四点共圆,,即,又∵OA=OB,∴,∠EAH+∠AEH=90°,∴AD⊥DE,即OA⊥DE∴AO∥FG.27. 解:延长AH交BC于P,连接DF,如图.由题知∠ADB=∠CDB=∠CEB=∠AEC=90°,∵BC=25,BD=20,BE=7,∴CD=15,CE=24.又∵∠DAB=∠EAC,∠ADB=∠AEC,∴△ADB∽△AEC,∴==,①由①得:,解得,∵∠AEC=90°,AD=CD=15,∴DE=AC=15.∵点F在以DE为直径的圆上,∴∠DFE=90°,∵DA=DE,∴AF=EF=AE=9.∵∠CDB=∠CEB=90°,∴D、E、B、C四点共圆,∴∠ADE=∠ABC.∵G、F、E、D四点共圆,∴∠AFG=∠ADE,∴∠AFG=∠ABC,∴GF∥BC.∴=.②∵H是△ABC的垂心,∴AP⊥BC,∴S△ABC=AB•CE=BC•AP,∵BA=BC=25,∴AP=CE=24,由②得AK===8.64.28. 证明:(1)连接BD,∵△ABC是Rt△,BE⊥AF∴∠BEA=∠ACB=90°,∴A,B,C,E四点共圆,且AB是此圆直径, 又∵CH⊥AB,CH=DH,∴D在此圆上,∴A,B,C,D,E五点共圆,∴∠CAF=∠CDE;(2)由(1)得:∠CDB=∠CAO,∠BCD=∠ACO,∴△AOC∽△DCB,同理可证:△AOF∽△DBG,△ACF∽△DCG,∴= , = , = ,∴= ,∴= ,∴GF∥BO,又∵O是AB的中点,∴CF=GF.29. 证明:∵CB是⊙O的切线,∴∠CBD=∠BAD.∵BD平分∠EBC,∴∠CBD=∠EBD.Rt△ABD中,∠EBD+∠BFD=90°,∠BAD+∠ABD=90°,∴∠BFD=∠ABD.又∵四边形AGDB内接于⊙O,∴∠CGD=∠ABD=∠BFD.过D作DM⊥BE于M,DN⊥AC于N,∵点D是∠EBC和∠ECB角平分线的交点,∴点D是△EBC的内心,则DM=DN.又∵∠DMF=∠DNG=90°,∠BFD=∠CGD,∴△DMF≌△DNG.∴DF=DG.30. 解:连接OC、BC,∵C是弧AB的中点,M是弦AC的中点,∴∠BOC=∠BHC=90°,则点O、B、C、H四点共圆,∴∠OHB=∠OCB=45°,∵∠BCM=90°,CH⊥BM,M为AC的中点,∴AM2=CM2=MH•MB,即=,∴△AMH∽△BMA,则∠MAH=∠MBA,∠AHN=∠BAM=45°,∴∠AHM=∠BHO,∴△AMH∽△BOH,∴=,则AH•OH=MH•BH,∵CH2=MH•HB,∴CH2=AH•OH.31.证明:连接CH并延长交AB于K,连接EQ,∵AD⊥BC,BE⊥AC,∴H是△ABC的垂心,∴CK⊥AB,∵∠CEH=∠BKH,∠EHC=∠KHB,∴∠3=∠4,∵∠AEB=Rt∠,P是AB的中点,∴EP=BP,∴∠1=∠4,∴∠1=∠3,∵∠CQH=∠CEH=Rt∠,∴C、H、E、Q四点共圆,∴∠2=∠3,∴∠1=∠2,∵∠EPH=∠QPE,∴△EPH∽△QPE,∴,∴PE2=PH•PQ.。
初三:第14课 四点共圆

第14课 四点共圆一、基本结论与方法:判断四点共圆的方法有:1.到定点等距离的几个点在同一个圆上;2.同斜边的直角三角形的各顶点共圆;3.同底同侧张角相等的三角形的各顶点共圆;4、如果一个四边形的一组对角互补,那么它的四个顶点共圆;5、如果四边形的一个外角等于它的内对角,则它的四个顶点共圆;6、四边形的对角线相交于点P ,且PA•PC=PB•PD,那么四个顶点共圆;7、四边形ABCD 的一组对边AB 、DC 的延长线交于点P ,若PA•PB=PC•PD, 那么四个顶点共圆.托勒密定理:圆内接四边形的对边之积的和,等于对角线之积。
即:如图,四边形ABCD 内接于圆,求证:BD AC BC AD CD AB ⋅=⋅+⋅.DB二、例题与习题例1、如图,ABCD 是等腰梯形,求证:BD 2=AB•CD+BC 2.CD 例2、△ABC 中,∠A:∠B:∠C=1:2:4,:求证:BC AC AB 111=+A D例3、在边长为1的正七边形中,对角线AD=a,BG=b,求证:22)()(ab b a b a =-+.C 例4、两圆相交于A 、B,P 是BA 延长线上一点,PCD 、PEF 分别是两圆的割线,求证:C 、D 、E 、F 四点共圆。
F例5、由圆外定直线上任意点,引圆的两条切线,求证:两切点的连线必经过某定点。
CA例6、点P 是正三角形外接圆的劣弧AB 上一点,连接PC 交AB 于D ,求证:(1)PA+PB=PC;(2)111PA PBPD +=.例7、P为△ABC内一点,D、E、F分别在三角形的边上,已知P、D、C、E四点共圆,P、E、A、F四点共圆,求证:B、D、P、F四点共圆。
例8、设凸四边形ABCD的对角线互相垂直,垂足为E,证明:点E关于AB、BC、CD、DA 的对称点也共圆。
A例9、两个圆彼此相交,从它们的对称中心引出两条射线交圆周于不在同一直线上的四个点,证明:这四个点共圆。
例10、梯形ABCD的两条对角线相交于点K,分别以梯形的两腰围直径作圆,点K位于两圆之外,证明:由K向两圆所作的切线长度相等。
初中四点共圆的判定定理

初中四点共圆的判定定理初中数学里有个很有趣的定理,叫做“四点共圆的判定定理”。
听起来是不是有点高大上?其实说白了就是:四个点如果能在同一个圆上,那它们之间的关系可是很特别的哦。
想象一下,四个好朋友,围成一圈,聊聊天,玩玩耍,生活多美好。
要是这四个点真能共圆,那可就意味着它们之间的角度关系得特别好,这个可不是随便说说的。
我们得聊聊什么是共圆。
简单来说,四个点能在一个圆上,就是说这四个点到圆心的距离是一样的。
这就像我们在生活中,有些朋友总是能聚在一起,无论走到哪里,关系都特别紧密。
好比说,吃饭时大家一起点的菜,总是能让每个人满意,恰到好处,圆满得很。
这就是共圆的魅力呀!怎么判断这四个点能不能共圆呢?其实很简单,大家只需要掌握一个小窍门。
记住了,四个点要共圆,就得看它们的对角线交点,看看这条线的乘积是否相等。
听上去可能有点复杂,但实际上就像打麻将一样,运气来了,胡牌就是这么简单。
只要细心算一下,就能得出结论,谁和谁能一圈儿走到一起。
这不,就拿生活中的事来举个例子。
假如有四个小伙伴,分别是小明、小红、小刚和小丽。
他们一起去游乐场玩,特别开心。
小明跟小红的关系特别好,像那对小鸳鸯,真是让人羡慕。
但小刚和小丽却有点小隔阂,感觉总是打不到一块儿。
这时候,若是他们能找到一个共同的兴趣,或者一起完成个任务,哎呀,那关系可就像那四个共圆的点一样,慢慢就能拉近了。
再说了,四点共圆的定理在生活中还可以提醒我们,朋友之间的关系也是要保持平衡的。
就像一个圆,缺了哪一块儿都不行。
要是某个朋友总是偏心,那就容易让其他人感到不舒服。
想想,我们的生活不就是要和谐、圆满吗?和朋友之间的相处也是如此。
当然了,这个定理还有个特别的地方,涉及到圆的外接圆。
四个点要是共圆,那就得存在一个圆把它们都包住。
这个圆就像我们生活中的大怀抱,能容纳各种不同的朋友,让大家在一起,互相包容,互相理解。
这就像家人一样,无论发生什么,始终围绕在一起,心连心。
九年级数学四点共圆例题讲解

九年级数学四点共圆例题讲解知识点、重点、难点四点共圆是圆的基本内容,它广泛应用于解与圆有关的问题.与圆有关的问题变化多,解法灵活,综合性强,题型广泛,因而历来是数学竞赛的热点内容。
在解题中,如果图形中蕴含着某四点在同一个圆上,或根据需要作出辅助圆使四点共圆,利用圆的有关性质定理,则会使复杂问题变得简单,从而使问题得到解决。
因此,掌握四点共圆的方法很重要。
判定四点共圆最基本的方法是圆的定义:如果A、B、C、D四个点到定点O的距离相等,即OA=OB=OC=OD,那么A、B、C、D四点共圆.由此,我们立即可以得出1.如果两个直角三角形具有公共斜边,那么这两个直角三角形的四个顶点共圆。
将上述判定推广到一般情况,得:2.如果四边形的对角互补,那么这个四边形的四个顶点共圆。
3.如果四边形的外角等于它的内对角,那么这个四边形的四个顶点共圆。
4.如果两个三角形有公共底边,且在公共底边同侧又有相等的顶角,那么这两个三角形的四个顶点共圆。
运用这些判定四点共圆的方法,立即可以推出:正方形、矩形、等腰梯形的四个顶点共圆。
其实,在与圆有关的定理中,一些定理的逆定理也是成立的,它们为我们提供了另一些证明四点共圆的方法.这就是:1.相交弦定理的逆定理:若两线段AB和CD相交于E,且AE·EB=CE·ED,则A、B、C、D四点共圆。
2.割线定理的逆定理:若相交于点P的两线段PB、PD上各有一点A、C,且PA·PB =PC·PD,则A、B、C、D四点共圆。
3.托勒密定理的逆定理:若四边形ABCD中,AB·CD+BC·DA=AC·BD,则ABCD是圆内接四边形。
另外,证多点共圆往往是以四点共圆为基础实现的一般可先证其中四点共圆,然后证其余各点均在这个圆上,或者证其中某些点个个共圆,然后判断这些圆实际是同一个圆。
例题精讲例1:如图,P为△ABC内一点,D、E、F分别在BC、CA、AB上。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
四点共圆专题讲义
例1.如图,E、F、G、H分别是菱形ABCD各边的中点.求证:E、F、G、H四点共圆.
例2.(1)如图,在△ABC中,BD、CE是AC、AB上的高,∠A=60°.求证:ED=1
2 BC
(2)已知:点O是△ABC的外心,BE,CD是高.求证:AO⊥DE
例3.如图,在△ABC中,AD⊥BC,DE⊥AB,DF⊥AC.求证:B、E、F、C四点共圆.
总结:四点共圆的方法:
1.__________________________________________________________
3.__________________________________________________________
4.__________________________________________________________
例4.求证:圆内接四边形对边乘积的和等于对角线的乘积,即图中AB·CD+BC·AD=AC·BD.
练习1.在ABC
△中,BA BC BAC
∠α
==
,,M是AC的中点,P是线段BM上的动点,将线段P A绕点P顺时针旋转2α得到线段PQ.
(1)若60
α=︒且点P与点M重合(如图1),线段CQ的延长线交射线BM于点D,请补全图形,并写出∠CDB 的度数;
(2)在图2中,点P不与点B,M重合,线段CQ的延长线与射线BM交于点D,猜想∠CDB的大小(用含α的代数式表示),并加以证明;
(3)对于适当大小的α,当点P在线段BM上运动到某一位置(不与点B,M重合)时,能使得线段CQ的延长线与射线BM交于点D,且PQ=QD,请直接写出α的范围.
OA=OB=OC∠ADC=∠ABC=90°∠ACD=∠ABD=90°∠B+∠D=180°或∠
A+∠BCD=180°或∠
A=∠DCE
∠A=∠D或∠B=∠
C
练习2.在△ABC 中,∠A =30°,AB =2
3,将△ABC 绕点B 顺时针旋转α(0°<α<90°),得到△DBE ,其中点A 的对应点是点D ,点C 的对应点是点E ,AC 、DE 相交于点F ,连接BF .
(1)如图1,若α=60°,线段BA 绕点B 旋转α得到线段BD .请补全△DBE ,并直接写出∠AFB 的度数; (2)如图2,若α=90°,求∠AFB 的度数和BF 的长; (3)如图3,若旋转α(0°<α<90°),请直接写出∠AFB 的度数及BF 的长(用含α 的代数式表示).
练习3.已知,点P 是∠MON 的平分线上的一动点,射线P A 交射线OM 于点A ,将射线P A 绕点P 逆时针旋转交射线ON 于点B ,且使∠APB +∠MON =180°. (1)利用图1,求证:P A =PB ;
(2)如图2,若点C 是AB 与OP 的交点,当S △POB =3S △PCB 时,求PB 与PC 的比值; (3)若∠MON =60°,OB =2,射线AP 交ON 于点D ,且满足且∠PBD =∠ABO ,请借助图3补全图形,并求OP 长.
图3 D
C B F
图1 D 图2 F D C B
练习4.已知,在△ABC中,AB=AC.过A点的直线a从与边AC重合的位置开始绕点A按顺时针方向旋转角θ,直线a交BC边于点P(点P不与点B、点C重合),△BMN的边MN始终在直线a上(点M在点N的上方),且BM=BN,连接CN.
(1)当∠BAC=∠MBN=90°时,
①如图a,当θ=45°时,∠ANC的度数为________ ;
②如图b,当θ≠45°时,①中的结论是否发生变化?说明理由;
(2)如图c,当∠BAC=∠MBN≠90°时,请直接写出∠ANC与∠BAC之间的数量关系,不必证明.
练习5.已知:Rt△''
BA C
∠=∠BAC=30°,现将Rt△''
A BC绕
∠=∠ACB=90°,''
A C B
A BC
∠和Rt△ABC重合,''
点B按逆时针方向旋转角α(60°≤α≤90°),设旋转过程中射线''
C C和线段'
AA相交于点D,连接BD.
(1)当α=60°时,'A B过点C,如图1所示,判断BD和'
AA之间的位置关系,不必证明;
(2)当α=90°时,在图2中依题意补全图形,并猜想(1)中的结论是否仍然成立,不必证明;
(3)如图3,对旋转角α(60°<α<90°),猜想(1)中的结论是否仍然成立;若成立,请证明你的结论;若不成立,请说明理由.
图1 图2 图3
图1
图2
图3
练习6.在等边△ABC 外侧作直线AP ,点B 关于直线AP 的对称点为D ,连接AD ,BD ,CD ,其中CD 交直线AP 于点E .设∠P AB =α,∠ACE =β,∠AEC =γ.
(1) 依题意补全图1; (2) 若α=15°,直接写出β和γ的度数; (3) 如图2,若60°<α<120°,①判断α,β的数量关系并加以证明; ②请写出求γ大小的思路.(可以不写出计算结果.........)
练习7.阅读下面材料:
小红遇到这样一个问题,如图1:在△ABC 中,AD ⊥BC ,BD =4,DC =6,且∠BAC =45°,求线段AD 的长.
小红是这样想的:作△ABC 的外接圆⊙O ,如图2:利用同弧所对圆周角和圆心角的关系,可以知道∠BOC =90°,然后过O 点作OE ⊥BC 于E ,作OF ⊥AD 于F ,在Rt △BOC 中可以求出⊙O 半径及OE ,在Rt △AOF 中可以求出AF ,最后利用AD =AF +DF 得以解决此题.
请你回答图2中线段AD 的长 . 参考小红思考问题的方法,解决下列问题:
如图3:在△ABC 中,AD ⊥BC ,BD =4,DC =6,且∠BAC =30°,则线段AD 的长 .
图2
A B
P
C
A
B C
P
图1
练习8.已知:A 、B 、C 三点不在同一直线上. (1)若点A 、B 、C 均在半径为R 的⊙O 上, (i )如图①,当∠A =45°,R =1时,求∠BOC 的度数和BC 的长; (ii )如图②,当∠A 为锐角时,求证:sinA =
2BC
R
; (2)若定长线段BC 的两个端点分别在∠MAN 的两边AM 、AN (B 、C 均与A 不重合)滑动,如图③,当∠MAN =60°,BC =2时,分别作BP ⊥AM ,CP ⊥AN ,交点为P ,试探索在整个滑动过程中,P 、A 两点间的距离是否保持不变?请说明理由.
练习9.在四边形ABCD 中,AB ∥DC ,AB >CD ,K ,M 分别在AD ,BC 上,∠DAM =∠CBK . 求证:∠DMA =∠CKB .
分析:连KM,由∠DAM=∠CBK,得到A,B,M,K四点共圆,则∠DAB=∠CMK,∠AKB=∠AMB,而∠DAB+∠ADC=180°,得到∠CMK+∠KDC=180°,因此C,D,K,M四点共圆,所以∠CMD=∠DKC,即可得到∠DMA=∠CKB.
解答:解:连KM,
∵∠DAM=∠CBK,
∴A,B,M,K四点共圆,
∴∠DAB=∠CMK,∠AKB=∠AMB,
又∵AB∥DC,
∴∠DAB+∠ADC=180°,
∴∠CMK+∠KDC=180°.
∴C,D,K,M四点共圆,
∴∠CMD=∠DKC,
∴180°-∠DKC-∠AKB=180°-∠CMD-∠AMB,
∴∠DMA=∠CKB.。
