设计一个补码定点小数乘法运算器
6位有符号补码阵列乘法器

6位有符号补码阵列乘法器一. 简介在计算机科学和数字电路设计中,6位有符号补码阵列乘法器是一种重要的电路组件。
补码是一种表示有符号数的编码方式,能够有效地表示负数。
本文将深入探讨6位有符号补码阵列乘法器的原理、设计和应用,并分享对该电路的观点和理解。
二. 原理1. 有符号补码表示有符号补码是一种在计算机中表示负数的常用编码方式。
在6位有符号补码中,最高位表示符号位,0代表正数,1代表负数。
其余位表示数值部分,通过取反加一的方式对负数进行编码。
2. 阵列乘法器阵列乘法器是一种用于执行乘法运算的电路。
6位有符号补码阵列乘法器能够以比较高的效率和较小的面积完成乘法运算。
其主要原理是将乘法运算拆分为多个部分,使用并行的方式进行计算,并最后将结果相加得到最终的乘积。
三. 设计1. 输入和输出6位有符号补码阵列乘法器一般包含两个输入,分别是被乘数和乘数,以及一个输出,即乘积。
被乘数和乘数的输入位数都为6位。
2. 乘法计算乘法计算是6位有符号补码阵列乘法器的核心部分。
它首先对乘数进行拆分,每一位与被乘数相乘,从而生成多个部分乘积。
接下来,对这些部分乘积进行累加,最后得到乘积的结果。
该阵列乘法器的设计需要考虑到乘法运算可能会出现的溢出和进位问题。
3. 控制逻辑6位有符号补码阵列乘法器还需要一些控制逻辑来控制乘法计算的顺序和结果的输出。
这些控制逻辑一般包括时钟信号、使能信号和清零信号等。
四. 应用1. 数字信号处理6位有符号补码阵列乘法器在数字信号处理领域得到广泛应用。
它能够高效地进行乘法运算,常用于滤波器等算法的实现。
2. 图像处理图像处理中经常需要进行像素之间的乘法运算,例如图像增强、滤波和特征提取等。
6位有符号补码阵列乘法器可以在图像处理中快速完成这些乘法运算。
3. 神经网络神经网络是人工智能领域的热门研究方向。
6位有符号补码阵列乘法器能够提供高效的乘法运算支持,可以在神经网络的训练和推理过程中扮演重要角色。
符号定点二进制小数(Qnformat)乘法原理

符号定点⼆进制⼩数(Qnformat)乘法原理⽆符号整数⼆进制乘法很简单,基本上就是补位到位数相同,然后乘数中的每⼀位与另⼀个乘数的每⼀位做AND(与)运算,然后移位累加就可以了。
那么把⽆符号⼆进制整数乘法拓展到⽆符号⼆进制⼩数乘法,就涉及⼩数格式的问题。
这⾥说定点⼆进制⼩数格式:Qn format;⼩数点位于第 n 位元之右侧,称为Qn 格式。
Q3.3就是3位整数3位⼩数。
乘数A是Qm.n整数部分m位,⼩数部分n位; 乘数B是Qo.p,整数部分o位,⼩数部分p位;那么积A*B 就是Q(m+o).(n+p),整数部分(m+o)位,⼩数部分(n+p)位;按照⽆符号⼆进制整数乘法进⾏,然后把输出从低到⾼按照位数划分整数和⼩数部分就可以得到正确的结果。
现在把⽆符号⼆进制整数乘法拓展到考虑符号的整数⼆进制乘法,这就涉及⼆进制符号位,补位的问题了。
考虑符号⼆进制整数,最⾼位是符号位,1表⽰负数,0表⽰正数。
负数的补码是所有位取反(反码)然后加1,正数的补码是正数本⾝。
1111是负数,它表⽰-1,它的补码是0001(反码加⼀后最⾼位溢出舍去),所以负数⼆进制的数值是补码视为正数的相反数。
符号位权位-2^(n-1)——n为⼆进制数的位数,计算符号⼆进制数的⼗进制也可以⽤权来计算。
(1111)2=1*(-2^3)+1*2^2+1*2^1+1*2^0=-8+4+2+1=-1;另外还需强调⼀点,就是符号⼆进制数的补位。
我们都知道不同位数⽆符号⼆进制数进⾏运算需要在位数⼩的数前⾯补0,例如⽆符号数1011和100相加,变成1011和0100相加,因为显然,100和0100, 00100, 000100都是相等的,⾼位补0产⽣0*2^(n),不对原始数值有影响。
但是负数⼆进制数的补位是要在⾼位补1:直接解释,假设仅要增补1位,如果不是1就改变了负数为正数。
由此递推到补n位,都是补1;也可以从权的⾓度来说明……符号⼆进制数的计算需要考虑每个乘数分别的符号,可以分为:正数*正数,正数*负数,负数*正数,负数*负数正数*正数:正常运算就⾏了,依次与然后移位累加。
6位有符号补码阵列乘法器

6位有符号补码阵列乘法器1. 介绍在计算机中,我们经常需要进行数字的乘法运算。
而对于有符号的整数,我们需要使用补码来表示。
本文将介绍一种用于进行6位有符号补码乘法运算的阵列乘法器。
2. 有符号补码表示首先,我们需要了解有符号补码的表示方法。
在6位有符号补码中,最高位为符号位,0代表正数,1代表负数。
其余5位用于表示数字的大小。
例如,+3可以用补码表示为0011,而-3可以用补码表示为1101。
3. 阵列乘法器结构阵列乘法器是一种常见且高效的硬件电路结构,用于实现数字乘法运算。
它由多个部件组成,包括乘法单元、加法单元和寄存器等。
在本文中,我们要设计一个6位有符号补码阵列乘法器。
它由以下几个部分组成:3.1 输入端口阵列乘法器需要接收两个输入操作数A和B。
每个操作数都是一个6位的二进制数,并且使用有符号补码表示。
3.2 控制单元控制单元用于控制乘法器的操作。
它根据输入操作数的符号位和乘法器的状态来确定乘法器的运算方式。
3.3 乘法单元乘法单元用于执行两个操作数的相乘操作。
对于6位有符号补码,我们可以使用标准的乘法算法,将两个6位数分别扩展到12位,并进行逐位相乘。
3.4 加法单元加法单元用于将乘法结果相加。
对于6位有符号补码,我们需要考虑进位和溢出情况。
3.5 结果寄存器结果寄存器用于存储最终的计算结果。
它是一个6位的寄存器,可以将计算结果保存在其中。
4. 工作原理下面我们将详细介绍6位有符号补码阵列乘法器的工作原理:1.首先,控制单元根据输入操作数A和B的符号位来确定运算方式。
2.如果A和B都为正数或者都为负数,则直接进行普通乘法运算。
3.如果A为正数而B为负数,则需要将B转换为正数,并在最后计算结果时取反。
4.如果A为负数而B为正数,则需要将A转换为正数,并在最后计算结果时取反。
5.控制单元将A和B送入乘法单元,进行逐位相乘操作。
6.乘法单元的输出经过加法单元,进行相加操作。
7.加法单元的输出经过结果寄存器,存储最终的计算结果。
补码一位乘法
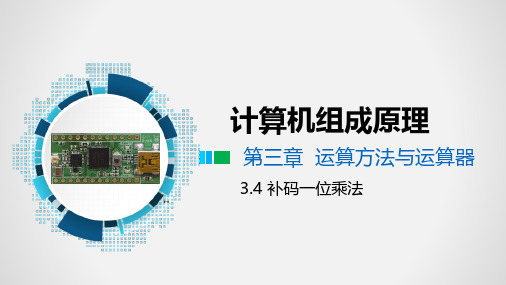
计算机组成原理第三章运算方法与运算器3.4 补码一位乘法1补码一位乘法的基本方法设[X]补= X0X1X2X3…X n[Y]补= Y0Y1Y2Y3…Y n可证明:[X⋅Y]补= [X]补•( 0.Y1Y2Y3…Yn) –Y0• [X]补进一步展开合并后可得:n[x•y]补=[x] 补•∑(y i+1-y i)2-i (符号位参加运算)i=01补码一位乘法的基本方法[x•y] 补=[x] 补• (y i+1-y i)2-i (符号位参加运算)补码一位乘法的运算规则如下:(1)如果y n+1=y n,部分积加0,部分积算术右移1位;(2)如果y n+1y n=10,部分积加[x]补,部分积算术右移1位;(3)如果y n+1y n=01,部分积加[-x]补,部分积算术右移1位.重复进行n+1步,但最后一步不移位。
包括一位符号位,所得乘积为2n+1位,其中n为数据位位数.1补码一位乘法的基本方法几个特殊问题的处理[x •y] 补=[x] 补• (y i+1-y i )2-i (符号位参加运算) 设[X]补= X 0X 1X 2X 3…X n [Y]补= Y 0Y 1Y 2Y 3…Y n(1)i=n 时,y n+1=?(2)y n+1是哪个寄存器?(3)算术右移的对象有哪些?y n+1=0在乘数寄存器Y 后增加的一位部分积和乘数寄存器均右移2补码一位乘法的举例例1 已知X= +1101 Y=+1011 用补码一位乘法求X⨯Y解:[X]补=01101 [Y]补=01011 [–X]补=10011部分积乘数说明000000 010110Y n+1< Y n部分积+[–X]补+ 110011110011→111001101011结果右移一位,Y n+1= Y n部分积+0+ 000000111001→111100 110101结果右移一位, Y n+1> Y n部分积+[X]补+ 0011010010012补码一位乘法的举例部分积乘数说明→000100 111010将结果右移一位, Y n+1< Y n部分积+[–X]补+ 110011110111→111011 111101将结果右移一位, Y n+1> Y n部分积+[X]补+ 001101001000∴[X⋅Y]补=010001111∴X⋅Y= 010001111。
补码一位乘法校正法

补码一位乘法校正法补码一位乘法校正法是一种用于检测和纠正乘法器误差的方法。
在数字电路中,乘法器是一种非常重要的组件,负责执行数字信号的乘法运算。
然而,由于硬件设计和制造的不完美,乘法器可能会产生误差,导致输出结果不准确。
补码一位乘法校正法就是一种常用的解决方案。
在理解补码一位乘法校正法之前,我们首先需要了解补码的概念。
补码是一种用于表示有符号整数的编码方式。
在计算机中,负数一般使用补码表示,这样可以简化运算。
补码的计算方法是将原码的符号位保持不变,其余位按位取反后加1。
例如,-5的原码为10000101,补码为11111011。
补码一位乘法校正法的基本思想是将乘法器的输出结果与真实的乘法结果进行比较,并根据比较结果来调整乘法器的输出。
具体步骤如下:1. 乘法器的输入为两个n位的补码数字,输出为一个2n位的补码数字。
2. 将乘法器的输出结果与真实的乘法结果进行比较。
如果两者相等,则乘法器的输出是正确的;如果不相等,则说明乘法器存在误差。
3. 根据乘法器输出的最高位进行判断。
如果最高位为1,说明乘法器的输出是负数,需要对乘法器的输出进行补码取反操作;如果最高位为0,则不需要进行操作。
4. 将乘法器的输出与校正后的结果进行比较。
如果两者相等,则乘法器的输出是正确的;如果不相等,则说明乘法器的误差无法通过补码一位乘法校正法进行修复。
补码一位乘法校正法的原理是通过对乘法器输出结果的最高位进行判断,来确定是否需要对乘法器的输出进行补码取反操作。
通过这种方法,可以有效地检测和纠正乘法器误差,提高乘法器的准确性和可靠性。
然而,补码一位乘法校正法只能处理一位乘法误差,对于多位乘法误差无法进行有效的修复。
在实际应用中,补码一位乘法校正法通常与其他纠错技术结合使用,以进一步提高乘法器的准确性。
例如,可以将补码一位乘法校正法与冗余校验码相结合,通过对乘法器输出结果进行校验和校正,来实现更可靠的乘法运算。
总结起来,补码一位乘法校正法是一种用于检测和纠正乘法器误差的方法。
Verilog实现补码一位乘法课程设计
计算机科学与工程学院课程设计报告题目全称:Verilog实现补码一位乘法课程名称:计算机组成原理指导老师:文泉职称:指导老师评语:指导签字:课程设计成绩:目录第 1 章序言 (1)1.1 课程设计目的 (1)1.2 课程设计作用 (2)1.3 课程设计需求 (2)1.3.1Xilinx设计软件 (2)1.3.2 在xilinx ISE集成开发环境下,使用Verilog HDL (2)第 2 章正文 (4)2.1 实现补码一位乘法的原理 (4)2.2 比较补码一位乘法方法 (6)2.2.1 分步乘法 (6)2.2.2 运算规则 (7)2.2.3 运算实例 (7)2.2.4算法流程图 (8)2.2.5 比较法(Booth算法) (8)2.3课程设计实验代码(概要设计) (10)2.4课程设计详细设计方案 (12)2.4.1顶层方案图的设计与实现 (13)2.4.2 功能模块的设计与实现 (14)2.4.3 仿真调试 (13)第 3 章结论 (16)3.1课程设计总结 (16)摘要本定点补码一位乘法器,具有良好的可移植性。
本文介绍了定点补码一位乘法的概念已及定点补码一位乘法的的原理和方法,分析了定点补码一位乘法器的设计,并详细介绍了使用EDA环境,Xilinx设计软件,在XCV200实验板的XCV200可编程逻辑芯片中上进行定点补码一位乘法器的移植。
通过测试,系统移植成功。
关键词:定点补码;EDA;一位乘法器;设计第1 章序言当今时代是一个信息的时代,我们的生活与信息紧密相连。
伴随着计算机的生活化,我们更近一步接触到信息技术的发展。
如今,计算机技术迅猛发展,它的发展不仅仅表现在软件领域取得辉煌的成就,同时也在硬件方面也取得了长足的发展。
因此,很多功能已经可以通过硬件来实现。
但是通常对嵌入式软件的基本要求是体积小、指令速度快、具有较好的裁减性和可移植性,目前这方面的设计已经很多也很优异,但是基于补码一位乘法器的实现,克服了定点补码乘法器的缺点,实现更加方便有效。
定点小数的乘法运算及实现

补码两位乘
将比较Yi-1Yi的状态与比较YiYi+1的状态所执行的运算合成一 步 对照:补码一位乘法 2(Yi- Yi-1 ) + (Yi+1-Yi) = Yi+ 1+ Yi - 2Yi-1 Yi+ Yi+1- 2Yi-1 0 1 1 2 -2 -1 -1 0 操作 +0,2→ +[X]补, 2→ +[X]补, 2→ +2[X]补, 2→ +2[-X]补, 2→ +[-X]补, 2→ +[-X]补, 2→ +0, 2→ 17
+
+
+ +
1 1 1 1
1 1 1 1
积低部
∴[Z]原=1,10001111
原码两位乘
原码一位乘依据Yi 决定操作,原码两位乘每次根据 连续两位乘数Yi+1Yi (=2Yi+1+Yi)决定本次操作 n位数的乘法一般只需n/2次操作
Yi+1 Yi 00
01 10 2 11
1 1 2 i 1 1 2 2
0
0→Cj,2→ -|X|
1→Cj,2→ +|X| 0→Cj,1→
00011100
1
00001110
0
积高位
积低位
最后一步只移一位 10
[Z]原=1,00111000000111
4.3.2 补码乘法运算
Booth法。目标:求[X· Y]补 设被乘数X、乘数Y均为n+1位的定点小数,
X补=x0.x1x2…xn, Y补=y0.y1y2…yn。 则[Y]补=y0· 20+y1· 2-1+· · · · · · +yn· 2-n
补码阵列乘法器例题

补码阵列乘法器例题
补码阵列乘法器是一种用于进行数字乘法运算的电子电路,常用于计算机中的算术逻辑单
元(ALU)中。
下面我们来看一个例题,了解补码阵列乘法器的工作原理。
假设我们要计算两个8位二进制数的乘积:A = 10101010,B = 01010101。
首先,我们需要将
这两个二进制数转换为补码表示。
由于A是正数,补码表示和原码相同,所以A的补码为10101010。
而B是负数,我们需要将其转换为补码表示。
对于B的补码表示,我们需要先将其转换为反码,即将所有位取反。
所以B的反码为10101010。
接下来,将反码的所有位加1,得到B的补码:10101011。
接下来,我们使用补码阵列乘法器进行乘法运算。
补码阵列乘法器的基本原理是将两个补码数
的每一位都和另一个数的每一位相乘,然后将乘积相加得到最终结果。
首先,我们将A的补码(10101010)和B的补码(10101011)分别输入到补码阵列乘法器中。
然后,乘法器开始执行乘法操作。
依次将A的每一位和B的每一位相乘,并将结果保留在乘
法器的不同位上。
在乘法过程中,如果某位的乘积超过了8位,乘法器会自动将其截断为低8位。
此外,在进行
乘法计算后,乘法器会将所有结果相加得到最终的乘积。
经过补码阵列乘法器的计算,我们得到的结果为11011000,即补码表示的乘积。
希望通过上面的例题,你能对补码阵列乘法器有更深入的理解。
补码阵列乘法器在计算机中扮
演着重要的角色,它能够高效地进行乘法运算,并且适用于各种数字表示形式。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
姓名:何飞龙 学号:13152120102.设计一个补码定点小数乘法运算器。
设被54321.y y y y y y =,乘数54321.x x x x x x =,积9871.q p p p p = ,均为补码形式的定点小数。
start 是启动信号,down 是除法完成信号,overflow 是“溢出”报警信号,reset 是清零信号,clock 是时钟信号。
请给出此除法器的VHDL 功能描述,并编写测试向量文件,通过分析模拟结果验证设计的正确性。
(X 补=1.0011,Y 补=1.0101)程序代码:LIBRARY IEEE;USE IEEE.STD_LOGIC_1164.ALL;USE IEEE.STD_LOGIC_UNSIGNED.ALL;ENTITY mult5 ISgeneric ( n: integer :=5;m: integer :=9 );PORT(start,reset,clock: IN STD_LOGIC;--kaishi,fuwei,shizhongdone,overflow: OUT STD_LOGIC;--wancheng,yichuy,x: IN STD_LOGIC_VECTOR(n DOWNTO 1);--bei cheng shu,chengshu p: OUT STD_LOGIC_VECTOR(m DOWNTO 1));--shuchuEND ENTITY mult5;ARCHITECTURE behav OF mult5 ISSIGNAL ry: STD_LOGIC_VECTOR(n DOWNTO 1); --SIGNAL pp: STD_LOGIC_VECTOR(m+1 DOWNTO 0);------------SIGNAL state: integer RANGE 0 TO 5;-------BEGINPROCESS(reset,clock)VARIABLE temp: STD_LOGIC_VECTOR(n+1 DOWNTO 1);BEGINIF reset='0' THENry <= (others=>'0');pp <= (others=>'0');state <= 0;done <= '0';ELSIF clock'EVENT AND clock='1' THENCASE state ISWHEN 0=> ry <= y; pp <= "00000" & x & '0';IF start= '1' THEN state <= 1; END IF;WHEN 5=> IF pp(1 DOWNTO 0) = "01" THEN temp := (pp(m+1) & pp(m+1 DOWNTO 6)) + (ry(n) & ry);ELSIF pp(1 DOWNTO 0) = "10" THEN temp:=(pp(m+1) & pp(m+1 DOWNTO n+1))+NOT(ry(n) & ry) + 1;ELSE temp := (pp(m+1) & pp(m+1 DOWNTO n+1)); END IF;p<=temp(n DOWNTO 1) & pp(n DOWNTO 2);if temp(n+1)='1' then overflow <='1'; else overflow <='0'; end if;done <= '1';state <= 0 ;WHEN OTHERS => IF pp(1 DOWNTO 0) = "01" THEN temp := (pp(m+1) & pp(m+1 DOWNTO n+1)) + ( ry(n) & ry);--01 +BELSIF pp(1 DOWNTO 0)="10" THEN temp := (pp(m+1) & pp(m+1 DOWNTO n+1)) + NOT(ry(n) & ry) + 1;--10-BELSE temp := (pp(m+1) & pp(m+1 DOWNTO n+1)); END IF;pp <= temp & pp(n DOWNTO 1); -------Cyou yistate <= state + 1;END CASE;END IF;END PROCESS;END behav;编译综合:运行结果:RTL 电路:2.设计一个正数定点小数除法运算器。
设被除数8760.y y y y y = ,除数4320.x x x x x = ,商4320.q q q q q = ,余数4320.r r r r r = ,均为正数。
start 是启动信号,down 是除法完成信号,overflow 是“溢出”报警信号,reset 是清零信号,clock 是时钟信号。
请给出此除法器的VHDL 功能描述,并编写测试向量文件,通过分析模拟结果验证设计的正确性。
原码恢复余数法或原码不恢复余数法(加减交替法)。
程序代码:LIBRARY IEEE;USE IEEE.STD_LOGIC_1164.ALL;USE IEEE.STD_LOGIC_UNSIGNED.ALL;ENTITY divi ISgeneric ( n: integer :=5);PORT(start,reset,clock: IN STD_LOGIC;done, overflow: OUT STD_LOGIC;x: IN STD_LOGIC_VECTOR(n-1 DOWNTO 0);---------chu shuy: IN STD_LOGIC_VECTOR(n+n-2 DOWNTO 0);--------bei chu shuq, r: OUT STD_LOGIC_VECTOR(n-1 DOWNTO 0));--------shang, yu shuEND ENTITY divi;ARCHITECTURE behav OF divi ISSIGNAL rx: STD_LOGIC_VECTOR(n DOWNTO 0);SIGNAL ry: STD_LOGIC_VECTOR(n DOWNTO 0);SIGNAL rq: STD_LOGIC_VECTOR(n-1 DOWNTO 0);SIGNAL flag: STD_LOGIC;SIGNAL state: integer RANGE 0 TO 7;BEGINPROCESS(reset,clock)VARIABLE rmd: STD_LOGIC_VECTOR(n DOWNTO 0);---------yushuVARIABLE sq: STD_LOGIC;---------shangshangBEGINIF reset='0' THENry <= (others=>'0');rx <= (others=>'0');rq <= (others=>'0');overflow <= '0';state <= 0 ;flag <= '1';done <= '0';rx <= "00" & x(n-2 DOWNTO 0); ry <= "00" & y(n+n-3 DOWNTO n-1); rq <= y(n-2 DOWNTO 0) & '0';ELSIF clock'EVENT AND clock='1' THENCASE state ISWHEN 0=> flag <= '1';done <= '0'; rx <= "00" & x(n-2 DOWNTO 0); ry <= "00" & y(n+n-3 DOWNTO n-1); rq <= y(n-2 DOWNTO 0) & '0';IF start= '1' THEN state <= 1; END IF;WHEN 1=> rmd := ry - rx;IF rmd(n DOWNTO n-1) = "00" THEN overflow <= '1'; state <= 0;ELSE sq := '0'; flag <= '0'; END IF;ry(n DOWNTO 0) <= rmd(n-1 DOWNTO 0) & rq(n-1); r q(n-1 DOWNTO 0) <= rq(n-2 DOWNTO 0) & sq; state <= state + 1;WHEN 5=> IF flag = '1' THEN rmd := ry - rx;ELSE rmd := ry + rx; END IF;IF rmd(n DOWNTO n-1) = "00" AND (ry>rx) THEN sq := '1';flag <= '1';ELSE sq := '0'; flag <= '0'; END IF;rq(n-1 DOWNTO 0) <= rq(n-2 DOWNTO 0) & sq; state <= state + 1;WHEN 6=> IF rq(0) = '0' THEN q <= rq ; r <= ry(n-1 DOWNTO 0); done <= '1'; state <= 0 ;ELSE ry <= ry + rx; state <= state + 1; END IF;WHEN 7=> q <= rq ; r <= ry(n-1 DOWNTO 0); done <= '1'; state <= 0 ;WHEN OTHERS => IF flag = '1' THEN rmd := ry - rx;ELSE rmd := ry + rx; END IF;IF rmd(n DOWNTO n-1) = "00" AND (ry>rx) THEN sq := '1'; flag <= '1';ELSE sq := '0'; flag <= '0'; END IF;ry(n DOWNTO 0) <= rmd(n-1 DOWNTO 0) & rq(n-1); r q(n-1 DOWNTO 0) <= rq(n-2 DOWNTO 0) & sq; state <= state + 1;END CASE;END IF;END PROCESS;END behav;运行结果:。
