matlab程序设计作业
完整版优化设计Matlab编程作业
化设计hl4HU©0⑥ 3 hlu 凹内r d X1州fci-rU-fFF卢F ♦ 忡下¥为+1 —*— S-ll-« F41:Si —MATLABoftiHMirjirCfiffliiiiJ PHI■1**■ 温不平?」11,・—喜M - 〜FT 文词一时y 片 34ml 3F*L9TR0i. Jill!-LkftLgWf 1S1CSI掰f 1 ■ >A A A »W I % :k Dnfl w I ■ J k^lXMprfaMk tjn nn Alflhw初选 x0=[1,1] 程序:Step 1: Write an Mfle objfunl.m.function f1=objfun1(x)f1=x(1)人2+2*x(2)入2-2*x(1)*x(2)-4*x(1);Step 2: Invoke one of the unconstrained optimization routinesx0=[1,1];>> options = 0Ptimset('LargeScale','off);>> [x,fval,exitflag,output] = fminunc(@objfun1,x0,options)运行结果: x =4.0000 2.0000 fval = -8.0000exitflag =1 output = iterations: 3 funcCount: 12 stepsize: 1 firstorderopt: 2.3842e-007algorithm: 'medium-scale: Quasi-Newton line search message: [1x85 char]非线性有约束优化1. Min f(x)=3 x : + x 2+2 x 1-3 x 2+5 Subject to:g 2(x)=5 X 1-3 X 2 -25 < 0 g (x)=13 X -41 X 2 < 0 3 12g 4(x)=14 < X 1 < 130无约束优化 min f(x)=X 2 + x 2-2 x 1 x 2-4 x 1g5 (x)=2 < X 2 < 57初选x0=[10,10]Step 1: Write an M-file objfun2.mfunction f2=objfun2(x)f2=3*x(1)人2+x(2)人2+2*x(1)-3*x(2)+5;Step 2: Write an M-file confunl.m for the constraints. function [c,ceq]=confun1(x) % Nonlinear inequality constraints c=[x(1)+x(2)+18;5*x(1)-3*x(2)-25;13*x(1)-41*x(2)人2;14-x(1);x(1)-130;2-x(2);x(2)-57];% Nonlinear inequality constraints ceq=[];Step 3: Invoke constrained optimization routinex0=[10,10]; % Make a starting guess at the solution>> options = optimset('LargeScale','off);>> [x, fval]=...fmincon(@objfun2,x0,[],[],[],[],[],[],@confun1,options)运行结果:x =3.6755 -7.0744 fval =124.14952.min f (x) =4x2 + 5x2s.t. g 1(x) = 2X] + 3x2- 6 < 0g (x) = x x +1 > 0初选x0=[1,1]Step 1: Write an M-file objfun3.m function f=objfun3(x) f=4*x(1)人2 + 5*x(2)人2Step 2: Write an M-file confun3.m for the constraints. function [c,ceq]=confun3(x) %Nonlinear inequality constraints c=[2*x(1)+3*x(2)-6;-x(1)*x(2)-1];% Nonlinear equality constraints ceq口;Step 3: Invoke constrained optimization routinex0=[1,1];% Make a starting guess at the solution>> options = optimset('LargeScale','off);>> [x, fval]=...fmincon(@objfun,x0,[],[],[],[],[],[],@confun,options)运行结果:Optimization terminated: no feasible solution found. Magnitude of search direction less than2*options.TolX but constraints are not satisfied.x =11fval =-13实例:螺栓连接的优化设计图示为一压气机气缸与缸盖连接的示意图。
matlab大作业实验报告,《Matlab程序设计》期末实验报告-大作业2015.doc

matlab⼤作业实验报告,《Matlab程序设计》期末实验报告-⼤作业2015.doc《MATLAB程序设计》实验报告学院: 学号: 姓名:⼀、题⽬:1、(10分)已知矩阵,⽤Matlab代码实现以下要求:(1)将矩阵赋给变量A,并在屏幕上显⽰A;(2)将A按列进列逆序重排,重排后的矩阵赋给变量B,并在屏幕上显⽰B;(3)⽤reshape命令将A重排为⼀个2⾏6列矩阵并赋给变量C;(4)将A重排为⼀个列向量,将其赋给变量D,求D的平均值,在屏幕上显⽰D和它的平均值;(5)⽤命令查看变量A的维数,并显⽰运⾏结果。
2、(10分)写代码实现以下要求:构造菜单项‘Plot’,菜单项Plot有两个⼦菜单项Plot sin(选择此项后执⾏画出曲线,线型为虚线,线条颜⾊为红⾊)和Plot cos(选择此项后执⾏画出曲线 ,线型为实线,线条宽度为2)。
3、(20分)已知,实现下列操作:(1)在同⼀个图形窗⼝,同⼀坐标系下⽤不同的颜⾊和线型绘制三条曲线,并添加图例来区分三条曲线(5分)。
(2)⽤subplot命令,以⼦图的⽅式绘制三条曲线,图形排列⽅式为三⾏⼀列(5分)。
(3) 分别⽤直⽅图(bar)、棒状图(stem)和填充图(fill)绘制三条曲线,以⼦图⽅式绘制,排列⽅式为3⾏3列,共9幅⼦图(10分)。
4、(10分)⽤surf命令绘制曲⾯图形,⽤shading interp命令进⾏插值着⾊处理并添加垂直颜⾊棒。
5、(15分)⾃2011年9⽉1⽇起,我国实⾏新的个⼈所得税征收办法,起征点为3500元,请⽤If-else if-else-end结构实现⼈⼯输⼊⽉收⼊后能计算出个⼈所得税的缴纳额并显⽰⽉收⼊10000元时应缴纳的税款。
级数应纳税所得额x(元)税率备注1x<=15003%x指⽉收⼊扣除起征点3500元之后的余额;215008000045%同上6. (10分)⽤while-end循环结构计算级数和的值,输⼊n值,能计算出f的值,并显⽰结果。
matlb课程设计作业

matlb课程设计作业一、教学目标本课程的教学目标是使学生掌握MATLAB基本语法、编程技巧以及应用方法,培养学生解决实际问题的能力。
具体目标如下:1.知识目标:(1)理解MATLAB的基本概念,如变量、数据类型、运算符等。
(2)掌握MATLAB编程的基本语法,如矩阵操作、函数定义与调用、循环结构、条件语句等。
(3)熟悉MATLAB与其他软件(如Mathematica、Python等)的接口转换。
(4)了解MATLAB在工程领域中的应用,如信号处理、控制系统、图像处理等。
2.技能目标:(1)能够运用MATLAB进行简单的数学计算、数据分析及图形绘制。
(2)具备编写MATLAB脚本文件和函数文件的能力。
(3)学会使用MATLAB解决实际问题,如编写程序实现线性方程组求解、最优化问题求解等。
(4)掌握MATLAB在实验数据处理、仿真实验等方面的应用。
3.情感态度价值观目标:(1)培养学生对科学探究的兴趣,提高其创新意识。
(2)培养学生团队协作、沟通交流的能力。
(3)培养学生具备良好的编程习惯和职业道德。
二、教学内容本课程的教学内容主要包括以下几个部分:1.MATLAB基本概念:变量、数据类型、运算符等。
2.MATLAB编程语法:矩阵操作、函数定义与调用、循环结构、条件语句等。
3.MATLAB高级应用:数组运算、图像处理、控制系统、信号处理等。
4.MATLAB与其他软件的接口转换。
5.实践项目:利用MATLAB解决实际问题,如线性方程组求解、最优化问题求解等。
三、教学方法本课程采用讲授法、案例分析法、实验法等多种教学方法相结合,以提高学生的学习兴趣和主动性。
1.讲授法:用于讲解MATLAB基本概念、语法和应用。
2.案例分析法:通过分析实际案例,使学生掌握MATLAB在各个领域的应用。
3.实验法:让学生亲自动手实践,培养其运用MATLAB解决实际问题的能力。
四、教学资源1.教材:选用《MATLAB教程》作为主要教材,辅助以相关参考书籍。
MATLAB程序设计与应用习题

X =
1 1 1 0
2.11设a=[0 100],求~a的值?(非运算)
答:>> clear
>> a=[0 1 0 0]
a =
0 1 0 0
>> x=not(a)
x =
1 0 1 1
2.12设a=[0 120],b=[21 0 0],求axor b的值?
答:>> clear
答:>> clear
>> a=[0 2 1 0]
a =
0 2 1 0
>> b=[2 1 0 0]
b =
2 1 0 0
>> x=and(a,b)
x =
0 1 0 0
2.10设a=[0 120],b=[120 0],求a|b的值?(或运算)
答:
>> clear
>> a=[0 1 2 0];b=[1 2 0 0];
答:quit:关闭MATLAB。
clear:清除内存中的变量。
cla:清除坐标。
clf:清除图形。
clc:清除MATLAB命令窗口的所有显示信息。
hold:控制当前图形窗口是否被刷新。
1.9学会打开并保存程序编辑窗口,并在M文档中编写1.4的运算程序并进行运算。
答:要打开程序编辑窗口,我们可以在Command Window窗口中,单击工具栏中最左端显示为一张白纸的工具按钮。这样就打开了一个空白的程序编辑窗口,如图1-6所示。
3.6已知
将a(2,3)=-1替换为a(2,3)=0。
答:
3.7已知
将a的第二行元素全部替换为0,然后将第二列元素全部替换为1。
matlab简单编程21个题目及答案
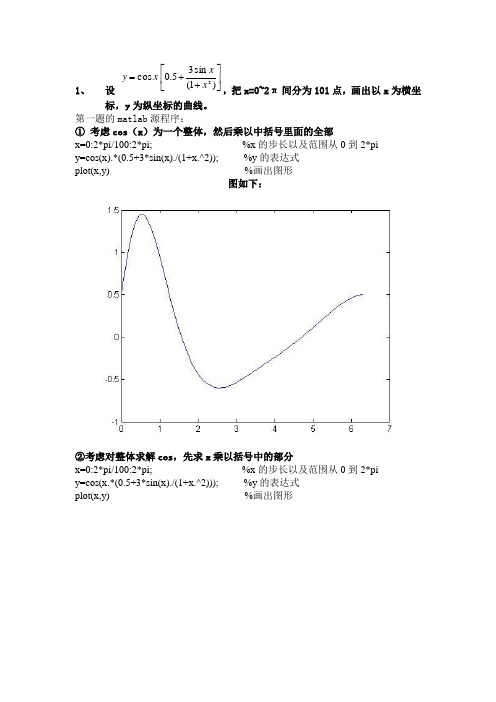
1、设⎥⎦⎤⎢⎣⎡++=)1(sin35.0cos2xxxy,把x=0~2π间分为101点,画出以x为横坐标,y为纵坐标的曲线。
第一题的matlab源程序:①考虑cos(x)为一个整体,然后乘以中括号里面的全部x=0:2*pi/100:2*pi; %x的步长以及范围从0到2*pi y=cos(x).*(0.5+3*sin(x)./(1+x.^2)); %y的表达式plot(x,y)%画出图形图如下:②考虑对整体求解cos,先求x乘以括号中的部分x=0:2*pi/100:2*pi; %x的步长以及范围从0到2*pi y=cos(x.*(0.5+3*sin(x)./(1+x.^2))); %y的表达式plot(x,y) %画出图形图如下:2、产生8×6阶的正态分布随机数矩阵R1, 求其各列的平均值和均方差。
并求该矩阵全体数的平均值和均方差。
第二题的matlab源程序如下:R1=randn(8,6) %产生正态分布随机矩阵R1 =1.0933 -0.7697 1.5442 -0.1924 1.4193 0.21571.1093 0.3714 0.0859 0.8886 0.2916 -1.1658-0.8637 -0.2256 -1.4916 -0.7648 0.1978 -1.14800.0774 1.1174 -0.7423 -1.4023 1.5877 0.1049-1.2141 -1.0891 -1.0616 -1.4224 -0.8045 0.7223-1.1135 0.0326 2.3505 0.4882 0.6966 2.5855-0.0068 0.5525 -0.6156 -0.1774 0.8351 -0.66691.5326 1.1006 0.7481 -0.1961 -0.2437 0.1873aver=(sum(R1(1:end,1:end)))./8 %产生各行的平均值aver =0.0768 0.1363 0.1022 -0.3473 0.4975 0.1044a=std(R1(1:end,1:end)) %产生各行的均方差也就是标准差a =1.0819 0.8093 1.3456 0.8233 0.8079 1.2150aver1=(sum(R1(:)))./48 %全体数的平均值aver1 =0.0950b=std(R1(:)) %全体数的均方差即标准差b =1.01033、设x=rcost+3t,y=rsint+3,分别令r=2,3,4,画出参数t=0~10区间生成的x~y 曲线。
matlab简单编程21个题目及答案

1、设⎥⎦⎤⎢⎣⎡++=)1(sin35.0cos2xxxy,把x=0~2π间分为101点,画出以x为横坐标,y为纵坐标的曲线。
第一题的matlab源程序:①考虑cos(x)为一个整体,然后乘以中括号里面的全部x=0:2*pi/100:2*pi; %x的步长以及范围从0到2*pi y=cos(x).*(0.5+3*sin(x)./(1+x.^2)); %y的表达式plot(x,y)%画出图形图如下:②考虑对整体求解cos,先求x乘以括号中的部分x=0:2*pi/100:2*pi; %x的步长以及范围从0到2*pi y=cos(x.*(0.5+3*sin(x)./(1+x.^2))); %y的表达式plot(x,y) %画出图形图如下:2、产生8×6阶的正态分布随机数矩阵R1, 求其各列的平均值和均方差。
并求该矩阵全体数的平均值和均方差。
第二题的matlab源程序如下:R1=randn(8,6) %产生正态分布随机矩阵R1 =1.0933 -0.7697 1.5442 -0.1924 1.4193 0.21571.1093 0.3714 0.0859 0.8886 0.2916 -1.1658-0.8637 -0.2256 -1.4916 -0.7648 0.1978 -1.14800.0774 1.1174 -0.7423 -1.4023 1.5877 0.1049-1.2141 -1.0891 -1.0616 -1.4224 -0.8045 0.7223-1.1135 0.0326 2.3505 0.4882 0.6966 2.5855-0.0068 0.5525 -0.6156 -0.1774 0.8351 -0.66691.5326 1.1006 0.7481 -0.1961 -0.2437 0.1873aver=(sum(R1(1:end,1:end)))./8 %产生各行的平均值aver =0.0768 0.1363 0.1022 -0.3473 0.4975 0.1044a=std(R1(1:end,1:end)) %产生各行的均方差也就是标准差a =1.0819 0.8093 1.3456 0.8233 0.8079 1.2150aver1=(sum(R1(:)))./48 %全体数的平均值aver1 =0.0950b=std(R1(:)) %全体数的均方差即标准差b =1.01033、设x=rcost+3t,y=rsint+3,分别令r=2,3,4,画出参数t=0~10区间生成的x~y 曲线。
MATLAB程序设计及应用习题

MATLAB 程序设计及应用习题二维平面绘图1. 椭圆的参数表示为⎩⎨⎧==)sin()cos(t b y t a x ,请利用这个公式画一个椭圆,其中a=5,b=3要求椭圆上有100个点。
2. Chebysheve 多项式的定义如下:11)),(cos cos(1≤≤-=-x x m y ;当m 的值从1变化到5时,得到五条曲线。
请将这五条曲线画在同一张图上。
使用legend 命令来标记每一条曲线。
3. 用contour 命令画出下列隐函数:2522=+y x 。
提示:画出函数:22y x z +=高度为25的等高线。
三维立体绘图1. 请利用surf 命令画出函数:)ex p(*22y x x z --=的图形。
其中x 在[-2,2]范围内均匀取21个点,y 在[-1,1]范围内均匀取21个点。
2. 一个空间的椭球可以表示为1222222=++cz b y a x ,请使用任何方法画出一个空间的光滑的椭球。
其中a=3,b=4,c=8。
3. 画出函数)cos()2/sin(),(y x y x f =的曲面图和等高线图,其中x 在[-2π,2π]范围内均匀取21个点,y 在[-1.5π,1.5π]范围内均匀取31个点。
用subplot(2,1,1)和subplot(2,1,2)将的曲面图和等高线图画在一个窗口中。
特殊图形1. 以下是某学校信息系各年度的人员组成表,请分别用bar 和bar3画出上述数据的统计图。
2. 请使用上题的数据作出(1)按每年度人数来划分的立体扇形图,并加上适当的说明。
(2)按每种类别人数来划分的立体扇形图,并加上适当的说明。
图象的显示与读写1.读入文件clown.mat中的小丑图象,显示图象,并将调色板colormap改为grey,你会发现图象偏暗,请调整调色板,使其亮度提高。
2.读入文件clown.mat中的小丑图象,显示图象,请调整调色板,使得显示的图象由全黑或全白的象素做成,且其个数的比例大约是1:1。
matlab课程设计大作业

matlab课程设计大作业一、教学目标本课程的教学目标是使学生掌握MATLAB基本语法、编程技巧以及MATLAB 在工程计算和数据分析中的应用。
通过本课程的学习,学生将能够熟练使用MATLAB进行简单数学计算、线性方程组求解、函数图像绘制等。
1.掌握MATLAB基本语法和编程结构。
2.了解MATLAB在工程计算和数据分析中的应用。
3.熟悉MATLAB的函数库和工具箱。
4.能够使用MATLAB进行简单数学计算。
5.能够使用MATLAB求解线性方程组。
6.能够使用MATLAB绘制函数图像。
7.能够利用MATLAB进行数据分析和处理。
情感态度价值观目标:1.培养学生对计算机辅助设计的兴趣和认识。
2.培养学生团队合作和自主学习的能力。
二、教学内容本课程的教学内容主要包括MATLAB基本语法、编程技巧以及MATLAB在工程计算和数据分析中的应用。
1.MATLAB基本语法:介绍MATLAB的工作环境、基本数据类型、运算符、编程结构等。
2.MATLAB编程技巧:讲解MATLAB的函数调用、脚本编写、函数文件编写等编程技巧。
3.MATLAB在工程计算中的应用:介绍MATLAB在数值计算、线性方程组求解、图像处理等方面的应用。
4.MATLAB在数据分析中的应用:讲解MATLAB在数据采集、数据分析、数据可视化等方面的应用。
三、教学方法本课程采用讲授法、案例分析法、实验法等多种教学方法相结合的方式进行教学。
1.讲授法:通过讲解MATLAB的基本语法、编程技巧以及应用案例,使学生掌握MATLAB的基本知识和技能。
2.案例分析法:通过分析实际工程案例,使学生了解MATLAB在工程计算和数据分析中的应用。
3.实验法:安排上机实验,使学生在实际操作中巩固所学知识,提高实际编程能力。
四、教学资源本课程的教学资源包括教材、实验设备、多媒体资料等。
1.教材:选用《MATLAB教程》作为主要教材,辅助以相关参考书籍。
2.实验设备:为学生提供计算机实验室,配备有MATLAB软件的计算机。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Matlab程序设计作业
姓名:
学号:
专业:
« MATLAB 程序设计》作业
1、考虑如下x-y 一组实验数据:
x=[1, 2, 3, 4, 5, 6, 7, 8, 9, 10] y 二[1.2, 3, 4, 4, 5, 4.7, 5, 5.2, 6, 7.2]
分别绘出plot 的原始数据、一次拟合曲线和三次拟合曲线,给出
原始曲线
MATLAB 代码和运行结果。
7
6
5
4
3
2
2 3 4 5 6 7 8 9 10
7
6.5
6
5.5
5
4.5
4
3.5
3
2.5
10
一次拟合
三次拟合
x=[1, 2, 3, 4, 5, 6, 7, 8, 9, 10]; y=[1.2, 3, 4, 4, 5, 4.7, 5, 5.2, 6, 7.2]; figure;
plot(x,y) p1=polyfit(x,y,1); y1=polyval(p1,x); figure;
plot(x,y1) p2=polyfit(x,y,3); y2=polyval(p2,x);
figure; plot(x,y2)
2、在[0, 3n区间,绘制y二Sin(x)曲线(要求消去负半波,即(n 2n)区间内的函数值置零),求出曲线y 的平均值,以及y 的最大值及其最大值的位置。
给出执行代码和运行结果。
x=0:pi/1000:3*pi;
y=Sin(x);
y1=(y>=0).*y; %消去负半波figure(1);
plot(x,y1, 'b' );
a=mean(y1) %求出y1 的平均值
b=max(y1) %求出y1 的最大值b, 以及最大值在矩阵中的位置;
d=x(find(y1==b))
>> ex1
a =
0.4243
b =
1
d =
1.5708 7.8540
>>
1
0.9
0.8
0.7
0.6
0.5
0.4 -
0.3 -
0.2 -
0.1 -
3、给出函数z=x A2+y A2的三维曲面的绘制结果和MATLAB代码, x=-3:0.1:3;
y=-4:0.1:4;
[x,y]=meshgrid(x,y);
z=x.A2+y.A2;
mesh(x,y,z);
12 3
4
-2
-4 -4 -2
4、将一幅彩色图像文件转换为灰度图像,存储并显示转换后的灰度图像,给出运行结果和执行代码
x=imread( 'hehua.jpg' ); x=rgb2gray(x);
figure(1);
imshow(x);
h=figure(1); saveas(h,'gray.jpg');
原图
处理后图像
5、结合自身研究方向,自拟一题目,采用MATLAB语言实现一具有完整功能的算法,给出运行结果和执行代码。
题目:用遗传算法找函数的最大
值
fun cti on mai n()
clear
clc
popsize = 100; %种群大小
chromle ngth = 10; %二进制编码长度
pc = 0.6; %交叉概率
pm = 0.001; %变异概率
pop = in itpop(popsize,chromle ngth);
for i=1:100
[objvalue] = cal_objvalue(pop);
fitvalue = objvalue;
[n ewpop] = selecti on( pop,fitvalue);
[n ewpop] = crossover (n ewpop,pc);
[n ewpop] = mutati on(n ewpop,pm);
pop = n ewpop;
[best in
dividual,bestfit]=best(pop,fitvalue); x2 = bin ary2decimal(besti ndividual);
x1 = bin ary2decimal( newpop);
%初始种群
%十算适应度值(函数值)
%选择操作
%交叉操作
%变异操作
%更新种群
%寻找最优解
[y1] = cal_objvalue( newpop); if mod(i,10)==0
figure; fplot( '10*si n(5*x)+7*abs(x-5)+10'
,[0 10]);
hold on ; title([ '迭代次数为 n=' num2str(i)]);
plot(x1,y1, '*');
end end
fprintf( 'the best X is --->>%5.2f\n' ,x2); fprintf(
'the best Y is --->>%5.2f\n'
,bestfit);
迭代次数为n=10
60
I [
L
i
L 1
50 M
-
- F i
「 \
1 /
40
- ■' r
i i
r i
\
I
*却
i 1 "i f \
*
I !
I )
/ \
30
[ 如
i 1
a
1
1
~1
J
1 1 r
1]
1 i
1
\
I
1
八
20
I
\ \ \ I i
i i t 1 i I \
1 j
\
1
1
i i r \ 1
'i i
10
-
f 1
J 1 I
f
1
■
0 J
r 『
r r
I
r r
1
23456789 10
迭代次数为n=20
0 1 23456789 10
n=30
迭代次数为
迭代次数为n=40
0 1 23456789 10
n=50
迭代次数为
迭代次数为n=60 60
10
0 L~ -------- 1 --------- [ --------- L
0 12 3
迭代次数为n=70
迭代次数为n=80 60
50
40
30
20
10
60
50
40
30
20
10
迭代次数为n=100
60
50
40
30
20
10
1 2 3 4 5 6 7 8 9 10。
