东南大学往年高数期末考试试题及答案-8篇整合
东南大学往年高数期末考试试题及答案-8篇整合

东 南 大 学 考 试 卷( A 卷))一.填空题(本题共5小题,每小题4分,满分20分) 1.22lim sin1x xx x →∞=+ 2 ; 2.当0x →时,()x α=与2()x kx β=是等价无穷小,则k =34; 3.设()1sin xy x =+,则d x yπ== d x π- ;)4.函数()e xf x x =在1x =处带有Peano 余项的二阶Taylor 公式为()223ee 2e(1)(1)(1)2x x x ο+-+-+- ; 5.已知函数32e sin ,0()2(1)9arctan ,0xa x x f xb x x x ⎧+<⎪=⎨-+≥⎪⎩可导,则a =1 ,b = -1 。
二.单项选择题(本题共4小题,每小题4分,满分16分) 6.设函数11()1ex xf x -=-,则 [ C ](A )0,1x x ==都是()f x 的第一类间断点(B )0,1x x ==都是()f x 的第二类间断点(C )0x =是()f x 的第一类间断点,1x =是()f x 的第二类间断点、(D )0x =是()f x 的第二类间断点,1x =是()f x 的第一类间断点7.设函数()y y x =由参数方程22ln(1)x t ty t ⎧=+⎨=+⎩确定,则曲线()y y x =在3x =处的切线与x 轴交点的横坐标是 [ C ] (A )1ln 238+ (B )1ln 238-+ (C )8ln 23-+ (D )8ln 23+ 8.以下四个命题中,正确的是 [ C ](A )若()f x '在(0,1)内连续,则()f x 在(0,1)内有界@(B )若()f x 在(0,1)内连续,则()f x 在(0,1)内有界 (C )若()f x '在(0,1)内有界,则()f x 在(0,1)内有界 (D )若()f x 在(0,1)内有界,则()f x '在(0,1)内有界9.当a 取下列哪个数值时,函数32()2912f x x x x a =-+-恰有两个不同的零点[ B ](A )2 (B )4 (C )6 (D )8、三.计算题(本题共5小题,每小题7分,满分35分) 10.011lim 1e x x x x -→+⎛⎫-⎪-⎝⎭()222000111e e 1lim lim lim 1e 1e x x x x x x x x x x x x x x x ----→→→++-++-+⎛⎫-== ⎪--⎝⎭ 20e 11lim xx x x -→-+=+22201()21lim x x x xο→+=+32= 11。
东南大学09-10-2医用高数期末试卷

09-10 邵雯 43211406共 4 页 第 1 页1.设sin ,0()1,0ax x f x x x x ⎧<⎪=⎨⎪-≥⎩,在0x =处连续 ,则a = ;2.若()sin f x x ''=,则()f x = ;3.积分()2sin +d x x x x ππ-=⎰ ;4.设z =d z = ; 5.改变积分次序后,2111d (,)d y y f x y x -=⎰⎰ ; 6.函数z =的间断点是 .7. 当0→x 时,无穷小量1cos2x -是22x 的 [ ]() A 高阶无穷小量; ()B 同阶但不等价的无穷小量;()C 等价无穷小量; ()D 低阶无穷小量.8.设32()6f x ax ax b =-+在区间[1,2]-上的最大值为3,最小值为29-,又知0a >则 )(A 2, 29a b ==-; )(B 3, 2a b ==; [ ])(C 2, 3a b ==; )(D 以上都不对.9. 微分方程95cos 2y y x ''+=的通解是 [ ]()A 3312e e cos 2x x C C x -++; ()B 12cos 2cos3sin 3x C x C x ++;()C ()312esin 2x C C x x -++; ()D 12sin 2cos3sin 3x C x C x ++. 10.设e ()()d xx F x f t t -=⎰,则=')(x F [ ]()A e (e )()x x f f x ----; ()B e (e )()x x f f x ---+;()C e (e )()x x f f x ---; () D e (e )()x x f f x --+.11. sin 2030sin d lim x x t t x →⎰12.设23e xyu x y =-+,求22u x ∂∂.09-10 邵雯 43211406共 4 页 第 2 页 13.设函数(,)z z x y =由方程23e 2x z z y -=+所确定,求3z z x y ∂∂+∂∂. 14.22e d 12e x x x x -⎰15.101)d x ⎰ 16.2d d y D xe x y -⎰⎰,其中D 是第一象限内由曲线224,9y x y x ==与1y =所围成的区域 17. 322211x x y y x x'+=++, 18. 2331y y y x '''+-=+ 19.据统计,某医院急性腹痛病人中30%患急性阑尾炎;急性阑尾炎病人中70%体温高于37.5︒ C ,而非急性阑尾炎病人中只有40%体温高于37.5︒ C. 若某急性腹痛者体温高于37.5︒ C ,求他患急性阑尾炎的概率。
东 南 大 学 高等数学下期末考试( A 卷)

共 5 页 第 1 页东 南 大 学 考 试 卷( A 卷)一. 填空题1.设一平面过原点及点()6,3,2-,且与平面428x y z -+=垂直,则此平面的方程是 .2. 幂级数()()1112ln 1nn nn x n ∞=-+∑的收敛域为 . 3. 交换积分次序:()()122001d ,d d ,d y yy f x y x y f x y x -+=⎰⎰⎰⎰.4. 设曲线C 为圆周221x y +=,则曲线积分()223d Cxy x s +-=⎰ .二. 单项选择题1.曲面24e 3zxy z +-=在点()1,2,0处的法线与直线12112x y z --==-的夹角为 [ ] (A) 4π (B) 3π (C) 2π(D) 0 2.设区域D 由直线,y x y x ==-和1x =围成,1D 是D 位于第一象限的部分,则[ ] (A )()()1sin d d 2d d DD xy y xy x y xy x y +=⎰⎰⎰⎰(B )()()()1sin d d 2sin d d DD xy y xy x y y xy x y +=⎰⎰⎰⎰(C )()()()()1sin d d 2sin d d DD xy y xy x y xy y xy x y +=+⎰⎰⎰⎰(D )()()sin d d 0Dxy y xy x y +=⎰⎰3.设∑为上半球面z =,则曲面积分∑的值为 [ ](A )4π (B )165π (C )163π (D )83π共 5 页 第 2 页4.二元函数(),f x y 在点()00,x y 处的两个偏导数()()0000,,,x y f x y f x y 存在是函数f 在该点可微的 [ ] (A ) 充分而非必要条件 (B )必要而非充分条件 (C )充分必要条件 (D )既非充分也非必要条件 三. (本题共5小题,每小题7分,满分3 5分)1.设(),z z x y =是由方程()2223x z f y z -=-所确定的隐函数,其中f 可微,求23z zyx x y∂∂+∂∂ .2.将函数()()2ln 2f x x x =+-展成2x -的幂级数。
06-07-2高数AB期末试卷答案 东南大学大一上学期高等数学试卷

1
a
1
a
e2a 1 e2 e2 e2a ch2 0 ,得 a ln ch2 为唯一驻点, I (a) 2e2a 0 , 2
I ln cha 为 I a 在[1,1]上的最小值,而最大值只能在端点 x 1, x 1 取得。
I
1
3 4
e2
1 4
e2
,
I
1
1 4
e2
5 4
e2
东南大学学生会 Students' Union of Southeast University
06-07-2高数AB期末试卷答案
止 于 至 善
一.填空题(本题共 9 小题,每小题 4 分,满分 36 分)
x
1. lim
x et2 dt
0
2;
x0 x(cos x 1) 3
2. y 3x 7 ;
1. 解: y2 2cot x y2 2cos x
y2 e 2 cot xdx 2
cos
2
xe
cot
xdx
dx
C
C
csc2
x
2 3
sin
x
2.解:
y
C1
cos
x
C2
sin
x
x
x 2
cos
x
,由题设条件得y(源自)0,y(0)3 2
,求得 C1
0, C2
1,于是
y
sin
x
x
x 2
cos
x
五.(本题满分 7 分) 解: I (a) 1 x a e2xdx a (a x)e2xdx 1(x a)e2xdx
1
1
a
a a e2xdx a xe2xdx 1 xe2xdx a 1e2xdx
东南大学考试卷(B)2006-2007学年高等数学期末试卷(后附答案)

东 南 大 学 考 试 卷(B 卷)课程名称 高等数学B 期末 考试学期06-07-3得分适用专业高数B考试形式闭卷 考试时间长度 150分钟一。
填空题(本题共10小题,每小题3分,满分30分)1.已知曲面z xy =上一点0000(,,)M x y z 处的法线垂直于平面390x y z +++=,则0x = ,0y = ,0z = ;2.已知三角形ABC ∆的顶点坐标为(0,1,2),(3,4,5),(6,7,8)A B C -,则ABC ∆的面积为 ;3. 曲线22221025x y y z ⎧+=⎪⎨+=⎪⎩在点(1,3,4)处的法平面为∏,则原点到∏的距离为 ;4.函数2u xyz =在点(1,1,1)处沿方向2=++e i j k 的方向导数等于 ;5.交换积分次序⎰⎰-221x -1-11- ),(dx x dy y x f = ;6.设222},,,{z y x r z y x r ++== ,则3rr div= ;7. 设正向闭曲线C :1x y +=,则曲线积分dy xy ydx x c 22+⎰= ;8.设2()e x f x =,则)0()2(n f= ;9.设0,0()1,0x f x x x ππ-<≤⎧=⎨+<≤⎩,其以2π为周期的Fourier 级数的和函数记为()S x ,则(3)S π= ;10.使二重积分()2244d Dxy σ--⎰⎰的值达到最大的平面闭区域D 为 。
14.求全微分方程22(cos 21)d (3)d 0x xy x x y y +++-+=的通解.二.(本题共2小题,每小题9分,满分18分) 11.计算二重积分()22d Dxy y σ+-⎰⎰,其中D 为由1,2y x y x ==及2y =围成的区域.12.计算三重积分zv Ω,其中Ω是yoz 平面上的直线121,3z y y =-=以及1z =围成的平面有界区域绕z 轴旋转一周得到的空间区域.三.(本题共2小题,每小题8分,满分16分) 13.计算曲线积分d Lz s ⎰,其中L 为圆锥螺线cos ,sin ,(02)x t t y t t z t t π===≤≤四.(15)(本题满分9分) 求函数(,)f x y xy =在圆周22(1)1x y -+=上的最大值和最小值.五.(16)(本题满分10分) 已知流体的流速函数 {}33333(,,),,2x y z y z z x z =--v ,求该流体流过由上半球面1z =+ z = 所围立体表面的外侧的流量.六.(17)(本题满分9分) 计算曲线积分(()ln d x y xy x y ++⎰,其中Γ是曲线1y =上从点(1,2)A 到点(0,1)C 的部分.七.(18)(本题满分8分) 设函数([0,1])f C ∈,且0()1f x ≤<,利用二重积分证明不等式:11100()d ()d 1()1()d f x x f x x f x f x x ≥--⎰⎰⎰06-07-3高数B 期末试卷参考答案及评分标准(A )一。
东南大学高数(上)至年期末考试(附答案)
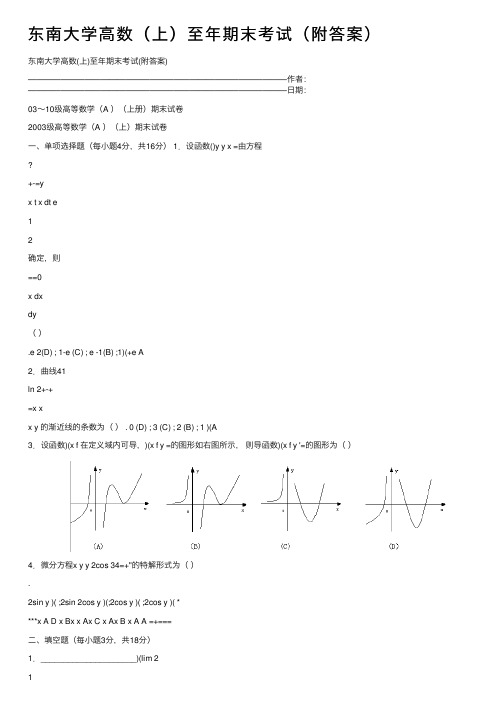
东南⼤学⾼数(上)⾄年期末考试(附答案)东南⼤学⾼数(上)⾄年期末考试(附答案)————————————————————————————————作者:————————————————————————————————⽇期:03~10级⾼等数学(A )(上册)期末试卷2003级⾼等数学(A )(上)期末试卷⼀、单项选择题(每⼩题4分,共16分) 1.设函数()y y x =由⽅程+-=yx t x dt e12确定,则==0x dxdy().e 2(D) ; 1-e (C) ; e -1(B) ;1)(+e A2.曲线41ln 2+-+=x xx y 的渐近线的条数为() . 0 (D) ; 3 (C) ; 2 (B) ; 1 )(A3.设函数)(x f 在定义域内可导,)(x f y =的图形如右图所⽰,则导函数)(x f y '=的图形为()4.微分⽅程x y y 2cos 34=+''的特解形式为().2sin y )( ;2sin 2cos y )(;2cos y )( ;2cos y )( ****x A D x Bx x Ax C x Ax B x A A =+===⼆、填空题(每⼩题3分,共18分)2.若)(cos 21arctanx f e x y +=,其中f 可导,则_______________=dxdy3.设,0,00,1sin )(=≠=αx x xx x f 若导函数)(x f '在0=x 处连续,则α的取值范围是__________。
4.若dt t t x f x ?+-=2324)(,则)(x f 的单增区间为__________,单减区间为__________. 5.曲线xxey -=的拐点是__________6.微分⽅程044='+''+'''y y y 的通解为__________________________=y 三、计算下列各题(每⼩题6分,共36分)1.计算积分dx x x+232)1(arctan 2.计算积分dx xxx ?5cos sin3. 计算积分dx e x x ?-2324. 计算积分?5.设)(x f 连续,在0=x 处可导,且4)0(,0)0(='=f f ,求xx dtdu u f t xtx sin ))((lim 3→6.求微分⽅程0)2(222=+-dx y x xydy 的通解四.(8分)求微分⽅程xxe y y y 223-=+'-''满⾜条件0,000='===x x y y 的特解五.(8分)设平⾯图形D 由x y x 222≤+与x y ≥所确定,试求D 绕直线2=x 旋转⼀周所⽣成的旋转体的体积。
07-08-2高数AB期末试卷 东南大学大一上学期高等数学试卷

六(16).(本题满分 8 分)设 f (x) 、 g(x) 满足 f (x) g(x) , g(x) 2ex f (x) ,且
f (0) 0, g(0) 2 ,求
0
g(x) 1 x
f (x) (1 x)2
dx
七(17).(本题满分 8 分)设直线 y ax (0 a 1) 与抛物线 y x2 所围成的图形面积 为 S1 ,它们与直线 x 1 所围成的图形面积为 S2 (1)试确定 a 的值,使 S1 S2 达到最小, 并求出最小值(2)求该最小值所对应的平面图形绕 x 轴旋转一周所得旋转体的体积
止 于 至 善
东南大学学生会 Students' Union of Southeast University
07-08-2高数AB期末试卷
一.填空题(本题共 9 小题,每小题 4 分,满分 36 分)
1
1. lim ex x x2
;
x0
sin 1
2.设 y x x ,则 dy
;
3.已知 f (3) 2,则 lim f (3 h) f (3)
n
n n2
3
n2
n 12
n2
n 3n2
;
8. 1 cos 2x cos x2 sin3 x dx
;
9.二阶常系数线性非齐次微分方程 y y 2sin x 的特解形式为
y*
.
二.计算下列积分(本题共 3 小题,每小题 7 分,满分 21 分)
10. 2 x2 2x x2 dx 0
;
h0 sin 2h
4.对数螺线 e 在 对应的点处的切线方程是
;
2
5.设 y y(x)
x 2
东南大学高数试卷及答案-06-07-3高数(B)期末考试

06-07-3高数B 期末试卷一。
填空题(本题共10小题,每小题3分,满分30分)1.已知曲面z xy =上一点0000(,,)M x y z 处的法线垂直于平面390x y z +++=,则0x = ,0y = ,0z = ;2.已知三角形ABC ∆的顶点坐标为(0,1,2),(3,4,5),(6,7,8)A B C -,则ABC ∆的面积为 ;3. 曲线22221025x y y z ⎧+=⎪⎨+=⎪⎩在点(1,3,4)处的法平面为∏,则原点到∏的距离为 ; 4.函数2u xyz =在点(1,1,1)处沿方向2=++e i j k 的方向导数等于 ;5.交换积分次序⎰⎰-221x -1-11- ),(dx x dy y x f = ;6.设222},,,{z y x r z y x r ++== ,则3rr div= ;7. 设正向闭曲线C :1x y +=,则曲线积分dy xy ydx x c 22+⎰= ;8.设2()e x f x =,则)0()2(n f= ;9.设0,0()1,0x f x x x ππ-<≤⎧=⎨+<≤⎩,其以2π为周期的Fourier 级数的和函数记为()S x ,则(3)S π= ;10.使二重积分()2244d Dxy σ--⎰⎰的值达到最大的平面闭区域D 为 。
二.(本题共2小题,每小题9分,满分18分) 11.计算二重积分()22d Dx y y σ+-⎰⎰,其中D 为由1,2y x y x ==及2y =围成的区域.12.计算三重积分zv Ω,其中Ω是yoz 平面上的直线121,3z y y =-=以及1z =围成的平面有界区域绕z 轴旋转一周得到的空间区域.三.(本题共2小题,每小题8分,满分16分) 13.计算曲线积分d Lz s ⎰,其中L 为圆锥螺线cos ,sin ,(02)x t t y t t z t t π===≤≤14.求全微分方程22(cos 21)d (3)d 0x xy x x y y +++-+=的通解.四.(15)(本题满分9分) 求函数(,)f x y xy =在圆周22(1)1x y -+=上的最大值和最小值.五.(16)(本题满分10分) 已知流体的流速函数 {}33333(,,),,2x y z y z z x z =--v ,求该流体流过由上半球面1z =z = 所围立体表面的外侧的流量.六.(17)(本题满分9分)计算曲线积分(()ln d x y xy x y ++⎰,其中Γ是曲线1y =上从点(1,2)A 到点(0,1)C 的部分.七.(18)(本题满分8分) 设函数([0,1])f C ∈,且0()1f x ≤<,利用二重积分证明不等式:11100()d ()d 1()1()d f x x f x x f x f x x ≥--⎰⎰⎰06-07-3高数B 期末试卷参考答案及评分标准(A )一。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
东 南 大 学 考 试 卷( A 卷)
)
一.填空题(本题共5小题,每小题4分,满分20分) 1.22lim sin
1
x x
x x →∞
=+ 2 ; 2.当0x →时
,()x α=与2
()x kx β=是等价无穷小,则
k =
34
; 3.设()1sin x
y x =+,则d x y
π
== d x π- ;
)
4.函数()e x
f x x =在1x =处带有Peano 余项的二阶Taylor 公式为
()223e
e 2e(1)(1)(1)2
x x x ο+-+
-+- ; 5.已知函数3
2e sin ,
0()2(1)9arctan ,0
x
a x x f x
b x x x ⎧+<⎪=⎨-+≥⎪⎩可导,则a =1 ,b = -1 。
二.单项选择题(本题共4小题,每小题4分,满分16分) 6.设函数1
1()1e
x x
f x -=
-,则 [ C ]
(A )0,1x x ==都是()f x 的第一类间断点(B )0,1x x ==都是()f x 的第二类间断点(C )0x =是()f x 的第一类间断点,1x =是()f x 的第二类间断点
、
(D )0x =是()f x 的第二类间断点,1x =是()f x 的第一类间断点
7.设函数()y y x =由参数方程22ln(1)
x t t
y t ⎧=+⎨=+⎩确定,则曲线()y y x =在3x =处的切线
与x 轴交点的横坐标是 [ C ] (A )1ln 238+ (B )1ln 238
-+ (C )8ln 23-+ (D )8ln 23+ 8.以下四个命题中,正确的是 [ C ]
(A )若()f x '在(0,1)内连续,则()f x 在(0,1)内有界
@
(B )若()f x 在(0,1)内连续,则()f x 在(0,1)内有界 (C )若()f x '在(0,1)内有界,则()f x 在(0,1)内有界 (D )若()f x 在(0,1)内有界,则()f x '在(0,1)内有界
9.当a 取下列哪个数值时,函数32
()2912f x x x x a =-+-恰有两个不同的零点[ B ]
(A )2 (B )4 (C )6 (D )8
、
三.计算题(本题共5小题,每小题7分,满分35分) 10.011lim 1e x x x x -→+⎛⎫
-
⎪-⎝
⎭
()
222000111e e 1lim lim lim 1e 1e x x x x x x x x x x x x x x x ----→→→++-++-+⎛⎫
-== ⎪--⎝⎭ 20e 11lim x
x x x -→-+=+22
201()21lim x x x x
ο→+=+32= 11。
()
3lim ln 12ln 1x x x →+∞
⎡⎤⎛⎫++
⎪⎢⎥⎝⎭⎣
⎦
】
()()()
33lim ln 12ln 1lim ln 2ln 12ln 1x x x x x x x -→+∞
→+∞⎡⎤⎡⎤⎛⎫⎛⎫++=+++ ⎪ ⎪⎢⎥⎢⎥⎝⎭⎝⎭⎣
⎦⎣⎦ 3
3lim ln 22x x x x x →+∞⎛⎫=⋅⋅+ ⎪⋅⎝⎭
3ln 2= 12
.1
1lim 1n n n
n →∞⎛+
+
++⎝
1111
n n n ≤++
≤++1n =
由夹逼定理得
11lim 11n n n n →∞
⎛+++
=
++⎝
*
13。
设,)
21(1
)(x x x f -=
求)()(x f n
12()12f x x x =+-()1!()(1)n n n n f x x
+=-112!(12)n n n x ++⋅+- 14.设函数()y y x =由方程2
2
2
sin()e 0x
x y xy ++-=所确定,求
d d y
x。
()222(22)cos e 20x x yy x y y xyy ''+++--=()()
()
222
22
2cos e d d 2cos x x x y y y
x y x x y ++-=-+ 四.(本题共4道题,满分29分)
#
15.(本题满分6分)如果以每秒3
50cm 的匀速给一个气球充气,假设气球内气压保持常值,且形状始终为球形,问当气球的半径为5cm 时,半径增加的速率是多少
324d d d d ,43d d d d V V r r V r t r t t ππ==⋅=d d 1
50100,d d 2r r t t ππ
==
16.(本题满分7分)证明不等式: 12
e 1e (0)x x
x x -≥+≥
设12
()e 1e
x x
F x x -=--11111
2
2222()e e
e e e 1e ()22x x x x x x
x x
F x x φ---+-⎛⎫'=--=--= ⎪⎝
⎭ 其中1
11
222
1()e
1,(0)e 10,()e 10(0)22x x x x x x φφφ++⎛⎫'=--=->=->≥ ⎪⎝⎭
¥
所以当0x ≥时,()x φ单增,又因(0)0φ>,所以()0x φ≥,从而()0F x '≥,所以()F x 单增,又因(0)0F =,所以当0x ≥时,()(0)0F x F ≥=,所要证不等式成立。
17.(本题满分8分)在抛物线214y x =
上求一点21,4P a a ⎛⎫
⎪⎝⎭
,(0)a >,使弦PQ 的长度最短,并求最短长度,其中Q 是过点P 的法线与抛物线的另一个交点。
法线方程2
224
a a
y x =-++,点Q 的坐标()222288,4a a a a ⎛⎫++ ⎪-
⎪⎝⎭
(2分) ()
()2
2
3
2
222
2
22484481()16a a a f a d a a a a a ⎛⎫++⎛⎫+ ⎪==++
-=
⎪ ⎪⎝⎭⎝
⎭
@
()()
2
22
5
848()0a
a
f a a
+-'=
=,
得唯一驻点a =
当0a <<()0f a '<,
当a >()0f a '>
,a =()f a 的唯一极小值点,因而是最小值点。
(
)
min ,P d =
18.(本题满分8分)设函数()f x 在闭区间[],a b 上连续,在开区间(),a b 内可导,且
(),()f a b f b a ==,证明:
(1) 至少存在一点(),c a b ∈,使得()f c c =;
(2) 至少存在互异的两点(),,a b ξη∈,使得 ()()1f f ξη''⋅= (1)令 ()()F x f x x =-
2()()(())(())()0F a F b f a a f b b b a ⋅=-⋅-=--<,[](),F x C a b ∈,所以
(),,()0,()c a b F c f c c ∃∈∍==即
(2)()()(),,()f c f a c b
a c f c a c a ξξ--'∃∈∍=
=
--, ()()(),,()f b f c a c
c b f b c b c
ηη--'∃∈∍==--,
()()1f f ξη''=。
