MATLAB语言与控制系统仿真-参考答案-第5章
MATLAB语言与控制系统仿真参考答案第5章

5、6控制系统的时域响应MATLAB 仿真实训5、6、1实训目的 123 4 5学会利用MATLAB绘制系统的单位阶跃响应曲线 ,掌握读取系统动态性能指标的方法 学会利用MATLAB 绘制系统的单位脉冲响应曲线的方法 掌握利用MATLAB 绘制系统的零输入响应曲线的方法 掌握利用MATLAB 绘制系统的一般输入响应曲线的方法 学会通过仿真曲线读取相关信息 ,并依据有关信息进行系统的时域分析。
5、6、2实训内容 1、编写程序求取下列各系统的单位阶跃响应 ,完成表5-5并记录相关曲线。
G(s) 16 ~2 s 3.2s 16 G 2(s) 16~2 s 2.4s 16 G a (s)16 s 21.6s 16G 4(s)16 -2s s 16解:>> n1=16; >> d 仁[1,3、2,16]; >> sys1=tf( n1,d1); >> step(sys1)-X r倚 25 3 7百'imeQ -4o.a■rp3±±-i_l r v>> n2=16; >> d2=[1,2、4,16]; >> sys2=tf( n2,d2); >> step(sys2)041.4D Q粘EEdE'luaJ 05 1 15 2 2.3 3 55 4<1.5Tim (lie)11-o02:>> n3=16;>> d3=[1,1、6,16];>> sys3=tf( n3,d3);>> step(sys3)lim* (t«c) >> n4=16; >> d4=[1,1,16];>> sys4=tf( n4,d4);>> step(sys4)表5-5序号nc maxt pt s (5%)计算值实验计算值实验计算值实验值1 0、4 4 1、2538 1、250、85690、8632、 18752、12 0、34 1 3723 1、370、 82330、8282、 91672、813 0、24 1、52661、530、80160、8 4 3750 4、940、125 4 1、6731 1、670、 79160、8037、 00007、33>> z1=0、4; w=4;cmax 1=1+exp(-z1*pi/sqrt(1-z1A2)); tp1=pi/(w*sqrt(1-z1A 2)); ts1=3、5/(z1*w); [cmax1,tp1,ts1] ans =>> z2=0、3;w=4;cmax2=1+exp(-z2*pi/sqrt(1-z2A2)); tp2=pi/(w*sqrt(1-z2A2)); ts2=3、5/(z2*w); [cmax2,tp2,ts2]ELIIds1、 2538 0、 85692、 1875ans =1、3723 0、82332、 9167>> z3=0、2;w=4;cmax3=1+exp(-z3*pi/sqrt(1-z3A2));tp3=pi/(w*sqrt(1-z3A2));ts3=3、5/(z3*w);[cmax3,tp3,ts3] ans =1、5266 0、8016 4、3750 >> z4=0、125;w=4;cmax4=1+exp(-z4*pi/sqrt(1-z4A2));tp4=pi/(w*sqrt(1-z4A2));ts4=3、5/(z4*w);[cmax4,tp4,ts4]ans =1、6731 0、7916 7、0000说明:对于二阶欠阻尼系统(0 1),若系统的闭环传递函数为则系统单位阶跃响应的输出最大值cmaxt pn 1 2调整时间估算值t s3.5n(以5%为误差带)t s 4.4(以2%为误差带)2、已知二阶系统的闭环传递函数如下,编程求取系统的单位阶跃响应并完成表峰值时间曲线。
系统辨识与自适应控制MATLAB仿真第5章模型参考自适应控制

[ky]
k
(t)
(t)
(5-13)
10
由式(5-13)和上式有
(t) k(t) (t)
(5-14)
式中,k(t) k(t) k。 于是可以看到,当 k(t) k 时, (t) 0
现给出规范化的性能指标函数:
J
(k)
1 2
2 (t)
m2
式中,m 1 2(t) 为规范化信号。
按优化理论,k变化使 J (k) 极小的方向应按负梯度确定:
梯度设计法来叙述。
例5.1.3 设有被控对象式(5-1),仍采用参考模型式(5-2)
和控制器结构式(5-6)。设aˆp (t) 是未知对象参数 ap的估计值,式
(5-6)中的 k(t) 由下式计算:
k(t) aˆp (t) am
(5-16)
为了产生参数估计aˆp (t) ,选择一个稳定的滤波器
系统辨识与自适应控制 MATLAB仿真
第5章模型参考自适应控制
1
模型参考自适应控制是一种不同于自校正控制的另一类自适应 控制形式。根据被控对象结构和控制要求,设计参考模型,使其输 出表达对输入指令的期望响应,然后通过模型输出与被控对象输出 之差来调整控制器参数,使差值趋向于零,也就是使对象输出向模 型输出靠近,最终达到完全一致。根据控制器参数更新方法的不 同,模型参考自适应控制可分为直接自适应控制和间接自适应控制 两种。推演参数自适应规律的方法有两种:梯度法和稳定理论法。 5.1简单自适应控制系统
本节目的:1)给出直接自适应控制和间接自适应控制的概 念;2)自适应控制系统的两种基本设计方法:李亚普诺夫法和2梯
度法。
5.1.1直接自适应控制
直接自适应控制是指控制器参数直接从一个自适应规律中获取
matlab的控制系统仿真与应用 第五章

[ n a n , n1 a n1 ,,1 a1 ] T 1
a n 2 a1 a n 3 1 0 1 0 0
a n 1 a n2 T b A b A n 1 b a1 1 函数bass_pp( ) 调用格式为:
1
2 n K v1 v2 vn
n v1 v2 vn
1
i K ,于是 vi
vi V,对于给定 i ,可以求出 i i
vi
一般说来
v1
v2 v n 可逆,否则重新选择 1 2 n 。
n V1 1 V2 2 Vn n
ai
(i=1,2,…,n - 1)为特征多项式系数,即
sI a s n a1 s n 1 an 1 s an 0
定义新的状态
ˆ x
x=T
ˆ x
1.变换法
由于系统可控,因此T可逆,系统变换成
1 1 ˆ T aTx ˆ T bu x
其中
0 0 1 T aT 0 an 1 0 0 an 1 0 1 0 a n 2 0 0 0 0 1 T b 1 0 a1 1
若假定 i 与A的特征值有相同的,或 i 中有重根时, i 1,2,, n 则可以对特征值相同的一个或几个加上一定的微小偏量,使之满足上面第一种 情形的条件。然后,再重新进行极点配置。如果效果不够理想,那么还可重新选择 1 2 n 阵来进行配置。 控制系统工具箱中place( )函数是基于鲁棒极点配置的算法,用来求取状态反馈 阵K,使得多输入系统具有指定的闭环极点P,即 p eig( A B * K ) 。 place( )函数调用格式为:
MATLAB教程课后实验报告题目及解答[第一至第五章]
![MATLAB教程课后实验报告题目及解答[第一至第五章]](https://img.taocdn.com/s3/m/512b4436f111f18583d05a96.png)
MATLAB教程实验报告实验项目名称实验一 Matlab基本操作学生姓名汪德旺专业班级 09数教(1)班学号 0301090131实验成绩日期一. 实验目的和要求1、了解MATLAB 的开发环境。
2、熟悉Matlab的基本操作。
3、掌握建立矩阵的方法。
4、掌握MATLAB各种表达式的书写规则以及常用函数的使用。
5、填写实验报告,实验报告文件取名为report1.doc。
6、于邮件附件形式将实验报告文件report1.doc 发到邮箱*******************,邮件主题为班级学号姓名,如:09数教1班15号张三。
二、实验内容1、先求下列表达式的值,然后显示MATLAB工作空间的使用情况并保存全部变量。
(1)0 122sin851ze =+(2)2212 1ln(0.4552i z x x+⎡⎤==⎢⎥-⎣⎦其中(3)0.30.330.3sin(0.3)ln,22a ae e az a--+=++a=-3.0,-2.9,-2.8,…, 2.8, 2.9,3.0(4)2242,011,12,0:0.5:2.521,23t tz t tt t t⎧≤<⎪=-≤<=⎨⎪-+≤<⎩其中t2.已知:1234413134787,2033657327 A B--⎡⎤⎡⎤⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦求下列表达式的值:(1)A+6*B和A-B+I(其中I为单位矩阵) (2)A*B和A.*B(3)A^3和A.^3(4)A/B和B\A(5)[A,B]和[A([1,3],:);B^2]3、设有矩阵A 和B123453016678910A=,B=17-691112131415023-41617181920970212223242541311⎡⎤⎢⎥⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎢⎥⎢⎥⎣⎦(1)求它们的乘积C 。
(2)将矩阵C 的右下角3*2子矩阵赋给D 。
(3)查看MATLAB 工作空间的使用情况。
控制系统数字仿真与CAD第五章习题答案
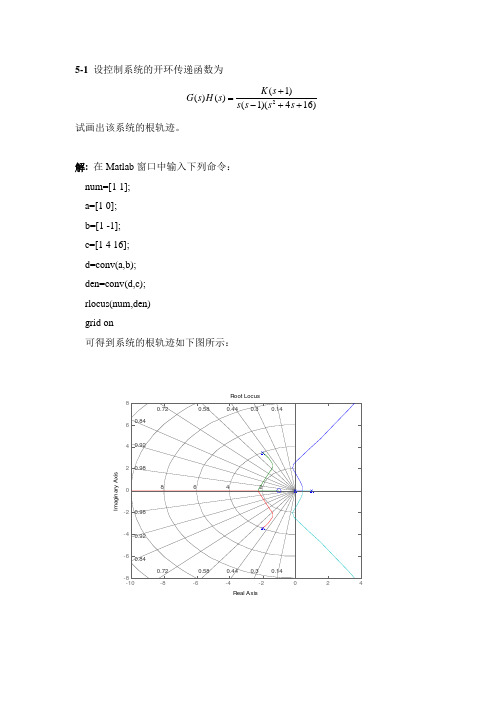
5-1 设控制系统的开环传递函数为2(1)()()(1)(416)K s G s H s s s s s +=-++试画出该系统的根轨迹。
解: 在Matlab 窗口中输入下列命令: num=[1 1]; a=[1 0]; b=[1 -1]; c=[1 4 16]; d=conv(a,b); den=conv(d,c); rlocus(num,den) grid on可得到系统的根轨迹如下图所示:5-2 某反馈控制系统的开环传递函数为()()()()24420KG s H s s s s s =+++ 试绘制其根轨迹。
解:在MATLAB 命令窗口中输入下列命令: num=1;den=conv(conv([1,0],[1,4]),[1,4,20]); rlocus(num,den) grid on 运行结果为:5-3.已知某系统传递函数为2180(1)100()11(1)[()20.31]40200200s W s s s s +=++⨯⨯+ 试绘制其伯德图。
解:分子分母同乘100*200得到280200(100)()(2.5100)(20.3200)200s W s s s s ⨯+=++⨯+在Matlab 窗口中输入下列命令:k=80*200; num=[1 100]; a=[2.5 100];b=[(1/200) 2*0.3 200]; den=conv(a,b); w=logspace(-1,1,100); [m,p]=bode(k*num,den,w); subplot(2,1,1);semilogx(w,20*log10(m)); grid;xlabel('Frequency(rad/sec)'); ylabel('Gain(dB)'); subplot(2,1,2); semilogx(w,p); grid;xlabel('Frequency(rad/s)'); ylabel('Phase(deg)');可绘制该系统的伯德图如下所示。
matlab语言第5章 Simulink仿真设计

信号源模块(Sources)
l Band-Limited White Noise:宽带限幅白噪声; l Chirp Signal:线性调频信号(频率随时间线性变 化的正弦波);
l Clock:时钟信号; l Constant:常数输入; l Counter Free-Running:自动计数器,发生溢出后, 从0开始重新计数;
分; lPID Controller:PID控制; lPID Controller(2DOF):二维PID控制; lState-Space:状态空间模型; lTransfer-Fcn:传递函数模型; lTransport Delay:输入信号延迟一个固定时间输出; lVariable Time Delay:输入可变时间信号延迟输出; lVariable Transport Delay:输入信号延迟可变输出; lZero-Pole:零极点模型。
3. Simulink模型的创建和仿真
以图示系统建立Simulink模型
模型建立
(1)启动工具箱 (2)建立Simulink空白模型 (3)根据系统模型选择模块 首先要确定所需模块所在的子模块库名称。例子中用 到的模块有单位阶跃信号﹑符号比较器﹑传递函数模 型和信号输出模块,分别属于信号源模块库﹑数学运 算模块库﹑连续模块库和输出模块库。在模块库浏览 器中打开相应的模块库,选择所需模块。
常用模块库(Commonly Used Blocks)
l Bus Creator:将输入信号合并为总线信号; l Bus Selector:由总线信号选择需要的信号输出; l Constant:常数信号; l Data Type Conversion:数据类型转换模块; l Delay:延迟模块; l Delux:信号分解模块; l Discrete-Time Integrator:离散时间积分器; l Gain:增益模块; l Ground:接地模块; l In1:输入模块; l Integrator:输入信号积分;
自动控制原理的MATLAB仿真与实践第5章 线性系统的频域分析

7
【例5-1】 试绘制惯性环节G(jω)=1/(2s+1)的Nyquist曲线 和Bode图。
解:程序如下:
>>clear
G=tf(1,[2,1]); %建立模型
nyquist (G); %绘制Nyquist图
figure(2); bode (G); %绘制Bode图
4
ngrid;ngrid(‘new’):绘制尼科尔斯坐标网格即等 20lgM圆和等角曲线组成的网格。‘new’代表清除以前 的图形,与后一个nichols()一起绘制网格。
semilogx(w,20*log10(mag)):绘制半对数坐标下的幅 频特性曲线。
semilogx(w,phase*180/pi):绘制半对数坐标下的相频 特性曲线。
MATLAB提供了许多用于线性系统频率分析 的函数命令,可用于系统频域的响应曲线、参数分析 和系统设计等。常用的频率特性函数命令格式及其功 能见表5-1。 bode (G):绘制传递函数的伯德图。其中:G为传递
函数模型,如:tf(), zpk(), ss()。 bode(num,den):num,den分别为传递函数的分子与
本节分别介绍利用MATLAB进行频域绘图和频 率分析的基本方法。
6
5.2.1 Nyquist曲线和Bode图
MATLAB频率特性包括幅频特性和相频特性。 当用极坐标图描述系统的幅相频特性时,通常称为 奈奎斯特(Nyquist)曲线;用半对数坐标描述系 统的幅频特性和相频特性时,称为伯德(Bode) 图;在对数幅值-相角坐标系上绘制等闭环参数( M和N)轨迹图,称为尼克尔斯(Nichols)图。
运行结果如图5-2所示。
2.5 应用MATLAB控制系统仿真-计算机-

图2-74 位置随动系统的结构图第一步求闭环传递函数GB (s)=q c(s) /q r(s),求解过程及结果如图2-75所示。第二步利用step()函数计算参考输入q r (t)为单阶跃信号时输出q c (t)的响应。
图2-63 分析弹簧—重物—阻尼器的MATLAB指 弹簧—重物—阻尼器的自由运动曲线MATLAB可分析以传递函数形式描述的系统。分子多项式和分母多项式都必须在MATLAB指令中指定。
在MATLAB中多项式由行向量组成,这些行向量包含了降次
>>y0=0.15;wn=sqrt(2);>>zeta1=3/(2*sqrt(2)); zeta2=1/(2*sqrt(2));
>>t=[0:0.1:10];>>unforced
(a)MATLAB指令窗口
* 计算系统在给定初始条件下的自由运动 t1=acos(zeta1)*ones(1,length(t)); t2=acos(zeta2)*ones(1,length(t));c1=(y0/sqrt(1-zeta1^2)); c2=(y0/sqrt(1-zeta2^2)); y1=c1*exp(-zeta1*wn*t)sin(wn*sqrt(1-zeta1^2)*t+t1); y2=c2*exp(-zeta2*wn*t)sin(wn*sqrt(1-zeta2^2)*t+t2);
图2-76 位置随动系统的阶跃响应曲线图2-76给出了位置随动系统的阶跃响应曲线。用plot()函数用画出y(t)曲线,grid函数用于给图形加上网格。
小结
本章讨论了如何建立控制系统以及元部件的数学模型问题。本章所涉及的数学模型共有三种,即微分方程、传递函数、结构图或信号流图。利用传递函数研究线性系统,可根据传递函数的极点和零点分布判定系统对不同输入信号的响应特性。利用结构图或信号流图可以了解系统中的每个变量,还可以通过梅逊(Mason)公式,方便地求得系统输入输出间的传递函数。利用MATLAB软件可求解系统在不同参数和输入情况下的响应。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
5.6 控制系统的时域响应MATLAB 仿真实训5.6.1实训目的 1. 学会利用MATLAB 绘制系统的单位阶跃响应曲线,掌握读取系统动态性能指标的方法; 2. 学会利用MATLAB 绘制系统的单位脉冲响应曲线的方法; 3. 掌握利用MATLAB 绘制系统的零输入响应曲线的方法; 4. 掌握利用MATLAB 绘制系统的一般输入响应曲线的方法;5.学会通过仿真曲线读取相关信息,并依据有关信息进行系统的时域分析。
5.6.2实训内容1.编写程序求取下列各系统的单位阶跃响应,完成表5-5并记录相关曲线。
162.316)(21++=s s s G 164.216)(22++=s s s G 166.116)(23++=s s s G 1616)(24++=s s s G 解:>> n1=16;>> d1=[1,3.2,16]; >> sys1=tf(n1,d1); >> step(sys1)>> n2=16;>> d2=[1,2.4,16]; >> sys2=tf(n2,d2); >> step(sys2)>> n3=16;>> d3=[1,1.6,16]; >> sys3=tf(n3,d3); >> step(sys3)>> n4=16;>> d4=[1,1,16]; >> sys4=tf(n4,d4); >> step(sys4)w=4;cmax1=1+exp(-z1*pi/sqrt(1-z1^2)); tp1=pi/(w*sqrt(1-z1^2));ts1=3.5/(z1*w);[cmax1,tp1,ts1]ans =1.2538 0.85692.1875 >> z2=0.3;w=4;cmax2=1+exp(-z2*pi/sqrt(1-z2^2)); tp2=pi/(w*sqrt(1-z2^2));ts2=3.5/(z2*w);[cmax2,tp2,ts2]ans =1.3723 0.82332.9167 >> z3=0.2; w=4;cmax3=1+exp(-z3*pi/sqrt(1-z3^2)); tp3=pi/(w*sqrt(1-z3^2)); ts3=3.5/(z3*w); [cmax3,tp3,ts3]ans =1.5266 0.8016 4.3750 >> z4=0.125; w=4;cmax4=1+exp(-z4*pi/sqrt(1-z4^2)); tp4=pi/(w*sqrt(1-z4^2)); ts4=3.5/(z4*w); [cmax4,tp4,ts4] ans =1.6731 0.7916 7.0000说明:对于二阶欠阻尼系统(10<<ξ),若系统的闭环传递函数为2222)(nn ns s s Φωξωω++= 则系统单位阶跃响应的输出最大值21max 1ξξπ--+=ec峰值时间21ξωπ-=n p t调整时间估算值ns t ξω5.3= (以5%为误差带) ns t ξω4.4=(以2%为误差带)2.已知二阶系统的闭环传递函数如下,编程求取系统的单位阶跃响应并完成表5-6,记录相关曲线。
(1)828)(21++=s s s Φ(2)10210)(22++=s s s Φ(3)12212)(23++=s s s Φ(4)16216)(24++=s s s Φ>> n1=8;>> d1=[1,2,8]; >> sys1=tf(n1,d1); >> impulse(sys1)>> n2=10;>> d2=[1,2,10]; >> sys2=tf(n2,d2); >> impulse(sys2)>> n3=12;>> d3=[1,2,12]; >> sys3=tf(n3,d3); >> impulse(sys3)>> n4=16;>> d4=[1,2,16]; >> sys4=tf(n4,d4); >> impulse(sys4)表5-63.已知某单位负反馈系统的开环传递函数为)11.0)(1(5)(++=s s s s G若系统的输入信号分别为(1)t u =1, )20,0(∈t (2)tteu 5.02-=, )20,0(∈t(3)te t u 5.03)2sin(-=,)20,0(∈t(4)te t u 34)2cos(-=,)20,0(∈t编写程序分别求取系统的在给定的输入信号下的响应,记录相应的曲线。
>> n=5;>> d=conv([1,1,0],[0.1,1]); >> [nc,dc]=cloop(n,d) >>sysc=tf(nc,dc); >> t=0:0.01:20; >> u1=t;>> u2=t.*exp(-0.5*t);>> u3=sin(2*t).*exp(-0.5*t); >> u4=cos(2*t).*exp(-3*t); >>subplot(221);lsim(sysc,u1,t);subplot(222);lsim(sysc,u2,t);subplot(223);lsim(sysc,u3,t);subplot(224);lsim(sysc,u4,t);4.编写程序绘制以下系统的单位阶跃响应曲线和单位脉冲响应曲线。
(1)u x x ⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡--=114001[]u x y 65.30+=>> a1=[-1,0;0,-4]; >> b1=[1;1]; >> c1=[0,3.5]; >> d1=6;>> sys1=ss(a1,b1,c1,d1);>> subplot(1,2,1);step(sys1);subplot(1,2,2);impulse(sys1);(2)u x x ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-=733412219553641251308342 x y ⎥⎦⎤⎢⎣⎡=05132301 >> a2=[2,4,3,8;0,3,1,5;2,1,4,6;3,5,-5,9]; >> b2=[1,2;2,1;4,3;3,7]; >> c2=[1,0,3,2;3,1,5,0]; >> d2=0;>> sys2=ss(a2,b2,c2,d2);>> step(sys2)>> impulse(sys2)(3))53)(4)(5()8.13.6)(2(5)(23++++++=s s s s s s s G >> sysa=zpk([-2],[-5;-4],[5]) Zero/pole/gain: 5 (s+2) ----------- (s+5) (s+4)>> sysb=tf([6.3,1.8],[1,3,0,5]) Transfer function: 6.3 s + 1.8 --------------- s^3 + 3 s^2 + 5 >> sys3=sysa*sysb Zero/pole/gain:31.5 (s+2) (s+0.2857)------------------------------------------------------- (s+5) (s+4) (s+3.426) (s^2 - 0.426s + 1.459) >> step(sys3)>> impulse(sys3)5.有三个系统如图5-17(a)、(b)、(c)所示,编程分别绘制各系统的单位阶跃响应和单位脉冲响应。
(a)>> sysa1=tf([5],[1,3,5]);>> sysa2=zpk([-2],[0;-3;-5],[20]);>> sysa3=tf([0.1,1],[2,1]);>> sysa=sysa1*sysa2*sysa3Zero/pole/gain:5 (s+2) (s+10)------------------------------------------------s (s+3) (s+5) (s+0.5) (s^2 + 3s + 5)>> step(sysa)>> impulse(sysa)(b)>> sysb1=tf([22,1],[1,5,23,15]);>> sysb2=zpk([-6],[0;-3;-10],[0.2]);>> sysb3=5*tf([0.6,1],[2,1])*tf([1.5,1],[3,7,1]);>> sysb=sysb1-sysb2+sysb3Zero/pole/gain:0.75 (s+32.84) (s+10.05) (s+3.02) (s+2.269) (s+0.5509) (s-0.0083) (s^2 + 0.6734s + 0.3865) -------------------------------------------------------------------------------------------------------------------- s (s+3) (s+2.18) (s+0.7582) (s+0.5) (s+10) (s+0.1529) (s^2 + 4.242s + 19.78)>> step(sysb)>> impulse(sysb)(c)>> G1=tf([10],[1,2,0]);>> G2=cloop(tf([1],[0.5,1]),1)Transfer function:1------------0.5 s + 1>> G2=feedback(tf([1],[0.5,1]),1,-1)Transfer function:1------------0.5 s + 2>> G=G1*G2Transfer function:10---------------------------0.5 s^3 + 3 s^2 + 4 s>> H=tf([3],[1,6,0])+tf([1],[0.1,1])Transfer function:s^2 + 6.3 s + 3-----------------------------0.1 s^3 + 1.6 s^2 + 6 s>> sys=G/(1+G*H)Transfer function:0.5 s^6 + 11 s^5 + 82 s^4 + 244 s^3 + 240 s^2------------------------------------------------------------------------------------------------------------------ 0.025 s^9 + 0.7 s^8 + 7.6 s^7 + 41.2 s^6 + 123 s^5 + 231.1 s^4 + 340 s^3 + 342 s^2 + 120 s >> step(sys)>> impulse(sys)6.设三阶系统闭环传递函数为81066)52()()(232+++++==Φs s s s s s R s C s )(试绘制其单位阶跃响应在]3.5,2.1[∈t 内的部分响应曲线。
