《解析几何》第三章(吕林根-许子道第四版)
解析几何课件(吕林根许子道第四版)

下一页
返回
定理1.4.2 如果向量e1, e2不共线,那么向量 r与
e1 , e2共面的充要条件是 r可以用向量 e1 , e2线性表示,
或者说向量 r可以分解成e1 , e2的线性组合,即
r xe1 ye2
(1.4-2)
并且系数x, y被e1 , e2 , r唯一确定. 这时e1 , e2叫做平面上向量的基底 . 定理1.4.3 如果向量e1 , e2 , e3不共面,那么空间
OC OA OB
下一页
返回
B
C
O
A
这种求两个向量和的方法叫做平行四边形法则
定理1.2.2 向量的加法满足下面的运算规律:
(1)交换律:
a
b
b
a.
(2)结合律:
a
b
c
(a
b)
c
a
(b
c).
(3)
a
(a)
0.
上一页 下一页
例2 证明四面体对边中点的连线交于一点,且
互相平分.
证 设四面体ABCD一组
D
对边AB,CD的中点E, F的连
线为EF ,它的中点为P1,其余
e3
两组对边中点分别为 P2 , P3 ,
下只需证P1 , P2 , P3三点重合
就可以了.取不共面的三向量 A
F
P1
e2
C
AB e1 , AC e2 , AD e3 ,
在不全为零的 n个数1 , 2 ,, n使得
1 a1 2 a2 n an=0,
(1.4 4)
解析几何_吕林根_许子道_第四版_课后习题解答
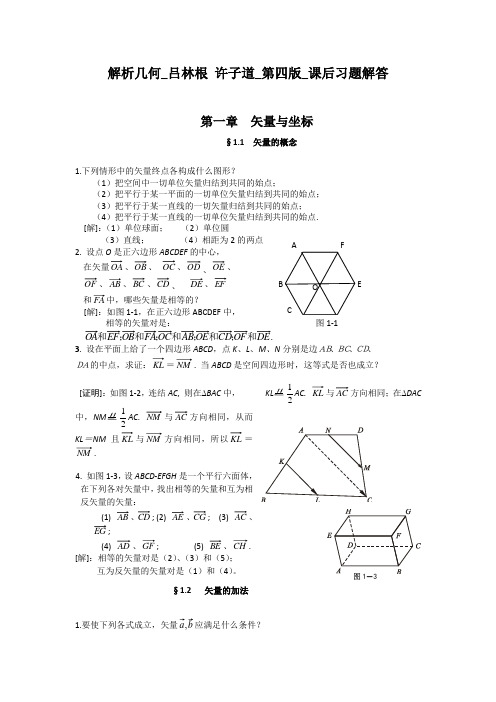
解析几何_吕林根 许子道_第四版_课后习题解答第一章 矢量与坐标§1.1 矢量的概念1.下列情形中的矢量终点各构成什么图形?(1)把空间中一切单位矢量归结到共同的始点;(2)把平行于某一平面的一切单位矢量归结到共同的始点; (3)把平行于某一直线的一切矢量归结到共同的始点;(4)把平行于某一直线的一切单位矢量归结到共同的始点. [解]:(1)单位球面; (2)单位圆(3)直线; (4)相距为2的两点2. 设点O 是正六边形ABCDEF 的中心,在矢量OA 、OB 、 OC 、OD 、OE 、 OF 、AB 、BC 、CD 、 DE 、EF 和FA 中,哪些矢量是相等的?[解]:如图1-1,在正六边形ABCDEF 中,相等的矢量对是: 图1-1 .DE OF CD OE AB OC FA OB EF OA 和;和;和;和;和3. 设在平面上给了一个四边形ABCD ,点K 、L 、M 、N 分别是边AB、BC、CD、DA的中点,求证:KL =NM . 当ABCD 是空间四边形时,这等式是否也成立?[证明]:如图1-2,连结AC , 则在∆BAC 中,21AC. KL 与AC 方向相同;在∆DAC 中,21AC . NM 与AC 方向相同,从而KL =NM 且KL 与NM 方向相同,所以KL =NM .4. 如图1-3,设ABCD -EFGH 是一个平行六面体,在下列各对矢量中,找出相等的矢量和互为相反矢量的矢量:(1) AB 、CD ; (2) AE 、CG ; (3) AC 、EG ;(4) AD 、GF ; (5) BE、CH . [解]:相等的矢量对是(2)、(3)和(5); 互为反矢量的矢量对是(1)和(4)。
§1.2 矢量的加法1.要使下列各式成立,矢量b a ,应满足什么条件?E(1=+ (2+=+ (3-=+ (4+=- (5=[解]:(1)b a ,-=+(2)b a ,+=+(3≥且b a ,-=+ (4)b a ,+=(5)b a ,≥-=-§1.3 数量乘矢量1 试解下列各题.⑴ 化简)()()()(→→→→-⋅+--⋅-b a y x b a y x .⑵ 已知→→→→-+=3212e e e a ,→→→→+-=321223e e e b ,求→→+b a ,→→-b a 和→→+b a 23.⑶ 从矢量方程组⎪⎩⎪⎨⎧=-=+→→→→→→by x ay x 3243,解出矢量→x ,→y .解 ⑴→→→→→→→→→→→→→→-=+-+---+=-⋅+--⋅-ay b x b y a y b x a x b y a y b x a x b a y x b a y x 22)()()()(⑵ →→→→→→→→→→+=+-+-+=+3132132142232e e e e e e e e b a ,→→→→→→→→→→→-+-=+---+=-321321321342)223(2e e e e e e e e e b a , →→→→→→→→→→→-+-=+---+=-3213213217103)223(2)2(323e e e e e e e e e b a . 2 已知四边形ABCD 中,→→→-=c a AB 2,→→→→-+=c b a CD 865,对角线→AC 、→BD 的中点分别为E 、F ,求→EF .解 →→→→→→→→→→→-+=-+-+=+=c b a c a c b a AB CD EF 533)2(21)865(212121.3 设→→→+=b a AB 5,→→→+-=b a BC 82,)(3→→→-=b a CD ,证明:A 、B 、D 三点共线. 证明 ∵→→→→→→→→→→=+=-++-=+=AB b a b a b a CD BC BD 5)(382∴→AB 与→BD 共线,又∵B 为公共点,从而A 、B 、D 三点共线.4 在四边形ABCD 中,→→→+=b a AB 2,→→→--=b a BC 4,→→→--=b a CD 35,证明ABCD 为梯形.证明∵→→→→→→→→→→→→→=--=-+--++=++=BC b a b a b a b a CD BC AB AD 2)4(2)35()4()2( ∴→AD ∥→BC ,∴ABCD 为梯形.6. 设L 、M 、N 分别是ΔABC 的三边BC 、CA 、AB 的中点,证明:三中线矢量AL , BM ,CN 可 以构成一个三角形.[证明]: )(21AC AB AL +=)(21BC BA BM +=)(21CB CA CN +=0)(21=+++++=++∴CB CA BC BA AC AB CN BM AL从而三中线矢量CN BM AL ,,构成一个三角形。
解析几何课件(吕林根许子道第四版)(精)

返回
第一章 向量与坐标
§1.3 数乘向量
表示与非零向量 设ea a 同方向的单位向量,
按照向量与数的乘积的规定,
a | a | ea
a . ea |a |
上式表明:一个非零向量除以它的模的结果是 一个与原向量同方向的单位向量.
上一页下一页ຫໍສະໝຸດ §1.2 向量的加法定 义1.2.1 设 已 知 矢 量 a、 b ,以空间任意一点 O为 始 点 接连作矢量 OA a, AB b得 一 折 线 OAB, 从 折 线 的 端 点 O到 另 一 端 点 B的 矢 量 OB c , 叫 做 两 矢 量 a与b的 和 , 记 做 cab
(2)结合律: a b c (a b ) c a (b c ). (3) a ( a ) 0.
上一页
下一页
返回
第一章 向量与坐标
§1.2 向量的加法
有限个矢量 a1 , a2 ,an 相 加 可 由 矢 量 的 三 角 求 形和 法则推广
解析几何课件(第四版)
吕林根 许子道等编
解析几何的基本思想是用代数的方法来研究 几何,为将代数运算引导几何中,采用的最根本最 有效的做法----有系统的把空间的几何结构代数 化,数量化.
第一章 第二章 第三章 第四章 向量与坐标 轨迹与方程 平面与空间直线 柱面锥面旋转曲面与二次曲面
第五章 二次曲线的一般理论
下一页
返回
第一章 向量与坐标
§1.4向量的线性关系与向量的分解
定理1.4.2 如果向量 e1 , e 2 不共线,那么向量 r与 e1 , e2 共面的充要条件是 r可以用向量 e1 , e2线性表示, 或者说向量 r可以分解成 e1 , e2的线性组合,即 r x e1 y e2 并且系数 x , y被 e1 , e2 , r唯一确定 . 这时 e1 , e 2叫做平面上向量的基底 . 定理1.4.3 如果向量 e1 , e 2 , e 3 不共面,那么空间 任意向量 r可以由向量 e1 , e 2 , e 3线性表示,或说空间 ( ) 1.4-2
【推荐下载】解析几何第四版答案-推荐word版 (17页)

本文部分内容来自网络整理,本司不为其真实性负责,如有异议或侵权请及时联系,本司将立即删除!== 本文为word格式,下载后可方便编辑和修改! ==解析几何第四版答案篇一:解析几何第四版吕林根课后习题答案第三章第三章平面与空间直线3.1平面的方程1.求下列各平面的坐标式参数方程和一般方程:(1)通过点M1(3,1,?1)和点M2(1,?1,0)且平行于矢量{?1,0,2}的平面(2)通过点M1(1,?5,1)和M2(3,2,?2)且垂直于xoy坐标面的平面;(3)已知四点A(5,1,3),B(1,6,2),C(5,0,4)D(4,0,6)。
求通过直线AB且平行于直线CD的平面,并求通过直线AB且与?ABC平面垂直的平面。
解:(1)? M1M2?{?2,?2,1},又矢量{?1,0,2}平行于所求平面,故所求的平面方程为:?x?3?2u?v??y?1?2u?z??1?u?2v?一般方程为:4x?3y?2z?7?0(2)由于平面垂直于xoy面,所以它平行于z轴,即{0,0,1}与所求的平面平行,又M1M2?{2,7,?3},平行于所求的平面,所以要求的平面的参数方程为:?x?1?2u??y??5?7u ?z?1?3u?v?一般方程为:7(x?1)?2(y?5)?0,即7x?2y?17?0。
(3)(ⅰ)设平面?通过直线AB,且平行于直线CD: ?{?4,5,?1},?{?1,0,2} 从而?的参数方程为:?x?5?4u?v??y?1?5u?z?3?u?2v?一般方程为:10x?9y?5z?74?0。
(ⅱ)设平面??通过直线AB,且垂直于?ABC所在的平面? ?{?4,5,?1}, ??{?4,5,?1}?{0,?1,1}?{4,4,4}?4{1,1,1}均与??平行,所以??的参数式方程为:?x?5?4u?v??y?1?5u?v ?z?3?u?v?一般方程为:2x?y?3z?2?0.2.化一般方程为截距式与参数式: ?:x?2y?z?4?0. 解:?与三个坐标轴的交点为:(?4,0,0),(0?2,0),(0,0,4),xyz???1. ?4?24所以,它的截距式方程为:又与所给平面方程平行的矢量为:{4,?2,0},{4,0,4},? 所求平面的参数式方程为:?x??4?2u?v??y??u?z?v?3.证明矢量v?{X,Y,Z}平行与平面Ax?By?Cz?D?0的充要条件为:AX?BY?CZ?0. 证明:不妨设A?0,则平面Ax?By?Cz?D?0的参数式方程为:DBC?x???u?v?AAA??y?u?z?v??BC故其方位矢量为:{?,1,0},{?,0,1},AA从而平行于平面Ax?By?Cz?D?0的充要条件为:v,{?BC,1,0},{?,0,1}共面? AAXYB?1AC?0A? AX?BY?CZ?0.Z0?0 14. 已知连接两点A(3,10,?5),B(0,12,z)的线段平行于平面7x?4y?z?1?0,求B 点的z坐标.解: ??{?3,2,5?z} 而AB平行于7x?4y?z?1?0 由题3知:(?3)?7?2?4?(z?5)?0 从而z?18.5. 求下列平面的一般方程.⑴通过点?1?2,?1,1?和?2?3,?2,1?且分别平行于三坐标轴的三个平面; ⑵过点??3,2,?4?且在x轴和y轴上截距分别为?2和?3的平面; ⑶与平面5x?y?2z?3?0垂直且分别通过三个坐标轴的三个平面; ⑷已知两点?1?3,?1,2?,?2?4,?2,?1?,求通过?1且垂直于?1,?2的平面; ⑸原点?在所求平面上的正射影为??2,9,?6?;⑹求过点?1?3,?5,1?和?2?4,1,2?且垂直于平面x?8y?3z?1?0的平面.x?2解:平行于x轴的平面方程为y?1z?1?1000?0.即z?1?0.11同理可知平行于y轴,z轴的平面的方程分别为z?1?0,x?y?1?0. ⑵设该平面的截距式方程为xyz24???1,把点??3,2,?4?代入得c?? ?2?3c19故一般方程为12x?8y?19z?24?0.⑶若所求平面经过x轴,则?0,0,0?为平面内一个点,?5,1,?2?和?1,0,0?为所求平面的方位矢量,x?0∴点法式方程为y?0z?010?2?0 051∴一般方程为2y?z?0.同理经过y轴,z轴的平面的一般方程分别为2x?5z?0,x?5y?0.1,?1,?3?.?1?2垂直于平面?, ⑷?1?2??1,?1,?3?,平面?通过点?1?3,?1,2?, ∴该平面的法向量n??因此平面?的点位式方程为?x?3???y?1??3?z?2??0. 化简得x?y?3z?2?0.??. (5) op??2,9,?6?p?op????4?81?36?11.op?p?n0?11?cos?,cos?,cos????2,9,?6?. 296,cos??,cos???. 111111296y?z?11?0. 则该平面的法式方程为:x?111111∴ cos??既 2x?9y?6z?121?0.1,?8,3?,M1M2??(6)平面x?8y?3z?1?0的法向量为n??1,6,1?,点从?4,1,2? ?x?4写出平面的点位式方程为y?1z?2?863111?83?0,则A???26,61B?313?2,C??14,D??26?4?2?28??74, 111则一般方程Ax?By?Cz?D?0,即:13x?y?7z?37?0. 6.将下列平面的一般方程化为法式方程。
解析几何_吕林根_许子道_第四版_课后习题解答

解析几何_吕林根 许子道_第四版_课后习题解答第一章 矢量与坐标§1.1 矢量的概念1.下列情形中的矢量终点各构成什么图形?(1)把空间中一切单位矢量归结到共同的始点;(2)把平行于某一平面的一切单位矢量归结到共同的始点; (3)把平行于某一直线的一切矢量归结到共同的始点;(4)把平行于某一直线的一切单位矢量归结到共同的始点. [解]:(1)单位球面; (2)单位圆(3)直线; (4)相距为2的两点2. 设点O 是正六边形ABCDEF 的中心,在矢量OA 、OB 、 OC 、OD 、OE 、 OF 、AB 、BC 、CD 、 DE 、EF 和FA 中,哪些矢量是相等的?[解]:如图1-1,在正六边形ABCDEF 中,相等的矢量对是: 图1-1 .DE OF CD OE AB OC FA OB EF OA 和;和;和;和;和3. 设在平面上给了一个四边形ABCD ,点K 、L 、M 、N 分别是边AB、BC、CD、DA的中点,求证:KL =NM . 当ABCD 是空间四边形时,这等式是否也成立?[证明]:如图1-2,连结AC , 则在∆BAC 中,21AC. KL 与AC 方向相同;在∆DAC 中,21AC . NM 与AC 方向相同,从而KL =NM 且KL 与NM 方向相同,所以KL =NM .4. 如图1-3,设ABCD -EFGH 是一个平行六面体,在下列各对矢量中,找出相等的矢量和互为相反矢量的矢量:(1) AB 、CD ; (2) AE 、CG ; (3) AC 、EG ;(4) AD 、GF ; (5) BE、CH . [解]:相等的矢量对是(2)、(3)和(5); 互为反矢量的矢量对是(1)和(4)。
§1.2 矢量的加法1.要使下列各式成立,矢量b a ,应满足什么条件?E(1=+ (2+=+ (3-=+ (4+=- (5=[解]:(1)b a ,-=+(2)b a ,+=+(3≥且b a ,-=+ (4)b a ,+=(5)b a ,≥-=-§1.3 数量乘矢量1 试解下列各题.⑴ 化简)()()()(→→→→-⋅+--⋅-b a y x b a y x .⑵ 已知→→→→-+=3212e e e a ,→→→→+-=321223e e e b ,求→→+b a ,→→-b a 和→→+b a 23.⑶ 从矢量方程组⎪⎩⎪⎨⎧=-=+→→→→→→by x ay x 3243,解出矢量→x ,→y .解 ⑴→→→→→→→→→→→→→→-=+-+---+=-⋅+--⋅-ay b x b y a y b x a x b y a y b x a x b a y x b a y x 22)()()()(⑵ →→→→→→→→→→+=+-+-+=+3132132142232e e e e e e e e b a ,→→→→→→→→→→→-+-=+---+=-321321321342)223(2e e e e e e e e e b a , →→→→→→→→→→→-+-=+---+=-3213213217103)223(2)2(323e e e e e e e e e b a . 2 已知四边形ABCD 中,→→→-=c a AB 2,→→→→-+=c b a CD 865,对角线→AC 、→BD 的中点分别为E 、F ,求→EF .解 →→→→→→→→→→→-+=-+-+=+=c b a c a c b a AB CD EF 533)2(21)865(212121.3 设→→→+=b a AB 5,→→→+-=b a BC 82,)(3→→→-=b a CD ,证明:A 、B 、D 三点共线. 证明 ∵→→→→→→→→→→=+=-++-=+=AB b a b a b a CD BC BD 5)(382∴→AB 与→BD 共线,又∵B 为公共点,从而A 、B 、D 三点共线.4 在四边形ABCD 中,→→→+=b a AB 2,→→→--=b a BC 4,→→→--=b a CD 35,证明ABCD 为梯形.证明∵→→→→→→→→→→→→→=--=-+--++=++=BC b a b a b a b a CD BC AB AD 2)4(2)35()4()2( ∴→AD ∥→BC ,∴ABCD 为梯形.6. 设L 、M 、N 分别是ΔABC 的三边BC 、CA 、AB 的中点,证明:三中线矢量AL , BM ,CN 可 以构成一个三角形.[证明]: )(21AC AB AL +=)(21BC BA BM +=)(21CB CA CN +=0)(21=+++++=++∴CB CA BC BA AC AB CN BM AL从而三中线矢量CN BM AL ,,构成一个三角形。
3-1解析几何吕林根第四版

R(0,0,c)(其中a 0,b 0,c 0),求此平面方程.
z
将 A D, B D, C D,
c
a
b
c
代入所设方程
Ax By Cz D 0,
o
xa
y
b
得
x y z 1 平面的截距式方程
a bc
x轴上截距 y轴上截距 z 轴上截距
5. 平面的截距式方程
若已知三点为平面与三坐标的交点 M1 a,0,0, M2 0,b,0,
化简得
n1
n2
2x 3 y z 6 0.
nr
例 求过点(1,0,-1), 且平行于向量 n1 {2,1,1} 和 n1 {1, 1, 0} 的平
面方程.
解 取所求平面法向量 n n1 n2 {1,1, 3},
所求平面方程为
1 ( x 1) 1 ( y 0) 3 ( z 1) 0, n1
为所求平面之法向.
故得平面方程为: r
( x x1, y y1, z z1) n 14( x 2) 9( y 1) (z 4)
14x 9 y z 15 0
或
r ( x x2, y y2, z z2) n
14( x 1) 9( y 3) (z 2)
14x 9 y-z 15 0
所以, 点B与C分居在平面的两侧.
的方位向量。
ur uur ur
uuuuur ur
在空间取仿射坐标系 O;e1, e2, e3 ,并设点 M0 的向 OM0 r0 ,平面
z
uuuur r
上任意一点 M 的向径为 OM r ,
b
r ur r r
M0
a
M
则平面 的向量式参数方程为 r r0 ua vb
《解析几何》(第四版)吕林根 许子道 编第3章平面与空间直线3.1平面的方程

x0 y0 z0 D X1 Y1 Z1 ,
因a,
b 不共线,
X2 所以A,
B,
Y2 Z2 C不全为零
,
这表明
:
任一平面都可用关于 x, y, z的三元一次方程表示 .
反之,可证 : 任一关于x, y, z的一次方程 (3.110)都表示平面.
事实上,因A, B, C不全为零,不妨设A 0,则(3.110)
在空间,
取仿射坐标系
O;e1
,
e2
,
e3
,
并设点
M
的向径
0
OM
0
r0
,
平面上任一点
M的向径OM
r
(图3
1),
则
a,
点 M在平面上 M
b不共线,由 定理 1.4.2知
0M
, a, z
b共面.
又 即
MM0 M0 Muarvrb0 ,, r r0 ua vb.
(3.1-1)
平面 的向量式参数方 x
2 11 3 3 2
问题:说明上式的由来 .
将方程组(*)变形为
A 5B D, 3A 2B D.
由克莱姆法则 , 有
D 5 5 1
D 2 2 1
A
D,
1 5 1 5
32 32
1 D 1 1 B 3 D 1 3 D,
1 5 1 5 32 32
5 1 1 1
2 1 13
A:B:D
D:
616
化简得 1 1 1 , 令 1 1 1 t 6a b 6c 6a b 6c
a 1 , b 1, c 1 ,
6t
t
6t 代入体积式
1 1 1 1 1 t 1 ,
解析几何课件(吕林根- 许子道第四版)

那么这一组向量就线性 相关.
推论 一组向量如果含有零向 量,那么这组向量必
线性相关 .
上一页 下一页
返回
定理1.4.6 两向量共线的充要条件 是它们线性相关 . 定理1.4.7 三个向量共面的充要条 件是它们线性相关 . 定理 1.4.8 空间任何四个向量总是 线性相关 .
上一页 下一页
返回
§1.5 标架与坐标
a就
是n个
矢
量a1
,
a2
,,
a
的
n
和
,
即
OA OA1 A1 A2 An1 An .
A1
A4
A3
A2
An-1
O
An
这种求和的方法叫做多边形法则
上一页 下一页
返回
定义1.2.2 当矢量b与矢量c的和等于矢量a,即b c a
时,我们把矢量c叫做矢量a与b的差,并记做c a b.
向量减法
叫 做 矢 量a1, a2 ,, an的 线 性 组 合. 定理1.4.1 如果矢量e 0,那么矢量r与矢量e共
线 的 充 要 条 件 是r可 以 用 矢 量e线 性 表 示 , 或 者 说r
是e的 线 性 组 合 , 即r=xe,
(1.4 1)
并且系数x被e, r唯一确定.
这时e称为用线性组合来表示共线矢量的基底.
所以 2AM ( AB AC) (BM CM ), A 但 BM CM BM MB 0,
因而 2AM AB AC
即
AM 1 (AB AC) 2
C
B
M
(图1.11)
上一页 下一页
返回
例2 用向量方法证明:联结三角形两边中点 的线段平行于第三边且等于第三边的一半.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
上一页 下一页
返回
例 2 求过点(1,1,1),且垂直于平面x y z 7和
3x 2 y 12z 5 0的平面方程.
解
n1 {1,1,1},
n2 {3,2,12}
取法向量
n n1 n2 {10,15, 5},
所求平面方程为
10( x 1) 15( y 1) 5(z 1) 0,
(2)
A 0,
D
0,
平面平行于x 轴;
类似地可讨论 B 0, C 0 情形.
(3) A B 0, 平面平行于xoy 坐标面;
类似地可讨论 A C 0, B C 0 情形.
(4)A B D 0, 有z 0,即xoy面.
上一页 下一页
返回
例 3 设平面过原点及点(6,3, 2) ,且与平面
(1) L A B C . mn p
(2) L // Am Bn Cp 0.
上一页 下一页
返回
例 1 设直线L : x 1 y z 1,平面 2 1 2
4x y 2z 8垂直,求此平面方程.
解 设平面为 Ax By Cz D 0, 由平面过原点知 D 0,
由平面过点(6,3, 2)知 6A 3B 2C 0
n{4,1,2},
4A B 2C 0
A B 2C, 3
所求平面方程为 2x 2 y 3z 0.
上一页 下一页
返回
例 4 设平面与x, y, z 三轴分别交于P(a,0,0)、 Q(0,b,0)、R(0,0,c)(其中a 0 ,b 0,c 0 ),
求此平面方程.
解 设平面为 Ax By Cz D 0,
aA D 0, 将三点坐标代入得 bB D 0,
cC D 0,
AD, BD, C D.
Pr jn P1P0 P1P0 en
A( x0 x1 ) B( y0 y1 ) C(z0 z1 ) A2 B2 C 2 A2 B2 C 2 A2 B2 C 2
Ax0 By0 Cz0 ( Ax1 By1 Cz1 ) , A2 B2 C 2
上一页 下一页
返回
Ax1 By1 Cz1 D 0 ( P1 )
Pr jnP1P0
Ax0 By0 Cz0 D , A2 B2 C 2
d | Ax0 By0 Cz0 D | . A2 B2 C 2 点到平面距离公式
上一页 下一页
返回
例 1 求两平面 z x 2y 1, 3x 6y 3z 4间的距离.
n2 {4,2,2}
2 1 1 , 两平面平行 4 2 2
M(1,1,0) 1 M(1,1,0) 2
两平面平行但不重合.
(3) 2 1 1 , 两平面平行 4 2 2
M(1,1,0) 1 M(1,1,0) 2
两平面重合.
上一页
返回
§3.4 空间直线的方程
一、空间直线的一般方程
方向向量的定义:
如果一非零向量平行于 一条已知直线,这个向量称 为这条直线的方向向量.
z
s
L
M
M0
M0 ( x0 , y0 , z0 ), M( x, y, z), o
y
M L,
M0M// s
x
s (m, n, p), M0M {x x0, y y0, z z0}
x x0 m
y y0 n
解析几何课件(第四版)
吕林根 许子道等编
第一章 向量与坐标
第二章 轨迹与方程 第三章 平面与空间直线
第四章 柱面锥面旋转曲面与二次曲面
第五章 二次曲线的一般理论
第三章 平面与空间直线
§3.1 平面的方程 §3.3 两平面的相关位置
§3.2 平面与点的相关位置 §3.4 空间直线的方程
§3.5 直线与平面的相关位置
2
返回
三、空间直线的参数式方程
由直线的对称式方程 x x0 y y0 z z0
m
n
p
令 x x0 y y0 z z0 t
m
n
p
x x0 mt
y
y0
nt
z
z0
pt
直线的参数方程
直线的一组方向数
方向向量的余弦称为直 线的方向余弦.
上一页 下一页
返回
例2 用对称式方程及参数方程表示直线
y 3z 1 0 4x 2y 2z 1 0 4x 2y 2z 2 0
解 (1) cos | 1 0 2 1 1 3 |
(1)2 22 (1)2 12 32
cos
1 60
两平面相交,夹角 arccos
1. 60
上一页 下一页
返回
(2) n1 {2,1,1},
上一页 下一页
返回
例 1 求过三点A(2,1,4)、B(1,3,2)和 C (0,2,3)的平面方程. 解 AB {3, 4,6}
AC {2, 3,1} 取 n AB AC {14, 9,1}, 所求平面方程为 14( x 2) 9( y 1) (z 4) 0,
化简得 14x 9 y z 15 0.
夹角.(通常取锐角)
n2
n1
1 : A1 x B1 y C1z D1 0,
2
2 : A2 x B2 y C2z D2 0,
n1 { A1, B1,C1},
1
n2 { A2 , B2 ,C2 },
下一页
返回
按照两向量夹角余弦公式有
cos
| A1 A2 B1B2 C1C2 |
外一点,求P0 到平面的距离.
解 P1( x1, y1, z1 ) d | Pr jnP1P0 |
n
P0
Pr jn P1P0 P1P0 en
P1
N
P1P0 { x0 x1, y0 y1, z0 z1}
下一页
返回
en
A
,
A2 B2 C 2
B
,
A2 B2 C 2
C
A2 B2 C 2
(4,1,3),
对称式方程 x 1 y 0 z 2 , 4 1 3
令 x 1 y 0 z 2 t, 4 1 3
x 1 4t
得参数方程
y
t
.
z 2 3t
上一页 下一页
返回
例 3 一直线过点A(2,3,4),且和y 轴垂直相
交,求其方程.
解 因为直线和 y轴垂直相交,
所以交点为 B(0,3, 0),
: Ax By Cz D 0, n ( A, B,C),
(s , n)
,
2
(s , n)
2
下一页
返回
sin cos cos .
2
2
sin
| Am Bn Cp |
A2 B2 C 2 m2 n2 p2
直线与平面的夹角公式
直线与平面的位置关系:
不妨设 A 0,则
A x
D A
By 0 Cz 0
0
,为一平面.
Ax By Cz D 0 平面的一般方程
法向量 n {A, B,C}.
上一页 下一页 返回
Ax By Cz D 0 平面的一般方程
平面一般式方程的几种特殊情况:
(1) D 0, 平面通过坐标原点;
D 0, 平面通过 x轴;
A12 B12 C12 A22 B22 C22
两平面夹角余弦公式
两平面位置特征:
(1) 1 2 A1 A2 B1B2 C1C2 0;
(2)
1
//
2
A1 A2
B1 B2
C1 C2
.
上一页 下一页
返回
例1 研究以下各组里两平面的位置关系:
(1) x 2 y z 1 0, (2) 2x y z 1 0, (3) 2x y z 1 0,
x y z 1 0 2x y 3z 4
. 0
解 在直线上任取一点 ( x0 , y0 , z0 )
取
x0 1
y0 y0
z0 2 0 , 3z0 6 0
解得 y0 0, z0 2
点坐标(1,0,2),
上一页 下一页
返回
因所求直线与两平面的法向量都垂直
取
s
n1
n2
z z0 p
直线的对称式方程 (点向式方程)
上一页 下一页
返回
注: 当 方 向向 量 的 某 个坐 标为 零 时, 比 如
m 0,n 0,p 0时 , 方 程 仍然 写 为
x x0 y y0 z z0 ,
0 此时
理解
n 为二
p x 平面的交线 y
x0 y0 n
0 z
z0 p
化简得 2x 3 y z 6 0.
上一页 下一页
返回
二、平面的一般式方程
由平面的点法式方程
A( x x0 ) B( y y0 ) C(z z0 ) 0
Ax By Cz ( Ax0 By0 Cz0 ) 0
表示
D
即 任一平面
?
Ax By Cz D 0
(A,B,C不同时为零)
§3.6 空间两直线的相关位置
§3.7 空间直线与点的相关位置
§3.1 平面的方程
一、平面的点法式方程
z
n
如果一非零向量垂直
M0
M
于一平面,这向量就叫做
该平面的法线向量.
o
y
x
法线向量的特征: 垂直于平面内的任一向量.
已知
n
{
A,
B,
C },
M0( x0 , y0 , z0 ),
设平面上的任一点为 M( x, y, z)
6t
t
6t 代入体积式
1 1 1 1 1 t 1 ,
