冉绍尔-汤森德效应
冉绍尔汤森效应验证和测量气体原子散射截面与电子能量的关系
散射截面用以表示A粒子与B粒子发生相互作用而离开入 射束的概率
3
测量原理
冉绍尔-汤森效应实验仪
4
• 测量气体原子总散射截面的原理图
5
• 灯丝被加热,电子自阴极逸出,设阴极电流为Ik,电子在 加速电压的作用下,有一部分电子在到达栅极之前,被屏 极接收,形成电流Is1;有一部分穿越屏极上的矩形孔,形 成电流I0,由于屏极上的矩形孔与板极P之间是一个等势 空间,所以电子穿越矩形孔后就以恒速运动,受到气体原 子散射的电子则到达屏极,形成散射电流Is2;而未受到散 射的电子则到达板极P,形成透射电流Ip
9
• 用测量所得数据作图,分别得到Ea- Is曲线、Ea-Ip曲线、 Ea- Is*曲线、 Ea- Ip*曲线、Ea-f曲线。与交流观察的现象吻 合,各个电流与加速电压的关 系基本成正比例,而Ea-Ip 曲线存在拐角,验证了在交流观察时看到的明显的凹陷。 同时得到的Ea-f曲线,f数值可以低至0.02左右,可视为 f<<1,故关系式(总有效散射截面) Q=-(1/L)*ln[(Ip/Is)*( Is*/ Ip*)]在实验处理时完全可以采用。
10
作出散射几率与电子能量平方根的关系图
Pห้องสมุดไป่ตู้s
0.9
0.8
0.7
0.6
0.5
0.4
0.3
0.2
0.1
0.5
1.0
1.5
2.0
2.5
3.0
3.5
(eV)1/2
11
曲线分析: 有效散射截面与电子的运动速度密切相关。电子能量
降到约6.5eV时,散射截面达到极大值;进一步降低电子 能量,散射截面急剧变小,当电子能量低至约0.9eV,散 射截面出现极小值,此时,气体原子呈现所谓的“透明” 现象,即电子经过原子气体时,几乎不与原子发生碰撞而 径直透过;再降低电子的能量,散射截面将迅速增大。
冉绍尔汤森效应实验

实验5-3 冉绍尔-汤森效应实验作者:任学智 同组者:关希望 指导老师:周丽霞一. 引言1921年,德国物理学家冉绍尔(Carl Ramsauer )用磁偏转法分离出单一速度的电子,对极低能量0.75~1.1eV 的电子在各种气体中的平均自由程做了研究。
结果发现,氩气(Ar )气中的平均自有程e λ远大于经典力学的理论计算值。
以后,他又把电子能量扩展到100eV 左右,发现Ar 原子对电子的弹性散射截面Q (与e λ成反比)随电子能量的减小而增大,在10eV 左右达到极大值,而后又随着电子能量的减小而减小。
1922年,现代气体放电理论的奠基人、英国物理学家汤森(J.S.Townsend )和贝利(Bailey )也发现了类似的现象。
进一步的研究表明,无论哪种气体原子的弹性散射截面(或电子平均自由程),在低能区都与碰撞电子的能量(或运动速度v )明显相关,而且类似的原子具有相似的行为,这就是著名的冉绍尔-汤森效应。
冉绍尔-汤森效应在当时是无法解释的。
因为经典的气体分子运动论把电子看成质点,把气体原子看成刚性小球,它们之间碰撞的散射截面仅决定于原子的尺寸,电子的平均自由程也仅决定于气体原子大小及其密度 n ,都与电子的运动速度无关。
不久,在德布罗意波粒二相性假设(1924年)和量子力学理论(1925~1928年)建立后,人们认识到,电子与原子的碰撞实际上是入射电子波在原子势场中的散射,是一种量子效应,以上实验事实才得到了圆满的理论解释。
冉绍尔-汤森效应是量子力学理论极好的实验例证,通过该实验,可以了解电子碰撞管的设计原则,掌握电子与原子的碰撞规则和测量原子散射截面的方法,测量低能电子与气体原子的散射几率以及有效弹性散射截面与电子速度的关系。
本实验的目的主要有:了解电子碰撞管的设计原则,掌握电子与原子的碰撞规则和测量的原子散射截面的方法;测量低能电子与气体原子的散射几率Ps 与电子速度的关系;测量气体原子的有效弹性散射截面Q 与电子速度的关系,测定散射截面最小时的电子能量;验证冉绍尔-汤森效应,并学习用量子力学理论加以解释。
冉绍尔-汤森效应
冉绍尔-汤森效应——验证和测量气体原子散射截面与电子能量的关系摘要:实验研究发现,电子与气体原子发生碰撞,散射截面的大小与电子的速度有关,惰性气体(Ar、Kr、Xe)原子对电子的弹性散射截面存在极大值与极小值;无论哪种气体原子的弹性散射截面,在低能区都与碰撞电子的能量明显有关,而且相似原子具有相似的行为,称为冉绍尔-汤森效应。
冉绍尔-汤森效应是量子力学理论极好的实验验证,通过实验可以研究分析,气体分子对低能电子的弹性散射几率以及散射截面和电子平均自由程与电子能量的关系。
关键词:电子能量散射截面充气闸流管加速电压室温与液氮条件实验历史背景:早在1921年,德国物理学家冉绍尔用磁偏转法分离出单一速度的电子,对极低能量0.75~1.1eV的电子在各种气体中的平均自由程作了研究。
结果发现,Ar气中的平均自由程远大于经典热力学的理论计算值。
惰性气体(主要讨论Ar)原子对电子的弹性散射截面在10eV左右存在极大值;同时在能量约为0.37eV时,电子的自由程出现极大值;在能量降到约0.2eV时,Ar的散射截面呈现极小值,且接近于零。
无论哪种气体原子的弹性散射截面,在低能区都与碰撞电子的能量明显有关,而且相似原子具有相似的行为。
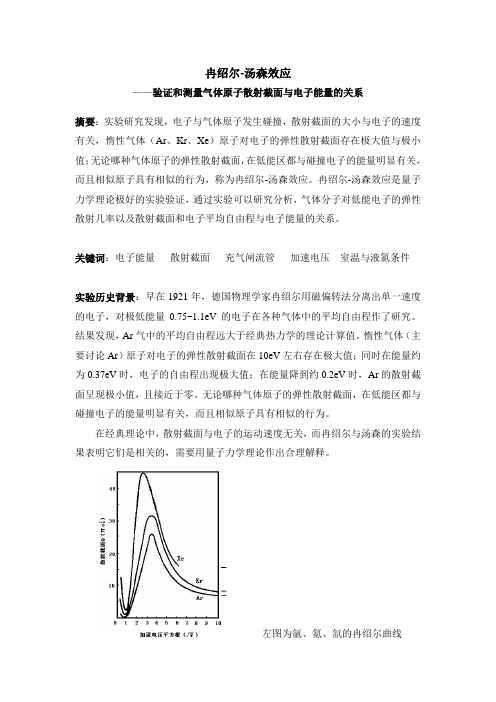
在经典理论中,散射截面与电子的运动速度无关,而冉绍尔与汤森的实验结果表明它们是相关的,需要用量子力学理论作出合理解释。
左图为氩、氪、氙的冉绍尔曲线实验原理:1.散射截面设想B粒子杂乱分布在一个很薄的平面层上,单位面积上平均有n个粒子,当一个A粒子垂直入射到这一平面层,可能会通过与B粒子的相互作用而离开入射束。
将这一事件的发生概率记为P,定义散射截面:σ=P/n . 在厚层下,经过路程x而散射的概率Ps(x)=1-exp(-x/λ).在经典物理学中,粒子的平均自由程等于总散射截面nσ的倒数(λ=1/nσ)。
2.测量原理测量气体原子总散射截面的原理图灯丝被加热,电子自阴极逸出,设阴极电流为Ik,电子在加速电压的作用下,有一部分电子在到达栅极之前,被屏极接收,形成电流Is1;有一部分穿越屏极上的矩形孔,形成电流I,由于屏极上的矩形孔与板极P之间是一个等势空间,所以电子穿越矩形孔后就以恒速运动,受到气体原子散射的电子则到达屏极,形成散射电流Is2;而未受到散射的电子则到达板极P,形成透射电流Ip.电子在等势区内的散射概率为: PS =1-Ip/II p 可以直接测得,至于I则需要用间接的方法测定。
冉绍尔一汤森效应 - 武汉大学物理实验教学中心解读

冉绍尔-汤森效应1912年,德国物理学家冉绍尔(Carl Ramsauer)在研究电子与气体原子的碰撞中,发现碰撞截面的大小与电子的速度有关。
当电子能量较高时,氩原子的截面散射截面随着电子能量的降低而增大;当电子能量小于十几个电子伏特后,发现散射截面却随着电子的能量的降低而迅速减小。
1922年,现代气体放电理论的奠基人、英国物理学家汤森(J.S.Townsend)和贝利(Bailey)也发现了类似的现象。
进一步的研究表明,无论哪种气体原子的弹性散射截面(或电子平均自由程),在低能区都与碰撞电子的能量(或运动速度υ)明显相关,而且类似的原子具有相似的行为,这就是著名的冉绍尔-汤森效应。
冉绍尔-汤森效应在当时是无法解释的。
因为经典的气体分子运动论把电子看成质点,把气体原子看成刚性小球,它们之间碰撞的散射截面仅决定于原子的尺寸,电子的平均自由程也仅决定于气体原子大小及其密度n,都与电子的运动速度无关。
不久,在德布罗意波粒二相性假设(1924年)和量子力学理论(1925~1928年)建立后,人们认识到,电子与原子的碰撞实际上是入射电子波在原子势场中的散射,是一种量子效应,以上实验事实才得到了圆满的理论解释。
一实验目的1.了解电子碰撞管的设计原则,掌握电子与原子的碰撞规则和测量原子散射截面的方法。
2.测量低能电子与气体原子的散射几率Ps与电子速度的关系。
3.测量气体原子的有效弹性散射截面Q与电子速度的关系,测定散射截面最小时的电子能量。
4.验证冉绍尔-汤森效应,并学习用量子力学理论加以解释。
二实验原理1.理论原理冉绍尔在研究极低能量电子(0.75eV-1.1eV)的平均自由程时,发现氩气中电子自由程比用气体分子运动论计算出来的数值大得多。
后来,把电子的能量扩展到一个较宽的范围内进行观察,发现氩原子对电子的弹性散射总有效截面Q随着电子能量的减小而增大,约在lOeV 附近达到一个极大值,而后开始下降,当电子能量逐渐减小到leV左右时,有效散射截面Q 出现一个极小值。
冉绍尔-汤森效应实验

冉绍尔-汤森效应实验【摘要】加速电子与充氙闸流管中的氙原子碰撞,电子被散射,把闸流管先后浸入77K 液氮和在室温下测俩观众的栅极及板极电流。
得出散射概率、散射截面与电子能量的关系,低能电子与气体原子的散射几率与电子速度的关系,验证冉绍尔-汤森效应。
用量子力学解释这一效应测量氙原子的电离电位。
【实验原理】当灯丝加热后,就有电子自阴极逸出,设阴极电流为K I ,电子在加速电压的作用下,有一部分电子在到达栅极之前,被屏极接收,形成电流1S I ;有一部分穿越屏极上的矩形孔,形成电流0I ,由于屏极上的矩形孔与板极P 之间是一个等势空间,所以电子穿越矩形孔后就以恒速运动,受到气体原子散射的电子则到达屏极,形成散射电流2S I ;而未受到散射的电子则到达板极P ,形成板流P I ,因此有10S K I I I +=21S S S I I I +=20S P I I I +=电子在等势区内的散射概率为:01I I P PS -= (1)可见,只要分别测量出P I 和0I 即可以求得散射几率。
从上面论述可知,P I 可以直接测得,至于0I 则需要用间接的方法测定。
由于阴极电流K I 分成两部分1S I 和0I ,它们不仅与K I 成比例,而且他们之间也有一定的比例关系,这一比值称为几何因子f ,即有10S I I f =(2)几何因子f 是由电极间相对张角及空间电荷效应所决定,即f 与管子的几何结构及所用的加速电压、阴极电流有关。
将式(2)带入(1)式得到111S PS I I f P -= (3)为了测量几何因子f ,我们把电子碰撞管的管端部分浸入温度为77K 的液氮中,这时,管内掉气体冻结,在这种低温状态下,气体原子的密度很小,对电子的散射可以忽略不计,几何因子f 就等于这时的板流*P I 与屏流*S I 之比,即**=SP I I f (4)如果这时阴极电流和加速电压保持与式(1)和(2)时的相同,那么上式中的f 值与式(3)中掉相等,因此有**-=PS S P S I II I P 11 (5)设L 为出射孔S 到板极P 之间的距离,则)exp(1QL P S --= (6)当f<<1时,由(5)、(6)两式得⎪⎪⎭⎫ ⎝⎛-=**P S S P I I I I L Q ln 1 测量不同的加速电压Ea 下的Ps 的值,即可由上式得到总有效散射截面Q 与a E 的关系曲线。
冉绍尔-汤森效应实验

冉绍尔-汤森效应实验【摘要】加速电子与充氙闸流管中的氙原子碰撞,电子被散射,把闸流管先后浸入77K 液氮和在室温下测俩观众的栅极及板极电流。
得出散射概率、散射截面与电子能量的关系,低能电子与气体原子的散射几率与电子速度的关系,验证冉绍尔-汤森效应。
用量子力学解释这一效应测量氙原子的电离电位。
【实验原理】当灯丝加热后,就有电子自阴极逸出,设阴极电流为K I ,电子在加速电压的作用下,有一部分电子在到达栅极之前,被屏极接收,形成电流1S I ;有一部分穿越屏极上的矩形孔,形成电流0I ,由于屏极上的矩形孔与板极P 之间是一个等势空间,所以电子穿越矩形孔后就以恒速运动,受到气体原子散射的电子则到达屏极,形成散射电流2S I ;而未受到散射的电子则到达板极P ,形成板流P I ,因此有10S K I I I +=21S S S I I I +=20S P I I I +=电子在等势区内的散射概率为:01I I P PS -= (1)可见,只要分别测量出P I 和0I 即可以求得散射几率。
从上面论述可知,P I 可以直接测得,至于0I 则需要用间接的方法测定。
由于阴极电流K I 分成两部分1S I 和0I ,它们不仅与K I 成比例,而且他们之间也有一定的比例关系,这一比值称为几何因子f ,即有10S I I f =(2)几何因子f 是由电极间相对张角及空间电荷效应所决定,即f 与管子的几何结构及所用的加速电压、阴极电流有关。
将式(2)带入(1)式得到111S PS I I f P -= (3)为了测量几何因子f ,我们把电子碰撞管的管端部分浸入温度为77K 的液氮中,这时,管内掉气体冻结,在这种低温状态下,气体原子的密度很小,对电子的散射可以忽略不计,几何因子f 就等于这时的板流*P I 与屏流*S I 之比,即**=SP I I f (4)如果这时阴极电流和加速电压保持与式(1)和(2)时的相同,那么上式中的f 值与式(3)中掉相等,因此有**-=PS S P S I II I P 11 (5)设L 为出射孔S 到板极P 之间的距离,则)exp(1QL P S --= (6)当f<<1时,由(5)、(6)两式得⎪⎪⎭⎫ ⎝⎛-=**P S S P I I I I L Q ln 1 测量不同的加速电压Ea 下的Ps 的值,即可由上式得到总有效散射截面Q 与a E 的关系曲线。
冉绍尔-汤森德效应
冉绍尔——汤森德效应摘要:冉绍尔——汤森德效应是在研究低能电子的平均自由程时发现的一种气体原子与电子弹性碰撞的散射截面Q与电子能量密切相关的现象。
此现象与经典理论相矛盾,需要用量子理论解释。
关键词:散射截面碰撞概率加速电压补偿电压电离电位一、引言1921年德国物理学家冉绍尔在研究低能电子的平均自由程时发现:在惰性气体中,当电子的能量降到几个电子伏时,气体原子与电子弹性碰撞的散射截面Q(与平均自由程成反比)迅速减小;当电子能量约为1电子伏时,Q出现极小值,而且接近零。
如果继续减少电子能量,则Q迅速增大,这说明弹性散射截面与电子能量密切相关。
1922年英国物理学家汤森德把电子能量进一步降低,用另外的方法研究平均自由程随电子速度变化的情况,也发现类似现象。
随后,冉绍尔用实验证明了汤森德的结果。
冉绍尔——汤森德效应在当时无法解释,因为经典理论认为气体原子与电子弹性碰撞的散射截面仅决定于原子的尺寸,而与电子的运动速度无关,只有在波粒二象性和量子力学建立后,这种效应才得到圆满解释。
因此冉绍尔——汤森德效应也验证了量子力学的正确性。
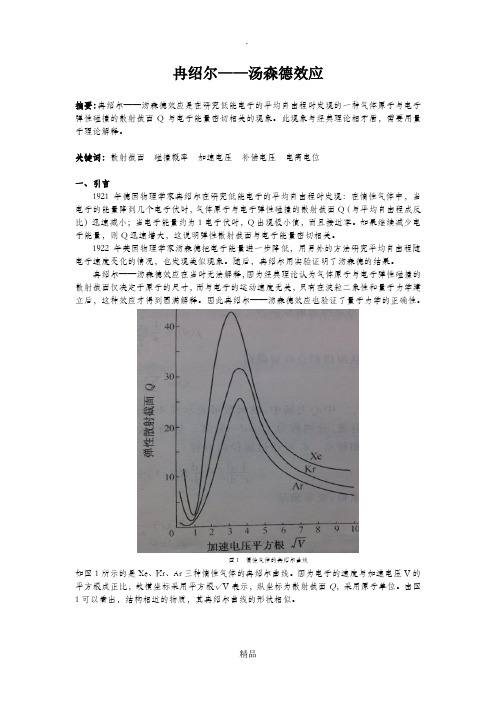
图1 惰性气体的冉绍尔曲线如图1所示的是Xe、Kr、Ar三种惰性气体的冉绍尔曲线。
因为电子的速度与加速电压V的平方根成正比,故横坐标采用平方根√V表示,纵坐标为散射截面Q,采用原子单位。
由图1可以看出,结构相近的物质,其冉绍尔曲线的形状相似。
二、冉绍尔——汤森德效应的理论描述在量子力学中,碰撞现象也称作散射现象。
粒子的碰撞过程有弹性碰撞与非弹性碰撞两大类。
在弹性碰撞过程中,粒子A 以波矢k|k|=(1)沿Z 入射到靶粒子B (即散射中心)上,受B 粒子作用偏离原方向而散射,散射程度可用总散射截面Q 表示。
讨论粒子受辏力场弹性散射的情况。
取散射中心为坐标原点;设入射粒子与散射中心之间的相互作用势能为U (r ),当r → ∞时,U (r )趋于零,则远离散射中心处的波函数Ψ由入射粒子的平面波Ψ1和散射粒子的球面散射波Ψ2组成12()ikrikzr e e f r ψψψθ→∞→+=+ (2) 这里考虑的是弹性散射,所以散射波的能量没有改变,即其波矢k 的数值不变。
冉绍尔-汤姆森效应实验

中国石油大学近代物理实验报告成绩:班级:姓名:同组者:教师:实验B8 冉绍尔-汤姆森效应实验【实验目的】1、了解电子碰撞管的设计原则,掌握电子与原子的碰撞规则和测量的原子散射截面的方法。
2、测量低能电子与气体原子的散射几率Ps与电子速度的关系。
3、测量气体原子的有效弹性散射截面Q与电子速度的关系,测定散射截面最小时的电子能量。
4、验证冉绍尔-汤森效应,并学习用量子力学理论加以解释。
【实验原理】一、理论原理冉绍尔在研究极低能量电子(0.75eV—1.1eV)的平均自由程时,发现氩气中电子自由程比用气体分子运动论计算出来的数值大得多。
后来,把电子的能量扩展到一个较宽的范围内进行观察,发现氩原子对电子的弹性散射总有效截面Q随着电子能量的减小而增大,约在10eV附近达到一个极大值,而后开始下降,当电子能量逐渐减小到1eV左右时,有效散射截面Q出现一个极小值。
也就是说,对于能量为1eV左右的电子,氩气竟好像是透明的。
电子能量小于1eV以后Q再度增大。
此后,冉绍尔又对各种气体进行了测量,发现无论哪种气体的总有效散射截面都和碰撞电子的速度有关。
并且,结构上类似的气体原子或分子,它们的总有效散射截面对电子速度的关系曲线Q (V为加速电压值)具有相同的形状,称为冉绍尔曲线。
图B8-1为氙(Xe),氪(Ke),氩(Ar)三种VF惰性气体的冉绍尔曲线。
图中横坐标是与电子速度成正比的加速电压平方根值,纵坐标是散射截面Q值,这里采用原子单位,其中a0为原子的玻尔半径。
图中右方的横线表示用气体分子运动论计算出的Q值。
显然,用两个钢球相碰撞的模型来描述电子与原子之间的相互作用是无法解释冉绍尔效应的,因为这种模型得出的散射截面与电子能量无关。
要解释冉绍尔效应需要用到粒子的波动性质,即把电子与原子的碰撞看成是入射粒子在原子势场中的散射,其散射程度用总散射截面来表示。
图B8-1 Xe、Kr、H气体对电子的散射截面二、测量原理测量气体原子对电子的总散射截面的方法很多,装置也各式各样。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
冉绍尔——汤森德效应摘要:冉绍尔——汤森德效应是在研究低能电子的平均自由程时发现的一种气体原子与电子弹性碰撞的散射截面Q与电子能量密切相关的现象。
此现象与经典理论相矛盾,需要用量子理论解释。
关键词:散射截面碰撞概率加速电压补偿电压电离电位一、引言1921年德国物理学家冉绍尔在研究低能电子的平均自由程时发现:在惰性气体中,当电子的能量降到几个电子伏时,气体原子与电子弹性碰撞的散射截面Q(与平均自由程成反比)迅速减小;当电子能量约为1电子伏时,Q出现极小值,而且接近零。
如果继续减少电子能量,则Q迅速增大,这说明弹性散射截面与电子能量密切相关。
1922年英国物理学家汤森德把电子能量进一步降低,用另外的方法研究平均自由程随电子速度变化的情况,也发现类似现象。
随后,冉绍尔用实验证明了汤森德的结果。
冉绍尔——汤森德效应在当时无法解释,因为经典理论认为气体原子与电子弹性碰撞的散射截面仅决定于原子的尺寸,而与电子的运动速度无关,只有在波粒二象性和量子力学建立后,这种效应才得到圆满解释。
因此冉绍尔——汤森德效应也验证了量子力学的正确性。
图1 惰性气体的冉绍尔曲线如图1所示的是Xe、Kr、Ar三种惰性气体的冉绍尔曲线。
因为电子的速度与加速电压V的平方根成正比,故横坐标采用平方根√V表示,纵坐标为散射截面Q,采用原子单位。
由图1可以看出,结构相近的物质,其冉绍尔曲线的形状相似。
二、冉绍尔——汤森德效应的理论描述在量子力学中,碰撞现象也称作散射现象。
粒子的碰撞过程有弹性碰撞与非弹性碰撞两大类。
在弹性碰撞过程中,粒子A 以波矢k2|k|=mE(1)沿Z 入射到靶粒子B (即散射中心)上,受B 粒子作用偏离原方向而散射,散射程度可用总散射截面Q 表示。
讨论粒子受辏力场弹性散射的情况。
取散射中心为坐标原点;设入射粒子与散射中心之间的相互作用势能为U (r ),当r → ∞时,U (r )趋于零,则远离散射中心处的波函数Ψ由入射粒子的平面波Ψ1和散射粒子的球面散射波Ψ2组成12()ikrikzr e e f r ψψψθ→∞→+=+ (2)这里考虑的是弹性散射,所以散射波的能量没有改变,即其波矢k 的数值不变。
θ为散射角,即粒子被散射后的运动方向与入射方向之间的夹角;f(θ)称散射振幅。
总散射截面220|()|2|()|sin Q f d f d πθπθθθ=Ω=⎰⎰ (3)利用分波法求解满足式(3)边界条件的薛定谔方程22()2U r E m ψψ⎛⎫-∆+= ⎪⎝⎭ (4)可求得散射振幅为1()(21)(cos )sin i elll f l P e k δθθδ∞==+∑ (5)从而得到总散射截面2004(21)sin l ll l Q Q l k πδ∞∞====+∑∑ (6)中心力场中,波函数可表成不同角动量l 的入射波和出射波的相干叠加,l =0, 1, 2…的分波,分别称为s , q , d …分波。
势场U (r )的作用仅使入射粒子散射后的每一个分波各自产生相移δl 。
δl 可通过解径向方程 2222212(1)()()()0l l d d m l l r R r k U r R r r dr dr r +⎡⎤⎡⎤+--=⎢⎥⎢⎥⎣⎦⎣⎦(7)求得,要满足1()sin()2l l kr l R r kr kr πδ→∞→-+ (8)这样,计算散射截在Q 的问题就归结为计算各分波的相移δl ;式(6)中的Q l 为第l 个分波的散射截面。
在冉绍尔-汤森德效应实验里,U (r )为电子与原子之间的相互用势,可以把惰性气体的势场近似地看成一个三维方势阱,()0,U r a U r r a -≤⎧=⎨>⎩ (9) U 0代表势阱深度,a 表征势阱宽度。
对于低能散射,ka <<1,δl 随l 增大而迅速减少,仅需考虑s 波的贡献,20024sin Q Q k πδ≈=(10)其分波相移'0'arctan(tan )k k a ka k δ=- (11)其中0'()E U k +可见在原子势特性(-U 0,a )确定的情况下,低能弹性散射截面的大小将随入射电子波波矢,即入射电子能量E 的变化而变化。
当入射电子能量(E ≠0),原子势特性满足''tan tan k a ka k k = (12)时,δ0=π,Q 0=0;而高l 分波的贡献又非常小,因此散射截面呈现极小值。
对图1的几种惰性气体来说,适当选择势阱参数,可使入射电子能量为leV 左右时,其总散射截面Q 为极小。
随着能量的逐渐增大,高l 分波的贡献不能忽略,各l 分波相移的总和使总散射截面不再出现极小值。
上述三维方势阱模型还是相当粗糙的,只能定性地用来解释冉绍尔曲线。
散射截面的更精确的计算要采用Hartree-Fock 自洽场方法。
但从以上分析我们可以看到,实验测定弹性散射截面与入射电子能量的关系,可以提供有关原子势场的信息,这是研究基本粒子间相互作用所常用的方法。
三、散射几率、散射截面和平均自由程之间的关系推导当入射粒子A 穿过由B 粒子组成的厚度为dz 的靶时,若其平均自由程为λ,则其散射几率为s dzP λ=(13)另一方面,若靶粒子的体密度为n ,单个靶粒子的散射截面为Q ,入射粒子穿过该靶时的散射几率又可表示为s P nQdz = (14)因此有1nQ λ=(15)既入射粒子的平均自由程λ与单位体积内靶粒子的总散射截面nQ 互为倒数关系。
在几种惰性气体(Ar, Kr, Xe )的冉绍尔-汤森德效应实验中,当电子能量约为leV 时,散射截面出现极小值,e λ为极大值,入射电子径直透过势阱,犹如不存在原子一样,原子对电子像是“透明”的,这种现象称为共振贯穿或共振透射。
密度为N (z )的入射粒子,经由B 粒子组成的厚度为dz 的靶散射后,出射粒子密度的减小量为()()()()s dzdN z P N z N z nQN z dzλ-=== (16)取不定积分得/()nQz z N z ce ce λ--== (17)设z=0 处的入射粒子密度为N 0,则/00()nQz z N z N e N e λ--== (18)于是求得密度N 0的入射粒子穿过厚度为z 的靶时,散射几率为/00()11nQz z s N N z P e e N λ---==-=- (19)n 代表了单位体积内所有靶粒子对于碰撞的总贡献。
当靶粒子密度n 一定时,散射截面Q 则是决定散射几率P s 的因子。
实验测得散射几率P s 后可得1ln(1)s nQ P z =-- (20) 和ln(1)s z P λ-=- (21)对于给定温度T 和压强p 的气体,其总散射截面ln(1)s kT Q P pz -=- (22)其中k 为玻耳兹曼常数。
四、实验仪器实验仪器由充气闸流管、R-T 实验仪(包括电源组和微电流计及交流测量两部分)示波器、液氮保温瓶等组成。
用ZQI 0.1/1.3型充氙闸流管作碰撞管,进行低能电子和气体原子弹性碰撞散射截面的测量。
图2是充氙闸流管结构示意图,K 为旁热式氧化物阴极,内有灯丝F ,M 为调制极,调制极与板极P 之间有一块中央开矩形孔的隔板,它与周围的屏蔽金属套相连,称为栅极或屏蔽极S ,调制极与屏蔽极连在一起作加速极用。
隔板右面区域是等电位区,通道隔板小孔的电子与氙原子在这一区域进行弹性碰撞,该区内的板极则收集未被散射的电子。
图2 闸流管结构示意图现将R-T 实验仪的电源组作简要说明:1、灯丝电源E f ,提供1.2---5V 交流电,连续可调。
2、加速极电源E a 有交流、直流两种。
示波器观察时用交流,直流测量时用直流。
交流和直流电压用同一个电位器调节。
3、直流补偿电源E c ,0-5.0V ,连续可调。
由于屏蔽极与板极材料表面状况不同,存在接触电位差,调节E c 进行补偿,可使板极区域空间等电位,不致影响散射几率的测量。
电源组面板示意图如图3所示。
微电流计及交流测量部分中,微电流计有2只数显表,用来测量收集极上的电流I c和加速极上的电流,交流测量用于在示波器上观察I c-V a和I a-V a曲线。
微电流计及交流测量仪器面板示意图如图4所示。
图3 电源组面板示意图图4 微电流计面板示意图⑴电源开关⑵灯丝电压调节电位器⑴电源开关⑵I s测量输入端子⑶灯丝电压输出⑷加速电压调节电位器⑶I s量程选择⑷数显表,显示I s⑸加速电压输出⑹补偿电压调节电位器⑸I c测量输入端子⑹I c量程选择⑺补偿电压输出⑻灯丝电压的数显表⑺数显表,显示I c ⑻K、S、P端子⑼加速电压的数显表⑼Y1、Y2,BNC插座(10)补偿电压的数显表(10)X,BNC插座(11)E c端子(12)W1电位器(13)W2电位器五、测量原理测量原理线路图如图5所示。
图5 测量原理线路图灯丝电源为E f,调制极M与屏蔽极S连在一起作加速极用,它与阴极之间接有加速电源E a,可以改变和控制到达屏蔽极隔离板孔处电子运动的速度;电源E c用来补偿板极与屏蔽极之间的接触势差,保证屏蔽极隔离板至板极的空间为等势空间;R a和R c为取样电阻,作测量加速极电流和收集极电流之用。
加速电源E a上还有一组交流可调电压输出,供双踪示波器动态观察I a-V a和I c-V a曲线。
六、实验内容1、交流定性观察(1)、按图6所示连接线路。
示波器X轴扫描由加速电源的交流输出电压提供,闸流管处于室温。
调节E f为某一值,电位器W1用来调节交变电压V a的幅度,W2用来调节X轴的扫描幅度,示波器上会出现图7(a)所示图形。
其中Ⅰ为I a-V a曲线,Ⅱ为I c-V a曲线。
其中曲线Ⅱ中凹陷是由散射几率的变化引起的。
图6 交流观察接线图图7 交流定性观察(2)、一只手扶住闸流管管座,另一只手旋松支架上的固定螺丝,小心地将闸流管玻壳缓慢移入装有液氮的保温瓶内,让管顶浸入液氮,切不可使金属管座接触液氮,否则会炸裂。
观察I c-V a曲线的变化, 其凹陷消失。
(3)、接触电势差的补偿:由于屏蔽极和板极间接触电势差的存在,碰撞空间不是等势空间。
V a很小时,I a和I c不同时出现。
(必要时将X轴扫描扩展10倍)仔细调节示波器Y1和Y2的放大倍数以及补偿电压E c的值,使曲线Ⅰ和Ⅱ基本上全部重合,如图7(b)所示,此时可认为接触电势差得到补偿。
以后操作保持E c不变。
2、直流测量(1)、按图8所示连接线路。
图8 直流测量接线图闸流管仍置于液氮中。
选择好灯丝电压,将V a调至较大负电压,使闸流管完全截止。
两微电流计置于最小量程。
(2)、测量液氮温度下一组V a,I a*、I c*值,由于实验曲线以√Va为横坐标,所以起始时V a 的间隔应取得小些。
