哈工大结构力学题库三章
(完整版)哈工大结构力学题库三章
第三章 虚功原理和结构的位移一 判 断 题1. 已知P M ,Mk 图，用图乘法 求位移的结果为：（ω1у1+ω2у2）/（EI ）。
（ ） （X ） 题1图 题2图 题3图2. 图示结构中B 点挠度不等于零。
（ ）（√）3. 图示桁架中腹杆截面的大小对C 点的竖向位移影响。
（ ）（X ）4. 求图示A 点竖向位移可用图乘法。
（ ）（X ）题4图 题5图5. 图示梁的跨中挠度为零。
（ ）（√）6. 在位移互等定理中，可以建立线位移和角位移的互等关系：12δ=21ϕ。
这里12δ，21ϕ与只是数值相等而量纲不同。
（ ）（X ）7. 三个刚片用不在同一直线上的三个虚铰两两相联，则所组成的体系是无多余约束的几何不变体系。
（ ）（√）8. 几何瞬变体系产生的运动非常微小并很快就转变成几何不变体系，因而可以用作工程结构。
（ ）（X ）9. 在任意荷载下，仅用静力平衡方程即可确定全部反力和内力的体系是几何不变体系。
（ ）（√）10. 两刚片或三刚片组成几何不变体系的规则中，不仅指明了必需的约束数目，而且指明了这些约束必须满足的条件。
（ ）（√）11. 在非荷载因素（支座移动，温度变化，材料收缩等）作用下，静定结构不产生内力，但会有位移，且位移只与杆件相对刚度有关。
（ ）（X ）12. 虚功中的力状态和位移状态是彼此独立无关的，这两个状态中的任一个都可看作是虚设的。
（ ）（√）13. 温度改变，支座位移，材料收缩和制造误差不会使静定结构产生内力，因而也不产生位移。
（ ）（X ）14. 计算自由度W 小于等于零是体系几何不变的充要条件。
（ ）（X ）15．若体系计算自由度W<0，则它一定是几何可变体系。
（ ）（X ）16．平面几何不变体系的三个基本组成规则是可以相互沟通的。
（ ）（√）17．三刚片由三个单铰或任意六根链杆两两相联，体系必为几何不变。
（ ）（X ）18．图示三铰刚架，EI 为常数，A 铰无竖向位移。
结构动力学哈工大版课后习题解答
.. .
..
第一章 单自由度系统
1.1 总结求单自由度系统固有频率的方法和步骤。 单自由度系统固有频率求法有：牛顿第二定律法、动量距定理法、拉格朗日方程法和能量守 恒定理法。 1、 牛顿第二定律法 适用范围：所有的单自由度系统的振动。 解题步骤：（1） 对系统进行受力分析,得到系统所受的合力；
（2） 利用牛顿第二定律 m x F ,得到系统的运动微分方程；
0
bi
2 T
T
F (t ) sin(it )dt
0
因为 F (t) H sin 2 (0t) 是偶函数，所以 bi 0 。
于是
F (t )
H 2
H 2
c os (2 0 t )
而
x(t)
H 2k
A s in(2 0 t
a
/
2)
；
式中
H
A
2m
；
( n 2 402 ) 16n202
1 2
K A A2 K B B 2
1 2
K
A
KB
rA 2 rB 2
A2 ;
系统的机械能为
图 1-36
c
）
T
U
1 4
m
A
mB rA2 A2
1 2
K
A
KB
rA 2 rB 2
A2
C；
由 d T U 0 得系统运动微分方程
dt
1 2
m A
mB rA2A
K
A
KB
rA 2 rB 2
48EIl3
；
m
48EI k1l 3 m
（b）此系统相当于两个弹簧并联, 等效刚度为:
(高清版)哈工大2019年《结构力学》考研真题和答案
哈尔滨工业大学2019年硕士研究生入学考试试题考试科目：结构力学报考专业：结构工程、工程力学等考试代码：【872】是否允许使用计算器：【是】一、填空题1.图是体系的计算自由度W= ，为体系。
2.图示静定结构，受荷载作用，求M A= ，侧受拉。
3.如图所示，求F H= 。
4.求C点的相对转角θC= 。
5.已知图示结构各杆长a，EI为常数，截面为矩形，截面高度为H，线膨胀系数为α。
当内部温度降低t℃，外侧温度不变时，求M AB= 。
6.用位移法计算图示结构时，F1P= 。
二、单项选择题1.图示结构的超静定次数是N= 。
A .0 B.8 C.10 D.142.如下图，EI为常数，CD杆的分配系数为。
A . 1/6 B.1/8 C.1/11 D.1/163.下列不一定满足线弹性要求的是。
ds D.W外=W内A．δij=δji B. r ij=r ji C.M1M PEI4.利用对称性求解图示结构时，位移法最少基本未知量的个数为。
A .1 B.2 C.3 D.45.影响静定结构内力影响线的因素是哪个。
A .外荷载 B.杆件的横截面面积 C.杆件的E D.约束条件6.如图所示，若斜杆A2增大，则F NBC。
A .增大 B.减小 C.不变 D.与A1/A2有关三、试求桁架1,2杆的内力。
四、求图示结构C截面的相对转角。
五、画出下图结构的弯矩、剪力、轴力图。
六、用力法计算图示结构的M图。
七、用位移法计算图示结构，作M图。
八、（1）作图示结构F NCD，M A,F QCB的影响线（F P=1从B E）；（2）由影响线求q作用下的M A。
答 案一、 填空题1. 0，无多余约束的几何不变2. m （上侧受拉）3. 10 3kN （←）4.2△l（ ） 5.3EI αt a+αEIt H（内侧受拉） 6. −1312ql （↓）二、 单项选择题1-6 BBDBDA三、 提示：荷载可分为正对称和反对称F 1= 55F P （拉） F 2=3 25F P （拉）四、 提示：图乘法−7qa 224EI −（4 2+4）qa （ ） 五、 提示：静定复合刚架六、 提示：超静定复合刚架。
结构力学第三章习题及答案
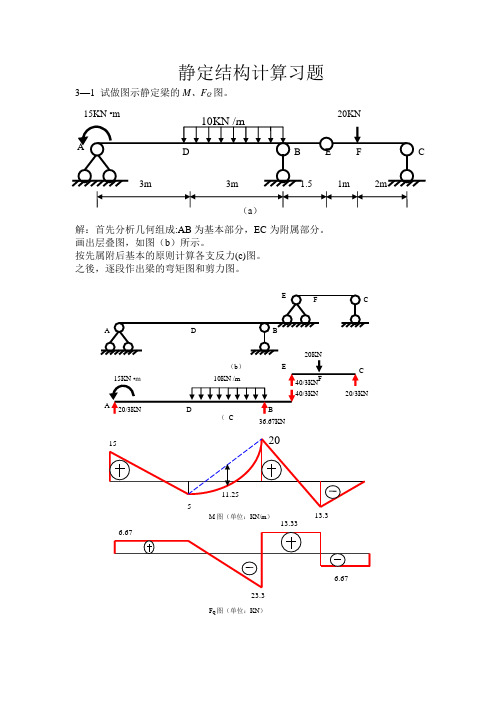
静定结构计算习题3—1 试做图示静定梁的M 、F Q 图。
解：首先分析几何组成:AB 为基本部分，EC 为附属部分。
画出层叠图，如图（b ）所示。
按先属附后基本的原则计算各支反力(c)图。
之後，逐段作出梁的弯矩图和剪力图。
36.67KN15KN •m 20KNM 图（单位：KN/m ）13.323.313.33F Q 图（单位：KN ）3—3 试做图示静定刚架的内力（M 、F Q 、F N ）图，并校核所得结果。
解：（1）计算支反力F AX =48kN （→） M A =60 KN •m (右侧受拉) （2）逐杆绘M 图 （3）绘F Q 图 （4）绘N 图（5）校核: 内力图作出后应进行校核。
(略)3—7 试做图示静定刚架的内力（M 、F Q 、F N ）图，并校核所得结果。
解：（1）计算支反力F AX =20kN （←） F AY =38kN(↑) F BY =62kN(↑) （2）逐杆绘M 图BCM 图（单位：KN/m ） F Q 图（单位：KN ）3030F AX F N图（单位：60）20）（3）绘F Q 图 （4）绘N 图（5）校核: 内力图作出后应进行校核。
(略)3—9 试做图示静定刚架的内力（M 、F Q 、F N ）图，并校核所得结果。
解：（1）计算支反力F AX =0.75qL （←） F AY =-0.25qL( ) F BY =0.25qL(↑) （2）逐杆绘M 图 （3）绘F Q 图 （4）绘N 图（5）校核: 内力图作出后应进行校核。
(略)3—11试做图示静定刚架的内力（M 、F Q 、F N ）图，并校核所得结果。
解：（1）计算支反力F BX =40KN （←） F AY =30KN (↑) F BY =50kN(↑) （2）逐杆绘M 图 （3）绘F Q 图 （4）绘N 图（5）校核: 内力图作出后应进行校核。
(略)C（a ）qBY 23—17 试求图示抛物线三铰拱的支座反力，并求截面D 和E 的内力。
哈尔滨工业大学01-03年春秋结构力学试卷及答案精品文档29页
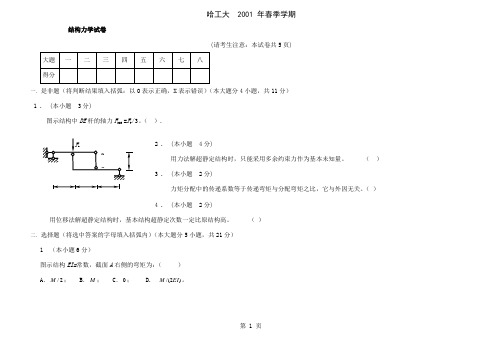
哈工大 2001 年春季学期结构力学试卷(请考生注意：本试卷共5页)一．是非题（将判断结果填入括弧：以O 表示正确，X 表示错误）（本大题分4小题，共11分）1 . (本小题 3分)图示结构中DE 杆的轴力F NDE =F P /3。
（ ）.2 . (本小题 4分)用力法解超静定结构时，只能采用多余约束力作为基本未知量。
（ ） 3 . (本小题 2分)力矩分配中的传递系数等于传递弯矩与分配弯矩之比，它与外因无关。
（） 4 . (本小题 2分)用位移法解超静定结构时，基本结构超静定次数一定比原结构高。
（ ）二．选择题（将选中答案的字母填入括弧内）（本大题分5小题，共21分）1 （本小题6分）图示结构EI=常数，截面A 右侧的弯矩为：（ ） A ．2/M ； B ．M ； C ．0； D. )2/(EI M 。
2. （本小题4分）图示桁架下弦承载，下面画出的杆件内力影响线，此杆件是：（ ） Ａ.ch ; B.ci; C.dj; D .cj .3. (本小题 4分)图a 结构的最后弯矩图为：A. 图b;B. 图c;C. 图d;D.都不对。
（ ）( a) (b) (c) (d)4. (本小题 4分)用图乘法求位移的必要条件之一是：A.单位荷载下的弯矩图为一直线；2=1/4 M /8 M /2B.结构可分为等截面直杆段；C.所有杆件EI 为常数且相同；D.结构必须是静定的。
( ) 5. （本小题3分）图示梁A 点的竖向位移为（向下为正）：( )Ａ．F P l 3/(24EI ); B . F P l 3/(!6EI ); C . 5F P l 3/(96EI ); D. 5F P l 3/(48EI ).三（本大题 5分）对图示体系进行几何组成分析。
四（本大题 9分）图示结构B 支座下沉4 mm ，各杆EI=2.0×105 kN ·m 2，用力法计算并作M 图。
五（本大题 11分） 用力矩分配法计算图示结构，并作M 图。
结构力学章节习题及参考答案
习题2.1(6)图
习题2.2填空
(1)习题2.2(1)图所示体系为_________体系。
习题2.2(1)图
(2)习题2.2(2)图所示体系为__________体系。
习题2-2(2)图
习题2.2(5)图
(6)习题2.2(6)图所示体系为_________体系，有_________个多余约束。
习题2.2(6)图
(7)习题2.2(7)图所示体系为_________体系，有_________个多余约束。
习题2.2(7)图
习题2.3对习题2.3图所示各体系进行几何组成分析。
习题2.3图
第3章静定梁与静定刚架习题解答
习题7.2(4)图
习题9.3用力矩分配法计算习题7.3图所示连续梁，作弯矩图和剪力图，并求支座B的反力。
（1）（2）
习题7.3图
习题9.4用力矩分配法计算习题7.4图所示连续梁，作弯矩图。
（1）（2）
习题7.4图
习题9.5用力矩分配法计算习题7.5图所示刚架，作弯矩图。
（1）（2）
习题7.5图
第11章影响线及其应用习题解答
习题11.1是非判断题
(1)习题8.1(1)图示结构BC杆轴力的影响线应画在BC杆上。（ ）
习题8.1(1)图习题8.1(2)图
(2)习题8.1(2)图示梁的MC影响线、FQC影响线的形状如图（a）、（b）所示。
(3)习题8.1(3)图示结构，利用MC影响线求固定荷载FP1、FP2、FP3作用下MC的值，可用它们的合力FR来代替，即MC=FP1y1+FP2y2+FP3y3=FR 。( )
结构力学 第三章 作业参考答案
40kN m
10kN m M图(kN m)
32.5kN
20kN
20kN F(kN) S
解：求支座反力。取整体：
47.5kN
∑M ∑F
A
=0
FB × 8 − 20 ×10 − 10 ×10 × 3 − 40 = 0 FAy + FB − 10 ×10 − 20 = 0
然后即可做出弯矩图，利用弯矩图即可作出剪力图。
1m
D 80
30
40 E
20 40
40 C F
80 E
40
A
解： （1） 求支座反力
B
40
∑F = 0 ∑M = 0 ∑F = 0
y A x
FC − 10 × 4 − 20 = 0 FA − FB = 0
⇒ FC = 60 kN ⇒ FC = 10 kN
（1） （2） （3）
FB ×1 − 50 − 10 × 4 × 6 − 20 × 10 = 0 ⇒ FB = 10 kN
然后即可做出弯矩图。
4
结构力学 第三章 习题 参考答案
3—10 试不计算反力绘出梁的 M 图。
A E B F C G D H
2M M
2M
2M
首先可作出悬臂段 AE 的弯矩图，如上图； B 点为铰结点，弯矩为零，故可作出 EB 段弯矩； B 铰左右两边的剪力相等，故弯矩图为一直线，就可以将 EB 段弯矩延长至 F，其余作法与之 相同。
4 = 77.6 kN 17
1 = −19.4 kN 17 = − FDy = −(20 + 20 × 7) = −160 kN
验证结点 B 的 FS 、 FN 的受力平衡如图（b）所示。
哈尔滨工程大学期末结构力学考试
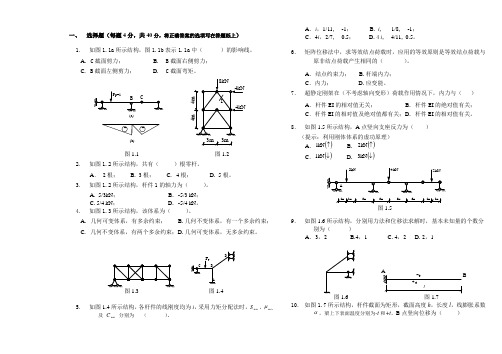
一、 选择题（每题4分，共40分，将正确答案的选项写在答题纸上） 1． 如图1.1a 所示结构，图1.1b 表示1.1a 中（ ）的影响线。
A . C 截面剪力； B . B 截面右侧剪力； C . B 截面左侧剪力； D . C 截面弯矩。
(a)(b)3m 3m图1.1 图1.22． 如图1.2所示结构，共有（ ）根零杆。
A ． 2根；B . 3根；C . 4根；D . 5根。
3． 如图1.2所示结构，杆件1的轴力为（ ）。
A . 5/3kN ； B . -5/3 kN ；C .5/4 kN ；D . -5/4 kN 。
4． 如图1.3所示结构，该体系为（ ）。
A . 几何可变体系，有多余约束；B .几何不变体系，有一个多余约束；C . 几何不变体系，有两个多余约束；D .几何可变体系，无多余约束。
图1.3 图1.45． 如图1.4所示结构，各杆件的线刚度均为i ，采用力矩分配法时，BD S ，BDμ及 BD C 分别为 （ ）。
A ．i ，1/11, -1；B . i , 1/8, -1；C ．4i ，2/7, 0.5；D .4 i , 4/11, 0.5。
6． 矩阵位移法中，求等效结点荷载时，应用的等效原则是等效结点荷载与原非结点荷载产生相同的（ ）。
A ．结点约束力； B .杆端内力；C ．内力；D .应变能。
7． 超静定刚架在（不考虑轴向变形）荷载作用情况下，内力与（ ）A ．杆件EI 的相对值无关；B . 杆件EI 的绝对值有关；C ．杆件EI 的相对值及绝对值都有关；D . 杆件EI 的相对值有关。
8． 如图1.5所示结构，A 点竖向支座反力为（ ）（提示：利用刚体体系的虚功原理） A ．()↑kN 1 B . ()↑kN 2C ．()↓kN 1D . ()↓kN 31m1m2m2m 2m 2m 1m 1m图1.59． 如图1.6所示结构，分别用力法和位移法求解时，基本未知量的个数分别为（ ）A ．3，2 B.4，1 C. 4，2 D. 2，1lAB-t+t图1.6 图1.710． 如图1.7所示结构，杆件截面为矩形，截面高度h ，长度l ，线膨胀系数α，梁上下表面温度分别为-t 和+t ，B 点竖向位移为（ ）2mq =1kN/m()↑=↑=kN 4kN 4B R RA F F对称结构对称荷载，从I-I 面剖开，取左侧作为隔离体，kN 40441615.020=⇒=⨯-⨯⨯+⇒=∑NDE NDE F F Mc利用D 点的平衡，求得kN 4-=NDF F （压杆），kN 66.5=NDA F 。
哈工大结构力学试卷参考答案
哈工大结构力学试卷参考答案呼伦贝尔学院建筑工程学院《结构力学》试卷1参考答案考试时间120分钟满分100分学院专业级班姓名学号题号得分评卷人一二三四总分能够减少自由度的装置称为约束。
5、图6所示结构的超静定次数是 6 次，此结构位移法基本未知量的个数是 6 个。
6、结构力学的研究对象是杆件结构。
图67、利用位移计算总公式计算结构位移时，对于桁架只须考虑轴力项，对于梁和刚架只须考虑弯矩项，对于拱要考虑弯矩、轴力项。
三、单项选择题（2分×10题，共20分） 1、下列结构内力只有轴力的是（C ）。
A、梁 B、刚架 C、桁架 D、拱2、图7所示平面体系的几何组成性质是（ D ）。
A、几何不变且无多余约束 B、几何可变C、几何不变且有多余约束D、几何瞬变图73、当一个竖向单位荷载沿结构移动时，表示某一量值变化规律的图形是（C ）。
A、弯矩图B、轴力图C、影响线D、剪力图 4、三个刚片用三个铰两两联结而成的体系是（ D ）。
A、几何不变B、几何可变C、几何瞬变D、以上三者均有可能 5、静定结构在几何构造上的特征是（ D ）。
A、有多余约束 B、计算自由度W等于零一、判断题（对的打“√”错的打“×”，2分×5题，共10分） 1、静定结构受温度改变影响会产生内力。
（× ）2、所谓零秆，既该杆的轴力为零，故从该静定结构去掉，并不影响结构的功能。
（× ）3、如图1所示为某超静定刚架对应的力法基本体系，其力法方程的主系数δ36/EI。
（× ）4、如图25所示结构的M图是正确的。
（√）X1 EI pl pl s θ i (a)6m l 22是X2 2EI M图p s θ i (b) 6m 图1 l图2 l 图3 5、如图3所示，（a）与（b）所示梁A端的转动刚度示相同的。
（√ ） l/2 l/2 l 二、填空题（每空1分,共15分）ql 2q B 1、图4所示结构支座A的支座反力为 3ql ，方向向上，B截面的剪力为 3ql/2 ，2A C、无多余约束 D、几何不变，且无多余约束 6、位移法的基本未知量是（ A）。
哈尔滨工程大学船舶结构力学课程习题目集答案word版
第1章绪论１．１题１）承受总纵弯曲构件：连续上甲板，船底板，甲板及船底纵骨，连续纵桁，龙骨等远离中和轴的纵向连续构件（舷侧列板等）２）承受横弯曲构件：甲板强横梁，船底肋板，肋骨３）承受局部弯曲构件：甲板板，平台甲板，船底板，纵骨等４）承受局部弯曲和总纵弯曲构件：甲板，船底板，纵骨，递纵桁，龙骨等１．２题甲板板：纵横力（总纵弯曲应力沿纵向，横向货物或上浪水压力，横向作用）舷侧外板：横向水压力等骨架限制力沿中面内底板：主要承受横向力货物重量，骨架限制力沿中面为纵向力舱壁板：主要为横向力如水，货压力也有中面力第2章单跨梁的弯曲理论２.1题设坐标原点在左跨时与在跨中时的挠曲线分别为v(x)与v(1x)１）图2.1333 2334243()()()424 ()26666l l ll l lp x p x p x M x N xv xEI EI EI EI EI---=++++原点在跨中：3230111104()4()266llp xM x N xv x vEI EI EI-=+++，'11'11()0()022(0)0(0)2l lv vpv N⎧==⎪⎨⎪==⎩２）3323()3 2.2()266llp xN xMxv x xEI EI EIθ-=+++图３）333002()2 2.3()666xx x llp xN x qx dxv x xEI EI EIθ-=++-⎰图２.２题a)33111311131(3)(2)616444641624 pp ppl plv v vEI EI⎡⎤⎡⎤=+=⨯⨯-+⨯-⨯⎢⎥⎢⎥⎣⎦⎣⎦=3512plEI333321911()61929641624pl pl pl V EI EI EI ⎡⎤⎛⎫=-++= ⎪⎢⎥⎝⎭⎣⎦b) 2'292(0)(1)3366Ml Ml Pl v EI EI EI-=+++ =2220.157316206327Pl Pl Pl EI EI EI-+=⨯2291()(1)3366Ml Ml Pl l EI EI EIθ-=+-+ =2220.1410716206327Pl Pl Pl EI EI EI---=⨯()()()2222133311121333363l l p l l v m m EIl EI ⎛⎫⎛⎫⎪ ⎪⎛⎫⎝⎭⎝⎭⎡⎤=----+ ⎪⎣⎦⎝⎭=2372430pl EIc) ()44475321927682304ql ql ql l v EI EI EI=-=()23233'11116(0)962416683612lq l ql plqlql v EI EI EIEIEI ⎡⎤=--=--=⎢⎥⎣⎦d)2.1图、2.2图和2.3图的弯矩图与剪力图如图2.1、图2.2和图2.3图2.1图2.2图2.32.3题1）()32212120624452313120Ml ql l l Mlq q EI EI EI EI q l M θ⎡⎤=---+=⎢⎥⎣⎦∴=右2）32101732418026q l Ml l l Ml lq EI EI EIEI θ⎡⎤=-++-⎢⎥⎣⎦=3311117131824360612080q l q l EI EI⎛⎫-++-=-⎪⨯⎝⎭ 2.4 题2.5图3000()6N x v x v x EIθ=++，()00v A p N =-300()6x v x Ap x A N EI θ⎛⎫∴=++- ⎪⎝⎭如图2.4， ()()0v l v l '==由得300200200060263l Ap l A N EI l N EI pl Ap l EI pN θθθ⎫⎛⎫++-=⎪⎪⎪⎝⎭⎬⎪+=⎪⎭⎧-==-⎪⎨⎪=⎩解出 3333()1922pl x x v x EI l l ⎛⎫∴=-+ ⎪⎝⎭图2.42.6图()()()()()()()2300122300012120001221223121212260,42026622M x N x v x x EI EIv l v l M l N l EI EI M l l l EI EIEI M l N l N l EI EI x x v x x l l θθθθθθθθθθθθθθ=++'==⎫⎧=--++=⎪⎪⎪⎪⎬⎨⎪⎪=+++=⎪⎪⎩⎭++∴=++由得解得 2.5题2.5图：（剪力弯矩图如２．５）()132023330222002332396522161848144069186pl Mp pR p ll p pl v AR EI EI v l Mlpl pl pl v EI EI EI EI v Ml pl pl pl v l EI EI EI EIθ-∴==-===⋅=⎛⎫=-=-=⎪⎝⎭-'==--=-=-()16A pa b b M A l K l ⎡⎤=++⎢⎥⎣⎦， 图2.5 111,0,6632A l a l b A K ====+=将代入得：()16312pl plM ==2.7图：（剪力弯矩图如２．６）341113422244440.052405021005112384240100572933844009600l ql ql v A R EI EI l ql ql v A R EI EIl qlql v EI EI ql ql EI EI==⋅===⋅=⎛⎫⎛⎫=++ ⎪ ⎪⎝⎭⎝⎭⎛⎫=+=⎪⎝⎭ 图２．６()()3331233312111202424401007511117242440100300v v ql ql ql EI l EI EIv v ql ql qll EI l EI EIθθ-⎛⎫=-=-+=⎪⎝⎭--⎛⎫=--=--+=⎪⎝⎭2.8图（剪力弯矩图如２．７）()2221401112124,,0,11,82411118243212121248243,82864AA Qa b M A K l Q qa a l b A K ql ql M ql qlql R ql v AR EIα⎡⎤⎛⎫=⋅++⎢⎥⎪⎝⎭⎢⎥⎣⎦======++==⨯⨯⨯+==-===由,代入得图２．７442433032355238412816384111(0)246246448192()6488l qlql Ml ql v EI EI EI EI v ql Ml ql EI l EI EI ql EIl ql ql l M EI EI θθα⎛⎫∴=+-=⎪⎝⎭⎛⎫=--=-- ⎪⎝⎭=-=-=-⋅=2.6题. []1max 2max 2113212132142.()()62()()62()()242(0)sN EIv s sss s N dv dx dx dx GGA N EI v dx v C GA GA EI ax bx v v v f x cx d f x ax b C GA EI EIax bx f x f x c a x d GA GA qx qx f x f x EI EIv v τγ'''====-''=−−−→-+⎡⎤''∴=+=++++-+++⎢⎥⎣⎦⎛⎫''=-+++-+ ⎪⎝⎭''==''=⎰式中由于11142323432342(0)00()()00242602,224()241222425()23848s s s ssd b v l v l ql EI ql al EI c a l EI GA EIGA qlal EIql ql c EI EIqx qlx qx qx qlv x x EI EI GA EI GA l ql ql v EI GA ===''==⎧⎛⎫-++-=⎪⎪⎪⎝⎭⎨⎪+=⎪⎩=⎛⎫∴=--++⎪⎝⎭∴=+可得出由得方程组：解出：a=2.8题 已知：20375225,1.8,751050kgl cm t cm s cm cm σ=⨯====1025100.7576.875kgq hs cm γ==⨯⨯=面积2cm 距参考轴cm面积距3cm惯性矩4cm自惯性矩4cm外板1.845⨯ 81 0 0 0 (21.87)略 球扁钢O N 24a38.75 9430.2 2232 ∑119.8 15.6 604.5 9430.22253.9ABC=11662224604.55.04116628610119.8BBe cm I C cm AA===-=-=275 1.838.75174min ,4555A cm l lI be s cm=⨯+=⎧⎫===⎨⎬⎩⎭计算外力时面积计算时，带板形心至球心表面1240.9 5.0419.862t y h e cm =+-=+-=形心至最外板纤维321186105.94433.5219.86t I y e cm w cm y =+=∴===()32206186101449.45.9422510501740.3662221086100.988,()0.980Iw cm y A l u EI x u u σϕ===⨯===⨯⨯== ()()()222212012020176.8752250.988320424.1212176.8752250.980158915)242415891510501416433.53204241050127114503204241050378433.5ql M x u kg cm ql M u kgcm M kg cm w M kg cm w M kg w ϕσσσσσσ==⨯⨯==-=-⨯⨯⨯=-=+=+==+=+==+=+=中中球头中板固端球头端（2max 21416kg cm cm σ⎫⎪⎪⎪⎪∴=⎬⎪⎪⎪⎪⎭若不计轴向力影响，则令u=0重复上述计算：222max 0176.875225241050142424433.5142414160.56%1424ql kg w cm σσσ⨯==+=+=⨯-=球头中相对误差：结论：轴向力对弯曲应力的影响可忽略不及计。
哈工大结构力学题库3
第四章 力 法一 判 断 题1. 图示结构，据平衡条件求出B 点约束力，进而得图示弯矩图，即最后弯矩图。
（ ）（X ）题1图 题2图2. 图示结构用力法求解时，可选切断杆件2，4后的体系作为基本结构。
（ ）（X ）3. 图a 结构，支座B 下沉a 。
取图b 中力法基本结构，典型方程中1C a ∆=-。
（ ） （X ）题3图 题4图4. 图a 所示桁架结构可选用图b 所示的体系作为力法基本体系。
（ ）（√）5. 图a 结构，取图为力法基本结构，1C l θ∆=。
（ ） （X ）题5图 题6图6. 图a 结构的力法基本体系如图b ，主系数3311/(3)/()l EI l EA δ=+。
（ ）（X ）7. 图示结构用力法解时，可选切断1，2，3，4杆中任一杆件后的体系作为基本结构.（ ）（X ）题7图 题9图 8. 图示结构受温度变化作用，已知α，h ，选解除支杆B 为力法基本体系(设B X 向上为正)，典型方程中自由项2121()/(4)t a t t l h ∆=--。
（ ）（X ）9. 图a 结构，力法基本体系如图b ，自由项412/(8)P ql EI ∆=-。
（ ）（X ）题10图 题11图10.图示超静定梁在支座转动1A ϕ=时的杆端弯矩26.310AB M KN m =⨯⋅，22( 6.310)EI KN m =⨯⋅。
（ ）（√） 11. 图a 结构，取图b 为力法基本结构，h 为截面高度，α为线胀系数，典型方程中2121()/(2)t a t t l h ∆=--。
（ ）（X ）题12图 题13图 12. 图a 结构，取力法基本体系如图b 所示，则1/C l ∆=∆（ ）。
（X ）13. 超静定结构在荷载作用下的反力和内力，只与各杆件刚度的相对数值有关。
（ ）（√）14. 图示结构的超静定次数为4。
（ ）（X ）题15图 题16图15. 图示结构，选切断水平杆为力法基本体系时，其3112/(3)h EI δ=。
哈工大版理论力学复习题
理论力学复习题一、是非题1. 若一平面力系向A，B两点简化的结果相同，则其主矢为零主矩必定不为零。
2. 首尾相接构成一封闭力多边形的平面力系是平衡力系。
3. 力系的主矢和主矩都与简化中心的位置有关。
4. 当力系简化为合力偶时，主矩与简化中心的位置无关5.平面一般力系平衡的充要条件是力系的合力为零。
二、选择题1.将平面力系向平面内任意两点简化，所得的主矢相等，主矩也相等，且主矩不为零，则该力系简化的最后结果为------。
①一个力②一个力偶③平衡2.关于平面力系的主矢和主矩，以下表述中正确的是①主矢的大小、方向与简化中心无关②主矩的大小、转向一定与简化中心的选择有关③当平面力系对某点的主矩为零时，该力系向任何一点简化结果为一合力④当平面力系对某点的主矩不为零时，该力系向任一点简化的结果均不可能为一合力3.下列表述中正确的是①任何平面力系都具有三个独立的平衡方程式②任何平面力系只能列出三个平衡方程式③在平面力系的平衡方程式的基本形式中，两个投影轴必须相互垂直④平面力系如果平衡，该力系在任意选取的投影轴上投影的代数和必为零4. 图示的四个平面平衡结构中,属于静定结构的是三、填空1. 图示桁架。
已知力1p 、 和长度a 。
则杆1内力=_________； 杆2内力=_________； 杆3内力=_________。
2. 矩为M =10k N .m 的力偶作用在图示结构上。
若 a =1m ，不计各杆自重，则支座D 的约束力=_________，图示方向。
3. 一平面汇交力系的汇交点为A ，B为力系平面内的另一点，且满足方程。
若此力系不平衡，则力系简化为_________。
4.若一平面平行力系中的力与Y 轴不垂直，且满足方程0y F =∑。
若此力系不平衡，则力系简化为_________。
答案：一、1、×2、×3、×4、√5、×二、1、② 2、① 3、④ 4、③三、1、0、P 1、0 2、=10KN(--)（提示：先从CB 及绳处断开，以右部分为研究对象，以B 为矩心，列力矩方程，则D 处竖直方向力为零，再以整体为研究对象以A 为矩心，列力矩方程可求出D 处）3.过A 、B 两点的一个力4、一个力偶第三章 练习题一、是非题1.力对点之矩是定位矢量，力对轴之矩是代数量。
哈工大结构力学考研题库
2
哈工大题库—几何组成分析
【内部资料】
3. 图示体系虽有三个多余约束，但为保证其几何不变，哪两根链杆是不能同时去掉的。
A．a 和 e B. a 和 b C. a 和 c D. c 和 e
（B）
4. 图示体系是
（B）
A．无多余联系的几何不变体系 B．有多余联系的几何不变体系
C．几何可变体系 D．瞬变体系
题7图
题8图
题9图
8. 图示体系的计算自由度为（D）
A．0 B．1 C．-1 D．-2
9. 图中体系是(C)
A.几何可变体系 B.几何瞬变体系 C.无多余联系的几何不变体系
D.有多余联系的几何不变体系
10. 图示平面体系的几何组成为(C)
A.几何不变无多余约束 B.几何不变有多余约束 C.瞬变体系 D.几何可变体系
既然我已经踏上这条道路，那么任何东西都不应妨碍我沿着这条路走下去——康德
4
哈工大题库—几何组成分析
【内部资料】
题 17 图
题 18 图
18. 图示体系为几何不变体系，且其多余联系数目为（D）
A．1 B．2 C．3 D．4
19. 图示体系的几何组成为（B）
A．几何不变无多余约束 B．几何不变有多余约束
C．瞬变体系 D．常变体系
20. 图示平面体系的几何组成性质是（A）
A．几何不变且无多余联系的 B．几何不变且有多余联系的
C．几何可变的 D．瞬变的
题 19 图
题 20 图
题 21 图 题 22 图
题 23 图
21. 图示平面体系的几何组成性质是（A）
A．几何不变且无多余联系的 B．几何不变且有多余联系的
16. 图示体系是(A)
结构力学教材习题第三章答案全解——哈工大老师提供
结构力学(王焕定第三版)教材习题答案全解第三章习题答案3-1 (a) 答：由图（a）、（b）可知结构对称（水平反力为零）荷载对称，因此内力对称。
所以可只对一半进行积分然后乘以 2 来得到位移。
如图示F P R(1−cos θ)M P = θ∈[0,π/2]；M=R sin θθ∈[0,π/2]2 代入位移计算公式可得M P M 1 π2 M P M 2 π2 F P R(1−cos θ)∆Bx = ∑∫ EI d s = 2⋅EI ∫0 EI R dθ= EI ∫0 2 R sin θR dθ=F P R3 =(→)2EI3-1 (b) 答：如图（a）、（b）可建立如下荷载及单位弯矩方程pR ∆Bx =∑∫ MEIM d s =∫0π2 MEI P M R dθ= qEI 4 ∫0π2 (1−2cosθ+cos 2 θ)R dθqR 4 ⎡ θ 1 ⎡3π ⎡ qR 4= EI ×⎡θ−2sinθ+ 2 + 4sin2θ⎡⎡0 =⎡⎡ 4 − 2⎡⎡ 2EI (→)2 ⎡3-2 答：作M P 图和单位力弯矩图如下图： 由此可得内力方程代入位移公式积分可得2 2 P 0s i n ( ) d (c o s ) (c o s )q M R q R M R θθ α α θ θ − == − = − ∫AqRBα θ( a θ( b )根据题意 EI (x ) = EI (l + x )2l 代入位移公式并积分（查积分表）可得M P M l2 q 0x 4∆Bx =∑∫ EI d x =∫0 6EI (l + x ) d x7 q 0l 4 ql 4= (ln 2− )× =(→)12 3EI EI3-3 答：分别作出荷载引起的轴力和单位力引起的轴力如下图所示：由此可得 C 点的竖向为移为：1 lM 图 x3 0 p x q M M xl= = xP M 图2 0 6q lABl q 05 83 8F NP F N1 F NP F N1 ∆Cy =∑∫EA d s=∑ EA l =6 5kN× ×6 m+2× kN× ×5 m+125 kN× ×5 m+75 kN× ×6 m)= 8 8EA=×10−4 m当求CD 和CE 杆之间的夹角改变使：施加如图所示单位广义力并求作出F N2 图，则F∆=∑∫ F NP EA F N2 ds=∑ NP EA F N2 l2× kN×(−×5 m+(− kN)××6 m =EA=−×10−4 rad ( 夹角减小）3-4 （a）答：先作出M p和M 如右图所示。
哈尔滨工业大学结构力学期末试卷及答案
哈工大 2003 年春季学期结构力学试卷一．是非题（将判断结果填入括弧：以O 表示正确，X 表示错误）（本大题分3小题，共7分） 1.（本小题 3分）图a. b 所示三铰拱的支座反力相同。
（ ）（a ）(b) 2.（本小题 2分）图示结构中的反力H =-M /L 。
（ ）3.（本小题 2分）力矩分配法中的分配系数 ，传递系数与外界因素（荷栽，温度变化等）有关。
（ ）二．选择题（将选中答案的字母填入括弧内，本大题分3小题，共9分）1． (本小题 4分) 连续梁和M 图如图所示，则支座B 的竖向反力F By 是：A. 1.21(↑)B.5.07( ↑)C.11.07(↓)D.17.07(↑)。
（ ）2 (本小题3分) 在位移法中，将铰接端的角位移，滑动支撑端的线位移作为基本未知量：A,绝对不可；B.一定条件下可以；C.可以，但不必；D.必须。
( )3 (本小题 2分) 图示体系为：A. 几何不变无多余约束B. 几何不变有多余约束C.几何常变 D. 几何瞬变三.填充题（将答案写在空格内）（本大题分2小题，共9分）1．（本小题 4分）图示刚架支座反力F By= ,C 截面的弯矩M C = ,剪力F Q C =2．（本小题 5分） 虚功原理应用条件是：力系满足 条件；位移是 的。
四（本大题 4分）对图示体系作几何组成分析q20 kN15.85五（本大题7分）用力法计算图示梁，取支座D的竖向链杆为多余约束，代以方向向上的多余力X1,求得δ11=l3/(EI)，Δ1P= -ql4/(24EI)，求作其M图。
六（本大题7分）求图示桁架杆件a，b的内力七（本大题8分）已知图示结构的M图, 作F Q , F N图。
八（本大题10分）作图示结构F Q B左，M F的影响线。
九（本大题12分）用力矩分配法计算并作图示对称结构的M图。
已知：q=40 kN/m各杆EI相同。
十（本大题13分）用位移法计算并作图示结构M图，横梁为无穷刚梁EI→∞，两柱刚度均为EI。
哈尔滨工业大学01-03年春秋结构力学试卷及答案共20页word资料
哈工大 2019 年春季学期结构力学试卷(请考生注意：本试卷共5页)11分）1 . (本小题 3分)图示结构中DE 杆的轴力F NDE =F P /3。
（ ）.2 . (本小题 4分) 用力法解超静定结构时，只能采用多余约束力作为基本未知量。
（ ）3 . (本小题 2分) 力矩分配中的传递系数等于传递弯矩与分配弯矩之比，它与外因无关。
（ ）4 . (本小题 2分)用位移法解超静定结构时，基本结构超静定次数一定比原结构高。
（ ） 二．选择题（将选中答案的字母填入括弧内）（本大题分5小题，共21分）1 （本小题6分）图示结构EI=常数，截面A 右侧的弯矩为：（ ）A ．2/M ；B ．M ； C ．0； D. )2/(EI M 。
2. （本小题4分）图示桁架下弦承载，下面画出的杆件内力影响线，此杆件是：（ ）Ａ.ch ; B.ci; C.dj; D .cj.23. (本小题 4分)图a 结构的最后弯矩图为：A. 图b;B. 图c;C. 图d;D.都不对。
（ ）( a) (b) (c) (d) 4. (本小题 4分) 用图乘法求位移的必要条件之一是： A.单位荷载下的弯矩图为一直线；B.结构可分为等截面直杆段；C.所有杆件EI 为常数且相同；D.结构必须是静定的。
( )5. （本小题3分） 图示梁A 点的竖向位移为（向下为正）：( )Ａ．F P l 3/(24EI ); B . F P l 3/(!6EI ); C . 5F P l 3/(96EI ); D. 5F P l 3/(48EI ).三（本大题 5分）对图示体系进行几何组成分析。
四（本大题 9分）图示结构B 支座下沉4 mm ，各杆EI=2.0×105 kN ·m 2，用力法计算并作M 图。
五（本大题 11分） 用力矩分配法计算图示结构，并作M 图。
EI =常数。
六（本大题14分）已知图示结构，422.110 kN m ,10 kN/m EI q =⨯⋅=求B 点的水平位移。
结构力学第3章习题答案
3-2 试作图示多跨静定梁的弯矩图和剪力图。
(a) 4P F a2P F a 2P F aＭ4PF Ｑ34P F 2P F(b) ４2020M Q10/326/3４10A B C a a a a a F P a D E F F P 2m 6m 2m 4m 2m A B C D 10kN 2kN/m (c) 21018018040M1560704040Q(d) 7.5514482.524MQ3m 2m2m AB C E F15kN 3m 3m 4m 20kN/m D 3m 2m 2m 2m2m 2m 2m ABC D E FG H 6kN ·m 4kN ·m 4kN 2m 3-3 试作图示刚架的内力图。
试作图示刚架的内力图。
(a) 242018616MQ1820(b) 3030301101010QM 2104kN ·m 3m 3m 2kN A CBD 6m 10kN 40kN ·m ABC D(c) 664275MQ(d) 444444/32MQN2kN/m 6kN 6m 4kN AB CD2kN 6m 2kN 4kN ·m ACB D E(e) 44814``(f) 2222200.815MQN4m ABC4m D4kN A B C2m 3m 4m 2kN/m 3-4试找出下列各弯矩图形的错误之处，并加以改正。
(a) F P(b) (c) F P(d) M(e) (f) F PF P3-5 试按图示梁的BC 跨跨中截面的弯矩与截面B 和C 的弯矩绝对值都相等的条件，确定E 、F 两铰的位置。
B C EFDA28ql M2221()222116121618c B C BC C qql M l x x qx xM M M M ql ql x ql x l=-+===\=\=\= 中FD()2ql x -lBC EFxDAql lx3-6 试作图示刚架的弯矩和剪力图。
结构力学各章练习题判断题
第二章：平面体系几何构造分析一．判断题1．几何可变体系在任何荷载作用下都不能平衡。
（）2．三个刚片由三个铰相连的体系一定是静定结构。
（）3．有多余约束的体系一定是超静定结构。
（）4．有些体系是几何可变体系，但却有多与约束存在。
（）5．在任意荷载作用下，仅用静力平衡方程即可确定全部反力和内力的体系是几何不变体系。
（）6．图1－16所示体系是几何不变体系。
（）图1－16 图1－17 图1－18 7．图1－17所示体系是几何不变体系。
（）8．几何瞬变体系的计算自由度一定等于零。
（）9．图1－18所示体系按三刚片法则分析，三铰共线故为几何瞬变。
（）10．图中链杆1和2的交点O可视为虚铰。
（）O2．8 多余约束的体系一定是几何可变体系。
（）2．9 只有无多余约束的几何不变体系才能作结构。
（）2．10 图示2－10铰结体系是无多余约束的几何不变体系。
（）图2－10 题2－112．11 图示2－11铰结体系是有多余约束的几何不变体系。
（）2．12 图示2－12体系是无多余约束的几何不变体系。
（）题2－12 题2－132．13 图示体系是有多余约束几何不变的超静定结构。
（）2．14 图示体系在给定荷载下可维持平衡，因此，此体系可作为结构承担荷载。
（）2．15 图示体系是有多余约束的超静定结构。
（）题2－14 题2－15答案：1 ×2 × 3 ×4 √5 √ 6 ×7 √8 ×9 ×10×；2.8 ×2.9×2.10√ 2.11× 2.12 ×2.13× 2.14 × 2.15 ×二、分析题：对下列平面体系进行几何组成分析。
3、4、C DB CDB5、 6、A CD BEABCDE7、 8、ABCD GE FA BCDEFGHK9、 10、11、 12、1234513、 14、15、 16、17、 18、19、 20、1245321、 22、123456781234523、 24、12345625、 26、27、28、29、30、31、32、33、BA CFDE三、在下列体系中添加支承链杆，使之成为无多余约束的几何不变体系。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第三章 虚功原理和结构的位移一 判 断 题1. 已知P M ,Mk 图，用图乘法 求位移的结果为：（ω1у1+ω2у2）/（EI ）。
（ ） （X ） 题1图 题2图 题3图2. 图示结构中B 点挠度不等于零。
（ ）（√）3. 图示桁架中腹杆截面的大小对C 点的竖向位移影响。
（ ）（X ）4. 求图示A 点竖向位移可用图乘法。
（ ）（X ）题4图 题5图5. 图示梁的跨中挠度为零。
（ ）（√）6. 在位移互等定理中，可以建立线位移和角位移的互等关系：12δ=21ϕ。
这里12δ，21ϕ与只是数值相等而量纲不同。
（ ）（X ）7. 三个刚片用不在同一直线上的三个虚铰两两相联，则所组成的体系是无多余约束的几何不变体系。
（ ）（√）8. 几何瞬变体系产生的运动非常微小并很快就转变成几何不变体系，因而可以用作工程结构。
（ ）（X ）9. 在任意荷载下，仅用静力平衡方程即可确定全部反力和内力的体系是几何不变体系。
（ ）（√）10. 两刚片或三刚片组成几何不变体系的规则中，不仅指明了必需的约束数目，而且指明了这些约束必须满足的条件。
（ ）（√）11. 在非荷载因素（支座移动，温度变化，材料收缩等）作用下，静定结构不产生内力，但会有位移，且位移只与杆件相对刚度有关。
（ ）（X ）12. 虚功中的力状态和位移状态是彼此独立无关的，这两个状态中的任一个都可看作是虚设的。
（ ）（√）13. 温度改变，支座位移，材料收缩和制造误差不会使静定结构产生内力，因而也不产生位移。
（ ）（X ）14. 计算自由度W 小于等于零是体系几何不变的充要条件。
（ ）（X ）15．若体系计算自由度W<0，则它一定是几何可变体系。
（ ）（X ）16．平面几何不变体系的三个基本组成规则是可以相互沟通的。
（ ）（√）17．三刚片由三个单铰或任意六根链杆两两相联，体系必为几何不变。
（ ）（X ）18．图示三铰刚架，EI 为常数，A 铰无竖向位移。
（ ） （√）题18图 题19图 题20图19．图示桁架，各杆EA 相同，AB 杆将发生转动。
（ ）（√）20．图示桁架，EA=常数，在力P 作用下，C 点竖向位移Δcv=1.414Pa/EA 。
（ ）（√）21．结构荷载和相应的弯矩图如图示，则C 点竖向位移Δcv 的算式如下：（X ）题21图 题22图 22．图示结构中EI ，EA 均为常数，铰C 两侧截面相对转角c ϕ为EI Pl /22。
（ ）（X ）23．功的互等，位移互等，反力互等和位移反力互等的四个普遍定理仅适用于线性变形体系。
（ ） （√）24．图示结构D 点的竖向位移()()EA Pa EI Pa DV 4/6/3+=∆。
（ ） （√）题24图 题25图25．图示结构A 点的竖向位移AV ∆为零。
（ ）（√）26．图示刚架A 点的水平位移2/3Pa AH =∆（方向相左）。
（ ） （X ）题26图 题27图 题28图27．图示结构梁式杆EI=常数，二力杆EA=常数，AB 杆的转角0=AB ϕ。
（ ）（√）28．图示结构铰C 两侧截面相对转角C ϕ可用下式求得：322211Pl l EI C ⨯⨯⨯⨯-=ϕ （ ）（X ） 29．图示结构，EI=常数，C ，B 两点相对水平位移值为()EI pl /53。
（ ） （X ）题29图 题30图30．图示为刚架的虚设力系，按此力系及位移计算公式可求出杆AC 的转角。
（ ）（√）31． 图示桁架EA=常数，图a 中C 点的竖向位移比图中b 中C 点的竖向位移大P l /（EA ）。
（ ）（X ）题31图 题32图32．图示结构宽度是高度的2/3，在P 力作用下，B 点的水平位移方向向右。
（ ）（√）33．已知图a 所示梁的Mp 图如图b ，各杆EI=常数，则铰B 左，右两侧截面的相对转角为()EI B /160=ϕ（铰B 左，右两侧向上转）。
（ ）（√）题33图 题34图 题35图 34．图示悬臂梁，EI 为常数，杆长为l ，B 点竖向位移()()↓=∆EI Ml BV 2/3。
（ ）（X ） 35．图示简支梁，当P1=1，P2=0时，1点的挠度为EI l /0165.03，2点挠度为EI l /077.03。
当P1=0，P2=1时，则1点的挠度为EI l /021.03。
（ ）（X ）36．结构的温度变化及单位荷载作用下的内力如图a ，b 所示，梁截面为矩形，h=0.6m ，材料线膨胀系数为α，则C ，D 两点的相对水平位移为400α。
（ ） （X ）题36图 题37图37．图示结构EI=常数，D 截面转角为零。
（ ）（√） 38．图示桁架EA=常数，在荷载P 作用下，结点C 的竖向位移为()EA Pl CV /828.5=∆。
（ ）（X ）题38图 题39图 题40图39．水平荷载P 分别作用于A 点和B 点时C 点产生的水平位移相同。
（ ）（X ）40．图示桁架，各杆EA 相同，EF 杆将无转动。
（ ）（√）41．图示桁架中，结点D 与结点E 的竖向位移相等。
（ ） （√）题41图 题 42图42．图a,b 为同一对称桁架，荷载不同，而K 点竖向位移相同。
（ ）（√）43．桁架及荷载如图，B 点将产生向左的水平位移。
（ ）（X ）（√）题43图 题44图 题 45图44．竖向荷载P 分别作用于A 点和B 点时，B 点产生的竖向位移是不同的。
（ ）（X ）45．图示桁架结点C 水平位移不等于零。
（ ）46．图示桁架B 点的竖向位移为零（EA=常数）。
（ ）（X ）题46图 题47图 题48图47．图示梁AB 在所示荷载作用下的M 图面积为3/3ql 。
（ ）（X ）48．图示梁EI=常数，C 点的竖向位移为EA qa 3/74（向下）。
（ ）（√）49．图示结构，EI=常数，q=p/a ，B 截面的转角位移为()EI Pa 2/2，顺时针方向。
（ ） （X ）题49图 题50图 题51图50．图示梁EI=常数，C 点的竖向位移方向向下。
（ ）（X ）51．位移互等定理为：第一个力的方向上由第二个力所引起的位移，等于第二个力的方向上由第一个力所引起的位移。
（ ）（X ）52．图示结构，EI=常数，q=2KN/m ，B 点的竖向位移为()()↓EI /3888。
（ ）（X ）53．图示结构中，增加杆AD ，CD 及BD 的EA 值，均能减小C 点的挠度。
（ ） （√）题53图54．应用虚力原理求体系的位移时，虚设力状态可在需求位移处添加相应的非单位力，亦可求得该位移。
（ ）（√）55．弹性体系虚功的特点是：（1）在作功过程中，力的数值保持不变；（2）作功的力与相应的位移无因果关系，位移由其他力系或其它因素所产生。
（ ）（√）56．若刚架中各杆均无内力，则整个刚架不存在位移。
（ ）（X ）57．变形体虚功原理也适用于塑性材料结构与刚体体系。
（ ）（√）58．虚功原理仅适用于线弹性的小变形体系。
（ ）（X ）59．在小变形条件下，结构位移计算和变形位移计算均可应用叠加原理。
（ ）（X ）60．图示桁架，已知线膨胀系数为α，杆AD ，DB 温度上升t ℃，则D 点竖向位移()↓3/16t α。
（ ） （X ）题60图 题61图 题62图61．图示桁架AB 杆的转角EA P AB /=ϕ（顺时针）。
（ ）（X ） 62．图示结构杆长l ，矩形截面，高为h=l/10，线膨胀系数为α。
内侧温度升高t ℃，外侧温度升高2t ℃。
则C 截面水平位移()→=∆tl CH α5。
（ ）（X ）63．图示结构BC 杆温度降低t ℃，线膨胀系数为α，则A 点的竖向位移是()↓=∆td AV α。
（ ） （X ）题63图 题64图 题65图64．图示混合结构，C 点的水平位移EI CH /5.7=∆。
（ ）（√） 65． 图示桁架各杆EA=常数，由于荷载P 是反对称性质的，故结点B 的竖向位移等于零。
（X ）66．图a,b 所示两结构中，除A 处的支承情况不同和图b 中多一根链杆DB 外，其余情况相同，则两图中B 点的竖向位移是相等的。
（ ）（√）题66图二 选 择 题1． 图示各种结构中，欲求A 点竖向位移，能用图乘法的为：（ ）（B ）题1图 题2图2．图示结构的两个状态，位移互等12δ=21ϕ，12δ和21ϕ的量纲为：（ ）A ．长度B ．无量纲C ．长 度/力D ．力/长 度（C ）3．图a,b 两种状态中，梁的转角ϕ与竖向位移δ间的关系为：（ ）A ．δ=ϕB ．δ与ϕ关系不定，取决于梁的刚度大小C ．δ>ϕD ．δ<ϕ（A ）题3图 题4图4．图示结构，求A ，B 两点相对线位移时，虚力状态应在两点分别施加的单位力为：（ ）A ．竖向反向力B ．水平反向力C ．连线方向反向力D ．反向力偶（C ）5．变形体虚位移原理的虚功方程中包含了力系与位移（及变形）两套物理量，其中：（ ）A ．力系必须是虚拟的，位移是实际的B ．位移必须是虚拟的，力系是实际的C ．力系与位移都必须是虚拟的D ．力系与位移两者都是实际的（B ）6．静定结构的位移与EA ，EI 的关系是：（ C ）A ．无关B ．相对值有关C ．绝对值有关D ．与E 无关，与A ，I 有关（C ）7．导出单位荷载法的原理：（ ）A ．虚位移原理B ．虚力原理C ．叠加原理D ．静力平衡条件（B ）8．按虚力原理所建立的虚功方程等价于：（ ）A ．静力方程B ．物理方程C ．平衡方程D ．几何方程（D ）9．四个互等定理适用于：（ ）A ．刚体B ．变形体C ．线性弹性体系D ．非线性体系（C ）10．图示结构两个状态中的反力互等定理 12γ=21γ，12γ和21γ的量纲为：（ ）A ．力X 长度B ．无量纲C ．力D ．长 度（A ）题10图 题16图11．刚体系与变形体系虚位移原理的虚功方程两者的区别在于：（ ）A ．前者用于求位移，后者用于求未知力B ．前者用于求未知力，后者用于求位移C ．前者的外力总虚功等于零，后者的外力总虚功等于其总虚应变能D ．前者的外力总虚功不等于零，后者的外力总虚功等于其总虚应变能（C ）12．功的互等定理：（ ）A ．适用于任意变形体结构B ．适用于任意线弹性体结构C ．仅适用于线弹性静定结构D ．仅适用于线弹性超静定结构（B ）13．静定结构温度改变时：（ ）A ．无变形，无位移，无内力B ．有变形，有内力，有位移C ．有变形，有位移，无内力D ．无变形，有位移，无内力（C ）14．线弹性结构的位移反力互等定理，其适用范围为：（ ）A ．只限于混合结构B ．只限于超静定结构C ．只限于静定结构D ．超静定和静定结构均可用（D ）15．变形体虚功原理：（ ）A ．只适用于静定结构B ．只适用于超静定结构C ．只适用于线弹性体系D ．适用于任何变形体系（D ）16. 图示为刚架在荷载作用下的Mp 图，曲线为二次抛物线，横梁的抗弯刚度为2EI ，竖柱为EI ，则横梁中点K 的竖向位移为：（ ）A ．87．75/（EI ）↓B ．43．875/（EI ）↓C ．94．5/（EI ）↓D ．47．25/（EI ）↓（B ）17. 图a,b 为同一结构的两个受力与变形状态，则在下列关系式中正确的是：（ ）A ．12c a ∆=∆B ．21a c ∆=θC ．12c c θθ=D ．12a c ∆=θ（B ）题17图18. 用图乘法求位移的必要条件之一是：（ ）A ．单位荷载下的弯矩图为一直线B ．结构可分为等截面直杆段C ．所有杆件EI 为常数且相同D ．结构必须是静定的（B ）图示为结构在荷载作用下的Mp ，Np 图，a=3m ，受弯杆件EI=常数，各链杆EA=常数，则D 点的竖向位移（ ↓ ）DV ∆=：（ ）A ．360/（EA ）+810/（EI ）B ．360（1+5）/（EA ）+810/（EI ）C ．360/（EA ）+900/（EI ）D ．360（1+5）/（EA ）+900/（EI ）（A ）题19图 题20图 19. 图示结构的受弯杆件的抗弯刚度为EI ，链杆的抗拉（压）刚度为EA ，且()230/m I A =，则D 端的转角（顺时针方向）为：（ ）A ．223/（3EI ）B ．137/（3EI ）C ．4673/（3EI ）D ．1500/（EI ）（C ）20. 图示梁当EI=常数时，B 端的转角是：( )A ．5q 3l /(48EI) （顺时针）B ．5q 3l /(48EI) （逆时针）C ．7q 3l /(48EI) （逆时针）D ．9q 3l /(48EI) （逆时针） （C ）题21图三 填 充 题1. 图示刚架，EI=常数，各杆长度为l ，A 点的竖向位移为 0 。