COMSOL周期性边界条件的应用
用周期性边界条件模拟导波介质的传播模式及其模式常数的后续分析计算

用周期性边界条件模拟导波介质的传播模式及其模式常数的后续分析计算 例子:平板波导基本参数:光波长1064nm ,导波介质为钕玻璃(n=1.54),介质厚度1000nm 。
波导中传播模式的理论值:通过理论计算(见附录),可知该频率的TE 光在这个波导中存在两个模式。
基模(m=0)的角度θ为74.533°,即β=k*n*sin74.533°,传播方向x 上的空间波长为x sin λλθ==1064nm/1.54/sin74.533°=716.871nm 。
1模(m=1)的角度θ为42.192°,传播方向x 上的空间波长为x sin λλθ==1064nm/1.54/sin42.192°=1028.72nm 。
在例子中我们就将通过数值模拟,处理得到空间波长从而得到各个模式的角度。
STEP1:建立EastFDTD 文档。
设置合适的参数:选择合适的单位:本例子的波导厚1微米,脉冲中心波长1.064微米,故长度单位取0.01微米比较合适。
选择边界类型:为了节省计算空间,边界条件x 方向为周期性的边界条件。
Y 方向为PML 吸收边界条件。
由于是2D 模型,Z 方向为周期性边界条件。
由于本例子的计算空间是相当大的2000*200,为保证y 方向上吸收干净,PML 吸收边界设置多一些,本例子用32层。
设置计算区域:为了避免脉冲在传播过一个周期长度后头尾相干叠加影响计算结果,x方向一个周期的长度不能小于光源脉冲的长度。
而且为了空间分辨率提高,要尽可能的增加一个周期的长度,但x方向越长计算时间也越长,所以要适当取舍。
本例子中的2D结构计算时间短,x方向不妨设得长一些,这里设为正负1000。
由于波导厚度为1微米,故y方向设置正负100。
为了达到平衡后,只留下导模的光,计算时间设得较长,为15000步。
STEP2:建立材料。
这个例子只有两种材料:空气和钕玻璃。
空气不用新建,所以只新建一个材料。
周期边界条件

周期边界条件aresaran(答网友问)(1)、究竟什么是"周期性边界条件"?如何去定义它的,为什么要引入这样一个定义。
周期边界条件源于这样的问题:宏观结构的信息不足以描述问题的细节,所以引入微观结构的信息来统计物质的宏观性质。
周期边界条件广泛用于molecular dynamics & micromechanics.Fig1.细观力学的RVE 代表单元尽管目前计算机的运算速度极大提高,但是仍然不能够用于进行大规模的宏微观联合计算。
因此引入了代表单元的概念,代表单元RVE 就如同是一个打开微观世界的一个窗口,看到的只是窗户里面的东西,我们假设整个微观世界是统计均匀的,因此无限量的复制了这个窗口,就可以得到所有微观信息。
当然这个代表单元有要求,如上图,宏观结构尺寸远远尺寸,但是这个达标单元的尺寸又要能足够多的包含微观颗粒的信息,有代表性,所以要求l L >>l A <<这是个一般性定义。
(2)、"周期性边界条件" 是不是只是在处理复合材料问题时才用,而且从众位大侠的讨论中似乎让我觉得这有点像"子结构"?Fig2. 2D or 3 D RVE子结构和代表单元根本不在一个层次上,RVE 的建模与普通建模没什么区别,当然你想得到随机的微观结构,就需要用外部程序比如matlab 书写相应的inp 文件。
Fig3. Ref. Frederic Feyel. Multiscale elastoviscoplastic analysis of compositestructures. Computational Materials Science,1999,16: 344~3542FE子结构模型适合多尺度计算。
如图三,是一个发动机叶片,局部区域希望能够用细观微结构描述,其余结构希望是均匀材料。
这个问题的模型就可以将复合材料区域SiC/Ti 用子模型/子结构实现代表单元,子结构传递边界条件给代表单元, 实现微观和宏观的关联。
cpml边界条件

cpml边界条件边界条件在计算流体力学(Computational Fluid Dynamics, CFD)中起着至关重要的作用。
边界条件是指在模拟流体运动时,对模型的边界进行设定的条件。
本文将介绍CFD中常用的一种边界条件,即CPML(Conformal Perfectly Matched Layer)边界条件。
CPML边界条件是一种用于模拟无限介质边界的技术。
在CFD模拟中,我们常常需要模拟有限领域内的流体运动,但为了避免边界效应对计算结果的影响,需要使用CPML边界条件。
CPML边界条件通过人工引入虚拟的吸收层来模拟无限边界。
这个虚拟的吸收层会吸收由模型边界反射回来的波,使其在模拟区域内几乎消失。
由于CPML边界条件能够避免反射,所以它在模拟波动现象(如声波、电磁波等)时特别有用。
CPML边界条件的应用通常需要考虑两个重要因素:吸收强度和吸收层厚度。
吸收强度决定了边界处能够吸收多少波动能量,而吸收层厚度则决定了虚拟吸收层的大小。
合理设置这两个参数可以使CPML边界条件在模拟中发挥较好的效果。
与其他边界条件相比,CPML边界条件具有一些优势。
首先,它可以减小反射和绘制出类似无限边界的模拟域。
其次,CPML边界条件对波动方向没有限制,能够很好地适应复杂的流体运动。
此外,CPML边界条件还能够模拟多种波动类型,并可用于求解各种物理现象。
总之,CPML边界条件是CFD模拟中常用的一种边界条件,它通过引入虚拟吸收层来模拟无限边界,有效消除了边界效应对计算结果的影响。
合理设置CPML 边界条件的吸收强度和吸收层厚度可以提高模拟的准确性和可靠性。
COMSOL使用技巧

COMSOL Multiphysics使用技巧(旧版通用)一、全局约束/全局定义对于多物理仿真,添加全局约束是COMSOL非常有用的功能之一。
例如,对于一个涉及传热的仿真,希望能够调整热源Q_0的大小,从而使得某一位置处的温度T_probe 恒定在指定值T_max,我们可以直接将这个全局约束添加进来即可。
有些情况下,全局约束可能包含有对时间的微分项,也就是常说的常微分方程(ODE ),COMSOL 同样也支持自定义ODE 作为全局约束。
例如,在一个管道内流体+物质扩散问题的仿真中,利用PID 算法控制管道入口的流速u_in_ctrl,从而使得某一位置处的浓度conc 恒定在指定值c_set 。
(基本模块模型库 〉 Multidisciplinary 〉 PID control )。
需要添加的PID 算法约束如下式:要添加上述约束,除变上限积分项外,另外两项都可以很容易的在边界条件中的“入口流速”设置中直接定义。
因此,这个变上限积分需要转化成一个ODE ,作为全局约束加入.令⎰-=tdt set c conc 0)_(int ,方程两边同对时间t 求导,得到set c conc dtd _int -=。
在COMSOL 中,变量u 对时间的导数,用ut 表示。
因此变量int 的时间导数即为intt.利用COMSOL 的“ODE 设定",我们可以很容易的将intt —(conc —c_set )=0这个ODE 全局约束添加入模型之中。
二、积分耦合变量COMSOL的语法中,变量u对空间的微分,分别默认为用ut,ux,uy,uz等来表示,这为仿真提供了极大的便利。
那么对变量u的空间积分呢?COMSOL提供了积分耦合变量来实现这一功能.积分耦合变量分为四种:点(point)积分耦合变量、边(edge)积分耦合变量、边界(boundary)积分耦合变量、求解域(subdomain)积分耦合变量。
根据模型的维度,会有相应积分耦合变量。
Comsol经典实例025:频率选择表面周期性互补开口谐振环

在COMSOL Multiphysics 5.5版本中创建Comsol经典实例025:频率选择表面周期性互补开口谐振环频率选择表面(FSS) 是一种具有带通或带阻频率响应的周期性结构。
此模型表明,只有中心频率附近的信号才能通过周期性互补开口谐振环层。
一、案例简介频率选择面(FSS) 是一种周期性结构,具有带通或带阻频率响应特性。
本案例演示了只有围绕中心频率的信号才能通过周期性互补开口谐振环层。
图A 一个互补开口谐振环单元由周期性边界条件建模,以模拟无限二维阵列。
单元顶部和底部的完美匹配层吸收激发模态和高阶模态二、模型定义在2 µm PTFE 基板表面(图A)的薄铜层上印有开口环槽。
铜层比所模拟的频率范围内的集肤深度厚得多,因此其被模拟为理想电导体(PEC)。
其余仿真域都充满空气。
Floquet 周期性边界条件用于单元的四个边,以模拟无限二维阵列。
单元顶部和底部的完美匹配层(PML)吸收源端口的激励模,以及由周期性结构生成的任何高阶模态。
波在与PML 边界垂直的方向传播时,PML会将其削弱。
由于本案例针对一系列入射角求解模型,因此PML中的波长设为2π/|k0cosθ|。
这说明了PML中波矢的法向分量如何随入射角变化。
“端口”边界条件位于PML的内部边界,与空气域相邻,可依据S参数自动确定反射和传输特性。
有PML背衬的内部端口边界需要狭缝条件。
为了定义S参数计算时的向内方向,需要指定端口方向。
高次衍射模不是本示例研究的重点,因此结合使用了有域背衬的狭缝端口和PML,而不是为每个衍射级和偏振添加衍射级端口。
周期性边界条件要求成对边界上的表面网格相同。
这通过两个步骤来实现:首先,只在其中一个边界上创建网格,然后对其他边界上的网格使用“复制面”操作。
使用物理场控制的网格时会自动设置该网格配置,如建模操作说明中所述。
如果您想了解有关网格的更多详细信息,可先使用物理场控制网格进行网格剖分,然后在网格设置中将网格序列类型更改为用户控制的网格,即可查看生成的网格序列详情。
Comsol软件介绍与应用

COMSOL软件介绍与应用
COMSOL软件介绍与应用
COMSOL软件介绍与应用
COMSOL软件介绍与应用
COMSOL软件介绍与应用
材案Βιβλιοθήκη 料例浏库
览
器
内置各种常用的物理模型,用户可轻松选择并进行必要的修改。 5.内嵌丰富的CAD 建模工具和全面的第三方CAD 导入功能
用户可直接在软件中进行二维和三维建模;全面的第三方CAD 导入功 能,支持当前主流CAD 软件格式文件的导入 6.强大的网格剖分能力
支持多种网格剖份,支持移动网格功能。 7.多国语言操作界面
COMSOL软件介绍与应用
目前Comsol在声学、生物科学、化学反应、弥散、电磁学、流体动力学、燃 料电池、地球科学、热传导、微系统、微波工程、光学、光子学、多孔介质、量 子力学、射频、半导体、结构力学、传动现象、波的传播等领域得到了广泛的应 用。
应 用 领 域
COMSOL软件介绍与应用
COMSOL特点: 1.求解多场问题 = 求解方程组
1.几何模型绘制 2.指定材料特性和边界条件 3.剖分网格 4.求解 5.结果后处理 各个步骤都非常的容易实现。 基于大量的预定义的应用模式,涵盖流 体、传热、结构力学、电磁场、化学反应、地球科学及多场耦合模型,以 及自定义偏微分方程,帮助用户十分迅速的建立分析模型。材料属性、载 荷、边界条件可以定义为基于独立变量的任意函数。
COMSOL软件介绍与应用
COMSOL Multiphysics 是一款大型的高级数值仿真软件,它是以有限元 法为基础,通过求解偏微分方程(单场)或偏微分方程组(多场)来实现 真实物理现象的仿真,被当今世界科学家称为“第一款真正的任意多物理 场直接耦合分析软件”。
周期性边界条件下多孔介质方腔内自然对流换热数值研究

计 算 物 理
CHINESE JOURNAL OF COMPUTATIONAL PHYSICS
[ 文章编号 ] 10012246X(2007) 0320282205
周期性边界条件下多孔介质方腔内 自然对流换热数值研究
Vol . 24 ,No. 3 May , 2007
1 物理问题描述及数值方法
如图 1 所示 ,倾斜方腔内充满各向同性 、均质的饱和 多孔介质 ,其 4 个壁面均为不可渗透固体壁面 ,方腔上 、 下两壁面绝热 ,表面 2 维持恒温 T0 ,表面 1 的温度以 T0 为平均值按正弦规律波动 ,振幅为 T1 . 方腔内固体骨架与 不可压缩牛顿流体的温度相等 ,即采用局部热平衡假设 ; 流体和固体骨架的热物性为常量 ,同时引入 Boussinesq 假 设来考虑自然对流效应 ;采用 Brinkman 扩展达西模型描 述多孔介质方腔内的流动 ,该模型考虑了黏性对流体流
算 ,用得到的 Nu 数与文[ 7 ]中的相应值进行对比 (表 1) ,验证了其可靠性. 对于本文所研究的问题 ,经过网格
考核 ,网格数为 50 ( X) ×50 ( Y) 时获得了网格无关解 ,最终计算均采用 50 ( X) ×50 ( Y) 的网格.
表 1 Nu 数计算值与文[ 7] 中 Nu 数的比较
+
Pr
Δ
2V - PrV + Ra Prθcosα,
Da
(3)
能量方程
σ
9θ 9τ
+
V
·θ=
ΔΔ
2θ.
(4)
上述方程中涉及的无量纲量定义为
τ = tamΠH2 , X = xΠH , Y = yΠH , U = uHΠam , V = vHΠam , P = pH2Π(ρ0 a2m) , θ = ( T - T0 ) ΠT1 , σ = (ρc) mΠ(ρcp ) f , Pr = νΠam , Da = KΠH2 , Ra = gβT1 H3Π(νam) , 其中 σ 为比热比 , am 为多孔介质的有效热扩散系数 , 其定义式为 am = kmΠ(ρcp ) f , 有 效 导 热 系 数 km =
COMSOL软件使用范例-碟形纳米颗粒阵列的斜入射
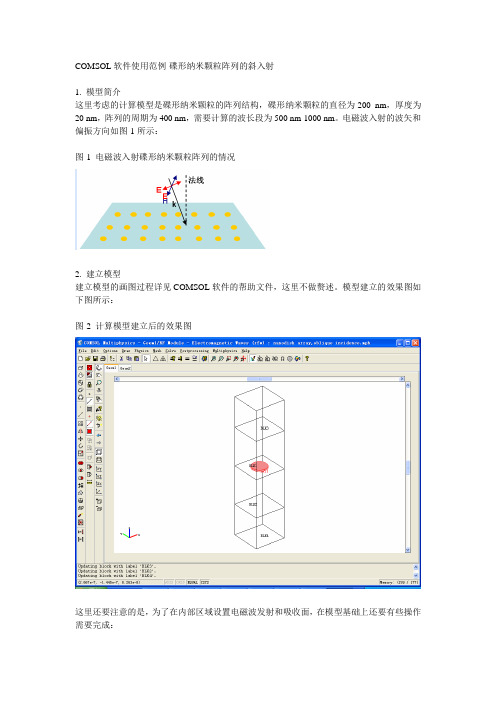
COMSOL软件使用范例-碟形纳米颗粒阵列的斜入射1. 模型简介这里考虑的计算模型是碟形纳米颗粒的阵列结构,碟形纳米颗粒的直径为200 nm,厚度为20 nm,阵列的周期为400 nm,需要计算的波长段为500 nm-1000 nm。
电磁波入射的波矢和偏振方向如图-1所示:图-1 电磁波入射碟形纳米颗粒阵列的情况2. 建立模型建立模型的画图过程详见COMSOL软件的帮助文件,这里不做赘述。
模型建立的效果图如下图所示:图-2 计算模型建立后的效果图这里还要注意的是,为了在内部区域设置电磁波发射和吸收面,在模型基础上还要有些操作需要完成:(1)中间的区域合并Union(2)所有区域全选(3)建立pairs3. 子区域物理参数的设定这里子区域的物理参数设定主要是对各个子区域的介电常数以及PML吸收层进行物理上的参数设定。
这里PML吸收层的作用是用来吸收电磁波入射和反射的杂波。
需要设定的参数如下图所示:图-3 各个子区域表示的意思设定步骤如下:(1)衬底层的设定(2)金的设定:注意这里金的介电常数我们赋予的是一个函数名称“gold ”。
这个gold 接下来会用一个确切的表达式表达。
(3)PML吸收层的设定4. 边界条件的设定(1)与H分量垂直的面全部设定为PMC边界条件(2)上下两个外端面设定成scattering 边界条件(3)先前设置的pairs 设定成入射和吸收电磁波的port 边界条件(3.1)出射电磁波端口的设定(3.2)吸收端口的设定端口数改成2(4)周期性边界条件的设定5. 物理常数、变量和表达式函数的设定将波长的参数设置成变量“wl”freqc=1.65*6.5e12点击“OK ”。
(2)设置入射波矢分量和入射角度:波矢分量为:kx=k0*sin(theta*pi/180), kz=k0*cos(theta*pi/180),其中k0=2*pi/wl ,是入射光波矢。
theta 是斜入射角度,这里我们设定theta=30°。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
COMSOL周期性边界条件的应用
在将真实的物理问题转化为仿真模型时,为了通过有限的计算资源获得尽可能高的计算精度,模型简化是必要的。
模型简化的前提是所模拟的物理问题具有结构、材料属性及边界条件的对称性或均匀性,以此为基础,可通过特定的方程及边界条件建立模型,例如降维方程,镜像/周期性/旋转对称边界条件,或根据工程经验将某些计算域简化为边界等等。
当处理空间或时间上具有周期性的物理问题时,采用周期性边界条件(Periodic/Cyclic Condition),可将复杂结构的模拟简化为周期单元,在不失精确度的前提下,大大降低计算量。
COMSOL提供的周期性边界条件包括四种类型:
•连续性周期边界(Continuity),指在源和目标边界上的场值相等;
•反对称周期边界(Antiperiodicity),源和目标边界上场值符号相反;
•弗洛奎特周期性边界(Floquet periodicity),源和目标边界上场值相差一个位相因子,位相因子由波矢和边界相对距离确定。
Continuity和Antiperiodicity边界可以认
为是Floquet periodicity边界在位相分别为0和π情况下的两个特例。
•循环对称性边界(Cyclic Symmetry),源和目标边界上场值相差一个位相因子,位相因子由计算域所对应的扇形角和角向模式数决定。
以下是几个典型应用:
1.微纳光学领域内的光子晶体(Photonic Crystal)、表面等离子体激元(Surface Plasmon)
阵列结构及超材料(Metamaterial),这几种结构均由空间上周期性重复的散射体构
成,当计算透射率及能带结构时,常常可采用Floquet perioidcity边界将结构简化。
超材料能带分析
Metamaterial.mph
2.作为压电传感器件的声表面波器件(Surface Acoustic Wave, SAW)的本征频率问题
计算。
压电声表面波器件的共振频率下的位移场(左)和电势(右)分布才
Acoustics Module/Industrial Models/Saw_gas_sensor
3. 飞机、轮船、风力发电机中的涡轮机,或是旋转电机结构往往具有旋转对称性,在
进行电磁场或振动模态分析时,可采用Cyclic Symmerty 类型周期性边界简化。
叶轮的振动模态
Structural Mechanics Module/Tutorial Models/impeller
值得注意的是,周期性条件的引入会导致模型的非线性增强,这常常会导致计算的收敛性问题。
为了提高计算收敛性,在网格剖分时,需要注意使互为周期性的两个边界上网格完全一致。
在COMSOL 中可先剖分周期性边界对中的一个边界,然后复制网格(Copy mesh )来实现两个边界上网格的一致性,详见参考模型。
/forum/post/show.html?tid=13539。
