7大学物理习题及综合练习答案详解
大学物理试题答案及解析

大学物理试题答案及解析一、选择题1. 光年是表示距离的单位,它等于()。
A. 一年内光所行进的距离B. 一年内光所行进的时间C. 一年内光所行进的路程D. 一年内光所行进的速度答案:A解析:光年是天文学中用来表示距离的单位,它表示光在真空中一年内所行进的距离。
2. 根据牛顿第二定律,一个物体的加速度与作用在它上面的力成正比,与它的质量成反比。
这个定律的数学表达式是()。
A. \( F = ma \)B. \( F = \frac{m}{a} \)C. \( a = \frac{F}{m} \)D. \( a = \frac{m}{F} \)答案:C解析:牛顿第二定律指出,物体的加速度与作用在它上面的力成正比,与它的质量成反比,数学表达式为 \( a = \frac{F}{m} \)。
二、填空题1. 根据热力学第一定律,能量守恒,即能量不能被创造也不能被消灭,只能从一种形式转化为另一种形式。
用公式表示为:\( \Delta U = Q- W \),其中 \( \Delta U \) 表示内能的变化,\( Q \) 表示系统吸收的热量,\( W \) 表示系统对外做的功。
2. 电磁波谱中,波长最长的是()。
答案:无线电波解析:电磁波谱中,波长从长到短依次为无线电波、微波、红外线、可见光、紫外线、X射线和伽马射线。
三、计算题1. 一辆质量为1000kg的汽车以20m/s的速度行驶,突然遇到紧急情况需要刹车。
假设刹车过程中汽车的加速度为-5m/s²,求汽车从开始刹车到完全停止所需的时间。
答案:4秒解析:根据公式 \( v = u + at \),其中 \( v \) 是最终速度,\( u \) 是初始速度,\( a \) 是加速度,\( t \) 是时间。
已知\( v = 0 \),\( u = 20 \)m/s,\( a = -5 \)m/s²,代入公式得\( 0 = 20 - 5t \),解得 \( t = 4 \)秒。
大学物理习题与答案解析

根据匀加速直线运动的速度公 式$v = v_0 + at$,代入已知的 $v_0 = 2m/s$和$a = 3m/s^2$,以及时间$t = 3s$, 计算得到$v = 2m/s + 3 times 3m/s^2 = 11m/s$。
一物体做匀减速直线运动,初 速度为10m/s,加速度为2m/s^2,则该物体在速度减为 零时的位移是多少?
04
答案解析
根据公式$v = lambda f$,频率$f = frac{v}{lambda} = frac{3 times 10^{8}}{500 times 10^{-9}}Hz = 6 times 10^{14}Hz$;根据公式 $E = hnu$,能量$E = h times f = 6.626 times 10^{-34} times 6 times
题目
答案解析
计算氢原子光谱线波长与频 率的关系。
根据巴尔末公式,氢原子光 谱线波长与频率的关系可以
表示为λ=R*(1/n1^2 1/n2^2),其中λ是光谱线波 长,R是里德伯常数,n1和 n2分别是两个能级的主量子
数。
பைடு நூலகம்
题目
一束光照射到某金属表面, 求光电子的最大初动能。
答案解析
根据爱因斯坦光电效应方程,光 电子的最大初动能Ekm=hν-W, 其中h是普朗克常数,ν是入射光 的频率,W是金属的逸出功。因 此,通过测量入射光的频率和金 属的逸出功,可以计算出光电子
题目
一定质量的理想气体,在等容升温过 程中,不吸热也不放热,则内能如何 变化?
答案解析
根据热力学第一定律,等容升温过程 中,气体不吸热也不放热,则内能增 加。
热传递习题及答案解析
题目
大学物理习题及综合练习答案详解

库仑定律 7-1 把总电荷电量为Q 的同一种电荷分成两部分,一部分均匀分布在地球上,另一部分均匀分布在月球上,使它们之间的库仑力正好抵消万有引力,已知地球的质量M = 5.98l024kg ,月球的质量m =7.34l022kg 。
(1)求 Q 的最小值;(2)如果电荷分配与质量成正比,求Q 的值。
解:(1)设Q 分成q 1、q 2两部分,根据题意有 2221r MmG r q q k=,其中041πε=k即 2221q k q GMm q q Q +=+=。
求极值,令0'=Q ,得 0122=-kq GMmC 1069.5132⨯==∴k GMm q ,C 1069.51321⨯==k q GMm q ,C 1014.11421⨯=+=q q Q (2)21q m q M =Θ,k GMm q q =21 kGMm m q mq Mq ==∴2122 解得C 1032.61222⨯==kGm q , C 1015.51421⨯==m Mq q ,C 1021.51421⨯=+=∴q q Q 7-2 三个电量为 –q 的点电荷各放在边长为 l 的等边三角形的三个顶点上,电荷Q (Q >0)放在三角形的重心上。
为使每个负电荷受力为零,Q 值应为多大?解:Q 到顶点的距离为 l r 33=,Q 与-q 的相互吸引力为 20141rqQ F πε=, 两个-q 间的相互排斥力为 220241l q F πε=据题意有 10230cos 2F F =,即 2022041300cos 412rqQl q πεπε=⨯,解得:q Q 33= 电场强度7-3 如图7-3所示,有一长l 的带电细杆。
(1)电荷均匀分布,线密度为+,则杆上距原点x 处的线元d x 对P 点的点电荷q 0 的电场力为何?q 0受的总电场力为何?(2)若电荷线密度=kx ,k 为正常数,求P 点的电场强度。
解:(1)线元d x 所带电量为x q d d λ=,它对q 0的电场力为200200)(d 41)(d 41d x a l x q x a l q q F -+=-+=λπεπεq 0受的总电场力 )(4)(d 4000200a l a l q x a l xq F l+=-+=⎰πελπελ00>q 时,其方向水平向右;00<q 时,其方向水平向左q 0 图7-3a λ lP x q-q-q-ll rQ rr(2)在x 处取线元d x ,其上的电量x kx x q d d d ==λ,它在P 点的电场强度为2020)(d 41)(d 41d x a l xkx x a l q E P -+=-+=πεπε)ln (4)(d 40020al aa l k x a l x x kE lP ++=-+=∴⎰πεπε 方向沿x 轴正向。
7大学物理习题及综合练习答案详解

7大学物理习题及综合练习答案详解库仑定律7-1 把总电荷电量为Q 的同一种电荷分成两部分,一部分均匀分布在地球上,另一部分均匀分布在月球上,使它们之间的库仑力正好抵消万有引力,已知地球的质量M =5.98⨯l024kg ,月球的质量m =7.34⨯l022kg 。
(1)求 Q 的最小值;(2)如果电荷分配与质量成正比,求Q 的值。
解:(1)设Q 分成q 1、q 2两部分,根据题意有2221r MmG r q q k=,其中041πε=k即2221q kq GMmq q Q +=+=。
求极值,令0'=Q ,得 0122=-kq GMm C 1069.5132⨯==∴kGMmq ,C 1069.51321⨯==kq GMmq,C1014.11421⨯=+=q qQ(2)21qmq M =,kGMmq q =21kGMm mq mq Mq==∴2122解得C1032.61222⨯==kGm q ,C 1015.51421⨯==mMq q ,C1021.51421⨯=+=∴q q Q7-2 三个电量为 –q 的点电荷各放在边长为 l 的等边三角形的三个顶点上,电荷Q (Q >0重心上。
为使每个负电荷受力为零,Q 解:Q 到顶点的距离为l r 33=,Q 与-q q-q -20141r qQ F πε=,两个-q 间的相互排斥力为 220241l q F πε=据题意有1230cos 2F F =,即2022041300cos 412r qQl q πεπε=⨯,解得:q Q 33=电场强度7-3 如图7-3所示,有一长l 的带电细杆。
(1)电荷均匀分布,线密度为+λ,则杆上距原点x 处的线元d x 对P 点的点电荷q 0 的电场力为何?受的总电场力为何?(2)若电荷线密度λ=kx ,k 为正常数,求P 点的电场强度。
解:(1)线元d x 所带电量为x q d d λ=,它对q 0的电场力为200200)(d 41)(d 41d x a l x q x a l q q F -+=-+=λπεπεq 0受的总电场力)(4)(d 4000200a l a l q x a l xq F l+=-+=⎰πελπελ0>q 时,其方向水平向右;0<q时,其方向水平向左(2)在x 处取线元d x ,其上的电量x kx x q d d d ==λ,它在P 点的电场强度为2020)(d 41)(d 41d x a l xkx x a l q E P -+=-+=πεπε)ln (4)(d 40020al aa l k x a l x x kE lP ++=-+=∴⎰πεπε 方向沿x 轴正向。
大学物理习题及综合练习答案详解

导体8-1两个同心导体球壳A 和B ,A 球壳带电+Q ,现从远处移来一带+q 的带电体(见图8-1),试问(请阐明理由):(1)两球壳间的电场分布与无+q 时相比有无变化(2)两球壳间的电势差是否变化(3)两球壳的电势是否变化(4)如将B 球壳接地,上述(1)、(2)、(3)的情况又如何 解:(1)由于静电屏蔽作用,+q 对两球壳间的电场没有影响。
(2)由⎰⋅=B A AB l E U ϖϖd 可知,由于E ϖ不变,所以AB U 不变,即两求壳间的电势差不变。
(3)由电势叠加原理,+q 使两球壳的电势升高。
(4)B 球壳接地,由于屏蔽作用,两球壳间的电场分布不变,从而AB U 不变。
因B 球壳接地,电势不变,所以A 球壳电势也不变。
8-2半径为R 1的导体球A ,带电q ,其外同心地套一导体球壳B ,内外半径分别为R 2和R 3(见图8-2),且R 2=2R 1,R 3=3R 1。
今在距球心O 为d =4R 1的P 处放一点电荷Q ,并将球壳接地。
问(1)球壳B 所带的净电荷Q ’ 为多少(2)如用导线将导体球A 与球壳B 相连,球壳所带电荷Q ” 为多少 解:(1)根据静电平衡条件,A 球上电荷q 分布在A 球表面上,B 球壳内表面带电荷-q 。
由高斯定理可得,R r R 21<<:0204r r q E ϖϖπε=A 球电势 10210208)11(4d 4d 21R q R R q r rq l E U R R BAA πεπεπε=-==⋅=⎰⎰ϖϖ 设B 球壳外表面带电荷q ’,由电势叠加原理,A 球球心处电势40302010044'44R Q R q R q R q U πεπεπεπε++-+=1010********'244RR q R q R q πεπεπεπε++-= 1010104434'8R Q R q R q πεπεπε++=108R q U A πε==, Q q 43'-=∴ B球壳所带净电荷 q Q q q Q --=-=43''(2)用导线将和相连,球上电荷与球壳内表面电荷相消。
大学物理试题讲解及答案

大学物理试题讲解及答案一、选择题(每题2分,共20分)1. 光在真空中的传播速度是()。
A. 3×10^5 km/sB. 3×10^8 m/sC. 3×10^9 km/sD. 3×10^11 m/s答案:B2. 根据牛顿第二定律,力和加速度的方向()。
A. 总是相同B. 总是相反C. 有时相同,有时相反D. 无关答案:A3. 一个物体的质量为2kg,受到的力为10N,那么它的加速度是()。
A. 5 m/s^2B. 10 m/s^2C. 20 m/s^2D. 无法确定答案:A4. 一个点电荷在电场中从静止开始运动,其电势能将()。
A. 增加B. 减少C. 保持不变D. 先增加后减少答案:B5. 根据热力学第一定律,一个系统在绝热过程中()。
A. 内能增加B. 内能减少C. 内能不变D. 无法确定答案:D6. 光的折射定律表明,入射角和折射角的关系是()。
A. 入射角大,折射角小B. 入射角小,折射角大C. 入射角和折射角成正比D. 入射角和折射角成反比答案:C7. 一个物体在自由下落过程中,其动能和重力势能的关系是()。
A. 动能增加,重力势能减少B. 动能减少,重力势能增加C. 动能和重力势能之和保持不变D. 动能和重力势能之和增加答案:C8. 根据麦克斯韦方程组,电磁波的传播速度是()。
A. 光速的一半B. 光速C. 超过光速D. 低于光速答案:B9. 在理想气体定律中,气体的压强与体积成()。
A. 正比B. 反比C. 无关D. 先正比后反比答案:B10. 根据欧姆定律,电阻两端的电压与通过电阻的电流之间的关系是()。
A. 正比B. 反比C. 无关D. 先正比后反比答案:A二、填空题(每题2分,共20分)1. 牛顿第三定律指出,作用力和反作用力大小相等、方向相反、作用在_________上。
答案:不同物体2. 在国际单位制中,力的单位是_________。
大学物理波动光学综合练习题(含答案)
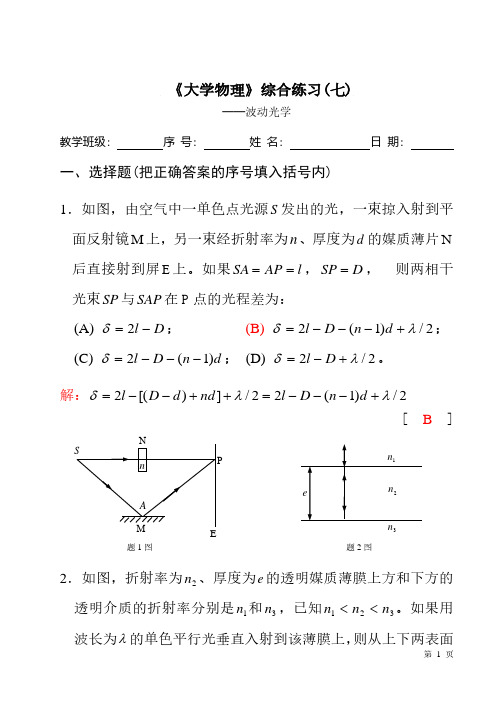
《大学物理》综合练习(七)——波动光学教学班级: 序 号: 姓 名: 日 期:一、选择题(把正确答案的序号填入括号内)1.如图,由空气中一单色点光源S 发出的光,一束掠入射到平面反射镜M 上,另一束经折射率为n 、厚度为d 的媒质薄片N 后直接射到屏E 上。
如果l AP SA ==,D SP =, 则两相干光束SP 与SAP 在P 点的光程差为:(A) D l −=2δ; (B) 2/)1(2λδ+−−−=d n D l ;(C) d n D l )1(2−−−=δ; (D) 2/2λδ+−=D l 。
解:2/)1(22/])[(2λλδ+−−−=++−−=d n D l nd d D l[ B ]2.如图,折射率为2n 、厚度为e 的透明媒质薄膜上方和下方的透明介质的折射率分别是1n 和3n ,已知321n n n <<。
如果用波长为λ的单色平行光垂直入射到该薄膜上,则从上下两表面3题1图 题2图反射的光束的光程差是(A) e n 22; (B) 2/22λ−e n ;(C) 2/322λ−e n ; (D) 222/2n e n λ−。
解:两反射面均有半波损失,e n 22=δ。
[ A ]3.设在双缝干涉实验中,屏幕E 上的P 点是亮条纹,如将缝2S 盖住,并在21S S 连线的垂直平分面处放一反射镜M (如图),则此时:(A) P 点处为暗条纹;(B) P 点处仍然是亮条纹;(C)无干涉条纹; (D)无法确定P 点是亮条纹还是暗条纹。
解:光在M 处发射有半波损失,故P 点处为暗条纹。
[ A ]4.用波长为λ的平行单色光垂直照射图示装置观察空气层上下表面反射光形成的等厚干涉条纹。
以下各图画出可能出现的暗条纹的形状和位置。
试判断哪一图是实际观察到的干涉暗条纹。
题3图解:λλλδ42247max =+⨯= 4max =k (明),故图(C )正确。
[ C ]5.在迈克尔耳逊干涉仪的一条光路中,放入一折射率为n 、厚度为d 的透明薄片,放入前后两条光路的光程差的改变量为(A) d n )1(−; (B) nd ; (C) d n )1(2−; (D) nd 2。
大学物理习题与答案解析

dvy dt
kv
2 y
v dvy kdt
2 y
设入水时为计时起点,水面为坐标原点, 0 时,y=0, v y v0 , t 运动过程中t时刻速度为 v y ,将上式两侧分别以 v y和t为积分变量, k 以 和 y 2 为被积函数作积分得: v
v v0 (kv0 t 1)
x x0 vdt A costdt A sin t
0 0
t
t
x A sin t
大学物理
4、一质点在XOY平面内运动,其运动方程为 x at , y b ct 2 式中a、b、c为常数,当质点运动方向与x 轴成 450角时,它的速率为 v 2a 。
则解得
2 t 9
3
3
2 于是角位移为 2 3t 2 3 0.67(rad) 9
大学物理 2 4、一质点作平面运动,加速度为 ax A cost , a y B 2 sin t ,A B,A 0 ,B 0。当 t 0
时,v x 0 0 ,x0 点的运动轨迹。
2 2 t 1s时,v 2e i 2e j (m/s)
t 1s时,a 4e2i 4e2 j (m/s2 )
dv 2t 2t a 4e i 4e j (m/s 2 ) dt
dr 2t 2t v 2e i 2e j (m/s) dt
0
大学物理 6、一质点沿x轴作直线运动,在 t 0时,质点位于x0 2m
2 处,该质点的速度随时间的变化规律是 v 12 3t , 当质点瞬时静止时,其所在的位置和加速度分别为(A) x=来自6m, a=-12 m/s2 .
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
7大学物理习题及综合练习答案详解-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN库仑定律7-1 把总电荷电量为Q 的同一种电荷分成两部分,一部分均匀分布在地球上,另一部分均匀分布在月球上,使它们之间的库仑力正好抵消万有引力,已知地球的质量M =5.98l024kg ,月球的质量m =7.34l022kg 。
(1)求 Q 的最小值;(2)如果电荷分配与质量成正比,求Q 的值。
解:(1)设Q 分成q 1、q 2两部分,根据题意有 2221rMmG r q q k=,其中041πε=k 即 2221q k q GMm q q Q +=+=。
求极值,令0'=Q ,得 0122=-kq GMmC 1069.5132⨯==∴k GMm q ,C 1069.51321⨯==k q GMm q ,C 1014.11421⨯=+=q q Q (2)21q m q M =,k GMm q q =21 kGMm m q mq Mq ==∴2122 解得C 1032.61222⨯==kGm q , C 1015.51421⨯==m Mq q ,C 1021.51421⨯=+=∴q q Q 7-2 三个电量为 –q 的点电荷各放在边长为 l 的等边三角形的三个顶点上,电荷Q (Q >0)放在三角形的重心上。
为使每个负电荷受力为零,Q 值应为多大?解:Q 到顶点的距离为 l r 33=,Q 与-q 的相互吸引力为 20141rqQ F πε=, 两个-q 间的相互排斥力为 220241l q F πε=据题意有 10230cos 2F F =,即 2022041300cos 412rqQl q πεπε=⨯,解得:q Q 33= 电场强度7-3 如图7-3所示,有一长l 的带电细杆。
(1)电荷均匀分布,线密度为+λ,则杆上距原点x 处的线元d x 对P 点的点电荷q 0 的电场力为何?q 0受的总电场力为何(2)若电荷线密度λ=kx ,k 为正常数,求P 点的电场强度。
解:(1)线元d x 所带电量为x q d d λ=,它对q 0的电场力为200200)(d 41)(d 41d x a l x q x a l q q F -+=-+=λπεπεq 0 图7-3aλl P xq -q-q-ll r Q rrq 0受的总电场力 )(4)(d 4000200a l a l q x a l xq F l+=-+=⎰πελπελ00>q 时,其方向水平向右;00<q 时,其方向水平向左(2)在x 处取线元d x ,其上的电量x kx x q d d d ==λ,它在P 点的电场强度为2020)(d 41)(d 41d x a l xkx x a l q E P -+=-+=πεπε)ln (4)(d 40020al aa l k x a l x x kE lP ++=-+=∴⎰πεπε 方向沿x 轴正向。
7-4一半径为R 的绝缘半圆形细棒,其上半段均匀带电量+q ,下半段均匀带电量-q ,如图7-4所示,求半圆中心处电场强度。
解:建立如图所示的坐标系,由对称性可知,+q 和-q 在O 点电场强度沿x 轴的分量之和为零。
取长为d l 的线元,其上所带电量为θπθππλd 2d 2d 21d d q R R q l R q l q ====,20d 41d R q E πε=∴ 方向如图 y 方向的分量 θεπθθπεcos 2d cos d 41d 20220R q R q E y -=-= j R qj R q E20220202d cos 22επθθεππ-=⨯-=∴⎰7-5一半径为R 的半球壳,均匀带有电荷,电荷面密度为σ ,求球心处电场强度。
解:沿半球面的对称轴建立x 轴,坐标原点为球心O 。
在球面上取半径为r 、宽为d l 的环带,如图,其面积为θππd 2d 2d R r l r S ⋅==,所带电荷 θπσσd 2d d R r S q ⋅⋅==d q 在O 处产生的电场强度为,2322023220)(d 2)(d 41d r x xr R r x qx E +=+=θεσπε 图7-4θsin R r = ,θcos R x = θθθεσd cos sin 2d 0=∴E 因为球面上所有环带在O 处产生的电场强度方向相同,i i E204d cos sin 2εσθθθεσπ==∴⎰7-6一无限大均匀带电薄平板,面电荷密度为σ ,平板中部有一半径为R 的圆孔, 如图7-6所示。
求圆孔中心轴线上的场强分布。
(提示:利用无穷大板和圆盘的电场及场强叠加原理)解:利用补偿法,将圆孔看作由等量的正、负电荷重叠而成,即等效为一个完整的带电无穷大平板和一个电荷面密度相反的圆盘叠加而成。
无穷大平板的电场为 n e E012εσ= 圆盘激发的电场为 n e R x x E )1(22202+--=εσ,其中n e为平板外法线的单位矢量。
圆孔中心轴线上的电场强度为 n e R x x E E E 220212+=+=εσ电通量7-7电场强度为E的匀强电场,其方向与半径为R 的半球面的对称轴平行,如图7-7所示,求通过该半球面的电场强度通量。
解:作半径为R 的平面S ’与半球面S 构成一个闭合曲面,由于该闭合曲面内无电荷,由高斯定理0d d d ''=⋅+⋅=⋅=Φ⎰⎰⎰+S SS S S E S E S EE R R E S E S E S SS 22'cos d d πππ=⋅-=⋅-=⋅=Φ∴⎰⎰7-8一边长为a 的立方体置于直角坐标系中,如图7-8所示。
现空间中有一非均匀电场j E i kx E E21)(++=,E 1、E 2为常量,求电场对立方体各表面及整个立方体表面的电场强度通量。
解:0=z E 0=Φ=Φ∴DEFG OABC⎰⎰==⋅++=⋅=ΦSSABGF a E S E j S j E i kx E S E 22221)(d ])[(d⎰⎰-=-⋅++=⋅=ΦSSCDEO a E j S j E i kx E S E 2221)d (])[(d⎰⎰-=-⋅+=⋅=ΦSSAOEF a E i S j E i E S E 2121)d ()(d⎰⎰+=⋅++=⋅=ΦSSBCDGa ka E i S j E i ka E S E 2121)()(d ])[(d整个立方体表面的电场强度通量 3ka ii =Φ=Φ∑ 高斯定理7-9有两个同心的均匀带电球面,内外半径分别为R 1和R 2,已知外球面的电荷面密度为+σ ,其外面各处的电场强度都是零。
试求:(1)内球面上的电荷面密度;(2)外球面以内空间的电场分布。
解:作一半径为r 的同心球面为高斯面。
设内球面上的电荷面密度为'σ。
(1)2R r >处:因为外球面外的电场强度处处为零,由高斯定理有0)4'4(11d 212203=⋅+⋅==⋅∑⎰R R q S E ii Sπσπσεε,得 σσ212)('R R -= (2)由高斯定理011=<E R r21R r R << 21024'1d R S E S πσε⋅=⋅⎰ 即 210224'14R r E πσεπ⋅=⋅2022202121220212)(44'rR r R R R r R E εσεσπεπσ-=⋅-=⋅=∴ 方向沿径向反向图7-87-10一对无限长的均匀带电共轴直圆筒,内外半径分别为R 1和R 2,沿轴线方向单位长度的电量分别为λ1和λ2。
(1)求各区域内的场强分布;(2)若λ1=-λ2,情况如何?画出此情形下的E ~ r 的关系曲线。
解:(1)作一半径为r 、长为h 的共轴圆柱面为高斯面,由高斯定理有 011=<E R r21R r R << h S E S1021d λε=⋅⎰h rh E 10212λεπ=⋅∴,得 rrE ˆ2012 πελ=2R r > h S E S )(1d 2103λλε+=⋅⎰ 得 r r E ˆ20213 πελλ+= (2)21λλ-=时,01=E,r rE ˆ2012 πελ=,03=E7-11设半径为R 的球体,电荷体密度 ρ ═ kr (r ≤ R ),其中k 为常量,r 为距球心的距离。
求电场分布,并画出E ~ r 的关系曲线。
解:作一半径为r 的同心球面为高斯面。
根据高斯定理R r < 402011d 41d 1d kr r r kr V S E rVSπεπερε=⋅==⋅⎰⎰⎰即 402114kr r E πεπ=⋅ 得 rkr E ˆ4021 ε= R r > 402021d 41d kR r r kr S E RSπεπε=⋅=⋅⎰⎰即 402214kR r E πεπ=⋅ 得 r rkR E ˆ42042 ε= 7-12一厚度为d =0.5cm 的无限大平板,均匀带电,电荷体密度 ρ ═ 1.0⨯10-4C/m 3,求(1)平板内外的电场分布;(2)讨论平板中央以及平板内与其表面相距0.1cm 处的电场强度。
12解:(1)设中心平面为S 0。
根据对称性,在距S 0处为x 处对称地取两面积均为S ∆的底面作一圆柱形高斯面,其侧面与板面垂直(如图所示),即侧面的电通量为零。
2dx <时 S x S E S E S ∆⋅=∆=⋅⎰ρε212d 011 , x E 01ερ=∴ 2dx >时 S d S E S E S ∆⋅⋅=∆=⋅⎰2212d 022ρε , 02ερd E =∴ (2)平板中央 0=x ,00=∴E平板内与表面相距0.1cm 处,cm 15.0=x 4123401069.11085.8105.1100.1⨯=⨯⨯⨯⨯==∴---ερx E V/m7-13一个电荷体密度为 ρ(常量)的球体。
(1)证明球内距球心r 处一点的电场强度为r E 03ερ=;(2)若在球内挖去一个小球,如图7-13所示,证明小球空腔内的电场是匀强电场a E 03ερ=,式中a是球心到空腔中心的距离矢量。
证:(1)作与球体同心的球面为高斯面,根据高斯定理⎰⎰=⋅VSV S E d 1d 0ρε 即 302344r r E περπ⋅=⋅ r E 03ερ=∴ 矢量式 r E3ερ= 得证(2)填充法:设在空腔中填充电荷密度分别为ρ和-ρ的电荷球体,形成电荷密度分别为ρ和-ρ的大球体和小球体。
对腔内任一点P (如图),由(1)的结果有大球 r E P 013ερ=; 小球 '302r E Pερ-= a r r E E E P P0213)'(3ερερ=-=+= 得证静电场的环路定理S∆7-14若电场中某一部分电场线的形状是以O 点为中心的同心圆弧。
