三角高程测量原理
三角高程测量方法

三角高程测量方法三角高程测量方法三角高程测量是一种常用的高程测量方法,其通过三角函数计算出两点之间的高差,从而得到目标点的高程。
三角高程测量方法具有精度高、操作简便、适用范围广等特点,广泛应用于工程测量、地形测量、城市规划等领域。
一、直接测量法直接测量法是一种简单而实用的高程测量方法。
其基本原理是利用水准仪和水准尺直接测量两点之间的高差。
在已知高程的基准点上设置水准仪,将水准尺放置在待测点上,读取水准尺上的读数,然后通过水准仪的水平视线读取水准尺上的高程。
直接测量法的优点是操作简便、精度高,适用于小范围的高程测量。
二、间接测量法间接测量法是一种通过测量角度和距离来计算高程的方法。
其基本原理是利用全站仪或测距仪测量两点之间的距离和角度,然后根据三角函数计算出两点之间的高差。
间接测量法的优点是不需要设置水准点,适用于大范围的高程测量。
但是,由于需要考虑地球曲率和大气折光等因素,间接测量法的精度相对较低。
三、水准测量法水准测量法是一种经典的几何高程测量方法。
其基本原理是利用水准仪和水准尺测量两点之间的高差。
水准仪由望远镜、水准器和基座组成,水准尺通常由玻璃钢或铝合金制成。
通过水准仪的望远镜和水准器,可以精确地读取水准尺上的读数和高程。
水准测量法的优点是精度高、操作简便,适用于各种地形的高程测量。
但是,由于需要设置多个水准点,水准测量法的劳动强度较大。
四、GPS测量法GPS测量法是一种利用全球定位系统进行高程测量的方法。
其基本原理是利用GPS接收机接收卫星信号,通过求解卫星至目标点之间的几何距离和卫星钟差等参数,计算出目标点的高程。
GPS测量法的优点是不需要设置水准点,适用于大范围的高程测量。
同时,GPS测量法的精度也较高,能够满足大多数工程测量的要求。
但是,由于信号受到建筑物、树木等遮挡物的影响,GPS测量法在城市地区的使用受到一定的限制。
综上所述,三角高程测量方法具有多种类型,每种方法都有其特点和应用范围。
三角高程测量原理

§ 5.9三角高程测量三角高程测量的基本思想是根据由测站向照准点所观测的垂直角(或天顶距)和它们之间的水平距离,计算测站点与照准点之间的高差。
这种方法简便灵活,受地形条件的限制较少,故适用于测定三角点的高程。
三角点的高程主要是作为各种比例尺测图的高程控制的一部分。
一般都是在一定密度的水准网控制下,用三角高程测量的方法测定三角点的高程。
5.9.1 三角高程测量的基本公式1.基本公式关于三角高程测量的基本原理和计算高差的基本公式,在测量学中已有过讨论,但公式的推导是以水平面作为依据的。
在控制测量中,由于距离较长,所以必须以椭球面为依据来推导三角高程测量的基本公式。
如图5-35所示。
设s o为A、B两点间的实测水平距离。
仪器置于 A点,仪器高度为i1。
…B为照准点,砚标高度为v2, R为参考椭球面上AB的曲率半径。
PE、AF分别为过一 P点和A点的水准面。
PC 是PE在P点的切线,PN为光程曲线。
当位于 P点的望远镜指向与PN相切的PM方向时,由于大气折光的影响,由N点出射的光线正好落在望远镜的横丝上。
这就是说,仪器置于A点测得P、M间的垂直角为a i,2。
图5-35 由图5-35可明显地看出,A、B两地面点间的高差为g,2 =BF =MC +CE +EF —MN —NB (5-54)式中,EF为仪器高i1; NB为照准点的觇标高度v2;而CE和MN分别为地球曲率和折光影响。
由CE — s2 MN 二丄s;2R 2R式中R•为光程曲线PN在N点的曲率半径。
设—=K,则RMN —.. —S2 = —S022R R 2RK称为大气垂直折光系数。
由于A 、B 两点之间的水平距离 S o 与曲率半径R 之比值很小(当S o =10km 时,s 0所 对的圆心角仅 5’多一点),故可认为 PC 近似垂直于 0M ,即认为PCMs^O :这样 .PCM 可视为直角三角形。
则(5-54 )式中的MC 为MC =S o tan 0(1,2将各项代入(5-54 )式,贝U A 、B 两地面点的高差为(5-56 )这就是表达实测距离 S 0与参考椭球面上的距离 S 之间的关系式。
三角高程测量
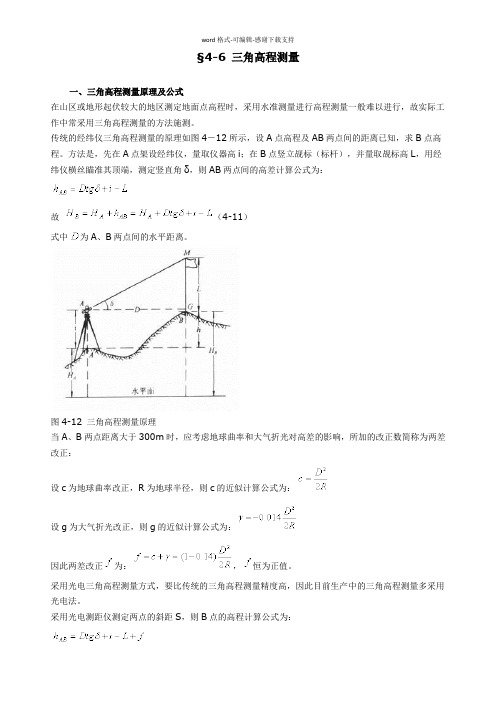
§4-6 三角高程测量一、三角高程测量原理及公式在山区或地形起伏较大的地区测定地面点高程时,采用水准测量进行高程测量一般难以进行,故实际工作中常采用三角高程测量的方法施测。
传统的经纬仪三角高程测量的原理如图4-12所示,设A点高程及AB两点间的距离已知,求B点高程。
方法是,先在A点架设经纬仪,量取仪器高i;在B点竖立觇标(标杆),并量取觇标高L,用经纬仪横丝瞄准其顶端,测定竖直角δ,则AB两点间的高差计算公式为:故(4-11)式中为A、B两点间的水平距离。
图4-12 三角高程测量原理当A、B两点距离大于300m时,应考虑地球曲率和大气折光对高差的影响,所加的改正数简称为两差改正:设c为地球曲率改正,R为地球半径,则c的近似计算公式为:设g为大气折光改正,则g的近似计算公式为:因此两差改正为:,恒为正值。
采用光电三角高程测量方式,要比传统的三角高程测量精度高,因此目前生产中的三角高程测量多采用光电法。
采用光电测距仪测定两点的斜距S,则B点的高程计算公式为:(4-12)为了消除一些外界误差对三角高程测量的影响,通常在两点间进行对向观测,即测定hAB和hBA,最后取其平均值,由于hAB和hBA反号,因此可以抵销。
实际工作中,光电三角高程测量视距长度不应超过1km,垂直角不得超过15°。
理论分析和实验结果都已证实,在地面坡度不超过8度,距离在1.5km以内,采取一定的措施,电磁波测距三角高程可以替代三、四等水准测量。
当已知地面两点间的水平距离或采用光电三角高程测量方法时,垂直角的观测精度是影响三角高程测量的精度主要因素。
二、光电三角高程测量方法光电三角高程测量需要依据规范要求进行,如《公路勘测规范》中光电三角高程测量具体要求见表4-6。
表4-6 光电三角高程测量技术要求往返各注:表4-6中为光电测距边长度。
对于单点的光电高程测量,为了提高观测精度和可靠性,一般在两个以上的已知高程点上设站对待测点进行观测,最后取高程的平均值作为所求点的高程。
三角高程测量原理及应用

三角高程测量及其误差分析与应用一、 三角高程测量的基本原理三角高程测量是通过观测两点间的水平距离和天顶距(或高度角)求定两点间的高差的方法。
它观测方法简单,不受地形条件限制,是测定大地控制点高程的基本方法。
如图1,所示,在地面上A,B 两点间测定高差h AB , A 点设置仪器,在B 点竖立标尺。
量取望远镜旋转轴中心I 至地面点上A 点的仪器高i 1,用望远镜中的十字丝的横丝照准B 点标尺上的一点M,它距B 点的高度称为目标高i 2,测出倾斜视线与水平线所夹的竖角为a ,若A,B 两点间的水平距离已知为S 0,则由图可得图1如图1,所示,在地面上A ,B 两点间测定高差h AB , A 点设置仪器,在B 点竖立标尺。
量取望远镜旋转轴中心至地面点上A 点的仪器高i ,用望远镜中的十字丝的横丝照准B 点标尺,它距B 点的高度称为目标高v ,测出倾斜视线与水平线所夹的竖角为a ,若A,B 两点间的水平距离已知为s ,则由图可得,AB 两点间高差的公式为:若A 点的高程已知为H A ,则B 点的高程为:但是,在实际的三角高程测量中,地球曲率、大气折光等因素对测量结果精度的影响非常大,必须纳入考虑分析的范围。
因而,出现了各种不同的三角高程AB h s tg i vα=•+-B A AB A H H h H s tg i v α=+=+•+-测量方法,主要分为:单向观测法,对向观测法,以及中间观测法.1。
1 单向观测法单向观测法是最基本最简单的三角高程测量方法,它直接在已知点对待测点进行观测,然后在①式的基础上加上大气折光和地球曲率的改正,就得到待测点的高程.这种方法操作简单,但是大气折光和地球曲率的改正不便计算,因而精度相对较低.1。
2 对向观测法对向观测法是目前使用比较多的一种方法。
对向观测法同样要在A点设站进行观测,不同的是在此同时,还在B点设站,在A架设棱镜进行对向观测.从而就可以得到两个观测量:直觇:h AB= S往tanα往+i往-v往+c往+r往②反觇:h BA= S返tanα返+i返-v返+c返+r返③S——A、B间的水平距离;α--观测时的高度角;i-—仪器高;v——棱镜高;c—-地球曲率改正;r——大气折光改正.然后对两次观测所得高差的结果取平均值,就可以得到A、B两点之间的高差值。
简析三角高程测量新方法原理

简析三角高程测量新方法原理三角高程测量是工程施工中传递高程的一种基本的测量方法,由于传统的三角高程测量精度不仅受大气折光、垂直角观测精度等因素影响,更重要的是受量取仪器的高度产生的垂线偏差因素影响,故在施工单位中使用并不广泛,随着几何水准测量的发展,几何水准测量成为了精密高程控制的主要方法,而使传统的三角高程测量只是在一些特殊情况下(如山区、丘陵区等高差较大地区)的几何水准测量的补充。
近几年,随着国内高速铁路大规模的建设,而高速铁路多设计为高架路段,桥梁工程所占比例在70%以上,有的桥长达几十公里,要保证桥上的无砟轨道高程定位精度达到±1mm,如何将地面上的高程精确地引测到十几米高的桥面上,这是施工单位所必须要解决的测量难题。
根据无砟轨道施工精度要求,桥上每2km左右应引测一个二等水准点,若采用精密几何水准测量法,不仅实施难度非常大且精度也难以保证,而传统的三角高程测量虽然现场实施较简单,但是受大气折光、垂直角及垂线偏差等因素影响,就很难满足精度要求。
要实现把地面上的高程高精度地引测至桥上,若采用三角测量方法,关键是要消除仪器高度产生的垂线偏差的影响。
三角高程测量新方法的原理新方法的原理:就是全站仪任意点设站,后视地面上已知的高程控制点,前视待测高程点,设定前后视点上的棱镜高度一致,在测量过程中不需要量取仪器高和棱镜高,测量完成后推算出待测点的高程。
A点为地面已知高程点,B点为待求高程点,为了测量A点与B点间高差,在中间位置设立全站仪,A点与B点处分别安置等高棱镜组,利用三角高程测量原理可得(暂不考虑大气折光因素):HA+V-△h1=HB+V-△h2则A点与B点间高差△HA-B为:△HA-B=HB-HA=△h2-△h1 (1)由上式可知,A点与B点间高差已自行消除了仪器高和棱镜高,故影响三角高程测量精度的一个重要因素就消除了。
三角高程测量新方法的计算公式及精度分析1、单向观测三角高程测量高差的计算公式:(2)或:(3)式中 -------------三角高程测量的高差;-------------全站仪至棱镜的斜距;--------------全站仪至棱镜的平距;--------------垂直角;---------------全站仪高度;--------------棱镜高;-------------地球平均曲率半径,约为6370km;-------------大气垂直折光系数,根据实际情况一般取0.08~0.14;2、单向观测三角高程测量高差的误差计算公式:(4)因新方法中是不需要量取仪器高和棱镜高的,故不存在仪器高和棱镜高的误差的,则式(4)可变换为:(5)3、测量精度分析:由式(5)可知,单向观测三角高程测量高差的误差只与距离、垂直角的误差和两气差有关,因此A点与B点间的高差计算公式为:(6)或:(7)由上式可推导出A点与B点的高差误差公式为:(8)单向观测三角测量误差分析如下:采用测角精度2"、测距精度2mm±(2*D)ppm全站仪和带气泡的对中杆棱镜组进行三角高程测量时,即、,控制测距在250m以内,垂直角在28°以内,球气差误差一般按()进行计算,則可达到三、四等水准精度(三等为,四等);若采用测角精度1"、测距精度1mm±(1*D)ppm全站仪、强制归心安装精密棱镜组,进行三角高程测量时,控制测距在100m之内、垂直角在25°以内,则可达到二等水准精度,即三角高程测量新方法的应用石武客运专线河北段,大部分路段为高架桥,架梁后桥面与地面的平均高差在20m左右,而根据无砟轨道施工要求,每2km一处应从地面高程控制点引测至桥面上。
全站仪三角高程的高差计算公式

全站仪三角高程的高差计算公式在测量工作中,全站仪三角高程测量是一种常用的高程测量方法。
它具有操作简便、效率高、精度能满足一定要求等优点,在地形起伏较大的地区应用广泛。
要准确进行全站仪三角高程测量,就必须掌握其高差计算公式。
首先,我们来了解一下全站仪三角高程测量的基本原理。
全站仪三角高程测量是通过测量两点之间的水平距离、垂直角以及仪器高和目标高,来计算两点之间的高差。
其高差计算公式的推导基于几何原理。
假设我们有 A、B 两点,A点为测站点,B 点为观测点。
在 A 点安置全站仪,测量出 A 点到 B 点的水平距离 D(也就是斜距在水平面上的投影),以及在 A 点观测 B点时的垂直角α(通常观测的是天顶距,然后通过 90 度减去天顶距得到垂直角)。
同时,我们还需要知道 A 点的仪器高 i 和 B 点的目标高 v。
那么,全站仪三角高程测量的高差计算公式可以表示为:h =D × tanα + i v + f其中,h 表示 A、B 两点之间的高差;D × tanα 这一项称为“直觇高差”,它是通过水平距离和垂直角计算得到的高差;i 是A 点的仪器高,即全站仪横轴中心到测站点地面的高度;v 是 B 点的目标高,即观测目标点的标志中心到地面的高度;f 则是球气差改正数。
接下来,我们详细说一说球气差改正数 f。
由于地球曲率和大气折光的影响,实际测量得到的高差与理论高差之间存在差异,这个差异就需要通过球气差改正来消除。
球气差改正数 f 的计算公式为:f = 043 × D²/ R其中,R 为地球平均曲率半径,一般取值为 6371km。
在实际测量中,如果两点之间的距离较短,球气差的影响较小,可以忽略不计。
但当距离较长时,忽略球气差改正会导致较大的误差。
再说说仪器高 i 和目标高 v 的测量。
仪器高的测量通常是使用小钢尺从全站仪横轴中心量至测站点地面标志点。
目标高的测量则是从观测目标点的标志中心量至地面。
三角高程测量的计算公式

三角高程测量的计算公式三角高程测量是地理测量中常用的一种方法,用于测量地面上的点的高程。
本文将介绍三角高程测量的计算公式,并解释其原理和应用。
三角高程测量是基于三角法原理的一种测量方法。
它利用三角形的一些特性和测量数据,通过计算可以得到被测点的高程。
三角高程测量适用于各种地形条件,无论是平原、山地还是高原,都可以通过三角高程测量来确定各个点的高程。
三角高程测量的计算公式如下:h = H + d * tan(a)其中,h表示被测点的高程,H表示参考点的高程,d表示两个测点之间的水平距离,a表示两个测点之间的夹角。
根据这个公式,我们可以通过测量参考点和被测点之间的距离和夹角,再加上参考点的高程,就可以计算出被测点的高程。
这个公式的原理是基于三角形的相似性原理,即两个三角形的对应边的比例相等。
在实际测量中,我们首先需要选择一个参考点,可以是已知高程的点或者固定测量设备的位置。
然后,利用测量仪器测量参考点和被测点之间的水平距离和夹角。
最后,根据测量数据和计算公式,我们可以计算出被测点的高程。
三角高程测量在地理测量中具有广泛的应用。
它可以用于绘制地形图、制作地图、建筑工程设计等。
通过三角高程测量,我们可以快速准确地确定地面上各个点的高程,为地理信息系统的建设和规划提供重要的数据支持。
在实际应用中,三角高程测量需要考虑一些误差因素。
例如,测量仪器的精度、天气条件、地形复杂度等都会对测量结果产生影响。
因此,在测量过程中要注意选择合适的测量仪器、控制测量误差,并进行合理的数据处理和分析。
三角高程测量是一种常用的地理测量方法,通过测量参考点和被测点之间的距离和夹角,再结合计算公式,可以准确地确定被测点的高程。
它在地理信息系统、地形图制作、建筑工程设计等领域具有重要的应用价值。
在实际应用中,我们需要注意测量误差的控制和数据处理,以提高测量结果的精度和可靠性。
通过三角高程测量,我们可以更好地了解地球表面的地形特征,为人类的生活和发展提供有益的信息。
中点单觇法三角高程测量的误差及精度分析

中点单觇法三角高程测量的误差及精度分析摘要:本文主要探讨了中点单觇法三角高程测量中可能出现的误差及其精度分析。
首先,介绍了中点单觇法三角高程测量的基本原理和方法,然后分析了误差来源及其影响因素,最后对精度进行了分析,并给出了精度计算公式和实例。
关键词:中点单觇法;三角高程测量;误差分析;精度分析正文:一、中点单觇法三角高程测量基本原理和方法中点单觇法是三角高程测量中常用的一种方法。
其基本原理是在一定水平距离上设置两个观测点(称为A点和B点),并以两个观测点及目标物(称为C点)形成的三角形为基础,通过测量三角形三个内角,计算出目标物的高程。
中点单觇法的测量方法如下:1. 在距离目标物一定距离的A、B两点上分别设置测距仪。
2. A、B两个测距仪同时测量目标物到各自测距仪的距离。
3. A、B两个测距仪同时记录目标物与A、B两点的连线在水平方向上的夹角。
4. 利用三角函数和测量数据计算出目标物的高程。
二、误差来源及其影响因素中点单觇法三角高程测量中可能存在的误差主要包括观测误差、仪器误差、环境误差和计算误差等。
其中观测误差是指由于人为或自然因素造成的误差;仪器误差是指由于仪器本身的精度、灵敏度等因素引起的误差;环境误差是指由于气象、地形、天气等环境因素引起的误差;计算误差是指由于计算方法和步骤引起的误差。
影响中点单觇法三角高程测量精度的因素主要包括:1. 测量设备的精度和灵敏度2. 测量人员的水平和经验3. 环境因素的影响4. 测量方法选择的科学性和合理性三、精度分析及计算公式为了提高中点单觇法三角高程测量的精度,需要针对误差来源和影响因素进行分析,并采取相应的措施加以消减。
一般情况下,中点单觇法的精度可以通过以下公式进行计算:(式中,K为系数,a为目标物与A点的距离,b为目标物与B点的距离,α、β、γ分别为A、B、C三角形三个内角)具体的精度计算实例如下:假设A、B两点距离为100米,目标物离A、B两点的距离分别为70米和50米,并且测量误差为±1毫米,则根据上述公式计算得到中点单觇法的测量精度为:K=0.00179α=54.44°β=35.56°γ=90.00°a=70mb=50m∆H=2.0303×10^-4m四、结论中点单觇法三角高程测量是一种简单、直观、可靠的高程测量方法,但其精度受到多种因素的影响。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
建筑工程测量
五、思考题与习题
1.根据表 1中所列数据,计算图根闭合 导线各点坐标。
建筑工程测量
2.控制测量分为哪几种?各有什么作用? 3.导线的布设形式有几种?分别需要哪些起算数据和观测数据? 4.选择导线点应注意哪些问题?导线测量的外业工作包括哪些内 容? 5.根据图1中所示数据,计算图根附合导线各点坐标。
2.控制测量 测定控制点位置的工作,称为控制测量。 测定控制点平面位置(x、y)的工作,称为平面控制测量。测 定控制点高程(H)的工作,称为高程控制测量。 控制网有国家控制网、城市控制网和小地区控制网等。
建筑工程测量
二、国家控制网
• 在全国范围内建立的控制网,称为国家控制网。它是全国各种比例尺 测图的基本控制,并为确定地球形状和大小提供研究资料。国家控制 网是用精密测量仪器和方法,依照施测精度按一、二、三、四等四个 等级建立的,它的低级点受高级点逐级控制。 • 国家平面控制网,主要布设成三角网,采用三角测量的方法。如图61所示,一等三角锁是国家平面控制网的骨干;二等三角网布设于一 等三角锁环内,是国家平面控制网的全面基础;三、四等三角网为二 等三角网的进一步加密。
第六章 小地区控制测量
教学要点
一、教学内容
• (1)控制测量的等级、精度要求和有关规 范; • (2)小地区控制平面控制测量、高程控制 测量的布设方法; • (3)导线测量,交会定点; • (4)三角高程测量。
建筑工程测量
二、重点和难点
重点 导线测量,交会定点;
难点 导线测量和交会定点的坐标计算。 三、教学要求 • (1)了解小地区控制平面控制测量、高程控制测 量的布设方法,控制测量的等级、精度要求和有 关规范; • (2)掌握导线测量的外业测量、内业计算,交会 定点的计算,三角高程的测量和计算方法。 四、教学方法
二、图根导线测量的外业工作
1.踏勘选点 2.建立标志 3.导线边长测知数据:AB,XB,YB;CD,XC,YC。点1、2、3、 4为新建导线点。
3 B DB1 1
C CD
D34 4 D4C
AB A
B (XB,YB)
1
图1 图根附合导线示意图
N
建筑工程测量
6.角度前方交会观测数据如图2所示,已知xA=1112.342m、yA= 351.727 m、xB=659.232m、yB=355.537m、xC=406.593m、yC= 654.051m,求P点坐标。 P
A
57°08′42″ 61°32′18″ 69°11′04″
x xB=875.44m yB=946.07m αAB=218°36′24″ 235°25′24″ B 267°33′17″ x xM=930.76m yM=1547.00m αMN=126°17′49″
A
M 63°47′26″ 100°17′57″ 140°36′06″ 2 178.43m 103.76m 154.65m 267.22m 3 1
建筑工程测量
建筑工程测量
建筑工程测量
三、城市控制网
在城市地区,为测绘大比例尺地形图、进行市政 工程和建筑工程放样,在国家控制网的控制下而 建立的控制网,称为城市控制网。
四、小地区控制测量
在面积小于15km2范围内建立的控制网,称为小 地区控制网。 建立小地区控制网时,应尽量与国家(或城市) 已建立的高级控制网连测,将高级控制点的坐标 和高程,作为小地区控制网的起算和校核数据。
D12
2
D23
3
4
(XC,YC)
C
D
2
附合导线图
观测数据:连接角B 、C ;
导线转折角 1 , 2 , 3 ,4 ; 建筑工程测量 导线各边长DB1,D12,……,D4C。
建筑工程测量
国家高程控制网,布设成水准网,采用精密水准测 量的方法。如图6-2所示,一等水准网是国家高程 控制网的骨干;二等水准网布设于一等水准环内, 是国家高程控制网的全面基础;三、四等水准网为 国家高程控制网的进一步加密。
建筑工程测量
图形1:国家一、二等平面控制网布置形式
一等三角 网
二等三角网
建筑工程测量
1 第一节 控制测量概述 2 第二节 导线测量的外业工作 3 第三节 导线测量的内业计算 4 第四节 交会测量
1 第五节 高程控制测量
建筑工程测量
第一节 控制测量概述
一、控制测量的概念
1.控制网 在测区范围内选择若干有控制意义的点(称为控制点),按一定 的规律和要求构成网状几何图形,称为控制网。 控制网分为平面控制网和高程控制网。
2.附合导线(connecting traverse)
多用于带状地区及公路、铁路、水利等工程的勘 测与施工。 3.支导线(open traverse) 支导线的点数不宜超过2个,仅作补点使用。
建筑工程测量 还有导线网,其多用于测区情况较复杂地区。
附合导线
闭合导线
单结点导线(导线网) 支导线
建筑工程测量
59°42′39″
C
B
图2 角度前方交会示意图
建筑工程测量
7.距离交会观测数据如图3所示,已知xA=1223.453m,yA= 462.838m,xB=770.343m,yB=466.648m,xC=517.704m,yC= 765.162m,求P点坐标。 P
A C
B
图3 距离交会示意图
8.如图6-17所示,已知A、B两点间的水平距离DAB=224.346m, A点的高程HA=40.48m。在A点设站照准B点测得垂直角为+ 4˚25′16″,仪器高iA=1.52m,觇标高vB=1.10m;B点设站照准A 点测得垂直角为-4˚35′40″,仪器高iB=1.50m,觇标高vA=1.20m。 求B点的高程?
建筑工程测量
第二节 导线测量的外业工作 定义及分类
1.导线的定义:将测区内相邻控制点(导线点)
(traverse point)连成直线而构成的折线图形。
2.适用范围:主要用于带状地区 (如:公路、铁路
和水利) 、隐蔽地区、城建区、地下工程等控
制点的测量。
建筑工程测量
一、导线布设形式 1.闭合导线(closed traverse) 多用于面积较宽阔的独立地区。
