2016文数—立体几何
高考立体几何知识点总结(详细)
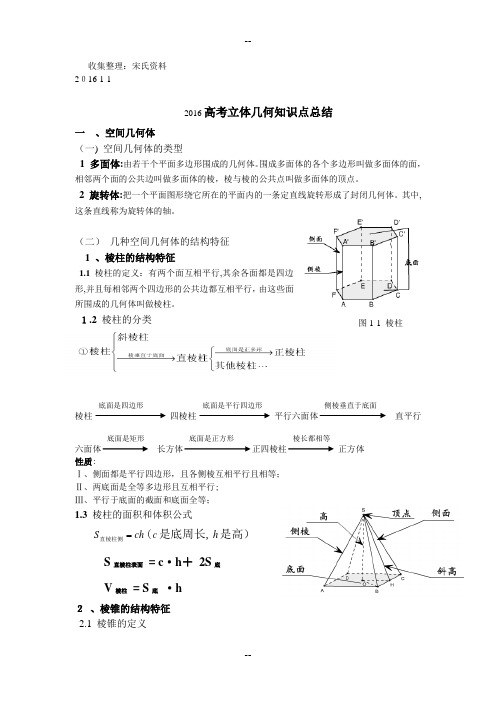
收集整理:宋氏资料 2016-1-12016高考立体几何知识点总结一 、空间几何体 (一) 空间几何体的类型1 多面体:由若干个平面多边形围成的几何体。
围成多面体的各个多边形叫做多面体的面,相邻两个面的公共边叫做多面体的棱,棱与棱的公共点叫做多面体的顶点。
2 旋转体:把一个平面图形绕它所在的平面内的一条定直线旋转形成了封闭几何体。
其中,这条直线称为旋转体的轴。
(二) 几种空间几何体的结构特征 1 、棱柱的结构特征1.1 棱柱的定义:有两个面互相平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行,由这些面所围成的几何体叫做棱柱。
1.2 棱柱的分类棱柱四棱柱平行六面体直平行六面体长方体正四棱柱正方体 性质:Ⅰ、侧面都是平行四边形,且各侧棱互相平行且相等; Ⅱ、两底面是全等多边形且互相平行; Ⅲ、平行于底面的截面和底面全等;1.3 棱柱的面积和体积公式ch S 直棱柱侧(c 是底周长,h 是高)S 直棱柱表面 = c ·h + 2S 底 V 棱柱 = S 底 ·h2 、棱锥的结构特征2.1 棱锥的定义棱长都相等底面是正方形底面是矩形侧棱垂直于底面底面是平行四边形底面是四边形图1-1 棱柱(1) 棱锥:有一个面是多边形,其余各面是有一个公共顶点的三角形,由这些面所围成的几何体叫做棱锥。
(2)正棱锥:如果有一个棱锥的底面是正多边形,并且顶点在底面的投影是底面的中心,这样的棱锥叫做正棱锥。
2.2 正棱锥的结构特征Ⅰ、 平行于底面的截面是与底面相似的正多边形,相似比等于顶点到截面的距离与顶点到底面的距离之比;它们面积的比等于截得的棱锥的高与原棱锥的高的平方比;截得的棱锥的体积与原棱锥的体积的比等于截得的棱锥的高与原棱锥的高的立方比;Ⅱ、 正棱锥的各侧棱相等,各侧面是全等的等腰三角形;正棱锥侧面积:1'2S ch =正棱椎(c 为底周长,'h 为斜高) 体积:13V Sh =棱椎(S 为底面积,h 为高)正四面体:对于棱长为a 正四面体的问题可将它补成一个边长为a 22的正方体问题。
立体几何第一章空间几何体单元测试题(含详细标准答案解析)

第一章综合素能检测时间120分钟,满分150分。
一、选择题(本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中只有一个是符合题目要求的)1.(2016·菏泽市高一检测)以边长为1的正方形的一边所在直线为旋转轴,将该正方形旋转一周所得圆柱的侧面积等于错误!()A.2πﻩB.πC.2ﻩD.1[答案] A[解析]所得旋转体是底面半径为1,高为1的圆柱,其侧面积S侧=2πRh=2π×1×1=2π.2.(2016·全国卷Ⅲ,文)如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的表面积为\x(导学号)()A.18+36\r(5) B.54+18错误!C.90 D.81[答案] B[解析]由三视图,知该几何体是一个斜四棱柱,所以该几何体的表面积S=2×3×6+2×3×3+2×3×35=54+18错误!,故选B.3.已知一个底面是菱形、侧面是矩形的四棱柱,侧棱长为5,菱形的对角线的长分别是9和15,则这个棱柱的侧面积是导学号()A.3034 B.60\r(34)C.30错误!+135ﻩD.135[答案] A[解析]由菱形的对角线长分别是9和15,得菱形的边长为错误!=错误!错误!,则这个菱柱的侧面积为4×错误!错误!×5=30错误!.4.已知圆柱与圆锥的底面积相等,高也相等,它们的体积分别为V1和V2,则V1:V2=错误!()A.1:3ﻩB.1:1C.2:1ﻩD.3:1[答案]D[解析]V1:V2=(Sh):(错误!Sh)=3:1.5.(2016·寿光现代中学高一月考)若两个球的表面积之比为1:4,则这两个球的体积之比为导学号( )A.1:2ﻩB.1:4C.1:8 D.1:16[答案]C[解析]设两个球的半径分别为r1、r2,∴S1=4πr2,1,S2=4πr错误!.∴\f(S1,S2)=错误!=错误!,∴错误!=错误!.∴错误!=错误!=(错误!)3=错误!.6.如图,△O′A′B′是水平放置的△OAB的直观图,则△OAB的面积为错误!()A.6ﻩB.3 2C.6\r(2) D.12[答案] D[解析]△OAB是直角三角形,OA=6,OB=4,∠AOB=90°,∴S△OAB=\f(1,2)×6×4=12.7.(2015·北京文)某四棱锥的三视图如图所示,该四棱锥最长棱的棱长为导学号( )A.1B .\r(2)C .\r(3)ﻩD .2[答案] C[解析] 根据三视图,可知几何体的直观图为如图所示的四棱锥V -ABCD ,其中VB ⊥平面AB CD ,且底面AB CD 是边长为1的正方形,VB =1.所以四棱锥中最长棱为VD.连接BD ,易知BD =\r(2),在Rt △VBD 中,VD =错误!=错误!.8.若一圆柱与圆锥的高相等,且轴截面面积也相等,那么圆柱与圆锥的体积之比为错误!( )A .1 ﻩB .\f (1,2)C .\f(\r (3),2)D.34 [答案] D[解析] 设圆柱与圆锥的底半径分别为R,r ,高都是h ,由题设,2R ·h=\f (1,2)×2r ·h , ∴r=2R ,V 柱=πR 2h ,V锥=13πr 2h =错误!πR 2h , ∴错误!=错误!,选D .9.半径为R 的半圆卷成一个圆锥,则它的体积为错误!( )D .错误!πR 3 ﻩB.错误!πR3C.错误!πR 3 ﻩD .错误!πR 3[答案] A[解析] 依题意,得圆锥的底面周长为πR ,母线长为R ,则底面半径为错误!,高为错误!R ,所以圆锥的体积为\f(1,3)×π×(错误!)2×错误!R =错误!πR 3.10.(2015·全国卷)《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问。
专题8.3 立体几何综合问题(原卷版)文科生

【考点1】空间角,距离的求法 【备考知识梳理】 1.空间的角(1)异面直线所成的角:如图,已知两条异面直线,a b ,经过空间任一点O 作直线','a a b b .则把'a 与'b 所成的锐角(或直角)叫做异面直线与所成的角(或夹角).异面直线所成的角的范围是0,2π⎛⎤⎥⎝⎦. (2)平面的一条斜线和它在平面内的射影所成的锐角,叫做这条直线和这个平面所成的角.①直线垂直于平面,则它们所成的角是直角;②直线和平面平行,或在平面内,则它们所成的角是0︒的角.直线与平面所成角的范围是0,2π⎡⎤⎢⎥⎣⎦.(3)二面角的平面角:如图在二面角l αβ--的棱上任取一点O ,以点O 为垂足,在半平面α和β内分别作垂直于棱的射线OA 和OB ,则AOB ∠叫做二面角的平面角.二面角的范围是[]0,π.(4)等角定理:如果一个角的两边和另一个角的两边分别平行,并且方向相同,那么这两个角相等. 推论:如果两条相交直线和另两条相交直线分别平行,那么这两组直线所成的锐角(或直角)相等. 3.空间距离:(1)两条异面直线的距离:两条异面直线的公垂线在这两条异面直线间的线段的长度,叫做两条异面直线的距离;常有求法①先证线段AB 为异面直线b a ,的公垂线段,然后求出AB 的长即可.②找或作出过且与平行的平面,则直线到平面的距离就是异面直线b a ,间的距离.③找或作出分别过b a ,且与,分别平行的平面,则这两平面间的距离就是异面直线b a ,间的距离.(2)点到平面的距离:点P到直线的距离为点P到直线的垂线段的长,常先找或作直线所在平面的垂线,得垂足为A,过A作的垂线,垂足为B连PB,则由三垂线定理可得线段PB即为点P到直线的距离.在直角三角形PAB中求出PB的长即可.常用求法①作出点P到平面的垂线后求出垂线段的长;②转移法,如果平面α的斜线上两点A,B到斜足C的距离AB,AC的比为n m :,则点A,B到平面α的距离之比也为n m :.特别地,AB=AC时,点A,B到平面α的距离相等;③体积法(3)直线与平面的距离:一条直线和一个平面平行,这条直线上任意一点到平面的距离,叫做这条直线和平面的距离;(4)平行平面间的距离:两个平行平面的公垂线段的长度,叫做两个平行平面的距离. 【规律方法技巧】1.空间中各种角包括:异面直线所成的角、直线与平面所成的角以及二面角. (1)异面直线所成的角的范围是]2,0(π.求两条异面直线所成的角的大小一般方法是通过平行移动直线,把异面问题转化为共面问题来解决具体步骤如下:①利用定义构造角,可固定一条,平移另一条,或两条同时平移到某个特殊的位置,顶点选择在特殊的位置上;②证明作出的角即为所求的角;③利用三角形来求角; ④补形法:将空间图形补成熟悉的、完整的几何体,这样有利于找到两条异面直线所成的角θ. (2)直线与平面所成的角的范围是]2,0[π.求线面角方法:①利用面面垂直性质定理,巧定垂足:由面面垂直的性质定理,可以得到线面垂直,这就为线面角中的垂足的确定提供了捷径. ②利用三棱锥的等体积,省去垂足,在构成线面角的直角三角形中,其中垂线段尤为关键.确定垂足,是常规方法.可是如果垂足位置不好确定,此时可以利用求点面距常用方法---等体积法.从而不用确定垂足的位置,照样可以求出线面角.因为垂线段的长度实际就是点面距h,利用三棱锥的等体积,只需求出h ,然后利用斜线段长h =θsin 进行求解.③妙用公式,直接得到线面角 课本习题出现过这个公式:21cos cos cos θθθ=,如图所示:21,,θθθ=∠=∠=∠OBC ABO ABC .其中1θ为直线AB 与平面所成的线面角.这个公式在求解一些选择填空题时,可直接应用.但是一定要注意三个角的位置,不能张冠李戴.(3)确定点的射影位置有以下几种方法:①斜线上任意一点在平面上的射影必在斜线在平面的射影上;②如果一个角所在的平面外一点到角的两边距离相等,那么这一点在平面上的射影在这个角的平分线上;如果一条直线与一个角的两边的夹角相等,那么这一条直线在平面上的射影在这个角的平分线上;③两个平面相互垂直,一个平面上的点在另一个平面上的射影一定落在这两个平面的交线上;④利用某些特殊三棱锥的有关性质,确定顶点在底面上的射影的位置:a.如果侧棱相等或侧棱与底面所成的角相等,那么顶点落在底面上的射影是底面三角形的外心;b. 如果顶点到底面各边距离相等或侧面与底面所成的角相等,那么顶点落在底面上的射影是底面三角形的内心(或旁心);c. 如果侧棱两两垂直或各组对棱互相垂直,那么顶点落在底面上的射影是底面三角形的垂心;(4)二面角的范围[]0,π,解题时要注意图形的位置和题目的要求.求二面角的方法:①直接法.直接法求二面角大小的步骤是:一作(找)、二证、三计算.即先作(找)出表示二面角大小的平面角,并证明这个角就是所求二面角的平面角,然后再计算这个角的大小. 用直接法求二面角的大小,其关键是确定表示二面角大小的平面角.而确定其平面角,可从以下几个方面着手:①利用三垂线定理(或三垂线定理的逆定理)确定平面角,自二面角的一个面上一点向另一面引垂线,再由垂足向棱作垂线得到棱上的点(即垂足),斜足与面上一点连线和斜足与垂足连线所夹的角,即为二面角的平面角;;②利用与二面角的棱垂直的平面确定平面角, 自空间一点作与棱垂直的平面,截二面角得两条射线,这两条射线所成的角就是二面角的平面角;③利用定义确定平面角, 在棱上任取一点,过这点在两个平面内分别引棱的垂线,这两条射线所成的角,就是二面角的平面角;DBA Cα②射影面积法.利用射影面积公式cos θ=S S';此方法常用于无棱二面角大小的计算;对于无棱二面角问题还有一条途径是设法作出它的棱,作法有“平移法”“延伸平面法”等. 【考点针对训练】1. .【2016高考浙江文数】如图,在三棱台ABC-DEF 中,平面BCFE ⊥平面ABC ,∠ACB =90°,BE=EF=FC =1,BC =2,AC =3.(I )求证:BF ⊥平面ACFD ;(II )求直线BD 与平面ACFD 所成角的余弦值.2. 【2016届湖北省武汉市武昌区高三5月调研】如图,PA 垂直圆O 所在的平面,C 是圆O 上的点,Q 是PA 的中点,G 为AOC ∆的重心,AB 是圆O 的直径,且22AB AC ==.(1)求证://QG 平面PBC ; (2)求G 到平面PAC 的距离. 【考点2】立体几何综合问题 【备考知识梳理】空间线、面的平行与垂直的综合考查一直是高考必考热点.归纳起来常见的命题角度有: 以多面体为载体综合考查平行与垂直的证明. 探索性问题中的平行与垂直问题. 折叠问题中的平行与垂直问题. 【考点针对训练】1. 【2016届宁夏高三三轮冲刺】如图,在三棱锥P ABC -中,平面PAC ⊥平面ABC ,PA AC ⊥,AB BC ⊥.设,D E 分别为,PA AC 中点.(1)求证://DE 平面PBC ; (2)求证:BC ⊥平面PAB ;(3)试问在线段AB 上是否存在点F ,使得过三点D ,,E F 的平面内的任一条直线都与平面PBC 平行?若存在,指出点F 的位置并证明;若不存在,请说明理由.2. 【2016届四川南充高中高三4月模拟三】如图,在正方形ABCD 中,点,E F 分别是,AB BC 的中点,将,AED DCF ∆∆分别沿DE 、DF 折起, 使,A C 两点重合于P .(Ⅰ)求证:平面PBD ⊥平面BFDE ; (Ⅱ)求四棱锥P BFDE -的体积. 【应试技巧点拨】 1.如何求线面角(1)利用面面垂直性质定理,巧定垂足:由面面垂直的性质定理,可以得到线面垂直,这就为线面角中的垂足的确定提供了捷径. (2)利用三棱锥的等体积,省去垂足在构成线面角的直角三角形中,其中垂线段尤为关键.确定垂足,是常规方法.可是如果垂足位置不好确定,此时可以利用求点面距常用方法---等体积法.从而不用确定垂足的位置,照样可以求出线面角.因为垂线段的长度实际就是点面距h !利用三棱锥的等体积,只需求出h ,然后利用斜线段长h=θsin 进行求解.(3)妙用公式,直接得到线面角 课本习题出现过这个公式:21cos cos cos θθθ=,如图所示:21,,θθθ=∠=∠=∠OBC ABO ABC .其中1θ为直线AB 与平面所成的线面角.这个公式在求解一些选择填空题时,可直接应用.但是一定要注意三个角的位置,不能张冠李戴. 2.如何求二面角(1)直接法.直接法求二面角大小的步骤是:一作(找)、二证、三计算.即先作(找)出表示二面角大小的平面角,并证明这个角就是所求二面角的平面角,然后再计算这个角的大小. 用直接法求二面角的大小,其关键是确定表示二面角大小的平面角.而确定其平面角,可从以下几个方面着手:①利用三垂线定理(或三垂线定理的逆定理)确定平面角;②利用与二面角的棱垂直的平面确定平面角;③利用定义确定平面角;(2)射影面积法.利用射影面积公式cos θ=S S';此方法常用于无棱二面角大小的计算;对于无棱二面角问题还有一条途径是设法作出它的棱,作法有“平移法”“延伸平面法”等. 3.探索性问题探求某些点的具体位置,使得线面满足平行或垂直关系,是一类逆向思维的题目.一般可采用两个方法:一是先假设存在,再去推理,下结论;二是运用推理证明计算得出结论,或先利用条件特例得出结论,然后再根据条件给出证明或计算.4.在推证线面平行时,一定要强调直线不在平面内,否则,会出现错误.5.在解决直线与平面垂直的问题过程中,要注意直线与平面垂直定义,判定定理和性质定理的联合交替使用,即注意线线垂直和线面垂直的互相转化.6.面面垂直的性质定理是作辅助线的一个重要依据.我们要作一个平面的一条垂线,通常是先找这个平面的一个垂面,在这个垂面中,作交线的垂线即可. 【三年高考】1. 【2016高考新课标1文数】平面α过正文体ABCD —A 1B 1C 1D 1的顶点A ,11//CB D α平面,ABCD m α=平面,11ABB A n α=平面,则m ,n 所成角的正弦值为( )(A )2 (B )2 (C )3(D )132. 【2016高考浙江文数】如图,已知平面四边形ABCD ,AB =BC =3,CD =1,AD ADC =90°.沿直线AC 将△ACD 翻折成△CD 'A ,直线AC 与D 'B 所成角的余弦的最大值是______.3. 【2016高考北京文数】如图,在四棱锥ABCD P -中,⊥PC 平面ABCD ,,AB DC DC AC ⊥∥(I )求证:DC PAC ⊥平面; (II )求证:PAB PAC ⊥平面平面;(III )设点E 为AB 的中点,在棱PB 上是否存在点F ,使得//PA 平面C F E ?说明理由.4. 【2016高考天津文数】如图,四边形ABCD 是平行四边形,平面AED ⊥平面ABCD ,EF||AB ,AB=2,BC=EF=1,DE=3,∠BAD=60º,G 为BC 的中点.(Ⅰ)求证://FG 平面BED ;(Ⅱ)求证:平面BED ⊥平面AED ;(Ⅲ)求直线EF 与平面BED 所成角的正弦值.5. 【2016高考新课标1文数】如图,在已知正三棱锥P -ABC 的侧面是直角三角形,PA =6,顶点P 在平面ABC 内的正投影为点E ,连接PE 并延长交AB 于点G . (I )证明G 是AB 的中点;(II )在答题卡第(18)题图中作出点E 在平面PAC 内的正投影F (说明作法及理由),并求四面体PDEF 的体积.PABD CGE6. 【2015高考浙江,文7】如图,斜线段AB 与平面α所成的角为60,B 为斜足,平面α上的动点P 满足30∠PAB =,则点P 的轨迹是( )A .直线B .抛物线C .椭圆D .双曲线的一支7.【2015高考福建,文20】如图,AB 是圆O 的直径,点C 是圆O 上异于,A B 的点,PO 垂直于圆O 所在的平面,且1PO =OB =.(Ⅰ)若D 为线段AC 的中点,求证C A ⊥平面D P O ; (Ⅱ)求三棱锥P ABC -体积的最大值;(Ⅲ)若BC =E 在线段PB 上,求CE OE +的最小值.8.【2015高考四川,文18】一个正方体的平面展开图及该正方体的直观图的示意图如图所示. (Ⅰ)请按字母F ,G ,H 标记在正方体相应地顶点处(不需要说明理由) (Ⅱ)判断平面BEG 与平面ACH 的位置关系.并说明你的结论. (Ⅲ)证明:直线DF ⊥平面BEGAB FHED C G CD EAB9.【2015高考重庆,文20】如题(20)图,三棱锥P-ABC 中,平面PAC ⊥平面ABC ,∠ABC=2π,点D 、E 在线段AC 上,且AD=DE=EC=2,PD=PC=4,点F 在线段AB 上,且EF//BC. (Ⅰ)证明:AB ⊥平面PFE.(Ⅱ)若四棱锥P-DFBC 的体积为7,求线段BC 的长.题(20)图AC10. 【2014高考重庆文第20题】如题(20)图,四棱锥P ABCD -中,底面是以O 为中心的菱形,PO ⊥底面ABCD ,2,3AB BAD π=∠=,M 为BC 上一点,且12BM=. (Ⅰ)证明:BC⊥平面POM ;(Ⅱ)若MP AP ⊥,求四棱锥P ABMO -的体积.11. 【2014高考全国1文第19题】如图,三棱柱111C B A ABC -中,侧面C C BB 11为菱形,C B 1的中点为O ,且⊥AO 平面C C BB 11. (1)证明:;1AB C B ⊥(2)若1AB AC ⊥,,1,601==∠BC CBB求三棱柱111C B A ABC -的高.12.【2014高考江西文第19题】如图,三棱柱111C B A ABC -中,111,BB B A BC AA ⊥⊥. (1)求证:111CC C A ⊥;(2)若7,3,2===BC AC AB ,问1AA 为何值时,三棱柱111C B A ABC -体积最大,并求此最大值.【一年原创真预测】1.已知AB ⊥平面ACD ,DE ⊥平面ACD ,ACD ∆为等边三角形,22AD DE AB ===,F 为CD 的中点.(Ⅰ)求证:平面平面BCE DCE ⊥; (Ⅱ)求B CDE 点到平面的距离.2.如图,直三棱柱111ABC A B C -中,底面ABC △是等腰直角三角形,且AB CB ==,且AA 1=3,D 为11AC 的中点,F 在线段1AA 上,设11A F tAA =(102t <<),设11=B C BC M .MFDC 1B 1A 1CBA(Ⅰ)当取何值时,CF ⊥平面1B DF ;(Ⅱ)在(Ⅰ)的条件下,求四面体1F B DM -的体积.3.如图,三棱锥P ABC -中,BC ⊥平面PAB ,PA PB AB BC 6====,点M ,N 分别为PB,BC 的中点.(I )求证:AM ⊥平面PBC ; (Ⅱ)E 是线段AC 上的点,且AM 平面PNE .①确定点E 的位置;②求直线PE 与平面PAB 所成角的正切值.4.如图,在直角三角形ABC 中,∠BAC=60°,点F 在斜边AB 上,且AB=4AF ,D ,E 是平面ABC 同一侧的两点,AD ⊥平面ABC ,BE ⊥平面ABC ,AD=3,AC=BE=4.(Ⅰ)求证:CD ⊥EF ;(Ⅱ)若点M 是线段BC 的中点,求点M 到平面EFC 的距离.5. 如图所示,在边长为12的正方形11ADD A 中,点,B C 在线段AD 上,且3,4AB BC ==,作11//BB AA ,分别交111,A D AD 于点1B ,P .作11//CC AA ,分别交111,A D AD 于点1C ,Q .将该正方形沿11,BB CC 折叠,使得1DD 与1AA 重合,构成如图的三棱柱111ABC A B C -.(1)求证:AB ⊥平面11BCC B ; (2)求四棱锥A BCQP -的体积.【考点1针对训练】 1.2.【考点2针对训练】 1.又因为EF ⊄平面PBC ,BC ⊂平面PBC ,所以//EF PBC .又因为DE EF E =,所以平面//DEF 平面PBC ,所以平面DEF 内的任一条直线都与平面PBC 平行.2.【三年高考】 1. 【答案】A//',//'m m n n ,则,m n 所成的角等于','m n 所成的角.延长AD ,过1D 作11//D E B C ,连接11,CE B D ,则CE 为'm ,同理11B F 为'n ,而111//,//BD CE B F A B ,则','m n 所成的角即为1,A B BD 所成的角,即为60 ,故,m n所成角的正弦值为2,故选A. 2.3. 【解析】(I )因为C P ⊥平面CD AB ,所以C DC P ⊥.又因为DC C ⊥A ,所以DC ⊥平面C PA . (II )因为//DC AB ,DC C ⊥A ,所以C AB ⊥A .因为C P ⊥平面CD AB ,所以C P ⊥AB .所以AB ⊥平面C PA .所以平面PAB ⊥平面C PA .(III )棱PB 上存在点,使得//PA 平面C F E .证明如下:取PB 中点,连结F E ,C E ,CF .又因为E 为AB 的中点,所以F//E PA .又因为PA ⊄平面CF E ,所以//PA 平面C F E .4.5.6. 【答案】C【解析】由题可知,当点运动时,在空间中,满足条件的AP绕AB旋转形成一个圆锥,用一个与圆锥高成60角的平面截圆锥,所得图形为椭圆.故选C.7.解法二:(I)、(II)同解法一.8.【解析】(Ⅰ)点F ,G ,H 的位置如图所示9.【解析】如题(20)图.由,DE EC PD PC ==知,E 为等腰PDC D 中DC 边的中点,故PE AC ^,又平面PAC ⊥平面ABC ,平面PAC 平面ABC AC =,PE Ì平面PAC ,PE AC ^,所以PE ^平面ABC ,从而PE AB ^.因ABC=,,AB EF 2EF BC p衈故. 从而AB 与平面PFE 内两条相交直线PE ,EF 都垂直,所以AB ^平面PFE .(2)解:设BC=x ,则在直角ABC D中,从而11S AB BC=22ABC D =?由EFBC ,知23AF AE AB AC ==,得AEF ABC DD ,故224()S 39AEF ABC S D D ==,即4S 9AEF ABC S D D =.FCDEAB GHO由1AD=2AE ,11421S S =S S 22999AFB AFE ABC ABC D D D D =?=从而四边形DFBC 的面积为DFBC11S S -=29ABC ADF S D D =718=(1)知,PE PE ^平面ABC ,所以PE 为四棱锥P-DFBC 的高.在直角PEC D 中,=体积DFBC 117S 73318P DFBC V PE -=鬃=?,故得42362430x x -+=,解得2297x x ==或,由于0x >,可得3x x ==或.所以3BC =或BC =10.11.12.【解析】(1)证明:由1AA BC ⊥知1BB BC ⊥,又11BB A B ⊥,故1BB ⊥平面1,BCA 即11BB AC ⊥,又11//BB CC ,所以11.AC CC ⊥(2)设1,AA x =在11Rt A BB ∆中1BA同理1AC 在1A BC ∆中,2222111111cos 2A B AC BC BAC BAC A B AC +-∠==∠=⋅11111sin 2A BCS A B A C BA C ∆=⋅∠=从而三棱柱111ABC A B C -的体积为11133A BC V BB S ∆=⨯⨯=因=故当x =时,即1AA =时,体积V取到最大值【一年原创真预测】1.【解析】(Ⅰ)DE ⊥平面ACD ,F A ⊂平面CD A ∴DE AF ⊥,又等边三角形ACD 中AF CD ⊥, D CD D E =,D E ⊂平面CD E ,CD ⊂平面CD E ,∴平面AF ECD ⊥,取CE 的中点M ,连接BM,MF ,则MF 为△CDE 的中位线,故1////,2MF DE AB MF DE AB ==,所以四边形ABMF 为平行四边形,即MB//AF,MB⊂平面C B E ,F A ⊄平面C B E ,//BCE 平面AF ∴,平面平面BCE DCE ∴⊥.(Ⅱ)因为AB ⊥平面ACD ,DE ⊥平面ACD ,所以AB //DE ,故AB //平面DCE ,B CDE 点到平面的距离h 等于A CDE 点到平面的距离d ,由体积相等A DCE E ACD V V --=得,1133DCE ADC S d S DE ∆∆⋅=⨯,011112222sin 6023232d ⋅⨯⨯⋅=⨯⨯⨯⨯,解得h d ==.2.(Ⅱ)由已知得111111==22F B DM M B DF C B DF B CDF V V V V ----=,因为FD FC 1=22CDF S DF FC ⋅=△,由(Ⅰ)得1B D ⊥平面DFC ,故112=21=33B CDF V -⨯⨯,故1F B DM -的体积为13.3.②作EH AB ⊥于H ,则EH //BC ,∴EH ⊥平面PAB ,∴EPH ∠是直线PE 与平面PAB 所成的角.∵1AH AB 23==,π6=3PA PAH =∠, ∴PH ==1EH BC 23==,∴EH tan EPH PH 7∠==,即直线PE 与平面PAB 所成角的正切值为7.4.5.。
2016-2017学年高中数学 第一章立体几何初步 1.1.2 简单多面体课件 北师大版必修2

探究一
探究二
探究三
探究四
思想方法
解:(1)错误.棱锥的侧面一定是三角形,可以是等腰三角形,也可以 是正三角形,例如棱长均相等的正三棱锥的各个面都是正三角形.
(2)正确.在三棱锥中,共有4个面,每一个面均可作为底面,每一个 顶点均可作为棱锥的顶点.
(3)错误.只有当棱锥被与其底面平行的平面所截时,才能截得一 个棱锥和一个棱台.
4.棱台 (1)棱台的定义:用一个平行于棱锥底面的平面去截棱锥,底面与截 面之间的部分叫作棱台.原棱锥的底面和截面叫作棱台的下底面和 上底面,其他各面叫作棱台的侧面,相邻侧面的公共边叫作棱台的 侧棱.如图所示.
(2)表示:用表示底面各顶点的字母表示棱台.如上图中的棱台可记 作:四棱台ABCD-A'B'C'D'. (3)分类:按底面多边形的边数分为三棱台、四棱台、五棱台…… (4)特殊的棱台:用正棱锥截得的棱台叫作正棱台.正棱台的侧面是 全等的等腰梯形.
锥的顶点,于是棱台的侧棱所在的直线均相交于同一点,故命题④
为真命题.故选A. 答案:A
探究一
探究二
探究三
探究四
思想方法
探究一
探究二
探究三
探究四
思想方法
变式训练1 下列说法中正确的是
.
①在正方体上任意选择4个不共面的顶点,它们可能是正四面体的4
个顶点;
②底面是等边三角形,侧面都是等腰三角形的三棱锥是正三棱锥;
其中假命题的个数是( )
A.0 B.1 C.2 D.3
探究一
探究二
探究三
探究四
思想方法
解析:解答本题可先根据棱柱、棱锥、棱台的结构特征进行详细
分析,再结合已知的各个命题具体条件进行具体分析.显然命题① ②③均是真命题.对于命题④,棱台的侧棱所在的直线就是截得原
高中数学高考专题(5)立体几何的高考解答题型及求解策略

高中数学高考专题(5)立体几何的高考解答题型及求解策略立体几何的解答题型主要采用“论证与计算”相结合的模式,即首先是利用定义、定理、公理等证明空间的线线、线面、面面平行或垂直,再计算几何体的体积.试题背景有折叠问题、探索性问题等,考查空间想象能力、逻辑思维能力及转化与化归思想的应用能力.题型一线面位置关系的证明题型概览:空间中线面的平行与垂直的证明有两种思路:一是利用相应的判定定理和性质定理去解决;二是利用空间向量法来论证,应用向量证明线、面的位置关系的关键是把空间线面位置关系的判定定理和性质定理与空间向量建立对应关系,把空间位置关系的证明转化为空间向量的运算,通过运算解决证明问题.这里以传统方法为例建立审题程序与答题模板,向量方法参照本专题题型二.如图,四边形ABCD是菱形,四边形MADN是矩形,平面MADN⊥平面ABCD,E、F分别为MA、DC的中点,求证:(1)EF∥平面MNCB;(2)平面MAC⊥平面BND.[审题程序]第一步:利用中位线、平行四边形的性质在四边形MNCB内确定与EF平行的直线;第二步:在平面MAC和平面BND中寻找与另一平面垂直的直线;第三步:应用面面垂直、菱形的性质,由线线垂直解决.[规范解答](1)如图,取NC的中点G,连接FG,MG.因为ME∥ND且ME=12ND,F、G分别为DC、NC的中点,FG∥ND且FG=12ND,所以FG与ME平行且相等,所以四边形MEFG是平行四边形,所以EF∥MG,又MG⊂平面MNCB,EF⊄平面MNCB,所以EF∥平面MNCB.(2)如图,连接BD、MC.因为四边形MADN是矩形,所以ND⊥AD.因为平面MADN⊥平面ABCD,平面ABCD∩平面MADN=AD,DN⊂平面MADN,所以ND⊥平面ABCD,所以ND⊥AC.因为四边形ABCD是菱形,所以AC⊥BD.因为BD∩ND=D,所以AC⊥平面BDN.又AC⊂平面MAC,所以平面MAC⊥平面BDN.[答题模板]解决这类问题的答题模板如下:1.(2016·北京西城区高三期末)如图,在多面体ABCDEF中,底面ABCD是边长为2的正方形,四边形BDEF是矩形,平面BDEF⊥平面ABCD,BF=3,G,H分别是CE,CF的中点.(1)求证:AC⊥平面BDEF;(2)求证:平面BDGH∥平面AEF;(3)求多面体ABCDEF的体积.[解](1)证明:因为四边形ABCD是正方形,所以AC⊥BD.又平面BDEF⊥平面ABCD,平面BDEF∩平面ABCD=BD,且AC⊂平面ABCD,所以AC⊥平面BDEF.(2)证明:在△CEF中,因为G,H分别是CE,CF的中点,所以GH∥EF.又GH⊄平面AEF,EF⊂平面AEF,所以GH∥平面AEF.设AC∩BD=O,连接OH.在△ACF中,因为OA=OC,CH=HF,所以OH∥AF.因为OH⊄平面AEF,AF⊂平面AEF,所以OH∥平面AEF.因为OH∩GH=H,OH,GH⊂平面BDGH,所以平面BDGH∥平面AEF.(3)由(1)得AC⊥平面BDEF.因为AO=2,四边形BDEF的面积S▱BDEF=3×22=62,=4.所以四棱锥A-BDEF的体积V1=13×AO×S▱BDEF同理,四棱锥C-BDEF的体积V2=4.所以多面体ABCDEF的体积V=V1+V2=8.题型二求空间几何体的体积题型概览:计算几何体的体积,关键是根据条件找出相应的底面和高,应注意充分利用多面体的截面和旋转体的轴截面,将空间问题转化为平面问题.(1)直接法:对于规则几何体,直接利用公式计算即可.(2)割补法:当一个几何体的形状不规则时,常通过分割或者补形的手段将此几何体变为一个或几个规则的、体积易求的几何体,然后再计算.经常考虑将三棱锥还原为三棱柱或长方体,将三棱柱还原为平行六面体,将台体还原为锥体.(3)等体积法:一般利用三棱锥的“等积性”求三棱锥体积,可以把任何一个面作为三棱锥的底面.注意两点:一是求体积时,可选择“容易计算”的方式来计算;二是利用“等积性”可求“点到面的距离”,关键是在面中选取三个点,与已知点构成三棱锥.(2016·全国卷Ⅲ)如图,四棱锥P-ABCD中,P A⊥底面ABCD,AD∥BC,AB=AD=AC=3,P A=BC=4,M为线段AD上一点,AM=2MD,N为PC的中点.(1)证明:MN∥平面P AB;(2)求四面体N-BCM的体积.[审题程序]第一步:由线线平行或面面平行证明(1);第二步:由N 为PC 中点,推证四面体N -BCM 的高与P A 的关系; 第三步:利用直接法求四面体的体积.[规范解答] (1)由已知得AM =23AD =2.取BP 的中点T ,连接AT ,TN ,由N 为PC 中点知TN ∥BC ,TN =12BC =2.又AD ∥BC ,故TN 綊AM ,四边形AMNT 为平行四边形, 于是MN ∥AT .因为AT ⊂平面P AB ,MN ⊄平面P AB , 所以MN ∥平面P AB .(2)因为P A ⊥平面ABCD ,N 为PC 的中点,所以N 到平面ABCD 的距离为12P A .取BC 的中点E ,连接AE .由AB =AC =3得AE ⊥BC ,AE =AB 2-BE 2= 5.由AM ∥BC 得M 到BC 的距离为5, 故S △BCM =12×4×5=2 5.所以四面体N -BCM 的体积V N -BCM =13×S △BCM ×P A 2=453. [答题模板] 解决这类问题的答题模板如下:2.(2016·深圳一模)如图所示,在四棱锥S-ABCD中,底面ABCD是平行四边形,侧面SBC是正三角形,E是SB的中点,且AE⊥平面SBC.(1)证明:SD∥平面ACE;(2)若AB⊥AS,BC=2,求点S到平面ABC的距离.[解](1)证明:连接BD,交AC于点F,连接EF.∵四边形ABCD是平行四边形,∴F是BD的中点,又∵E是SB的中点,∴EF∥SD.∵SD⊄平面ACE,EF⊂平面ACE,∴SD∥平面ACE.(2)∵AB⊥AS,BC=BS=2,且E是SB的中点,∴AE=1.∵AE⊥平面SBC,BS、CE⊂平面SBC,∴AE⊥BS,AE⊥CE.∴AB=AE2+BE2= 2.又侧面SBC 是正三角形,∴CE =3, ∴AC =AE 2+CE 2=2,∴△ABC 是底边长为2,腰长为2的等腰三角形, ∴S △ABC =12×2×4-12=72.设点S 到平面ABC 的距离为h .由V 三棱锥S -ABC =V 三棱锥A -SBC ,得13h ·S △ABC =13AE ·S △SBC ,∴h =AE ·S △SBC S △ABC =237=2217.题型三 立体几何中的探索性问题题型概览:如果知道的是试题的结论,而要求的却是试题的某一个存在性条件(如存在某个定点、定直线、定值等),这种试题称为存在探索型试题.解题策略一般是先假设结论成立,然后以该结论作为一个已知条件,再结合题目中的其他已知条件,逆推(即从后往前推),一步一步推出所要求的特殊条件,即要求的存在性条件.若能求出,则存在;若不能求出,则不存在.(2016·石家庄调研)如图,在三棱柱ABC -A 1B 1C 1中,A 1A ⊥平面ABC ,AC ⊥BC ,E 在线段B 1C 1上,B 1E =3EC 1,AC =BC =CC 1=4.(1)求证:BC ⊥AC 1;(2)试探究:在AC 上是否存在点F ,满足EF ∥平面A 1ABB 1?若存在,请指出点F 的位置,并给出证明;若不存在,请说明理由.[审题程序]第一步:由B 1E =3EC 1及EF ∥平面A 1ABB 1猜想点F 的位置;第二步:在平面A 1ABB 1内探求与EF 平行的直线或寻找经过EF 与平面A 1ABB 1平行的平面; 第三步:由线线平行或面面平行推理论证.[规范解答] (1)证明:∵AA 1⊥平面ABC ,BC ⊂平面ABC ,∴BC ⊥AA 1. 又∵BC ⊥AC ,AA 1∩AC =A ,∴BC ⊥平面AA 1C 1C . 又AC 1⊂平面AA 1C 1C ,∴BC ⊥AC 1.(2)解法一:当AF=3FC时,EF∥平面A1ABB1.证明如下:如图1,在平面A1B1C1内过点E作EG∥A1C1交A1B1于点G,连接AG.∵B1E=3EC1,∴EG=34A1C1.又AF∥A1C1且AF=3,4A1C1∴AF∥EG且AF=EG,∴四边形AFEG为平行四边形,∴EF∥AG.又EF⊄平面A1ABB1,AG⊂平面A1ABB1,∴EF∥平面A1ABB1.解法二:当AF=3FC时,EF∥平面A1ABB1.证明如下:如图2,在平面BCC1B1内过点E作EG∥BB1交BC于点G,连接FG. ∵EG∥BB1,EG⊄平面A1ABB1,BB1⊂平面A1ABB1,∴EG∥平面A1ABB1.∵B1E=3EC1,∴BG=3GC,∴FG∥AB.又AB⊂平面A1ABB1,FG⊄平面A1ABB1,∴FG∥平面A1ABB1.又EG⊂平面EFG,FG⊂平面EFG,EG∩FG=G,∴平面EFG∥平面A1ABB1.∵EF⊂平面EFG,∴EF∥平面A1ABB1.[答题模板]解决这类问题的答题模板如下:3.如图,三棱柱ABC-A1B1C1的底面是边长为4的正三角形,侧棱AA1⊥底面ABC,M为A1B1的中点.(1)证明:MC⊥AB;(2)若AA1=26,侧棱CC1上是否存在点P,使得MC⊥平面ABP?若存在,求PC的长;若不存在,请说明理由.[解](1)证明:取AB的中点N,连接MN,CN,则MN⊥底面ABC,MN⊥AB.因为△ABC是正三角形,所以NC⊥AB.因为MN∩NC=N,MN⊂平面MNC,NC⊂平面MNC,所以AB⊥平面MNC,所以AB⊥MC.(2)由(1)知MC⊥AB,若存在点P使得MC⊥平面ABP,则必有MC⊥BP.过M作MQ⊥B1C1,垂足为Q,连接QC,则QC是MC在平面BCC1B1内的射影,只需QC⊥BP即可,此时Rt△QC1C与Rt△PCB相似,QC1C1C =PCCB,所以PC=QC1·CBC1C=3×426=6,点P恰好是CC1的中点.。
2016届高三数学一轮阶段性测试题9《立体几何》(含解析)新人教A版

阶段性测试题九(立体几何)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
满分150分。
考试时间120分钟。
第Ⅰ卷(选择题共60分)一、选择题(本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的.)1.(文)(2014·辽宁师大附中期中)已知两个不同的平面α、β和两条不重合的直线m、n,有下列四个命题①若m∥n,m⊥α,则n⊥α②若m⊥α,m⊥β,则α∥β③若m⊥α,m∥n,n⊂β,则α⊥β④若m∥α,α∩β=n,则m∥n其中正确命题的个数是()A.0个B.1个C.2个D.3个[答案] D[解析]由线面垂直的性质知①正确;垂直于同一条直线的两个平面平行,∴②正确;由m⊥α,m∥n知n⊥α,又n⊂β,∴α⊥β,∴③正确;如图,正方体ABCD-A1B1C1D1中,平面ABCD与平面ADD1A1分别为α、β,CC1为m,则m∥α,α∩β=n,但m与n不平行,∴④错,故选D.(理)(2014·浙江台州中学期中)设a、b是两条不同的直线,α、β是两个不同的平面,则下列四个命题①若a⊥b,a⊥α,则b∥α②若a∥α,α⊥β,则a⊥β③a⊥β,α⊥β,则a∥α④若a⊥b,a⊥α,b⊥β,则α⊥β其中正确的命题的个数是()A.0个B.1个C.2个D.3个[答案] B[解析]①中可能有b⊂α;②中a⊂β,或a∥β,a与β斜交,a⊥β,都有可能;③中可能有a⊂α;若a⊥b,a⊥α,则b∥α或b⊂α,又b⊥β,∴α⊥β,∴④正确,故选B.2.(2014·山东省博兴二中质检)设m、n是两条不同直线,α、β是两个不同的平面,下列命题正确的是()A.m∥α,n∥β且α∥β,则m∥nB.m⊥α,n⊥β且α⊥β,则m⊥nC.m⊥α,n⊂β,m⊥n,则α⊥βD .m ⊂α,n ⊂α,m ∥β,n ∥β,则α∥β[答案] B[解析] 设m 与n 相交,m 、n 都在平面γ内,γ∥α,γ∥β时,满足A 的条件,∴A 错;若m ⊥α,α⊥β,则m ⊂β或m ∥β,又n ⊥β,∴n ⊥m ,∴B 正确;若m ⊥α,m ⊥n ,则n ∥α或n ⊂α,结合n ⊂β得不出α⊥β,故C 错;当m ∥n 且满足D 的条件时,得不出α∥β,故D 错.3.(2015·河南八校联考)一个几何体的三视图如图所示,其中正视图是一个正三角形,则这个几何体的外接球的表面积为( )A .16π3B .8π3C .43D .23π[答案] A [解析] 由三视图知该几何体为三棱锥,底面是等腰三角形,其底长为2,高为1,棱锥高为3,顶点在底面射影为等腰直角三角形底边的中点D ,直观图如图,BD ⊥AC ,PD ⊥平面ABC ,DA=DB =DC =1,故球心O 在PD 上,设OP =R ,则(3-R)2+12=R2,∴R =233.∴S 球=4πR2=16π3.4.(文)(2014·吉林市摸底)下图是某四棱锥的三视图,则该几何体的表面积等于( )A .17+65B .34+6 5C .6+65+43D .6+63+413[答案] B[解析] 由三视图知,这是一个底面是矩形的四棱锥,矩形的长和宽分别是6,2,四棱锥的高是4,其直观图如图,作PE ⊥平面ABCD ,则垂足E 为AD 的中点,PE =4,作EF ⊥BC ,垂足为F ,则PF ⊥BC ,∵EF =2,∴PF =25,∵AB ⊥AD ,∴AB ⊥PA ,PA =PE2+AE2=5,∴S =6×2+12×6×4+12×6×25+2×(12×2×5)=34+65,故选B .(理)(2015·豫南九校联考)已知四棱锥的三视图如图所示,则四棱锥的四个侧面中面积最大的是( )A .3B .25C .6D .8 [答案]C [解析] 由三视图知,该几何体是四棱锥,其直观图如图,其四个侧面中面积最大的是△PBC ,由图中数据知AB =2,BC =4,PA =PD =3,∴PE =5,取BC 中点F ,则EF ⊥BC ,∴PF ⊥BC ,PF =PE2+EF2=3,∴S △PBC =12BC·PF =6.5.(2014·云南景洪市一中期末)一个几何体的三视图如图所示,其中俯视图与左视图均为半径是1的圆,则这个几何体的体积是( )A .4π3B .πC .2π3D .π3[答案] B[解析] 由三视图知,这是一个半径为1的球,截去14,故其体积为V =34·(4π3·13)=π.6.(2015·江西三县联考)平面α与平面β平行的条件可以是( )A .α内有无穷多条直线与β平行B .直线a ∥α,a ∥βC .直线a ⊂α,直线b ⊂β,且a ∥β,b ∥αD .α内的任何直线都与β平行[答案] D[解析] 当α∩β=l 时,α内与l 平行的直线都与β平行,故A 错;当α∩β=l ,a ∥l ,a ⊄α,a ⊄β时,满足B 的条件,∴B 错;当α∩β=l ,a ⊂α,a ∥l ,b ⊂β,b ∥l 时,有a ∥β,b ∥α,∴C 错,故选D .7.(2014·长春市一调)某几何体的三视图如图(其中俯视图中的圆弧是半圆),则该几何体的表面积为( )A .92+14πB .82+14πC .92+24πD .82+24π[答案] A[解析] 由三视图知,该几何体是一个组合体,下部是长宽分别为5、4,高为4的长方体,上部为底半径为2,高为5的半圆柱,故其表面积S =5×4+(5+4)×2×4+π·22+12(2π×2×5)=92+14π,故选A .8.(2015·许昌、平顶山、新乡调研)一个几何体的三视图如图所示,则该几何体的体积为( )A .103B .10C .30D .24+2 5[答案] B[解析] 由三视图可知,该几何体为直四棱柱,底面为直角梯形,S 底=12×(2+3)×2=5,棱柱高为2,V =5×2=10.9.(2015·广东揭阳一中期中)下列命题中,错误的是( )A .一条直线与两个平行平面中的一个相交,则必与另一个平面相交B .平行于同一平面的两个不同平面平行C .如果平面α不垂直平面β,那么平面α内一定不存在直线垂直于平面βD .若直线l 不平行平面α,则在平面α内不存在与l 平行的直线[答案] D[解析] 当直线l 在平面α内时可知D 错误.10.(文)(2015·广东执信中学期中)将正方体(如图1所示)截去两个三棱锥,得到如图2所示的几何体,则该几何体的左视图为( )[答案] B[解析] 其左视图可考虑在原正方体中,将该几何体投射到平面BCC1B1上,则A 点射影为B ,D 点射影为C ,D1点射影为C1,AD1的射影为BC1,应为实线,DD1的射影CC1为实线,B1C 应为虚线(左下到右上),故应选B .(理)(2015·甘肃天水一中段测)在正方体ABCD -A1B1C1D1中,点E1,F1分别是线段A1B1,A1C1的中点,则直线BE1与AF1所成角的余弦值是( )A .3010B .12C .3015D .1510[答案] A[解析] 以A 为原点,直线AB 、AD 、AA1分别为x 轴、y 轴、z 轴建立空间直角坐标系A -xyz ,设棱长为1,则B(1,0,0),E1(12,0,1),F1(12,12,1),∴AF1→=(12,12,1),BE1→=(-12,0,1).cos 〈AF1→,BE1→〉=AF1→·BE1→|AF1→||BE1→|=3452×62=3010,故选A . 11.(2015·深圳市五校联考)一个多面体的三视图如图所示,则该多面体的体积为( )A .233B .223C .6D .7[答案] A[解析] 由三视图可知,该多面体是由正方体截去两个正三棱锥所成的几何体,如图,正方体棱长为2,正三棱锥侧棱互相垂直,侧棱长为1,故几何体的体积为:V =V 正方体-2V 三棱锥=2×2×2-2×(13×12×1×1×1)=233.12.(2014·长沙市重点中学月考)某几何体的三视图如图所示,则它的表面积为( )A .2+1+52πB .2+1+252πC .2+(1+5)πD .2+2+52π[答案] A[解析] 由三视图知,该几何体是倒立的半个圆锥,圆锥的底半径为1,高为2,故其表面积为S =12π·12+12×2×2+12π·1·22+12=2+1+52π,故选A .第Ⅱ卷(非选择题 共90分)二、填空题(本大题共4个小题,每小题4分,共16分,把正确答案填在题中横线上.)13.(2015·甘肃天水一中段测)若某几何体的三视图如下,该几何体的体积为2,则俯视图中的x =________.[答案] 2[解析] 由三视图可知,该几何体为四棱锥,高为2,底面为直角梯形,面积S =12(1+x)×2=1+x ,因此V =13Sh =13·(1+x)·2=2,解得x =2.14.(2014·成都七中模拟)已知正方体ABCD -A1B1C1D1的棱长为1,点M 是BC1的中点,P 是BB1一动点,则(AP +MP)2的最小值为________.[答案] 52[解析] 将平面ABB1A1展开到与平面CBB1C1共面,如下图,易知当A 、P 、M 三点共线时(AP +MP)2最小.AM2=AB2+BM2-2AB×BMcos135°=12+(22)2-2×1×22×(-22)=52.15.(2014·海南省文昌市检测)边长是22的正三角形ABC 内接于体积是43π的球O ,则球面上的点到平面ABC 的最大距离为________.[答案] 433[解析] 设球半径为R ,则由条件知43πR3=43π,∴R =3,正三角形ABC 所在平面截球得截面如图,OO1⊥平面ABC(O1为△ABC 的中心),OA =3,O1A =23×32×22=263,∴OO1=OA2-O1A2=33,∴球面上的点到平面ABC 的最大距离为PO1=PO +OO1=433.16.一个几何体的三视图如图所示,则这个几何体的体积为________.[答案] 9[解析] 由三视图可得该几何体是一个三棱锥,底面是等腰三角形,底边长为6,高为3,三棱锥的高为3,所以V =13×(12×6×3)×3=9.三、解答题(本大题共6个小题,共74分,解答应写出文字说明,证明过程或演算步骤.)17.(本小题满分12分)(2015·石光中学月考)如图所示,在四棱锥P -ABCD 中,底面ABCD 是边长为a 的正方形,侧面PAD ⊥底面ABCD ,且PA =PD =22AD ,若E ,F 分别为PC ,BD 的中点.(1)求证:EF ∥平面PAD ;(2)求证:平面PDC ⊥平面PAD ;(3)求四棱锥P -ABCD 的体积.[解析] (1)连接EF ,AC ,∵四棱锥P -ABCD 中,底面ABCD 是边长为a 的正方形且点F 为对角线BD 的中点, ∴对角线AC 经过F 点,又点E 为PC 的中点,∴EF 为△PAC 的中位线,∴EF ∥PA .又PA ⊂平面PAD ,EF ⊄平面PAD ,∴EF ∥平面PAD .(2)∵底面ABCD 是边长为a 的正方形,∴CD ⊥AD ,又侧面PAD ⊥底面ABCD ,侧面PAD ∩底面ABCD =AD ,∴CD ⊥平面PAD .又CD ⊂平面PCD ,∴平面PDC ⊥平面PAD .(3)过点P 作AD 的垂线PG ,垂足为点G ,∵侧面PAD ⊥底面ABCD ,PG ⊂平面PAD ,侧面PAD ∩底面ABCD =AD ,∴PG ⊥平面ABCD ,即PG 为四棱锥P -ABCD 的高,又PA =PD =22AD 且AD =a ,∴PG =a 2.∴V 四棱锥P -ABCD =13S 正方形ABCD·PG =13×a2×a 2=16a3.18.(本小题满分12分)(文)(2014·合肥市质检)如图,在多面体ABCDFE中,底面ABCD 是梯形,且AD =DC =CB =12AB .直角梯形ACEF 中,EF 綊12AC ,∠ECA 是直角,且平面ACEF ⊥平面ABCD .(1)求证:BC ⊥AF ;(2)试判断直线DF 与平面BCE 的位置关系,并证明你的结论.[解析] (1)证明:取AB 的中点H ,连接CH ,∵底面ABCD 是梯形,且AD =DC =CB =12AB ,易证四边形AHCD 为菱形,∴AD =HC =12AB ,∴∠ACB =90°,∴BC ⊥AC .∵平面ACEF ⊥平面ABCD ,且平面ACEF ∩平面ABCD =AC ,∴BC ⊥平面ACEF ,而AF ⊂平面ACEF ,故BC ⊥AF.(2)DF ∥平面BCE.证明如下:连接DH 交AC 于点M ,易知M 为AC 的中点,连接FM.在菱形AHCD 中,DM ⊥AC ,由第一问知BC ⊥AC ,故DM ∥BC .在直角梯形ACEF 中,EF 綊CM ,四边形EFMC 是平行四边形,故FM ∥EC .而BC ,CE ⊂平面BCE ,BC ∩CE =C ,而DM ,MF ⊂平面DMF ,DM ∩MF =M ,故平面BCE ∥平面DMF ,DF ⊂平面DMF ,从而,DF ∥平面BCE.(理)(2014·天津南开中学月考)如图,三棱柱ABC -A1B1C1的底面为边长为2的等边三角形,侧棱长为3,且侧棱与底面垂直,D 为B1C1的中点.(1)求证AC1∥平面A1BD ;(2)求异面直线AC1与BD 所成角的余弦值;(3)求二面角B1-A1B -D 的平面角的正弦值.[解析] 因为三棱柱的侧棱垂直于底面,所以平面BB1C1C ⊥平面A1B1C1.在等腰三角形A1B1C1中,D 为B1C1中点,∴A1D ⊥B1C1,∴A1D ⊥平面BB1C1C .取BC 的中点E ,连接DE ,则直线ED ,B1C1,A1D 两两垂直.如图,以D 为坐标原点建立空间直角坐标系,在等边三角形A1B1C1中,边长为2,所以A1D =3,所以D(0,0,0),B1(1,0,0),C1(-1,0,0),A1(0,0,3),B(1,-3,0),C(-1,-3,0),A(0,-3,3).(1)证明:DA1→=(0,0,3),DB →=(1,-3,0).设平面A1BD 的一个法向量为m =(x1,y1,z1),则⎩⎨⎧ 3z =0,x1-3y1=0.令y1=3,则x1=3,z1=0. 所以m =(3,3,0).又AC1→=(-1,3,-3),AC1→·m =0,∴AC1→⊥m ,又∵AC1⊄平面BDA1,∴AC1∥平面BDA1.(2)AC1→=(-1,3,-3),DB →=(1,-3,0),cos 〈AC1→,DB →〉=AC1→·DB →|AC1→|·|DB →|=-1-37·2=-277. 异面直线AC1与BD 所成角的余弦值为277.(3)B1B →=(0,-3,0),B1A1→=(-1,0,3),设平面B1BA1的一个法向量为n =(x2,y2,z2),则⎩⎨⎧ -3y2=0,-x2+3z2=0.令z2=3,则x2=3. 所以n =(3,0,3).cos 〈m ,n 〉=m·n |m|·|n|=912=34.∴二面角B1-A1B -D 的平面角的正弦值为74.19.(本小题满分12分)(文)(2015·江西三县联考)如图,四边形ABEF 是等腰梯形,AB ∥EF ,AF =BE =2,EF =42,AB =22,ABCD 是矩形.AD ⊥平面ABEF ,其中Q ,M 分别是AC ,EF 的中点,P 是BM 中点.(1)求证:PQ ∥平面BCE ;(2)求证:AM ⊥平面BCM ;(3)求点F 到平面BCE 的距离.[解析] (1)因为AB ∥EM ,且AB =EM ,所以四边形ABEM 为平行四边形.连接AE ,则AE 过点P ,且P 为AE 中点,又Q 为AC 中点,所以PQ 是△ACE 的中位线,于是PQ ∥CE.∵CE ⊂平面BCE ,PQ ⊄平面BCE ,∴PQ ∥平面BCE.(2)AD ⊥平面ABEF ⇒BC ⊥平面ABEF ⇒BC ⊥AM.在等腰梯形ABEF 中,由AF =BE =2,EF =42,AB =22,可得∠BEF =45°,BM =AM =2,∴AB2=AM2+BM2,∴AM ⊥BM.又BC ∩BM =B ,∴AM ⊥平面BCM.(3)解法一:点F 到平面BCE 的距离是M 到平面BCE 的距离的2倍,∵EM2=BE2+BM2,∴MB ⊥BE ,∵MB ⊥BC ,BC ∩BE =B ,∴MB ⊥平面BCE ,∴d =2MB =4.解法二:VC -BEF =13S △BEF·BC =43BC ,VF -BCE =13S △BCE·d =d 3BC .∵VC -BEF =VF -BCE ,∴d =4.(理)(2014·成都七中模拟)如图,四棱锥P -ABCD 中,底面ABCD 是平行四边形,PG ⊥平面ABCD ,垂足为G ,G 在AD 上且AG =13GD ,GB ⊥GC ,GB =GC =2,E 是BC 的中点,四面体P -BCG 的体积为83.(1)求过P 、C 、B 、G 四点的球的表面积;(2)求直线DP 与平面PBG 所成角的正弦值;(3)在棱PC 上是否存在一点F ,使DF ⊥GC ,若存在,确定点F 的位置,若不存在,说明理由.[解析] (1)∵四面体P -BCG 的体积为83,GB ⊥GC ,GB =GC =2,PG ⊥平面ABCD ,∴PG =4,以GP ,GB ,GC 为棱构造长方体,外接球的直径为长方体的对角线.∴(2R)2=16+4+4,∴R =6,∴S =4π×6=24π.(2)∵GB =GC =2,∠BGC =π2,E 为BC 的中点,∴GE =2,BGsin ∠AGB =2,∴∠AGB =π4,作DK ⊥BG 交BG 的延长线于K ,∴DK ⊥平面BPG ,∵BC =BG2+CG2=22,∴DG =34BC =322,∴DK =GK =32,PD =412. 设直线DP 与平面PBG 所成角为α,∴sinα=DK DP =38282.(3)假设F 存在,过F 作FF ′⊥GC 交GC 于F ′,则必有DF ′⊥GC .因为AG =13GD ,且AD =22,所以GD =322,又∠DGF ′=45°,∴GF ′=32=34GC ,∴PF =34PC .∴当CF CP =14时满足条件.20.(本小题满分12分)(2015·大连市二十中期中)如图,四边形ABCD 中,AB ⊥AD ,AD ∥BC ,AD =6,BC =4,AB =2,E 、F 分别在BC 、AD 上,EF ∥AB .现将四边形ABEF 沿EF 折起,使得平面ABEF ⊥平面EFDC .(1)当BE =1时,是否在折叠后的AD 上存在一点P ,使得CP ∥平面ABEF ?若存在,指出P 点位置,若不存在,说明理由;(2)设BE =x ,问当x 为何值时,三棱锥A -CDF 的体积有最大值?并求出这个最大值.[解析] (1)存在点P 使得满足条件CP ∥平面ABEF ,且此时AP AD =35.证明如下:AP AD =35,过点P 作MP ∥FD ,与AF 交于点M ,则有MP FD =35,又FD =5,故MP =3,又因为EC =3,MP ∥FD ∥EC ,故有MP 綊EC ,故四边形MPCE 为平行四边形,所以PC ∥ME ,又CP ⊄平面ABEF ,ME ⊂平面ABEF ,故有CP ∥平面ABEF 成立.(2)因为平面ABEF ⊥平面EFDC ,平面ABEF ∩平面EFDC =EF ,又AF ⊥EF ,所以AF ⊥平面EFDC . 由已知BE =x ,所以AF =x(0<x<4),FD =6-x.故VA -CDF =13·(12DF·EF)·AF =13·12·2·(6-x)·x =13(6x -x2)=13[-(x -3)2+9]=-13(x -3)2+3.所以,当x =3时,VA -CDF 有最大值,最大值为3.21.(本小题满分12分)(文)如图,在直三棱柱ABC -A1B1C1中,BC =2,AB =AC =AA1=1,D 是棱CC1上的一点,P 是AD 的延长线与A1C1的延长线的交点,且PB1∥平面BDA1.(2)求证:CD =C1D ;(2)求点C 到平面B1DP 的距离.[解析] (1)证明:连接B1A 交BA1于O ,∵PB1∥平面BDA1,B1P ⊂平面AB1P ,平面AB1P ∩平面BA1D =OD ,∴B1P ∥OD .又∵O 为B1A 的中点,∴D 为AP 的中点,∴C1为A1P 的中点,∴△ACD ≌△PC1D ,∴CD =C1D ;(2)因为VC -B1PD =VB1-PCD所以13h·S △B1PD =13A1B1·S △PCD ,∵A1B1=1,S △PCD =12CD·PC1=14,在△B1PD 中,B1D =32,B1P =5,PD =52,∴cos ∠DB1P =255,sin ∠DB1P =55.∴S △B1PD =12×32×5×55=34,∴h =13.(理) (2014·康杰中学、临汾一中、忻州一中、长治二中四校联考)如图,四边形ABCD 与BDEF 均为菱形,设AC 与BD 相交于点O ,若∠DAB =∠DBF =60°,且FA =FC .(1)求证:FC ∥平面EAD ;(2)求二面角A -FC -B 的余弦值.[解析] (1)证明:∵四边形ABCD 与BDEF 均为菱形,∴AD ∥BC ,DE ∥BF.∵AD ⊄平面FBC ,DE ⊄平面FBC ,∴AD ∥平面FBC ,DE ∥平面FBC ,又AD ∩DE =D ,AD ⊂平面EAD ,DE ⊂平面EAD ,∴平面FBC ∥平面EAD ,又FC ⊂平面FBC ,∴FC ∥平面EAD .(2)连接FO 、FD ,∵四边形BDEF 为菱形,且∠DBF =60°,∴△DBF 为等边三角形, ∵O 为BD 中点.所以FO ⊥BD ,O 为AC 中点,且FA =FC ,∴AC ⊥FO ,又AC ∩BD =O ,∴FO ⊥平面ABCD ,∴OA 、OB 、OF 两两垂直,建立如图所示的空间直角坐标系O -xyz ,设AB =2,因为四边形ABCD 为菱形,∠DAB =60°,则BD =2,OB =1,OA =OF =3,∴O(0,0,0),A(3,0,0),B(0,1,0),C(-3,0,0),F(0,0,3),∴CF →=(3,0,3),CB →=(3,1,0),设平面BFC 的一个法向量为n =(x ,y ,z),则有⎩⎪⎨⎪⎧ n·CF →=0,n·CB →=0,∴⎩⎨⎧3x +3z =0,3x +y =0, 令x =1,则n =(1,-3,-1),∵BD ⊥平面AFC ,∴平面AFC 的一个法向量为OB →=(0,1,0).∵二面角A -FC -B 为锐二面角,设二面角的平面角为θ,∴cosθ=|cos 〈n ,OB →〉|=|n·OB →||n|·|OB →|=⎪⎪⎪⎪⎪⎪-35=155, ∴二面角A -FC -B 的余弦值为155.22.(本小题满分14分)(文)(2014·黄石二中检测)如图,在直三棱柱ABC -A1B1C1中,AA1=AC =2AB =2,且BC1⊥A1C .(1)求证:平面ABC1⊥平面A1ACC1;(2)设D 是A1C1的中点,判断并证明在线段BB1上是否存在点E ,使DE ∥平面ABC1;若存在,求三棱锥E -ABC1的体积.[解析] (1)证明:在直三棱柱ABC -A1B1C1中,有A1A ⊥平面ABC .∴A1A ⊥AC ,又A1A =AC ,∴A1C ⊥AC1.又BC1⊥A1C ,∴A1C ⊥平面ABC1,∵A1C ⊂平面A1ACC1,∴平面ABC1⊥平面A1CC1.(2)存在,E 为BB1的中点.取A1A 的中点F ,连EF ,FD ,当E 为B1B 的中点时,EF ∥AB ,DF ∥AC1,∴平面EFD ∥平面ABC1,则有ED ∥平面ABC1.当E 为BB1的中点时,VE -ABC1=VC1-ABE =13×2×12×1×1=13.(理)(2014·浙北名校联盟联考)已知在长方体ABCD -A ′B ′C ′D ′中,点E 为棱CC ′上任意一点,AB =BC =2,CC ′=1.(1)求证:平面ACC ′A ′⊥平面BDE ;(2)若点P 为棱C ′D ′的中点,点E 为棱CC ′的中点,求二面角P -BD -E 的余弦值.[解析] (1)∵ABCD 为正方形,∴AC ⊥BD ,∵CC ′⊥平面ABCD ,∴BD ⊥CC ′,又CC ′∩AC =C ,∴BD ⊥平面ACC ′A ′,∴平面BDE ⊥平面ACC ′A ′.(2)以DA 为x 轴,以DC 为y 轴,以DD ′为z 轴建立空间直角坐标系,则D(0,0,0),B(2,2,0),E(0,2,12),P(0,1,1),设平面BDE 的法向量为m =(x ,y ,z),∵DB →=(2,2,0),DE →=(0,2,12),∴⎩⎪⎨⎪⎧ m·DB →=2x +2y =0,m·DE →=2y +12z =0, 令x =1,则y =-1,z =4,∴m =(1,-1,4),设平面PBD 的法向量为n =(x ,y ,z), ∵DP →=(0,1,1),∴⎩⎪⎨⎪⎧ n·DB →=2x +2y =0,n·DP →=y +z =0, 令x =1,则y =-1,z =1,∴n =(1,-1,1),∴cos 〈m ,n 〉=m·n |m|·|n|=63,∴二面角P -BD -E 的余弦值为63.。
2016届高三数学一轮总复习课件:第七章 立体几何7-4

符号语言
l⊄α
a⊂α ⇒l∥α a∥l
第六页,编辑于星期五:二十点 十二分。
2.性质定理: 文字语言
如果一条直线和一个平 性 面平行,经过这条直线 质 的平面和这个平面相 定 交,那么这条直线就和 理 交线平行(简记线面平行
⇒线线平行).
图形语言
符号语言
a∥α
a⊂β ⇒a∥b α∩β=b
答案 平行
第十三页,编辑于星期五:二十点 十二分。
知识点二
平面与平面平行
4.设l为直线,α,β是两个不同的平面.下列命题中正确的是
() A.若l∥α,l∥β,则α∥β
B.若l⊥α,l⊥β,则α∥β
C.若l⊥α,l∥β,则α∥β
D.若α⊥β,l∥α,则l⊥β
第十四页,编辑于星期五:二十点 十二分。
解析 l∥α,l∥β,则α与β可能平行,也可能相交,故A项 错;由面面平行的判定定理可知B项正确;由l⊥α,l∥β可知α⊥ β,故C项错;由α⊥β,l∥α可知l与β可能平行,也可能相交,故 D项错.
第二十页,编辑于星期五:二十点 十二分。
问题3 证明面面平行有哪些常见的方法? (1)利用定义:即证两个平面没有公共点(不常用). (2)利用面面平行的判定定理(主要方法). (3)利用垂直于同一条直线的两平面平行(客观题可用). (4)利用平面平行的传递性,即两个平面同时平行于第三个平 面,则这两个平面平行(客观题可用).
第十九页,编辑于星期五:二十点 十二分。
问题2 证明线面平行有哪些常见的方法? (1)利用线面平行的定义(无公共点); (2)利用线面平行的判定定理(a⊄α,b⊂α,a∥b⇒a∥α); (3)利用面面平行的性质(α∥β,a⊂α⇒a∥β); (4)利用面面平行的性质(α∥β,a⊄α,a⊄β,a∥α⇒a∥β).
2016年上海市高考数学立体几何复习训练2

九、直线、平面、简单几何体考试要求:1、掌握平面的基本性质,会用斜二侧的画法画水平放置的平面图形的直观图;能够画出空间两条直线、直线和平面的各种位置关系的图形,能够根据图形想象它们的位置关系。
2、掌握直线和平面平行的判定定理和性质定理;理解直线和平面垂直的概念,掌握直线和平面垂直的判定定理;掌握三垂线定理及其逆定理。
3、理解空间向量的概念,掌握空间向量的加法、减法和数乘。
4、了解空间向量的基本定理;理解空间向量坐标的概念,掌握空间向量的坐标运算。
5、掌握空间向量的数量积的定义及其性质;掌握用直角坐标计算空间向量数量积的公式;掌握空间两点间距离公式。
6、理解直线的方向向量,平面的法向量、向量在平面内的射影等概念。
7、掌握直线和直线、直线和平面、平面和平面所成的角、距离的概念。
对于异面直线的距离,只要求会计算已给出公垂线或在坐标表示下的距离。
掌握直线和平面垂直的性质定理。
掌握两个平面平行、垂直的判定定理和性质定理。
8、了解多面体、凸多面体的概念,了解正多面体的概念。
9、了解棱柱的概念,掌握棱柱的性质,会画直棱柱的直观图。
10、了解棱锥的概念,掌握正棱锥的性质,会画正棱锥的直观图。
11、了解球的概念,掌握球的性质,掌握球的表面积、体积公式。
1、已知直线m ,n ,平面βα,,给出下列命题:①若βαβα⊥⊥⊥则,,m m ;②若βαβα//,//,//则m m ;③若βαβα⊥⊥则,//,m m ; ④若异面直线m ,n 互相垂直,则存在过m 的平面与n 垂直.其中正确的命题是: A .②③ B .①③ C .②④ D .③④ 2、已知平面α、β、γ,直线l 、m ,且l m m l ==⊥⊥βγαγγα ,,,,给出下列四个结论:①γβ⊥;②α⊥l ;③β⊥m ;④αβ⊥.则其中正确的个数是:A .0B .1C .2D .33、如图,点E 是正方体ABCD —A 1B 1C 1D 1的棱DD 1的中点,则过点E 且与直线AB 、B 1C 1都相交的 直线的条数是: A .0 B .1C .2D .无数条4、已知四个命题: ①若直线l ∥平面α,则直线l 的垂线必平行于平面α; ②若直线l 与平面α相交,则有且只有一个平面经过l 与平面α垂直; ③若一个三棱锥每两个相邻侧面所成的角都相等,则这个三棱锥是正三棱锥; ④若四棱住的任意两条对角线都相交且互相平分,则这个四棱柱为平行六面体. 其中正确的命题是: A .① B .② C .③ D .④5、在正三棱锥S —ABC 中,侧棱SC ⊥侧面SAB ,侧棱SC=32,则此正三棱锥的外接球的表面积为6、在空间中,下列命题中正确的是:①若两直线a 、b 分别与直线l 平行,则a //b ②若直线a 与平面β内的一条直线b 平行,则a //β ③若直线a 与平面β内的两条直线都垂直,则a ⊥β ④若平面β内的一条直线a 垂直平面γ,则β⊥γ A .①②④ B .①④ C .①③④ D .①②③④7、如图正三棱柱ABC —A 1B 1C 1底面边长与高相等,截面PAC 把棱柱分成两部分的体积之比为5∶1,则二面角P —AC —B 的大小为 : A .30° B .45°C .60°D .75°8、球面上有A 、B 、C 三点,其中任意两点的球面距离都等于大圆周长的61,过A 、B 、C的小圆圆心到△ABC 的边BC 的距离为1,那么球的面积为 9、P 是正三棱柱ABC —A 1B 1C 1的侧棱CC 1上一点(侧棱端点除外),则∠APB 的大小满足: A .︒<∠<︒600APB B .︒=∠60APB C .︒<∠<︒9060APB D .以上都有可能 10、锥体体积V 可以由底面积S 与高h 求得:Sh V 31=. 已知正三棱锥P —ABC 底面边长为23,体积为43,则底面三角形ABC 的中心O 到侧面PAB 的距离为 . 11、如图,在棱长为3的正方体ABCD —A 1B 1C 1D 1中,M 、N 分别是棱A 1B 1、A 1D 1的中点,则点B 到平 面AMN 的距离是 ( )A .29 B .3C .556 D .212、如图,矩形ABCD 中,DC=3,AD=1,在DC 上截取DE=1, 将△ADE 沿AE 翻折到D 1点,点D 1在平面ABC 上的射影落在 AC 上时,二面角D 1—AE —B 的平面角的余弦值是 .PABCDD 1A 1B 1C 113、如图:直三棱柱ABC-A 1B 1C 1中,AB BC ⊥,E 是A 1C 的中点,ED A C ⊥1且交AC 于D ,A A AB BC 122==。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2016年全国各省市高考文数——立体几何1.全国2文(4) 体积为8的正方体的顶点都在同一球面上,则该球面的表面积为
(A)12π(B)32
3
π(C)8π(D)4π
2.全国3文(11)在封闭的直三棱柱ABC-A1B1C1内有一个体积为V的球.若AB⊥BC,AB=6,BC=8,AA1=3,则V的最大值是
(A)4π(B)9π
2
(C)6π(D)
32π
3
3.山东文(6)已知直线a,b分别在两个不同的平面β
α,内,则“直线a和直线b相交”是“平面α和平面β相交”的
(A)充分不必要条件(B)必要不充分条件
(C)充要条件(D)既不充分也不必要条件
4.上海文16.如图,在正方体ABCD−A1B1C1D1中,E、F分别为BC、BB1的中点,则下列直线中与直线EF相交的是()
(A)直线AA1 (B)直线A1B1(C)直线A1D1(D)直线B1C1
5.浙江文2. 已知互相垂直的平面αβ
,交于直线l.若直线m,n满足m∥α,n⊥β,则()
A.m∥l
B.m∥n
C.n⊥l
D.m⊥n
6.浙江文14.如图,已知平面四边形ABCD,AB=BC=3,CD=1,AD ADC=90°.沿直线AC将△ACD翻折成△ACD',直线AC与BD'所成角的余弦的最大值是______.
参考答案:
1.A
2.B
3.A
4.D
5. C 6
.。
