反比例函数压轴题精选(含答案)

合集下载

反比例函数压轴题精选(含标准答案)

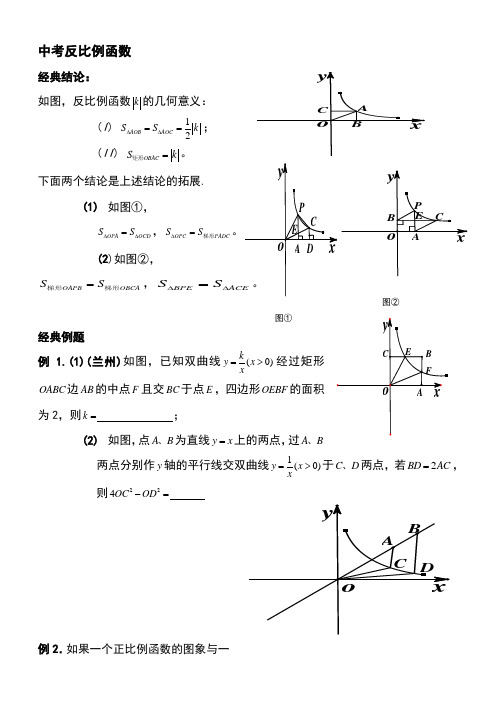
中考反比例函数经典结论：如图，反比例函数k 的几何意义： (I ) 12AOB AOC S S k ∆∆==； (II ) OBAC S k =矩形。

下面两个结论是上述结论的拓展.(1) 如图①，OPA OCD S S ∆∆=，OPC PADC S S ∆=梯形(2)如图②，OAPB OBCA S S =梯形梯形，BPE S S ∆∆=经典例题例 1.(1)(兰州)如图，已知双曲线(0)ky x x=>经过矩形OABC边AB 的中点F 且交BC 于点E ，四边形OEBF 的面积为2，则k = ；(2) 如图，点A B 、为直线y x =上的两点，过A B、两点分别作y 轴的平行线交双曲线1(0)y x x=>于C D 、两点，若2BD AC =，则224OC OD -=例2．如果一个正比例函数的图象与一个反比例函数xy 6=的图象交),(),,(2211y x B y x A ，那么))((1212y y x x --值为 .例3．如图，一次函数b kx y +=的图象与反比例函数xm y =的图象交于点A ﹙－2，－5﹚，C ﹙5，n ﹚，交y 轴于点B ，交x 轴于点D ．(1) 求反比例函数xm y =和一次函数kx y +=(2) 连接OA ，OC ．求△AOC 的面积．例4．如图，已知直线12y x =与双曲线(0)k y k x=>交于A B ，两点，且点A 的横坐标为4．（1）求k 的值；（2）若双曲线(0)k y k x=>上一点C 的纵坐标为8，求AOC △的面积；（3）过原点O 的另一条直线l 交双曲线(0)k y k x=>于P Q ，两点（P 点在第一象限），若由点A B P Q ，，，为顶点组成的四边形面积为24，求点P 的坐标．例5.(山东淄博) 如图，正方形AOCB 的边长为4，反比例函数的图象过点E （3，4）．（1）求反比例函数的解读式；图2图4y图1（2）反比例函数的图象与线段BC交于点D，直线1=-+过点D，与线段AB相y x b2交于点F，求点F的坐标；（3）连接OF，OE，探究∠AOF与∠EOC的数量关系，并证明．。

中考数学——反比例函数的综合压轴题专题复习附答案解析

一、反比例函数真题与模拟题分类汇编（难题易错题）1．在平面直角坐标系内，双曲线：y= （x＞0）分别与直线OA：y=x和直线AB：y=﹣x+10，交于C，D两点，并且OC=3BD．（1）求出双曲线的解析式；（2）连结CD，求四边形OCDB的面积．【答案】（1）解：过点A、C、D作x轴的垂线，垂足分别是M、E、F，∴∠AMO=∠CEO=∠DFB=90°，∵直线OA：y=x和直线AB：y=﹣x+10，∴∠AOB=∠ABO=45°，∴△CEO∽△DEB∴= =3，设D（10﹣m，m），其中m＞0，∴C（3m，3m），∵点C、D在双曲线上，∴9m2=m（10﹣m），解得：m=1或m=0（舍去）∴C（3，3），∴k=9，∴双曲线y= （x＞0）（2）解：由（1）可知D（9，1），C（3，3），B（10，0），∴OE=3，EF=6，DF=1，BF=1，∴S四边形OCDB=S△OCE+S梯形CDFE+S△DFB= ×3×3+ ×（1+3）×6+ ×1×1=17，∴四边形OCDB的面积是17【解析】【分析】（1）过点A、C、D作x轴的垂线，垂足分别是M、E、F，由直线y=x和y=﹣x+10可知∠AOB=∠ABO=45°，证明△CEO∽△DEB，从而可知 = =3，然后设设D（10﹣m，m），其中m＞0，从而可知C的坐标为（3m，3m），利用C、D在反比例函数图象上列出方程即可求出m的值．（2）求分别求出△OCE、△DFB△、梯形CDFE的面积即可求出答案．2．如图．一次函数y=x+b的图象经过点B（﹣1，0），且与反比例函数（k为不等于0的常数）的图象在第一象限交于点A（1，n）．求：（1）一次函数和反比例函数的解析式；（2）当1≤x≤6时，反比例函数y的取值范围．【答案】（1）解：把点B（﹣1，0）代入一次函数y=x+b得： 0=﹣1+b，∴b=1，∴一次函数解析式为：y=x+1，∵点A（1，n）在一次函数y=x+b的图象上，∴n=1+1，∴n=2，∴点A的坐标是（1，2）．∵反比例函数的图象过点A（1，2）．∴k=1×2=2，∴反比例函数关系式是：y=（2）解：反比例函数y= ，当x＞0时，y随x的增大而减少，而当x=1时，y=2，当x=6时，y= ，∴当1≤x≤6时，反比例函数y的值：≤y≤2【解析】【分析】（1）根据题意首先把点B（﹣1，0）代入一次函数y=x+b求出一次函数解析式，又点A（1，n）在一次函数y=x+b的图象上，再利用一次函数解析式求出点A的坐标，然后利用代入系数法求出反比例函数解析式，（2）根据反比例函数的性质分别求出当x=1，x=6时的y值，即可得到答案．3．如图，在平面直角坐标系中，菱形ABCD的顶点C与原点O重合，点B在y轴的正半轴上，点A在反比例函数y= （k＞0，x＞0）的图象上，点D的坐标为（，2）．（1）求k的值；（2）若将菱形ABCD沿x轴正方向平移，当菱形的一个顶点恰好落在函数y= （k＞0，x ＞0）的图象上时，求菱形ABCD平移的距离．【答案】（1）解：作DE⊥BO，DF⊥x轴于点F，∵点D的坐标为（，2），∴DO=AD=3，∴A点坐标为：（，5），∴k=5 ；（2）解：∵将菱形ABCD向右平移，使点D落在反比例函数y= （x＞0）的图象上D′，∴DF=D′F′=2，∴D′点的纵坐标为2，设点D′（x，2）∴2= ，解得x= ，∴FF′=OF′﹣OF= ﹣ = ，∴菱形ABCD平移的距离为，同理，将菱形ABCD向右平移，使点B落在反比例函数y= （x＞0）的图象上，菱形ABCD平移的距离为，综上，当菱形ABCD平移的距离为或时，菱形的一个顶点恰好落在函数图象上．【解析】【分析】（1）根据菱形的性质和D的坐标即可求出A的坐标，代入求出即可；（2）B和D可能落在反比例函数的图象上，根据平移求出即可．4．已知反比例函数y= 的图象经过点A（﹣，1）．（1）试确定此反比例函数的解析式；（2）点O是坐标原点，将线段OA绕O点顺时针旋转30°得到线段OB．判断点B是否在此反比例函数的图象上，并说明理由；（3）已知点P（m， m+6）也在此反比例函数的图象上（其中m＜0），过P点作x轴的垂线，交x轴于点M．若线段PM上存在一点Q，使得△OQM的面积是，设Q点的纵坐标为n，求n2﹣2 n+9的值．【答案】（1）解：由题意得1= ，解得k=﹣，∴反比例函数的解析式为y=﹣（2）解：过点A作x轴的垂线交x轴于点C．在Rt△AOC中，OC= ，AC=1，∴OA= =2，∠AOC=30°，∵将线段OA绕O点顺时针旋转30°得到线段OB，∴∠AOB=30°，OB=OA=2，∴∠BOC=60°．过点B作x轴的垂线交x轴于点D．在Rt△BOD中，BD=OB•sin∠BOD= ，OD= OB=1，∴B点坐标为（﹣1，），将x=﹣1代入y=﹣中，得y= ，∴点B（﹣1，）在反比例函数y=﹣的图象上（3）解：由y=﹣得xy=﹣，∵点P（m， m+6）在反比例函数y=﹣的图象上，其中m＜0，∴m（ m+6）=﹣，∴m2+2 m+1=0，∵PQ⊥x轴，∴Q点的坐标为（m，n）．∵△OQM的面积是，∴OM•QM= ，∵m＜0，∴mn=﹣1，∴m2n2+2 mn2+n2=0，∴n2﹣2 n=﹣1，∴n2﹣2 n+9=8．【解析】【分析】（1）由于反比例函数y= 的图象经过点A（﹣，1），运用待定系数法即可求出此反比例函数的解析式；（2）首先由点A的坐标，可求出OA的长度，∠AOC的大小，然后根据旋转的性质得出∠AOB=30°，OB=OA，再求出点B的坐标，进而判断点B是否在此反比例函数的图象上；（3）把点P（m， m+6）代入反比例函数的解析式，得到关于m的一元二次方程；根据题意，可得Q点的坐标为（m，n），再由△OQM的面积是，根据三角形的面积公式及m＜0，得出mn的值，最后将所求的代数式变形，把mn的值代入，即可求出n2﹣2 n+9的值．5．已知：如图，正比例函数y=ax的图象与反比例函数y= 的图象交于点C（3，1）（1）试确定上述比例函数和反比例函数的表达式；（2）根据图象回答，在第一象限内，当x取何值时，反比例函数的值大于正比例函数的值？（3）点D（m，n）是反比例函数图象上的一动点，其中0＜m＜3，过点C作直线AC⊥x 轴于点A，交OD的延长线于点B；若点D是OB的中点，DE⊥x轴于点E，交OC于点F，试求四边形DFCB的面积．【答案】（1）解：将点C（3，1）分别代入y= 和y=ax，得：k=3，a= ，∴反比例函数解析式为y= ，正比例函数解析式为y= x；（2）解：观察图象可知，在第二象限内，当0＜x＜3时，反比例函数值大于正比例函数值；（3）解：∵点D（m，n）是OB的中点，又在反比例函数y= 上，∴OE= OA= ，点D（，2），∴点B（3，4），又∵点F在正比例函数y= x图象上，∴F（，），∴DF= 、BC=3、EA= ，∴四边形DFCB的面积为 ×（ +3）× = ．【解析】【分析】（1）利用待定系数法把C坐标代入解析式即可；（2）须数形结合，先找出交点，在交点的左侧与y轴之间，反比例函数值大于正比例函数值.（3）求出DF、BC、EA，代入梯形面积公式即可.6．已知点P在一次函数y=kx+b（k，b为常数，且k＜0，b＞0）的图象上，将点P向左平移1个单位，再向上平移2个单位得到点Q，点Q也在该函数y=kx+b的图象上．（1）k的值是________；（2）如图，该一次函数的图象分别与x轴、y轴交于A，B两点，且与反比例函数y=图象交于C，D两点（点C在第二象限内），过点C作CE⊥x轴于点E，记S1为四边形CEOB的面积，S2为△OAB的面积，若 = ，则b的值是________．【答案】（1）﹣2（2）3【解析】【解答】解：（1）设点P的坐标为（m，n），则点Q的坐标为（m﹣1，n+2），依题意得：，解得：k=﹣2．故答案为：﹣2．（2）∵BO⊥x轴，CE⊥x轴，∴BO∥CE，∴△AOB∽△AEC．又∵ = ，∴ = = ．令一次函数y=﹣2x+b中x=0，则y=b，∴BO=b；令一次函数y=﹣2x+b中y=0，则0=﹣2x+b，解得：x= ，即AO= ．∵△AOB∽△AEC，且 = ，∴．∴AE= AO= b，CE= BO= b，OE=AE﹣AO= b．∵OE•CE=|﹣4|=4，即 b2=4，解得：b=3 ，或b=﹣3 （舍去）．故答案为：3 ．【分析】（1）设出点P的坐标，根据平移的特性写出Q点的坐标，由点P,Q均在一次函数y=kx+b（k，b为常数，且k＜0，b＞0）的图象上，即可得出关于k,m,n,b的四元次一方程组，两式作差即可求出k的值；（2）由BO⊥x轴，CE⊥x轴，找出△AOB∽△AEC．再由给定图形的面积比即可求出==，根据一次函数的解析式可以用含b的式子表示出OA,OB,由此即可得出线段CE,AE 的长，利用OE=AE﹣AO求出OE的长，再借助反比例函数K的几何意义得出关于b的一元二次方程，解方程即可得出结论。

中考数学与反比例函数有关的压轴题附答案解析

中考数学与反比例函数有关的压轴题附答案解析一、反比例函数1．如图，在平面直角坐标系中，反比例函数y= 的图象与一次函数y=ax+b的图象交于点A（﹣2，3）和点B（m，﹣2）．（1）求反比例函数和一次函数的解析式；（2）直线x=1上有一点P，反比例函数图象上有一点Q，若以A、B、P、Q为顶点的四边形是以AB为边的平行四边形，直接写出点Q的坐标．【答案】（1）解：∵点A（﹣2，3）在反比例函数y= 的图形上，∴k=﹣2×3=﹣6，∴反比例函数的解析式为y=﹣，∵点B在反比例函数y=﹣的图形上，∴﹣2m=﹣6，∴m=3，∴B（3，﹣2），∵点A，B在直线y=ax+b的图象上，∴，∴，∴一次函数的解析式为y=﹣x+1（2）解：∵以A、B、P、Q为顶点的四边形是以AB为边的平行四边形，∴AB=PQ，AB∥PQ，设直线PQ的解析式为y=﹣x+c，设点Q（n，﹣），∴﹣ =﹣n+c，∴c=n﹣，∴直线PQ的解析式为y=﹣x+n﹣，∴P（1，n﹣﹣1），∴PQ2=（n﹣1）2+（n﹣﹣1+ ）2=2（n﹣1）2，∵A（﹣2，3）．B（3，﹣2），∴AB2=50，∵AB=PQ，∴50=2（n﹣1）2，∴n=﹣4或6，∴Q（﹣4. ）或（6，﹣1）【解析】【分析】（1）先利用待定系数法求出反比例函数解析式，进而求出点B的坐标，再用待定系数法求出直线解析式；（2）先判断出AB=PQ，AB∥PQ，设出点Q的坐标，进而得出点P的坐标，即可求出PQ，最后用PQ=AB建立方程即可得出结论．2．抛物线y= +x+m的顶点在直线y=x+3上，过点F（﹣2，2）的直线交该抛物线于点M、N两点（点M在点N的左边），MA⊥x轴于点A，NB⊥x轴于点B．（1）先通过配方求抛物线的顶点坐标（坐标可用含m的代数式表示），再求m的值；（2）设点N的横坐标为a，试用含a的代数式表示点N的纵坐标，并说明NF=NB；（3）若射线NM交x轴于点P，且PA•PB= ，求点M的坐标．【答案】（1）解：y= x2+x+m= （x+2）2+（m﹣1）∴顶点坐标为（﹣2，m﹣1）∵顶点在直线y=x+3上，∴﹣2+3=m﹣1，得m=2；（2）解：过点F作FC⊥NB于点C，∵点N在抛物线上，∴点N的纵坐标为： a2+a+2，即点N（a， a2+a+2）在Rt△FCN中，FC=a+2，NC=NB﹣CB= a2+a，∴NF2=NC2+FC2=（ a2+a）2+（a+2）2，=（ a2+a）2+（a2+4a）+4，而NB2=（ a2+a+2）2，=（ a2+a）2+（a2+4a）+4∴NF2=NB2，NF=NB（3）解：连接AF、BF，由NF=NB，得∠NFB=∠NBF，由（2）的思路知，MF=MA，∴∠MAF=∠MFA，∵MA⊥x轴，NB⊥x轴，∴MA∥NB，∴∠AMF+∠BNF=180°∵△MAF和△NFB的内角总和为360°，∴2∠MAF+2∠NBF=180°，∠MAF+∠NBF=90°，∵∠MAB+∠NBA=180°，∴∠FBA+∠FAB=90°，又∵∠FAB+∠MAF=90°，∴∠FBA=∠MAF=∠MFA，又∵∠FPA=∠BPF，∴△PFA∽△PBF，∴ = ，PF2=PA×PB= ，过点F作FG⊥x轴于点G，在Rt△PFG中，PG= = ，∴PO=PG+GO= ，∴P（﹣，0）设直线PF：y=kx+b，把点F（﹣2，2）、点P（﹣，0）代入y=kx+b，解得k= ，b= ，∴直线PF：y= x+ ，解方程 x2+x+2= x+ ，得x=﹣3或x=2（不合题意，舍去），当x=﹣3时，y= ，∴M（﹣3，）．【解析】【分析】（1）利用配方法将二次函数化成顶点式，写出顶点坐标，由顶点再直线y=x+3上，建立方程求出m的值。

中考数学反比例函数-经典压轴题

，解得
，
∴ 一次函数解析式为 y=2x+2，
∵ 点 A 的横坐标是 1，
∴ 当 x=1 时，y=4，即 A（1，4），
把 A（1，4）代入反比例函数 y= ，可得 k=4，
∴ 反比例函数解析式为 y=
（2）解：解方程组
，可得
或
，
∴ B（﹣2，﹣2），
又∵ A（1，4），BH⊥y 轴，
∴ △ ABH 面积= ×2×（4+2）=6．【解析】【分析】（1）先由 tan∠ CDO=2 可求出 C 坐标，再把 D 点坐标代入直线解析式，可求出一次函数解析式，再由直线解析式求出 A 坐标，代入双曲线解析式，可求出双曲线解析式；（2）△ ABH 面积可以 BH 为底，高=yA-yB=4-(-2)=6.
5．函数学习中，自变量取值范围及相应的函数值范围问题是大家关注的重点之一，请解决下面的问题．
（1）分别求出当 2≤x≤4 时，三个函数：y=2x+1，y= ，y=2（x﹣1）2+1 的最大值和最小值；
（2）若 y= 的值不大于 2，求符合条件的 x 的范围；
（3）若 y= ，当 a≤x≤2 时既无最大值，又无最小值，求 a 的取值范围；（4）y=2（x﹣m）2+m﹣2，当 2≤x≤4 时有最小值为 1，求 m 的值．【答案】（1）解：y=2x+1 中 k=2＞0， ∴ y 随 x 的增大而增大， ∴ 当 x=2 时，y 最小=5；当 x=4 时，y 最大=9．
联立
，解得直线 PA 的方程为 y= x+ ﹣1，
联立
，解得直线 PB 的方程为 y=﹣ x+ +1，
∴ M（m﹣4，0），N（m+4，0），

中考数学压轴题专题复习——反比例函数的综合及详细答案

点 C 为（﹣1，3），对应的函数的解析式是 y= x2+ ； e、当点 A 在 x 轴负半轴上，点 B 在 y 轴负半轴上，点 C 坐标为（3，4）时，另一个顶点 D
的坐标是（7，﹣3）时，对应的函数解析式是 y=﹣ x2+ ； f、当点 A 在 x 轴负半轴上，点 B 在 y 轴负半轴上，点 C 坐标为（3，4）时，另一个顶点 D
3．已知点 A，B 分别是 x 轴、y 轴上的动点，点 C，D 是某个函数图象上的点，当四边形 ABCD（A，B，C，D 各点依次排列）为正方形时，我们称这个正方形为此函数图象的“伴侣正方形”．例如：在图 1 中，正方形 ABCD 是一次函数 y=x+1 图象的其中一个“伴侣正方形”．
（1）如图 1，若某函数是一次函数 y=x+1，求它的图象的所有“伴侣正方形”的边长；
∵ 反比例函数 ∴ k=1×2=2，
的图象过点 A（1，2）．
∴ 反比例函数关系式是：y=
（2）解：反比例函数 y= ，当 x＞0 时，y 随 x 的增大而减少，而当 x=1 时，y=2，当
x=6 时，y= ，
∴ 当 1≤x≤6 时，反比例函数 y 的值： ≤y≤2 【解析】【分析】（1）根据题意首先把点 B（﹣1，0）代入一次函数 y=x+b 求出一次函数解析式，又点 A（1，n）在一次函数 y=x+b 的图象上，再利用一次函数解析式求出点 A 的坐标，然后利用代入系数法求出反比例函数解析式，（2）根据反比例函数的性质分别求出当 x=1，x=6 时的 y 值，即可得到答案．
（3）解：∠ PAQ=∠ PBQ．理由如下：
过点 Q 作 QT⊥x 轴于 T，设 AQ 交 x 轴于 D，QB 的延长线交 x 轴于 E，如图 3．可设点 Q 为（c，），直线 AQ 的解析式为 y=px+q，则有

中考数学与反比例函数有关的压轴题及答案

一、反比例函数真题与模拟题分类汇编（难题易错题）1．如图，已知直线y=ax+b与双曲线y= （x＞0）交于A（x1， y1），B（x2， y2）两点（A与B不重合），直线AB与x轴交于P（x0，0），与y轴交于点C．（1）若A，B两点坐标分别为（1，3），（3，y2），求点P的坐标．（2）若b=y1+1，点P的坐标为（6，0），且AB=BP，求A，B两点的坐标．（3）结合（1），（2）中的结果，猜想并用等式表示x1，x2，x0之间的关系（不要求证明）．【答案】（1）解：∵直线y=ax+b与双曲线y= （x＞0）交于A（1，3），∴k=1×3=3，∴y= ，∵B（3，y2）在反比例函数的图象上，∴y2= =1，∴B（3，1），∵直线y=ax+b经过A、B两点，∴解得，∴直线为y=﹣x+4，令y=0，则x=4，∴P（4，O）（2）解：如图，作AD⊥y轴于D，AE⊥x轴于E，BF⊥x轴于F，BG⊥y轴于G，AE、BG 交于H，则AD∥BG∥x轴，AE∥BF∥y轴，∴= ，= = ，∵b=y1+1，AB=BP，∴= ，= = ，∴B（，y1）∵A，B两点都是反比例函数图象上的点，∴x1•y1= • y1，解得x1=2，代入= ，解得y1=2，∴A（2，2），B（4，1）（3）解：根据（1），（2）中的结果，猜想：x1， x2， x0之间的关系为x1+x2=x0【解析】【分析】（1）先把A（1，3）），B（3，y2）代入y= 求得反比例函数的解析式，进而求得B的坐标，然后把A、B代入y=ax+b利用待定系数法即可求得直线的解析式，继而即可求得P的坐标；（2）作AD⊥y轴于D，AE⊥x轴于E，BF⊥x轴于F，BG⊥y轴于G，AE、BG交于H，则AD∥BG∥x轴，AE∥BF∥y轴，得出 = ， = = ，根据题意得出 = ， = = ，从而求得B（， y1），然后根据k=xy得出x1•y1= • y1，求得x1=2，代入 = ，解得y1=2，即可求得A、B的坐标；（3）合（1），（2）中的结果，猜想x1+x2=x0．2．如图，已知点D在反比例函数y= 的图象上，过点D作x轴的平行线交y轴于点B （0，3）．过点A（5，0）的直线y=kx+b与y轴于点C，且BD=OC，tan∠OAC= ．（1）求反比例函数y= 和直线y=kx+b的解析式；（2）连接CD，试判断线段AC与线段CD的关系，并说明理由；（3）点E为x轴上点A右侧的一点，且AE=OC，连接BE交直线CA与点M，求∠BMC的度数．【答案】（1）解：∵A（5，0），∴OA=5．∵，∴，解得OC=2，∴C（0，﹣2），∴BD=OC=2，∵B（0，3），BD∥x轴，∴D（﹣2，3），∴m=﹣2×3=﹣6，∴，设直线AC关系式为y=kx+b，∵过A（5，0），C（0，﹣2），∴，解得，∴；（2）解：∵B（0，3），C（0，﹣2），∴BC=5=OA，在△OAC和△BCD中∴△OAC≌△BCD（SAS），∴AC=CD，∴∠OAC=∠BCD，∴∠BCD+∠BCA=∠OAC+∠BCA=90°，∴AC⊥CD；（3）解：∠BMC=45°．如图，连接AD，∵AE=OC，BD=OC，AE=BD，∴BD∥x轴，∴四边形AEBD为平行四边形，∴AD∥BM，∴∠BMC=∠DAC，∵△OAC≌△BCD，∴AC=CD，∵AC⊥CD，∴△ACD为等腰直角三角形，∴∠BMC=∠DAC=45°．【解析】【分析】（1）由正切定义可求C坐标，进而由BD=OC求出D坐标，求出反比例函数解析式；由A、C求出直线解析式；（2）由条件可判定△OAC≌△BCD，得出AC=CD，∠OAC=∠BCD，进而AC⊥CD；（3）由已知可得AE=OC，BD=OC，得出AE=BD，再加平行得四边形AEBD为平行四边形，推出△OAC≌△BCD，∴AC=CD，∵AC⊥CD，∴△ACD为等腰直角三角形，∴∠BMC=∠DAC=45°.3．如图，已知直线y=x+k和双曲线y= （k为正整数）交于A，B两点．（1）当k=1时，求A、B两点的坐标；（2）当k=2时，求△AOB的面积；（3）当k=1时，△OAB的面积记为S1，当k=2时，△OAB的面积记为S2，…，依此类推，当k=n时，△OAB的面积记为S n，若S1+S2+…+S n= ，求n的值．【答案】（1）解：当k=1时，直线y=x+k和双曲线y= 化为：y=x+1和y= ，解得，，∴A（1，2），B（﹣2，﹣1）（2）解：当k=2时，直线y=x+k和双曲线y= 化为：y=x+2和y= ，解得，，∴A（1，3），B（﹣3，﹣1）设直线AB的解析式为：y=mx+n，∴∴，∴直线AB的解析式为：y=x+2∴直线AB与y轴的交点（0，2），∴S△AOB= ×2×1+ ×2×3=4；（3）解：当k=1时，S1= ×1×（1+2）= ，当k=2时，S2= ×2×（1+3）=4，…当k=n时，S n= n（1+n+1）= n2+n，∵S1+S2+…+S n= ，∴ ×（…+n2）+（1+2+3+…n）= ，整理得：，解得：n=6．【解析】【分析】（1）两图像的交点就是求联立的方程组的解；（2）斜三角形△AOB的面积可转化为两水平（或竖直）三角形（有一条边为水平边或竖直边的三角形称为水平或竖直三角形）的面积和或差；（3）利用n个数的平方和公式和等差数列的和公式可求出.4．如图，在平面直角坐标系中，OA⊥OB，AB⊥x轴于点C，点A（，1）在反比例函数y= 的图象上．（1）求反比例函数y= 的表达式；（2）在x轴的负半轴上存在一点P，使得S△AOP= S△AOB，求点P的坐标；（3）若将△BOA绕点B按逆时针方向旋转60°得到△BDE．直接写出点E的坐标，并判断点E是否在该反比例函数的图象上．【答案】（1）解：∵点A（，1）在反比例函数y= 的图象上，∴k= ×1= ，∴反比例函数表达式为y= .（2）解：∵A（，1），AB⊥x轴于点C，∴OC= ，AC=1，∵OA⊥OB，OC⊥AB，∴∠A=∠COB，∴tan∠A= =tan∠COB= ，∴OC2=AC•BC，即BC=3，∴AB=4，∴S△AOB= × ×4=2 ，∴S△AOP= S△AOB= ，设点P的坐标为（m，0），∴ ×|m|×1= ，解得|m|=2 ，∵P是x轴的负半轴上的点，∴m=﹣2 ，∴点P的坐标为（﹣2 ，0）（3）解：由（2）可知tan∠COB= = = ，∴∠COB=60°，∴∠ABO=30°，∵将△BOA绕点B按逆时针方向旋转60°得到△BDE，∴∠OBD=60°，∴∠ABD=90°，∴BD∥x轴，在Rt△AOB中，AB=4，∠ABO=30°，∴AO=DE=2，OB=DB=2 ，且BC=3，OC= ，∴OD=DB﹣OC= ，BC﹣DE=1，∴E（﹣，﹣1），∵﹣ ×（﹣1）= ，∴点E在该反比例函数图象上【解析】【分析】（1）由点A的坐标，利用待定系数法可求得反比例函数表达式；（2）由条件可求得∠A=∠COB，利用三角函数的定义可得到OC2=AC•BC，可求得BC的长，可求得△AOB的面积，设P点坐标为（m，0），由题意可得到关于m的方程，可求得m的值；（3）由条件可求得∠ABD=90°，则BD∥x轴，由BD、DE的长，可求得E点坐标，代入反比例函数解析式进行判断即可．5．如图，在平面直角坐标系中，直线AB与x轴交于点B、与y轴交于点A，与反比例函数y= 的图象在第二象限交于C，CE⊥x轴，垂足为点E，tan∠ABO= ，OB=4，OE=2．（1）求反比例函数的解析式；（2）若点D是反比例函数图象在第四象限内的点，过点D作DF⊥y轴，垂足为点F，连接OD、BF．如果S△BAF=4S△DFO，求点D的坐标．（3）若动点D在反比例函数图象的第四象限上运动，当线段DC与线段DB之差达到最大时，求点D的坐标．【答案】（1）解：∵tan∠ABO= ，∴ = ，且OB=4，∴OA=2，∵CE⊥x轴，即CE∥AO，∴△AOB∽△CEB，∴ = ，即 = ，解得CE=3，∴C（﹣2，3），∴m=﹣2×3=﹣6，∴反比例函数解析式为y=﹣（2）解：设D（x，﹣），∵D在第四象限，∴DF=x，OF= ，∴S△DFO= DF•OF= x× =3，由（1）可知OA=2，∴AF=x+ ，∴S△BAF= AF•OB= （x+ ）×4=2（x+ ），∵S△BAF=4S△DFO，∴2（x+ ）=4×3，解得x=3+ 或x=3﹣，当x=3+ 时，﹣的值为3﹣，当x=3﹣时，﹣的值为3+ ，∵D在第四象限，∴x=3﹣不合题意，舍去，∴D（3+ ，3﹣）（3）解：∵D在第四象限，∴在△BCD中，由三角形三边关系可知CD﹣CB≤BC，即当B、C、D三点共线时，其差最大，设直线AB解析式为y=kx+b，由题意可得，解得，∴直线AB解析式为y=﹣ x+2，联立直线AB和反比例函数解析式可得，解得或（舍去），∴D（6，﹣1），即当线段DC与线段DB之差达到最大时求点D的坐标为（6，﹣1）【解析】【分析】（1）由条件可求得OA，由△AOB∽△CEB可求得CE，则可求得C点坐标，代入反比例函数解析式可求得m的值，可求得反比例函数解析式；（2）设出D的坐标，从而可分别表示出△BAF和△DFO的面积，由条件可列出方程，从而可求得D点坐标；（3）在△BCD中，由三角形三边关系可知CD﹣CB≤BC，当B、C、D三点共线时，其差最大，联立直线BC与反比例函数解析式可求得D点坐标．6．如图，在菱形ABCD中，， ,点E是边BC的中点，连接DE,AE.（1）求DE的长；（2）点F为边CD上的一点，连接AF，交DE于点G，连接EF，若 ,①求证：△△；②求DF的长.【答案】（1）解：连结BD（2）解：①②【解析】【分析】（1）连结BD ，根据菱形的性质及等边三角形的判定方法首先判定出△CDB是等边三角形，根据等边三角形的性质得出DE⊥BC，CE=2，然后利用勾股定理算出DE的长；（2）①首先判断出△AGD∽△EGF，根据相似三角形对应边成比例得出，又∠AGE=∠DGF，故△AGE∽△DGF；②根据相似三角形的性质及含30°直角三角形的边之间的关系及勾股定理得出EF的长，然后过点E作EH⊥DC于点H，在Rt△ECH中，利用勾股定理算出FH的长，从而根据线段的和差即可算出答案.7．如图，二次函数（其中a，m是常数，且a>0，m>0）的图象与x轴分别交于点A，B（点A位于点B的左侧），与y轴交于点C(0，－3)，点D在二次函数的图象上，CD∥AB，连接AD.过点A作射线AE交二次函数的图象于点E，AB平分∠DAE.（1）用含m的代数式表示a；（2）求证：为定值；（3）设该二次函数图象的顶点为F.探索：在x轴的负半轴上是否存在点G，连接CF，以线段GF、AD、AE的长度为三边长的三角形是直角三角形？如果存在，只要找出一个满足要求的点G即可，并用含m的代数式表示该点的横坐标；如果不存在，请说明理由.【答案】（1）解：将C（0，-3）代入函数表达式得，，∴（2）证明：如答图1，过点D、E分别作x轴的垂线，垂足为M、N.由解得x1=－m，x2=3m.∴A(－m，0)，B(3m，0).∵CD∥AB，∴点D的坐标为（2m，－3）.∵AB平分∠DAE.∴∠DAM=∠EAN.∵∠DMA=∠ENA=900，∴△ADM∽△AEN, ∴ .设点E的坐标为（x, ）,∴ ,∴x=4m.∴为定值.（3）解：存在，如答图2，连接FC并延长，与x轴负半轴的交点即为所求点G.由题意得：二次函数图像顶点F的坐标为（m，-4），过点F作FH⊥x轴于点H，在Rt△CGO和Rt△FGH中,∵tan∠CGO＝ , tan∠FGH＝ , ∴ = .∴OG="3m,"由勾股定理得，GF= ，AD=∴ .由（2）得，，∴AD∶GF∶AE=3∶4∶5.∴以线段GF、AD、AE的长度为三边长的三角形是直角三角形，此时点G的横坐标为－3m.【解析】【分析】1）将C点代入函数解析式即可求得.（2）令y=0求A、B的坐标，再根据，CD∥AB，求点D的坐标，由△ADM∽△AEN,对应边成比例，将求的比转化成求比，结果不含m即为定值.（3）连接FC并延长，与x轴负半轴的交点即为所求点G..过点F作FH⊥x轴于点H，在Rt△CGO和Rt△FGH中根据同角的同一个三角函数相等，可求OG（用m表示），然后利用勾股定理求GF和AD（用m表示），并求其比值，由（2）是定值，所以可得AD∶GF∶AE=3∶4∶5，由此可根据勾股定理逆定理判断以线段GF、AD、AE的长度为三边长的三角形是直角三角形，直接得点G的横坐标.8．已知如图，二次函数的图象经过A（3，3），与x轴正半轴交于B 点，与y轴交于C点，△ABC的外接圆恰好经过原点O.（1）求B点的坐标及二次函数的解析式；（2）抛物线上一点Q（m，m+3），（m为整数），点M为△ABC的外接圆上一动点，求线段QM长度的范围；（3）将△AOC绕平面内一点P旋转180°至△A'O'C'（点O'与O为对应点），使得该三角形的对应点中的两个点落在的图象上，求出旋转中心P的坐标.【答案】（1）解：如图，过点A作AD⊥y轴于点D，AE⊥x轴于点E，∴∠ADC=∠AEB=90°∵二次函数与y轴交于点C，点C坐标为（0，2）∵点A坐标（3，3）∴DA=AE=3∵∠DAC+∠CAE=90°∠EAB+∠CAE=90°∴∠DAC=∠EAB∴△ACD≌△ABE∴EB=CD=3-2=1OB=3+1=4∴点B的坐标为（4，0）将A（3，3）B（4，0）代入二次函数中得：解得：二次函数的解析式为：（2）解：将点Q（m，m+3）代入二次函数解析式得：m1=1；m2= （舍）∴m=1∴点Q坐标为(1,4)由勾股定理得：BC=2设圆的圆心为N∵圆经过点O，且∠COB=90°∴BC是圆N的直径，∴圆N的半径为，N的坐标为（2,1）由勾股定理得，QN=半径r= ，则≤QM≤（3）解：当点A的对称点，点O的对称点在抛物线上时，如图设点的横坐标为m，则点的横坐标为m-3得：解得：∴的坐标为（）∴旋转中心P的坐标为当点A的对称点，点C的对称点在抛物线上时，如图设点的横坐标为m，则点的横坐标为m-3得：解得：∴的坐标为（）∴旋转中心P的坐标为综上所述，旋转中心P的坐标为或【解析】【分析】（1）过点A作AD⊥y轴于点D，AE⊥x轴于点E，求证△ACD≌△ABE，进而求得点B坐标，再将A、B两点坐标代入二次函数解析式，即可解答；（2）将点Q （m，m+3）代入二次函数解析式，求得m的值，进而且得点Q坐标，根据圆的性质得到BC是圆N的直径，利用勾股定理即可求得BC，进而求得N的坐标，再利用勾股定理求得QN的长，确定取值范围即可；（3）分两种情况：当点A的对称点，点O的对称点在抛物线上时，利用旋转180°可知，∥，设点的横坐标为m，则点的横坐标为m-3，利用列出式子，即可求得m的值，利用旋转中心和线段中点的特点，即可求得旋转中心P的坐标；当点A的对称点，点C的对称点在抛物线上时，设点的横坐标为m，则点的横坐标为m-3，同理可求得m的值以及旋转中心P 的坐标.9．【问题】如图1，在Rt△ABC中，∠ACB=90°，AC=BC，过点C作直线l平行于AB.∠EDF=90°，点D 在直线l上移动，角的一边DE始终经过点B，另一边DF与AC交于点P，研究DP和DB的数量关系.（1）【探究发现】如图2，某数学兴趣小组运用“从特殊到一般”的数学思想，发现当点D 移动到使点P与点C重合时，通过推理就可以得到DP=DB，请写出证明过程；（2）【数学思考】如图3，若点P是AC上的任意一点（不含端点A、C），受（1）的启发，这个小组过点D作DG⊥CD交BC于点G，就可以证明DP=DB，请完成证明过程；（3）【拓展引申】如图4，在（1）的条件下，M是AB边上任意一点（不含端点A、B），N是射线BD上一点，且AM=BN，连接MN与BC交于点Q，这个数学兴趣小组经过多次取M点反复进行实验，发现点M在某一位置时BQ的值最大.若AC=BC=4，请你直接写出BQ的最大值.【答案】（1）解：∵∠ACB=90°，AC=BC∴∠CAB=∠CBA=45°∵CD∥AB∴∠CBA=∠DCB=45°，且BD⊥CD∴∠DCB=∠DBC=45°∴DB=DC即DB=DP（2）解：∵DG⊥CD，∠DCB=45°∴∠DCG=∠DGC=45°∴DC=DG，∠DCP=∠DGB=135°，∵∠BDP=∠CDG=90°∴∠CDP=∠BDG，且DC=DG，∠DCP=∠DGB=135°，∴△CDP≌△GDB（ASA）∴DB=DP（3）解：如图4，过点M作MH⊥MN交AC于点H，连接CM，HQ，∵MH⊥MN，∴∠AMH+∠NMB=90°∵CD∥AB，∠CDB=90°∴∠DBM=90°∴∠NMB+∠MNB=90°∴∠HMA=∠MNB，且AM=BN，∠CAB=∠CBN=45°∴△AMH≌△BNQ（ASA）∴AH=BQ∵∠ACB=90°，AC=BC=4，∴AB=4 ，AC-AH=BC-BQ∴CH=CQ∴∠CHQ=∠CQH=45°=∠CAB∴HQ∥AB∴∠HQM=∠QMB∵∠ACB=∠HMQ=90°∴点H，点M，点Q，点C四点共圆，∴∠HCM=∠HQM∴∠HCM=∠QMB，且∠A=∠CBA=45°∴△ACM∽△BMQ∴∴∴BQ= +2∴AM=2 时，BQ有最大值为2.【解析】【分析】（1）DB=DP，理由如下：根据等腰直角三角形的性质得出∠CAB=∠CBA=45°，根据二直线平行，内错角相等得出∠CBA=∠DCB=45°，根据三角形的内角和得出∠DCB=∠DBC=45°，最后根据等角对等边得出 DB=DC ，即DB=DP；（2）利用ASA判断出△CDP≌△GDB ，再根据全等三角形的对应边相等得出DB=DP；（3）如图4，过点M作MH⊥MN交AC于点H，连接CM，HQ，利用ASA判断出△AMH≌△BNQ 根据全等三角形的对应边相等得出AH=BQ，进而判断出点H，点M，点Q，点C四点共圆，根据圆周角定理得出∠HCM=∠HQM ，然后判断出△ACM∽△BMQ ，根据相似三角形的对应边成比例得出,根据比例式及偶数次幂的非负性即可得出求出答案.10．综合与探究如图，抛物线的图象经过坐标原点O，且与轴的另一交点为( ，0).（1）求抛物线的解析式；（2）若直线与抛物线相交于点A和点B(点A在第二象限)，设点A′是点A关于原点O的对称点，连接A′B，试判断ΔAA′B的形状，并说明理由；（3）在问题(2)的基础上，探究：平面内是否存在点P，使得以点A，B，A′，P为顶点的四边形是菱形？若存在直接写出点P的坐标；若不存在，请说明理由.【答案】（1）解：∵抛物线y=x2+bx+c的图象经过点（0，0）和( ，0)，∴，解得：；∴ .（2）解：ΔAA′B是等边三角形；∵，解得：，∴A( )，B( )，过点A分别作AC⊥轴，AD⊥A′B，垂足分别为C，D，∴AC= ，OC= ，在RtΔAOC中OA= ，∵点A′与点A关于原点对称，∴A′( )，AA′= ，∵B( )，∴A′B=2-(- )= ，又∵A( )，B( )，∴AD= ，BD= ，在RtΔABD中AB= ，∴AA′=A′B=AB，∴ΔAA′B是等边三角形（3）解：存在正确的点P，且以点A、B、A′、P为顶点的菱形分三种情况；设点P的坐标为：（x，y）．①当A′B为对角线时，有，解得：，∴点P为：；②当AB为对角线时，有，解得：，∴点P为：；③当AA′为对角线时，有，解得：，∴点P为：；综合上述， , ,【解析】【分析】（1）根据点的坐标，利用待定系数法即可求出抛物线F的解析式；（2）先求出点A、B的坐标，利用对称性求出点A′的坐标，利用两点间的距离公式（勾股定理）可求出AB、AA′、A′B的值，由三者相等即可得出△AA′B为等边三角形；（3）根据等边三角形的性质结合菱形的性质，可得出存在正确得点P，设点P的坐标为（x，y），分三种情况考虑：①当A′B为对角线时，根据菱形的性质（对角线互相平分）可求出点P 的坐标；②当AB为对角线时，根据菱形的性质（对角线互相平分）可求出点P的坐标；③当AA′为对角线时，根据菱形的性质（对角线互相平分）可求出点P的坐标．综上即可得出结论．11．如图，正方形、等腰的顶点在对角线上(点与、不重合)，与交于，延长线与交于点，连接 .（1）求证： .（2）求证：（3）若，求的值.【答案】（1）解：∵是正方形，∴，，∵是等腰三角形，∴，，∴，∴，∴（2）解：∵是正方形，∴，，∵是等腰三角形，∴，∵，∵，∴，∴，∴，∴，∴，（3）解：由(1)得，，，∴，由(2) ，∴，∵，∴，在中，，∴【解析】【分析】（1）证出∠ABP=∠CBQ，由SAS证明△ABP≌△CBQ可得结论；（2）根据正方形的性质和全等三角形的性质得到，∠APF=∠ABP，可证明△APF∽△ABP，再根据相似三角形的性质即可求解；（3）根据全等三角形的性质得到∠BCQ=∠BAC=45°，可得∠PCQ=90°，根据三角函数和已知条件得到，由（2）可得，等量代换可得∠CBQ=∠CPQ即可求解．12．在平面直角坐标系xOy中，抛物线y=-x2+mx+n与x轴交于点A，B（A在B的左侧）．（1）抛物线的对称轴为直线x=-3，AB=4．求抛物线的表达式；（2）平移（1）中的抛物线，使平移后的抛物线经过点O，且与x正半轴交于点C，记平移后的抛物线顶点为P，若△OCP是等腰直角三角形，求点P的坐标；（3）当m=4时，抛物线上有两点M（x1， y1）和N（x2， y2），若x1＜2，x2＞2，x1+x2＞4，试判断y1与y2的大小，并说明理由．【答案】（1）解：抛物线 y=-x2+mx+n的对称轴为直线x=-3，AB=4．∴点 A（-5，0），点B（-1，0）．∴抛物线的表达式为y=-（x+5）（ x+1）∴y=-x2-6x-5．（2）解：如图1，依题意，设平移后的抛物线表达式为：y=-x2+bx．∴抛物线的对称轴为直线x＝，抛物线与x正半轴交于点C（b，0）．∴b＞0．记平移后的抛物线顶点为P，∴点P的坐标（，），∵△OCP是等腰直角三角形，∴ =∴b=2．∴点P的坐标（1，1）．（3）解：如图2，当m=4时，抛物线表达式为：y=-x2+4x+n．∴抛物线的对称轴为直线 x=2．∵点M（x1， y1）和N（x2， y2）在抛物线上，且x1＜2，x2＞2，∴点M在直线x=2的左侧，点N在直线x=2的右侧．∵x1+x2＞4，∴2-x1＜x2-2，∴点M到直线x=2的距离比点N到直线x=2的距离近，∴y1＞y2．【解析】【分析】（1）先根据抛物线和x轴的交点及线段的长，求出抛物线的解析式；（2）根据平移后抛物线的特点设出抛物线的解析式，再利用等腰直角三角形的性质求出抛物线解析式；（3）根据抛物线的解析式判断出点M，N的大概位置，再关键点M，N的横坐标的范围即可得出结论．13．小明利用函数与不等式的关系，对形如 ( 为正整数)的不等式的解法进行了探究．（1）下面是小明的探究过程，请补充完整：①对于不等式，观察函数的图象可以得到如表格：的范围的符号+﹣由表格可知不等式的解集为．②对于不等式，观察函数的图象可以得到如表表格：的范围的符号+﹣+由表格可知不等式的解集为________．③对于不等式，请根据已描出的点画出函数(x+1)的图象；观察函数的图象补全下面的表格：的范围的符号+﹣________________由表格可知不等式的解集为________．……小明将上述探究过程总结如下：对于解形如 ( 为正整数)的不等式，先将按从大到小的顺序排列，再划分的范围，然后通过列表格的办法，可以发现表格中的符号呈现一定的规律，利用这个规律可以求这样的不等式的解集．（2）请你参考小明的方法，解决下列问题：①不等式的解集为________．②不等式的解集为________．【答案】（1）或；+；-；或（2）或或；或且【解析】【解答】(1)②由表格可知不等式的解集为或，故答案为：或；③当时，，当时，，由表格可知不等式的解集为或，故答案为：+，﹣，或；(2)①不等式的解集为或或，故答案为：或或；②不等式的解集为或且，故答案为：或且【分析】根据题意可知在表格中写出相应的函数值的正负性，借此来判断相应的不等式的解集.（1）②根据表格中的数据可以直接写出不等式的解集；③根据表格中的数据可以直接写出不等式的解集；（2）①根据小明的方法，可以直接写出该不等式的解集；②根据小明的方法，可以直接写出该不等式的解集．14．如图，一次函数y=kx+b（k＜0）与反比例函数y= 的图象相交于A、B两点，一次函数的图象与y轴相交于点C，已知点A（4，1）（1）求反比例函数的解析式；（2）连接OB（O是坐标原点），若△BOC的面积为3，求该一次函数的解析式．【答案】（1）解：∵点A（4，1）在反比例函数y= 的图象上，∴m=4×1=4，∴反比例函数的解析式为y=（2）解：∵点B在反比例函数y= 的图象上，∴设点B的坐标为（n，）．将y=kx+b代入y= 中，得：kx+b= ，整理得：kx2+bx﹣4=0，∴4n=﹣，即nk=﹣1①．令y=kx+b中x=0，则y=b，即点C的坐标为（0，b），∴S△BOC= bn=3，∴bn=6②．∵点A（4，1）在一次函数y=kx+b的图象上，∴1=4k+b③．联立①②③成方程组，即，解得：，∴该一次函数的解析式为y=﹣x+3【解析】【分析】（1）由点A的坐标结合反比例函数系数k的几何意义，即可求出m的值；（2）设点B的坐标为（n，），将一次函数解析式代入反比例函数解析式中，利用根与系数的关系可找出n、k的关系，由三角形的面积公式可表示出来b、n的关系，再由点A在一次函数图象上，可找出k、b的关系，联立3个等式为方程组，解方程组即可得出结论．15．如果三角形的两个内角α与β满足2α+β=90°，那么我们称这样的三角形为“准互余三角形”.（1）若△ABC是“准互余三角形”，∠C＞90°，∠A=60°，则∠B=________°；（2）如图①，在Rt△ABC中，∠ACB=90°，AC=4，BC=5.若AD是∠BAC的平分线，不难证明△ABD是“准互余三角形”.试问在边BC上是否存在点E（异于点D），使得△ABE也是“准互余三角形”？若存在，请求出BE的长；若不存在，请说明理由.（3）如图②，在四边形ABCD中，AB=7，CD=12，BD⊥CD，∠ABD=2∠BCD，且△ABC是“准互余三角形”，求对角线AC的长.【答案】（1）15（2）解：如图①中，在Rt△ABC中，∵∠B+∠BAC=90°，∠BAC=2∠BAD，∴∠B+2∠BAD=90°，∴△ABD是“准互余三角形”，∵△ABE也是“准互余三角形”，∴只有2∠B+∠BAE=90°，∵∠B+∠BAE+∠EAC=90°，∴∠CAE=∠B，∵∠C=∠C=90°，∴△CAE∽△CBA，可得CA2=CE•CB，∴CE= ，∴BE=5﹣ = .（3）解：如图②中，将△BCD沿BC翻折得到△BCF.∴CF=CD=12，∠BCF=∠BCD，∠CBF=∠CBD，∵∠ABD=2∠BCD，∠BCD+∠CBD=90°，∴∠ABD+∠DBC+∠CBF=180°，∴A、B、F共线，∴∠A+∠ACF=90°∴2∠ACB+∠CAB≠90°，∴只有2∠BAC+∠ACB=90°，∴∠FCB=∠FAC，∵∠F=∠F，∴△FCB∽△FAC，∴CF2=FB•FA，设FB=x，则有：x（x+7）=122，∴x=9或﹣16（舍去），∴AF=7+9=16，在Rt△ACF中，AC=【解析】【解答】（1）∵△ABC是“准互余三角形”，∠C＞90°，∠A=60°，∴2∠B+∠A=90°，解得，∠B=15°；【分析】（1）根据“准互余三角形”的定义构建方程即可解决问题；（2）只要证明△CAE∽△CBA，可得CA2=CE•CB，由此即可解决问题；（3）如图②中，将△BCD沿BC翻折得到△BCF.只要证明△FCB∽△FAC，可得CF2=FB•FA，设FB=x，则有：x（x+7）=122，推出x=9或﹣16（舍弃），再利用勾股定理求出AC即可；。

中考数学压轴题之反比例函数(中考题型整理,突破提升)及详细答案

y1= 中，当 x=1 时，y=4， ∴ P（1，4）．设直线 AP 的函数关系式为 y=mx+n，把点 A（﹣4，﹣1）、P（1，4）代入 y=mx+n，
则
，
解得
．
故直线 AP 的函数关系式为 y=x+3，
则点 C 的坐标（0，3），OC=3，
∴ S△ AOP=S△ AOC+S△ POC
= OC•AR+ OC•PS
又∵ 点 F 在反比例函数
（k＞0）的图象上，∴ k=12，
∴ 该函数的解析式为 y= （x＞0）
（2）解：由题意知 E，F 两点坐标分别为 E（，4），F（6，
∴ 当 k=12 时，S 有最大值．S 最大=3
【解析】【分析】）当 F 为 AB 的中点时，点 F 的坐标为（3，1），由此代入求得函数解
C 与 D 横纵坐标乘积相等，求出 b 的值确定出 B 坐标，进而求出 k 的值，确定出双曲线解析式；（3）抓住两个关键点，将 A 坐标代入双曲线解析式求出 b 的值；将 C 坐标代入双曲线解析式求出 b 的值，即可确定出平行四边形与双曲线总有公共点时 b 的范围．
5．如图，正比例函数和反比例函数的图象都经过点 A（3，3），把直线 OA 向下平移后，与反比例函数的图象交于点 B（6，m），与 x 轴、y 轴分别交于 C、D 两点．
（1）求 m 的值；（2）求过 A、B、D 三点的抛物线的解析式；（3）若点 E 是抛物线上的一个动点，是否存在点 E，使四边形 OECD 的面积 S1
，是四边
形 OACD 面积 S 的？若存在，求点 E 的坐标；若不存在，请说明理由．【答案】（1）解：∵ 反比例函数的图象都经过点 A（3，3），

中考数学反比例函数-经典压轴题附答案解析

中考数学反比例函数 -经典压轴题附答案解析一、反比例函数1．如图，矩形 OABC 的顶点 A 、 C 分别在 x 、y 轴的正半轴上，点 D 为 BC 边上的点，反比2）将矩形 OABC 的进行折叠，使点 O 于点 D 重合，折痕分别与 x 轴、 y 轴正半轴交于点 F ，G ，求折痕 FG 所在直线的函数关系式．【答案】（1）∵反比例函数 y= （k ≠0）在第一象限内的图象经过点E （3，）， ∴反比例函数的表达式为 y= ．又∵点 D （m ，2）在反比例函数 y= 的图象上， ∴2m=2 ，解得： m=1（2）解：设 OG=x ，则 CG=OC ﹣OG=2﹣x ，∵点 D （ 1， 2）， ∴CD=1．在 Rt △CDG 中，∠DCG=9°0，CG=2﹣x ，CD=1，DG=OG=x ， ∴CD 2+CG 2=DG 2 ，即 1+（ 2﹣ x ） 2=x 2 ，解得： x= ，∴点 G （0，）．过点 F 作 FH ⊥ CB 于点 H ，如图所示．D （m ，2）和 AB 边上的点E （3，由折叠的特性可知： ∠GDF=∠GOF=9°0 ，OG=DG ，OF=DF ． ∵∠ CGD+∠CDG=90 ，°∠CDG+∠ HDF=90 ，° ∴∠ CGD=∠HDF ，∵∠ DCG=∠ FHD=90 ，°∴△ GCD ∽△DHF ，∴ =2 ，∴DF=2GD= ，∴点 F 的坐标为（，0）．设折痕 FG 所在直线的函数关系式为 y=ax+b ，∴折痕 FG 所在直线的函数关系式为 y=﹣ x+【解析】【分析】（ 1）由点 E 的坐标利用反比例函数图象上点的坐标特征即可求出 k 值，再由点 B 在反比例函数图象上，代入即可求出 m 值；（ 2）设 OG=x ，利用勾股定理即可得出关于 x 的一元二次方程，解方程即可求出 x 值，从而得出点 G 的坐标．再过点 F 作 FH ⊥CB 于点 H ，由此可得出 △GCD ∽△DHF ，根据相似三角形的性质即可求出线段 DF 的长度，从而得出点 F 的坐标，结合点 G 、 F 的坐标利用待定系数法即可求出结论．∴有，解得：2．如图，一次函数y=kx+b 的图象交反比例函数y= （x> 0）的图象于A（4，-8）、 B （m，-2）两点，交x 轴于点C．（1）求反比例函数与一次函数的关系式；（2）根据图象回答：当x 为何值时，一次函数的值大于反比例函数的值？（3）以O、A、B、P为顶点作平行四边形，请直接写出点P 的坐标．【答案】（1）解：∵反比例函数y= （x>0）的图象于A（4，-8），∴k=4 ×（-8）=-32．∵双曲线y= 过点B（m，-2），∴m=16 ．由直线y=kx+b 过点 A ， B 得：，解得，反比例函数关系式为，一次函数关系式为（2）解：观察图象可知，当0<x<4或x>16时，一次函数的值大于反比例函数的值（3）解：∵ O（0，0），A（4，-8）、B（16，-2），分三种情况：① 若OB∥AP，OA∥ BP，∵O（0，0），A（4，-8），∴由平移规律，点B（16，-2）向右平移 4 个单位，向下平移8 个单位得到P 点坐标为（20，-10）；② 若OP∥ AB，OA∥ BP，∵A（4，-8），B（16，-2），∴由平移规律，点O（0，0）向右平移12 个单位，向上平移 6 个单位得到P 点坐标为（12，6）；③ 若OB∥ AP，OP∥AB，∵B（16，-2），A（4，-8），∴由平移规律，点O（0，0）向左平移12 个单位，向下平移 6 个单位得到P 点坐标为（- 12，-6）；∴以O，A，B，P为顶点作平行四边形，第四个顶点P的坐标为（12，6）或（-12，-6）或（20，-10）【解析】【分析】（1）将点A（4，-8），B（m ，-2）代入反比例函数y= （x> 0）中，可求k、a；再将点A（4，-8），B（m，-2）代入y=kx+b 中，列方程组求k、b 即可；（2）根据两函数图象的交点，图象的位置可确定一次函数的值大于反比例函数的值时x 的范围；（3）根据平行四边形的性质，即可直接写出．3．如图，已知A（3，m），B（﹣2，﹣3）是直线AB 和某反比例函数的图象的两个交点．（1）求直线AB 和反比例函数的解析式；（2）观察图象，直接写出当x 满足什么范围时，直线AB 在双曲线的下方；（3）反比例函数的图象上是否存在点C，使得△OBC 的面积等于△OAB 的面积？如果不存在，说明理由；如果存在，求出满足条件的所有点 C 的坐标．【答案】（1）解：设反比例函数解析式为y= ，把B（﹣2，﹣3）代入，可得k=﹣2×（﹣ 3 ）=6，∴反比例函数解析式为y= ；把A（3，m）代入y= ，可得3m=6，即m=2 ，∴A（3，2），设直线AB 的解析式为y=ax+b，把A（3，2），B（﹣2，﹣3）代入，可得解得，∴直线AB 的解析式为y=x﹣1（2）解：由题可得，当x满足：x<﹣2或0<x<3时，直线AB在双曲线的下方（3）解：存在点C．如图所示，延长AO 交双曲线于点C1 ，∵点 A 与点C1 关于原点对称，∴AO=C1O，∴△ OBC1的面积等于△ OAB的面积，此时，点C1的坐标为（﹣3，﹣2）；如图，过点C1作BO的平行线，交双曲线于点C2 ，则△OBC2的面积等于△ OBC1的面积，∴△ OBC2的面积等于△ OAB的面积，由B（﹣2，﹣3）可得OB 的解析式为y= x ，可设直线C1C2 的解析式为y= x+b'，把C1（﹣3，﹣2）代入，可得﹣2= ×（﹣3）+b'，解得b'= ，∴直线C1C2 的解析式为y= x+ ，解方程组，可得C2（）；如图，过 A 作OB的平行线，交双曲线于点C3 ，则△OBC3 的面积等于△ OBA的面积，设直线AC3 的解析式为y= x+ ，把A（3，2）代入，可得2= ×3+ ，解得=﹣，∴直线AC3 的解析式为y= x﹣，解方程组，可得C3（）；综上所述，点C的坐标为（﹣3，﹣2），（（））．【解析】【分析】（1）用待定系数法求出反比例函数解析式,一次函数解析式,将已知的点A,B 的坐标代入设的函数解析式列出关于待定系数的方程（组）求出系数，再回代到解析式（2）结合图像判断直线AB 在双曲线的交点坐标为A,B，X 取值范围为双曲线所在象限交点的横坐标，第一象限为为小于横坐标大于零，第三象限为小于横坐标（3）结合已知条件根据同底等高、等底同高作出与原三角形面积相等的三角形，再结合已知条件用待定系数法求出与双曲线有交点的直线的解析式，得出点的坐标，注意要考虑满足条件的所有点 C 的坐标。

中考数学反比例函数-经典压轴题含答案

一、反比例函数真题与模拟题分类汇编（难题易错题）1．如图，一次函数y1=k1x+b与反比例函数y2= 的图象交于点A（4，m）和B（﹣8，﹣2），与y轴交于点C．（1）m=________，k1=________；（2）当x的取值是________时，k1x+b＞；（3）过点A作AD⊥x轴于点D，点P是反比例函数在第一象限的图象上一点．设直线OP 与线段AD交于点E，当S四边形ODAC：S△ODE=3：1时，求点P的坐标．【答案】（1）4；（2）﹣8＜x＜0或x＞4（3）解：由（1）知，y1= x+2与反比例函数y2= ，∴点C的坐标是（0，2），点A 的坐标是（4，4）．∴CO=2，AD=OD=4．∴S梯形ODAC= •OD= ×4=12，∵S四边形ODAC：S△ODE=3：1，∴S△ODE= S梯形ODAC= ×12=4，即OD•DE=4，∴DE=2．∴点E的坐标为（4，2）．又点E在直线OP上，∴直线OP的解析式是y= x，∴直线OP与y2= 的图象在第一象限内的交点P的坐标为（4 ，2 ）．【解析】【解答】解：（1）∵反比例函数y2= 的图象过点B（﹣8，﹣2），∴k2=（﹣8）×（﹣2）=16，即反比例函数解析式为y2= ，将点A（4，m）代入y2= ，得：m=4，即点A（4，4），将点A（4，4）、B（﹣8，﹣2）代入y1=k1x+b，得：，解得：，∴一次函数解析式为y1= x+2，故答案为：4，；（2）∵一次函数y1=k1x+2与反比例函数y2= 的图象交于点A（4，4）和B（﹣8，﹣2），∴当y1＞y2时，x的取值范围是﹣8＜x＜0或x＞4，故答案为：﹣8＜x＜0或x＞4；【分析】（1）由A与B为一次函数与反比例函数的交点，将B坐标代入反比例函数解析式中，求出k2的值，确定出反比例解析式，再将A的坐标代入反比例解析式中求出m的值，确定出A的坐标，将B坐标代入一次函数解析式中即可求出k1的值；（2）由A与B 横坐标分别为4、﹣8，加上0，将x轴分为四个范围，由图象找出一次函数图象在反比例函数图象上方时x的范围即可；（3）先求出四边形ODAC的面积，由S四边形ODAC：S△ODE=3：1得到△ODE的面积，继而求得点E的坐标，从而得出直线OP的解析式，结合反比例函数解析式即可得．2．如图，一次函数y=kx+b的图象分别与反比例函数y= 的图象在第一象限交于点A（4，3），与y轴的负半轴交于点B，且OA=OB．（1）求函数y=kx+b和y= 的表达式；（2）已知点C（0，5），试在该一次函数图象上确定一点M，使得MB=MC，求此时点M 的坐标．【答案】（1）解：把点A（4，3）代入函数y= 得：a=3×4=12，∴y= ．OA= =5，∵OA=OB，∴OB=5，∴点B的坐标为（0，﹣5），把B（0，﹣5），A（4，3）代入y=kx+b得：解得：∴y=2x﹣5．（2）解：∵点M在一次函数y=2x﹣5上，∴设点M的坐标为（x，2x﹣5），∵MB=MC，∴解得：x=2.5，∴点M的坐标为（2.5，0）．【解析】【分析】（1）先求反比例函数关系式，由OA=OB，可求出B坐标，再代入一次函数解析式中求出解析式；（2）M点的纵坐标可用x 的式子表示出来，可套两点间距离公式，表示出MB、MC，令二者相等，可求出x .3．如图，P1、P2（P2在P1的右侧）是y= （k＞0）在第一象限上的两点，点A1的坐标为（2，0）．（1）填空：当点P1的横坐标逐渐增大时，△P1OA1的面积将________（减小、不变、增大）（2）若△P1OA1与△P2A1A2均为等边三角形，①求反比例函数的解析式；②求出点P2的坐标，并根据图象直接写在第一象限内，当x满足什么条件时，经过点P1、P2的一次函数的函数值大于反比例函数y= 的函数值．【答案】（1）减小（2）解：①如图所示，作P1B⊥OA1于点B，∵A1的坐标为（2，0），∴OA1=2，∵△P1OA1是等边三角形，∴∠P1OA1=60°，又∵P1B⊥OA1，∴OB=BA1=1，∴P1B= ，∴P1的坐标为（1，），代入反比例函数解析式可得k= ，∴反比例函数的解析式为y= ；②如图所示，过P2作P2C⊥A1A2于点C，∵△P2A1A2为等边三角形，∴∠P2A1A2=60°，设A1C=x，则P2C= x，∴点P2的坐标为（2+x， x），代入反比例函数解析式可得（2+x） x= ，解得x1= ﹣1，x2=﹣﹣1（舍去），∴OC=2+ ﹣1= +1，P2C= （﹣1）= ﹣，∴点P2的坐标为（ +1，﹣），∴当1＜x＜ +1时，经过点P1、P2的一次函数的函数值大于反比例函数y= 的函数值【解析】【解答】解：（1）当点P1的横坐标逐渐增大时，点P1离x轴的距离变小，而OA1的长度不变，故△P1OA1的面积将减小，故答案为：减小；【分析】（1）当点P1的横坐标逐渐增大时，点P1离x轴的距离变小，而OA1的长度不变，故△P1OA1的面积将减小；（2）①由A1的坐标为（2，0），△P1OA1是等边三角形，求出P1的坐标，代入反比例函数解析式即可；②由△P2A1A2为等边三角形，求出点P2的坐标，得出结论.4．如图，已知正比例函数y=2x和反比例函数的图象交于点A（m，﹣2）.（1）求反比例函数的解析式；（2）观察图象，直接写出正比例函数值大于反比例函数值时自变量x的取值范围；（3）若双曲线上点C（2，n）沿OA方向平移个单位长度得到点B，判断四边形OABC 的形状并证明你的结论.【答案】（1）解：设反比例函数的解析式为（k＞0）∵A（m，﹣2）在y=2x上，∴﹣2=2m，∴解得m=﹣1。

中考数学反比例函数-经典压轴题附答案解析

反比例函数压轴题精选(含标准答案)

中考反比例函数经典结论：如图，反比例函数k 的几何意义： (I ) 12AOB AOC S S k ∆∆==； (II ) OBAC S k =矩形。

下面两个结论是上述结论的拓展.(1) 如图①，OPA OCD S S ∆∆=，OPC PADC S S ∆=梯形(2)如图②，OAPB OBCA S S =梯形梯形，BPE S S ∆∆=经典例题例1.(1)(兰州)如图，已知双曲线(0)ky x x=>经过矩形OABC边AB 的中点F 且交BC 于点E ，四边形OEBF 的面积为2，则k = ；(2) 如图，点A B 、为直线y x =上的两点，过A B 、两点分别作y 轴的平行线交双曲线1(0)y x x=>于C D 、两点，若2BD AC =，则224OC OD -=例2．如果一个正比例函数的图象与一个反比例函数xy 6=的图象交),(),,(2211y x B y x A ，那么))((1212y y x x --值为 .例3．如图，一次函数b kx y +=的图象与反比例函数xm y =的图象交于点A ﹙－2，－5﹚，C ﹙5，n ﹚，交y 轴于点B ，交x 轴于点D ．(1) 求反比例函数xm y =和一次函数b kx y +=(2) 连接OA ，OC ．求△AOC 的面积．例4．如图，已知直线12y x =与双曲线(0)k y k x=>交于A B ，两点，且点A 的横坐标为4．（1）求k 的值；（2）若双曲线(0)k y k x=>上一点C 的纵坐标为8，求AOC △的面积；（3）过原点O 的另一条直线l 交双曲线(0)k y k x=>于P Q ，两点（P 点在第一象限），若由点A B P Q ，，，为顶点组成的四边形面积为24，求点P 的坐标．图2图4y例5.(山东淄博) 如图，正方形AOCB的边长为4，反比例函数的图象过点E（3，4）．（1）求反比例函数的解读式；过点D，与线段AB （2）反比例函数的图象与线段BC交于点D，直线1y x b2相交于点F，求点F的坐标；（3）连接OF，OE，探究∠AOF与∠EOC的数量关系，并证明．。

中考数学与反比例函数有关的压轴题附答案

中考数学与反比例函数有关的压轴题附答案一、反比例函数1．已知反比例函数y= 的图象经过点A（﹣，1）．（1）试确定此反比例函数的解析式；（2）点O是坐标原点，将线段OA绕O点顺时针旋转30°得到线段OB．判断点B是否在此反比例函数的图象上，并说明理由；（3）已知点P（m， m+6）也在此反比例函数的图象上（其中m＜0），过P点作x轴的垂线，交x轴于点M．若线段PM上存在一点Q，使得△OQM的面积是，设Q点的纵坐标为n，求n2﹣2 n+9的值．【答案】（1）解：由题意得1= ，解得k=﹣，∴反比例函数的解析式为y=﹣（2）解：过点A作x轴的垂线交x轴于点C．在Rt△AOC中，OC= ，AC=1，∴OA= =2，∠AOC=30°，∵将线段OA绕O点顺时针旋转30°得到线段OB，∴∠AOB=30°，OB=OA=2，∴∠BOC=60°．过点B作x轴的垂线交x轴于点D．在Rt△BOD中，BD=OB•sin∠BOD= ，OD= OB=1，∴B点坐标为（﹣1，），将x=﹣1代入y=﹣中，得y= ，∴点B（﹣1，）在反比例函数y=﹣的图象上（3）解：由y=﹣得xy=﹣，∵点P（m， m+6）在反比例函数y=﹣的图象上，其中m＜0，∴m（ m+6）=﹣，∴m2+2 m+1=0，∵PQ⊥x轴，∴Q点的坐标为（m，n）．∵△OQM的面积是，∴OM•QM= ，∵m＜0，∴mn=﹣1，∴m2n2+2 mn2+n2=0，∴n2﹣2 n=﹣1，∴n2﹣2 n+9=8．【解析】【分析】（1）由于反比例函数y= 的图象经过点A（﹣，1），运用待定系数法即可求出此反比例函数的解析式；（2）首先由点A的坐标，可求出OA的长度，∠AOC的大小，然后根据旋转的性质得出∠AOB=30°，OB=OA，再求出点B的坐标，进而判断点B是否在此反比例函数的图象上；（3）把点P（m， m+6）代入反比例函数的解析式，得到关于m的一元二次方程；根据题意，可得Q点的坐标为（m，n），再由△OQM的面积是，根据三角形的面积公式及m＜0，得出mn的值，最后将所求的代数式变形，把mn的值代入，即可求出n2﹣2 n+9的值．2．如图1，已知一次函数y=ax+2与x轴、y轴分别交于点A，B，反比例函数y= 经过点M．（1）若M是线段AB上的一个动点（不与点A、B重合）．当a=﹣3时，设点M的横坐标为m，求k与m之间的函数关系式．（2）当一次函数y=ax+2的图象与反比例函数y= 的图象有唯一公共点M，且OM= ，求a的值．（3）当a=﹣2时，将Rt△AOB在第一象限内沿直线y=x平移个单位长度得到Rt△A′O′B′，如图2，M是Rt△A′O′B′斜边上的一个动点，求k的取值范围．【答案】（1）解：当a=﹣3时，y=﹣3x+2，当y=0时，﹣3x+2=0，x= ，∵点M的横坐标为m，且M是线段AB上的一个动点（不与点A、B重合），∴0＜m＜，，DANG则，﹣3x+2= ，当x=m时，﹣3m+2= ，∴k=﹣3m2+2m（0＜m＜）（2）解：由题意得：，ax+2= ，ax2+2x﹣k=0，∵直线y=ax+2（a≠0）与双曲线y= 有唯一公共点M时，∴△=4+4ak=0，ak=﹣1，∴k=﹣，则，解得：，∵OM= ，∴12+（﹣）2=（）2，a=±（3）解：当a=﹣2时，y=﹣2x+2，∴点A的坐标为（1，0），点B的坐标为（0，2），∵将Rt△AOB在第一象限内沿直线y=x平移个单位得到Rt△A′O′B′，∴A′（2，1），B′（1，3），点M是Rt△A′O′B′斜边上一动点，当点M′与A′重合时，k=2，当点M′与B′重合时，k=3，∴k的取值范围是2≤k≤3【解析】【分析】（1）当a=﹣3时，直线解析式为y=﹣3x+2，求出A点的横坐标，由于点M的横坐标为m，且M是线段AB上的一个动点（不与点A、B重合）从而得到m的取值范围，由﹣3x+2= ,由X=m得k=﹣3m2+2m（0＜m＜）；（2）由ax+2= 得ax2+2x﹣k=0，直线y=ax+2（a≠0）与双曲线y= 有唯一公共点M时，△=4+4ak=0，ak=﹣1，由勾股定理即可；（3）当a=﹣2时，y=﹣2x+2，从而求出A、B两点的坐标，由平移的知识知A′，B′点的坐标，从而得到k的取值范围。

中考数学压轴题专题复习—反比例函数的综合含答案解析

一、反比例函数真题与模拟题分类汇编（难题易错题）1．如图，已知抛物线y=﹣x2+9的顶点为A，曲线DE是双曲线y= （3≤x≤12）的一部分，记作G1，且D（3，m）、E（12，m﹣3），将抛物线y=﹣x2+9水平向右移动a个单位，得到抛物线G2．（1）求双曲线的解析式；（2）设抛物线y=﹣x2+9与x轴的交点为B、C，且B在C的左侧，则线段BD的长为________；（3）点（6，n）为G1与G2的交点坐标，求a的值．（4）解：在移动过程中，若G1与G2有两个交点，设G2的对称轴分别交线段DE和G1于M、N两点，若MN＜，直接写出a的取值范围．【答案】（1）把D（3，m）、E（12，m﹣3）代入y= 得，解得，所以双曲线的解析式为y= ；（2）2（3）解：把（6，n）代入y= 得6n=12，解得n=2，即交点坐标为（6，2），抛物线G2的解析式为y=﹣（x﹣a）2+9，把（6，2）代入y=﹣（x﹣a）2+9得﹣（6﹣a）2+9=2，解得a=6± ，即a的值为6± ；（4）抛物线G2的解析式为y=﹣（x﹣a）2+9，把D（3，4）代入y=﹣（x﹣a）2+9得﹣（3﹣a）2+9=4，解得a=3﹣或a=3+ ；把E（12，1）代入y=﹣（x﹣a）2+9得﹣（12﹣a）2+9=1，解得a=12﹣2 或a=12+2；∵G1与G2有两个交点，∴3+ ≤a≤12﹣2 ，设直线DE的解析式为y=px+q，把D（3，4），E（12，1）代入得，解得，∴直线DE的解析式为y=﹣ x+5，∵G2的对称轴分别交线段DE和G1于M、N两点，∴M（a，﹣ a+5），N（a，），∵MN＜，∴﹣ a+5﹣＜，整理得a2﹣13a+36＞0，即（a﹣4）（a﹣9）＞0，∴a＜4或a＞9，∴a的取值范围为9＜a≤12﹣2 ．【解析】【解答】解：（2）当y=0时，﹣x2+9=0，解得x1=﹣3，x2=3，则B（﹣3，0），而D（3，4），所以BE= =2 ．故答案为2 ；【分析】（1）把D（3，m）、E（12，m﹣3）代入y= 得关于k、m的方程组，然后解方程组求出m、k，即可得到反比例函数解析式和D、E点坐标；（2）先解方程﹣x2+9=0得到B（﹣3，0），而D（3，4），然后利用两点间的距离公式计算DE的长；（3）先利用反比例函数图象上点的坐标特征确定交点坐标为（6，2），然后把（6，2）代入y=﹣（x ﹣a）2+9得a的值；（4）分别把D点和E点坐标代入y=﹣（x﹣a）2+9得a的值，则利用图象和G1与G2有两个交点可得到3+ ≤a≤12﹣2 ，再利用待定系数法求出直线DE的解析式为y=﹣ x+5，则M（a，﹣ a+5），N（a，），于是利用MN＜得到﹣ a+5﹣＜，然后解此不等式得到a＜4或a＞9，最后确定满足条件的a的取值范围．2．如图，已知直线y=x+k和双曲线y= （k为正整数）交于A，B两点．（1）当k=1时，求A、B两点的坐标；（2）当k=2时，求△AOB的面积；（3）当k=1时，△OAB的面积记为S1，当k=2时，△OAB的面积记为S2，…，依此类推，当k=n时，△OAB的面积记为S n，若S1+S2+…+S n= ，求n的值．【答案】（1）解：当k=1时，直线y=x+k和双曲线y= 化为：y=x+1和y= ，解得，，∴A（1，2），B（﹣2，﹣1）（2）解：当k=2时，直线y=x+k和双曲线y= 化为：y=x+2和y= ，解得，，∴A（1，3），B（﹣3，﹣1）设直线AB的解析式为：y=mx+n，∴∴，∴直线AB的解析式为：y=x+2∴直线AB与y轴的交点（0，2），∴S△AOB= ×2×1+ ×2×3=4；（3）解：当k=1时，S1= ×1×（1+2）= ，当k=2时，S2= ×2×（1+3）=4，…当k=n时，S n= n（1+n+1）= n2+n，∵S1+S2+…+S n= ，∴ ×（…+n2）+（1+2+3+…n）= ，整理得：，解得：n=6．【解析】【分析】（1）两图像的交点就是求联立的方程组的解；（2）斜三角形△AOB的面积可转化为两水平（或竖直）三角形（有一条边为水平边或竖直边的三角形称为水平或竖直三角形）的面积和或差；（3）利用n个数的平方和公式和等差数列的和公式可求出.3．如图，在平面直角坐标系xOy中，一次函数y=kx+b（k≠0）的图象与反比例函数的图象交于二四象限内的A、B 两点，与x轴交于C点，点B的坐标为（6，n），线段OA=5，E为x轴负半轴上一点，且sin∠AOE=．（1）求该反比例函数和一次函数的解析式；（2）求△AOC的面积；（3）直接写出一次函数值大于反比例函数值时自变量x的取值范围．【答案】（1）解：作AD⊥x轴于D，如图，在Rt△OAD中，∵sin∠AOD= = ，∴AD= OA=4，∴OD= =3，∴A（﹣3，4），把A（﹣3，4）代入y= 得m=﹣4×3=﹣12，所以反比例函数解析式为y=﹣；把B（6，n）代入y=﹣得6n=﹣12，解得n=﹣2，把A（﹣3，4）、B（6，﹣2）分别代入y=kx+b得，解得，所以一次函数解析式为y=﹣x+2（2）解：当y=0时，﹣x+2=0，解得x=3，则C（3，0），所以S△AOC= ×4×3=6（3）解：当x＜﹣3或0＜x＜6时，一次函数的值大于反比例函数的值【解析】【分析】（1）作AD⊥x轴于D，如图，先利用解直角三角形确定A（﹣3，4），再把A点坐标代入y= 可求得m=﹣12，则可得到反比例函数解析式；接着把B（6，n）代入反比例函数解析式求出n，然后把A和B点坐标分别代入y=kx+b得到关于a、b的方程组，再解方程组求出a和b的值，从而可确定一次函数解析式；（2）先确定C点坐标，然后根据三角形面积公式求解；（3）观察函数图象，找出一次函数图象在反比例函数图象上方所对应的自变量的范围即可．4．如图，在平面直角坐标系中，平行四边形的边，顶点坐标为，点坐标为 .（1）点的坐标是________，点的坐标是________（用表示）；（2）若双曲线过平行四边形的顶点和，求该双曲线的表达式；（3）若平行四边形与双曲线总有公共点，求的取值范围.【答案】（1）；（2）解：∵双曲线过点和点，∴，解得，∴点的坐标为，点的坐标为，把点的坐标代入，解得，∴双曲线表达式为（3）解：∵平行四边形与双曲线总有公共点，∴当点在双曲线，得到，当点在双曲线，得到，∴的取值范围 .【解析】【分析】（1）由四边形ABCD为平行四边形，得到A与B纵坐标相同，C与D纵坐标相同，横坐标相差2，得出B、C坐标即可；（2）根据B与D在反比例图象上，得到C与D横纵坐标乘积相等，求出b的值确定出B坐标，进而求出k的值，确定出双曲线解析式；（3）抓住两个关键点，将A坐标代入双曲线解析式求出b的值；将C坐标代入双曲线解析式求出b的值，即可确定出平行四边形与双曲线总有公共点时b的范围．5．阅读理解：配方法是中学数学的重要方法，用配方法可求最大（小）值。

反比例函数压轴题精选(含答案)

中考反比例函数经典结论：如图,反比例函数k 的几何意义： (I) 12AOB AOC S S k ∆∆==; (II) OBAC S k =矩形. 下面两个结论是上述结论的拓展.(1) 如图①,OPA OCD S S ∆∆=,OPC PADC S S ∆=梯形.(2)如图②,OAPB OBCA S S =梯形梯形,BPE ACE S S ∆∆=.经典例题例 1.(1)(兰州)如图,已知双曲线(0)k y x x=>经由矩形OABC 边AB 的中点F 且交BC 于点E ,四边形OEBF 的面积为2,则k = 2 ;(2)如图,点A B 、为直线y x =上的两点,过A B 、两点分离作y 轴的平行线交双曲线1(0)y x x=>于C D 、两点,若2BD AC =,则224OC OD -= 6 例2．(陕西)假如一个正比例函数的图象与一个反比例函数xy 6=的图象交),(),,(2211y x B y x A ,那么))((1212y y x x --值为 24 .解析：因为A,B 在反比例函数xy 6=上,所以611=y x ,我们知道正比例函数与反比例函数的交点坐标关于原点成中间对称,是以),(),,(2211y x B y x A 中有1212,y y x x -=-=,所以24644))(())((1111111212=⨯==----=--y x y y x x y y x x例3．(山东威海)如图,一次函数b kx y +=的图象与反比例函数xm y =的图象交于点A ﹙－2,－5﹚,C ﹙5,n ﹚,交y 轴于点B,交x 轴于点D ．(1) 求反比例函数xm y =和一次函数b kx y +=(2) 衔接OA,OC ．求△AOC 的面积．解：(1)∵反比例函数xm y =的图象经由点A ﹙－2,－5﹚,∴m=(－2)×( －5)＝10．∴反比例函数的表达式为xy 10=．∵点C ﹙5,n ﹚在反比例函数的图象上,∴2510==n ．∴C 的坐标为﹙5,2﹚．∵一次函数的图象经由点A,C,将这两个点的坐标代入b kx y +=,得⎩⎨⎧+=+-=-.5225b k b k ，解得⎩⎨⎧-==.31b k ， ∴所求一次函数的表达式为y ＝x －3．(2) ∵一次函数y=x －3的图像交y 轴于点B,∴B 点坐标为﹙0,－3﹚．∴OB＝3．∵A 点的横坐标为－2,C 点的横坐标为5,∴S△AOC= S△AOB+ S△BOC=()22152215212-21=+⋅⋅=⋅⋅+⋅⋅OB OB OB ．例4．（福建福州）如图,已知直线12y x =与双曲线(0)k y k x=>交于A B ，两点,且点A 的横坐标为4．（1）求k 的值;（2）若双曲线(0)k y k x=>上一点C 的纵坐标为8,求AOC △的面积;（3）过原点O 的另一条直线l 交双曲线(0)k y k x=>于P Q ，两点（P 点在第一象面积为24,限）,若由点A B P Q ，，，为极点构成的四边形求点P 的坐标．解：（1）点A 横坐标为4,∴当4x =时,2y =．∴点A 的坐标为(42)，．点A 是直线12y x =与双曲线(0)k y k x=>的交点,428k ∴=⨯=．（2）解法一：如图1,点C 在双曲线上,当8y =时,1x =∴点C 的坐标为(18)，．过点A C ，分离做x 轴,y 轴的垂线,垂足为M N ，,得矩形DMON ．32ONDM S =矩形,4ONC S =△,9CDA S =△,4OAM S =△．3249415AOC ONC CDA OAM ONDM S S S S S =---=---=△△△△矩形解法二：如图2,过点C A ，分离做x 轴的垂线,垂足为E F ，,点C 在双曲线8y x=上,当8y =时,1x =．∴点C 的坐标为(18)，．点C ,A 都在双曲线8y x=上,4COEAOF S S ∴==△△COE COA AOF CEFA S S S S ∴+=+△△△梯形．COA CEFA S S ∴=△梯形．1(28)3152CEFA S =⨯+⨯=梯形,15COA S ∴=△．（3）反比例函数图象是关于原点O OP OQ ∴=,OA OB =．∴四边形APBQ 是平行四边形． 1124644POA APBQ S S ∴==⨯=△平行四边形．设点P 横坐标为(04)m m m >≠且,得8()P m m，．过点P A ，分离做x 轴的垂线,垂足为E F ，, 点P A ，在双曲线上,4PQE AOF S S ∴==△△．若04m <<,如图3,POE POA AOF PEFA S S S S +=+△△△梯形,6POA PEFA S S ∴==△梯形．182(4)62m m ⎛⎫+-= ⎪⎝⎭∴·．解得2m =,8m =-（舍去）．∴(24)P ，．若4m >,如图4,AOF AOP POE AFEP S S S S +=+△△△梯形,图2图3图46POA PEFA S S ∴==△梯形．182(4)62m m ⎛⎫∴+-= ⎪⎝⎭,解得8m =,2m =-（舍去）．(81)P ∴，． ∴点P 的坐标是(24)P ，或(81)P ，．例 5.(山东淄博) 如图,正方形AOCB 的边长为4,反比例函数的图象过点E （3,4）．（1）求反比例函数的解析式;（2）反比例函数的图象与线段BC 交于点D,直线1yx b 2过点D,与线段AB 订交于点F,求点F 的坐标;（3）衔接OF,OE,探讨∠AOF 与∠EOC 的数目关系,并证实．【答案】解：（1）设反比例函数的解析式k yx , ∵反比例函数的图象过点E （3,4）,∴k 43,即k=12.∴反比例函数的解析式12yx. （2）∵正方形AOCB 的边长为4,∴点D 的横坐标为4,点F 的纵坐标为4.∵点D 在反比例函数的图象上,∴点D 的纵坐标为3,即D （4,3）. ∵点D 在直线1y x b 2上,∴134b 2,解得b=5.∴直线DF 为1yx 52.将y4代入1yx 52,得14x 52,解得x 2.∴点F 的坐标为（2,4）.（3）∠AOF＝12∠EOC.证实如下：在CD 上取CG=CF=2,衔接OG,衔接EG 并延伸交ｘ轴于点H.∵AO=CO=4,∠OAF=∠OCG=900,AF=CG=2, ∴△OAF≌△OCG（SAS ）.∴∠AOF=∠COG. ∵∠EGB=∠HGC,∠B=∠GCH=900,BG=CG=2,∴△EGB≌△HGC（AAS ）.∴EG=HG. 设直线EG ：ymxn ,∵E（3,4）,G （4,2）,∴43m n 24m n =+⎧⎨=+⎩,解得,m 2n=10=⎧⎨⎩－. ∴直线EG ：y 2x10.令y2x10=0,得x 5.∴H（5,0）,OH=5.在R ｔ△AOF 中,AO=4,AE=3,依据勾股定理,得OE=5.∴OH=OE.∴OG 是等腰三角形底边EH 上的中线.∴OG 是等腰三角形顶角的等分线. ∴∠EOG=∠GOH.∴∠EOG=∠GOC=∠AOF,即∠AOF＝12∠EOC.例 6.(山东威海)一次函数y ax b =+的图象分离与x 轴.y 轴交于点,M N ,与反比例函数ky x=的图象订交于点,A B ．过点A 分离作AC x ⊥轴,AE y ⊥轴,垂足分离为,C E ;过点B 分离作BF x ⊥轴,BD y ⊥轴,垂足分离为F D ，，AC 与BD 交于点K ,衔接CD ．（1）若点A B ，在反比例函数k y x=的图象的统一分支上,如图1,试证实： ①AEDK CFBK S S =四边形四边形; ②AN BM =．（2）若点A B ，分离在反比例函数k y=的图象的不合分支上,如图2,则AN 与BM还相等吗？试证实你的结论．解：（1）①AC x ⊥轴,AE y ⊥BF x ⊥轴,BD y ⊥轴,∴四边形AC x ⊥轴,BD y ⊥轴,∴四边形1111OC x AC y x y k ===，，,∴11AEOC S OC AC x y k ===矩形 2222OF x FB y x y k ===，，,∴22BDOF S OF FB x y k ===矩形．∴AEOC BDOF S S =矩形矩形．AEDK AEOC DOCK S S S =-矩形矩形矩形,CFBK BDOF DOCK S S S =-矩形矩形矩形,∴AEDK CFBK S S =矩形矩形)②由（1）知AEDK CFBK S S =矩形矩形．∴AK DK BK CK =．∴AK BKCK DK= 90AKB CKD ∠=∠=°,∴AKB CKD △∽△．∴CDK ABK ∠=∠．∴AB CD∥AC y ∥轴,∴四边形ACDN 是平行四边形．∴AN CD =．同理BM CD =．AN BM ∴=．（2）AN 与BM 仍然相等．AEDK AEOC ODKC S S S =+矩形矩形矩形,BKCF BDOF ODKC S S S =+矩形矩形矩形,又AEOC BDOF S S k ==矩形矩形,∴AEDK BKCF S S =矩形矩形∴AK DK BK CK =．∴CK DKAK BK=．K K ∠=∠,∴CDK ABK △∽△．∴CDK ABK ∠=∠．∴AB CD ∥．AC y ∥轴,∴四边形ANDC 是平行四边形．∴AN CD =．同理BM CD =．∴AN BM =．第一部分演习一.选择题1.(鄂州)如图,直线y=mx 与双曲线y=xk 交于A.B 两点,过点A 作AM⊥x 轴,垂足为M,贯穿连接BM,若ABM S ∆=2,则k 的值是2.(兰州) 如图,若正方形OABC 的极点B 和正方形ADEF 的极点E 都在函数1y x=（0x >）的图象上,则点E 的坐标是（,）.3.(泰安）如图,双曲线)0(＞k xk y =经由矩形OABC 的边BC 的中点E, 交AB 于点D.若梯形ODBC 的面积为3,则双曲线的解析式为A ．xy 1=B ．xy 2= C ．x y 3=D ．xy 6=OAB4.（仙桃）如图,已知双曲线)0k (xk y ＞=经由直角三角形斜边OB 的中点D,与直角边AB 订交于点C ．若△OBC 的面积为3,则k ＝____________．OC D KF E N yxABM图2xyABO1S2Sy xO P 1P 2P 3P 4 P 5A 1 A 2 A 3 A 4 A 52x 5.(牡丹江市)如图,点A .B 是双曲线3y x=上的点,分离经由A .B 两点向x 轴.y 轴作垂线段,若1S =阴影，则12S S +=．6.（莆田）如图,在x 轴的正半轴上依次截取112233445OA A A A A A A A A ====,过点12345A A A A A 、、、、分离作x 轴的垂线与反比例函数()20y x x=≠的图象订交于点12345P P P P P 、、、、,得直角三角形1112233344455OPA A P A A P A A P A A P A 2、、、、，并设其面积分离为12345S S S S S 、、、、，则5S 的值为．．第4题图第5题图第6题图7.（包头）已知一次函数1y x =+与反比例函数ky x =的图象在第一象限订交于点A ,与x 轴订交于点C AB x ，⊥轴于点B ,AOB △的面积为1,则AC 的长为8.（嵊州市）如图,直线)0(<=k kx y 与双曲线xy 2-=交于),(),,(2211y x B y x A 两点,则122183y x y x -的值为A.－5 B.－10 C.5 D.10【答案】B9.（江苏无锡）如图,已知梯形ABCO 的底边AO 在x 轴上,BC∥AO,AB⊥AO,过点C 的双曲线ky x=交OB 于D,且OD ：DB=1:2,若△OBC 的面积等于3,则k 的值A ．等于2 B ．等于34C ．等于245D ．无法肯定【答案】B第7题图第8题图第9题图10.（江苏盐城）如图,A.B 是双曲线y= kx(k>0) 上的点,A.B 两点的横坐标分离是a.2a,线段AB 的延伸线交x 轴于点C,若S△AOC=6．则k=．【答案】4 11.（安徽蚌埠二中）已知点（1,3）在函数)0(>=x xk y 的图像上.正方形ABCD 的边BC 在x 轴上,点E 是对角线BD 的中点,函数)0(>=x x k y 的图像又经由A .E 两点,则点E 的横坐标为__________.612.（四川内江）如图,反比例函数y ＝kx(x ＞0)的图象经由矩形OABC 对角线的交点M,分离与AB.BC 订交于点D.E ．若四边形ODBE 的面积为6,则k 的值为y O AC B yBAoO ABCDxy图6yx O BC AAB C D E yxOMA ．1B ．2C ．3D ．4【答案】B第10题图第11题图第12题图13.（山东东营）如图,直线l 和双曲线(0)k y k x=>交于A.B 亮点,P 是线段AB 上的点（不与A.B 重合）,过点A.B.P 分离向x 轴作垂线,垂足分离是C.D.E,衔接OA.OB.OP,设△AOC 面积是S1.△BOD 面积是S2.△POE 面积是S3.则 A. S1＜S2＜S3B. S1>S2>S3C. S1=S2>S3D. S1=S2<S3 【答案】D①x＜0时,x2y =,②△OPQ 的面积为定值, ③x＞0时,y 随x 的增大而增大 ④MQ=2PM⑤∠POQ 可以等于90°个中准确的结论是A ．①②④B②④⑤C．③④⑤D．②③⑤ 【答案】B15.（甘肃兰州,15,4分）如图,矩形ABCD 的对角线BD 经由坐标原点,矩形的边分离平行于坐标轴,点C 在反比例函数221k k y x++=的图象上.若点A 的坐标为（－2,－2）,则k 的值为A ．1B ．－3C ．4D ．1或－3【答案】D轴于A.B 16.（四川乐山）如图,直线6y x =-交x 轴.y 直线下两点,P 是反比例函数4(0)y x x=>图象上位于xyOABCD方的一点,过点P 作x 轴的垂线,垂足为点M,交AB 于点E,过点P 作y 轴的垂线,垂足为点N,交AB 于点F.则AF BE ⋅= A ．8 B ．6 C ．4 D ．62 【答案】A17.（•德州）如图,两个反比例函数和的图象分离是l1和l2．设点P在l1上,PC⊥x 轴,垂足为C,交l2于点A,PD⊥y 轴,垂足为D,交l2于点B,则三角形PAB 的面积为A ． 3B ． 4C ．D ．5 解解：∵点P 在y=上,∴设P 的坐标是（a,）, ∵PA ⊥x 轴,∴A 的横坐标是a,∵A 在y=﹣上,∴A 的坐标是（a,﹣）, ∵PB ⊥y 轴,∴B 的纵坐标是, ∵B 在y=﹣上,∴代入得：﹣, 解得：x=﹣2a,∴B 的坐标是（﹣2a,）, ∴PA=﹣（﹣）=,PB=a ﹣（﹣2a ）=3a, ∵PA ⊥x 轴,PB ⊥y 轴,x 轴⊥y 轴,∴PA ⊥PB,∴△PAB 的面积是：PA ×PB=××3a=．故选C ．18.（福州）如图,过点C(1,2)分离作x 轴.y 轴的平行线,交直线y ＝－x ＋6于A. B 两点,若反比例函数y ＝kx (x ＞0)的图像与△ABC 有公共点,则k 的取值规模是A ．2≤k≤9 B．2≤k≤8C ．2≤k≤5D ．5≤k≤8 解答：解：∵点C(1,2),BC∥y 轴,AC∥x 轴,ABCOxy∴当x ＝1时,y ＝－1＋6＝5,当y ＝2时,－x ＋6＝2,解得x ＝4, ∴点A.B 的坐标分离为A(4,2),B(1,5),依据反比例函数系数的几何意义,当反比例函数与点C 订交时,k ＝1×2＝2最小,设与线段AB 订交于点(x,－x ＋6)时k 值最大,则k ＝x(－x ＋6)＝－x2＋6x ＝－(x －3)2＋9,∵ 1≤x≤4,∴当x ＝3时,k 值最大,此时交点坐标为(3,3), 是以,k 的取值规模是2≤k≤9．故选A ．19.（临沂）如图,若点M 是x 轴正半轴上随意率性一点,过点M 作PQ∥y 轴,分离交函数1(0)k y x x =>和2(0)ky x x=>的图象于点P 和Q,衔接OP 和OQ ．则下列结论准确的是A ．∠POQ 不成能等于90°B．12k PM QM k = C ．这两个函数的图象必定关于x 轴对称; D ．△POQ 的面积是()1212k k + 故选：D ．20.（湖北黄石）如图所示,已知11(,)2A y ,2(2,)B y 为反比例函数1y x=图像上的两点,动点(,0)P x 在x 正半轴上活动,当线段AP 与线段BP 之差达到最大时,点P 的坐标是DA. 1(,0)2B. (1,0)C. 3(,0)2D. 5(,0)2【解答】解：∵把A （1/2 ,y1）,B （2,y2）代入反比例函数y=1/ x 得：y1=2,y2=1/2 ,yxOABP∴A（1/2 ,2）,B （2,1/2 ）,∵在△ABP 中,由三角形的三边关系定理得：|AP－BP|＜AB,∴延伸AB 交x 轴于P′,当P 在P′点时,PA－PB=AB,即此时线段AP 与线段BP 之差达到最大,设直线AB 的解析式是y=kx+b,把 A.B 的坐标代入得： 2=1/2k+b ,1/2=2k+b,解得：k=－1,b=5/2 ,∴直线AB 的解析式是y=－x+5/2 ,当y=0时,x=5/2 ,即P （5/2 ,0）,故选D ．21.(湖北随州)如图,直线l 与反比例函数x y 2=的图象在第一象限内交于A.B 两点,交x 轴的正半轴于C 点,若AB ：BC=(m 一l)：1(m>l)则△OAB 的面积(用m 暗示)为A.m m 212-B.mm 12- C. m m )1(32- D.m m 2)1(32- 答案：B22.（江苏姑苏）如图,菱形OABC 的极点C 的坐标为(3,4),极点A 在x 轴的正半轴上．反比例函数y ＝k x(x ＞0)的图象经由极点B,则k 的值为A ．12B ．20C ．24D ．32【答案】D ．解：过C 点作CD⊥x 轴,垂足为D ．B AoxylO xyB A C∵点C 的坐标为（3,4）,∴OD=3,CD=4．∴OC= OD2+CD2=32+42=5．∴OC=BC=5．∴点B 坐标为（8,4）, ∵反比例函数y=k x（x ＞0）的图象经由极点B,∴k=32．23.（山东临沂）如图,等边三角形OAB 的一边OA 在x 轴上,双曲线y ＝3x在第一象限内的图象经由OB 边的中点C,则点B 的坐标是 A ．（1,3）B ．（3,1）C ．（2,23）D ．（23,2）【答案】：C ．24.(湖北孝感）如图,函数y=﹣x 与函数的图象订交于A,B 两点,过A,B 两点分离作y 轴的垂线,垂足分离为点C,D ．则四边形ACBD 的面积为A ．2 B ．4 C ． 6 D ．8 解答：解：∵过函数的图象上A,B 两点分离作y 轴的垂线,垂足分离为点C,D,∴S △AOC=S △ODB=|k|=2, 又∵OC=OD,AC=BD,∴S △AOC=S △ODA=S △ODB=S △OBC=2, ∴四边形ABCD 的面积为：S △AOC+S △ODA+S △ODB+S △OBC=4×2=8．故选D ．25.（四川内江）如图,反比例函数（x ＞0）的图象经由矩形OABC 对角线的交点M,分离于AB.BC 交于点D.E,若四边形ODBE 的面积为9,则k 的值为A ． 1B ．2 C ．3 D ．4 解答：解：由题意得：E.M.D 位于反比例函数图象上,则S △OCE=,S △OAD=,过点M 作MG ⊥y 轴于点G,作MN ⊥x 轴于点N,则S □ONMG=|k|,又∵M 为矩形ABCO 对角线的交点, ∴S 矩形ABCO=4S □ONMG=4|k|, 因为函数图象在第一象限,k ＞0,则++9=4k, 解得：k=3．故选C ．26.(四川乐山)如图,已知第一象限内的点A 在反比例函数y = 2x 的图象上,第二象限内的点B 在反比例函数y = k x 的图象上,且OA⊥0B,cotA= 33,则k 的值为A ．－3 B.－6 C.－ 3 D.－2 3 在第一象27.（黔东南州）如图,直线y=2x 与双曲线y=限的交点为A,过点A 作AB⊥x 轴于B,将△ABO 绕点O 扭转90°,得到△A′B′O,则点A′的坐标为A.()1,0B. ()1,0或()1,0-C. ()2,0或()0,2-D. ()2,1-或()2,1-解答：解：联立直线与反比例解析式得：,消去y 得到：x2=1,解得：x=1或﹣1,∴y=2或﹣2, ∴A （1,2）,即AB=2,OB=1,依据题意画出响应的图形,如图所示,可得A ′B ′=A ′′B ′′=AB=2,OB ′=OB ′′=OB=1,依据图形得：点A ′的坐标为（﹣2,1）或（2,﹣1）．故选D ．Ox y ABC28. （•威海）如图,在平面直角坐标系中,∠AOB=90°,∠OAB=30°,反比例函数的图象经由点A,反比例函数的图象经由点B,则下列关于m,n 的关系准确的是（）A ． m =﹣3nB ． m =﹣nC ．m=﹣nD ．m=n解答：解：过点B 作BE ⊥x 轴于点E,过点A 作AF ⊥x 轴于点F,设点B 坐标为（a,）,点A 的坐标为（b,）,∵∠OAB=30°,∴OA=OB,设点B 坐标为（a,）,点A 的坐标为（b,）,则OE=﹣a,BE=,OF=b,AF=,∵∠BOE+∠OBE=90°,∠AOF+∠BOE=90°, ∴∠OBE=∠AOF,又∵∠BEO=∠OFA=90°, ∴△BOE ∽△OAF,∴==,即==,解得：m=﹣ab,n=,故可得：m=﹣3n ．故选A ．二.填空题1.（湖北武汉）如图,直线y ＝33x b -+与y 轴交于点A,与双4,则k曲线y ＝k x在第一象限交于点B,C 两点,且AB ⋅AC ＝＝．答案：3（0x >）交2.（福建德化）如图,直线43y x =与双曲线ky x =于点A ．将直线43y x =向下平移个6单位后,与双曲线k y x=（0x >）交于点B ,与x 轴交于点C,则C 点的坐标为___________;若2AO BC=,则k =．【答案】（)0,29,123.（湖南衡阳）如图,已知双曲线)0k (xk y ＞=经由直角三角形OAB 斜边OB 的中点D,与直角边AB 订交于点C ．若△OBC 的面积为3, 则k ＝____________．【答案】24.（宁波市）如图,正方形A1B1P1P2的极点P1.P2在反比例函数y ＝2x （x ＞0）的图像上,极点A1.B1分离在x 轴和y 轴的正半轴上,再在其右侧作正方形P2P3A2B2,极点P3在反比例函数y ＝2x （x ＞0）的图象上,极点A3在x 轴的正半轴上,则点P3的坐标为【答案】（3＋1,3－1）5.（安徽芜湖）如图,在平面直角坐标系中有一正方形AOBC,半径为反比例函数k y x=经由正方形AOBC 对角线的交点,（422）的圆内切于△ABC,则k 的值为．【答案】46.（湖北武汉市）如图,ABCD 的极点A,B 的坐标分离是A AD 交（－1,0）,B （0,－2）,极点C,D 在双曲线y=xk 上,边y 轴于点E,且四边形BCDE 的面积是△ABE 面积的5倍,则k=_____．【答案】12在双曲7.（湖北孝感）如图,点A 在双曲线1y x上,点B ABCD 的线3yx上,且AB∥x 轴,C.D 在x 轴上,若四边形面积为矩形,则它的面积为. 【答案】2xy第16题图BCEDoQ PA xy第16题图HF BCEDoQ PA 8.（湖北荆州,16,4分）如图,双曲线2(0)yx x经由四边形OABC 的极点A.C,∠ABC＝90°,OC等分OA 与x 轴正半轴的夹角,AB∥x 轴,将△ABC 沿AC 翻折后得到△AB＇C,B ＇点落在OA 上,则四边形OABC 的面积是.【答案】29.（浙江温州）如图,已知动点A 在函数点C,延4=y x(x>o)的图象上,AB⊥x 轴于点B,AC⊥y 轴于伸CA 至点D,使AD=AB,延伸BA 至点Ｅ,使AE=AC.直线DE 分离交x 轴,y 轴于点P,Q.当QE ：DP=4:9时,图中的暗影部分的面积等于____________. 如图,作EF⊥y 轴,DH⊥x 轴,由题意得：△QEF∽△DHP,∵QE：DP=4:9设AC= a,则AB=4a,49EF HP ,HP=94a ,∵△AED∽△DHP,∴424648==,==49934EA AD a a a a a DH HP a 得到：得：得：S暗影=2218+2a a=413+3=33） 10.（•聊城）如图,在直角坐标系中,正方形的中间在原点O,且正方形的一组对边与x 轴平行,点P （3a,a ）是反比例函数y=（k ＞0）的图象上与正方形的一个交点．若图中暗影部分的面积等于9,则这个反比例函数的解析式为．解答：解答：解：∵反比例函数的图象关于原点对称,∴暗影部分的面积和正好为正方形面积的,设正方形的边长为b ,则b 2=9,解得b =6,∵正方形的中间在原点O , ∴直线AB 的解析式为：x =3, ∵点P （3a ,a ）在直线AB 上, ∴3a =3,解得a =1,∴P （3,1）, ∵点P 在反比例函数y =（k ＞0）的图象上,∴k=3, ∴此反比例函数的解析式为：y=．故答案为：y=的图象交11.（•衢州）如图,已知函数y=2x和函数于A.B两点,过点A作AE⊥x轴于点E,若△AOE的面积为4,P是坐标平面上的点,且以点B.O.E.P为极点的四边形是平行四边形,则知足前提的P点坐标是P1（0,﹣4）P2（﹣4,﹣4）P3（4,4）解答：解：如图∵△AOE的面积为4,函数的图象过一.三象限,∴k=8,∵函数y=2x和函数的图象交于A.B两点,∴A.B两点的坐标是：（2,4）（﹣2,﹣4）,∵以点B.O.E.P为极点的平行四边形共有3个,∴知足前提的P点有3个,分离为：P1（0,﹣4）,P2（﹣4,﹣4）,P3（4,4）．故答案为：P1（0,﹣4）,P2（﹣4,﹣4）,P3（4,4）．12.(甘肃兰州)如图,M为双曲线y＝3x上的一点,过点M作x轴.y轴的垂线,分离交直线y＝－x＋m于点D.C两点,若直线y＝－x＋m与y轴交于点A,与x 轴订交于点B,则AD•BC的值为．解答：解：作CE⊥x轴于E,DF⊥y轴于F,如图,对于y＝－x＋m,令x＝0,则y＝m;令y＝0,－x＋m＝0,解得x＝m,∴A(0,m),B(m,0),∴△OAB等腰直角三角形,∴△ADF和△CEB都是等腰直角三角形,设M的坐标为(a,b),则ab＝,CE＝b,DF＝a,∴AD＝DF＝a,BC＝CE＝b,∴AD•BC＝a•b＝2ab＝2．故答案为2．13.（.深圳）如图,双曲线ky(k0)x=>与⊙O在第一象限内交于P.Q两点,分离过P.Q 两点向x 轴和y 轴作垂线,已知点P 坐标为(1,3),则图中暗影部分的面积为．【答案】4.【剖析】∵⊙O 在第一象限关于y=x 对称,k y (k 0)x=>也关于y=x 对称,P 点坐标是（1,3）,∴Q 点的坐标是（3,1）,∴S 暗影=1×3+1×3－2×1×1=4.14.(•扬州)如图,双曲线y ＝经由Rt△OMN 斜边上的点A,与直角边MN 订交于点B,已知OA ＝2AN,△OAB 的面积为5,则k 的值是 12 ．解答：过A 点作AC ⊥x 轴于点C,如图,则AC ∥NM,∴△OAC ∽△ONM,∴OC ：OM ＝AC ：NM ＝OA ：ON,而OA ＝2AN,即OA ：ON ＝2：3,设A 点坐标为(a,b),则OC ＝a,AC ＝b, ∴OM ＝a,NM ＝b,∴N 点坐标为(a,b), ∴点B 的横坐标为a,设B 点的纵坐标为y, ∵点A 与点B 都在y ＝图象上,∴k ＝ab ＝a •y, ∴y ＝b,即B 点坐标为(a,b),∵OA ＝2AN,△OAB 的面积为5,∴△NAB 的面积为, ∴△ONB 的面积＝5＋＝,∴NB •OM ＝,即×(b －b)×a ＝,∴ab ＝12,∴k ＝12．故答案为12．15.（武汉）如图,点A 在双曲线y=的第一象限的那一支上,AB 垂直于x 轴与点B,点C 在x 轴正半轴上,且OC=2AB,点E 在线段AC 上,且AE=3EC,点D 为OB 的中点,若△ADE 的面积为3,则k 的值为．解答：解：连DC,如图,C∵AE=3EC,△ADE 的面积为3,∴△CDE 的面积为1, ∴△ADC 的面积为4,设A 点坐标为（a,b ）,则AB=a,OC=2AB=2a,而点D 为OB 的中点,∴BD=OD=b,∵S 梯形OBAC=S△ABO+S△ADC+S△ODC,∴（a+2a ）×b=a×b+4+×2a×b,∴ab=, 把A （a,b ）代入双曲线y=,∴k=ab=．16.(成都)如图,在平面直角坐标系xOy 中,直线AB 与x 轴.y 轴分离交于点A,B, 与反比例函数k y x=(k 为常数,且0k >)在第一象限的图象交于点E,F ．过点E 作EM⊥y 轴于M,过点F 作FN⊥x 轴于N,直线EM 与FN 交于点C ．若BE 1BF m=(m 为大于l的常数)．记△CEF 的面积为1S ,△OEF 的面积为2S ,则12S S=________． (用含m 的代数式暗示) 答案：11m m （k 的几何意义,线段比的转化,面积的几种求法）17.（湖北黄冈）已知反比例函数y ＝6x在第一象限的图象如图所示,点A 在其图象上,点B 为x 轴正半轴上一点,衔接AO.AB,且AO ＝AB,则S△AOB＝．【答案】6．【解析】如下图,过点A 作AC⊥OB 于点C,∵AO＝AB,∴OC＝BC ．而AC ＝AC,AO ＝AB,∴△AOC≌△ABC．∴S△AOC＝S△ABC．设点A 的坐标为(x,y)(x ＞0,y ＞0),则xy ＝6,AC ＝y,OC ＝x,∴S△AOB＝2S△AOC＝2×12×OC·AC＝xy ＝6．18.（四川宜宾）如图,直线x y 34=与双曲线)0(>=x x k y 交于点A,将直线x y 34=向右平移29个单位后,与双曲线)0(>=x x k y 交于点B,与x 轴交于点C,若2=BCAO,则k=．【答案】12．【解析】起首求出平移后直线的解析式,然后直线x y 34=与双曲线)0(>=x xk y 两解析式联立方程组求出点A 的纵坐标,平移后的直线解析式x y 34=－6与双曲线)0(>=x xky 两解析式联立方程组,求出点B 的纵坐标,依据类似三角形对应边成比例的性质可得A.B 的纵坐标的比等于AO ：BC,然后列出方程求解即可．19.（四川泸州）如图,()111P ,x y ,()222P ,x y ,……()P ,n n n x y 在函数()10y x x=>的图像上,11P OA ∆,212P A A ∆,323P A A ∆,……1P A A n n n -∆都是等腰直角三角形,斜边1OA .12A A .23A A ,……1A A n n -都在x 轴上（n是大于或等于2的正整数）,则点3P 的坐标是;点n P 的坐标是（用含n 的式子暗示）．【答案】;【解析】过点P1作P1E⊥x 轴于点E,过点P2作P2F⊥x 轴于点F,过点P3作P3G⊥x 轴于点G,依据△P1OA1,△P2A1A2,△P3A2A3都是等腰直角三角形,可求出P1,P2,P3的坐标,从而总结出一般纪律得出点Pn 的坐标．21.（山东日照）如右图,直线AB 交双曲线xk y =于Ａ.B,交x 轴于点C,B 为线段AC 的中点,过点B 作BM⊥x 轴于M,贯穿连接OA.若OM=2MC,S⊿OAC=12.则k 的值为___________. 【答案】8【解析】过点A 作AD⊥x 轴于点D,则△ADO 的面积为21k,∵BM⊥x 轴,∴AD∥BM, ∵B 为线段AC 的中点,∴BM 为△ADC 的中位线,∴DM=MC, ∵OM=2MC, ∴OD=DM=MC.∴S⊿OAC=3S⊿OAD,=12=k 23,∴k=8.22.（•宁波）如图,等腰直角三角形ABC极点A在x轴上,∠BCA=90°,AC=BC=2,反比例函数y=（x＞0）的图象分离与AB,BC交于点D,E．贯穿连接DE,当△BDE∽△BCA时,点E的坐标为．【答案】．（,）．【解析】如图,∵∠BCA=90°,AC=BC=2,反比例函数y=（x＞0）的图象分离与AB,BC交于点D,E,∴∠BAC=∠ABC=45°,且可设E（a,）,D（b,）,∴C（a,0）,B（a,2）,A（2﹣a,0）,∴易求直线AB的解析式是：y=x+2﹣a．又∵△BDE∽△BCA,∴∠BDE=∠BCA=90°,∴直线y=x与直线DE垂直,=,即ab=3．∴点D.E关于直线y=x对称,则又∵点D在直线AB上,∴=b+2﹣a,即2a2﹣2a﹣3=0,解得,a=,∴点E的坐标是（,）．23.（•自贡）如图,在函数的图象上有点P1.P2.P3….Pn.Pn+1,点P1的横坐标为2,且后面每个点的横坐标与它前面相邻点的横坐标的差都是2,过点P1.P2.P3….Pn.Pn+1分离作x轴.y轴的垂线段,构成若干个矩形,如图所示,将图中暗影部分的面积从左至右依次记为S1.S2.S3….Sn,则S1=4 ,Sn=．（用含n的代数式暗示）解答：解：当x=2时,P1的纵坐标为4,当x=4时,P2的纵坐标为2,当x=6时,P3的纵坐标为, 当x=8时,P4的纵坐标为1, 当x=10时,P5的纵坐标为：, 则S1=2×（4﹣2）=4=2[﹣]; S2=2×（2﹣）=2×=2[﹣]; S3=2×（﹣1）=2×=2[﹣];Sn=2[﹣]=;故答案为：4,．24.（•遵义）如图,已知直线y=x 与双曲线y=（k ＞0）交于A.B 两点,点B 的坐标为（﹣4,﹣2）,C 为双曲线y=（k ＞0）上一点,且在第一象限内,若△AOC 的面积为6,则点C 的坐标为（2,4）．解答：解：∵点B （﹣4,﹣2）在双曲线y=上,∴=﹣2,∴k=8, 依据中间对称性,点A.B 关于原点对称,所以,A （4,2）, 如图,过点A 作AE ⊥x 轴于E,过点C 作CF ⊥x 轴于F,设点C 的坐标为（a,）,则S △AOC=S △COF+S 梯形ACFE ﹣S △AOE=×8+×（2+）（4﹣a ）﹣×8,=4+﹣4,=,∵△AOC 的面积为6,∴=6,整顿得,a2+6a ﹣16=0,解得a1=2,a2=﹣8（舍去）,∴==4,∴点C 的坐标为（2,4）．故答案为：（2,4）．25.(武汉)如图,已知四边形ABCD 是平行四边形,BC ＝2AB,A,B 两点的坐标分离是（－1,0）,（0,2）,C,D 两点在反比例函数)0(<=x xk y 的图象上,则k 的值等于．答案：－12解析：如图,过C.D 两点作x 轴的垂线,垂足为F.G,CG 交AD于M 点,过D 点作DH⊥CG,垂足为H,∵CD∥AB,CD=AB,∴△CDH≌△ABO（AAS ）,∴DH=AO=1,CH=OB=2,设C （m,n ）,D （m －1,n －2）, 则mn ＝（m －1）（n －2）=k,解得n=2－2m, 设直线BC 解析式为y=ax+b,将B.C 两点坐标代入得2b n am b=⎧⎨=+⎩,又n=2－2m, BC ＝22(2)m n +-＝25m ,AB ＝5,因为BC ＝2AB,解得：m ＝－2,n ＝6,所以,k ＝mn ＝－12轴交于26.(咸宁)如图,一次函数y ax b =+的图像与x 轴.y两点,A B 、两点,与反比例函数k y x=的图象订交于C D、衔接分离过C D 、两点作y 轴.x 轴的垂线,垂足为E F 、,CF DE、.有以下四个结论：①CEF DEF S S ∆∆=;②AOB FOE ∆∆∽;③DCE CDF ∆∆≌;④AC BD =.个中准确的结论是 . 三.解答题1.(兰州) 如图,P1是反比例函数)0(＞k x ky =在第一象限图像上的一点,点A1的坐标为(2,0)．（1）当点P1的横坐标逐渐增大时,△P1OA1的面积将若何变更？（2）若△P1OA1与△P2A1A2均为等边三角形,求此反比例函数的解析式及A2点的坐标．FE D CB A o xyyx第15题图DCBAO2.（内蒙呼和浩特）在平面直角坐标系中,函数y＝mx（x＞0,m是常数）的图像经过点A（1,4）.点B（a,b）,个中a＞1.过点A作x中的垂线,垂足为C,过点B 作y轴的垂线,垂足为D,AC与BD订交于点M,贯穿连接AD.DC.CB与AB.（1）求m的值;（2）求证：DC∥AB;（3）当AD＝BC时,求直线AB的函数解析式.【答案】解：（1）∵点A（1,4）在函数y＝mx的图像上,∴4＝1m,得m＝4.……………………………2分（2）∵点B（a,b）在函数y＝mx的图像上,∴ab＝4.又∵AC⊥x轴于C,BD⊥y轴于D交AC于M,∴AC⊥BD于M∴M（1,b）,D（0,b）,C（1,0）∴tan∠BAC＝BMAM ＝14ab--＝1aab b--＝1b,tan∠DCM＝DMMC＝1b……………4分∴tan∠BAC＝tan∠DCM,所以锐角∠BAC＝∠DCM,DC∥AB………………………………………………6分（3）设直线AB的解析式为y＝kx＋b∵AB∥CD,AD＝BC,∴四边形ABCD是平行四边形或等腰梯形.①四边形ABCD是平行四边形时,AC与BD互相等分,又∵AC⊥BD,∴B（2,2）∴422k b k b +=⎧⎨+=⎩,解得26k b =-⎧⎨=⎩∴直线AB 的解析式为：y ＝－2x ＋6.………………8分 ②当四边形ABCD 是等腰梯形时, BD 与AC 相等且垂直,∵AC＝BD ＝4, ∴B（4,1）∴同理可求直线AB 的解析式为y ＝－x ＋5.…………………10分可以应用这一结论解决问题.如图,在统一向角坐标系中,正比例函数的图象可以看作是：将x 轴地点的直线绕着原点O xy 3=的图象分离交于第一.三象限的点B .D ,已知点)0,(m A -.)0,(mC .（1）直接断定并填写：不管α取何值,四边形ABCD 的外形必定是; （2）①当点B 为)1,(p 时,四边形ABCD 是矩形,试求p .α.和m 有值;②不雅察猜测：对①中的m 值,能使四边形ABCD 为矩形的点B 共有几个？(不必说理)（3）试探讨：四边形ABCD 能不克不及是菱形？若能, 直接写出B 点的坐标, 若不克不及, 解释来由. 【答案】解：（1）平行四边形 …………（3分）（2）①∵点)1,(p B 在xy 3=的图象上,∴p31=∴3=p ………………………………（4分）过B 作E x BE 轴于⊥,则13==，BE OE 在BOE Rt ∆中,3331tan ===OE BE α α=30°∴2=OB又∵点B.D 是正比例函数与反比例函数图象的交点,∴点B.D 关于原点O 成中间对称∴OB=OD=2 ∵四边形ABCD 为矩形,且)0,(m A -)0,(m C ∴2====OD OC OB OA ∴2=m ;②能使四边形ABCD 为矩形的点B 共有2个; （3）四边形ABCD 不克不及是菱形. 法一：∵点A .C 的坐标分离为)0,(m -.)0,(m ∴四边形ABCD 的对角线AC 在x 轴上.又∵点B .D 分离是正比例函数与反比例函数在第一.三象限的交点. ∴对角线AC 与BD 不成能垂直. ∴四边形ABCD 不克不及是菱形法二：若四边形ABCD 为菱形,则对角线AC⊥BD,且AC 与BD 互相等分, 因为点A.C 的坐标分离为（－m,0）.（m,0）所以点A.C 关于原点O 对称,且AC 在x 轴上. 所以BD 应在y 轴上,这与“点B.D 分离在第一.三象限”抵触,所以四边形ABCD 不成能为菱形.4.（广西柳州）如图,过点P(－4,3)作x 轴.y 轴的垂线,分离交x 轴.y 轴于A.B 两点,交双曲线xk y =（k≥2）于E.F 两点．（1）点E 的坐标是________,点F 的坐标是________;（均用含k 的式子暗示）（2）断定EF 与AB 的地位关系,并证实你的结论; 如有,（3）记OEF PEF S S S ∆∆-=,S 是否有最小值？求出其最小值;若没有,请解释来由．解：（1）E （－4,－4k ）,F （3k ,3） ……3分（2）（证法一）结论：EF∥AB证实：∵P（－4,3）∴E（－4,－4k ）,F （3k ,3）,即得：PE=3+4k ,PF=3k +4 …∵1212433+=+=k k PEPA ,1212344+=+=k k PFPB ∠APB=∠EPF ∴△PAB∽△PEF∴∠PAB=∠PEF∴EF∥AB （证法二）结论：EF∥AB证实：∵P（－4,3）∴E（－4,－4k ）,F （3k ,3）,即得：PE=3+4k ,PF=3k +4 …在Rt△PAB 中,tan∠PAB=34=PAPB在Rt △PEF中,tan∠PEF=344343=++=k k PEPF ∴tan∠PAB= tan∠PEF∴∠PAB=∠PEF ∴ EF∥AB （3）（办法一）S 有最小值 ∵k S S S S FBO EAO PAOB PEDF +=++=∆∆12矩形四边形∴k S S S S PEF PEF PEDF EOF+-=-=∆∆∆12四边形由（2）知,)43)(43(2121++=⋅⋅=∆k k PF PE S PEF∴S=k S S S PEF OEFPEF --=-∆∆∆122=3)6(1211222-+=+k k k 又∵k≥2,此时S 的值随k 值增大而增大,∴当k=2时,37=最小S ∴S 的最小值是37（办法二）S 有最小值．分离过点E.F 作PF.PE 的平行线,交点为P′．由（2）知,P′⎪⎭⎫⎝⎛-43k k ，∵四边形PEP′为矩形,∴S△P′EF= S△PEF∴S=S△PEF－ S△OEF = S△P′EF－ S△OEF = S△OME +S 矩形OMP′N+ S△ONF=21222k k k ++=22k +k =3)6(1212-+k 又∵k≥2,此时S 的值随k 值增大而增大, ∴当k=2时,S 最小=37∴S 的最小值是37．5.（四川绵阳）如图,已知正比例函数y = ax （a≠0）的图象与反比例函致另—个交xk y =（k≠0）的图象的一个交点为A （－1,2－k2）,点为B,且A.B 关于原点O 对称,D 为OB 的中点,过点D 的线段OB 的垂直等分线与x 轴.y 轴分离交于C.E ．（1）写出反比例函数和正比例函数的解析式; （2）试盘算△COE 的面积是△ODE 面积的若干倍．【答案】（1）由图知k ＞0,a ＞0．∵点A （－1,2－k2）在xk y =图象上,∴ 2－k2 =－k,即k2－k －2 = 0,解得k = 2（k =－1舍去）,得反比例函数为xy 2=．此时A （－1,－2）,代人y = ax,解得a = 2,∴正比例函数为y = 2x ．（2）过点B 作BF⊥x 轴于F ．∵A（－1,－2）与B 关于原点对称, ∴B（1,2）,即OF = 1,BF = 2,得OB =5．由图,易知Rt△OBF∽Rt△OCD,∴OB : OC = OF : OD,而OD = OB∕2 =5∕2,∴OC = OB · OD∕OF = 2.5．由Rt△COE∽Rt△ODE 得5)5225()(22=⨯==∆∆OD OC S S ODE COE , 所以△COE 的面积是△ODE 面积的5倍． 7.（湖北荆州）已知：关于x 的一元二次方程()01222=+-+k x k x 的两根21,x x 知足02221=-x x ,双曲线xky 4=(x ＞0)经由Rt△OAB 斜边OB 的中点D,与直角边AB 交于C （如图）,求OBC △S ．【答案】解：()01222=+-+k x k x 有两根 ∴()041222≥--=∆k k 即41≤k 由02221=-x x 得：()()02121=+-x x x x当021=+x x 时,()012=--k 解得21=k ,不合题意,舍去当021=-x x 时,21x x =,()041222=--=∆k k 解得：41=k 相符题意 ∴双曲线的解析式为：xy 1=过D 作DE⊥OA 于E,则21121S S OCA ODE =⨯==∆∆ ∵DE⊥OA,BA⊥OA∴DE∥AB∴△ODE∽△OBA∴42=⎪⎭⎫ ⎝⎛=∆∆OD OB S S ODE OBA ∴2214=⨯=∆OBA S∴23212=-=-=∆∆∆OCA OBA OBC S S S 8．（北京）已知反比例函数y= k x的图像经由点A （—3,1）（1）试肯定此反比例函数的解析式．（2）点O 是坐标原点,将线段OA 绕点O 顺时针扭转30°得到线段OB,断定点B 是否在反比例函数的图像上,并解释来由．（3）已知点P （）也在此反比例函数的图像上（个中m ＜0）,过p点作x 轴的的垂线,交x 轴于点M,若线段PM 上消失一点Q,使得△OQM 的面积是12,设Q 点的纵坐标为n,求n2－的值．【答案】解：（1）由题意德k=∴反比例函数的解析式为y= （2）过点A 作x 轴的垂线交x 轴于点C,在Rt△AOC 中可得由题意,∠AOC=30°,OB=OA=2,∴∠BOC=60°过点B 做x 轴的垂线交x 轴于点D,在Rt△BOD 中,可得∴点B 坐标（－x=－1代入y= ,得∴点B （－y= x-的图像上．（3）由y=得xy=∵点P （）在反比例函数的y= 的图像上,m ＜0）=210m ++= ∵PQ⊥x 轴∴Q 点的坐标（m,n ） ∵△OQM 的面积为12∴12OM.QM=12∵m＜0 ∴m .n=－1 ∴22220m n n ++=∴21n -=-∴298n ++=．9.（广东广州市）已知Rt△ABC 的斜边AB 在平面直角坐标系的x 轴上,点C（1,3）在反比例函数y = k x 的图象上,且sin∠BAC= 35．（1）求k 的值和边AC 的长; （2）求点B 的坐标．【答案】（1）把C （1,3）代入y = kx 得k=3设斜边AB 上的高为CD,则sin∠BAC=CD AC =35∵C（1,3）∴CD=3,∴AC=5（2）分两种情形,当点B 在点A 右侧时,如图1有： AD=52－32=4,AO=4－1=3∵△ACD∽ABC∴AC2=AD·AB∴AB=AC2AD =254∴OB=AB－AO=254－3=134此时B 点坐标为（134,0）图1 图2当点B 在点A 左侧时,如图2此时AO=4＋1=5OB= AB －AO=254－5=54此时B 点坐标为（－54,0）所以点B 的坐标为（134,0）或（－54,0）．10.（山东聊城）如图,已知一次函数y ＝kx ＋b 的图象交反比例函数42my x-=（x>0）图象于点A.B,交x 轴于点C ．x yB A CD O O xyB A CD（1）求m 的取值规模;（2）若点A 的坐标是（2,－4）,且13BC AB =,求m 的值和一次函数的解析式;【答案】（1）因反比例函数的图象在第四象限,所以4－2m ＜0,解得m ＞2;（2）因点A(2,－4)在反比例函数图象上,所以－4＝224m-,解得m ＝6,过点A.B分离作AM⊥OC 于点M,BN⊥OC 于点N,所以∠BNC＝∠AMC ＝90°,又因为∠BCN ＝∠AMC,所以△BCN∽△ACM,所以ACBCAM BN =,因为31=AB BC ,所以41=AC BC ,即41=AM BN ,因为AM ＝4,所以BN ＝1,所以点B 的纵坐标为－1,因为点B 在反比例函数的图象上,所以当y ＝－1时,x ＝8,所以点B 的坐标为（8,－1）,因为一次函数y ＝kx ＋b 的图象过点A(2,－4),B(8,－1),所以⎩⎨⎧-=+-=+1842b k b k ,解得⎪⎩⎪⎨⎧-==521b k ,所以一次函数的解析式为y ＝21x －511.（江苏南通）如图,直线l 经由点A(1,0),且与双曲线y ＝m x（x ＞0）交于点B(2,1),过点P(p,p －1)（p ＞1）作x 轴的平行线分离交曲线y ＝m x（x ＞0）和y＝－m x（x ＜0）于M,N 两点.（1）求m 的值及直线l 的解析式;（2）若点P 在直线y ＝2上,求证：△PMB∽△PNA;（3）是否消失实数p,使得S△AMN＝4S△APM？若消失,要求出所有知足前提的p 的值;若不消失,请解释来由.【答案】（1）∵点B(2,1)在双曲线y ＝m x上,∴12m =,得m ＝2.设直线l 的解析式为y ＝kx ＋b∵直线l 过A(1,0)和B(2,1) ∴021k b k b +=⎧⎨+=⎩,解得11k b =⎧⎨=-⎩∴直线l 的解析式为y ＝x －1.(2) 证实：当x ＝p 时,y ＝p －1,点P(p,p －1)（p ＞。

2020-2021中考数学反比例函数-经典压轴题

2020-2021中考数学反比例函数-经典压轴题一、反比例函数1．如图，点A在函数y=（x＞0）图象上，过点A作x轴和y轴的平行线分别交函数y=图象于点B，C，直线BC与坐标轴的交点为D，E．（1）当点C的横坐标为1时，求点B的坐标；（2）试问：当点A在函数y=（x＞0）图象上运动时，△ABC的面积是否发生变化？若不变，请求出△ABC的面积，若变化，请说明理由．（3）试说明：当点A在函数y=（x＞0）图象上运动时，线段BD与CE的长始终相等．【答案】（1）解：∵点C在y=的图象上，且C点横坐标为1，∴C（1，1），∵AC∥y轴，AB∥x轴，∴A点横坐标为1，∵A点在函数y=（x＞0）图象上，∴A（1，4），∴B点纵坐标为4，∵点B在y=的图象上，∴B点坐标为（，4）；△SABC =AB•AC= × × = ，（2）解：设 A （a ，），则 C （a ，），B （，），∴ AB=a ﹣ = a ，AC= ﹣ = ， ∴ △即 ABC 的面积不发生变化，其面积为；（3）解：如图，设 AB 的延长线交 y 轴于点 G ，AC 的延长线交 x 轴于点 F ，∵ AB ∥ x 轴， ∴ △ ABC ∽ △ EFC ，∴ =，即= ，∴ EF= a ，由（2）可知 BG= a ， ∴ BG=EF ，∵ AE ∥ y 轴， ∴ ∠ BDG=∠ FCE ， △在 DBG △和 CFE 中∴ △ DBG ≌ △ CEF （AAS ），∴ BD=EF ．【解析】【分析】（1）由条件可先求得A点坐标，从而可求得B点纵坐标，再代入y=可求得B点坐标；（2）可设出A点坐标，从而可表示出C、B的坐标，则可表示出AB和AC的长，可求得△ABC的面积；（3）可证明△ABC∽△EFC，利用（2）中，AB和AC的长可表示出EF，可得到BG=EF，从而可证明△DBG≌△CFE，可得到DB=CF．2．如图，一次函数y=x+4的图象与反比例函数y=（k为常数，且k≠0）的图象交于A （﹣1，a），B（b，1）两点．（1）求反比例函数的表达式；（2）在x轴上找一点P，使PA+PB的值最小，求满足条件的点P的坐标；（3△）求PAB的面积．【答案】（1）解：当x=﹣1时，a=x+4=3，∴点A的坐标为（﹣1，3）．将点A（﹣1，3）代入y=中，3=，解得：k=﹣3，∴反比例函数的表达式为y=﹣（2）解：当y=b+4=1时，b=﹣3，∴点B的坐标为（﹣3，1）．作点B关于x轴的对称点D，连接AD，交x轴于点P，此时PA+PB的值最小，如图所示．∵ 点 B 的坐标为（﹣3，1）， ∴ 点 D 的坐标为（﹣3，﹣1）．设直线 AD 的函数表达式为 y=mx+n ，将点 A （﹣1，3）、D （﹣3，﹣1）代入 y=mx+n 中，，解得：，∴ 直线 AD 的函数表达式为 y=2x+5．当 y=2x+5=0 时，x=﹣ ，∴ 点 P 的坐标为（﹣ ，0）（3）解：△SPAB △=S ABD﹣△S BDP = ×2×2﹣ ×2× =【解析】【分析】（1）由一次函数图象上点的坐标特征可求出点 A 的坐标，根据点 A 的坐标利用待定系数法，即可求出反比例函数的表达式；（2）利用一次函数图象上点的坐标特征可求出点 B 的坐标，作点 B 关于 x 轴的对称点 D ，连接 AD ，交 x 轴于点 P ，此时 PA+PB 的值最小，由点 B 的坐标可得出点 D 的坐标，根据点 A 、D 的坐标利用待定系数法，即可求出直线 AB 的函数表达式，再由一次函数图象上点的坐标特征即可求出点 P 的坐标；（3）根据三角形的面积公式结合 △S PAB △=S ABD ﹣△S BDP ，即可得出结论．3．如图，已知抛物线 y=﹣x 2+9 的顶点为 A ，曲线 DE 是双曲线 y= （3≤x≤12）的一部分，记作 G 1 ，且 D （3，m ）、E （12，m ﹣3），将抛物线 y=﹣x 2+9 水平向右移动 a 个单位，得到抛物线 G 2 ．（1）求双曲线的解析式；（2）设抛物线 y=﹣x 2+9 与 x 轴的交点为 B 、C ，且 B 在 C 的左侧，则线段 BD 的长为________；（3）点（6，n ）为 G 1 与 G 2 的交点坐标，求 a 的值．（4）解：在移动过程中，若 G 1 与 G 2 有两个交点，设 G 2 的对称轴分别交线段 DE 和 G 1 于M 、N 两点，若 MN ＜，直接写出 a 的取值范围．∵ G 与 G 有两个交点，∵ G 的对称轴分别交线段 DE 和 G 于 M 、N 两点，【答案】（1）把 D （3，m ）、E （12，m ﹣3）代入 y= 得，解得，所以双曲线的解析式为 y=；（2）2（3）解：把（6，n ）代入 y= 得 6n=12，解得 n=2，即交点坐标为（6，2），抛物线 G 2 的解析式为 y=﹣（x ﹣a ）2+9，把（6，2）代入 y=﹣（x ﹣a ）2+9 得﹣（6﹣a ）2+9=2，解得 a=6±即 a 的值为 6± ；（4）抛物线 G 2 的解析式为 y=﹣（x ﹣a ）2+9，，把 D （3，4）代入 y=﹣（x ﹣a ）2+9 得﹣（3﹣a ）2+9=4，解得 a=3﹣或 a=3+把 E （12，1）代入 y=﹣（x ﹣a ）2+9 得﹣（12﹣a ）2+9=1，解得 a=12﹣2；12∴ 3+≤a≤12﹣2，设直线 DE 的解析式为 y=px+q ，；或 a=12+2把 D （3，4），E （12，1）代入得，解得，∴ 直线 DE 的解析式为 y=﹣ x+5，2 1∴ M （a ，﹣ a+5），N （a ，），∵ MN ＜， ∴ ﹣ a+5﹣＜，整理得 a 2﹣13a+36＞0，即（a ﹣4）（a ﹣9）＞0，∴ a ＜4 或 a ＞9，∴ a 的取值范围为 9＜a≤12﹣2 ．【解析】【解答】解：（2）当 y=0 时，﹣x 2+9=0，解得 x 1=﹣3，x 2=3，则 B （﹣3，0），而 D （3，4），所以 BE=故答案为 2；=2 ．【分析】（1）把D（3，m）、E（12，m﹣3）代入y=得关于k、m的方程组，然后解方程组求出m、k，即可得到反比例函数解析式和D、E点坐标；（2）先解方程﹣x2+9=0得到B（﹣3，0），而D（3，4），然后利用两点间的距离公式计算DE的长；（3）先利用反比例函数图象上点的坐标特征确定交点坐标为（6，2），然后把（6，2）代入y=﹣（x ﹣a）2+9得a的值；（4）分别把D点和E点坐标代入y=﹣（x﹣a）2+9得a的值，则利用图象和G1与G2有两个交点可得到3+≤a≤12﹣2，再利用待定系数法求出直线DE的解析式为y=﹣x+5，则M（a，﹣a+5），N（a，），于是利用MN＜得到﹣a+5﹣＜，然后解此不等式得到a＜4或a＞9，最后确定满足条件的a的取值范围．4．已知：O是坐标原点，P（m，n）（m＞0）是函数y=（k＞0）上的点，过点P作直线PA⊥OP于P，直线PA与x轴的正半轴交于点A（a，0）（a＞m）．设△OPA的面积为s，且s=1+．（1）当n=1时，求点A的坐标；（2）若OP=AP，求k的值；（3）设n是小于20的整数，且k≠，求OP2的最小值．【答案】（1）解：过点P作PQ⊥x轴于Q，则PQ=n，OQ=m，当n=1时，s=，∴ a== ．（2）解：解法一：∵ OP=AP ，PA ⊥OP ， ∴ △ OPA 是等腰直角三角形．∴ m=n= ． ∴ 1+= •an ．即 n 4﹣4n 2+4=0， ∴ k 2﹣4k+4=0， ∴ k=2．解法二：∵ OP=AP ，PA ⊥OP ， ∴ △ OPA 是等腰直角三角形．∴ m=n ．△设 OPQ 的面积为 s 1则：s 1= ∴•mn= （1+ ），即：n 4﹣4n 2+4=0， ∴ k 2﹣4k+4=0， ∴ k=2．（3）解：解法一：∵ PA ⊥OP ，PQ ⊥OA ， ∴ △ OPQ ∽ △ OAP ．△设： OPQ 的面积为 s 1 ，则=即： = 化简得：化简得：2n 4+2k 2﹣kn 4﹣4k=0 （k ﹣2）（2k ﹣n 4）=0， ∴ k=2 或 k=（舍去），∴ 当 n 是小于 20 的整数时，k=2．∵ OP 2=n 2+m 2=n 2+ 又 m ＞0，k=2， ∴ n 是大于 0 且小于 20 的整数．当n=1时，OP2=5，当n=2时，OP2=5，当n=3时，OP2=32+=9+=，当n是大于3且小于20的整数时，即当n=4、5、6…19时，OP2的值分别是：42+、52+、62+…192+，∵192+＞182+＞32+＞5，∴OP2的最小值是5．【解析】【分析】（1）利用△OPA面积定义构建关于a的方程，求出A的坐标；（2）由已知OP=AP，PA⊥OP，可得△OPA是等腰直角三角形，由其面积构建关于n的方程，转化为k的方程，求出k;（3）利用相似三角形的面积比等于相似比的平方构建关于k的方程，最值问题的基本解决方法就是函数思想，利用勾股定理用m、n的代数式表达OP2,,在n的范围内求出OP2的最值.5．如图，在平面直角坐标系中，平行四边形点坐标为.的边，顶点坐标为，（1）点的坐标是________，点的坐标是________（用表示）；（2）若双曲线（3）若平行四边形【答案】（1）（2）解：∵双曲线过平行四边形与双曲线；过点的顶点和，求该双曲线的表达式；总有公共点，求的取值范围.和点，∴，解得，∴点的坐标为，点的坐标为，把点的坐标代入，解得，∴双曲线表达式为（3）解：∵平行四边形与双曲线总有公共点，∴当点当点在双曲线在双曲线，得到，得到，，∴的取值范围.【解析】【分析】（1）由四边形ABCD为平行四边形，得到A与B纵坐标相同，C与D纵坐标相同，横坐标相差2，得出B、C坐标即可；（2）根据B与D在反比例图象上，得到C与D横纵坐标乘积相等，求出b的值确定出B坐标，进而求出k的值，确定出双曲线解析式；（3）抓住两个关键点，将A坐标代入双曲线解析式求出b的值；将C坐标代入双曲线解析式求出b的值，即可确定出平行四边形与双曲线总有公共点时b的范围．6．【阅读理解】对于任意正实数a、b，因为≥0，所以≥0，所以≥2，只有当时，等号成立．【获得结论】在≥2（a、b均为正实数）中，若为定值，则≥2，只有当时，有最小值2．（1）根据上述内容，回答下列问题：若>0，只有当=________时，________．（2）【探索应用】如图，已知A（－3，0），B（0，－4），P为双曲线有最小值（＞0）上的任意一点，过点P作PC⊥x轴于点C，PD⊥y轴于点D．求四边形ABCD面积的最小值，并说明此时四边形ABCD的形状．【答案】（1）1；2（2）解：设P（x，），则C（x，0），D（0，），∴CA=x+3，BD=+4，∴S四边形=ABCD CA×BD=（x+3）（+4），化简得：S=2（x+）+12．∵x＞0，＞0，∴x+≥2 =6，只有当x=，即x=3时，等号成立，∴S≥2×6+12=24，∴四边形ABCD的面积有最小值24，此时，P（3，4），C（3，0），D（0，4），AB=BC=CD=DA=5，∴四边形ABCD是菱形．【解析】【解答】解：（1）根据题目所给信息可知m+≥2，且当m=时等号，∴当m=1时，m+≥2，即当m=1时，m+有最小值2．故答案为：1，2；【分析】（1）此题是一道阅读题，根据题中所给的信息可知：，只有当m=时等号成立，一个正数只有1和它的倒数相等，从而得出答案；（2）根据双曲线上点的坐标特点设出P点的坐标，根据垂直于坐标轴上的点的坐标特点表示出C,D两点的坐标，从而表示出AC,BD的长，根据对角线互相垂直的四边形的面积等于两对角线积的一半建立出S与x的函数关系式，根据题干提供的信息得出得出,只有在，即x=3时，等号成立，从而得出S的最小值，从而得出P,C,D三点的坐标，进而算出AB=BC=CD=DA=5，根据四边相等的四边形是菱形得出结论。

中考数学复习---《反比例函数综合》压轴题练习(含答案解析)

中考数学复习---《反比例函数综合》压轴题练习（含答案解析）一．反比例函数系数k的几何意义（共4小题）1．（2022•十堰）如图，正方形ABCD的顶点分别在反比例函数y＝（k1＞0）和y＝（k2＞0）的图像上．若BD∥y轴，点D的横坐标为3，则k1+k2＝（）A．36B．18C．12D．9【答案】B【解答】解：连接AC交于E，延长BD交x轴于F，连接OD、OB，如图：∵四边形ABCD是正方形，∴AE＝BE＝CE＝DE，设AE＝BE＝CE＝DE＝m，D（3，a），∵BD∥y轴，∴B（3，a+2m），A（3+m，a+m），∵A，B都在反比例函数y＝（k1＞0）的图像上，∴k1＝3（a+2m）＝（3+m）（a+m），∵m≠0，∴m＝3﹣a，∴B（3，6﹣a），∵B（3，6﹣a）在反比例函数y＝（k1＞0）的图像上，D（3，a）在y＝（k2＞0）的图像上，∴k1＝3（6﹣a）＝18﹣3a，k2＝3a，∴k1+k2＝18﹣3a+3a＝18；故选：B．2．（2022•通辽）如图，点D是▱OABC内一点，AD与x轴平行，BD与y轴平行，BD＝，∠BDC＝120°，S△BCD＝，若反比例函数y＝（x＜0）的图像经过C，D两点，则k的值是（）A．﹣6B．﹣6C．﹣12D．﹣12【答案】C【解答】解：过点C作CE⊥y轴，延长BD交CE于点F，∵四边形OABC为平行四边形，∴AB∥OC，AB＝OC，∴∠COE＝∠1，∵BD与y轴平行，∴∠1＝∠ABD，∠ADB＝90°，∴∠COE＝∠ABD，在△COE和△ABD中，，∴△COE≌△ABD（AAS），∴OE＝BD＝，∵S△BDC＝BD•CF＝，∴CF＝9，∵∠BDC＝120°，∴∠CDF＝60°，∴DF＝3，点D的纵坐标为4，设C（m，），则D（m+9，4），∵反比例函数y＝（x＜0）的图像经过C，D两点，∴k＝m＝4（m+9），∴m＝﹣12，∴k＝﹣12，故选：C．3．（2022•宜宾）如图，△OMN是边长为10的等边三角形，反比例函数y＝（x ＞0）的图像与边MN、OM分别交于点A、B（点B不与点M重合）．若AB ⊥OM于点B，则k的值为．【答案】9【解答】解：过点B作BC⊥x轴于点C，过点A作AD⊥x轴于点D，如图，∵△OMN是边长为10的等边三角形，∴OM＝ON＝MN＝10，∠MON＝∠M＝∠MNO＝60°设OC＝b，则BC＝，OB＝2b，∴BM＝OM﹣OB＝10﹣2b，B（b，b），∵∠M＝60°，AB⊥OM，∴AM＝2BM＝20﹣4b，∴AN＝MN﹣AM＝10﹣（20﹣4b）＝4b﹣10，∵∠AND＝60°，∴DN＝＝2b﹣5，AD＝AN＝2b﹣5，∴OD＝ON﹣DN＝15﹣2b，∴A（15﹣2b，2b﹣5），∵A、B两点都在反比例函数y＝（x＞0）的图像上，∴k＝（15﹣2b）（2b﹣5）＝b•b，解得b＝3或5，当b＝5时，OB＝2b＝10，此时B与M重合，不符题意，舍去，∴b＝3，∴k＝b•b＝9，故答案为：9．4．（2022•乐山）如图，平行四边形ABCD的顶点A在x轴上，点D在y＝（k ＞0）上，且AD⊥x轴，CA的延长线交y轴于点E．若S△ABE＝，则k＝．【答案】3【解答】解：设BC与x轴交于点F，连接DF、OD，∵四边形ABCD为平行四边形，∴AD∥BC，∴S△ODF＝S△EBC，S△ADF＝S△ABC，∴S△OAD＝S△ABE＝，∴k＝3，故答案为：3．二．反比例函数图像上点的坐标特征（共4小题）5．（2022•宿迁）如图，点A在反比例函数y＝（x＞0）的图像上，以OA为一边作等腰直角三角形OAB，其中∠OAB＝90°，AO＝AB，则线段OB长的最小值是（）A．1B．C．2D．4【答案】C【解答】解：∵三角形OAB是等腰直角三角形，∴当OB最小时，OA最小，设A点坐标为（a，），∴OA＝，∵≥0，即：﹣4≥0，∴≥4，∵≥0，两边同时开平方得：a﹣＝0，∴当a＝时，OA有最小值，解得a1＝，a2＝﹣（舍去），∴A点坐标为（，），∴OA＝2，∵三角形OAB是等腰直角三角形，OB为斜边，∴OB＝OA＝2．故选：C．6．（2022•枣庄）如图，正方形ABCD的边长为5，点A的坐标为（4，0），点B在y轴上，若反比例函数y＝（k≠0）的图像过点C，则k的值为（）A．4B．﹣4C．﹣3D．3【答案】C【解答】解：如图，过点C作CE⊥y轴于E，在正方形ABCD中，AB＝BC，∠ABC＝90°，∴∠ABO+∠CBE＝90°，∵∠OAB+∠ABO＝90°，∴∠OAB＝∠CBE，∵点A的坐标为（4，0），∴OA＝4，∵AB＝5，∴OB＝＝3，在△ABO和△BCE中，，∴△ABO≌△BCE（AAS），∴OA＝BE＝4，CE＝OB＝3，∴OE＝BE﹣OB＝4﹣3＝1，∴点C的坐标为（﹣3，1），∵反比例函数y＝（k≠0）的图像过点C，∴k＝xy＝﹣3×1＝﹣3，故选：C．7．（2022•江西）已知点A在反比例函数y＝（x＞0）的图像上，点B在x 轴正半轴上，若△OAB为等腰三角形，且腰长为5，则AB的长为．【答案】5或2或【解答】解：当AO＝AB时，AB＝5；当AB＝BO时，AB＝5；当OA＝OB时，设A（a，）（a＞0），B（5，0），∵OA＝5，∴＝5，解得：a1＝3，a2＝4，∴A（3，4）或（4，3），∴AB＝＝2或AB＝＝；综上所述，AB的长为5或2或．故答案为：5或2或．8．（2022•宁波）如图，四边形OABC为矩形，点A在第二象限，点A关于OB的对称点为点D，点B，D都在函数y＝（x＞0）的图像上，BE⊥x 轴于点E．若DC的延长线交x轴于点F，当矩形OABC的面积为9时，的值为，点F的坐标为．【答案】，（，0）．【解答】解：如图，方法一：作DG⊥x轴于G，连接OD，设BC和OD交于I，设点B（b，），D（a，），由对称性可得：△BOD≌△BOA≌△OBC，∴∠OBC＝∠BOD，BC＝OD，∴OI＝BI，∴DI＝CI，∴＝，∵∠CID＝∠BIO，∴△CDI∽△BOI，∴∠CDI＝∠BOI，∴CD∥OB，∴S△BOD＝S△AOB＝S矩形AOCB＝，∵S△BOE＝S△DOG＝＝3，S四边形BOGD＝S△BOD+S△DOG＝S梯形BEGD+S△BOE，∴S梯形BEGD＝S△BOD＝，∴•（a﹣b）＝，∴2a2﹣3ab﹣2b2＝0，∴（a﹣2b）•（2a+b）＝0，∴a＝2b，a＝﹣（舍去），∴D（2b，），即：（2b，），在Rt△BOD中，由勾股定理得，OD2+BD2＝OB2，∴[（2b）2+（）2]+[（2b﹣b）2+（﹣）2]＝b2+（）2，∴b＝，∴B（，2），D（2，），∵直线OB的解析式为：y＝2x，∴直线DF的解析式为：y＝2x﹣3，当y＝0时，2﹣3＝0，∴x＝，∴F（，0），∵OE＝，OF＝，∴EF＝OF﹣OE＝，∴＝，方法二：如图，连接BF，BD，作DG⊥x轴于G，直线BD交x轴于H，由上知：DF∥OB，∴S△BOF＝S△BOD＝，∵S△BOE＝|k|＝3，∴＝＝，设EF＝a，FG＝b，则OE＝2a，∴BE＝，OG＝3a+b，DG＝，∵△BOE∽△DFG，∴＝，∴＝，∴a＝b，a＝﹣（舍去），∴D（4a，），∵B（2a，），∴＝＝，∴GH＝EG＝2a，∵∠ODH＝90°，DG⊥OH，∴△ODG∽△DHG，∴，∴，∴a＝，∴3a＝，∴F（，0）故答案为：，（，0）．三．待定系数法求反比例函数解析式（共1小题）9．（2022•湖州）如图，已知在平面直角坐标系xOy中，点A在x轴的负半轴上，点B在y轴的负半轴上，tan∠ABO＝3，以AB为边向上作正方形ABCD．若图像经过点C的反比例函数的解析式是y＝，则图像经过点D的反比例函数的解析式是．【答案】y＝﹣【解答】解：如图，过点C作CT⊥y轴于点T，过点D作DH⊥CT交CT的延长线于点H．∵tan∠ABO＝＝3，∴可以假设OB＝a，OA＝3a，∵四边形ABCD是正方形，∴AB＝BC，∠ABC＝∠AOB＝∠BTC＝90°，∴∠ABO+∠CBT＝90°，∠CBT+∠BCT＝90°，∴∠ABO＝∠BCT，∴△AOB≌△BTC（AAS），∴BT＝OA＝3a，OB＝TC＝a，∴OT＝BT﹣OB＝2a，∴C（a，2a），∵点C在y＝上，∴2a2＝1，同法可证△CHD≌△BTC，∴DH＝CT＝a，CH＝BT＝3a，∴D（﹣2a，3a），设经过点D的反比例函数的解析式为y＝，则有﹣2a×3a＝k，∴k＝﹣6a2＝﹣3，∴经过点D的反比例函数的解析式是y＝﹣．故答案为：y＝﹣．四．反比例函数与一次函数的交点问题（共2小题）10．（2022•怀化）如图，直线AB交x轴于点C，交反比例函数y＝（a＞1）的图像于A、B两点，过点B作BD⊥y轴，垂足为点D，若S△BCD＝5，则a 的值为（）A．8B．9C．10D．11【答案】D【解答】解：设点B的坐标为（m，），∵S△BCD＝5，且a＞1，∴×m×＝5，解得：a＝11，故选：D．11．（2022•巴中）将双曲线y＝向右平移2个单位，再向下平移1个单位，得到的新双曲线与直线y＝k i（x﹣2）﹣1（k i＞0，i＝1，2，3， (1011)相交于2022个点，则这2022个点的横坐标之和为．【答案】4044【解答】解：直线y＝k i（x﹣2）﹣1（k i＞0，i＝1，2，3，⋅⋅⋅，1011）可由直线y＝k i x（k i＞0，i＝1，2，3，⋅⋅⋅，1011）向右平移2个单位，再向下平移1个单位得到，∴直线y＝k i x（k i＞0，i＝1，2，3，⋅⋅⋅，1011）到直线y＝k i（x﹣2）﹣1（k i＞0，i＝1，2，3，⋅⋅⋅，1011）的平移方式与双曲线双曲线的相同，∴新双曲线与直线y＝k i（x﹣2）﹣1（k i＞0，i＝1，2，3，⋅⋅⋅，1011）的交点也可以由双曲线与直线y＝k i x（k i＞0，i＝1，2，3，⋅⋅⋅，1011）的交点以同样的方式平移得到，设双曲线与直线y＝k i x（k i＞0，i＝1，2，3，⋅⋅⋅，1011）的交点的横坐标为x i，x'i，（i＝1，2，3，⋅⋅⋅，1011），则新双曲线与直线y＝k i（x﹣2）﹣1（k i＞0，i＝1，2，3，⋅⋅⋅，1011）的交点的横坐标为x i+2，x'i+2（i＝1，2，3，⋅⋅⋅，1011），根据双曲线与直线y＝k i x（k i＞0，i＝1，2，3，⋅⋅⋅，1011）图像都关于原点对称，可知双曲线与直线y＝k i x（k i＞0，i＝1，2，3，⋅⋅⋅，1011）的交点也关于原点对称，∴x i+x'i＝0，（i＝1，2，3，⋅⋅⋅，1011），∴（x i+2）+（x'i+2）＝4（i＝1，2，3，⋅⋅⋅，1011），即新双曲线与直线y＝k i（x﹣2）﹣1（k i＞0，i＝1，2，3，⋅⋅⋅，1011）的交点的横坐标之和都是4，∴这2022个点的横坐标之和为：4×1011＝4044．故答案是：4044．。

中考数学反比例函数-经典压轴题附答案

中考数学反比例函数-经典压轴题附答案一、反比例函数1．如图，反比例函数y= 的图象与一次函数y=kx+b的图象交于A、B两点，点A的坐标为（2，3n），点B的坐标为（5n+2，1）．（1）求反比例函数与一次函数的表达式；（2）将一次函数y=kx+b的图象沿y轴向下平移a个单位，使平移后的图象与反比例函数y= 的图象有且只有一个交点，求a的值；（3）点E为y轴上一个动点，若S△AEB=5，则点E的坐标为________．【答案】（1）解：∵A、B在反比例函数的图象上，∴2×3n=（5n+2）×1=m，∴n=2，m=12，∴A（2，6），B（12，1），∵一次函数y=kx+b的图象经过A、B两点，∴，解得，∴反比例函数与一次函数的表达式分别为y= ，y=﹣ x+7．（2）解：设平移后的一次函数的解析式为y=﹣ x+7﹣a，由，消去y得到x2+（2a﹣14）x+24=0，由题意，△=0，（21a﹣14）2﹣4×24=0，解得a=7±2 ．（3）（0，6）或（0，8）【解析】【解答】（3）设直线AB交y轴于K，则K（0，7），设E（0，m），由题意，PE=|m﹣7|．∵S△AEB=S△BEP﹣S△AEP=5，∴ ×|m﹣7|×（12﹣2）=5．∴|m﹣7|=1．∴m1=6，m2=8．∴点E的坐标为（0，6）或（0，8）．故答案为（0，6）或（0，8）．【分析】（1）由A、B在反比例函数的图象上，得到n，m的值和A、B的坐标，用待定系数法求出反比例函数与一次函数的表达式；（2）由将一次函数y=kx+b的图象沿y轴向下平移a个单位，得到平移后的一次函数的解析式，由平移后的图象与反比例函数的图象有且只有一个交点，得到方程组求出a的值；（3）由点E为y轴上一个动点和S△AEB=5，求出点E的坐标.2．如图1，经过原点的抛物线y=ax2+bx+c与x轴的另一个交点为点C；与双曲线y= 相交于点A，B；直线AB与分别与x轴、y轴交于点D，E．已知点A的坐标为（﹣1，4），点B在第四象限内且到x轴、y轴的距离相等．（1）求双曲线和抛物线的解析式；（2）计算△ABC的面积；（3）如图2，将抛物线平移至顶点在原点上时，直线AB随之平移，试判断：在y轴的负半轴上是否存在点P，使△PAB的内切圆的圆心在y轴上？若存在，求出点P的坐标；若不存在，请说明理由．【答案】（1）解：把点A的坐标代入双曲线的解析式得：k=﹣1×4=﹣4．所以双曲线的解析式为y=﹣．设点B的坐标为（m，﹣m）．∵点B在双曲线上，∴﹣m2=﹣4，解得m=2或m=﹣2．∵点B在第四象限，∴m=2．∴B（2，﹣2）．将点A、B、C的坐标代入得：，解得：．∴抛物线的解析式为y=x2﹣3x．（2）解：如图1，连接AC、BC．令y=0，则x2﹣3x=0，∴x=0或x=3，∴C（3，0），∵A（﹣1，4），B（2，﹣2），∴直线AB的解析式为y=﹣2x+2，∵点D是直线AB与x轴的交点，∴D（1，0），∴S△ABC=S△ADC+S△BDC= ×2×4+ ×2×2=6；（3）解：存在，理由：如图2，由原抛物线的解析式为y=x2﹣3x=（x﹣）2﹣，∴原抛物线的顶点坐标为（，﹣），∴抛物线向左平移个单位，再向上平移个单位，而平移前A（﹣1，4），B（2，﹣2），∴平移后点A（﹣，），B（，），∴点A关于y轴的对称点A'（，），连接A'B并延长交y轴于点P，连接AP，由对称性知，∠APE=∠BPE，∴△APB的内切圆的圆心在y轴上，∵B（，），A'（，），∴直线A'B的解析式为y=3x﹣，∴P（0，﹣）．【解析】【分析】（1）首先将点A的坐标代入反比例函数的解析式求得k的值，然后再求得B的值，最后根据点A的坐标求出双曲线的解析式，进而得出点B的坐标，最后，将点A、B、O三点的坐标代入抛物线的解析式，求得a、b、c的值即可；（2）由点A和点B的坐标可求得直线AB的解析式，然后将y=0可求得点D的横坐标，最后用三角形的面积和求解即可；（3）先确定出平移后点A，B的坐标，进而求出点A关于y轴的对称点的坐标，求出直线BA'的解析式即可得出点P的坐标.3．如图，在平面直角坐标系中，平行四边形的边，顶点坐标为，点坐标为 .（1）点的坐标是________，点的坐标是________（用表示）；（2）若双曲线过平行四边形的顶点和，求该双曲线的表达式；（3）若平行四边形与双曲线总有公共点，求的取值范围.【答案】（1）；（2）解：∵双曲线过点和点，∴，解得，∴点的坐标为，点的坐标为，把点的坐标代入，解得，∴双曲线表达式为（3）解：∵平行四边形与双曲线总有公共点，∴当点在双曲线，得到，当点在双曲线，得到，∴的取值范围 .【解析】【分析】（1）由四边形ABCD为平行四边形，得到A与B纵坐标相同，C与D纵坐标相同，横坐标相差2，得出B、C坐标即可；（2）根据B与D在反比例图象上，得到C与D横纵坐标乘积相等，求出b的值确定出B坐标，进而求出k的值，确定出双曲线解析式；（3）抓住两个关键点，将A坐标代入双曲线解析式求出b的值；将C坐标代入双曲线解析式求出b的值，即可确定出平行四边形与双曲线总有公共点时b的范围．4．如图，过原点O的直线与双曲线交于上A（m，n）、B，过点A的直线交x轴正半轴于点D，交y轴负半轴于点E，交双曲线于点P.（1）当m＝2时，求n的值；（2）当OD：OE＝1：2，且m＝3时，求点P的坐标；（3）若AD＝DE，连接BE，BP，求△PBE的面积.【答案】（1）解：∵点A（m，n）在双曲线y＝上，∴mn＝6，∵m＝2，∴n＝3；（2）解：由（1）知，mn＝6，∵m＝3，∴n＝2，∴A（3，2），∵OD：OE＝1：2，设OD＝a，则OE＝2a，∵点D在x轴坐标轴上，点E在y轴负半轴上，∴D（a，0），E（0，﹣2a），∴直线DE的解析式为y＝2x﹣2a，∵点A（3，2）在直线y＝2x﹣2a上，∴6﹣2a＝2，∴a＝2，∴直线DE的解析式为y＝2x﹣4①，∵双曲线的解析式为y＝②，联立①②解得，（点A的横纵坐标，所以舍去）或，∴P（﹣2，﹣3）；（3）解：∵AD＝DE，点D在x轴坐标轴上，点E在y轴负半轴上，A（m，n），∴E（0，﹣n），D（ m，0），∴直线DE的解析式为y＝ x﹣n，∵mn＝6，∴m＝，∴y＝ x﹣n③，∵双曲线的解析式为y＝④，联立③④解得，∴（点A的横纵坐标，所以舍去）或，∴P（﹣2m，﹣2n），∵A（m，n），∴直线AB的解析式为y＝x⑤.联立④⑤解得，（点A的横纵坐标，所以舍去）或∴B（﹣m，﹣n），∵E（0，﹣n），∴BE∥x轴，∴S△PBE＝ BE×|y E﹣y P|＝ ×m×|﹣n﹣（﹣2n）|＝ mn＝3.【解析】【分析】（1）把A（2，n）代入解析式即可求出n；（2）先求出A点坐标，设OD＝a，则OE＝2a，得D（a，0），E（0，﹣2a），直线DE的解析式为y＝2x﹣2a，把点A（3，2）代入求出a，再联立两函数即可求出交点P；（3）由AD＝DE，点D在x轴坐标轴上，点E在y轴负半轴上，故A（m，n），E（0，﹣n），D（ m，0），求得直线DE 的解析式为y＝ x﹣n，又mn＝6，得y＝ x﹣n，与y＝联立得，即为P点坐标，由直线AB的解析式为y＝ x与双曲线联立解得B （﹣m，﹣n），再根据S△PBE＝ BE×|y E﹣y P|＝ ×m×|﹣n﹣（﹣2n）|求出等于3.5．如图，已知A（3，m），B（﹣2，﹣3）是直线AB和某反比例函数的图象的两个交点．（1）求直线AB和反比例函数的解析式；（2）观察图象，直接写出当x满足什么范围时，直线AB在双曲线的下方；（3）反比例函数的图象上是否存在点C，使得△OBC的面积等于△OAB的面积？如果不存在，说明理由；如果存在，求出满足条件的所有点C的坐标．【答案】（1）解：设反比例函数解析式为y= ，把B（﹣2，﹣3）代入，可得k=﹣2×（﹣3）=6，∴反比例函数解析式为y= ；把A（3，m）代入y= ，可得3m=6，即m=2，∴A（3，2），设直线AB 的解析式为y=ax+b，把A（3，2），B（﹣2，﹣3）代入，可得，解得，∴直线AB 的解析式为y=x﹣1（2）解：由题可得，当x满足：x＜﹣2或0＜x＜3时，直线AB在双曲线的下方（3）解：存在点C．如图所示，延长AO交双曲线于点C1，∵点A与点C1关于原点对称，∴AO=C1O，∴△OBC1的面积等于△OAB的面积，此时，点C1的坐标为（﹣3，﹣2）；如图，过点C1作BO的平行线，交双曲线于点C2，则△OBC2的面积等于△OBC1的面积，∴△OBC2的面积等于△OAB的面积，由B（﹣2，﹣3）可得OB的解析式为y= x，可设直线C1C2的解析式为y= x+b'，把C1（﹣3，﹣2）代入，可得﹣2= ×（﹣3）+b'，解得b'= ，∴直线C1C2的解析式为y= x+ ，解方程组，可得C2（）；如图，过A作OB的平行线，交双曲线于点C3，则△OBC3的面积等于△OBA的面积，设直线AC3的解析式为y= x+ ，把A（3，2）代入，可得2= ×3+ ，解得 =﹣，∴直线AC3的解析式为y= x﹣，解方程组，可得C3（）；综上所述，点C的坐标为（﹣3，﹣2），（（））．【解析】【分析】（1）用待定系数法求出反比例函数解析式,一次函数解析式,将已知的点A,B的坐标代入设的函数解析式列出关于待定系数的方程（组）求出系数，再回代到解析式（2）结合图像判断直线AB在双曲线的交点坐标为A,B，X取值范围为双曲线所在象限交点的横坐标，第一象限为为小于横坐标大于零，第三象限为小于横坐标（3）结合已知条件根据同底等高、等底同高作出与原三角形面积相等的三角形，再结合已知条件用待定系数法求出与双曲线有交点的直线的解析式，得出点的坐标，注意要考虑满足条件的所有点C的坐标。

中考数学反比例函数-经典压轴题附答案

中考数学压轴题专题复习——反比例函数的综合及答案

中考数学压轴题专题复习——反比例函数的综合及答案一、反比例函数1．如图，反比例函数y= 的图象经过点A（﹣1，4），直线y=﹣x+b（b≠0）与双曲线y= 在第二、四象限分别相交于P，Q两点，与x轴、y轴分别相交于C，D两点．（1）求k的值；（2）当b=﹣2时，求△OCD的面积；（3）连接OQ，是否存在实数b，使得S△ODQ=S△OCD？若存在，请求出b的值；若不存在，请说明理由．【答案】（1）解：∵反比例函数y= 的图象经过点A（﹣1，4），∴k=﹣1×4=﹣4；（2）解：当b=﹣2时，直线解析式为y=﹣x﹣2，∵y=0时，﹣x﹣2=0，解得x=﹣2，∴C（﹣2，0），∵当x=0时，y=﹣x﹣2=﹣2，∴D（0，﹣2），∴S△OCD= ×2×2=2（3）解：存在．当y=0时，﹣x+b=0，解得x=b，则C（b，0），∵S△ODQ=S△OCD，∴点Q和点C到OD的距离相等，而Q点在第四象限，∴Q的横坐标为﹣b，当x=﹣b时，y=﹣x+b=2b，则Q（﹣b，2b），∵点Q在反比例函数y=﹣的图象上，∴﹣b•2b=﹣4，解得b=﹣或b= （舍去），∴b的值为﹣．【解析】【分析】（1）根据反比例函数的图象上点的坐标特征易得k=﹣4；（2）当b=﹣2时，直线解析式为y=﹣x﹣2，则利用坐标轴上点的坐标特征可求出C（﹣2，0），D（0，﹣2），然后根据三角形面积公式求解；（3）先表示出C（b，0），根据三角形面积公式，由于S△ODQ=S△OCD，所以点Q和点C到OD的距离相等，则Q的横坐标为（﹣b，0），利用直线解析式可得到Q（﹣b，2b），再根据反比例函数的图象上点的坐标特征得到﹣b•2b=﹣4，然后解方程即可得到满足条件的b的值．2．已知点A，B分别是x轴、y轴上的动点，点C，D是某个函数图象上的点，当四边形ABCD（A，B，C，D各点依次排列）为正方形时，我们称这个正方形为此函数图象的“伴侣正方形”．例如：在图1中，正方形ABCD是一次函数y=x+1图象的其中一个“伴侣正方形”．（1）如图1，若某函数是一次函数y=x+1，求它的图象的所有“伴侣正方形”的边长；（2）如图2，若某函数是反比例函数（k＞0），它的图象的“伴侣正方形”为ABCD，点D（2，m）（m＜2）在反比例函数图象上，求m的值及反比例函数的解析式；（3）如图3，若某函数是二次函数y=ax2+c（a≠0），它的图象的“伴侣正方形”为ABCD，C，D中的一个点坐标为（3，4），请你直接写出该二次函数的解析式．【答案】（1）解：（I）当点A在x轴正半轴、点B在y轴负半轴上时：正方形ABCD的边长为．（II）当点A在x轴负半轴、点B在y轴正半轴上时：设正方形边长为a，易得3a= ，解得a= ，此时正方形的边长为．∴所求“伴侣正方形”的边长为或（2）解：如图，作DE⊥x轴，CF⊥y轴，垂足分别为点E、F，易证△ADE≌△BAO≌△CBF．∵点D的坐标为（2，m），m＜2，∴DE=OA=BF=m，∴OB=AE=CF=2﹣m．∴OF=BF+OB=2，∴点C的坐标为（2﹣m，2）．∴2m=2（2﹣m），解得m=1．∴反比例函数的解析式为y=（3）解：实际情况是抛物线开口向上的两种情况中，另一个点都在（3，4）的左侧，而开口向下时，另一点都在（3，4）的右侧，与上述解析明显不符合a、当点A在x轴正半轴上，点B在y轴正半轴上，点C坐标为（3，4）时：另外一个顶点为（4，1），对应的函数解析式是y=﹣ x2+ ；b、当点A在x 轴正半轴上，点 B在 y轴正半轴上，点D 坐标为（3，4）时：不存在，c、当点A 在 x 轴正半轴上，点 B在 y轴负半轴上，点C 坐标为（3，4）时：不存在d、当点A在x 轴正半轴上，点B在y轴负半轴上，点D坐标为（3，4）时：另外一个顶点C为（﹣1，3），对应的函数的解析式是y= x2+ ；e、当点A在x轴负半轴上，点B在y轴负半轴上，点C坐标为（3，4）时，另一个顶点D的坐标是（7，﹣3）时，对应的函数解析式是y=﹣ x2+ ；f、当点A在x轴负半轴上，点B在y轴负半轴上，点C坐标为（3，4）时，另一个顶点D 的坐标是（﹣4，7）时，对应的抛物线为y= x2+ ；故二次函数的解析式分别为：y= x2+ 或y=﹣ x2+ 或y=﹣ x2+ 或y= x2+【解析】【分析】（1）先正确地画出图形，再利用正方形的性质确定相关点的坐标从而计算正方形的边长.（2）因为ABCD为正方形，所以可作垂线得到等腰直角三角形，利用点D（2，m）的坐标表示出点C的坐标，可求出m的值，即可得到反比例函数的解析式．（3）由抛物线开口既可能向上，也可能向下．当抛物线开口向上时，正方形的另一个顶点也是在抛物线上，这个点既可能在点（3，4）的左边，也可能在点（3，4）的右边，过点（3，4）向x轴作垂线，利用全等三角形确定线段的长即可确定抛物线上另一个点的坐标；当抛物线开口向下时也是一样地分为两种情况来讨论，即可得到所求的结论．3．【阅读理解】对于任意正实数a、b，因为≥0，所以≥0，所以≥2 ，只有当时，等号成立．【获得结论】在≥2 （a、b均为正实数）中，若为定值，则≥2 ，只有当时，有最小值2 ．（1）根据上述内容，回答下列问题：若 >0，只有当 =________时，有最小值________．（2）【探索应用】如图，已知A（－3，0），B（0，－4），P为双曲线（＞0）上的任意一点，过点P作PC⊥x轴于点C，PD⊥y轴于点D．求四边形ABCD面积的最小值，并说明此时四边形ABCD的形状．【答案】（1）1；2（2）解：设P（x，），则C（x，0），D（0，），∴CA=x+3，BD= +4，∴S四边形= CA×BD= （x+3）（ +4），化简得：S=2（x+ ）+12．∵x＞0，＞0，∴x+ ≥2 ABCD=6，只有当x= ，即x=3时，等号成立，∴S≥2×6+12=24，∴四边形ABCD的面积有最小值24，此时，P（3，4），C（3，0），D（0，4），AB=BC=CD=DA=5，∴四边形ABCD是菱形．【解析】【解答】解：（1）根据题目所给信息可知m+ ≥2 ，且当m= 时等号，∴当m=1时，m+ ≥2，即当m=1时，m+ 有最小值2．故答案为：1，2；【分析】（1）此题是一道阅读题，根据题中所给的信息可知：，只有当m=时等号成立，一个正数只有1和它的倒数相等，从而得出答案；（2）根据双曲线上点的坐标特点设出P点的坐标，根据垂直于坐标轴上的点的坐标特点表示出C,D两点的坐标，从而表示出AC,BD的长，根据对角线互相垂直的四边形的面积等于两对角线积的一半建立出S与x的函数关系式，根据题干提供的信息得出得出,只有在，即x=3时，等号成立，从而得出S的最小值，从而得出P,C,D三点的坐标，进而算出AB=BC=CD=DA=5，根据四边相等的四边形是菱形得出结论。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

2009-2013年中考反比例函数经典结论：如图，反比例函数k 的几何意义： (I ) 12AOB AOC S S k ∆∆==； (II ) OBAC S k =矩形。

下面两个结论是上述结论的拓展.(1) 如图①，OPA OCD S S ∆∆=，OPC PADC S S ∆=梯形。

(2)如图②，OAPB OBCA S S =梯形梯形，BPE ACE S S ∆∆=。

经典例题例 1.(1)(兰州)如图，已知双曲线(0)ky x x=>经过矩形OABC 边AB 的中点F 且交BC 于点E ，四边形OEBF 的面积为2，则k = 2 ；(2)如图，点A B 、为直线y x =上的两点，过A B 、两点分别作y 轴的平行线交双曲线1(0)y x x=>于C D 、两点，若2BD AC =，则224OC OD -例2．(2013陕西) 如果一个正比例函数的图象与一个反比例函数x y 6=),(),,(2211y x B y x A ，那么))((1212y y x x --值为 24 .解析：因为A，B 在反比例函数xy 6=上，所以611=y x ，我们知道正比例函数与反比例函数的交点坐标关于原点成中心对称，因此),(),,(2211y xBy x A 中有1212,y y x x -=-=，所以24644))(())((1111111212=⨯==----=--y x y y x x y y x x例3．(2010山东威海) 如图，一次函数b kx y +=的图象与反比例函数xmy =的图象交于点A ﹙－2，－5﹚，C ﹙5，n ﹚，交y 轴于点B ，交x 轴于点D ．(1) 求反比例函数xmy =和一次函数b kx y +=的表达式； (2) 连接OA ，OC ．求△AOC 的面积．解：(1)∵ 反比例函数xmy =的图象经过点A ﹙－2，－5﹚， ∴ m =(－2)×( －5)＝10．∴ 反比例函数的表达式为xy 10=． ∵ 点C ﹙5，n∴ 2510==n ． ∴ C 的坐标为﹙5，2﹚． ∵ 一次函数的图象经过点A ，C ，将这两个点的坐标代入b kx y +=，得 ⎩⎨⎧+=+-=-.5225b k b k ，解得⎩⎨⎧-==.31b k ，∴ 所求一次函数的表达式为y ＝x －3．(2) ∵ 一次函数y =x －3的图像交y 轴于点B ， ∴ B 点坐标为﹙0，－3﹚． ∴ OB ＝3． ∵ A 点的横坐标为－2，C 点的横坐标为5，∴ S △AOC = S △AOB + S △BOC =()22152215212-21=+⋅⋅=⋅⋅+⋅⋅OB OB OB ．例4．（2007福建福州）如图，已知直线12y x =与双曲线(0)ky k x=>交于A B ，两点，且点A 的横坐标为4．（1）求k 的值；（2）若双曲线(0)ky k x=>上一点C 的纵坐标为8，求AOC △的面积；（3）过原点O 的另一条直线l 交双曲线(0)ky k x=>于P Q ，两点（P 点在第一象限），若由点A B P Q，，，为顶点组成的四边形面积为24，求点P 的坐标．解：（1）点A 横坐标为4，∴当4x =时，2y =．∴点A 的坐标为(42)，．点A 是直线12y x =与双曲线(0)ky k x=>的交点，428k ∴=⨯=．（2）解法一：如图1，点C 在双曲线上，当8y =时，1x =∴点C 的坐标为(18)，．过点A C ，分别做x 轴，y 轴的垂线，垂足为M N ，，得矩形DMON ．32ONDM S =矩形，4ONC S =△，9CDA S =△，4OAM S =△．3249415AOC ONC CDA OAM ONDM S S S S S =---=---=△△△△矩形解法二：如图2，过点C A ，分别做x 轴的垂线，垂足为E F ，，点C 在双曲线8y x =上，当8y =时，1x=．∴点C 的坐标为(18)，．点C ，A 都在双曲线8y x=上， 4COE AOF S S ∴==△△ COE COA AOF CEFA S S S S ∴+=+△△△梯形． COA CEFA S S ∴=△梯形．1(28)3152CEFA S =⨯+⨯=梯形，15COA S ∴=△．（3）反比例函数图象是关于原点O 的中心对称图形，OP OQ ∴=，OA OB =．∴四边形APBQ 是平行四边形．1124644POA APBQ S S ∴==⨯=△平行四边形．设点P 横坐标为(04)m m m >≠且，得8()P m m，．过点P A ，分别做x 轴的垂线，垂足为E F ，，点P A ，在双曲线上，4PQE AOF S S ∴==△△．若04m <<，如图3，POE POA AOF PEFA S S S S +=+△△△梯形，6POA PEFA S S ∴==△梯形．182(4)62m m ⎛⎫+-= ⎪⎝⎭∴·．解得2m =，8m =-（舍去）．∴(24)P ，．若4m >，如图4，AOF AOP POE AFEP S S S S +=+△△△梯形，6POA PEFA S S ∴==△梯形．182(4)62m m ⎛⎫∴+-= ⎪⎝⎭，解得8m =，2m =-（舍去）．(81)P ∴，． ∴点P 的坐标是(24)P ，或(81)P ，．图2图3图4例5.(山东淄博) 如图，正方形AOCB的边长为4，反比例函数的图象过点E（3，4）．（1）求反比例函数的解析式；（2）反比例函数的图象与线段BC交于点D，直线1y x b2过点D，与线段AB相交于点F，求点F的坐标；（3）连接OF，OE，探究∠AOF与∠EOC的数量关系，并证明．【答案】解：（1）设反比例函数的解析式kyx，∵反比例函数的图象过点E（3，4），∴k43，即k=12。

∴反比例函数的解析式12yx。

（2）∵正方形AOCB的边长为4，∴点D的横坐标为4，点F的纵坐标为4。

∵点D在反比例函数的图象上，∴点D的纵坐标为3，即D（4,3）。

∵点D在直线1y x b2上，∴134b2，解得b=5。

∴直线DF为1y x52。

将y4代入1y x52，得14x52，解得x2。

∴点F的坐标为（2，4）。

（3）∠AOF＝12∠EOC。

证明如下：在CD上取CG=CF=2，连接OG，连接EG并延长交ｘ轴于点H。

∵AO=CO=4，∠OAF=∠OCG=900，AF=CG=2，∴△OAF≌△OCG（SAS）。

∴∠AOF=∠COG。

∵∠EGB=∠HGC，∠B=∠GCH=900，BG=CG=2，∴△EGB≌△HGC（AAS）。

∴EG=HG。

设直线EG：y mx n，∵E（3，4），G（4，2），∴43m n24m n=+⎧⎨=+⎩，解得，m2n=10=⎧⎨⎩－。

∴直线EG：y2x10。

令y2x10=0，得x5。

∴H（5，0），OH=5。

在Rｔ△AOF中，AO=4，AE=3，根据勾股定理，得OE=5。

∴OH=OE。

∴OG是等腰三角形底边EH上的中线。

∴OG是等腰三角形顶角的平分线。

∴∠EOG=∠GOH。

∴∠EOG=∠GOC=∠AOF，即∠AOF＝12∠EOC。

例6.(2009山东威海) 一次函数y ax b =+的图象分别与x 轴、y 轴交于点,M N ，与反比例函数ky x=的图象相交于点,A B ．过点A 分别作AC x ⊥轴，AE y ⊥轴，垂足分别为,C E ；过点B 分别作BF x ⊥轴，BD y ⊥轴，垂足分别为F D ，，AC 与BD 交于点K ，连接CD ．（1）若点A B ，在反比例函数ky x=的图象的同一分支上，如图1，试证明： ①AEDK CFBK S S =四边形四边形； ②AN BM =．（2）若点A B ，分别在反比例函数ky x=的图象的不同分支上，如图2，则AN 与BM 还相等吗？试证明你的结论．解：（1）①AC x ⊥轴，AE y ⊥轴，∴四边形AEOC 为矩形．BF x ⊥轴，BD y ⊥轴，∴四边形BDOF 为矩形．AC x ⊥轴，BD y ⊥轴，∴四边形AEDK DOCK CFBK ，，均为矩形．1111OC x AC y x y k ===，，， ∴11AEOC S OC AC x y k ===矩形2222OF x FB y x y k ===，，，∴22BDOF S OF FB x y k ===矩形． ∴AEOC BDOF S S =矩形矩形．AEDK AEOC DOCK S S S =-矩形矩形矩形，CFBK BDOF DOCK S S S =-矩形矩形矩形， ∴AEDK CFBK S S =矩形矩形 ②由（1）知AEDK CFBK S S =矩形矩形．∴AK DK BK CK =．∴AK BKCK DK=90AKB CKD ∠=∠=°，∴AKB CKD △∽△．∴CDK ABK ∠=∠．∴AB CD∥AC y ∥轴，∴四边形ACDN 是平行四边形．∴AN CD =．同理BM CD =．AN BM ∴=．（2）AN 与BM 仍然相等．AEDK AEOC ODKC S S S =+矩形矩形矩形，BKCF BDOF ODKC S S S =+矩形矩形矩形，又AEOC BDOF S S k ==矩形矩形，)yy2y x=∴AEDK BKCF S S =矩形矩形 ∴AK DK BK CK =． ∴CK DKAK BK=． K K ∠=∠，∴CDK ABK △∽△．∴CDK ABK ∠=∠． ∴AB CD ∥．AC y ∥轴， ∴四边形ANDC 是平行四边形． ∴AN CD =．同理BM CD =． ∴AN BM =．第一部分练习一、选择题1.(2009年鄂州)如图，直线y =mx 与双曲线y =xk交于A 、B 两点，过点A 作AM ⊥x 轴，垂足为M ，连结BM ,若ABM S ∆=2，则k 的值是A .2B .m －2C .mD .42.(2009兰州) 如图，若正方形OABC 的顶点B 和正方形ADEF 的顶点E 都在函数1y x=（0x >）的图象上，则点E 的坐标是（，）. 3.(2009泰安）如图，双曲线)0(＞k xky =经过矩形OABC 的边BC 的中点E ，交AB 于点D 。

若梯形ODBC 的面积为3，则双曲线的解析式为A ．x y 1=B ．x y 2=C ． x y 3=D ．xy 6=4.（2009仙桃）如图，已知双曲线)0k (xky ＞=经过直角三角形OAB 斜边OB 的中点D ，与直角边AB 相交于点C ．若△OBC 的面积为3，则k ＝____________． 5.(2009年牡丹江市)如图，点A 、B 是双曲线3y x=上的点，分别经过A 、B 两点向x 轴、y 轴作垂线段，若1S =阴影，则12S S += ．6.（2009年莆田）如图，在x 轴的正半轴上依次截取112233445OA A A A A A A A A ====，过点12345A A A A A 、、、、分别作x 轴的垂线与反比例函数()20y x x=≠的图象相交于点12345P P P P P 、、、、，得直角三角形1112233344455OP A A P A A P A A P A A P A 2、、、、，并设其面积分别为12345S S S S S 、、、、，则5S 的值为．．yAB E y第4题图第5题图第6题图 7.（2009年包头）已知一次函数1y x =+与反比例函数ky x=的图象在第一象限相交于点A ，与x 轴相交于点C AB x ，⊥轴于点B ，AOB △的面积为1，则AC 的长为8.（2010 嵊州市）如图,直线)0(<=k kx y 与双曲线xy 2-=交于),(),,(2211y x B y x A 两点,则122183y x y x -的值为 A .－5 B .－10 C .5 D .10 【答案】B9.（2010江苏无锡）如图，已知梯形ABCO 的底边AO 在x 轴上，BC ∥AO ，AB ⊥AO ，过点C 的双曲线k y x= 交OB 于D ，且OD ：DB=1:2，若△OBC 的面积等于3，则k 的值 A ．等于2 B ．等于34C ．等于5D ．无法确定【答案】B第7题图第8题图第9题图10.（2010江苏盐城）如图，A 、B 是双曲线 y = kx (k >0) 上的点， A 、B 两点的横坐标分别是a 、2a ，线段AB 的延长线交x 轴于点C ，若S △AOC =6．则k= ．【答案】4 11.（2010安徽蚌埠二中）已知点（1，3）在函数)0(>=x xky 的图像上。