2021年中考数学压轴题专项训练反比例函数含解析202102192297
反比例函数压轴题精选(含答案)
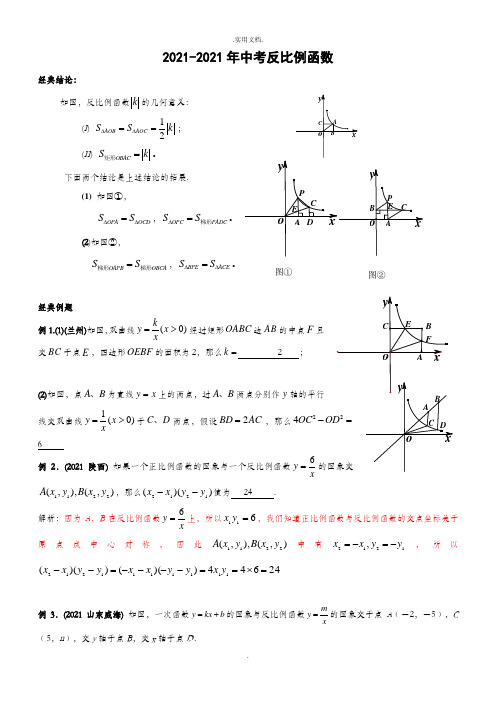
2021-2021年中考反比例函数经典结论：如图，反比例函数k 的几何意义： (I ) 12AOB AOC S S k ∆∆==； (II ) OBAC S k =矩形。
下面两个结论是上述结论的拓展.(1) 如图①，OPA OCD S S ∆∆=，OPC PADC S S ∆=梯形。
(2)如图②，OAPB OBCA S S =梯形梯形，BPE ACE S S ∆∆=。
经典例题例1.(1)(兰州)如图，双曲线(0)ky x x=>经过矩形OABC边AB 的中点F 且交BC 于点E ，四边形OEBF 的面积为2，那么k = 2 ；(2)如图，点A B 、为直线y x =上的两点，过A B 、两点分别作y 轴的平行线交双曲线1(0)y x x=>于C D 、两点，假设2BD AC =，那么24OC -6例2．(2021陕西) 如果一个正比例函数的图象与一个反比例函数xy 6=),(),,(2211y x B y x A ，那么))((1212y y x x --值为 24 .解析：因为A ，B 在反比例函数xy 6=上，所以611=y x ，我们知道正比例函数与反比例函数的交点坐标关于原点成中心对称，因此),(),,(2211y x B y x A 中有1212,y y x x -=-=，所以24644))(())((1111111212=⨯==----=--y x y y x x y y x x例3．(2021山东威海) 如图，一次函数b kx y +=的图象与反比例函数xmy =的图象交于点A ﹙－2，－5﹚，C ﹙5，n ﹚，交y 轴于点B ，交x 轴于点D ．(1) 求反比例函数xmy =和一次函数b kx y +=的表达式； (2) 连接OA ，OC ．求△AOC 的面积． 解：(1)∵ 反比例函数xmy =的图象经过点A ﹙－2，－5﹚， ∴ m =(－2)×( －5)＝10．∴ 反比例函数的表达式为xy 10=． ∵ 点C ﹙5，n∴ 2510==n ． ∴ C 的坐标为﹙5，2﹚． ∵ 一次函数的图象经过点A ，C ，将这两个点的坐标代入b kx y +=，得 ⎩⎨⎧+=+-=-.5225b k b k ，解得⎩⎨⎧-==.31b k ，∴ 所求一次函数的表达式为y ＝x －3．(2) ∵ 一次函数y =x －3的图像交y 轴于点B ， ∴ B 点坐标为﹙0，－3﹚． ∴ OB ＝3． ∵ A 点的横坐标为－2，C 点的横坐标为5，∴ S △AOC = S △AOB + S △BOC =()22152215212-21=+⋅⋅=⋅⋅+⋅⋅OB OB OB ．例4．〔2007福建福州〕如图，直线12y x =与双曲线(0)ky k x=>交于A B ，两点，且点A 的横坐标为4． 〔1〕求k 的值；〔2〕假设双曲线(0)ky k x=>上一点C 的纵坐标为8，求AOC △的面积； 〔3〕过原点O 的另一条直线l 交双曲线(0)ky k x=>于P Q ，两点〔P 点在第一象限〕，假设由点A B P Q ，，，为顶点组成的四边形面积为24，求点P 的坐标．解：〔1〕点A 横坐标为4，∴当4x =时，2y =．∴点A 的坐标为(42)，． 点A 是直线12y x =与双曲线(0)ky k x =>的交点，428k ∴=⨯=．〔2〕解法一：如图1，点C 在双曲线上，当8y =时，1x =∴点C 的坐标为(18)，． 过点A C ，分别做x 轴，y 轴的垂线，垂足为M N ，，得矩形DMON ．32ONDM S =矩形，4ONC S =△，9CDA S =△，4OAM S =△．3249415AOC ONC CDA OAM ONDM S S S S S =---=---=△△△△矩形．解法二：如图2，过点C A ，分别做x 轴的垂线，垂足为E F ，，点C 在双曲线8y x=上，当8y =时，1x =．∴点C 的坐标为(18)，．点C ，A 都在双曲线8y x=上， 4COE AOF S S ∴==△△ COE COA AOF CEFA S S S S ∴+=+△△△梯形．COA CEFA S S ∴=△梯形．1(28)3152CEFA S =⨯+⨯=梯形，15COA S ∴=△．〔3〕反比例函数图象是关于原点O 的中心对称图形，OP OQ ∴=，OA OB =．∴四边形APBQ 是平行四边形． 1124644POA APBQ S S ∴==⨯=△平行四边形． 设点P 横坐标为(04)m m m >≠且，得8()P m m，．过点P A ，分别做x 轴的垂线，垂足为E F ，， 点P A ，在双曲线上，4PQE AOF S S ∴==△△． 假设04m <<，如图3，POE POA AOF PEFA S S S S +=+△△△梯形，6POA PEFA S S ∴==△梯形．182(4)62m m ⎛⎫+-= ⎪⎝⎭∴·． 解得2m =，8m =-〔舍去〕．∴(24)P ，． 假设4m >，如图4，AOF AOP POE AFEP S S S S +=+△△△梯形，6POA PEFA S S ∴==△梯形．182(4)62m m ⎛⎫∴+-= ⎪⎝⎭，解得8m =，2m =-〔舍去〕．(81)P ∴，． ∴点P 的坐标是(24)P ，或(81)P ，． 例5.(山东淄博) 如图，正方形AOCB 的边长为4，反比例函数的图象过点E 〔3，4〕．图2O x AyBFE C图3O AyBFQE P x图4O x AyBF E QP〔1〕求反比例函数的解析式；〔2〕反比例函数的图象与线段BC 交于点D ，直线1y x b 2过点D ，与线段AB 相交于点F ，求点F 的坐标；〔3〕连接OF ，OE ，探究∠AOF 与∠EOC 的数量关系，并证明．【答案】解：〔1〕设反比例函数的解析式k y x， ∵反比例函数的图象过点E 〔3，4〕，∴k43，即k=12。
完整版中考反比例函数压轴题
完美WORD格式资料反比例函数一．填空题〔共19小题〕1．〔2021?湖州〕如图，点A是第一象限内横坐标为2的一个定点，AC⊥x轴于点M，交直线y=﹣x于点N．假设点P是线段ON上的一个动点，∠APB=30°，BA⊥PA，那么点P在线段ON上运动时， A点不变，B点随之运动．求当点P从点O运动到点N时，点B运动的路径长是．2．〔2021?市中区一模〕如图，双曲线经过直角三角形OAB斜边OA的中点D，且与直角边AB相交于点C．假设点A的坐标为〔﹣6，4〕，那么△AOC的面积为．3．〔2021?石家庄校级一模〕如图，Rt△ABC的直角边BC在x轴正半轴上，斜边AC上的中线BD反向延长线交y轴负半轴于E，双曲线y= 的图象经过点A，假设S△BEC=8，那么k= ．4．〔2021?同安区校级质检〕如图，直线y=﹣x+b与双曲线y=﹣〔x＜0〕交于点A，与x轴交于点B，那么OA2﹣OB2= ．专业整理分享完美WORD格式资料5．〔2021?邳州市二模〕如图，点P在双曲线y= 〔x＞0〕上，以P为圆心的⊙P与两坐标轴都相切，点E为y轴负半轴上的一点，过点P作PF⊥PE交x轴于点F，假设OF﹣OE=6，那么k的值是．6．〔2021?遵义二模〕如图，矩形ABCD的对角线 BD经过坐标原点，矩形的边分别平行于坐标轴，点C在反比例函数的图象上．假设点A的坐标为〔﹣2，﹣2〕，那么k的值为．7．〔2021?黄石〕如下图，在平面直角坐标系中，一次函数y=ax+b〔a≠0〕的图象与反比例函数〔k≠0〕的图象交于二、四象限的A、B两点，与x轴交于C点．A 〔﹣2，m〕，B〔n，﹣2〕，tan∠BOC=，那么此一次函数的解析式为．专业整理分享8．〔2021?遵〕如，直y= x与双曲y= 〔k＞0〕交于A、B两点，点 B的坐〔4，2〕，C双曲y= 〔k＞0〕上一点，且在第一象限内，假设△AOC的面6，点C的坐．9．〔2021?州〕如，点P1〔x1，y1〕，点P2〔x2，y2〕，⋯，点Pn〔xn，yn〕在函数〔x ＞0〕的象上，△P1OA1，△P2A1A2，△P3A2A3，⋯，△P n A n﹣1A n都是等腰直角三角形，斜OA1、A1A2、A2A3，⋯，An﹣1An都在x上〔n是大于或等于2的正整数〕，点P3的坐是；点Pn的坐是〔用含n的式子表示〕．10．〔2021?宁波〕如，等腰直角三角形ABC点A在x上，∠BCA=90°，AC=BC=2 ，反比例函数y= 〔x＞0〕的象分与AB，BC交于点D，E．DE，当△BDE∽△BCA，点E的坐．11．〔2021?重〕如，菱形OABC的点O是坐原点，点A在x的正半上，点B、C均在第一象限，OA=2，∠AOC=60°．点D在AB上，将四形OABC沿直0D翻折，使点B和点C分落在个坐平面的点B′和C′，且∠C′DB′=60．°假设某反比例函数的象点B′，个反比例函数的解析式．专业整理分享12．〔2021?芦淞区模拟〕双曲线，的局部图象如下图，P是y轴正半轴上一点，过点P作AB∥x轴，分别交两个图象于点A，B．假设PB=2PA，那么k= ．13．〔2021?阜宁县二模〕如图，D是反比例函数的图象上一点，过D作DE⊥x轴于E，DC⊥y轴于C，一次函数y=﹣x+m与的图象都经过点C，与x轴分别交于A、B两点，四边形DCAE的面积为 4，那么k的值为．14．〔2021?邓州市校级一模〕如图，梯形ABCO的底边AO在x轴上，BC∥AO，AB⊥AO，过点C的双曲线交OB于D，且OD：DB=1：2，假设△OBC的面积等于3，那么k的值是．15．〔2021?三明〕如图，点A在双曲线上，点B在双曲线上，且AB∥y轴，点P是y轴上的任意一点，那么△PAB的面积为．专业整理分享完美WORD格式资料16．〔2021?十堰〕如图，直线y=6x，y= x分别与双曲线y= 在第一象限内交于点A，B，假设S△OAB=8，那么k=．17．〔2021?漳州〕如图，点A〔3，n〕在双曲线y=上，过点A作AC⊥x轴，垂足为C．线段OA的垂直平分线交OC于点M，那么△AMC周长的值是．18．〔2021?淄博模拟〕如图，直线y= x与双曲线 y=〔x＞0〕交于点A，将直线y= x向下平移个6单位后，与双曲线y=〔x＞0〕交于点B，与x轴交于点C，那么C点的坐标为；假设=2，那么k=．19．〔2021?桐乡市校级三模〕如图，点A〔a，b〕在双曲线上，AB⊥x轴于点B，假设点是双曲线上异于点A的另一点．专业整理分享完美WORD 格式资料〔1 〕k=；〔2〕假设a 2=169﹣b 2，那么△OAB 的内切圆半径r= ．二．解答题〔共 11小题〕20．解方程组：21．〔2021?淄博〕如图，点A 与点B 的坐标分别是〔 1，0〕，〔5，0〕，点P 是该直角坐标系内的一个动点．〔1 〕使∠APB=30°的点P 有 个；〔2 〕假设点P 在y 轴上，且∠APB=30°，求满足条件的点P 的坐标；〔3 〕当点P 在y 轴上移动时，∠APB 是否有最大值？假设有，求点 P 的坐标，并说明此时∠APB最大的理由；假设没有，也请说明理由．22．〔2021?湖州〕如图①， O 为坐标原点，点 B 在x 轴的正半轴上，四边形 OACB 是平行四边形，sin ∠AOB= ，反比例函数 y= 〔k ＞0〕在第一象限内的图象经过点 A ，与BC 交于点F ．1〕假设OA=10，求反比例函数解析式；2〕假设点F 为BC 的中点，且△AOF 的面积S=12，求OA 的长和点C 的坐标；〔3〕在〔2〕中的条件下，过点F 作EF ∥OB ，交OA 于点E 〔如图②〕，点P 为直线EF 上的一个动点，连接PA ，PO ．是否存在这样的点P ，使以P 、O 、A 为顶点的三角形是直角三角形？假设存在，请直接写出所有点 P 的坐标；假设不存在，请说明理由．专业整理分享完美WORD格式资料23．〔2021?泉州〕如图，直线y=﹣x+3与x，y轴分别交于点A，B，与反比例函数的图象交于点P〔2，1〕．1〕求该反比例函数的关系式；2〕设PC⊥y轴于点C，点A关于y轴的对称点为A′；①求△A′BC的周长和sin∠BA′C的值；②对大于1的常数m，求x轴上的点M的坐标，使得sin∠BMC=．24．〔2021?巴中〕如图，在平面直角坐标系xOy中，一次函数y=kx+b〔k≠0〕的图象与反比例函数y=的图象交于一、三象限内的A、B两点，直线A B与x轴交于点C，点B的坐标为〔﹣6，n〕，线段OA=5，E为x轴正半轴上一点，且tan∠AOE=．（1〕求反比例函数的解析式；2〕求△AOB的面积．专业整理分享完美WORD格式资料25．〔2021?龙岩〕如图，将边长为4的等边三角形AOB放置于平面直角坐标系xoy中，F是AB边上的动点〔不与端点A、B重合〕，过点F的反比例函数y=〔k＞0，x＞0〕与OA边交于点E，过点F作FC⊥x轴于点C，连结EF、OF．〔1〕假设S△OCF=，求反比例函数的解析式；〔2〕在〔1〕的条件下，试判断以点E为圆心，EA长为半径的圆与y轴的位置关系，并说明理由；〔3〕AB边上是否存在点F，使得EF⊥AE？假设存在，请求出BF：FA的值；假设不存在，请说明理由．26．〔2021?广元〕如图，双曲线y=经过点D〔6，1〕，点C是双曲线第三象限上的动点，过C作CA⊥x轴，过D作DB⊥y轴，垂足分别为A，B，连接AB，BC．1〕求k的值；2〕假设△BCD的面积为12，求直线CD的解析式；3〕判断AB与CD的位置关系，并说明理由．27．〔2021?北海〕如图，在平面直角坐标系中有Rt△ABC，∠A=90°，AB=AC，A〔﹣2，0〕、B〔0，1〕、C〔d，2〕．〔1〕求d的值；〔2〕将△ABC沿x轴的正方向平移，在第一象限内B、C两点的对应点B′、C′正好落在某反比例函数图象上．请求出这个反比例函数和此时的直线B′C′解析式；的专业整理分享完美WORD 格式资料〔3〕在〔2〕的条件下，直线 BC 交y 轴于点G ．问是否存在 x 轴上的点 M 和反比例函数图象 上的点P ，使得四边形 PGMC ′是平行四边形？如果存在，请求出点M 和点P 的坐标；如果不存 在，请说明理由．28．〔2021?泰州〕如图，一次函数y 1=kx+b 图象与x 轴相交于点 A ，与反比例函数 的图象相交于B 〔﹣1，5〕、C 〔，0〕两点．点P 〔m ，n 〕是一次函数 y 1=kx+b 的图象上的动点．〔1 〕求k 、b 的值；〔2 〕设﹣1＜m ＜，过点P 作x 轴的平行线与函数的图象相交于点D ．试问△PAD 的面积是否存在最大值？假设存在，请求出面积的最大值及此时点 P 的坐标；假设不存在，请说明理由；〔3 〕设m=1﹣a ，如果在两个实数m 与n 之间〔不包括m 和n 〕有且只有一个整数，求实数a的取值范围．29．〔2021?淄博〕如图，正方形 AOCB 的边长为 4，反比例函数的图象过点E 〔3，4〕．〔1 〕求反比例函数的解析式；〔2 〕反比例函数的图象与线段 BC 交于点D ，直线过点D ，与线段AB 相交于点F ，求点F 的坐标；〔3 〕连接OF ，OE ，探究∠AOF 与∠EOC 的数量关系，并证明．专业整理分享完美WORD格式资料30．〔2021?长春一模〕如图，在平面直角坐标系中，△ABC的顶点A、B分别落在x轴、y轴的正半轴上，顶点C在第一象限，BC与x轴平行．BC=2，△ABC的面积为1．〔1〕求点C的坐标．〔2〕将△ABC绕点C顺时针旋转90°，△ABC旋转到△A1B1C的位置，求经过点B1的反比例函数关系式．专业整理分享完美WORD格式资料2021年03月05日1161622024的初中数学组卷参考答案与试题解析一．填空题〔共19小题〕1．〔2021?湖州〕如图，点A是第一象限内横坐标为2的一个定点，AC⊥x轴于点M，交直线y=﹣x于点N．假设点P是线段ON上的一个动点，∠APB=30°，BA⊥PA，那么点P在线段ON上运动时，A点不变，B点随之运动．求当点P从点O运动到点N时，点B运动的路径长是．考点：一次函数综合题．专题：压轴题．分析：〔1〕首先，需要证明线段B0B n就是点B运动的路径〔或轨迹〕，如答图②所示．利用相似三角形可以证明；〔2〕其次，如答图①所示，利用相似三角形△AB0n0n的长度，B∽△AON，求出线段BB即点B运动的路径长．解答：解：由题意可知，OM=，点N在直线y=﹣x上，AC⊥x轴于点M，那么△OMN为等腰直角三角形，ON=OM=×=．如答图①所示，设动点P在O点〔起点〕时，点B的位置为B0，动点P在N点〔终点〕时，点B的位置为B n，连接B0B nAO⊥AB0，AN⊥AB n，∴∠OAC=∠B0AB n，又∵AB0=AO?tan30°，AB n=AN?tan30°，∴AB0：AO=AB n：AN=tan30°〔此处也可用30°角的Rt△三边长的关系来求得〕，∴△AB0B n∽△AON，且相似比为tan30°，∴B0B n=ON?tan30°=×=．现在来证明线段B0B n就是点B运动的路径〔或轨迹〕．如答图②所示，当点P运动至ON上的任一点时，设其对应的点B为B i，连接AP，AB i，B0B iAO⊥AB0，AP⊥AB i，∴∠OAP=∠B0AB i，又∵AB0=AO?tan30°，AB i=AP?tan30°∴，AB0：AO=AB i：AP，∴△AB0B i∽△AOP，∴∠AB0B i=∠AOP．又∵△AB0B n∽△AON，∴∠AB0B n=∠AOP，专业整理分享完美WORD格式资料∴∠AB0B i=∠AB0B n，∴点B i在线段B0B n上，即线段B0B n就是点B运动的路径〔或轨迹〕．综上所述，点B运动的路径〔或轨迹〕是线段B0B n，其长度为．故答案为：．点评：此题考查坐标平面内由相似关系确定的点的运动轨迹，难度很大．此题的要点有两个：首先，确定点B的运动路径是此题的核心，这要求考生有很好的空间想象能力和分析问题的能力；其次，由相似关系求出点B运动路径的长度，可以大幅简化计算，防止陷入坐标关系的复杂运算之中．2．〔2021?市中区一模〕如图，双曲线经过直角三角形OAB斜边OA的中点D，且与直角边AB相交于点C．假设点A的坐标为〔﹣6，4〕，那么△AOC的面积为9．考点：反比例函数系数k的几何意义．专题：压轴题；数形结合．分析：要求△AOC的面积，OB为高，只要求AC长，即点C的坐标即可，由点D为三角形OAB斜边OA的中点，且点A的坐标〔﹣6，4〕，可得点D的坐标为〔﹣3，2〕，代入双曲线可得k，又AB⊥OB，所以C点的横坐标为﹣ 6，代入解析式可得纵坐标，继而可求得面积．解答：解：∵点D为△OAB斜边OA的中点，且点A的坐标〔﹣6，4〕，∴点D的坐标为〔﹣3，2〕，专业整理分享完美WORD格式资料把〔﹣3，2〕代入双曲线，可得k=﹣6，即双曲线解析式为y=﹣，AB⊥OB，且点A的坐标〔﹣6，4〕，∴C点的横坐标为﹣6，代入解析式y=﹣，y=1，即点C坐标为〔﹣6，1〕，AC=3，又∵OB=6，S△AOC=×AC×OB=9．故答案为：9．点评：此题考查反比例函数系数k的几何意义及其函数图象上点的坐标特征，表达了数形结合的思想．3．〔2021?石家庄校级一模〕如图，Rt△ABC的直角边BC在x轴正半轴上，斜边AC上的中线BD反向延长线交y轴负半轴于E，双曲线y=的图象经过点A，假设S△BEC=8，那么k=16．考点：反比例函数系数k的几何意义．专题：压轴题．分析：方法1：因为S△BEC=8，根据k的几何意义求出k值即可；方法2：先证明△ABC与△OBE相似，再根据相似三角形的对应边成比例列式整理即可得到k=2S△BEC=16．专业整理分享完美WORD 格式资料解答：解：方法 1：设OB=x ，那么AB=，过D 作DH ⊥x 轴于H ，∵D 为AC 中点， ∴DH 为△ABC 中位线， DH=AB=，∵∠EBO=∠DBC=∠DCB ， ∴△ABC ∽△EOB ， 设BH 为y ， 那么EO=，BC=2y ， S △EBC =BC?OE=??2y==8，k=16．方法2：∵BD 是Rt △ABC 斜边上的中线， BD=CD=AD ， ∴∠DBC=∠ACB ，又∠DBC=∠OBE ，∠BOE=∠ABC=90°， ∴△ABC ∽△EOB ， ∴=， AB?OB=BC?OE ， S △BEC =×BC?OE=8， AB?OB=16， k=xy=AB?OB=16． 故答案为：16．点评：主要考查了用待定系数法求反比例函数的解析式和反比例函数系数k 的几何意义．反比例函数系数k 的几何意义为：反比例函数图象上的点的横纵坐标之积是定值 k ，同时|k|也是 该点到两坐标轴的垂线段与两坐标轴围成的矩形面积．此题综合性强，考查知识面广，能较全面考查学生综合应用知识的能力．4．〔2021?同安区校级质检〕如图，直线 y=﹣x+b 与双曲线 y=﹣ 〔x ＜0〕交于点 A ，与x 轴交于点B ，那么OA 2﹣OB 2= 2 ．专业整理分享完美WORD 格式资料考点：反比例函数综合题．专题：压轴题．分析：由直线y=﹣x+b 与双曲线y=﹣〔x ＜0〕交于点A 可知：x+y=b ，xy=﹣1，又OA 2=x 2+y 2，222﹣OB2的值． OB=b ，由此即可求出OA 解答：y=﹣x+b 与双曲线y=﹣ 〔x ＜0〕交于点A ， 解：∵直线设A 的坐标〔x ，y 〕，∴x+y=b ，xy=﹣1，而直线y=﹣x+b 与x 轴交于B 点，∴OB=b2 2 2 2 2，∴又OA=x+y ，OB=b ∴ OA 2﹣OB 2=x 2+y 2﹣b 2=〔x+y 〕2﹣2xy ﹣b 2=b 2+2﹣b 2=2．故答案为：2．点评：此题难度较大，主要考查一次函数与反比例函数的图形和性质， 也考查了图象交点坐标和解析式的关系．∴ 5．〔2021?邳州市二模〕如图，点 P 在双曲线 y=〔x ＞0〕上，以 P 为圆心的⊙P 与两坐标轴都相切，点 E 为y 轴负半轴上的一点，过点 P 作PF ⊥PE 交x 轴于点F ，假设OF ﹣OE=6，那么k 的值是9．考点：反比例函数综合题．专题：计算题；压轴题．分析：过P 点作x 轴、y 轴的垂线，垂足为A 、B ，根据⊙P 与两坐标轴都相切可知，PA=PB ，由∠APB=∠EPF=90°可证△BPE ≌△APF ，得BE=AF ，利用OF﹣OE=6，求圆的半径，根据k=OA ×PA 求解．解答：解：如图，过 P 点作x 轴、y 轴的垂线，垂足为A 、B ，∵⊙P 与两坐标轴都相切，PA=PB ，四边形OAPB 为正方形，∵∠APB=∠EPF=90°，专业整理分享完美WORD 格式资料∴∠BPE=∠APF ， Rt △BPE ≌Rt △APF ， BE=AF ， OF ﹣OE=6，∴〔OA+AF 〕﹣〔BE ﹣OB 〕=6，即2OA=6，解得OA=3，k=OA ×PA=3×3=9．故答案为：9．点评：此题考查了反比例函数的综合运用． 关键是根据圆与坐标轴相切的关系作辅助线， 构造全等三角形，正方形，将有关线段进行转化．6．〔2021?遵义二模〕如图，矩形 ABCD 的对角线 BD 经过坐标原点，矩形的边分别平行于坐标轴，点C 在反比例函数 的图象上．假设点 A 的坐标为〔﹣ 2，﹣2〕，那么k 的值为 1或﹣3 ．∴考点：反比例函数综合题．专题：综合题；压轴题．分析：根据矩形的对角线将矩形分成面积相等的两个直角三角形， 找到图中的所有矩形及相等的三角形，即可推出 S 四边形CEOF =S 四边形HAGO ，根据反比例函数比例系数的几何意义即可求出k 2+4k+1=4，再解出k 的值即可．解答：解：如图：∵四边形ABCD 、HBEO 、OECF 、GOFD 为矩形，又∵BO 为四边形 HBEO 的对角线，OD 为四边形OGDF 的对角线，S △BEO =S △BHO ，S △OFD =S △OGD ，S △CBD =S △ADB ，S△CBD ﹣S △BEO ﹣S △OFD =S △ADB ﹣S △BHO ﹣S △OGD ，∴ S 四边形HAGO =S 四边形CEOF =2×2=4，xy=k 2+2k+1=4，解得k=1或k=﹣3．专业整理分享完美WORD格式资料故答案为1或﹣3．点评：此题考查了反比例函数k的几何意义、矩形的性质、一元二次方程的解法，关键是判断出S四边形CEOF=S四边形HAGO．7．〔2021?黄石〕如下图，在平面直角坐标系中，一次函数y=ax+b〔a≠0〕的图象与反比例函数〔k≠0〕的图象交于二、四象限的A、B两点，与x轴交于C点．A〔﹣2，m〕，B 〔n，﹣2〕，tan∠BOC=，那么此一次函数的解析式为y=﹣x+3．考点：反比例函数与一次函数的交点问题．专题：计算题；压轴题．分析：过点B作BD⊥x轴，在直角三角形BOD中，根据的三角函数值求出OD的长，得到点B的坐标，把点B的坐标代入反比例函数的解析式中，求出反比例函数的解析式，然后把点A的横坐标代入反比例函数的解析式中求出点A的坐标，最后分别把点A和点B的坐标代入一次函数解析式，求出a和b的值即可得到一次函数解析式．解答：解：过点B作BD⊥x轴，在Rt△BOD中，∵tan∠BOC===，∴OD=5，那么点B的坐标为〔5，﹣2〕，把点B的坐标为〔5，﹣2〕代入反比例函数〔k≠0〕中，那么﹣2=，即k=﹣10，∴反比例函数的解析式为y=﹣，把A〔﹣2，m〕代入y=﹣中，m=5，专业整理分享完美WORD格式资料∴A的坐标为〔﹣2，5〕，把A〔﹣2，5〕和B〔5，﹣2〕代入一次函数y=ax+b〔a≠0〕中，得：，解得，那么一次函数的解析式为y=﹣x+3．故答案为：y=﹣x+3．点评：此题考查了反比例函数和一次函数的交点问题，以及三角函数值，用待定系数法确定函数的解析式，是常用的一种解题方法．同学们要熟练掌握这种方法．8．〔2021?遵义〕如图，直线y= x与双曲线 y=〔k＞0〕交于A、B两点，点B的坐标为〔﹣4，﹣2〕，C为双曲线y=〔k＞0〕上一点，且在第一象限内，假设△AOC的面积为6，那么点C的坐标为〔2，4〕．考点：反比例函数与一次函数的交点问题．专题：压轴题．分析：把点B的坐标代入反比例函数解析式求出k值，再根据反比例函数图象的中心对称性求出点A的坐标，然后过点A作AE⊥x轴于E，过点C作CF⊥x轴于F，设点C的坐标为〔a，〕，然后根据S△AOC=S△COF+S梯形ACFE﹣S△AOE列出方程求解即可得到a的值，从而得解．解答：解：∵点B〔﹣4，﹣2〕在双曲线y=上，=﹣2，k=8，根据中心对称性，点A、B关于原点对称，专业整理分享完美WORD 格式资料所以，A 〔4，2〕，如图，过点 A 作AE ⊥x 轴于E ，过点 C 作CF ⊥x 轴于F ，设点 C 的坐标为〔a ， 〕，假设S △AOC =S △COF +S 梯形ACFE ﹣S △AOE ，×8+×〔2+〕〔4﹣a 〕﹣×8，=4+ ﹣4， = ，∵△AOC 的面积为 6，∴ =6，整理得，a 2+6a ﹣16=0，解得a 1=2，a 2=﹣8〔舍去〕， ==4，∴点C 的坐标为〔2，4〕．假设S =S +S 梯形ACFE ﹣S△COF=，△AOC △AOE∴=6，解得：a=8或a=﹣2〔舍去〕∴点C 的坐标为〔8，1〕〔与图不符，舍去〕．故答案为：〔 2，4〕．专业整理分享完美WORD 格式资料点：本考了反比例函数与一次函数的交点， 反比例函数系数的几何意， 作助并表示出△ABC 的面是解的关．9．〔2021?州〕如，点P 1〔x 1，y 1〕，点P 2〔x 2，y 2〕，⋯，点P n 〔x n ，y n 〕在函数 〔x＞0〕的象上， △P 1OA 1，△P 2A 1A 2，△P 3A 2A 3，⋯，△P n A n ﹣1A n 都是等腰直角三角形，斜OA 1 12 2 3 ，⋯，A n ﹣1n 都在x 上〔n 是大于或等于 2的正整数〕，点 3、AA 、A A A P 的坐是〔 + ， 〕 ；点P n 的坐是 〔+ ， 〕 〔用含n的式子表示〕．考点：反比例函数合．：合；．分析：12 23 3点P1于点E ，点PG ⊥x 于点G ，作PE ⊥x作PF ⊥x 于点F ，点P 作P 根据△P 1 121232 A 3都是等腰直角三角形，可求出 1 23的坐，OA，△PAA ，△PAP ，P ，P从而出一般律得出点P n 的坐．解答：解：点P 1作P 1E ⊥x 于点E ，点P 2作P 2F ⊥x 于点F ，点P 3作P 3G ⊥x 于点G ，∵△P 1OA 1是等腰直角三角形，P 1E=OE=A 1E=OA 1，点P 1的坐〔 a ，a 〕，〔a ＞0〕，将点P 1〔a ，a 〕代入y= ，可得a=1，故点P 1的坐〔 1，1〕，OA 1=2a ，点P 2的坐〔b+2，b 〕，将点 2，b 〕代入y= ，可得b=1，P 〔b+2故点P 2 的坐〔 +1，1〕，A 1F=A 2F= 1，OA 2=OA 1+A 1A 2=2，点P 3的坐〔c+2，c 〕，将点P 3〔c+2，c 〕代入y=，可得c=，故点P 3的坐〔+，〕，上可得：P 1的坐〔1，1〕，P 2的坐〔 +1，1〕，P 3的坐〔+，〕，律可得： P n 坐：〔 +，〕．专业整理分享完美WORD格式资料故答案为：〔+，﹣〕、〔+，﹣〕．点评：此题考查了反比例函数的综合，涉及了点的坐标的规律变化，解答此题的关键是根据等腰三角形的性质结合反比例函数解析式求出P123的坐标，从而总结出一般规律，难，P，P度较大．10．〔2021?宁波〕如图，等腰直角三角形ABC顶点A在x轴上，∠BCA=90°，AC=BC=2，反比例函数y=〔x＞0〕的图象分别与AB，BC交于点D，E．连结DE，当△BDE∽△BCA时，点E的坐标为〔，〕．考点：反比例函数综合题．专题：压轴题．分析：由相似三角形的对应角相等推知△BDE的等腰直角三角形；根据反比例函数图象上点的坐标特征可设E〔a，〕，D〔b，〕，由等腰直角三角形的性质可以求得ab=3；最后，将其代入直线AD的解析式即可求得a的值．解答：解：如图，过点D作DF⊥BC于点F，∵∠BCA=90°，AC=BC=2，反比例函数y=〔x＞0〕的图象分别与AB，BC交于点D，E，∴∠BAC=∠ABC=45°，且可设E〔a，〕，D〔b，〕，∴C〔a，0〕，B〔a，2〕，A〔a﹣2，0〕，∴易求直线AB的解析式是：y=x+2﹣a．∵△BDE∽△BCA，∴△BDE也是等腰直角三角形，∴DF=EF，专业整理分享完美WORD 格式资料a ﹣b=﹣，即ab=3．又∵点 D 在直线 AB 上，∴ =b+2 ﹣a ，即2a 2﹣2 a ﹣3=0，解得，a= ，∴点E 的坐标是〔，〕．故答案是：〔，〕．点评：此题综合考查了相似三角形的性质、 反比例函数图象上点的坐标特征、 一次函数图象上的点的坐标特征、待定系数法求一次函数的解析式．解题时，注意双曲线的对称性的应用．11．〔2021?重庆〕如图，菱形OABC 的顶点O 是坐标原点，顶点A 在x 轴的正半轴上，顶点B 、C 均在第一象限，OA=2，∠AOC=60°．点D 在边AB 上，将四边形OABC 沿直线0D 翻折，使点B 和点C 分别落在这个坐标平面的点 B ′和C ′处，且∠C ′DB ′=60．°假设某反比例函数的图象经过点B ′，那么这个反比例函数的解析式为y=﹣ ．考点：反比例函数综合题．专题：压轴题．分析：连接AC ，求出△BAC 是等边三角形，推出 AC=AB ，求出△DC ′B ′是等边三角形，推出C ′D=B ′D，得出CB=BD=B ′C ′，推出A 和D 重合，连接BB ′交x 轴于E ，求出AB ′=AB=2，∠B ′AE=60°，求出B ′的坐标是〔3，﹣ 〕，设经过点 B ′反比例函数的解析式是 y= ，代入求出即可．专业整理分享完美WORD格式资料解答：解：连接AC，∵四边形OABC是菱形，CB=AB，∠CBA=∠AOC=60°，∴△BAC是等边三角形，AC=AB，∵将四边形OABC沿直线0D翻折，使点B和点C分别落在这个坐标平面的点B′和C′处，BD=B′D，CD=C′D，∠DB′C′=∠ABC=60°，∵∠B′DC′=60，°∴∠DC′B′=60，°∴△DC′B′是等边三角形，C′D=B′D，CB=BD=B′C′，即A和D重合，连接BB′交x轴于E，那么AB′=AB=2，∠B′AE=180°﹣〔180°﹣60°〕=60°，在Rt△AB′E中，∠B′AE=60°，AB′=2，∴AE=1，B′E=，OE=2+1=3，即B′的坐标是〔3，﹣〕，设经过点B′反比例函数的解析式是y=，代入得：k=﹣3，即y=﹣，故答案为：y=﹣．点评：此题考查了折叠性质，菱形性质，等边三角形的性质和判定的应用，主要考查学生的计算能力，题目比拟好，有一定的难度．12．〔2021?芦淞区模拟〕双曲线，的局部图象如下图，P是y轴正半轴上一点，过点P作AB∥x轴，分别交两个图象于点A，B．假设PB=2PA，那么k=﹣4．专业整理分享完美WORD格式资料考点：反比例函数综合题．专题：压轴题；数形结合．分析：因为AB∥x轴，PB=2PA，所以可知A和B点的纵坐标相同，B点的横坐标的长度是A横坐标的2倍，从而可求出k的值，因为过第二象限，所以k＜0．解答：解：∵AB∥x轴，PB=2PA，∴=∴k=﹣4．故答案为：﹣4．点评：此题考查反比例函数图象的性质，以及从反比例函数获得信息，关键是看到纵坐标相同时，横坐标的不同，从而求出解．13．〔2021?阜宁县二模〕如图，D是反比例函数的图象上一点，过D作DE⊥x轴于E，DC⊥y轴于C，一次函数 y=﹣x+m与的图象都经过点C，与x轴分别交于A、B两点，四边形 DCAE的面积为4，那么k的值为﹣2．考点：反比例函数综合题．专题：计算题；压轴题．分析：由的图象经过点C，可求C〔0，2〕，代入一次函数y=﹣x+m求m的值，得出A点坐标，计算△AOC的面积，由四边形DCAE的面积为4，可知矩形OCDE的面积，从而得出k的值．解答：的图象经过点C，∴C〔0，2〕，解：∵∴将点C代入一次函数y=﹣x+m中，得m=2，y=﹣x+2，令y=0得x=2，∴A〔2，0〕，S△AOC=×OA×OC=2，专业整理分享完美WORD格式资料∵四边形DCAE的面积为4，∴S矩形OCDE=4﹣2=2，∴k=﹣2．故答案为：﹣2．点评：此题考查了一次函数、反比例函数图象上点的坐标求法，矩形面积与反比例系数的关系．关键是通过求三角形的面积确定矩形的面积．14．〔2021?邓州市校级一模〕如图，梯形ABCO的底边AO在x轴上，BC∥AO，AB⊥AO，过点C的双曲线交OB于D，且OD：DB=1：2，假设△OBC的面积等于3，那么k的值是．考点：反比例函数综合题．专题：压轴题．分析：设C〔x，y〕，BC=a．过D点作DE⊥OA于E点．根据DE∥AB得比例线段表示点D坐标；根据△OBC的面积等于3得关系式，列方程组求解．解答：解：设C〔x，y〕，BC=a．那么AB=y，OA=x+a．过D点作DE⊥OA于E点．∵OD：DB=1：2，DE∥AB，∴△ODE∽△OBA，相似比为OD：OB=1：3，DE=AB=y，OE=OA=〔x+a〕．∵D点在反比例函数的图象上，且D〔〔x+a〕，y〕，y?〔x+a〕=k，即xy+ya=9k，∵C点在反比例函数的图象上，那么xy=k，ya=8k．∵△OBC的面积等于3，ya=3，即ya=6．8k=6，k=．故答案为：．专业整理分享完美WORD格式资料点评：此题考查了反比例函数的应用、平行线分线段成比例及有关图形面积的综合运用，综合性较强．15．〔2021?三明〕如图，点A在双曲线上，点B在双曲线上，且AB∥y轴，点 P是y轴上的任意一点，那么△PAB的面积为1．考点：反比例函数系数k的几何意义．专题：压轴题；探究型．分析：设A〔x，〕，那么B〔x，〕，再根据三角形的面积公式求解．解答：解：设A〔x，〕，AB∥y轴，∴B〔x，〕，S△ABP=AB?x=〔﹣〕×x=1．故答案为：1．点评：此题考查的是反比例函数系数k的几何意义，先根据题意设出A点坐标，再由AB∥y轴得出B点坐标是解答此题的关键．16．〔2021?十堰〕如图，直线y=6x，y= x分别与双曲线y=在第一象限内交于点A，B，假设S△OAB=8，那么k= 6．专业整理分享完美WORD格式资料考点：反比例函数与一次函数的交点问题；反比例函数系数k的几何意义．专题：压轴题．分析：过点A作AC⊥x轴于点C，过点B作BD⊥x轴于点D，根据双曲线设出点并用直线与双曲线解析式联立求出点A、B的横坐标，再根据﹣S△OBD，然后列式整理即可得到关于k的方程，求解即可．解答：解：如图，过点A作AC⊥x轴于点C，过点B作BD⊥x轴于点D，设点A〔x1，〕，B〔x2，〕，A、B的坐标，梯形ACDB联立，解得x1=，联立，解得x2=，S△OAB=S△OAC+S梯形ACDB﹣S△OBD，= x1? +〔+〕×〔x2﹣x1〕﹣x2?，= k+〔k﹣k+k﹣k〕﹣k，= ?k，∵=×k，×k，k，S△OAB=8，∴k=8，专业整理分享S△OAB=S△OAC+S完美WORD格式资料解得k=6．故答案为：6．点评：此题考查了反比例函数与一次函数的交点问题，反比例函数系数的几何意义，作出辅助线表示出△AOB的面积并整理成只含有k的形式是解题的关键．17．〔2021?漳州〕如图，点A〔3，n〕在双曲线y=上，过点A作AC⊥x轴，垂足为C．线段OA的垂直平分线交OC于点M，那么△AMC周长的值是4．考点：反比例函数综合题．专题：压轴题．分析：先求出点A的坐标，根据点的坐标的定义得到OC=3，AC=1，再根据线段垂直平分线的性质可知AM=OM，由此推出△AMC的周长=OC+AC．解答：解：∵点A〔3，n〕在双曲线y=上，∴n==1，∴A〔3，1〕，∴OC=3，AC=1．∵OA的垂直平分线交OC于M，∴AM=OM，∴△AMC的周长=AM+MC+AC=OM+MC+AC=OC+AC=3+1=4．故答案为：4．点评：此题主要考查了反比例函数的图象性质和线段中垂线的性质，将求△AMC的周长转换成求OC+AC是解题的关键．专业整理分享完美WORD格式资料18．〔2021?淄博模拟〕如图，直线y= x与双曲线 y=〔x＞0〕交于点A，将直线y= x向下平移个6单位后，与双曲线y=〔x＞0〕交于点B，与x轴交于点C，那么C点的坐标为〔，0〕；假设=2，那么k= 12．考点：反比例函数综合题．专题：计算题；压轴题．分析：根据题意得到直线BC的解析式，令y=0，得到点C的坐标；根据直线AO和直线BC的解析式与双曲线y=联立求得A，B的坐标，再由条件=2，从而求出k值．解答：x向下平移个6单位后得到直线BC，解：∵将直线y=∴直线BC解析式为：y=x﹣6，令y=0，得x﹣6=0，∴C点坐标为〔，0〕；∵直线y= x与双曲线 y=〔x＞0〕交于点A，∴A〔，〕，又∵直线y= x﹣6与双曲线y=〔x＞0〕交于点B，且=2，∴B〔+，〕，将B的坐标代入y=中，得〔+〕=k，解得k=12．故答案为：〔，0〕，12．专业整理分享完美WORD 格式资料点评：此题考查一次函数与反比例函数的性质， 联立方程求出点的坐标， 同时还考查学生的计算能力．19．〔2021?桐乡市校级三模〕如图，点 A 〔a ，b 〕在双曲线上，AB ⊥x 轴于点B ，假设点 是双曲线上异于点 A 的另一点．1〕k=60；〔2〕假设a 2=169﹣b 2，那么△OAB 的内切圆半径 r=2 ．考点：反比例函数综合题． 专题：压轴题；数形结合．分析：〔1〕把P 点坐标代入反比例函数，即可求 k ；〔2〕先把A 点坐标代入反比例函数可得 ab=60，再结合 a 2=169﹣b 2组成方程组，解可得a 、b 的值，进而利用勾股定理可求 OA ，再结合直角三角形内切圆半径公式，易求 r ．解答：解：〔1〕把〔5 ，4 〕代入反比例函数，可得k=5 ×4 =60；〔2〕把〔a ，b 〕代入反比例函数，得ab=60与a 2=169﹣b 2联合组成方程组为： ，解得 或，即知OB=12，AB=5或OB=5，AB=12，在Rt △AOB 中，OA=13， 故△AOB 内切圆的半径 r= = =2．点评：此题考查了反比例函数的知识、勾股定理，解题的关键是能根据所给的点，求出 k ，并能解二元二次方程组．二．解答题〔共 11小题〕专业整理分享。
2021年九年级中考数学专题训练反比例几何专题(含答案)
反比例几何综合基础知识梳理反比例函数的定义形如y＝kx(k为常数，k≠0)的函数叫做反比例函数．注意：反比例函数图象上的点的横、纵坐标之积为定值．反比例函数的图象和性质在y＝k2＋1x的图象上有三个点A(1，y1)，B(2，y2)，C(－5，y3)，则y1，y2，y3的大小为________．(用小于号表示)答案y3<y2<y1反比例函数中比例系数k的几何意义1．k的几何意义：在反比例函数y＝kx(k≠0)上任取一点P(x，y)，过这一点分别作x轴、y轴的垂线PM，PN，与坐标轴围成的矩形PMON的面积S＝|xy|＝□01|k|.2．计算与双曲线上的点有关的图形面积如图，点A 是反比例函数y ＝kx (k ≠0)的图象上的一点，过点A 作AB ⊥x 轴，垂足为B ，点C 为y 轴上的一点，连接AC ，BC ，若△ABC 的面积为5，则反比例函数的解析式为________．重难点破译一 反比例函数的图象、性质及解析式的确定已知反比例函数y ＝kx (k ≠0)，若该函数图象过(2,5)． (1)反比例函数的解析式为y ＝________；(2)反比例函数图象位于第________象限，在每个象限内，y 随x 的增大而________；(3)若A (x 1，y 1)，B (x 2，y 2)在反比例函数图象上，且x 1>x 2>0，则y 1________y 2(填“>”“<”或“＝”)；(4)若点(－5，a )，(2，b )，(3，c )在该反比例函数的图象上，则a ，b ，c 的大小关系是________(用“>”连接)．答案 (1)10x (2)一、三 减小 (3)< (4)b >c >a 二 反比例函数与几何图形1．如图，反比例函数y ＝kx (x >0)的图象经过矩形OABC 对角线的交点M ，分别与AB ，BC 交于点D ，E ，若四边形ODBE 的面积为24，则k 的值为( )A ．2B ．4C ．6D ．8 答案 D解析 由题意得E ，M ，D 三点位于反比例函数的图象上，则S △OCE ＝12|k |，S △OAD ＝12|k |，如图，过点M 作MG ⊥y 轴于点G ，作MN ⊥x 轴于点N ，则S 四边形ONMG ＝|k |，又M 为矩形ABCO 对角线的交点，则S矩形ABCO＝4S四边形ONMG＝4|k |，由于函数图象在第一象限，则k >0，则k 2＋k2＋24＝4k ，解得k ＝8，故选D.2．(2019·西南大学附属中学第七次月考)如图，四边形ABCD 是平行四边形，A ，B 两点的坐标分别是(－1,0)，(0,2)，C ，D 两点在反比例函数y ＝kx (k <0)的图象上，DA 的延长线交y 轴负半轴于点E ，CB ∶DE ＝2∶3，则k 的值为( )A ．－12B ．－8C ．－6D ．－4 答案 A解析如图，作DK⊥y轴于点K，过C点作平行于y轴的直线交DK于H.∵四边形ABCD是平行四边形，∴AD＝BC.又CB∶DE＝2∶3，∴AE∶DE＝1∶3，△AOE∽△DKE.∴DK＝3OA＝3.∴D的横坐标为－3.根据题意可得△CHD≌△BOA，∴DH＝1，CH＝2.设D(－3，a)，则C(－2，a＋2)．∵D，C均在y＝kx的图象上，∴－3a＝－2(a＋2)，解得a＝4.∴D(－3,4)．∴k＝－12.故选A.方法技巧突破— 反比例函数中的典型面积问题类型一图形面积的大小和k有直接关系模型1一点一垂线型模型特征反比例函数图象上一点及过这点向坐标轴作垂线的垂足与另一坐标轴上一点(含原点)构成的三角形面积等于12|k|(同底等高面积转化)．1．如图，点A在反比例函数y＝kx(k≠0)的图象上，AB⊥x轴于点B，点C在x轴上，且CO＝OB，△ABC的面积为2，则此反比例函数的解析式为________．答案y＝2 x解析连接OA，∵OC＝OB，∴S△AOB ＝S△AOC＝1.∴k＝2×1＝2，∴y＝2x.模型2一点两垂线模型特征过反比例函数图象上一点作两条坐标轴的垂线，垂线与坐标轴围成的矩形面积等于|k|.2.如图，点A是反比例函数y＝－6x(x<0)的图象上的一点，过点A作平行四边形ABCD，使B，C在x轴上，点D在y轴上，则平行四边形ABCD的面积为________．答案6解析过点A作AH⊥OB于H，如图，∵四边形ABCD是平行四边形，∴AD∥OB，∴S▱ABCD＝S矩形AHOD.∵点A是反比例函数y＝－6x(x<0)的图象上的一点，∴S矩形AHOD＝|－6|＝6，∴S▱ABCD＝6.模型3两点一垂线(两点两垂线)模型特征反比例函数和正比例函数的图象相交，由交点向坐标轴作垂线所围成的图形的面积．3．如图，反比例函数y＝5x的图象与直线y＝kx(k>0)相交于A，B两点，AC∥BH∥y轴，BC∥x轴，BC交y轴于点M，AC交x轴于点N，BH交x轴于点H，则S△ABC＝________，S四边形AHBN＝________，S△ABH＝________，S梯形ABMN＝________.答案1010515 2模型4两曲一平行模型特征两条双曲线上的两点的连线与一条坐标轴平行，求该两点与原点或坐标轴上的点构成图形的面积，一般是过两点向另一坐标轴作垂线，结合k的几何意义求解．4．(2019·宁波模拟)如图，平行于x轴的直线与y＝k1x(k1>0，x>0)，y＝k2x(k2>0，x>0)的图象分别交于A，B两点，点A在点B的右侧，C为x轴上一个动点，△ABC的面积为4，则k1－k2的值为________．解析 如图，连接OA ，OB .∵AB ∥x 轴，∴S △AOB ＝S △ACB ＝4，S △AOB ＝S △AOD －S △BOD ，∴4＝k 12－k 22，∴k 1－k 2＝8.类型二 图形面积的大小和k 没有直接关系 模型5 两点一轴点模型特征 反比例函数与一次函数图象的交点及坐标轴上一点所构成的三角形的面积为坐标轴所分的两个三角形面积之和．5．如图，一次函数y ＝x －1的图象与x 轴、y 轴分别交于E ，F 两点，与反比例函数y ＝2x 的图象交于A ，B 两点，C 在x 轴上，C 点坐标为(－3,0)，则S △ABC 的面积为________．答案 6解析 解方程组⎩⎪⎨⎪⎧y ＝x －1，y ＝2x.令x －1＝2x ，解得x 1＝2，x 2＝－1.把x ＝2代入y ＝x －1得y ＝1.把x ＝－1代入y ＝x －1得y ＝－2.即A (2,1)，B (－1，－2)．在y ＝x －1中，令y ＝0得x ＝1，即E (1,0)，∴S △ABC ＝S △CEA ＋S △CEB ＝12CE ·|y A －y B |＝12×4×3＝6.模型6 两点一原点模型特征 反比例函数与一次函数图象的交点及原点所围成的三角形面积，若两交点在同一支上，用减法．解法一：S △AOB ＝S △COD －S △AOC －S △BOD .解法二：作AE ⊥x 轴于E ，交OB 于M ，作BF ⊥x 轴于F ，则S △OAB ＝S 直角梯形AEFB.⎝ ⎛⎭⎪⎪⎫∵S △OAE＝S △OBF ＝|k |2，∴S △OAM ＝S 直角梯形MEFB .∴S △OAB ＝S △AMB ＋S 直角梯形MEFB .∴S△OAB＝S 直角梯形AEFB .6．如图，O 为坐标原点，四边形OACB 是菱形，OB 在x 轴的正半轴上，sin∠AOB ＝45，反比例函数y ＝12x 在第一象限内的图象经过点A ，与BC 交于点F ，则△AOF 的面积等于( )A ．10B ．9C ．8D ．6 答案 A解析 如图所示，过点A 作AE ⊥OB 于点E ，过 点F 作GH ⊥AC 于点G ，交x 轴于点H ，设AE ＝m (m >0)，因为sin ∠AOB ＝45，所以OA ＝54m ，在Rt △AEO 中，∠AEO ＝90°，由勾股定理可得OE ＝OA 2－AE 2＝⎝ ⎛⎭⎪⎫54m 2－m 2＝34m ，因此点A 的坐标为⎝ ⎛⎭⎪⎫34m ，m ，又因为点A 在反比例函数的图象上，所以将点⎝ ⎛⎭⎪⎫34m ，m 代入反比例函数解析式得m ＝1234m ，解得m ＝±4.因为m >0，所以m ＝4，则点A 的坐标为(3,4)，所以OA ＝5.又因为四边形OACB 是菱形，所以OA ＝OB ＝BC ＝AC ＝5，所以S △AOF ＝S菱形OACB －S △OBF －S △AFC ＝AE ·OB －12FH ·OB －12FG ·AC ＝4×5－12×4×5＝10，故选A.课后作业1．(2019·重庆八中九(下)第二次周考)若函数y ＝m ＋2x 的图象在其所在的每一象限内，函数值y 随自变量x 的增大而增大，则m 的取值范围是( )A ．m <－2B ．m <0C ．m >－2D ．m >0答案 A解析 ∵在每一象限内，y 随x 的增大而增大， ∴m ＋2<0，∴m <－2，∴选A.2．(2019·南开中考)若点A (－3，y 1)，B (－2，y 2)，C (1，y 3)都在反比例函数y ＝－12x 的图象上，则y 1，y 2，y 3的大小关系是( )A ．y 2<y 1<y 3B ．y 3<y 1<y 2C ．y 1<y 2<y 3D ．y 3<y 2<y 1 答案 B解析 代入计算y 1，y 2，y 3的值即可．3．(2019·衡阳中考)如图，一次函数y 1＝kx ＋b (k ≠0)的图象与反比例函数y 2＝mx (m 为常数且m ≠0)的图象都经过点A (－1,2)，B (2，－1)，结合图象，则不等式kx ＋b >mx 的解集是( )A ．x <－1B ．－1<x <0C ．x <－1或0<x <2D ．－1<x <0或x >2答案 C解析 观察一次函数与反比例函数的图象及两个交点A ，B 可知，A 点左侧部分和B 点左侧与y 轴之间的部分均符合kx ＋b >mx ，故选C.4．(2018·南阳一模)如图，点A 在反比例函数y ＝kx 的图象上，AM ⊥y 轴于点M ，P 是x 轴上一动点，当△APM 的面积是4时，k 的值是( )A ．8B ．－8C ．4D ．－4答案 B解析 设点A 的坐标为⎝ ⎛⎭⎪⎫x ，k x ，由题意，得12×|x |×kx ＝4，解得|k |＝8.又∵反比例函数y ＝kx 的图象在第四象限，∴k ＝－8.5．(2019·黑龙江龙东中考)如图，在平面直角坐标系中，点O 为坐标原点，平行四边形OABC 的顶点A 在反比例函数y ＝1x 上，顶点B 在反比例函数y ＝5x 上，点C 在x 轴的正半轴上，则平行四边形OABC 的面积是( )A.32 B.52 C ．4 D ．6答案 C解析 设A (a ，b )，B (c ，b )，∵A ，B 两点分别在y ＝1x ，y ＝5x 上，∴a ＝1b ，c ＝5b ，∴AB ＝x B －x A ＝5b －1b ＝4b ，∴S ▱OABC ＝4b ·b ＝4，故选C.6．(2019·台州中考)已知某函数的图象C 与函数y ＝3x 的图象关于直线y ＝2对称．下列命题：①图象C 与函数y ＝3x 的图象交于点⎝ ⎛⎭⎪⎫32，2；②点⎝ ⎛⎭⎪⎫12，－2在图象C 上；③图象C 上的点的纵坐标都小于4；④A (x 1，y 1)，B (x 2，y 2)是图象C 上任意两点，若x 1>x 2，则y 1<y 2.其中真命题是( )A ．①②B ．①③④C ．②③④D ．①②③④答案 A解析 函数y ＝3x 的图象在第一、第三象限，图象C 与其关于直线y ＝2对称，则点⎝ ⎛⎭⎪⎫32，2是图象C 与函数y ＝3x 图象的交点，∴①正确；点⎝ ⎛⎭⎪⎫12，－2关于y ＝2对称的点为点⎝ ⎛⎭⎪⎫12，6. ∵⎝⎛⎭⎪⎫12，6在函数y ＝3x 的图象上， ∴点⎝ ⎛⎭⎪⎫12，－2在图象C 上，∴②正确； ∵y ＝3x 中，y ≠0，x ≠0，即y ＝3x 上任意一点为(x ，y )，则点(x ，y )关于y ＝2对称的点的纵坐标为4－3x ，当x <0时，4－3x >4，∴③错误；A (x 1，y 1)，B (x 2，y 2)关于y ＝2对称的点(x 1,4－y 1)，B (x 2，4－y 2)在函数y ＝3x 的图象上．∴4－y 1＝3x 1，4－y 2＝3x 2，∵x 1>x 2>0或0>x 1>x 2时，有4－y 1<4－y 2，即y 1>y 2， ∴④错误．故选A.7．(2019·北京中考)在平面直角坐标系xOy 中，点A (a ，b )(a >0，b >0)在双曲线y ＝k 1x 上，点A 关于x 轴的对称点B 在双曲线y ＝k 2x 上，则k 1＋k 2的值为________．答案 0解析 因点A (a ，b )在y ＝k 1x 上，则k 1＝ab .点A (a ，b )关于x 轴的对称点B (a ，－b )在y ＝k 2x 上，则k 2＝－ab ，∴k 1＋k 2＝0.8．(2019·重庆北碚区教学联盟模拟试卷)如图，一次函数y ＝ax ＋b 的图象与反比例函数y ＝kx 的图象相交于A ，B 两点，与y 轴交于点C ，与x 轴交于点D ，点D 的坐标为(－2,0)，点A 的横坐标是2，tan ∠CDO ＝12.(1)求点A 的坐标；(2)求一次函数和反比例函数的解析式； (3)求△AOB 的面积．解 (1)作AH ⊥x 轴于点H ，∵D 的坐标为(－2,0)，A 的横坐标为2，∴DH ＝4.又∵tan ∠CDO ＝12，∴在Rt △ADH 中，tan ∠CDO ＝AHDH . 即AH 4＝12，∴AH ＝2. ∴A 点坐标为(2,2)．(2)把A (2,2)代入y ＝k x 中，即2＝k2，k ＝4， ∴反比例函数的解析式为y ＝4x ， 把A (2,2)，D (－2,0)代入y ＝ax ＋b 中，得⎩⎪⎨⎪⎧2a ＋b ＝2，－2a ＋b ＝0，解得⎩⎨⎧a ＝12，b ＝1.∴一次函数的解析式为y ＝12x ＋1. (3)令12x ＋1＝4x ，解得x 1＝－4，x 2＝2， ∴B (－4，－1)．在y ＝12x ＋1中，令x ＝0，得y ＝1，即OC ＝1， ∴S △AOB ＝S △OCA ＋S △OCB ＝12×1×2＋12×1×4＝1＋2＝3. 9．(2019·长寿区模拟)如图，在平面直角坐标系中有三点(1,2)，(3,1)，(－2，－1)，其中有两点同时在反比例函数y ＝kx 的图象上，将这两点分别记为A ，B ，另一点记为C .(1)求出k 的值；(2)求直线AB 对应的一次函数的表达式；(3)设点C 关于直线AB 的对称点为D ，又在x 轴上有一个动点P ，请直接写出PC ＋PD 的最小值(不必说明理由但要在图中标出)．解 (1)∵1×2＝(－2)×(－1)≠3×1，∴(1,2)，(－2，－1)两点同时在反比例函数y ＝kx 的图象上， ∴k ＝2.(2)设直线AB 对应的函数表达式为y ＝k 1x ＋b ， 把(1,2)，(－2，－1)代入y ＝k 1x ＋b ，得⎩⎪⎨⎪⎧ k 1＋b ＝2，－2k 1＋b ＝－1，解得⎩⎪⎨⎪⎧k 1＝1，b ＝1. ∴y ＝x ＋1.(3)设点C 关于直线AB 的对称点为点D ，则CD ⊥AB ，则k CD ＝－1，设直线CD 的解析式为y ＝－x ＋b ′， 把(3,1)代入y ＝－x ＋b ′，得b ′＝4， ∴l CD ：y ＝－x ＋4，设直线CD 与直线AB 交于点H ， 令－x ＋4＝x ＋1，解得x ＝32，把x ＝32代入y ＝x ＋1得y ＝52，∴H ⎝⎛⎭⎪⎫32，52，设D (r ，t )，则r ＋32＝32，t ＋12＝52，得 r ＝0，t ＝4，∴D (0,4)， 又C 的坐标为(3,1)，∴点C 关于x 轴的对称点为C ′(3，－1)， ∴PC ＋PD 的最小值为 DC ′＝(0－3)2＋(4＋1)2＝34.高分直通车1．(2019·扬州中考)若反比例函数y ＝－2x 的图象上有两个不同的点关于y 轴的对称点都在一次函数y ＝－x ＋m 的图象上，则m 的取值范围是( )A ．m >22B ．m <－22C ．m >22或m <－22D ．－22<m <22 答案 C解析 反比例函数y ＝－2x 的图象上两个不同的点关于y 轴对称的点在一次函数y ＝－x ＋m 的图象上，∴反比例函数y ＝2x 的图象与一次函数y ＝－x ＋m 的图象有两个不同的交点．联立两个函数解析式⎩⎨⎧y ＝2x，y ＝－x ＋m ，即2x ＝－x ＋m ，即x 2－mx ＋2＝0有两个不相等的实根，Δ＝m 2－8>0，结合二次函数图象得出不等式的解集为m >22或m <－22，∴选C.2．(2019·济宁中考)如图，点A 的坐标是(－2,0)，点B 的坐标是(0,6)，C 为OB 的中点，将△ABC 绕点B 逆时针旋转90°后得到△A ′BC ′.若反比例函数y ＝kx 的图象恰好经过A ′B 的中点D ，则k 的值是( )A ．9B ．12C ．15D ．18答案 C解析 如图，作A ′H ⊥y 轴，垂足为H ，易证△A ′HB ≌△BOA ，∴A ′H ＝OB ＝6，BH ＝AO ＝2，∴A ′的坐标为(6,4)，又D 是A ′B 的中点，∴D 的坐标为⎝ ⎛⎭⎪⎫0＋62，6＋42，即D (3，5)，又y ＝kx 的图象经过A ′B 的中点D ，∴k ＝15，∴选C.3．(2019·重庆南开九(下)期考试)如图，矩形OABC 的顶点C 在反比例函数y ＝kx 的图象上，且点A 的坐标为(1，－3)，点B 的坐标为(7，－1)，则k 的值为( )A ．3B ．7C ．12D ．21答案 C解析 如图，过点C 作CD ⊥y 轴，垂足为D ，过A ，B 分别作x 轴、y 轴的平行线交于点H .易证△ABH ≌△COD ，∵点A 的坐标为(1，－3)，点B 的坐标为(7，－1)，∴AH ＝7－1＝6，BH ＝3－1＝2，∴CD ＝6，OD ＝2，∴点C 的坐标为(6,2)，∵y ＝kx 的图象过点C (6,2)，∴2＝k6，∴k ＝12.故选C.4．(2019·育才南开一诊)如图，正方形OABC 的边长为6，A ，C 分别在x 轴、y 轴上，点P 在AB 上，CP 交OB 于点Q ，函数y ＝kx 的图象经过点Q ，若S △BPQ ＝14S △OQC ，则k 的值为( )A ．－12B ．12C ．16D ．18答案 C解析 ∵S △BPQ ＝14S △OQC ，∴BQ OQ ＝12.∵正方形OABC 的边长为6，∴OB ＝62，∴OQ ＝4 2.过Q 作QH ⊥y 轴于点H ，在等腰直角三角形OHQ 中，QH ＝OH ＝4，∴点Q 的坐标为(4,4)．∵y ＝kx 的图象过点Q (4,4)，∴4＝k4，∴k ＝16.5．如图，四边形OABC 放置在平面直角坐标系中，AB ∥CO ，OA 在x 轴上，OC 在y 轴上，反比例函数y ＝kx (k >0，x >0)的图象经过AB 的中点D ，并且与CB 交于点E .已知CE CB ＝13，OC ＝72，则AB 的长等于( )A ．2.5B ．2C ．1.5D ．1答案 B解析 如图所示，作EF ⊥OA 于点F ，BN ⊥CO 于点N ，且交EF 于点V .DM ⊥CO 于点M ，且交EF 于点H .∵反比例函数y ＝kx (k >0，x >0)的图象经过AB 的中点D . ∴设AD ＝a ，AO ＝3b ，则AB ＝2a . ∵EF ∥CO ，∴△BEV ∽△BCN . ∵CE CB ＝13，∴NV NB ＝EC CB ＝13.∴NV ＝b . 由题意可得CN ＝72－2a ，EV CN ＝BE BC ＝23. 则EV72－2a＝23.解得EV ＝73－43a ， 故EF ＝73－43a ＋2a ＝73＋23a .∴E ⎝ ⎛⎭⎪⎫b ，73＋23a ，D (3b ，a )，故b ⎝ ⎛⎭⎪⎫73＋23a ＝3ab . 解得a ＝1，则AB ＝2a ＝2.故选B.6．(2019·厦门中考)如图，菱形ABCD 的顶点A 在函数y ＝3x (x >0)的图象上，函数y ＝kx (k >3，x >0)的图象关于直线AC 对称，且过B ，D 两点．若AB ＝2，∠BAD ＝30°，则k ＝________.答案 6＋23解析 如图，连接OC ，过点A 作AE ⊥x 轴于点E ，延长DA 与x 轴交于点F ，过点D 作DG ⊥x 轴于点G .∵函数y ＝kx (k >3，x >0)的图象关于直线AC 对称，∴O ，A ，C 三点在同一条直线上，且∠COE ＝45°，∴OE ＝AE ，设OE ＝AE ＝a ，则A (a ，a )．∵点A 在反比例函数y ＝3x (x >0)的图象上， ∴a 2＝3，∴a ＝3，∴AE ＝OE ＝3， ∵∠BAD ＝30°，∴∠OAF ＝∠CAD ＝12∠BAD ＝15°， ∵∠OAE ＝∠AOE ＝45°，∴∠EAF ＝30°， ∴AF ＝AEcos30°＝2，EF ＝AE tan30°＝1. ∵AD ＝AB ＝2＝AF ，AE ∥DG ， ∴EG ＝EF ＝1，DG ＝2AE ＝2 3.∴OG ＝OE ＋EG ＝3＋1.∴D (3＋1,23)． 故k ＝(3＋1)×23＝6＋2 3.。
2021年九年级中考数学 专题训练 反比例函数及其应用(含答案)
2021中考数学 专题训练 反比例函数及其应用一、选择题（本大题共10道小题） 1. （2019·上海）下列函数中，函数值y 随自变量x 的值增大而增大的是( )A ．y ＝3xB ．y ＝－3xC ．y ＝3xD ．y ＝－3x2. （2020·海南）下列各点中，在反比例函数y ＝8x图象上的点是( )A ．(－1，8)B ．(－2，4)C ．(1，7)D ．(2，4) 3. （2020·湖北孝感）已知蓄电池的电压为定值，使用蓄电池时，电流I(单位：A)与电阻R(单位：Ω)是反比例函数关系，它的图像如图所示，则这个反比例函数的解析式为( )A.I =24RB.I =36RC.I =48RD.I =64R4. 若点A (-4，y 1)，B (-2，y 2)，C (2，y 3)都在反比例函数y=-的图象上，则y 1，y 2，y 3的大小关系是 ( ) A .y 1>y 2>y 3 B .y 3>y 2>y 1 C .y 2>y 1>y 3 D .y 1>y 3>y 25. （2020·黔东南州）如图，点A 是反比例函数y （x ＞0）上的一点，过点A 作AC ⊥y 轴，垂足为点C ，AC 交反比例函数y 的图象于点B ，点P 是x 轴上的动点，则△P AB 的面积为（ ）A ．2B ．4C ．6D ．86. （2020·黔西南州）如图，在菱形ABOC 中，AB ＝2，∠A ＝60°，菱形的一个顶点C 在反比例函数y ＝kx（k ≠0）的图象上，则反比例函数的解析式为（ ）A ．y ＝B ．y ＝C ．y ＝3x-D ．y7. （2020·内江）如图，点A 是反比例函数ky x=图象上的一点，过点A 作AC x ⊥轴，垂足为点C ，D 为AC 的中点，若AOD ∆的面积为1，则k 的值为（ ）A.43B.83C. 3D. 48. 若一次函数y ＝mx ＋6的图象与反比例函数y ＝nx 在第一象限的图象有公共点，则有( )A. mn ≥－9B. －9≤mn ＜0C. mn ≥－4D. －4≤mn ≤09. 如图，☉O的半径为2，双曲线的解析式分别为y=和y=-，则阴影部分的面积为 ( )A .4πB .3πC .2πD .π10. (2019·湖北咸宁)在平面直角坐标系中，将一块直角三角板如图放置，直角顶点与原点O 重合，顶点A ，B 恰好分别落在函数y =﹣1x (x <0)，y =4x(x >0)的图象上，则sin ∠ABO 的值为A ．13BCD二、填空题（本大题共8道小题）11. 已知反比例函数y＝kx(k≠0)的图象如图所示，则k的值可能是________(写一个即可)．12. 如图，直线y1＝kx(k≠0)与双曲线y2＝2x(x>0)交于点A(1，a)，则y1>y2的解集为________．13. 已知点(m－1，y1)，(m－3，y2)是反比例函数y＝mx(m<0)图象上的两点，则y1________y2(填“>”或“＝”或“<”)．14. 如图，在平面直角坐标系中，菱形OABC的面积为12，点B在y轴上，点C在反比例函数y＝kx的图象上，则k的值为________．15. 如图，点A为函数y＝9x(x＞0)图象上一点，连接OA，交函数y＝1x(x＞0)的图象于点B，点C是x轴上一点，且AO＝AC，则△ABC的面积为________．16. （2019•山西）如图，在平面直角坐标中，点O为坐标原点，菱形ABCD的顶点B在x轴的正半轴上，点A坐标为（–4，0），点D的坐标为（–1，4），反比例函数y=kx（x＞0）的图象恰好经过点C，则k的值为__________．17. 如图所示，反比例函数y＝kx(k≠0，x>0)的图象经过矩形OABC的对角线AC 的中点D，若矩形OABC的面积为8，则k的值为________．18. (2019·浙江宁波)如图，过原点的直线与反比例函数ykx(k>0)的图象交于A，B两点，点A在第一象限．点C在x轴正半轴上，连结AC交反比例函数图象于点D．AE为∠BAC的平分线，过点B作AE的垂线，垂足为E，连结DE．若AC=3DC，△ADE的面积为8，则k的值为__________．三、解答题（本大题共6道小题）19. 如图，已知反比例函数y=(x>0)的图象与一次函数y=-x+4的图象交于A和B(6，n)两点.(1)求k和n的值;(2)若点C(x，y)也在反比例函数y=(x>0)的图象上，求当2≤x≤6时，函数值y的取值范围.20. 如图，在平面直角坐标系中，一次函数y1=kx+b(k≠0)的图象与反比例函数y2= (m≠0)的图象相交于第一、三象限内的A(3，5)，B(a，-3)两点，与x轴交于点C.(1)求该反比例函数和一次函数的解析式;(2)在y轴上找一点P使PB-PC最大，求PB-PC的最大值及点P的坐标;(3)直接写出当y1>y2时，x的取值范围.21. 如图，一次函数y=kx+b与反比例函数y=的图象交于A(m，4)，B(2，n)两点，与坐标轴分别交于M，N两点.(1)求一次函数的解析式;(2)根据图象直接写出kx+b->0中x的取值范围;(3)求△AOB的面积.22. 如图，一次函数y＝kx＋b(k≠0)与y轴交于点B(0，9)，与x轴的负半轴交于点A，且tan∠BAO＝1.反比例函数y＝mx与一次函数y＝kx＋b的图象交于C、D两点，且BD2＋BC2＝90.(1)求一次函数的解析式；(2)求反比例函数的解析式；(3)某二次函数的图象经过线段CD的中点，且以B点为顶点，求此二次函数的解析式．23. 如图，在平面直角坐标系中，一次函数的图象与反比例函数的图象交于第二、四象限内的A，B两点，与x轴交于点C，与y轴交于点D，点B的坐标是(m，－4)，连接AO，AO＝5，sin∠AOC＝3 5.(1)求反比例函数的解析式；(2)连接OB，求△AOB的面积．24. （2019•甘肃）如图，一次函数y=kx+b的图象与反比例函数y=mx的图象相交于A（–1，n）、B（2，–1）两点，与y轴相交于点C．（1）求一次函数与反比例函数的解析式；（2）若点D与点C关于x轴对称，求△ABD的面积；（3）若M（x1，y1）、N（x2，y2）是反比例函数y=mx上的两点，当x1<x2<0时，比较y2与y1的大小关系．2021中考数学专题训练反比例函数及其应用-答案一、选择题（本大题共10道小题）1. 【答案】A【解析】A、该函数图象是直线，位于第一、三象限，y随x的增大而增大，故本选项正确．B、该函数图象是直线，位于第二、四象限，y随x的增大而减小，故本选项错误．C、该函数图象是双曲线，位于第一、三象限，在每一象限内，y随x的增大而减小，故本选项错误．D、该函数图象是双曲线，位于第二、四象限，在每一象限内，y随x的增大而增大，故本选项错误．2. 【答案】D【解析】∵反比例函数的系数8，∴该反比例函数图象上的点的横坐标与纵坐标之积为8，故选D.3. 【答案】C【解析】设反比例函数解析式为I=kR,把图中点（8，6）代入得：k=8×6=48.故选C.4. 【答案】C[解析]由图象可知y2>y1>y3，故选C.5. 【答案】A【解析】利用反比例函数中比例系数k 的几何意义求解.如图，连接OA 、OB 、PC ．∵AC ⊥y 轴，∴S △APC ＝S △AOC |6|＝3，S △BPC ＝S △BOC|2|＝1，∴S △PAB ＝S △APC ﹣S △BPC ＝2．6. 【答案】B【解析】本题考查了待定系数法、菱形的性质、点的坐标的意义．因为在菱形ABOC 中，∠A ＝60°，菱形边长为2，所以OC ＝2，∠COB ＝60°．如答图，过点C 作CD ⊥OB 于点D ，则OD ＝OC·cos ∠COB ＝2×cos 60°＝2×12＝1，CD ＝OC·sin ∠COB ＝2×sin 60°＝C 在第二象限，所以点C 的坐标为（－1．因为顶点C 在反比例函数y ═kx1k -，得k＝所以反比例函数的解析式为y＝B ．7. 【答案】D【解析】本题考查了反比例函数系数k 的几何意义、反比例函数图象上点的坐标特征，解答本题的关键是明确题意，找出所求问题需要的条件，利用反比例函数的性质解答．先设出点A 的坐标，进而表示出点D 的坐标，利用△ADO 的面积建立方程求出2mn =，即可得出结论．∵点A 的坐标为（m ，2n ），∴2mn k =，∵D 为AC 的中点，∴D （m ，n ），∵AC ⊥x 轴，△ADO 的面积为1，∴()ADO 11121222S AD OC n n m mn =⋅=-⋅==，∴2mn =，∴24k mn ==，因此本题选D ．8. 【答案】A 【解析】如解图，根据题意，两个函数的图象在第一象限有公共点，则关于x 的方程nx ＝mx ＋6有实数根，方程化简为：mx 2＋6x －n ＝0，显然m ≠0，Δ＝36＋4mn ≥0，所以mn ≥－9，由于一次函数与反比例函数y ＝nx 在第一象限的图象有公共点，所以n ＞0，显然当一次函数y 随x 的增大而增大时，两个函数图象在第一象限有交点，即mn ≥－9符合题意．9. 【答案】C[解析]根据反比例函数y=，y=-及圆的中心对称性和轴对称性知，将二、四象限的阴影部分旋转到一、三象限对应部分，显然所有阴影部分的面积之和等于一、三象限内两个扇形的面积之和，也就相当于一个半径为2的半圆的面积.∴S 阴影=π×22=2π.故选C .10. 【答案】D【解析】如图，过点A ，B 分别作AD ⊥x 轴，BE ⊥x 轴，垂足为D ，E ，∵点A 在反比例函数y =﹣1x (x <0)上，点B 在y =4x(x >0)上， ∴S △AOD =1，S △BOE =4，又∵∠AOB =90°∴∠AOD =∠OBE，∴△AOD ∽△OBE ，∴(AO OB)2=14AOD OBES S =，∴12AO OB =． 设OA =m ，则OB =2m ，AB=， 在Rt △AOB 中，sin ∠ABO=OA AB ==，故选D ．二、填空题（本大题共8道小题）11. 【答案】－2(答案不唯一) 【解析】根据反比例函数的图象在二、四象限，则k ＜0，如k ＝－2(答案不唯一)．12. 【答案】x ＞1 【解析】当x ＞1时，直线的图象在双曲线图象的上方，即y 1＞y 2.因此，y 1＞y 2的解集为x ＞1.13. 【答案】＞ 【解析】∵m ＜0，∴反比例函数y ＝mx的图象位于第二、四象限，且在每一象限内y 随x 的增大而增大，又∵m －1＞m －3，∴y 1＞y 2.14. 【答案】－6 【解析】如解图，连接AC 交y 轴于点D ，因为四边形ABCO 是菱形，且面积为12，则△OCD 的面积为3，利用反比例函数k 的几何意义可得k ＝－6.15. 【答案】6【解析】 设A 点的坐标为(a ，9a )，直线OA 的解析式为y ＝kx ，于是有9a ＝ka ，∴k ＝9a 2，直线为y ＝9a 2x ，联立得方程组⎩⎪⎨⎪⎧y ＝9a 2x y ＝1x ，解得B 点的坐标为(a 3，3a )，∵AO ＝AC ，A(a ，9a )，∴C(2a ，0)，∴S △ABC ＝S △AOC －S △BOC ＝12×2a×9a －12×2a×3a ＝9－3＝6.16. 【答案】16 【解析】过点C 、D 作CE ⊥x 轴，DF ⊥x 轴，垂足为E 、F ，∵四边形ABCD 是菱形，∴AB =BC =CD =DA ， 易证△ADF ≌△BCE ，∵点A （–4，0），D （–1，4），∴DF =CE =4，OF =1，AF =OA –OF =3，在Rt △ADF 中，AD 5，∴OE =EF –OF =5–1=4，∴C （4，4），∴k =4×4=16，故答案为：16．17. 【答案】2 【解析】由题意可知，D 点在反比例函数图象上，如解图所示，过点D 作DE ⊥x 轴于点E ，作DF ⊥y 轴于点F ，则k ＝x D ·y D ＝DF·DE ＝S 矩形OEDF ，又D 为对角线AC 中点，所以S 矩形OEDF ＝14S 矩形OABC ＝2，∴k ＝2.18. 【答案】6【解析】如图，连接OE ，CE ，过点A 作AF ⊥x 轴，过点D 作DH ⊥x 轴，过点D 作DG ⊥AF ，∵过原点的直线与反比例函数y k x=(k >0)的图象交于A ，B 两点， ∴A 与B 关于原点对称，∴O 是AB 的中点，∵BE ⊥AE ，∴OE =OA ，∴∠OAE =∠AEO ，∵AE 为∠BAC 的平分线，∴∠BAE =∠DAE ，∴∠DAE =∠AEO ，∴AD ∥OE ，∴S △ACE =S △AOC ，∵AC =3DC ，△ADE 的面积为8，∴S △ACE =S △AOC =12，设点A (m ，k m)， ∵AC =3DC ，DH ∥AF ，∴3DH =AF ，∴D (3m ，3k m)， ∵CH ∥GD ，AG ∥DH ，∴△DHC ∽△AGD ，∴S △HDC 14=S △ADG ， ∵S △AOC =S △AOF +S 梯形AFHD +S △HDC 1122k =+⨯(DH +AF )×FH +S △HDC 114223k k m =+⨯⨯2m 112142243236k k k m k m +⨯⨯⨯=++=12， ∴2k =12，∴k =6；故答案为6．三、解答题（本大题共6道小题）19. 【答案】解:(1)把B (6，n )代入一次函数y=-x +4中，可得n=-×6+4=1，所以B 点的坐标为(6，1).又B 在反比例函数y=(x>0)的图象上，所以k=xy=1×6=6，所以k 的值为6，n 的值为1.(2)由(1)知反比例函数的解析式为y=.当x=2时，y==3;当x=6时，y==1，由函数图象可知，当2≤x≤6时函数值y的取值范围是1≤y≤3.20. 【答案】解:(1)将A(3，5)的坐标代入y2=得，5=，∴m=15.∴反比例函数的解析式为y2=.当y2=-3时，-3=，∴x=-5，∴点B的坐标为(-5，-3).将A(3，5)，B(-5，-3)的坐标代入y1=kx+b得，解得∴一次函数的解析式为y1=x+2.(2)令y1=0，则x+2=0，解得x=-2.∴点C的坐标为(-2，0).设一次函数图象与y轴交于点D.令x=0，则y1=2.∴点D的坐标为(0，2).连接PB，PC，当B，C和P不共线时，由三角形三边关系知，PB-PC<BC; 当B，C和P共线时，PB-PC=BC，∴PB-PC≤BC.由勾股定理可知，BC==3.∴当P与D重合，即P点坐标为(0，2)时，PB-PC取最大值，最大值为3.(3)当y1>y2时，x的取值范围为x>3或-5<x<0.21. 【答案】解:(1)∵点A在反比例函数y=图象上，∴=4，解得m=1，∴点A 的坐标为(1，4).又∵点B 也在反比例函数y=图象上，∴=n ，解得n=2，∴点B 的坐标为(2，2).∵点A ，B 在y=kx +b 的图象上，∴，解得∴一次函数的解析式为y=-2x +6.(2)根据图象得:kx +b ->0时，x 的取值范围为x<0或1<x<2.(3)∵直线y=-2x +6与x 轴的交点为N ，∴点N 的坐标为(3，0)，∴S △AOB =S △AON -S △BON =×3×4-×3×2=3.22. 【答案】(1)∵tan ∠BAO ＝1，∴OA ＝OB ，∵点B (0，9)，∴点A (－9，0)，∴⎩⎨⎧b ＝9－9k ＋b ＝0，解得⎩⎨⎧k ＝1b ＝9， ∴一次函数的解析式为y ＝x ＋9；(2)联立⎩⎪⎨⎪⎧y ＝x ＋9y ＝m x 得x 2＋9x －m ＝0， 设点C 、D 的横坐标分别为x 1、x 2，∵BD 2＋BC 2＝90，∴(2x 2)2＋(2x 1)2＝90即2(x 21＋x 22)＝90，∴x 21＋x 22＝(x 1＋x 2)2－2x 1x 2＝(－9)2－2(－m )＝45，即81＋2m ＝45，解得m ＝－18，∴反比例函数解析式为y ＝－18x ；(3)设所求的二次函数的解析式为y ＝ax 2＋9(a ≠0)，由(1)和(2)得⎩⎪⎨⎪⎧y ＝x ＋9y ＝－18x ， 解得⎩⎨⎧x 1＝－3y 1＝6或⎩⎨⎧x 2＝－6y 2＝3， 则线段CD 的中点为(x 1＋x 22，y 1＋y 22)即(－92，92)，代入y ＝ax 2＋9得92＝(－92)2a ＋9，解得a ＝－29， 故所求的二次函数的解析式为y ＝－29x 2＋9.23. 【答案】(1)【思路分析】如解图，过点A 作AE ⊥x 轴于点E ，由三角函数求出点A 坐标，再用待定系数法求出反比例函数的解析式便可．解：如解图过点A 作AE ⊥x 轴于点E ，∵OA ＝5，sin ∠AOC ＝35，∴AE ＝OA·sin ∠AOC ＝5×35＝3，OE ＝OA 2－AE 2＝4，∴A(－4，3)，(3分)设反比例函数的解析式为y ＝k x (k≠0)，把A(－4，3)代入解析式，得k ＝－12，∴反比例函数的解析式为y ＝－12x.(5分) (2)【思路分析】先把B 点坐标代入所求出的反比例函数解析式，求出m 的值，进而求出直线AB 的解析式，再求出点D 的坐标，便可求△AOD 与△BOD 的面积之和，即△AOB 的面积．解：把B(m ，－4)代入y ＝－12x 中，得m ＝3，∴B(3，－4)．设直线AB 的解析式为y ＝kx ＋b ，把A(－4，3)和B(3，－4)代入得，⎩⎨⎧－4k ＋b ＝33k ＋b ＝－4， 解得⎩⎨⎧k ＝－1b ＝－1，(7分) ∴直线AB 的解析式为y ＝－x －1，(8分)则AB 与y 轴的交点D(0，－1)，∴S △AOB ＝S △AOD ＋S △BOD ＝12×1×4＋12×1×3＝3.5.(10分)24. 【答案】（1）一次函数的解析式为y =–x +1，反比例函数的解析式为y =–2x ． （2）S △ABD =3．（3）y 1<y 2．【解析】（1）∵反比例函数y =m x 经过点B （2，–1），∴m =–2， ∵点A （–1，n ）在y =2x-上，∴n =2，∴A （–1，2）， 把A ，B 坐标代入y =kx +b ，则有221k b k b -+=+=-⎧⎨⎩，解得11k b =-=⎧⎨⎩， ∴一次函数的解析式为y =–x +1，反比例函数的解析式为y =–2x． （2）∵直线y =–x +1交y 轴于C ，∴C （0，1），∵D ，C 关于x 轴对称，∴D （0，–1），∵B （2，–1），∴BD ∥x 轴，∴S △ABD =12×2×3=3． （3）∵M （x 1，y 1）、N （x 2，y 2）是反比例函数y =–2x上的两点，且x 1<x 2<0，s ∴y 1<y 2．。
2020-2021中考数学—反比例函数的综合压轴题专题复习及答案
2020-2021中考数学—反比例函数的综合压轴题专题复习及答案一、反比例函数1．如图．一次函数y=x+b的图象经过点B（﹣1，0），且与反比例函数（k为不等于0的常数）的图象在第一象限交于点A（1，n）．求：（1）一次函数和反比例函数的解析式；（2）当1≤x≤6时，反比例函数y的取值范围．【答案】（1）解：把点B（﹣1，0）代入一次函数y=x+b得： 0=﹣1+b，∴b=1，∴一次函数解析式为：y=x+1，∵点A（1，n）在一次函数y=x+b的图象上，∴n=1+1，∴n=2，∴点A的坐标是（1，2）．∵反比例函数的图象过点A（1，2）．∴k=1×2=2，∴反比例函数关系式是：y=（2）解：反比例函数y= ，当x＞0时，y随x的增大而减少，而当x=1时，y=2，当x=6时，y= ，∴当1≤x≤6时，反比例函数y的值：≤y≤2【解析】【分析】（1）根据题意首先把点B（﹣1，0）代入一次函数y=x+b求出一次函数解析式，又点A（1，n）在一次函数y=x+b的图象上，再利用一次函数解析式求出点A的坐标，然后利用代入系数法求出反比例函数解析式，（2）根据反比例函数的性质分别求出当x=1，x=6时的y值，即可得到答案．2．如图，一次函数y=kx+b（k＜0）与反比例函数y= 的图象相交于A、B两点，一次函数的图象与y轴相交于点C，已知点A（4，1）（1）求反比例函数的解析式；（2）连接OB（O是坐标原点），若△BOC的面积为3，求该一次函数的解析式．【答案】（1）解：∵点A（4，1）在反比例函数y= 的图象上，∴m=4×1=4，∴反比例函数的解析式为y=（2）解：∵点B在反比例函数y= 的图象上，∴设点B的坐标为（n，）．将y=kx+b代入y= 中，得：kx+b= ，整理得：kx2+bx﹣4=0，∴4n=﹣，即nk=﹣1①．令y=kx+b中x=0，则y=b，即点C的坐标为（0，b），∴S△BOC= bn=3，∴bn=6②．∵点A（4，1）在一次函数y=kx+b的图象上，∴1=4k+b③．联立①②③成方程组，即，解得：，∴该一次函数的解析式为y=﹣x+3【解析】【分析】（1）由点A的坐标结合反比例函数系数k的几何意义，即可求出m的值；（2）设点B的坐标为（n，），将一次函数解析式代入反比例函数解析式中，利用根与系数的关系可找出n、k的关系，由三角形的面积公式可表示出来b、n的关系，再由点A在一次函数图象上，可找出k、b的关系，联立3个等式为方程组，解方程组即可得出结论．3．如图，已知一次函数y= x+b的图象与反比例函数y= （x＜0）的图象交于点A（﹣1，2）和点B，点C在y轴上．（1）当△ABC的周长最小时，求点C的坐标；（2）当 x+b＜时，请直接写出x的取值范围．【答案】（1）解：作点A关于y轴的对称点A′，连接A′B交y轴于点C，此时点C即是所求，如图所示．∵反比例函数y= （x＜0）的图象过点A（﹣1，2），∴k=﹣1×2=﹣2，∴反比例函数解析式为y=﹣（x＜0）；∵一次函数y= x+b的图象过点A（﹣1，2），∴2=﹣ +b，解得：b= ，∴一次函数解析式为y= x+ ．联立一次函数解析式与反比例函数解析式成方程组：，解得：，或，∴点A的坐标为（﹣1，2）、点B的坐标为（﹣4，）．∵点A′与点A关于y轴对称，∴点A′的坐标为（1，2），设直线A′B的解析式为y=mx+n，则有，解得：，∴直线A′B的解析式为y= x+ ．令y= x+ 中x=0，则y= ，∴点C的坐标为（0，）（2）解：观察函数图象，发现：当x＜﹣4或﹣1＜x＜0时，一次函数图象在反比例函数图象下方，∴当 x+ ＜﹣时，x的取值范围为x＜﹣4或﹣1＜x＜0【解析】【分析】（1）作点A关于y轴的对称点A′，连接A′B交y轴于点C，此时点C即是所求．由点A为一次函数与反比例函数的交点，利用待定系数法和反比例函数图象点的坐标特征即可求出一次函数与反比例函数解析式，联立两函数解析式成方程组，解方程组即可求出点A、B的坐标，再根据点A′与点A关于y轴对称，求出点A′的坐标，设出直线A′B的解析式为y=mx+n，结合点的坐标利用待定系数法即可求出直线A′B的解析式，令直线A′B解析式中x为0，求出y的值，即可得出结论；（2）根据两函数图象的上下关系结合点A、B的坐标，即可得出不等式的解集．4．已知：如图，正比例函数y=ax的图象与反比例函数y= 的图象交于点C（3，1）（1）试确定上述比例函数和反比例函数的表达式；（2）根据图象回答，在第一象限内，当x取何值时，反比例函数的值大于正比例函数的值？（3）点D（m，n）是反比例函数图象上的一动点，其中0＜m＜3，过点C作直线AC⊥x 轴于点A，交OD的延长线于点B；若点D是OB的中点，DE⊥x轴于点E，交OC于点F，试求四边形DFCB的面积．【答案】（1）解：将点C（3，1）分别代入y= 和y=ax，得：k=3，a= ，∴反比例函数解析式为y= ，正比例函数解析式为y= x；（2）解：观察图象可知，在第二象限内，当0＜x＜3时，反比例函数值大于正比例函数值；（3）解：∵点D（m，n）是OB的中点，又在反比例函数y= 上，∴OE= OA= ，点D（，2），∴点B（3，4），又∵点F在正比例函数y= x图象上，∴F（，），∴DF= 、BC=3、EA= ，∴四边形DFCB的面积为 ×（ +3）× = ．【解析】【分析】（1）利用待定系数法把C坐标代入解析式即可；（2）须数形结合，先找出交点，在交点的左侧与y轴之间，反比例函数值大于正比例函数值.（3）求出DF、BC、EA，代入梯形面积公式即可.5．如图，P1、P2（P2在P1的右侧）是y= （k＞0）在第一象限上的两点，点A1的坐标为（2，0）．（1）填空：当点P1的横坐标逐渐增大时，△P1OA1的面积将________（减小、不变、增大）（2）若△P1OA1与△P2A1A2均为等边三角形，①求反比例函数的解析式；②求出点P2的坐标，并根据图象直接写在第一象限内，当x满足什么条件时，经过点P1、P2的一次函数的函数值大于反比例函数y= 的函数值．【答案】（1）减小（2）解：①如图所示，作P1B⊥OA1于点B，∵A1的坐标为（2，0），∴OA1=2，∵△P1OA1是等边三角形，∴∠P1OA1=60°，又∵P1B⊥OA1，∴OB=BA1=1，∴P1B= ，∴P1的坐标为（1，），代入反比例函数解析式可得k= ，∴反比例函数的解析式为y= ；②如图所示，过P2作P2C⊥A1A2于点C，∵△P2A1A2为等边三角形，∴∠P2A1A2=60°，设A1C=x，则P2C= x，∴点P2的坐标为（2+x， x），代入反比例函数解析式可得（2+x） x= ，解得x1= ﹣1，x2=﹣﹣1（舍去），∴OC=2+ ﹣1= +1，P2C= （﹣1）= ﹣，∴点P2的坐标为（ +1，﹣），∴当1＜x＜ +1时，经过点P1、P2的一次函数的函数值大于反比例函数y= 的函数值【解析】【解答】解：（1）当点P1的横坐标逐渐增大时，点P1离x轴的距离变小，而OA1的长度不变，故△P1OA1的面积将减小，故答案为：减小；【分析】（1）当点P1的横坐标逐渐增大时，点P1离x轴的距离变小，而OA1的长度不变，故△P1OA1的面积将减小；（2）①由A1的坐标为（2，0），△P1OA1是等边三角形，求出P1的坐标，代入反比例函数解析式即可；②由△P2A1A2为等边三角形，求出点P2的坐标，得出结论.6．如图，四边形ABCD的四个顶点分别在反比例函数与（x＞0，0＜m＜n）的图象上，对角线BD∥y轴，且BD⊥AC于点P．已知点B的横坐标为4．（1）当m=4，n=20时．①若点P的纵坐标为2，求直线AB的函数表达式．②若点P是BD的中点，试判断四边形ABCD的形状，并说明理由．（2）四边形ABCD能否成为正方形？若能，求此时m，n之间的数量关系；若不能，试说明理由．【答案】（1）①当x=4时，∴点B的坐标是（4，1）当y=2时，由得得x=2∴点A的坐标是（2，2）设直线AB的函数表达式为∴解得∴直线AB的函数表达式为②四边形ABCD为菱形，理由如下：如图，由①得点B（4，1），点D（4，5）∵点P为线段BD的中点∴点P的坐标为（4，3）当y=3时，由得，由得，∴PA= ，PC=∴PA=PC而PB=PD∴四边形ABCD为平行四边形又∵BD⊥AC∴四边形ABCD是菱形（2）四边形ABCD能成为正方形当四边形ABCD时正方形时，PA=PB=PC=PD（设为t，t≠0），当x=4时，∴点B的坐标是（4，）则点A的坐标是（4-t，）∴，化简得t=∴点D的纵坐标为则点D的坐标为（4，）所以，整理得m+n=32【解析】【分析】（1）①分别求出点A，B的坐标，运用待定系数法即可求出直线AB的表达示；②由特殊的四边形可知，对角线互相垂直的是菱形和正方形，则可猜测这个四边形是菱形或是正方形，先证明其为菱形先，则需要证明四边形ABCD是平行四边形，运用“对角线互相平分的四边形是平行四边形”的判定定理证明会更好些；再判断对角线是否相等，若不相等则不是正方形；（2）要使m，n有具体联系，根据A,B，C，D分别在两个函数图象，且由正方形的性质，可用只含m的代数式表示出点D或点C的坐标代入y= ，即可得到只关于m和n的等式．7．如图1，已知直线y=x+3与x轴交于点A，与y轴交于点B，将直线在x轴下方的部分沿x轴翻折，得到一个新函数的图象（图中的“V形折现”）（1）类比研究函数图象的方法，请列举新函数的两条性质，并求新函数的解析式；（2）如图2，双曲线y= 与新函数的图象交于点C(1，a)，点D是线段AC上一动点(不包括端点)，过点D作x轴的平行线，与新函数图象交于另一点E，与双曲线交于点P．①试求△PAD的面积的最大值；②探索：在点D运动的过程中，四边形PAEC能否为平行四边形?若能，求出此时点D的坐标；若不能，请说明理由．【答案】（1）解：如图1，新函数的性质：1.函数的最小值为0；2.函数图象的对称轴为直线x=3.由题意得，点A的坐标为（-3，0），分两种情况：①当x-3时，y=x+3；②当x<-3时，设函数解析式为y=kx+b，在直线y=x+3中，当x=-4时，y=-1，则点（-4，-1）关于x轴的对称点为（-4，1），把点（-4，1），（-3，0），代入y=kx+b中，得：，解得：，∴y=-x-3.综上，新函数的解析式为y=.（2）解：如图2，①∵点C（1，a）在直线y=x+3上，∴a=4，∵点C（1，4）在反比例函数y=上，∴k=4，∴反比例函数的解析式为y=.∵点D是线段AC上一动点，∴设点D的坐标为（m，m+3），且-3<m<1，∵DP∥x轴，且点P在双曲线上，∴点P的坐标为（，m+3），∴PD=-m，∴S△PAD=（-m）（m+3）=m2-m+2=（m+）2+，∵a=<0，∴当m=时，S有最大值，最大值为，又∵-3<<1，∴△PAD的面积的最大值为.②在点D的运动的过程中，四边形PAEC不能为平行四边形，理由如下：当点D为AC的中点时，其坐标为（-1，2），此时点P的坐标为（2，2），点E的坐标为（-5，2），∵DP=3，DE=4，∴EP与AC不能互相平分，∴四边形PAEC不能为平行四边形.【解析】【分析】（1）根据一次函数的性质，结合函数图象写出新函数的两条性质；利用待定系数法求新函数解析式，注意分两种情况讨论；（2）①先求出点C的坐标，再利用待定系数法求出反比例函数解析式，设出点D的坐标，进而得到点P的坐标，再根据三角形的面积公式得出函数解析式，利用二次函数的性质求解即可；②先求出A的中点D的坐标，再计算DP、DE的长度，如果对角线互相平分，则能成为平行四边形，如若对角线不互相平分，则不能成为平行四边形.8．如图，在矩形OABC中，OA=6，OC=4，F是AB上的一个动点（F不与A，B重合），过点F的反比例函数的图象与BC边交于点E.（1）当F为AB的中点时，求该函数的解析式；（2）当k为何值时，△EFA的面积最大，最大面积是多少？【答案】（1）解：∵在矩形OABC中，OA=6，OC=4，∴B（6，4），∵F为AB的中点，∴F（6，2），又∵点F在反比例函数（k＞0）的图象上，∴k=12，∴该函数的解析式为y= （x＞0）（2）解：由题意知E，F两点坐标分别为E（，4），F（6，），∴，==== ，∴当k=12时，S有最大值．S最大=3【解析】【分析】）当F为AB的中点时，点F的坐标为（3，1），由此代入求得函数解析式即可；根据图中的点的坐标表示出三角形的面积，得到关于k的二次函数，利用二次函数求出最值即可．9．如图，在平面直角坐标系xOy中，直线y=kx+b（k≠0）与双曲线y= 相交于点A（m，3），B（﹣6，n），与x轴交于点C．（1）求直线y=kx+b（k≠0）的解析式；（2）若点P在x轴上，且S△ACP= S△BOC，求点P的坐标（直接写出结果）．【答案】（1）解：）∵点A（m，3），B（﹣6，n）在双曲线y= 上，∴m=2，n=﹣1，∴A（2，3），B（﹣6，﹣1）．将（2，3），B（﹣6，﹣1）带入y=kx+b，得：，解得．∴直线的解析式为y= x+2（2）解：当y= x+2=0时，x=﹣4，∴点C（﹣4，0）．设点P的坐标为（x，0），∵S△ACP= S△BOC， A（2，3），B（﹣6，﹣1），∴×3|x﹣（﹣4）|= × ×|0﹣（﹣4）|×|﹣1|，即|x+4|=2，解得：x1=﹣6，x2=﹣2．∴点P的坐标为（﹣6，0）或（﹣2，0）．【解析】【分析】（1）利用反比例函数图象上点的坐标特征可求出点A、B的坐标，再利用待定系数法即可求出直线AB的解析式；（2）利用一次函数图象上点的坐标特征可求出点C的坐标，设点P的坐标为（x，0），根据三角形的面积公式结合S△ACP= S△BOC，即可得出|x+4|=2，解之即可得出结论．10．如图1，抛物线y＝ax2+bx﹣3经过点A，B，C，已知点A（﹣1，0），点B（3，0）（1）求抛物线的解析式（2）点D为抛物线的顶点，DE⊥x轴于点E，点N是线段DE上一动点①当点N在何处时，△CAN的周长最小？②若点M（m，0）是x轴上一个动点，且∠MNC＝90°，求m的取值范围．【答案】（1）解：函数的表达式为：y=a（x+1）（x﹣3）=a（x2﹣2x﹣3），故﹣3a=﹣3，解得：a=1，故函数的表达式为：y=x2﹣2x﹣3（2）解：①过点C作x轴的平行线交抛物线于点C'（2，﹣3），连接AC'交DE于点N，则此时△CAN的周长最小．设过点A、C'的一次函数表达式为y=kx+b，则：，解得：，故直线AC'的表达式为：y=﹣x﹣1，当x=1时，y=﹣2，故点N（1，﹣2）；②如图2，过点C作CG⊥ED于点G．设NG=n，则NE=3﹣n．∵∠CNG+∠GCN=90°，∠CNG+∠MNE=90°，∴∠NCG=∠MNE，则tan∠NCG=n=tan∠MNE，故ME=﹣n2+3n，∴﹣1＜0，故ME有最大值，当n时，ME，则m的最小值为：；如下图所示，当点N与点D重合时，m取得最大值．过C作CG⊥ED于G．∵y=x2﹣2x﹣3= y=（x－1）2﹣4，∴D（1，－4），∴CG=OE=1．∵EG=OC=3∴GD=4－3=1，∴CG=DG=1，∴∠CDG=45°．∵∠CDM=90°，∴∠EDM=45°，∴△EDM是等腰直角三角形，∴EM=ED=4，∴OM=OE+EM=1+4=5，∴m=5．故：m≤5．【解析】【分析】（1）函数的表达式为：y=a（x+1）（x﹣3）=a（x2﹣2x﹣3），即可求解；（2）①过点C作x轴的平行线交抛物线于点C'（2，﹣3），连接AC'交DE于点N，则此时△CAN的周长最小，即可求解；②如图2，ME=﹣n2+3n，求出ME最大值，则可求出m的最小值；当点N与点D处时，m取得最大值，求解即可．11．已知：如图，在平面直角坐标系中，△ABC是直角三角形，∠ACB＝90°，点A，C的坐标分别为A（﹣3，0），C（1，0），BC＝AC．（1）在x轴上找一点D，连接DB，使得△ADB与△ABC相似（不包括全等），并求点D的坐标；（2）在（1）的条件下，如P，Q分别是AB和AD上的动点，连接PQ，设AP＝DQ＝m，问是否存在这样的m，使得△APQ与△ADB相似？如存在，请求出m的值；如不存在，请说明理由．【答案】（1）解：如图1，过点B作BD⊥AB，交x轴于点D，∵∠A＝∠A，∠ACB＝∠ABD＝90°，∴△ABC∽△ADB，∴∠ABC＝∠ADB，且∠ACB＝∠BCD＝90°，∴△ABC∽△BDC，∴∵A（﹣3，0），C（1，0），∴AC＝4，∵BC＝AC．∴BC＝3，∴AB＝＝＝5，∵，∴，∴CD＝，∴AD＝AC+CD＝4+ ＝，∴OD＝AD﹣AO＝，∴点D的坐标为：（，0）；（2）解：如图2，当∠APC＝∠ABD＝90°时，∵∠APC＝∠ABD＝90°，∠BAD＝∠PAQ，∴△APQ∽△ABD，∴，∴∴m＝，如图3，当∠AQP＝∠ABD＝90°时，∵∠AQP＝∠ABD＝90°，∠PAQ＝∠BAD，∴△APQ∽△ADB，∴，∴∴m＝；综上所述：当m＝或时，△APQ与△ADB相似．【解析】【分析】（1）如图1，过点B作BD⊥AB，交x轴于点D，可证△ABC∽△ADB，可得∠ABC＝∠ADB，可证△ABC∽△BDC，可得，可求CD 的长，即可求点D坐标；（2）分两种情况讨论，由相似三角形的性质可求解．12．在平面直角坐标系xOy中，抛物线y=-x2+mx+n与x轴交于点A，B（A在B的左侧）．（1）抛物线的对称轴为直线x=-3，AB=4．求抛物线的表达式；（2）平移（1）中的抛物线，使平移后的抛物线经过点O，且与x正半轴交于点C，记平移后的抛物线顶点为P，若△OCP是等腰直角三角形，求点P的坐标；（3）当m=4时，抛物线上有两点M（x1， y1）和N（x2， y2），若x1＜2，x2＞2，x1+x2＞4，试判断y1与y2的大小，并说明理由．【答案】（1）解：抛物线 y=-x2+mx+n的对称轴为直线x=-3，AB=4．∴点 A（-5，0），点B（-1，0）．∴抛物线的表达式为y=-（x+5）（ x+1）∴y=-x2-6x-5．（2）解：如图1，依题意，设平移后的抛物线表达式为：y=-x2+bx．∴抛物线的对称轴为直线x＝，抛物线与x正半轴交于点C（b，0）．∴b＞0．记平移后的抛物线顶点为P，∴点P的坐标（，），∵△OCP是等腰直角三角形，∴ =∴b=2．∴点P的坐标（1，1）．（3）解：如图2，当m=4时，抛物线表达式为：y=-x2+4x+n．∴抛物线的对称轴为直线 x=2．∵点M（x1， y1）和N（x2， y2）在抛物线上，且x1＜2，x2＞2，∴点M在直线x=2的左侧，点N在直线x=2的右侧．∵x1+x2＞4，∴2-x1＜x2-2，∴点M到直线x=2的距离比点N到直线x=2的距离近，∴y1＞y2．【解析】【分析】（1）先根据抛物线和x轴的交点及线段的长，求出抛物线的解析式；（2）根据平移后抛物线的特点设出抛物线的解析式，再利用等腰直角三角形的性质求出抛物线解析式；（3）根据抛物线的解析式判断出点M，N的大概位置，再关键点M，N的横坐标的范围即可得出结论．。
2021年四川省各市中考数学真题汇编压轴题：《反比例函数》及答案
2021年四川省各市中考数学真题汇编压轴题：《反比例函数》1．（2021•德阳）如图，一次函数y1＝ax+b与反比例函数y2＝的图象交于A、B两点．点A的横坐标为2，点B的纵坐标为1．（1）求a，b的值．（2）在反比例y2＝第三象限的图象上找一点P，使点P到直线AB的距离最短，求点P的坐标．2．（2021•眉山）已知一次函数y＝kx+b与反比例函数y＝的图象交于A（﹣3，2）、B（1，n）两点．（1）求一次函数和反比例函数的表达式；（2）求△AOB的面积；（3）点P在x轴上，当△PAO为等腰三角形时，直接写出点P的坐标．3．（2021•雅安）如图，一次函数y＝kx+b（k、b为常数，k≠0）的图象与x轴、y轴分别交于A、B两点，且与反比例函数y＝（m为常数且m≠0）的图象在第二象限交于点C，CD⊥x轴，垂足为D，若OB＝2OA＝3OD＝6．（1）求一次函数与反比例函数的解析式；（2）求两个函数图象的另一个交点E的坐标；（3）请观察图象，直接写出不等式kx+b≤的解集．4．（2021•绵阳）如图，在平面直角坐标系xOy中，一次函数的图象与反比例函数y＝（k ＜0）的图象在第二象限交于A（﹣3，m），B（n，2）两点．（1）当m＝1时，求一次函数的解析式；（2）若点E在x轴上，满足∠AEB＝90°，且AE＝2﹣m，求反比例函数的解析式．5．（2021•宜宾）如图，一次函数y＝kx+b的图象与反比例函数y＝（x＜0）的图象相交于点A（﹣3，n），B（﹣1，﹣3）两点，过点A作AC⊥OP于点C．（1）求一次函数和反比例函数的表达式；（2）求四边形ABOC的面积．6．（2021•攀枝花）如图，过直线y＝kx+上一点P作PD⊥x轴于点D，线段PD交函数y ＝（x＞0）的图象于点C，点C为线段PD的中点，点C关于直线y＝x的对称点C'的坐标为（1，3）．（1）求k、m的值；（2）求直线y＝kx+与函数y＝（x＞0）图象的交点坐标；（3）直接写出不等式＞kx+（x＞0）的解集．7．（2021•泸州）如图，在平面直角坐标系xOy中，已知一次函数y＝x+b的图象与反比例函数y＝的图象相交于A，B两点，且点A的坐标为（a，6）．（1）求该一次函数的解析式；（2）求△AOB的面积．8．（2021•凉山州）如图，已知直线l：y＝﹣x+5．（1）当反比例函数y＝（k＞0，x＞0）的图象与直线l在第一象限内至少有一个交点时，求k的取值范围．（2）若反比例函数y＝（k＞0，x＞0）的图象与直线l在第一象限内相交于点A（x1，y1）、B（x2，y2），当x2﹣x1＝3时，求k的值，并根据图象写出此时关于x的不等式﹣x+5＜的解集．9．（2021•乐山）如图，已知点A（﹣2，﹣2）在双曲线y＝上，过点A的直线与双曲线的另一支交于点B（1，a）．（1）求直线AB的解析式；（2）过点B作BC⊥x轴于点C，连结AC，过点C作CD⊥AB于点D．求线段CD的长．10．（2021•甘孜州）如图，一次函数y＝x+1的图象与反比例函数y＝的图象相交于A （2，m）和B两点．（1）求反比例函数的解析式；（2）求点B的坐标．11．（2021•成都）在平面直角坐标系xOy中，反比例函数y＝（x＞0）的图象经过点A （3，4），过点A的直线y＝kx+b与x轴、y轴分别交于B，C两点．（1）求反比例函数的表达式；（2）若△AOB的面积为△BOC的面积的2倍，求此直线的函数表达式．12．（2021•遂宁）如图，在平面直角坐标系中，已知点A的坐标为（0，2），点B的坐标为（1，0），连结AB，以AB为边在第一象限内作正方形ABCD，直线BD交双曲线y═（k≠0）于D、E两点，连结CE，交x轴于点F．（1）求双曲线y＝（k≠0）和直线DE的解析式．（2）求△DEC的面积．13．（2021•南充）如图，反比例函数y＝（k≠0，x＞0）的图象与y＝2x的图象相交于点C，过直线上点A（a，8）作AB⊥y轴交于点B，交反比例函数图象于点D，且AB＝4BD．（1）求反比例函数的解析式．（2）求四边形OCDB的面积．参考答案1．解：（1）∵一次函数y1＝ax+b与反比例函数y2＝的图象交于A、B两点．点A的横坐标为2，点B的纵坐标为1，∴A（2，2），B（4，1），则有，解得．（2）过点P作直线PM∥AB，当直线PM与反比例函数只有一个交点时，点P到直线AB的距离最短，设直线PM的解析式为y＝﹣x+n，由，消去y得到，x2﹣2nx+8＝0，由题意得，△＝0，∴4n2﹣32＝0，∴n＝﹣2或2（舍弃），解得，∴P（﹣2，﹣）．2．解：（1）∵反比例函数y＝经过点A（﹣3，2），∴m ＝﹣6，∵点B （1，n ）在反比例函数图象上，∴n ＝﹣6．∴B （1，﹣6），把A ，B 的坐标代入y ＝kx +b ， 则有， 解得， ∴一次函数的解析式为y ＝﹣2x ﹣4，反比例函数的解析式为y ＝﹣．（2）如图设直线AB 交y 轴于C ，则C （0，﹣4），∴S △AOB ＝S △OCA +S △OCB ＝×4×3+×4×1＝8．（3）由题意OA ＝＝，当AO ＝AP 时，可得P 1（﹣6，0），当OA ＝OP 时，可得P 2（﹣，0），P 4（，0），当PA ＝PO 时，过点A 作AJ ⊥x 轴于J ．设OP 3＝P 3A ＝x ， 在Rt △AJP 3中，则有x 2＝22+（3﹣x ）2，解得x ＝， ∴P 3（﹣，0），综上所述，满足条件的点P 的坐标为（﹣6，0）或（﹣，0）或（，0）或（﹣，0）．3．解：（1）∵OB＝2OA＝3OD＝6，∴OB＝6，OA＝3，OD＝2，∵CD⊥OA，∴DC∥OB，∴＝，∴＝，∴CD＝10，∴点C坐标是（﹣2，10），∵B（0，6），A（3，0），∴，解得，∴一次函数为y＝﹣2x+6．∵反比例函数y＝经过点C（﹣2，10），∴m＝﹣20，∴反比例函数解析式为y＝﹣．（2）由解得或，∴E的坐标为（5，﹣4）．（3）由图象可知kx+b≤的解集是：﹣2≤x＜0或x≥5．4．解：（1）当m＝1时，点A（﹣3，1），∵点A在反比例函数y＝的图象上，∴k＝﹣3×1＝﹣3，∴反比例函数的解析式为y＝﹣；∵点B（n，2）在反比例函数y＝﹣图象上，∴2n＝﹣3，∴n＝﹣，设直线AB的解析式为y＝ax+b，则，∴，∴直线AB的解析式为y＝x+3；（2）如图，过点A作AM⊥x轴于M，过点B作BN⊥x轴于N，过点A作AF⊥BN于F，交BE于G，则四边形AMNF是矩形，∴FN＝AM，AF＝MN，∵A（﹣3，m），B（n，2），∴BF＝2﹣m，∵AE＝2﹣m，∴BF＝AE，在△AEG和△BFG中，，∴△AEG≌△BFG（AAS），∴AG＝BG，EG＝FG，∴BE＝BG+EG＝AG+FG＝AF，∵点A（﹣3，m），B（n，2）在反比例函数y＝的图象上，∴k＝﹣3m＝2n，∴m＝﹣n，∴BF＝BN﹣FN＝BN﹣AM＝2﹣m＝2+n，MN＝n﹣（﹣3）＝n+3，∴BE＝AF＝n+3，∵∠AEM+∠MAE＝90°，∠AEM+∠BEN＝90°，∴∠MAE＝∠NEB，∵∠AME＝∠ENB＝90°，∴△AME∽△ENB，∴＝＝＝＝，∴ME＝BN＝，在Rt△AME中，AM＝m，AE＝2﹣m，根据勾股定理得，AM2+ME2＝AE2，∴m2+（）2＝（2﹣m）2，∴m＝，∴k＝﹣3m＝﹣，∴反比例函数的解析式为y＝﹣．5．解：（1）B（﹣1，﹣3）代入y＝得，m＝3，∴反比例函数的关系式为y＝；把A（﹣3，n）代入y＝得，n＝﹣1∴点A（﹣3，﹣1）；把点A（﹣3，﹣1），B（﹣1，﹣3）代入一次函数y＝kx+b得，，解得：，∴一次函数的关系式为：y＝﹣x﹣4；答：一次函数的关系式为y ＝﹣x ﹣4，反比例函数的关系式为y ＝；（2）如图，过点B 作BM ⊥OP ，垂足为M ，由题意可知，OM ＝1，BM ＝3，AC ＝1，MC ＝OC ﹣OM ＝3﹣1＝2，∴S 四边形ABOC ＝S △BOM +S 梯形ACMB ， ＝+×（1+3）×2， ＝．6．解：（1）∵C ′的坐标为（1，3），代入y ＝（x ＞0）中，得：m ＝1×3＝3， ∵C 和C ′关于直线y ＝x 对称，∴点C 的坐标为（3，1），∵点C 为PD 中点，∴点P （3，2），将点P 代入y ＝kx +，∴解得：k ＝；∴k 和m 的值分别为：3，；（2）联立：，得：x 2+x ﹣6＝0，解得：x 1＝2，x 2＝﹣3（舍），∴直线y ＝kx +与函数y ＝（x ＞0）图象的交点坐标为（2，）；（3）∵两个函数的交点为：（2，），由图象可知：当0＜x ＜2时，反比例函数图象在一次函数图象上面， ∴不等式（x ＞0）的解集为：0＜x ＜2．7．解：（1）如图，∵点A （a ，6）在反比例函数y ＝的图象上，∴6a ＝12，∴a ＝2，∴A （2，6）， 把A （2，6）代入一次函数y ＝x +b 中得：＝6，∴b ＝3，∴该一次函数的解析式为：y ＝x +3； （2）由得：，，∴B （﹣4，﹣3），当x ＝0时，y ＝3，即OC ＝3，∴△AOB 的面积＝S △ACO +S △BCO ＝＝9．8．解：（1）将直线l 的表达式与反比例函数表达式联立并整理得：x 2﹣5x +k ＝0， 由题意得：△＝25﹣4k ≥0，解得：k ≤，故k 的取值范围0＜k ≤；（2）设点A（m，﹣m+5），而x2﹣x1＝3，则点B（m+3，﹣m+2），点A、B都在反比例函数上，故m（﹣m+5）＝（m+3）（﹣m+2），解得：m＝1，故点A、B的坐标分别为（1，4）、（4，1）；将点A的坐标代入反比例函数表达式并解得：k＝4×1＝4，观察函数图象知，当﹣x+5＜时，0＜x＜1或x＞4．9．解：（1）将点A（﹣2，﹣2）代入，得k＝4，即，将B（1，a）代入，得a＝4，即B（1，4），设直线AB的解析式为y＝mx+n，将A（﹣2，﹣2）、B（1，4）代入y＝mx+n，得，解得，∴直线AB的解析式为y＝2x+2；（2）∵A（﹣2，﹣2）、B（1，4），∴，∵，∴．10．解：（1）∵一次函数y＝x+1的图象过点A（2，m），∴m＝×2+1＝2，∴点A（2，2），∵反比例函数y＝的图象经过点A（2，2），∴k＝2×2＝4，∴反比例函数的解析式为：y＝；（2）联立方程组可得：，解得：或，∴点B（﹣4，﹣1）．11．解：（1）∵反比例函数y＝（x＞0）的图象经过点A（3，4），∴m＝3×4＝12，∴反比例函数的表达式为y＝；（2）∵直线y＝kx+b过点A，∴3k+b＝4，∵过点A的直线y＝kx+b与x轴、y轴分别交于B，C两点，∴B（﹣，0），C（0，b），∵△AOB的面积为△BOC的面积的2倍，∴×4×|﹣|＝2×|﹣|×|b|，∴b＝±2，当b＝2时，k＝，当b＝﹣2时，k＝2，∴直线的函数表达式为：y＝x+2或y＝2x﹣2．12．解：（1）∵点A的坐标为（0，2），点B的坐标为（1，0），∴OA＝2，OB＝1，作DM⊥y轴于M，∵四边形ABCD是正方形，∴∠BAD＝90°，AB＝AD，∴∠OAB+∠DAM＝90°，∵∠OAB+∠ABO＝90°，∴∠DAM＝∠ABO，在△AOB和△DMA中，∴△AOB≌△DMA（AAS），∴AM＝OB＝1，DM＝OA＝2，∴D（2，3），∵双曲线y═（k≠0）经过D点，∴k＝2×3＝6，∴双曲线为y＝，设直线DE的解析式为y＝mx+n，把B（1，0），D（2，3）代入得，解得，∴直线DE的解析式为y＝3x﹣3；（2）连接AC，交BD于N，∵四边形ABCD是正方形，∴BD垂直平分AC，AC＝BD，解得或，∴E（﹣1，﹣6），∵B（1，0），D（2，3），∴DE＝＝3，DB＝＝，∴CN＝BD＝，＝DE•CN＝×＝．∴S△DEC13．解：（1）∵点A（a，8）在直线y＝2x上，∴a＝4，A（4，8），∵AB⊥y轴于点B，AB＝4BD，∴BD＝1，即D（1，8），∵点D在y＝上，∴k＝8．∴反比例函数的解析式为y＝．（2）由，解得或（舍弃），∴C（2，4），∴S四边形OBDC ＝S△AOB﹣S△ADC＝×4×8﹣×4×3＝10．。
反比例函数中考真题(含答案解析)
反比例函数中考真题学校:___________姓名：___________班级：___________考号：___________ 一、单选题1．（2021·西藏·中考真题）如图．在平面直角坐标系中，△AOB 的面积为278，BA 垂直x 轴于点A ，OB 与双曲线y ＝kx相交于点C ，且BC △OC ＝1△2，则k 的值为（ ）A ．﹣3B ．﹣94C ．3D ．922．（2021·黑龙江牡丹江·中考真题）如图，矩形OABC 的面积为36，它的对角线OB 与双曲线y kx=相交于点D ，且OD ：OB ＝2：3，则k 的值为（ ）A ．12B ．﹣12C ．16D ．﹣163．（2021·辽宁营口·中考真题）如图，在平面直角坐标系中，菱形ABCD 的边BC 与x 轴平行，A ，B 两点纵坐标分别为4，2，反比例函数ky x=经过A ，B 两点，若菱形ABCD 面积为8，则k 值为（ ）A ．-B ．-C ．8-D ．-4．（2021·四川内江·中考真题）如图，菱形ABCD 的顶点分别在反比例函数1k y x=和2k y x=的图象上，若60BCD ∠=︒，则12k k 的值为（ ）AB ．23C．D ．13-5．（2021·江苏南通·中考真题）平面直角坐标系xOy 中，直线2y x =与双曲线()2ky k x=>相交于A ，B 两点，其中点A 在第一象限．设(),2M m 为双曲线()2ky k x=>上一点，直线AM ，BM 分别交y 轴于C ，D 两点，则OC OD -的值为（ ） A ．2B ．4C ．6D ．86．（2021·内蒙古·中考真题）如图，在平面直角坐标系中，矩形OABC 的OA 边在x 轴的正半轴上，OC 边在y 轴的正半轴上，点B 的坐标为（4，2），反比例函数2(0)y x x=>的图象与BC 交于点D ，与对角线OB 交于点E ，与AB 交于点F ，连接OD ，DE ，EF ，DF ．下列结论：△sin cos DOC BOC ∠=∠；△OE BE =；△DOE BEF S S =△△；△:2:3OD DF =．其中正确的结论有（ ）A ．4个B ．3个C ．2个D ．1个二、填空题7．（2021·辽宁鞍山·中考真题）如图，ABC 的顶点B 在反比例函数(0)k y x x=>的图象上，顶点C 在x 轴负半轴上，//AB x 轴，AB ，BC 分别交y 轴于点D ，E ．若32BE CO CE AD ==，13ABCS =，则k =_____．8．（2021·辽宁锦州·中考真题）如图，在平面直角坐标系中，△OABC 的顶点A ，B 在第一象限内，顶点C 在y 轴上，经过点A 的反比例函数y ＝kx（x ＞0）的图象交BC 于点D ．若CD ＝2BD ，△OABC 的面积为15，则k 的值为______．9．（2021·四川巴中·中考真题）如图，平行于y 轴的直线与函数y 1kx=（x ＞0）和y 22x =（x ＞0）的图象分别交于A 、B 两点，OA 交双曲线y 22x=于点C ，连接CD ，若OCD 的面积为2，则k ＝_______．10．（2021·贵州毕节·中考真题）如图，直线AB 与反比例函数()0,0ky k x x=>>的图象交于A ，B 两点，与x 轴交于点C ，且AB BC =，连接OA ．已知OAC 的面积为12，则k 的值为_____________．11．（2021·山东潍坊·中考真题）如图，在直角坐标系中，O 为坐标原点a y x =与by x=（a ＞b ＞0）在第一象限的图象分别为曲线C 1，C 2，点P 为曲线C 1上的任意一点，过点P 作y 轴的垂线交C 2于点A ，作x 轴的垂线交C 2于点B ，则阴影部分的面积S △AOB ＝_______．（结果用a ，b 表示）12．（2021·黑龙江绥化·中考真题）如图，在平面直角坐标系中，O 为坐标原点，MN 垂直于x 轴，以MN 为对称轴作ODE 的轴对称图形，对称轴MN 与线段DE 相交于点F ，点D 的对应点B 恰好落在(0,0)ky k x x=≠<的双曲线上．点O E 、的对应点分别是点C A 、．若点A 为OE 的中点，且1AEF S =△，则k 的值为____．13．（2021·广西柳州·中考真题）如图，一次函数2y x =与反比例数()0ky k x=>的图像交于A ，B 两点，点M 在以()2,0C 为圆心，半径为1的C 上，N 是AM 的中点，已知ON 长的最大值为32，则k 的值是_______．14．（2021·山东菏泽·中考真题）如图，一次函数y x =与反比例函数1y x=（0x >）的图象交于点A ，过点A 作AB OA ⊥，交x 轴于点B ；作1//BA OA ，交反比例函数图象于点1A ；过点1A 作111A B A B ⊥交x 轴于点B ；再作121//B A BA ，交反比例函数图象于点2A ，依次进行下去，……，则点2021A 的横坐标为_______．三、解答题15．（2021·四川绵阳·中考真题）如图，在平面直角坐标系xOy 中，直角ABC 的顶点A ，B 在函数()0,0ky k x x=>>图象上，//AC x 轴，线段AB 的垂直平分线交CB 于点M ，交AC 的延长线于点E ，点A 纵坐标为2，点B 横坐标为1，1CE =．（1）求点C和点E的坐标及k的值；（2）连接BE，求MBE△的面积．参考答案：1．A 【解析】 【分析】过C 作CD △x 轴于D ，可得△DOC △△AOB ，根据相似三角形的性质求出S △DOC ，由反比例函数系数k 的几何意义即可求得k ． 【详解】解：过C 作CD △x 轴于D ，△BC OC＝12， △OC OB＝23， △BA △x 轴， △CD △AB ， △△DOC △△AOB ， △DOC AOB S S ∆∆＝（OC OB ）2＝（23）2＝49， △S △AOB ＝278， △S △DOC ＝49S △AOB ＝49×278＝32，△双曲线y ＝kx 在第二象限，△k ＝﹣2×32＝﹣3，故选：A ． 【点睛】本题主要考查了反比例函数系数k 的几何意义，相似三角形的性质和判定，根据相似三角形的性质和判定求出S △DOC 是解决问题的关键．2．D 【解析】 【分析】过D 点作DE △OA ，DF △OC ，垂足为E 、F ，由双曲线的解析式可知S 矩形OEDF =|k |，由于D 点在矩形的对角线OB 上，可知矩形OEDF △矩形OABC ，并且相似比为OD :OB ＝2:3，由相似多边形的面积比等于相似比的平方可求出S 矩形OEDF =16，再根据在反比例函数y k x=图象在第二象限，即可算出k 的值． 【详解】解：过D 点作DE △OA ，DF △OC ，垂足为E 、F ，△D 点在双曲线y kx=上， △S 矩形OEDF =|xy |=|k |，△D 点在矩形的对角线OB 上， △矩形OEDF △矩形OABC ， △29()4OEDF OABC OD OB S S ==， △S 矩形OABC =36， △S 矩形OEDF =16， △|k |=16， △双曲线y kx=在第二象限， △k =-16， 故选：D ． 【点睛】本题考查了反比例函数的综合运用．关键是过D 点作坐标轴的垂线，构造矩形，再根据相似多边形的面积的性质求出|k |． 3．A【解析】 【分析】过点A 作AE BC ⊥，设,44k A ⎛⎫⎪⎝⎭，,22k B ⎛⎫ ⎪⎝⎭，根据菱形的面积得到AB 的长度，在Rt ABE△中应用勾股定理即可求解． 【详解】解：过点A 作AE BC ⊥，△A ，B 两点纵坐标分别为4，2，反比例函数ky x=经过A ，B 两点， △设,44k A ⎛⎫⎪⎝⎭，,22k B ⎛⎫ ⎪⎝⎭，△2AE =，244k k k BE =-+=-， △菱形ABCD 面积为8， △8BC AE ⋅=，解得4BC =， △4AB BC ==，在Rt ABE △中，222AB AE BE =+，即22242BE =+，解得BE = △k =- 故选：A ． 【点睛】本题考查反比例函数图象上点的坐标特征、菱形的性质等内容，根据提示做出辅助线是解题的关键． 4．D 【解析】 【分析】连接AC 、BD ，根据菱形的性质和反比例函数的对称性，即可得出△BOC =90°，△BCO =12△BCD =30°，解直角三角形求得tan 30OB OC ︒==，作 BM △x 轴于M ，CN △x 轴于N ，证得△OMB △△CNO ，得到2()BOMCONS OB S OC∆∆=，根据反比例函数系数 k 的几何意义即可求得结果． 【详解】解：连接AC 、BD ，四边形ABCD 是菱形，AC BD ∴⊥，菱形ABCD 的顶点分别在反比例函数1k y x=和2ky x =的图象上，A ∴与C 、B 与D 关于原点对称，AC ∴、BD 经过点O ，90BOC ∴∠=︒，1302BCO BCD ∠=∠=︒，tan30OB OC ∴︒=作BM x ⊥轴于M ，CN x ⊥轴于N ，90BOM NOC NOC NCO ∠+∠=︒=∠+∠， BOM NCO ∴∠=∠， 90OMB CNO ∠=∠=︒， OMB CNO ∴∆∆∽，∴2()BOM CON S OB S OC∆∆=， ∴12112132k k =-， ∴1213k k =-， 故选：D ．【点睛】本题考查反比例函数图象上点的坐标特征，菱形的性质，解直角三角形，三角形相似的判定和性质，反比例函数系数k 的几何意义，解题关键是熟练掌握反比例函数的性质与菱形的性质．5．B【解析】【分析】根据直线2y x =与双曲线()2k y k x=>相交于A ，B 两点，其中点A在第一象限求得A ⎝，B ⎛ ⎝，再根据(),2M m 为双曲线()2k y k x =>上一点求得,22k M ⎛⎫ ⎪⎝⎭；根据点A 与点M 的坐标求得直线AM解析式为y而求得OC =B 与点M 的坐标求得直线BM解析式为2k y -=OD =OC OD -即可． 【详解】 解：△直线2y x =与双曲线()2k y k x =>相交于A ，B 两点， △联立可得：2,,y x k y x =⎧⎪⎨=⎪⎩解得：11x y ⎧=⎪⎨⎪=⎩或22x y ⎧=⎪⎨⎪=⎩ △点A 在第一象限，△A ⎝，B ⎛ ⎝． △(),2M m 为双曲线()2k y k x=>上一点， △2k m =． 解得：2k m =． △,22k M ⎛⎫ ⎪⎝⎭． 设直线AM 的解析式为11y k x b =+，将点A ⎝与点,22k M ⎛⎫ ⎪⎝⎭代入解析式可得：1111,2?,2k b k k b ⎨⎪=+⎪⎩解得：11k b ⎧⎪⎪⎨⎪=⎪⎩△直线AM的解析式为y x ． △直线AM 与y 轴交于C 点，△0C x =．△2202C k yk -=+=． △C ⎛⎝．△2k >，△OC == 设直线BM 的解析式为22y k x b =+，将点B ⎛ ⎝与点,22k M ⎛⎫ ⎪⎝⎭代入解析式可得：2222?,2?,2k b k k b ⎧⎛+⎪ ⎪⎝⎭⎨⎪=+⎪⎩解得：22k b ⎧=⎪⎪⎨⎪=⎪⎩△直线BM的解析式为y ． △直线BM 与y 轴交于D 点，△0D x =．△2202D k yk -=+ △D ⎛⎝．△2k >，△OD =．△OC OD -k k22842k k k k-=- ()22422k k k k -=-=4．故选：B ．【点睛】本题考查了一次函数和反比例函数的综合应用，涉及到分式方程，一元二次方程和二元一次方程组的求解，正确求出点的坐标和直线解析式是解题关键．6．A【解析】【分析】 根据题意，图中各点的坐标均可以求出来，sin CD DOC OD ∠=，cos =OC BOC OB∠，只需证明CD OC OD OB=即可证明结论△；先求出直线OB 的解析式，然后求直线OB 与反比例函数2(0)y x x =>的交点坐标，即可证明结论△；分别求出DOE S △和BEF S ，进行比较即可证明结论△；只需证明OCD DBF ∽，即可求证结论△．【详解】解：△OABC 为矩形，点B 的坐标为（4，2），△A 点坐标为(4，0)，C 点坐标为(0，2)， 根据反比例函数2(0)y x x=>， 当2y =时，1x =，即D 点坐标为(1，2)，当4x =时，12y =，即F 点坐标为(4，12)， △21OC CD ==，，△OD△24OC CB ==，，△OB△sinCD DOC OD ∠=，cos =OC BOC OB ∠， △sin cos DOC BOC ∠=∠，故结论△正确；设直线OB 的函数解析式为：y kx =，点B 代入则有：2=4k ，解得：12k =， 故直线OB 的函数解析式为：12y x =， 当122x x =时，1222x x ==-；(舍)即2x =时，1y =，△点E 的坐标为(2，1)，△点E 为OB 的中点，△OE BE =，故结论△正确； △112CD AF ==，， △332BD BF ==，， 由△得：13122DOE DBE SS BD ==⨯⨯=， 13222BEF S BF =⨯⨯=， △DOE BEF S S =△△， 故结论△正确；在Rt OCD △和Rt DBF 中，32232OC DB CD BF ===，， △OCD DBF ∽，△::2:3OD DF OC DB ==，故结论△正确，综上：△△△△均正确，故选：A ．【点睛】本题主要考查矩形的性质，相似三角形判定与性质，锐角三角函数，反比例函数与几何综合，结合题意求出图中各点坐标是解决本题的关键．7．18【解析】【分析】过点B 作BF x ⊥轴于点F ，通过设参数表示出△ABC 的面积，从而求出参数的值，再利用△ABC 与矩形ODBF 的关系求出矩形面积，即可求得 k 的值．【详解】解：如图，过点B 作BF x ⊥轴于点F ．//AB x 轴，DBE COE ∴∽，DB BE DE CO CE EO∴==， 32BE CO CE AD ==， 32DB DE BE CO CO EO CE AD ∴====， 设3CO a =，3DE b =，则2AD a =，2OE b =，332DB a ∴=，5OD b =， 92a BD ∴=， 132a AB AD DB ∴=+=， 1113513222ABC a S AB OD b =⋅⋅=⨯⨯=， 45ab ∴=， 94551822ODBF a ab S BD OD b ⋅=⋅===矩形， 又反比例函数图象在第一象限，18k ∴=，故答案为18．【点睛】此题考查反比例函数知识，涉及三角形相似及利用相似求长度，矩形面积公式等，难度一般．8．18【解析】【分析】过点D 作DN △y 轴于N ，过点B 作BM △y 轴于M ，可得2CN MN =，设OC ＝a ，CN ＝2b ，则MN ＝b ，根据△OABC 的面积为15表示出BM 的长度，根据CD ＝2BD 求出ND 的长，进而表示出A ，D 两点的坐标，根据反比例函数系数k 的几何意义即可求出．【详解】解：过点D 作DN △y 轴于N ，过点B 作BM △y 轴于M ，△//DN BM ， △CN CD MN BD= ， △CD ＝2BD ， △2CN CD MN BD==，即2CN MN = ， 设OC ＝a ，CN ＝2b ，则MN ＝b ，△△OABC 的面积为15，△BM ＝15a， △//DN BM ，△CDN CBM ， △DN CD BM CB= ， △CD ＝2BD ， △23CD CB = ，△ND ＝23BM ＝10a， △A ，D 点坐标分别为（15a ，3b ），（10a ，a ＋2b ）， △15a •3b ＝10a（a ＋2b ）， △b ＝25a ， △k ＝15a •3b ＝15a •3×25a ＝18， 故答案为：18．【点睛】本题主要考查了平行四边形的性质和反比例函数的几何意义，相似三角形的性质和判定，利用数形结合思想是解题的关键．9．8【解析】【分析】设A （m ，k m ），则B （m ，2m），D （m ，0），C （n ，k n ），由112=222OCD C m S OD y m n n ===△得出12n m =，再根据()1122OCD OAD ACD k S S S k m n m=-=--△△△求解即可得到答案. 【详解】解：设A （m ，k m ），则B （m ，2m ），D （m ，0），C （n ，k n ）， △112=222OCD C m S OD y m n n ===△， △12n m =， 又△()1122OCD OAD ACD k S S S k m n m=-=--△△△ 112m n k m -⎛⎫=- ⎪⎝⎭ 12n k m =14k = △124k =解得8k故答案为：8.【点睛】本题主要考查了反比例函数与一次函数的交点问题，反比例函数比例系数的几何意义，函数图像上点的坐标特征，三角形的面积，解题的关键在于能够熟练掌握相关知识进行求解. 10．8.【解析】【分析】过点A作AE△x交x轴于E，过点B作BF△x交x轴于F，根据AB=BC，可以得到EF=FC，再根据三角形面积公式即可求解.【详解】解：如图所示，过点A作AE△x轴交x轴于E，过点B作BF△x轴交x轴于F△AE△x轴，BF△x轴，AB=BC△EF=FC，AE=2BF（中位线定理）设A点坐标为（a，ka），则B点坐标为（2a，2ka）△OC=OE+EF+FC△OC=OE+EF+FC=3a△11=31222OACkS OC AE aa==△解得8k故答案为：8.【点睛】本题主要考查了中位线定理，反比例函数的性质和三角形面积公式，解题的关键在于能够熟练运用相关知识进行求解.11．12a 22b a- 【解析】【分析】设B （m ，b m ），A （b n，n ），则P （m ，n ），阴影部分的面积S △AOB ＝矩形的面积﹣三个直角三角形的面积可得结论．【详解】解：设B （m ，b m ），A （b n，n ），则P （m ，n ）， △点P 为曲线C 1上的任意一点，△mn ＝a ，△阴影部分的面积S △AOB ＝mn 12-b 12-b 12-（m b n -）（n b m-） ＝mn ﹣b 12-（mn ﹣b ﹣b 2b mn+） ＝mn ﹣b 12-mn +b 22b mn- 12=a 22b a-． 故答案为：12a 22b a-． 【点睛】本题考查了反比例函数的系数k 的几何意义，矩形的面积，反比例函数图象上点的坐标特征等知识，本题利用参数表示三角形和矩形的面积并结合mn ＝a 可解决问题．12．24-【解析】【分析】先利用轴对称和中点的定义，确定EG 和EO 之间的关系，再利用平行线分线段成比例定理及推论，得到FG 和OD 之间的关系，设EG =x ，FG =y ，用它们表示出D 点坐标，接着得到B 点坐标，利用1AEF S =△，得到1xy =，再利用反比例函数的定义，计算出B 点横纵坐标的积，即为所求k 的值．【详解】解：如图所示，由轴对称的性质可知：GE =GA ，CG =OG ，BC =OD ，△点A 为OE 的中点，△AE =OA ， △1244EG EG EG OE AE EG ===, △MN △y 轴， △14FG EG OD EO ==， △=4OD FG ，△1AEF S =△， △112AE FG ⋅=, △1212EG FG ⨯⋅=， △1EG FG ⋅=，设EG =x ，FG =y ，则OG =3x ，OD =4y ，△()0,4D y ，因为D 点和B 点关于MN 对称，△()6,4B x y -△1EG FG ⋅=，△1xy =△6424x y -⋅=-,△点B 恰好落在(0,0)k y k x x=≠<的双曲线上， △24k =-，故答案为：24-．【点睛】本题考查了轴对称的性质、中点的定义、平行线分线段成比例定理的推论、反比例函数的定义等内容，解决本题的关键是牢记相关定义与性质，能根据题意在图形中找到对应关系，能挖掘图形中的隐含信息等，本题蕴含了数形结合的思想方法等．13．32 25【解析】【分析】根据题意得出ON是ABM的中位线，所以ON取到最大值时，BM也取到最大值，就转化为研究BM也取到最大值时k的值，根据,,B C M三点共线时，BM取得最大值，解出B的坐标代入反比例函数即可求解．【详解】解：连接BM，如下图：在ABM 中，,O N 分别是,AB AM 的中点，ON ∴是ABM 的中位线，12ON BM ∴=， 已知ON 长的最大值为32， 此时的3BM =，显然当,,B C M 三点共线时，取到最大值：3BM =，13BM BC CM BC =+=+=，2BC ∴=，设(,2)B t t ，由两点间的距离公式：2BC ==，22(2)44t t ∴-+=， 解得：124,05t t ==（取舍）， 48(,)55B ∴， 将48(,)55B 代入()0k y k x=>， 解得：3225k =， 故答案是：3225． 【点睛】 本题考查了一次函数、反比例函数、三角形的中位线、圆，研究动点问题中线段最大值问题，解题的关键是：根据中位线的性质，利用转化思想，研究BM 取最大值时k 的值．14【解析】【分析】由点A 是直线y x =与双曲线1y x=的交点，即可求出点A 的坐标，且可知45AOB ∠=︒，又AB AO ⊥可知AOB ∆是等腰直角三角形，再结合1BA OA //可知11BA B ∆是等腰直角三角形，同理可知图中所有三角形都是等腰直角三角形，由求2021A 的坐标，即n A 的坐标（n=1,2,3……），故想到过点2021A 作20212021A C x ⊥轴，即过n A 作n n A C x ⊥轴．设1A 的纵坐标为()10m m >，则1A 的横坐标为2m +，再利用点1A 在双曲线上即可求解1A 坐标，同理可得2021A 的坐标．【详解】解：过n A 作n n A C x ⊥轴于点n C点A 是直线y x =与双曲线1y x=的交点1y x y x =⎧⎪∴⎨=⎪⎩解得11x y =⎧⎨=⎩ ()1,1A ∴1,45OC AC AOC ∴==∠=︒AB AO ⊥∴AOB ∆是等腰直角三角形∴22OB AC ==1BA OA //∴11BA B ∆是等腰直角三角形∴111AC BC =设1A 的纵坐标为()10m m >，则1A 的横坐标为12m +点1A 在双曲线上∴()1121m m +=解得11m设2A 的纵坐标为()20m m >，则2A的横坐标为12222m m m ++=∴()221m m =解得2m同理可得3m由以上规律知：n m2021m ∴2021A∴2021A =【点睛】本题考察一次函数、反比例函数、交点坐标的求法、等腰直角三角形的性质、一元二次方程的应用和规律探究，属于综合几何题型，难度偏大．解题的关键是结合等腰直角三角形的性质做出辅助线，并在计算过程中找到规律．15．（1）()1,2，()2,2，23k =；（2）512 【解析】【分析】（1）由点A 的纵坐标为2，点B 的横坐标为1，可以用k 表示出A ，B 两点坐标，又//AC x 轴，ABC 为直角三角形，所以可以得到点C 的纵坐标为2，点C 的横坐标为1，由此得到C 点坐标，又由于1CE =，可以得到E 点坐标，因为EM 垂直平分AB ，所以AE BE =，根据此等式列出关于k 的方程，即可求解；（2）由（1）中的k 值，可以求出A ，B 的坐标，利用勾股定理，求出线段AB 的长度，从而得到BD 的长度，先证明BDM BCA △∽△，利用相似三角形对应边成比例，求出BM 的长度，即可求出MBE △的面积．【详解】解：（1）如图，连接BE ，由题意得点A 的坐标为(2k ，2)，点B 的坐标为(1,)k ， 又//AC x 轴，且ACB △为直角三角形，∴点C 的坐标为(1,2)，又△1CE =，∴点E 的坐标为(2,2)，点E 在线段AB 的垂直平分线上，EA EB ∴=，在Rt BCE 中，222EB BC CE =+，221(2)(2)2k k ∴+-=-， 2k ∴=或23，当2k =时，点A ，B ，C 三点重合，不能构成三角形，故舍去，23k ∴=， (1,2)C ∴，(2,2)E ，23k =； （2）由（1）可得，23AC =，43BC =，1CE =， 设AB 的中点为D ，AB =12BD AB ==， ABC MBD ∠=∠，90BDM BCA ∠=∠=︒，BDM BCA ∴△∽△， ∴BM BD BA BC=，53463BM ∴=， 1155122612MBE S BM CE ∆∴=⨯=⨯⨯=．【点睛】本题是一道反比例函数的综合题，考查了反比例函数的图象性质，垂直平分线的性质，勾股定理，相似三角形的判定与性质等相关知识，熟知平行于坐标轴的直线上的点的坐标特征，是解决此题的关键．。
2021年中考数学专题复习：函数压轴 反比例函数综合 练习题(含答案)
2021年中考数学专题复习：函数压轴反比例函数综合练习题1．如图，Rt△ABP的直角顶点P在第四象限，顶点A、B分别落在反比例函数y＝图象的两支上，且PB⊥x轴于点C，PA⊥y轴于点D，AB分别与x轴，y轴相交于点F和E．已知点B的坐标为（1，3）．（1）填空：k＝；（2）证明：CD∥AB；（3）当四边形ABCD的面积和△PCD的面积相等时，求点P的坐标．2．如图，在平面直角坐标系xOy中，矩形OABC的顶点A在x轴上，顶点C在y轴上，D是BC的中点，过点D的反比例函数图象交AB于E点，连接DE．若OD＝5，tan∠COD＝．（1）求过点D的反比例函数的解析式；（2）求△DBE的面积；（3）x轴上是否存在点P使△OPD为直角三角形？若存在，请直接写出P点的坐标；若不存在，请说明理由．3．如图1，在平面直角坐标系中，平行四边形OABC的一个顶点与坐标原点重合，OA边落在x轴上，且OA＝4，OC＝2，∠COA＝45°．反比例函数y＝（k＞0，x＞0）的图象经过点C，与AB交于点D，连接CD．（1）求反比例函数的解析式；（2）求点D的坐标；（3）如图2，连接OD，在反比例函数图象上是否存在一点P，使得S△POC＝S△COD？如果存在，请直接写出点P的坐标．如果不存在，请说明理由．4．已知点A在x轴负半轴上，点B在y轴正半轴上，线段OB的长是方程x2﹣2x﹣8＝0的解，tan∠BAO＝．（1）求点A的坐标；（2）点E在y轴负半轴上，直线EC⊥AB，交线段AB于点C，交x轴于点D，S△DOE ＝16．若反比例函数y＝的图象经过点C，求k的值；（3）在（2）条件下，点M是DO中点，点N，P，Q在直线BD或y轴上，是否存在点P，使四边形MNPQ是矩形？若存在，请直接写出点P的坐标；若不存在，请说明理由．。
2020-2021 中考数学(反比例函数提高练习题)压轴题训练及答案
2020-2021 中考数学(反比例函数提高练习题)压轴题训练及答案一、反比例函数1．如图，反比例函数y1= 的图象与一次函数y2= x的图象交于点A、B，点B的横坐标是4，点P（1，m）在反比例函数y1= 的图象上．（1）求反比例函数的表达式；（2）观察图象回答：当x为何范围时，y1＞y2；（3）求△PAB的面积．【答案】（1）解：把x=4代入y2= x，得到点B的坐标为（4，1），把点B（4，1）代入y1= ，得k=4．反比例函数的表达式为y1=（2）解：∵点A与点B关于原点对称，∴A的坐标为（﹣4，﹣1），观察图象得，当x＜﹣4或0＜x＜4时，y1＞y2（3）解：过点A作AR⊥y轴于R，过点P作PS⊥y轴于S，连接PO，设AP与y轴交于点C，如图，∵点A与点B关于原点对称，∴OA=OB，∴S△AOP=S△BOP，∴S△PAB=2S△AOP．y1= 中，当x=1时，y=4，∴P（1，4）．设直线AP的函数关系式为y=mx+n，把点A（﹣4，﹣1）、P（1，4）代入y=mx+n，则，解得．故直线AP的函数关系式为y=x+3，则点C的坐标（0，3），OC=3，∴S△AOP=S△AOC+S△POC= OC•AR+ OC•PS= ×3×4+ ×3×1= ，∴S△PAB=2S△AOP=15．【解析】【分析】（1）把x=4代入y2= x，得到点B的坐标，再把点B的坐标代入y1=，求出k的值，即可得到反比例函数的表达式；（2）观察图象可知，反比例函数的图象在一次函数图象上方的部分对应的自变量的取值范围就是不等式y1＞y2的解集；（3）过点A作AR⊥y轴于R，过点P作PS⊥y轴于S，连接PO，设AP与y轴交于点C，由点A与点B关于原点对称，得出OA=OB，那么S△AOP=S△BOP，S△PAB=2S△AOP．求出P点坐标，利用待定系数法求出直线AP的函数关系式，得到点C的坐标，根据S△AOP=S△AOC+S△POC求出S△AOP= ，则S△PAB=2S△AOP=15．2．已知点P在一次函数y=kx+b（k，b为常数，且k＜0，b＞0）的图象上，将点P向左平移1个单位，再向上平移2个单位得到点Q，点Q也在该函数y=kx+b的图象上．（1）k的值是________；（2）如图，该一次函数的图象分别与x轴、y轴交于A，B两点，且与反比例函数y=图象交于C，D两点（点C在第二象限内），过点C作CE⊥x轴于点E，记S1为四边形CEOB的面积，S2为△OAB的面积，若 = ，则b的值是________．【答案】（1）﹣2（2）3【解析】【解答】解：（1）设点P的坐标为（m，n），则点Q的坐标为（m﹣1，n+2），依题意得：，解得：k=﹣2．故答案为：﹣2．（2）∵BO⊥x轴，CE⊥x轴，∴BO∥CE，∴△AOB∽△AEC．又∵ = ，∴ = = ．令一次函数y=﹣2x+b中x=0，则y=b，∴BO=b；令一次函数y=﹣2x+b中y=0，则0=﹣2x+b，解得：x= ，即AO= ．∵△AOB∽△AEC，且 = ，∴．∴AE= AO= b，CE= BO= b，OE=AE﹣AO= b．∵OE•CE=|﹣4|=4，即 b2=4，解得：b=3 ，或b=﹣3 （舍去）．故答案为：3 ．【分析】（1）设出点P的坐标，根据平移的特性写出Q点的坐标，由点P,Q均在一次函数y=kx+b（k，b为常数，且k＜0，b＞0）的图象上，即可得出关于k,m,n,b的四元次一方程组，两式作差即可求出k的值；（2）由BO⊥x轴，CE⊥x轴，找出△AOB∽△AEC．再由给定图形的面积比即可求出==，根据一次函数的解析式可以用含b的式子表示出OA,OB,由此即可得出线段CE,AE 的长，利用OE=AE﹣AO求出OE的长，再借助反比例函数K的几何意义得出关于b的一元二次方程，解方程即可得出结论。
2021全国各地中考数学真题专项汇编： 反比例函数(含答案解析)
专题09 反比例函数一、单选题1．（2021·山西）已知反比例函数6y x=，则下列描述不正确的是（ ） A ．图象位于第一，第三象限 B ．图象必经过点34,2⎛⎫ ⎪⎝⎭C ．图象不可能与坐标轴相交D ．y 随x 的增大而减小【答案】D【分析】根据反比例函数图像的性质判断即可． 【详解】解：A 、反比例函数6y x=，0k ＞，经过一、三象限，此选项正确，不符合题意； B 、将点34,2⎛⎫ ⎪⎝⎭代入6y x=中，等式成立，故此选项正确，不符合题意； C 、反比例函数不可能坐标轴相交，此选项正确，不符合题意；D 、反比例函数图像分为两部分，不能一起研究增减性，故此选项错误，符合题意；故选：D ． 【点睛】本题主要考查反比例函数图像的性质，熟知反比例函数的图像的性质是解题关键．2．（2021·四川达州市）在反比例函数21k y x+=（k 为常数）上有三点()11,A x y ，()22,B x y ，()33,C x y ，若1230x x x <<<，则1y ，2y ，3y 的大小关系为（ ） A ．123y y y << B ．213y y y <<C ．132y y y <<D ．321y y y <<【答案】C【分析】根据k >0判断出反比例函数的增减性，再根据其坐标特点解答即可． 【详解】解：∵210k +>，∴反比例函数图象的两个分支在第一、三象限，且在每个象限内y 随x 的增大而减小， ∵B （x 2，y 2），C （x 3，y 3）是双曲线ky x=上的两点，且320x x >>，∴点B 、C 在第一象限，0＜y 3＜y 2， ∵A （x 1，y 1）在第三象限，∵y 1＜0，∴132y y y <<．故选：C ．【点睛】本题考查了由反比例函数图象的性质判断函数图象上点的坐标特征，理解基本性质是解题关键． 3．（2021·浙江杭州市）已知1y 和2y 均是以x 为自变量的函数，当x m =时，函数值分别为1M 和2M ，若存在实数m ，使得120M M +=，则称函数1y 和2y 具有性质P ．以下函数1y 和2y 具有性质P 的是（ ）A ．212y x x =+和21y x =--B ．212y x x =+和21y x =-+C ．11y x =-和21y x =-- D ．11y x=-和21y x =-+【答案】A【分析】根据题中所给定义及一元二次方程根的判别式可直接进行排除选项．【详解】解：当x m =时，函数值分别为1M 和2M ，若存在实数m ，使得120M M +=，对于A 选项则有210m m +-=，由一元二次方程根的判别式可得：241450b ac -=+=>，所以存在实数m ，故符合题意；对于B 选项则有210m m ++=，由一元二次方程根的判别式可得：241430b ac -=-=-<，所以不存在实数m ，故不符合题意； 对于C 选项则有110m m---=，化简得：210m m ++=，由一元二次方程根的判别式可得：241430b ac -=-=-<，所以不存在实数m ，故不符合题意；对于D 选项则有110m m--+=，化简得：210m m -+=，由一元二次方程根的判别式可得：241430b ac -=-=-<，所以不存在实数m ，故不符合题意；故选A ．【点睛】本题主要考查一元二次方程根的判别式、二次函数与反比例函数的性质，熟练掌握一元二次方程根的判别式、二次函数与反比例函数的性质是解题的关键．4．（2021·天津）若点()()()1235,,1,,5,A y B y C y -都在反比例函数5y x=-的图象上，则123,,y y y 的大小关系是（ ） A ．123y y y << B ．231y y y <<C ．132y y y <<D ．312y y y <<【答案】B【分析】将A 、B 、C 三点坐标代入反比例函数解析式，即求出123、、y y y 的值，即可比较得出答案． 【详解】分别将A 、B 、C 三点坐标代入反比例函数解析式得：1515y =-=-、2551y =-=-、3515y =-=-．则231y y y <<．故选B ． 【点睛】本题考查比较反比例函数值．掌握反比例函数图象上的点的坐标满足其解析式是解答本题的关键．5．（2021·四川乐山市）如图，直线1l 与反比例函数3(0)y x x=>的图象相交于A 、B 两点，线段AB 的中点为点C ，过点C 作x 轴的垂线，垂足为点D ．直线2l 过原点O 和点C ．若直线2l 上存在点(,)P m n ，满足APB ADB ∠=∠，则m n +的值为（ ）A ．3B ．3或32C ．3+3D ．3【答案】A【分析】根据题意，得()1,3A ，()3,1B ，直线2l ：y x =；根据一次函数性质，得m n =；根据勾股定理，得PC =PA ，PB ，FB ，根据等腰三角形三线合一性质，得()2,2C ，OC AB ⊥；根据勾股定理逆定理，得90ABD ∠=︒；结合圆的性质，得点A 、B 、D 、P 共圆，直线2l 和AB 交于点F ，点F 为圆心；根据圆周角、圆心角、等腰三角形的性质，得FC =；分PC PF FC =+或PC PF FC =-两种情况，根据圆周角、二次根式的性质计算，即可得到答案． 【详解】根据题意，得3,33A ⎛⎫ ⎪⎝⎭，33,3B ⎛⎫ ⎪⎝⎭，即()1,3A ，()3,1B∵直线2l 过原点O 和点C ∴直线2l ：y x = ∵(,)P m n 在直线2l 上∴m n = ∴PC =连接PA ，PB ，FB ∴PA PB =，线段AB 的中点为点C ∴()2,2C ，OC AB ⊥ 过点C 作x 轴的垂线，垂足为点D ∴()2,0D∴AD ==AB ==BD ==∴222AD AB BD =+ ∴90ABD ∠=︒∴点A 、B 、D 、P 共圆，直线2l 和AB 交于点F ，点F为圆心∴cos BD ADB AD ∠==∵AC BC =，12FB FA AD ==∴12BFC AFB ∠=∠ ∵APB ADB ∠=∠，且12APB AFB ∠=∠ ∴APB ADB BFC ∠=∠=∠∴cos cos FC APB BFC FB ∠=∠===FC = ∴PC PF FC =+或PC PF FC =- 当PC PF FC =-时，APB ∠和ADB ∠位于直线AB 两侧，即180APB ADB ∠+∠=︒ ∴PC PF FC =-不符合题意∴22PC PF FC =+=+，且2m < ∴)2PC m ==-)2m -=+∴32m =∴23m n m +==A ．【点睛】本题考查了圆、等腰三角形、反比例函数、一次函数、三角函数、勾股定理、二次根式的知识；解题的关键是熟练掌握圆心角、圆周角、等腰三角形三线合一、三角函数、勾股定理的性质，从而完成求解．6．（2021·重庆）如图，在平面直角坐标系中，菱形ABCD 的顶点D 在第二象限，其余顶点都在第一象限，AB ∥X 轴，AO ⊥AD ，AO =A D ．过点A 作AE ⊥CD ，垂足为E ，DE =4CE ．反比例函数()0ky x x=>的图象经过点E ，与边AB 交于点F ，连接OE ，OF ，EF ．若118EOFS=，则k的值为（ ）A ．73B ．214C ．7D ．212【答案】A【分析】延长EA 交x 轴于点G ，过点F 作x 轴的垂线，垂足分别为H ，则可得△DEA ≌△AGO ，从而可得DE =AG ，AE =OG ，若设CE =a ，则DE =AG =4a ，AD =DC =DE +CE =5a ，由勾股定理得AE =OG =3a ，故可得点E 、A 的坐标，由AB 与x 轴平行，从而也可得点F 的坐标，根据EOFEOGFOHEGHF S SS S=+-梯形 ，即可求得a 的值，从而可求得k 的值．【详解】如图，延长EA 交x 轴于点G ，过点F 作x 轴的垂线，垂足分别为H∵四边形ABCD 是菱形∴CD =AD =AB ，CD ∥AB ∵AB ∥x 轴，AE ⊥CD ∴EG ⊥x 轴，∠D +∠DAE =90゜ ∵OA ⊥AD ∴∠DAE +∠GAO =90゜∴∠GAO =∠D ∵OA =OD ∴△DEA ≌△AGO (AAS )∴DE =AG ，AE =OG 设CE =a ，则DE =AG =4CE =4a ，AD =AB =DC =DE +CE =5a在Rt △AED 中，由勾股定理得：AE =3a ∴OG =AE =3a ，GE =AG +AE =7a ∴A （3a ,4a ），E (3a ,7a ) ∵AB ∥x 轴，AG ⊥x 轴，FH ⊥x 轴∴四边形AGHF 是矩形 ∴FH =AG =3a ，AF =GH∵E 点在双曲线()0ky x x=>上∴221ka = 即221a y x= ∵F 点在双曲线221a y x =上，且F 点的纵坐标为4a ∴214a x = 即214a OH =∴94a GH OH OG =-=∵EOF EOG FOHEGHF SSS S=+-梯形∴1191211137(74)4224248a a a a a a a ⨯⨯++⨯-⨯⨯= 解得：219a = ∴217212193k a ==⨯= 故选：A ．【点睛】本题是反比例函数与几何的综合题，考查了菱形的性质，矩形的判定与性质，三角形全等的判定与性质等知识，关键是作辅助线及证明△DEA ≌△AGO ，从而求得E 、A 、F 三点的坐标． 7．（2021·江苏扬州市）如图，点P 是函数()110,0k y k x x=>>的图像上一点，过点P 分别作x 轴和y 轴的垂线，垂足分别为点A 、B ，交函数()220,0k y k x x=>>的图像于点C 、D ，连接OC 、OD 、CD 、AB ，其中12k k >，下列结论：①//CD AB ；②122OCDk kS-=；③()21212DCPk k Sk -=，其中正确的是（ ）A ．①②B ．①③C ．②③D ．①【答案】B 【分析】设P （m ，1k m ），分别求出A ，B ，C ，D 的坐标，得到PD ，PC ，PB ，P A 的长，判断PD PB 和PC PA的关系，可判断①；利用三角形面积公式计算，可得△PDC 的面积，可判断③；再利用OCD OAPB OBD OCA DPC S S S S S =---△△△△计算△OCD 的面积，可判断②．【详解】解：∵PB ⊥y 轴，P A ⊥x 轴，点P 在1k y x =上，点C ，D 在2k y x =上，设P （m ，1km）， 则C （m ，2k m ），A （m ，0），B （0，1k m ），令12k km x =，则21k m x k =，即D （21k m k ，1k m），∴PC =12k k m m-=12k k m -，PD =21k m m k -=()121m k k k -，∵()121121m k k k k k PD PB m k --==，121211k k k k PC m k PA k m--==，即PD PCPB PA=，又∠DPC =∠BP A ，∴△PDC ∽△PBA ，∴∠PDC =∠PBC ，∴CD ∥AB ，故①正确； △PDC 的面积=12PD PC ⨯⨯=()1212112m k k k k k m --⨯⨯=()21212k k k-，故③正确；OCDOAPB OBD OCA DPC S S S S S =---△△△△=()112221222112k k k k k k ----=()2121122k k k k k ---=()()21121112222k k k k k k k ---=()22112211222k k k k k k ---=221212k k k -，故②错误；故选B ． 【点睛】此题主要考查了反比例函数的图象和性质，k 的几何意义，相似三角形的判定和性质，解题关键是表示出各点坐标，得到相应线段的长度．8．（2021·浙江宁波市）如图，正比例函数()1110y k x k =<的图象与反比例函数()2220k y k x=<的图象相交于A ，B 两点，点B 的横坐标为2，当12y y >时，x 的取值范围是（ ）A ．2x <-或2x >B ．20x -<<或2x >C ．2x <-或02x <<D ．20x -<<或02x << 【答案】C【分析】根据轴对称的性质得到点A 的横坐标为-2，利用函数图象即可确定答案． 【详解】解：∵正比例函数与反比例函数都关于原点对称，∴点A 与点B 关于原点对称， ∵点B 的横坐标为2，∴点A 的横坐标为-2，由图象可知，当2x <-或02x <<时，正比例函数()1110y k x k =<的图象在反比例函数()2220k y k x=<的图象的上方，∴当2x <-或02x <<时，12y y >，故选：C ．【点睛】此题考查正比例函数与反比例函数的性质及相交问题，函数值的大小比较，正确理解图象是解题的关键．9．（2021·浙江金华市）已知点()()1122,,,A x y B x y 在反比例函数12y x=-的图象上．若120x x <<，则（ ）A ．120y y <<B ．210y y <<C ．120y y <<D ．210y y <<【答案】B【分析】根据反比例函数的图象与性质解题． 【详解】解：反比例函数12y x=-图象分布在第二、四象限， 当0x <时，0y > 当0x >时，0y < 120x x <<120y y ∴>>故选：B ．【点睛】本题考查反比例函数的图象与性质，是重要考点，难度较易，掌握相关知识是解题关键． 10．（2021·江苏连云港市）关于某个函数表达式，甲、乙、丙三位同学都正确地说出了该函数的一个特征．甲：函数图像经过点(1,1)-；乙：函数图像经过第四象限；丙：当0x >时，y 随x 的增大而增大．则这个函数表达式可能是（ ） A ．y x =- B ．1y x=C ．2yx D ．1y x=-【答案】D【分析】根据所给函数的性质逐一判断即可．【详解】解：A .对于y x =-，当x =-1时，y =1，故函数图像经过点(1,1)-；函数图象经过二、四象限；当0x >时，y 随x 的增大而减小．故选项A 不符合题意； B .对于1y x=，当x =-1时，y =-1，故函数图像不经过点(1,1)-；函数图象分布在一、三象限；当0x >时，y 随x 的增大而减小．故选项B 不符合题意； C .对于2yx ，当x =-1时，y =1，故函数图像经过点(1,1)-；函数图象分布在一、二象限；当0x >时，y随x 的增大而增大．故选项C 不符合题意； D .对于1y x=-，当x =-1时，y =1，故函数图像经过点(1,1)-；函数图象经过二、四象限；当0x >时，y 随x 的增大而增大．故选项D 符合题意；故选：D【点睛】本题考查的是一次函数、二次函数以及反比例函数性质，熟知相关函数的性质是解答此题的关键．11．（2021·浙江温州市）如图，点A ，B 在反比例函数ky x=（0k >，0x >）的图象上，AC x ⊥轴于点C ，BD x ⊥轴于点D ，BE y ⊥轴于点E ，连结AE ．若1OE =，23OC OD =，AC AE =，则k 的值为（ ）A ．2BC ．94D ．【答案】B【分析】设OD =m ，则OC =23m ，设AC =n ，根据213m n m =⨯求得32n =，在Rt △AEF 中，运用勾股定理可求出m ，故可得到结论． 【详解】解：如图，设OD =m ，∵23OC OD =∴OC =23m∵BD x ⊥轴于点D ，BE y ⊥轴于点E ，∴四边形BEOD 是矩形∴BD =OE =1∴B (m ，1)设反比例函数解析式为ky x=，∴k =m ×1=m 设AC =n ∵AC x ⊥轴∴A （23m ，n ）∴23m n k m ==，解得，n =32，即AC =32∵AC =AE ∴AE =32在Rt △AEF 中，23EF OC m ==，31122AF AC FC =-=-=由勾股定理得，222321()()()232m =+ 解得，2m =（负值舍去）∴2k =故选：B 【点睛】此题考查了反比例函数的性质、待定系数法求函数的解析式．此题难度较大，注意掌握数形结合思想与方程思想的应用．12．（2021·浙江嘉兴市）已知三个点()11,x y ，()22,x y ，()33,x y 在反比例函数2y x=的图象上，其中1230x x x <<<，下列结论中正确的是（ ）A ．2130y y y <<< B ．1230y y y <<< C ．3210y y y <<<D ．3120y y y <<<【答案】A【分析】根据反比例函数图像的增减性分析解答． 【详解】解：反比例函数2y x=经过第一，三象限，在每一象限内，y 随x 的增大而减小， ∴当1230x x x <<<时，2130y y y <<<故选：A ．【点睛】本题考查反比例函数的图像性质，掌握反比例函数的图像性质，利用数形结合思想解题是关键． 13．（2021·重庆）如图，在平面直角坐标系中，矩形ABCD 的顶点A ，B 在x 轴的正半轴上，反比例函数(0,0)ky k x x =>>的图象经过顶点D ，分别与对角线AC ，边BC 交于点E ，F ，连接EF ，AF ．若点E 为AC的中点，AEF 的面积为1，则k 的值为（ ）A ．125B ．32C ．2D ．3【答案】D【分析】设D 点坐标为()k a a，，表示出E 、F 、B 点坐标，求出ABF 的面积，列方程即可求解．【详解】解：设D 点坐标为()ka a ，，∵四边形ABCD 是矩形，则A 点坐标为(0)a ，，C 点纵坐标为k a， ∵点E 为AC 的中点，则E 点纵坐标为022kk a a +=，∵点E 在反比例函数图象上，代入解析式得2k ka x=，解得，2x a =， ∴E 点坐标为(2)2k a a ，，同理可得C 点坐标为(3)ka a，，∵点F 在反比例函数图象上，同理可得F 点坐标为(3)3ka a，，∵点E 为AC 的中点，AEF 的面积为1， ∴2ACFS=，即122CF AB ⋅=，可得，1()(3)223k ka a a a--=，解得3k =，故选：D ．【点睛】本题考查了反比例函数的性质和矩形的性质，解题关键是设出点的坐标，依据面积列出方程． 14．（2021·四川自贡市）已知蓄电池的电压为定值，使用蓄电池时，电流O （单位：A ）与电阻R （单位：Ω）是反比例函数关系，它的图象如图所示．下列说法正确的是（ ）A ．函数解析式为13I R= B ．蓄电池的电压是18V C ．当10A I ≤时， 3.6R ≥Ω D ．当6R =Ω时，4A I = 【答案】C【分析】将将()4,9代入UI R=求出U 的值，即可判断A ，B ，D ，利用反比例函数的增减性可判断C ． 【详解】解：设U I R=，将()4,9代入可得36I R =，故A 错误；∴蓄电池的电压是36V ，故B 错误；当10A I ≤时， 3.6R ≥Ω，该项正确； 当当6R =Ω时，6A I =，故D 错误，故选：C ．【点睛】本题考查反比例函数的实际应用，掌握反比例函数的图象与性质是解题的关键．15．（2021·浙江丽水市）一杠杆装置如图，杆的一端吊起一桶水，水桶对杆的拉力的作用点到支点的杆长固定不变．甲、乙、丙、丁四位同学分别在杆的另一端竖直向下施加压力 F F F F 丁乙甲丙、、、，将相同重量的水桶吊起同样的高度，若 F F F F <<<甲丁丙乙，则这四位同学对杆的压力的作用点到支点的距离最远的是（ ）A ．甲同学B ．乙同学C ．丙同学D ．丁同学【答案】B【分析】根据物理知识中的杠杆原理：动力×动力臂=阻力×阻力臂，力臂越大，用力越小，即可求解． 【详解】解：由物理知识得，力臂越大，用力越小，根据题意，∵ F F F F <<<甲丁丙乙，且将相同重量的水桶吊起同样的高度， ∴乙同学对杆的压力的作用点到支点的距离最远，故选：B ．【点睛】本题考查反比例函数的应用，属于数学与物理学科的结合题型，立意新颖，掌握物理中的杠杆原理是解答的关键． 二、填空题1．（2021·浙江绍兴市）如图，在平面直角坐标系中，正方形ABCD 的顶点A 在x 轴正半轴上，顶点B ，C 在第一象限，顶点D 的坐标5(,2)2． 反比例函数k y x=（常数0k >，0x >）的图象恰好经过正方形ABCD 的两个顶点，则k 的值是_______．【答案】5或22.5【分析】先设一个未知数用来表示出B 、C 两点的坐标，再利用反比例函数图像恰好经过B 、C 、D 的其中两个点进行分类讨论，建立方程求出未知数的值，符合题意时进一步求出k 的值即可．【详解】解：如图所示，分别过B 、D 两点向x 轴作垂线，垂足分别为F 、E 点，并过C 点向BF 作垂线，垂足为点G ；∵正方形ABCD ，∴∠DAB =90°，AB =BC =CD =DA ，∴∠DAE +∠BAF =90°， 又∵∠DAE +∠ADE =90°，∠BAF +∠ABF =90°，∴∠DAE =∠ABF ，∠ADE =∠BAF ，∴ADE ≌BAF ，同理可证△ADE ≌△BAF ≌△CBG ；∴DE =AF =BG ，AE =BF =CG ；设AE =m ，∵点D 的坐标 (52,2) ，∴OE=52，DE =AF =BG =2，∴B （92m +，m ），C （92，2m +）, ∵5252⨯=，当()9252m +=时，809m =-<，不符题意，舍去；当952m m ⎛⎫+=⎪⎝⎭时，由0m ≥解得m =,符合题意；故该情况成立，此时 5k =； 当()99222m m m ⎛⎫+=+⎪⎝⎭时，由 0m ≥解得3m =,符合题意，故该情况成立，此时()93222.52k =⨯+=;故答案为：5或22.5．【点睛】本题综合考查了全等三角形的判定与性质、正方形的性质、反比例函数的图像与性质、解一元二次方程等内容，解题的关键是牢记相关概念与性质，能根据题意建立相等关系列出方程等，本题涉及到了分类讨论和数形结合的思想方法等． 2．（2021·湖南）在反比例函数3m y x-=的图象的每一支曲线上，函数值y 随自变量x 的增大而增大，则m 的取值范围是________． 【答案】m ＜3【分析】根据反比例函数的增减性，列出关于m 的不等式，进而即可求解． 【详解】解：∵在反比例函数3m y x-=的图象的每一支曲线上，函数值y 随自变量x 的增大而增大， ∴m -3＜0，即：m ＜3．故答案是：m ＜3．【点睛】本题主要考查反比例函数的性质，掌握反比例函数ky x=，在反比例函数的图象的每一支曲线上，函数值y 随自变量x 的增大而增大，则k ＜0，是解题的关键．3．（2021·湖北武汉市）已知点()1,A a y ，()21,B a y +在反比例函数21m y x+=（m是常数）的图象上，且12y y <，则a 的取值范围是__________． 【答案】10a -<<【分析】根据反比例函数的增减性解答．【详解】解：∵210m +>，∴图象经过第一、三象限，在每个象限内，y 随着x 的增大而减小，∵点()1,A a y ，()21,B a y +在反比例函数21m y x+=（m是常数）的图象上，且12y y <，1a a <+ ，∴010a a <⎧⎨+>⎩，∴10a -<<，故答案为：10a -<<．【点睛】此题考查反比例函数的性质：当0k >时，在每个象限内y 随着x 的增大而增大；当0k <时，在每个象限内y 随x 的增大而减小．4．（2021·湖南株洲市）点()11,A x y 、()121,B x y +是反比例函数ky x=图像上的两点，满足：当1>0x 时，均有12y y <，则k 的取值范围是__________． 【答案】k <0【分析】先分析该两点所在的图像的象限和增减性，最后确定k 的取值范围即可． 【详解】解：因为当10x >时，110x +>，说明A 、B 两点同时位于第一或第四象限， ∵当10x >时，均有12y y <，∴在该图像上，y 随x 的增大而增大， ∴A 、B 两点同时位于第四象限，所以k <0，故答案为：k <0．【点睛】本题考查了反比例函数的图像和性质，解决本题的关键是理解并牢记反比例函数的图像和性质，能根据点的坐标情况分析其图像特点等，涉及了数形结合的思想方法． 5．（2021·陕西）若()11,A y ，()23,B y 是反比例函数2112m y m x -⎛⎫=< ⎪⎝⎭图象上的两点，则1y 、2y 的大小关系是1y ______2y （填“>”、“=”或“<”） 【答案】<【分析】先根据不等式的性质判断2-10m <，再根据反比例函数的增减性判断即可． 【详解】解：∵12m <∴1222m <⨯即2-10m < ∴反比例函数图像每一个象限内，y 随x 的增大而增大∵1<3∴1y <2y 故答案为：<．【点睛】本题考查反比例函数的增减性、不等式的性质、熟练掌握反比例函数的性质是关键． 6．（2021·浙江宁波市）在平面直角坐标系中，对于不在坐标轴上的任意一点(),A x y ，我们把点11,B x y ⎛⎫⎪⎝⎭称为点A 的“倒数点”．如图，矩形OCDE 的顶点C 为()3,0，顶点E 在y 轴上，函数()20=>y x x的图象与DE 交于点A ．若点B 是点A 的“倒数点”，且点B 在矩形OCDE 的一边上，则OBC 的面积为_________．【答案】14或32【分析】根据题意，点B 不可能在坐标轴上，可对点B 进行讨论分析：①当点B 在边DE 上时；②当点B 在边CD 上时；分别求出点B 的坐标，然后求出OBC 的面积即可． 【详解】解：根据题意，∵点11,B x y ⎛⎫⎪⎝⎭称为点(),A x y 的“倒数点”， ∴0x ≠，0y ≠，∴点B 不可能在坐标轴上； ∵点A 在函数()20=>y x x 的图像上，设点A 为2(,)x x ，则点B 为1(,)2xx ， ∵点C 为()3,0，∴3OC =，①当点B 在边DE 上时；点A 与点B 都在边DE 上，∴点A 与点B 的纵坐标相同，即22xx =，解得：2x =， 经检验，2x =是原分式方程的解；∴点B 为1(,1)2，∴OBC 的面积为：133122S =⨯⨯=；②当点B 在边CD 上时；点B 与点C 的横坐标相同，∴13x =，解得：13x =，经检验，13x =是原分式方程的解；∴点B 为1(3,)6，∴OBC 的面积为：1113264S =⨯⨯=；故答案为：14或32．【点睛】本题考查了反比例函数的图像和性质，矩形的性质，解分式方程，坐标与图形等知识，解题的关键是熟练掌握反比例函数的性质，运用分类讨论的思想进行分析．7．（2021·云南）若反比例函数的图象经过点()1,2-，则该反比例函数的解析式（解析式也称表达式）为_________． 【答案】2y x=-【分析】先设ky x=，再把已知点的坐标代入可求出k 值，即得到反比例函数的解析式． 【详解】解：设反比例函数的解析式为ky x=（k ≠0），∵函数经过点（1，-2），∴21k -=，得k =-2，∴反比例函数解析式为2y x =-，故答案为：2y x=-． 【点睛】此题比较简单，考查的是用待定系数法求反比例函数的解析式，是中学阶段的重点． 三、解答题1．（2021·湖北随州市）如图，一次函数1y kx b =+的图象与x 轴、y 轴分别交于点A ，B ，与反比例函数2my x=（0m >）的图象交于点()1,2C ，()2,D n ．（1）分别求出两个函数的解析式；（2）连接OD ，求BOD 的面积． 【答案】（1）22y x=，13y x =-+；（2）3 【分析】（1）将点C 、D 的横、纵坐标代入反比例函数的解析式，求得m 、n 的值，从而点D 纵坐标已知，将点C 、D 的横、纵坐标代入一次函数的解析式，求得k 、b 的值，从而两个函数解析式可求； （2）求出点B 的坐标，可知OB 的长，利用三角形的面积公式可求三角形BOD 的面积． 【详解】解：（1）∵双曲线2my x=（m >0）过点C （1，2）和D （2，n ）， ∴212mm n ⎧=⎪⎪⎨⎪=⎪⎩，解得，21m n =⎧⎨=⎩．∴反比例函数的解析式为22y x =． ∵直线1y kx b =+过点C （1，2）和D （2，1），∴221k b k b +=⎧⎨+=⎩，解得，13k b =-⎧⎨=⎩．∴一次函数的解析式为13y x =-+．（2）当x =0时，y 1=3，即B （0，3）．∴3OB =．如图所示，过点D 作DE ⊥y 轴于点E ．∵D （2，1），∴DE =2．∴1132322BOD S OB DE ==⨯⨯=△． 【点睛】本题考查了待定系数法求函数解析式、二元一次方程组、三角形的面积等知识点，熟知解析式、点坐标、线段长三者的相互转化是解题的关键．2．（2021·湖北恩施州）如图，在平面直角坐标系中，Rt ABC 的斜边BC 在x 轴上，坐标原点是BC 的中点，30ABC ∠=︒，4BC =，双曲线ky x=经过点A ．（1）求k ；（2）直线AC 与双曲线y =D ．求ABD △的面积．【答案】（1）k =（2）ABD △的面积【分析】（1）过点A 作AE ⊥x 轴于点E ，由题意易得2,60AC ACB =∠=︒，进而可得1,==CE AE然后可得点(A ，最后问题可求解；（2）由（1）可先求出直线AC 的解析式为y =+，然后联立直线AC 的解析式与反比例函数y =D 的坐标，最后利用割补法求解三角形的面积即可．【详解】解：（1）过点A 作AE ⊥x 轴于点E ，如图所示：∵30ABC ∠=︒，4BC =，90BAC ∠=︒， ∴122AC BC ==，60ACB ∠=︒，∴30EAC ∠=︒，∴112EC AC ==， ∴在Rt △AEC中，AE ==∵点O 是BC 的中点，∴OC =2，∴OE =1，∴(A，∴1k == （2）由（1）可得：(A ，()2,0C ，∴设直线AC 的解析式为y kx b =+，则把点A 、C代入得：20k b k b ⎧+=⎪⎨+=⎪⎩k b ⎧=⎪⎨=⎪⎩，∴直线AC的解析式为y =+联立y =+与反比例函数y =+， 解得：123,1x x ==-（不符合题意，舍去），∴点(3,D ，∴142ABDABCBCDSSS=+=⨯⨯=【点睛】本题主要考查反比例函数与几何的综合及含30°直角三角形的性质、勾股定理，熟练掌握反比例函数与几何的综合及含30°直角三角形的性质、勾股定理是解题的关键．3．（2021·四川广安市）如图，一次函数()1y kx b k 0=+≠的图象与反比例函数()2my m 0x=≠的图象交于()1,A n -，()3,2B -两点．（1）求一次函数和反比例函数的解析式；（2）点P 在x 轴上，且满足ABP △的面积等于4，请直接写出点P 的坐标．【答案】（1）124y x =-+，26y x=-；（2）（1，0）或（3，0） 【分析】（1）根据点B 坐标求出m ，得到反比例函数解析式，据此求出点A 坐标，再将A ，B 代入一次函数解析式；（2）设点P 的坐标为（a ，0），求出直线AB 与x 轴交点，再结合△ABP 的面积为4得到关于a 的方程，解之即可．【详解】解：（1）由题意可得：点B （3，-2）在反比例函数2my x=图像上， ∴23m-=，则m =-6，∴反比例函数的解析式为26y x=-， 将A （-1，n ）代入26y x=-，得：661n =-=-，即A （-1，6），将A ，B 代入一次函数解析式中，得236k b k b -=+⎧⎨=-+⎩，解得：24k b =-⎧⎨=⎩，∴一次函数解析式为124y x =-+；（2）∵点P 在x 轴上，设点P 的坐标为（a ，0），∵一次函数解析式为124y x =-+，令y =0，则x =2，∴直线AB 与x 轴交于点（2，0），由△ABP 的面积为4，可得：()1242A B y y a ⨯-⨯-=，即18242a ⨯⨯-=，解得：a =1或a =3，∴点P 的坐标为（1，0）或（3，0）．【点睛】本题考查一次函数和反比例函数相交的有关问题；通常先求得反比例函数解析式；较复杂三角形的面积可被x 轴或y 轴分割为2个三角形的面积和． 4．（2021·浙江杭州市）在直角坐标系中，设函数11k y x=（1k 是常数，10k >，0x >）与函数22y k x =（2k 是常数，20k ≠）的图象交于点A ，点A 关于y 轴的对称点为点B ．（1）若点B 的坐标为()1,2-，①求1k ，2k 的值．②当12y y <时，直接写出x 的取值范围． （2）若点B 在函数33k y x=（3k 是常数，30k ≠）的图象上，求13k k +的值． 【答案】（1）①12k =，22k =；②1x >；（2）0【分析】（1）①根据点A 关于y 轴的对称点为点B ，可求得点A 的坐标是()1,2，再将点A 的坐标分别代入反比例函数、正比例函数的解析式中，即可求得12k =，22k =；②观察图象可解题； （2）将点B 代入33k y x=，解得3k 的值即可解题． 【详解】解（1）①由题意得，点A 的坐标是()1,2， 因为函数11k y x=的图象过点A ，所以12k =，同理22k =． ②由图象可知，当12y y <时，反比例函数的图象位于正比例函数图象的下方，即当12y y <时，1x >． （2）设点A 的坐标是()00,x y ，则点B 的坐标是()00,x y -，所以100k x y =，300k x y =-，所以310k k +=． 【点睛】本题考查关于y 轴对称的点的特征、待定系数法求反比例函数、正比例函数的解析式等知识，是重要考点，难度较易，掌握相关知识是解题关键．5．（2021·山东临沂市）已知函数()()()31 31131x x y x x x x⎧≤-⎪⎪=-⎨⎪⎪≥⎩＜＜（1）画出函数图象；列表：描点，连线得到函数图象：（2）该函数是否有最大或最小值？若有，求出其值，若没有，简述理由； （3）设1122(,),(,)x y x y 是函数图象上的点，若120x x +=，证明：120y y +=．【答案】（1）见解析；（2）有，当1x =时，最大值为3；当1x =-时，函数有最小值3-；（3）见解析 【分析】（1）选取特殊值，代入函数解析式，求出y 值，列表，在图像中描点，画出图像即可；（2）观察图像可得函数的最大值；（3）根据120x x +=，得到1x 和2x 互为相反数，再分111x -<<，11x ≤-，11x ≥，分别验证120y y +=．【详解】解：（1）列表如下：函数图像如图所示：（2）根据图像可知：当x =1时，函数有最大值3；当1x =-时，函数有最小值3-； （3）∵1122(,),(,)x y x y 是函数图象上的点，120x x +=，∴1x 和2x 互为相反数，当111x -<<时，211x -<<，∴113y x =，223y x =，∴()1212123330y y x x x x +=+=+=； 当11x ≤-时，21x ≥，则()121212123330x x y y x x x x ++=+==； 同理：当11x ≥时，21x ≤-，()121212123330x x y y x x x x ++=+==，综上：120y y +=．【点睛】本题主要考查正比例函数，反比例函数的图像和性质，描点法画函数图像，准确画出图像，理解120x x +=是解题的关键．6．（2021·安徽）已知正比例函数(0)y kx k =≠与反比例函数6y x=的图象都经过点A （m ，2）． （1）求k ，m 的值；（2）在图中画出正比例函数y kx =的图象，并根据图象，写出正比例函数值大于反比例函数值时x 的取值范围．【答案】（1）,k m 的值分别是23和3；（2）30x -<<或3x > 【分析】（1）把点A （m ，2）代入6y x=求得m 的值，从而得点A 的坐标，再代入(0)y kx k =≠求得k 值即可；（2）在坐标系中画出y kx =的图象，根据正比例函数(0)y kx k =≠的图象与反比例函数6y x=图象的两个交点坐标关于原点对称，求得另一个交点的坐标，观察图象即可解答．【详解】（1）将(,2)A m 代入6y x=得62m =， 3m ∴=， (3,2)A ∴，将(3,2)A 代入y kx =得23k =， 23k ∴=， ,k m ∴的值分别是23和3．（2）正比例函数23y x =的图象如图所示，∵正比例函数(0)y kx k =≠与反比例函数6y x =的图象都经过点A （3，2）， ∴正比例函数(0)y kx k =≠与反比例函数6y x=的图象的另一个交点坐标为（-3，-2），由图可知：正比例函数值大于反比例函数值时x 的取值范围为30x -<<或3x >． 【点睛】本题是正比例函数与反比例函数的综合题，利用数形结合思想是解决问题的关键． 7．（2021·浙江）已知在平面直角坐标系xOy 中，点A 是反比例函数1(0)y x x=>图象上的一个动点，连结,AO AO 的延长线交反比例函数(0,0)ky k x x=><的图象于点B ，过点A 作AE y ⊥轴于点E ．（1）如图1，过点B 作BF x ⊥轴于点F ，连结EF ．①若1k =，求证：四边形AEFO 是平行四边形； ②连结BE ，若4k =，求BOE △的面积．（2）如图2，过点E 作//EP AB ，交反比例函数(0,0)ky k x x=><的图象于点P ，连结OP ．试探究：对于确定的实数k ，动点A 在运动过程中，POE △的面积是否会发生变化？请说明理由．【答案】（1）①证明见解析，②1；（2）不改变，见解析【分析】（1）①计算得出AE OF a ==，利用平行四边形的判定方法即可证明结论；②证明AEO BDO ∽，利用反比例函数k 的几何意义求得212()2AO BO=，即可求解； （2）点A 的坐标为1()a a ，，点P 的坐标为()k b b，，可知四边形AEGO 是平行四边形，由AEO GHP ∽，利用相似三角形的性质得到关于ba的一元二次方程，利用三角形的面积公式即可求解．【详解】（1）①证明：设点A 的坐标为1()a a ，，则当1k =时，点B 的坐标为1()a a--，，AE OF a ∴==， AE y ⊥轴，//AE OF ∴，∴四边形AEFO 是平行四边形；②解：过点B 作BD y ⊥轴于点D ，AE y ⊥轴，//AE BD ∴，AEO BDO ∴∽， 2()AEO BDOS AO SBO ∴=， ∴当4k =时，则212()2AO BO=，即12AO BO =．21BOEAOES S∴==；（2）解 不改变． 理由如下：过点P 作PH x ⊥轴于点H PE ，与x 轴交于点G ，设点A 的坐标为1()a a ，，点P 的坐标为()k b b，， 则1kAE a OE PH a b===-，，，OH =b ，由题意，可知四边形AEGO 是平行四边形， ∴OG =AE =a ，∠HPG =∠OEG =∠EOA ，且∠PHG =∠OEA =90°，。
2021年九年级中考数学第三轮压轴题：反比例函数的综合 专题复习(含答案)
2021年中考数学第三轮压轴题：反比例函数的综合专题复习1、如图，在平面直角坐标系中，直线y=﹣x与反比例函数y=（k≠0）在第二象限内的图象相交于点A（m，1）．（1）求反比例函数的解析式；（2）将直线y=﹣x向上平移后与反比例函数图象在第二象限内交于点B，与y 轴交于点C，且△ABO的面积为，求直线BC的解析式．2、如图，已知反比例函数y=（x＞0）的图象与一次函数y=﹣x+4的图象交于A和B（6，n）两点．（1）求k和n的值；（2）若点C（x，y）也在反比例函数y=（x＞0）的图象上，求当2≤x≤6时，函数值y的取值范围．3、如图，一次函数y=x+4的图象与反比例函数y=（k为常数且k≠0）的图象交于A（﹣1，a），B两点，与x轴交于点C．（1）求此反比例函数的表达式；（2）若点P在x轴上，且S△ACP =S△BOC，求点P的坐标．4、如图所示，在平面直角坐标系中，一次函数y=kx+b（k≠0）与反比例函数y=（m≠0）的图象交于第二、四象限A、B两点，过点A作AD⊥x轴于D，AD=4，sin∠AOD=，且点B的坐标为（n，﹣2）．（1）求一次函数与反比例函效的解析式；（2）E是y轴上一点，且△AOE是等腰三角形，请直接写出所有符合条件的E 点坐标．5、如图，已知点A在反比例函数y=（x＞0）的图象上，过点A作AC⊥x轴，垂足是C，AC=OC．一次函数y=kx+b的图象经过点A，与y轴的正半轴交于点B．（1）求点A的坐标；（2）若四边形ABOC的面积是3，求一次函数y=kx+b的表达式．6、如图，一次函数y=kx+b（k≠0）的图象与反比例函数y=（a≠0）的图象在第二象限交于点A（m，2）．与x轴交于点C（﹣1，0）．过点A作AB⊥x轴于点B，△ABC的面积是3．（1）求一次函数和反比例函数的解析式；（2）若直线AC与y轴交于点D，求△BCD的面积．7、如图，直线y=kx+b（k≠0）与双曲线y=（m≠0）交于点A（﹣，2），B （n，﹣1）．（1）求直线与双曲线的解析式．（2）点P在x轴上，如果S=3，求点P的坐标．△ABP8、如图所示，四边形ABCD是菱形，边BC在x轴上，点A（0，4），点B（3，0），双曲线y=与直线BD交于点D、点E．（1）求k的值；（2）求直线BD的解析式；（3）求△CDE的面积．9、如图已知函数y=kx(k>0,x>0)的图象与一次函数y=mx+5(m<0)的图象相交不同的点A、B，过点A作AD⊥x轴于点D，连接AO，其中点A的横坐标为x0，△AOD的面积为2．(1)求k的值及x0=4时m的值；(2)记[x]表示为不超过x的最大整数，例如：[1,4]=1，[2]=2，设t=OD⋅DC，若−32<m<−54，求[m2⋅t]值．10、如图，直线y1=﹣x+4，y2=x+b都与双曲线y=交于点A（1，m），这两条直线分别与x轴交于B，C两点．（1）求y与x之间的函数关系式；（2）直接写出当x＞0时，不等式x+b＞的解集；（3）若点P在x轴上，连接AP把△ABC的面积分成1：3两部分，求此时点P 的坐标．11、如图，一次函数y=kx+b（k、b为常数，k≠0）的图象与x轴、y轴分别交于A、B两点，且与反比例函数y=（n为常数，且n≠0）的图象在第二象限交于点C．CD⊥x轴，垂足为D，若OB=2OA=3OD=12．（1）求一次函数与反比例函数的解析式；（2）记两函数图象的另一个交点为E，求△CDE的面积；（3）直接写出不等式kx+b≤的解集．12、如图，A（4，3）是反比例函数y=在第一象限图象上一点，连接OA，过A 作AB∥x轴，截取AB=OA（B在A右侧），连接OB，交反比例函数y=的图象于点P．（1）求反比例函数y=的表达式；（2）求点B的坐标；（3）求△OAP的面积．13、矩形AOBC 中，OB=4，OA=3．分别以OB ，OA 所在直线为x 轴，y 轴，建立如图1所示的平面直角坐标系．F 是BC 边上一个动点（不与B ，C 重合），过点F 的反比例函数y=（k ＞0）的图象与边AC 交于点E ．（1）当点F 运动到边BC 的中点时，求点E 的坐标；（2）连接EF ，求∠EFC 的正切值；（3）如图2，将△CEF 沿EF 折叠，点C 恰好落在边OB 上的点G 处，求此时反比例函数的解析式．14、如图，在平面直角坐标系中，矩形OAOB 的顶点,A B 的坐标分别为(6,0)A -,(0,4)B .过点(6,1)C -的双曲线(0)k y k x=≠与矩形OAOB 的边BD 交于点E . (1)填空：OA =_____,k =_____,点E 的坐标为__________；(2)当16t ≤≤时，经过点213(1,5)22M t t t --+-与点217(3,3)22N t t t ---+-的直线交y 轴于点F ，点P 是过,M N 两点的抛物线212y x bx c =-++的顶点. ①当点P 在双曲线k y x =上时，求证：直线MN 与双曲线k y x=没有公共点；②当抛物线212y x bx c =-++与矩形OAOB 有且只有三个公共点，求t 的值； ③当点F 和点P 随着t 的变化同时向上运动时，求t 的取值范围，并求在运动过程中直线MN 在四边形．．．OAEB 中扫过的面积.15、平面直角坐标系xOy 中，横坐标为a 的点A 在反比例函数y 1═（x ＞0）的图象上，点A ′与点A 关于点O 对称，一次函数y 2=mx+n 的图象经过点A ′．（1）设a=2，点B （4，2）在函数y 1、y 2的图象上．①分别求函数y 1、y 2的表达式；②直接写出使y 1＞y 2＞0成立的x 的范围；（2）如图①，设函数y 1、y 2的图象相交于点B ，点B 的横坐标为3a ，△AA'B 的面积为16，求k 的值；（3）设m=，如图②，过点A 作AD ⊥x 轴，与函数y 2的图象相交于点D ，以AD为一边向右侧作正方形ADEF ，试说明函数y 2的图象与线段EF 的交点P 一定在函数y 1的图象上．参考答案2021年中考数学第三轮压轴题：反比例函数的综合专题复习二象限内的图象相交于点A（m，1）．（1）求反比例函数的解析式；（2）将直线y=﹣x向上平移后与反比例函数图象在第二象限内交于点B，与y 轴交于点C，且△ABO的面积为，求直线BC的解析式．【解答】解：（1）∵直线y=﹣x过点A（m，1），∴﹣m=1，解得m=﹣2，∴A（﹣2，1）．∵反比例函数y=（k≠0）的图象过点A（﹣2，1），∴k=﹣2×1=﹣2，∴反比例函数的解析式为y=﹣；（2）设直线BC的解析式为y=﹣x+b，∵三角形ACO与三角形ABO面积相等，且△ABO的面积为，∴△ACO的面积=OC•2=，∴OC=，∴b=，∴直线BC的解析式为y=﹣x+．2、如图，已知反比例函数y=（x＞0）的图象与一次函数y=﹣x+4的图象交于A和B（6，n）两点．（1）求k和n的值；（2）若点C（x，y）也在反比例函数y=（x＞0）的图象上，求当2≤x≤6时，函数值y的取值范围．【解答】解：（1）当x=6时，n=﹣×6+4=1，∴点B的坐标为（6，1）．∵反比例函数y=过点B（6，1），∴k=6×1=6．（2）∵k=6＞0，∴当x＞0时，y随x值增大而减小，∴当2≤x≤6时，1≤y≤3．3、如图，一次函数y=x+4的图象与反比例函数y=（k为常数且k≠0）的图象交于A（﹣1，a），B两点，与x轴交于点C．（1）求此反比例函数的表达式；（2）若点P在x轴上，且S△ACP =S△BOC，求点P的坐标．【解答】解：（1）把点A（﹣1，a）代入y=x+4，得a=3，∴A（﹣1，3）把A（﹣1，3）代入反比例函数y=∴k=﹣3，∴反比例函数的表达式为y=﹣（2）联立两个函数的表达式得解得或∴点B的坐标为B（﹣3，1）当y=x+4=0时，得x=﹣4∴点C（﹣4，0）设点P的坐标为（x，0）∵S△ACP =S△BOC∴解得x1=﹣6，x2=﹣2∴点P（﹣6，0）或（﹣2，0）4、如图所示，在平面直角坐标系中，一次函数y=kx+b（k≠0）与反比例函数y=（m≠0）的图象交于第二、四象限A、B两点，过点A作AD⊥x轴于D，AD=4，sin∠AOD=，且点B的坐标为（n，﹣2）．（1）求一次函数与反比例函效的解析式；（2）E是y轴上一点，且△AOE是等腰三角形，请直接写出所有符合条件的E 点坐标．【解答】解：（1）∵一次函数y=kx+b与反比例函数y=图象交于A与B，且AD ⊥x轴，∴∠ADO=90°，在Rt△ADO中，AD=4，sin∠AOD=，∴=，即AO=5，根据勾股定理得：DO==3，∴A（﹣3，4），代入反比例解析式得：m=﹣12，即y=﹣，把B坐标代入得：n=6，即B（6，﹣2），代入一次函数解析式得：，解得：，即y=﹣x+2；（2）当OE3=OE2=AO=5，即E2（0，﹣5），E3（0，5）；当OA=AE1=5时，得到OE1=2AD=8，即E1（0，8）；当AE4=OE4时，由A（﹣3，4），O（0，0），得到直线AO解析式为y=﹣x，中点坐标为（﹣1.5，2），∴AO垂直平分线方程为y﹣2=（x+），令x=0，得到y=，即E4（0，），综上，当点E（0，8）或（0，5）或（0，﹣5）或（0，）时，△AOE是等腰三角形．5、如图，已知点A在反比例函数y=（x＞0）的图象上，过点A作AC⊥x轴，垂足是C，AC=OC．一次函数y=kx+b的图象经过点A，与y轴的正半轴交于点B．（1）求点A的坐标；（2）若四边形ABOC的面积是3，求一次函数y=kx+b的表达式．【解答】解：（1）∵点A在反比例函数y=（x＞0）的图象上，AC⊥x轴，AC=OC，∴AC•OC=4，∴AC=OC=2，∴点A的坐标为（2，2）；（2）∵四边形ABOC的面积是3，∴（OB+2）×2÷2=3，解得OB=1，∴点B的坐标为（0，1），依题意有，解得．故一次函数y=kx+b的表达式为y=x+1．6、如图，一次函数y=kx+b（k≠0）的图象与反比例函数y=（a≠0）的图象在第二象限交于点A（m，2）．与x轴交于点C（﹣1，0）．过点A作AB⊥x轴于点B，△ABC的面积是3．（1）求一次函数和反比例函数的解析式；（2）若直线AC与y轴交于点D，求△BCD的面积．【解答】解：（1）∵AB⊥x轴于点B，点A（m，2），∴点B（m，0），AB=2．=AB•BC=﹣1﹣m=3，∴m=﹣4，∴点A ∵点C（﹣1，0），∴BC=﹣1﹣m，∴S△ABC（﹣4，2）．∵点A在反比例函数y=（a≠0）的图象上，∴a=﹣4×2=﹣8，∴反比例函数的解析式为y=﹣．将A（﹣4，2）、C（﹣1，0）代入y=kx+b，得：，解得：，∴一次函数的解析式为y=﹣x﹣．=BC•（2）当x=0时，y=﹣x﹣=﹣，∴点D（0，﹣），∴OD=，∴S△BCDOD=×3×=1．7、如图，直线y=kx+b（k≠0）与双曲线y=（m≠0）交于点A（﹣，2），B （n，﹣1）．（1）求直线与双曲线的解析式．=3，求点P的坐标．（2）点P在x轴上，如果S△ABP【解答】解：（1）∵双曲线y=（m≠0）经过点A（﹣，2），∴m=﹣1．∴双曲线的表达式为y=﹣．∵点B（n，﹣1）在双曲线y=﹣上，∴点B的坐标为（1，﹣1）．∵直线y=kx+b经过点A（﹣，2），B（1，﹣1），∴，解得，∴直线的表达式为y=﹣2x+1；（2）当y=﹣2x+1=0时，x=，∴点C（，0）．设点P的坐标为（x，0），∵S△ABP=3，A（﹣，2），B（1，﹣1），∴×3|x﹣|=3，即|x﹣|=2，解得：x1=﹣，x2=．∴点P的坐标为（﹣，0）或（，0）．8、如图所示，四边形ABCD是菱形，边BC在x轴上，点A（0，4），点B（3，0），双曲线y=与直线BD交于点D、点E．（1）求k的值；（2）求直线BD的解析式；（3）求△CDE的面积．【解答】解：（1）∵点A（0，4），点B（3，0），∴OA=4，OB=3，由勾股定理得：AB=5，过D作DF⊥x轴于F，则∠AOB=∠DFC=90°，∵四边形ABCD是菱形，∴AB=DC=CD=AD=5，AD∥BC，∴AO=DF=4，∵AD∥BC，AO⊥OB，DF⊥x轴，∴∠DAO=∠AOF=∠DFO=90°，∴四边形AOFD是矩形，∴AD=OF=5，∴D点的坐标为（5，4），代入y=得：k=5×4=20；（2）设直线BD的解析式为y=ax+b，把B（3，0），D（5，4）代入得：，解得：a=2，b=﹣6，所以直线BD的解析式是y=2x﹣6；（3）由（1）知：k=20，所以y=，解方程组得：，，∵D点的坐标为（5，4），∴E点的坐标为（2，10），∵BC=5，∴△CDE的面积S=S△CDB +S△CBE=+=35．9、如图已知函数y=kx(k>0,x>0)的图象与一次函数y=mx+5(m<0)的图象相交不同的点A、B，过点A作AD⊥x轴于点D，连接AO，其中点A的横坐标为x0，△AOD的面积为2．(1)求k的值及x0=4时m的值；(2)记[x]表示为不超过x的最大整数，例如：[1,4]=1，[2]=2，设t=OD⋅DC，若−32<m<−54，求[m2⋅t]值．【答案】解：(1)设A(x0,y0)，则OD=x0，AD=y0，∴S△AOD=12OD⋅AD=12x0y0=2，∴k=x0y0=4；当x0=4时，y0=1，∴A(4,1)，代入y=mx+5中得4m+5=1，m=−1；(2)∵{y=4xy=mx+5，4x=mx+5，mx2+5x−4=0，∵A的横坐标为x0，∴mx02+5x0=4，当y=0时，mx+5=0，x=−5m，∵OC=−5m，OD=x0，∴m2⋅t=m2⋅(OD⋅DC)，=m2⋅x0(−5m−x0)，=m(−5x0−mx02)，=−4m，∵−32<m<−54，∴5<−4m<6，∴[m2⋅t]=5．10、如图，直线y1=﹣x+4，y2=x+b都与双曲线y=交于点A（1，m），这两条直线分别与x轴交于B，C两点．（1）求y与x之间的函数关系式；（2）直接写出当x＞0时，不等式x+b＞的解集；（3）若点P在x轴上，连接AP把△ABC的面积分成1：3两部分，求此时点P 的坐标．=﹣x+4，可得m=﹣1+4=3，【解答】解：（1）把A（1，m）代入y1∴A（1，3），把A（1，3）代入双曲线y=，可得m=1×3=3，∴y与x之间的函数关系式为：y=；（2）∵A（1，3），∴当x＞0时，不等式x+b＞的解集为：x＞1；=﹣x+4，令y=0，则x=4，（3）y1∴点B的坐标为（4，0），=x+b，可得3=+b，把A（1，3）代入y2∴b=，=x+，∴y2令y=0，则x=﹣3，即C（﹣3，0），∴BC=7，∵AP把△ABC的面积分成1：3两部分，∴CP=BC=，或BP=BC=，∴OP=3﹣=，或OP=4﹣=，∴P（﹣，0）或（，0）．11、如图，一次函数y=kx+b（k、b为常数，k≠0）的图象与x轴、y轴分别交于A、B两点，且与反比例函数y=（n为常数，且n≠0）的图象在第二象限交于点C．CD⊥x轴，垂足为D，若OB=2OA=3OD=12．（1）求一次函数与反比例函数的解析式；（2）记两函数图象的另一个交点为E，求△CDE的面积；（3）直接写出不等式kx+b≤的解集．【解答】解：（1）由已知，OA=6，OB=12，OD=4∵CD⊥x轴∴OB∥CD∴△ABO∽△ACD∴∴∴CD=20∴点C坐标为（﹣4，20）∴n=xy=﹣80∴反比例函数解析式为：y=﹣把点A（6，0），B（0，12）代入y=kx+b得：解得：∴一次函数解析式为：y=﹣2x+12 （2）当﹣=﹣2x+12时，解得x 1=10，x2=﹣4当x=10时，y=﹣8∴点E坐标为（10，﹣8）∴S△CDE =S△CDA+S△EDA=（3）不等式kx+b≤，从函数图象上看，表示一次函数图象不低于反比例函数图象∴由图象得，x≥10，或﹣4≤x＜012、如图，A（4，3）是反比例函数y=在第一象限图象上一点，连接OA，过A 作AB∥x轴，截取AB=OA（B在A右侧），连接OB，交反比例函数y=的图象于点P．（1）求反比例函数y=的表达式；（2）求点B的坐标；（3）求△OAP的面积．【解答】解：（1）将点A（4，3）代入y=，得：k=12，则反比例函数解析式为y=；（2）如图，过点A作AC⊥x轴于点C，则OC=4、AC=3，∴OA==5，∵AB∥x轴，且AB=OA=5，∴点B的坐标为（9，3）；（3）∵点B坐标为（9，3），∴OB所在直线解析式为y=x，由可得点P坐标为（6，2），过点P作PD⊥x轴，延长DP交AB于点E，则点E坐标为（6，3），∴AE=2、PE=1、PD=2，则△OAP的面积=×（2+6）×3﹣×6×2﹣×2×1=5．13、矩形AOBC中，OB=4，OA=3．分别以OB，OA所在直线为x轴，y轴，建立如图1所示的平面直角坐标系．F是BC边上一个动点（不与B，C重合），过点F 的反比例函数y=（k＞0）的图象与边AC交于点E．（1）当点F运动到边BC的中点时，求点E的坐标；（2）连接EF，求∠EFC的正切值；（3）如图2，将△CEF沿EF折叠，点C恰好落在边OB上的点G处，求此时反比例函数的解析式．【解答】解：（1）∵OA=3，OB=4，∴B（4，0），C（4，3），∵F是BC的中点，∴F（4，），∵F在反比例y=函数图象上，∴k=4×=6，∴反比例函数的解析式为y=，∵E点的坐标为3，∴E（2，3）；（2）∵F点的横坐标为4，∴F（4，），∴CF=BC﹣BF=3﹣=∵E的纵坐标为3，∴E（，3），∴CE=AC﹣AE=4﹣=，在Rt△CEF中，tan∠EFC==，（3）如图，由（2）知，CF=，CE=，，过点E作EH⊥OB于H，∴EH=OA=3，∠EHG=∠GBF=90°，∴∠EGH+∠HEG=90°，由折叠知，EG=CE ，FG=CF ，∠EGF=∠C=90°，∴∠EGH+∠BGF=90°，∴∠HEG=∠BGF ，∵∠EHG=∠GBF=90°，∴△EHG ∽△GBF ，∴=，∴， ∴BG=，在Rt △FBG 中，FG 2﹣BF 2=BG 2，∴（）2﹣（）2=， ∴k=，∴反比例函数解析式为y=．14、如图，在平面直角坐标系中，矩形OAOB 的顶点,A B 的坐标分别为(6,0)A -,(0,4)B .过点(6,1)C -的双曲线(0)k y k x=≠与矩形OAOB 的边BD 交于点E . (1)填空：OA =_____,k =_____,点E 的坐标为__________；(2)当16t ≤≤时，经过点213(1,5)22M t t t --+-与点217(3,3)22N t t t ---+-的直线交y 轴于点F ，点P 是过,M N 两点的抛物线212y x bx c =-++的顶点. ①当点P 在双曲线k y x =上时，求证：直线MN 与双曲线k y x=没有公共点；②当抛物线212y x bx c =-++与矩形OAOB 有且只有三个公共点，求t 的值； ③当点F 和点P 随着t 的变化同时向上运动时，求t 的取值范围，并求在运动过程中直线MN 在四边形．．．OAEB 中扫过的面积.解：(1)天空：6,6OA k ==-，点E 的坐标为3,42⎛⎫- ⎪⎝⎭； (2)①设直线11,MN y k x b =+ 由题意得211211135(1)22173(3)22t t k t b t t k t b ⎧-+-=-+⎪⎪⎨⎪-+-=--+⎪⎩ 解得211111,422k b t t ==-+- ∴直线211:422MN y x t t =-+- ∵抛物线212y x bx c =-++过点,M N 22221315(1)(1)2221713(3)(3)222t t t b t c t t t b t c ⎧-+-=--+-+⎪⎪∴⎨⎪-+-=---+--+⎪⎩解得1,52b c t =-=- ∴抛物线21522y x x t =--+- ∴顶点3(1,5)2P t --∵顶点3(1,5)2P t --在双曲线6y x-=上 3(5)(1)62t ∴-⨯-=- 32t ∴= 此时直线35:8MN y x =+ 联立3586y x y x ⎧=+⎪⎪⎨⎪=-⎪⎩，得3568x x -+= 2835480x x ∴++=2354848122515360∴∆=-⨯⨯=-<∴直线MN 与双曲线6y x=-没有公共点 ②当抛物线过B 点，此时抛物线与矩形OADB 有且只有三个公共点， 则6452,5t t =-= 当顶点P 在线段DB 上，此时抛物线与矩形OADB 有且只有三个公共点， 则10342t -=，1110t = 65t ∴=或1110t = ③点P 的坐标为3(1,5)2t --， 352r y t ∴=- 当16t ≤≤时，p y 随着t 的增大而增大，此时，当16t ≤≤时，随着t 的增大，点P 在直线1x =-上向上运动. 又点F 的坐标为211(0,4)22t t -+- 2115(4)22F y t ∴=--+ ∴当14t ≤≤时，F y 随着t 的增大而增大，此时当14t ≤≤时，随着t 的增大而增大，点F 在y 轴上向上运动. 14t ∴≤≤当1t =时，直线:3MN y x =+与x 轴交于(3,0)G -，与y 轴交于()0,3H当4t =MN 过点A ，当14t ≤≤时，直线MN 在四边形AEBO 中扫过的面积为1312164332222GHO AEBO S S S ∆⎛⎫=-=⨯+⨯-⨯⨯= ⎪⎝⎭四边形15、平面直角坐标系xOy 中，横坐标为a 的点A 在反比例函数y 1═（x ＞0）的图象上，点A ′与点A 关于点O 对称，一次函数y 2=mx+n 的图象经过点A ′．（1）设a=2，点B （4，2）在函数y 1、y 2的图象上．①分别求函数y 1、y 2的表达式；②直接写出使y 1＞y 2＞0成立的x 的范围；（2）如图①，设函数y 1、y 2的图象相交于点B ，点B 的横坐标为3a ，△AA'B 的面积为16，求k 的值；（3）设m=，如图②，过点A 作AD ⊥x 轴，与函数y 2的图象相交于点D ，以AD 为一边向右侧作正方形ADEF ，试说明函数y 2的图象与线段EF 的交点P 一定在函数y 1的图象上．【解答】解：（1）①由已知，点B （4，2）在y 1═（x ＞0）的图象上∴k=8∴y 1=∵a=2∴点A坐标为（2，4），A′坐标为（﹣2，﹣4）把B（4，2），A（﹣2，﹣4）代入y2=mx+n解得∴y2=x﹣2②当y1＞y2＞0时，y1=图象在y2=x﹣2图象上方，且两函数图象在x轴上方∴由图象得：2＜x＜4（2）分别过点A、B作AC⊥x轴于点C，BD⊥x轴于点D，连BO∵O为AA′中点S△AOB =S△AOA′=8∵点A、B在双曲线上∴S△AOC =S△BOD∴S△AOB =S四边形ACDB=8由已知点A、B坐标都表示为（a，）（3a，）∴解得k=6（3）由已知A（a，），则A′为（﹣a，﹣）把A′代入到y=﹣∴n=∴A′B解析式为y=﹣当x=a时，点D纵坐标为∴AD=∵AD=AF，∴点F和点P横坐标为∴点P纵坐标为═（x＞0）的图象上∴点P在y1。
2021年中考数学压轴题专项训练反比例函数含解析202102192297.doc
2021年中考数学压轴题专项训练《反比例函数》1．如图，反比例函数y1＝和一次函数y2＝mx+n相交于点A（1，3），B（﹣3，a），（1）求一次函数和反比例函数解析式；（2）连接OA，试问在x轴上是否存在点P，使得△OAP为以OA为腰的等腰三角形，若存在，直接写出满足题意的点P的坐标；若不存在，说明理由．解：（1）∵点A（1，3）在反比例函数y1＝的图象上，∴k＝1×3＝3，∴反比例函数的解析式为y1＝，∵点B（﹣3，a）在反比例函数y1＝的图象上，∴﹣3a＝3，∴a＝﹣1，∴B（﹣3，﹣1），∵点A（1，3），B（﹣3，﹣1）在一次函数y2＝mx+n的图象上，∴，∴，∴一次函数的解析式为y2＝x+2；（2）如图，∵△OAP为以OA为腰的等腰三角形，∴①当OA＝OP时，∵A（1，3），∴OA＝，∵OP＝，∵点P在x轴上，∴P（﹣，0）或（，0），②当OA＝AP时，则点A是线段OP的垂直平分线上，∵A（1，3），∴P（2，0），即：在x轴上存在点P，使得△OAP为以OA为腰的等腰三角形，此时，点P的坐标为（﹣，0）或（2，0）或（，0）．2．在平面直角坐标系xOy中，函数y＝（x＞0）的图象G经过点A（3，2），直线l：y＝kx﹣1（k≠0）与y轴交于点B，与图象G交于点C．（1）求m的值；（2）横、纵坐标都是整数的点叫做整点．记图象G在点A，C之间的部分与线段BA，BC 围成的区域（不含边界）为W．①当直线l过点（2，0）时，直接写出区域W内的整点个数；②若区域W内的整点不少于4个，结合函数图象，求k的取值范围．解：（1）把A（3，2）代入y＝得m＝3×2＝6，（2）①当直线l过点（2，0）时，直线解析式为y＝x﹣1，解方程＝x﹣1得x1＝1﹣（舍去），x2＝1+，则C（1+，），而B（0，﹣1），如图1所示，区域W内的整点有（3，1）一个；②如图2，直线l在AB的下方时，直线l：y＝kx﹣1过（6，1）时，1＝6k﹣1，解得k＝，当直线在OA的上方时，直线经过（1，4）时，4＝k﹣1，解得k＝5，观察图象可知：当k≤或k≥5时，区域W内的整点不少于4个．3．如图，在平面直角坐标系中，四边形OABC的顶点坐标分别为O（0，0），A（6，0），B（4，3），C（0，3）．动点P从点O出发，以每秒个单位长度的速度沿边OA向终点A运动；动点Q从点B同时出发，以每秒1个单位长度的速度沿边BC向终点C运动，设运动的时间为t秒，PQ2＝y．（1）直接写出y关于t的函数解析式及t的取值范围：；（2）当PQ＝时，求t的值；（3）连接OB交PQ于点D，若双曲线y＝经过点D，问k的值是否变化？若不变化，请求出k的值；若变化，请说明理由．解：（1）过点P作PE⊥BC于点E，如图1所示．当运动时间为t秒时（0≤t≤4）时，点P的坐标为（t，0），点Q的坐标为（4﹣t，3），∴PE＝3，EQ＝|4﹣t﹣t|＝|4﹣t|，∴PQ2＝PE2+EQ2＝32+|4﹣t|2＝t2﹣20t+25，∴y关于t的函数解析式及t的取值范围：；故答案为：．（2）当时，整理，得5t2﹣16t+12＝0，解得：t1＝2，．（3）经过点D的双曲线的k值不变．连接OB，交PQ于点D，过点D作DF⊥OA于点F，如图2所示．∵OC＝3，BC＝4，∴．∵BQ∥OP，∴△BDQ∽△ODP，∴，∴OD＝3．∵CB∥OA，∴∠DOF＝∠OBC．在Rt△OBC中，，，∴，，∴点D的坐标为，∴经过点D的双曲线的k值为．4．如图，一次函数y＝kx+b的图象与反比例函数y＝的图象交于点A（﹣3，m+8），B（n，﹣6）两点．（1）求一次函数与反比例函数的解析式；（2）求△AOB的面积；（3）若P（x1，y1），Q（x2，y2）是该反比例函数图象上的两点，且当x1＜x2时，y1＞y2，指出点P、Q各位于哪个象限？解：（1）将A（﹣3，m+8）代入反比例函数y＝得﹣3（m+8）＝m，解得m＝﹣6，∴点A的坐标为（﹣3，2），反比例函数解析式为y＝﹣，将点B（n，﹣6）代入y＝﹣得﹣6n＝﹣6，解得n＝1，∴点B的坐标为（1，﹣6），将点A（﹣3，2），B（1，﹣6）代入y＝kx+b得，解得，∴一次函数解析式为y＝﹣2x﹣4；（2）设AB与x轴相交于点C，如图，当﹣2x﹣4＝0，解得x＝﹣2，则点C的坐标为（﹣2，0），∴S△AOB＝S△AOC+S△BOC，＝×2×2+×2×6，＝2+6，＝8；（3）∵当x1＜x2时，y1＞y2，∴点P和点Q不在同一象限，∴P在第二象限，Q在第四象限．5．如图，平面直角坐标系中，一次函数y＝x﹣1的图象与x轴，y轴分别交于点A，B，与反比例函数y＝的图象交于点C，D，CE⊥x轴于点E，＝．（1）求反比例函数的表达式与点D的坐标；（2）以CE为边作▱ECMN，点M在一次函数y＝x﹣1的图象上，设点M的横坐标为a，当边MN与反比例函数y＝的图象有公共点时，求a的取值范围．解：（1）由题意A（1，0），B（0，﹣1），∴OA＝OB＝1，∴∠OAB＝∠CAE＝45°∵AE＝3OA，∴AE＝3，∵EC⊥x轴，∴∠AEC＝90°，∴∠EAC＝∠ACE＝45°，∴EC＝AE＝3，∴C（4，3），∵反比例函数y＝经过点C（4，3），∴k＝12，由，解得或，∴D（﹣3，﹣4）．（2）如图，设M（a，a﹣1）．当点N在反比例函数的图象上时，N（a，），∵四边形ECMN是平行四边形，∴MN＝EC＝3，∴|a﹣1﹣|＝3，解得a＝6或﹣2或﹣1±（舍弃），∴M（6，5）或（﹣2，﹣3），观察图象可知：当边MN与反比例函数y＝的图象有公共点时4＜a≤6或﹣3≤a≤﹣2．6．如图，一次函数y＝kx+2的图象与y轴交于点A，正方形ABCD的顶点B在x轴上，点D 在直线y＝kx+2上，且AO＝OB，反比例函数y＝（x＞0）经过点C．（1）求一次函数和反比例函数的解析式；（2）点P是x轴上一动点，当△PCD的周长最小时，求出P点的坐标；（3）在（2）的条件下，以点C、D、P为顶点作平行四边形，直接写出第四个顶点M的坐标．解：（1）设一次函数y＝kx+2的图象与x轴交于点E，连接BD，如图1所示．当x＝0时，y＝kx+2＝2，∴OA＝2．∵四边形ABCD为正方形，OA＝OB，∴∠BAE＝90°，∠OAB＝∠OBA＝45°，∴∠OAE＝∠OEA＝45°，∴OE＝2，点E的坐标为（﹣2，0）．将E（﹣2，0）代入y＝kx+2，得：﹣2k+2＝0，解得：k＝1，∴一次函数的解析式为y＝x+2．∵∠OBD＝∠ABD+∠OBA＝90°，∴BD∥OA．∵OE＝OB＝2，∴BD＝2OA＝4，∴点D的坐标为（2，4）．∵四边形ABCD为正方形，∴点C的坐标为（2+2﹣0，0+4﹣2），即（4，2）．∵反比例函数y＝（x＞0）经过点C，∴n＝4×2＝8，∴反比例函数解析式为y＝．（2）作点D关于x轴的对称点D′，连接CD′交x轴于点P，此时△PCD的周长取最小值，如图2所示．∵点D的坐标为（2，4），∴点D′的坐标为（2，﹣4）．设直线CD′的解析式为y＝ax+b（a≠0），将C（4，2），D′（2，﹣4）代入y＝ax+b，得：，解得：，∴直线CD′的解析式为y＝3x﹣10．当y＝0时，3x﹣10＝0，解得：x＝，∴当△PCD的周长最小时，P点的坐标为（，0）．（3）设点M的坐标为（x，y），分三种情况考虑，如图3所示．①当DP为对角线时，，解得：，∴点M1的坐标为（，2）；②当CD为对角线时，，解得：，∴点M2的坐标为（，6）；③当CP为对角线时，，解得：，∴点M3的坐标为（，﹣2）．综上所述：以点C、D、P为顶点作平行四边形，第四个顶点M的坐标为（，2），（，6）或（，﹣2）．7．如图在平面直角坐标系中，一次函数y＝﹣2x﹣4的图象与反比例函数y＝的图象交于点A（1，n），B（m，2）（1）求反比例函数关系式及m的值；（2）若x轴正半轴上有一点M满足△MAB的面积为16，求点M的坐标；（3）根据函数图象直接写出关于x的不等式在＜﹣2x﹣4的解集解：（1）∵一次函数y＝﹣2x﹣4的图象过点A（1，n），B（m，2）∴n＝﹣2﹣4，2＝﹣2m﹣4∴n＝﹣6，m＝﹣3，∴A（1，﹣6）把A（1，﹣6）代入y＝得，k＝﹣6，∴反比例函数关系式为y＝﹣；（2）设直线AB与x轴交于N点，则N（﹣2，0），设M（m，0），m＞0，∵S△MAB＝S△BMN+S△AMN，△MAB的面积为16，∴|m+2|×（2+6）＝16，解得m＝2或﹣6（不合题意舍去），∴M（2，0）；（3）由图象可知：不等式在＜﹣2x﹣4的解集是x＜﹣3或0＜x＜1．8．如图，在平面直角坐标系中，点A（3，5）与点C关于原点O对称，分别过点A、C作y 轴的平行线，与反比例函数的图象交于点B、D，连结AD、BC，AD与x 轴交于点E（﹣2，0）．（1）求直线AD对应的函数关系式；（2）求k的值；（3）直接写出阴影部分图形的面积之和．解：（1）设直线AD对应的函数关系式为y＝ax+b．∵直线AD过点A（3，5），E（﹣2，0），∴解得∴直线AD的解析式为y＝x+2．（2）∵点A（3，5）关于原点O的对称点为点C，∴点C的坐标为（﹣3，﹣5），∵CD∥y轴，∴设点D的坐标为（﹣3，a），∴a＝﹣3+2＝﹣1，∴点D的坐标为（﹣3，﹣1），∵反比例函数y＝的图象经过点D，∴k＝﹣3×（﹣1）＝3；（3）如图：∵点A和点C关于原点对称，∴阴影部分的面积等于平行四边形CDGF的面积，∴S阴影＝4×3＝12．9．如图，一次函数y＝kx+b的图象分别与反比例函数y＝的图象在第一象限交于点A（4，3），与y轴的负半轴交于点B，且OA＝OB．（1）求函数y＝kx+b和y＝的表达式；（2）已知点C（0，8），试在该一次函数图象上确定一点M，使得MB＝MC，求此时点M 的坐标．解：（1）把点A（4，3）代入函数得：a＝3×4＝12，∴y＝，OA＝5，∵OA＝OB，∴OB＝5，∴点B的坐标为（0，﹣5），把B（0，﹣5），A（4，3）代入y＝kx+b得：∴y＝2x﹣5；（2）作MD⊥y轴．∵点M在一次函数y＝2x﹣5上，∴设点M的坐标为（x，2x﹣5）．∵MB＝MC，∴CD＝BD，∴x2+（8﹣2x+5）2＝x2+（﹣5﹣2x+5）2∴8﹣（2x﹣5）＝2x﹣5+5解得：x＝∴2x﹣5＝，∴点M的坐标为（，）．10．如图，矩形OABC的顶点A、C分别在x、y轴的正半轴上，点B在反比例函数y＝（k ≠0）的第一象限内的图象上，OA＝3，OC＝5，动点P在x轴的上方，且满足S△PAO＝S．矩形OABC（1）若点P在这个反比例函数的图象上，求点P的坐标；（2）连接PO、PA，求PO+PA的最小值；（3）若点Q是平面内一点，使得以A、B、P、Q为顶点的四边形是菱形，则请你直接写出满足条件的所有点Q的坐标．解：（1）由题意，可知：点B的坐标为（3，5）．∵点B在反比例函数y＝（k≠0）的第一象限内的图象上，∴k＝3×5＝15，∴反比例函数的解析式为y＝．∵S△PAO＝S矩形OABC，∴×3×y P＝×3×5，∴y P＝3．当y＝3时，＝3，解得：x＝5，∴当点P在这个反比例函数的图象上时，点P的坐标为（5，3）．（2）由（1）可知：点P在直线y＝3上，作点O关于直线y＝3的对称点O′，连接AO′交直线y＝3于点P，此时PO+PA取得最小值，如图1所示．∵点O的坐标为（0，0），∴点O′的坐标为（0，6）．∵点A的坐标为（3，0），∴AO′＝＝3，∴PO+PA的最小值为3．（3）∵AB∥y轴，AB＝5，点P的纵坐标为3，∴AB不能为对角线，只能为边．设点P的坐标为（m，3），分两种情况考虑，如图2所示：①当点Q在点P的上方时，AP＝AB＝5，即（m﹣3）2+（3﹣0）2＝25，解得：m1＝﹣1，m2＝7，∴点P1的坐标为（﹣1，3），点P2的坐标为（7，3）．又∵PQ＝5，且PQ∥AB∥y轴，∴点Q1的坐标为（﹣1，8），点Q2的坐标为（7，8）；②当点Q在点P的下方时，BP＝AB＝5，即（m﹣3）2+（3﹣5）2＝25，解得：m3＝3﹣，m4＝3+，同理，可得出：点Q3的坐标为（3﹣，﹣2），点Q4的坐标为（3+，﹣2）．综上所述：当以A、B、P、Q为顶点的四边形是菱形时，点Q的坐标为（﹣1，8），（7，8），（3﹣，﹣2）或（3+，﹣2）．11．如图，已知C，D是反比例函数y＝图象在第一象限内的分支上的两点，直线CD分别交x轴、y轴于A，B两点，设C，D的坐标分别是（x1，y1）、（x2，y2），且x1＜x2，连接OC、OD．（1）若x1+y1＝x2+y2，求证：OC＝OD；（2）tan∠BOC＝，OC＝，求点C的坐标；（3）在（2）的条件下，若∠BOC＝∠AOD，求直线CD的解析式．（1）证明：∵C，D是反比例函数y＝图象在第一象限内的分支上的两点，∴y1＝，y2＝．∵x1+y1＝x2+y2，即x1+＝x2+，∴x1﹣x2＝．又∵x1＜x2，∴＝1，∴＝x2＝y1，＝x1＝y2．∴OC＝＝，OD＝＝，∴OC＝OD．（2）解：∵tan∠BOC＝，∴＝．又∵OC＝，∴+＝10，∴x1＝1，y1＝3或x1＝﹣1，y1＝﹣3．∵点C在第一象限，∴点C的坐标为（1，3）．（3）解：∵∠BOC＝∠AOD，∴tan∠AOD＝，∴＝．∵点C（1，3）在反比例函数y＝的图象上，∴m＝1×3＝3，∴x2•y2＝3，∴x2＝3，y2＝1或x2＝﹣3，y2＝﹣1．∵点D在第一象限，∴点D的坐标为（3，1）．设直线CD的解析式为y＝kx+b（k≠0），将C（1，3），D（3，1）代入y＝kx+b，得：，解得：，∴直线CD的解析式为y＝﹣x+4．12．如图，在平面直角坐标系中，矩形OABC的两边分别在x轴、y轴上，D是对角线的交点，若反比例函数y＝的图象经过点D，且与矩形OABC的两边AB，BC分别交于点E，F．（1）若D的坐标为（4，2）①则OA的长是8 ，AB的长是 4 ；②请判断EF是否与AC平行，井说明理由；③在x轴上是否存在一点P．使PD+PE的值最小，若存在，请求出点P的坐标及此时PD+PE的长；若不存在．请说明理由．（2）若点D的坐标为（m，n），且m＞0，n＞0，求的值．解：（1）①∵点D的坐标为（4，2），∴点B的坐标为（8，4），∴OA＝8，AB＝4．故答案为：8；4．②EF∥AC，理由如下：∵反比例函数y＝的图象经过点D（4，2），∴k＝4×2＝8．∵点B的坐标为（8，4），BC∥x轴，AB∥y轴，∴点F的坐标为（2，4），点E的坐标为（8，1），∴BF＝6，BE＝3，∴＝，＝，∴＝．∵∠ABC＝∠EBF，∴△ABC∽△EBF，∴∠BCA＝∠BFE，∴EF∥AC．③作点E关于x轴对称的点E′，连接DE′交x轴于点P，此时PD+PE的值最小，如图所示．∵点E的坐标为（8，1），∴点E′的坐标为（8，﹣1），∴DE′＝＝5．设直线DE′的解析式为y＝ax+b（a≠0），将D（4，2），E′（8，﹣1）代入y＝ax+b，得：，解得：，∴直线DE′的解析式为y＝﹣x+5．当y＝0时，﹣x+5＝0，解得：x＝，∴当点P的坐标为（，0）时，PD+PE的值最小，最小值为5．（2）∵点D的坐标为（m，n），∴点B的坐标为（2m，2n）．∵反比例函数y＝的图象经过点D（m，n），∴k＝mn，∴点F的坐标为（m，2n），点E的坐标为（2m， n），∴BF＝m，BE＝n，∴＝，＝，∴＝．又∵∠ABC＝∠EBF，∴△ABC∽△EBF，∴＝＝．13．如图，一次函数y＝kx+b（k≠0）的图象与反比例函数y＝（m≠0）的图象交于A（﹣3，1），B（1，n）两点．（1）求反比例函数和一次函数解析式；（2）结合图象直接写出不等式﹣kx﹣b＞0的解．解：（1）∵点A（﹣3，1）在反比例函数y＝（m≠0）的图象上，∴m＝（﹣3）×1＝﹣3，∴反比例函数的表达式为y＝﹣，∵点B（1，n）也在反比例函数y＝﹣的图象上，∴n＝﹣＝﹣3，即B（1，﹣3），把点A（﹣3，1），点B（1，﹣3）代入一次函数y＝kx+b中，得，解得，∴一次函数的表达式为y＝﹣x﹣2；（2）如图所示，当＞kx+b时，x的取值范围是﹣3＜x＜0或x＞1，所以不等式﹣kx﹣b＞0的解是：﹣3＜x＜0或x＞1．14．如图，在平面直角坐标系xOy内，函数y＝的图象与反比例函数y＝（k≠0）图象有公共点A，点A的坐标为（8，a），AB⊥x轴，垂足为点B．（1）求反比例函数的解析式；（2）点P在线段OB上，若AP＝BP+2，求线段OP的长；（3）点D为射线OA上一点，在（2）的条件下，若S△ODP＝S△ABO，求点D的坐标．解：（1）∵函数y＝的图象过点A（8，a），∴a＝×8＝4，∴点A的坐标为（8，4），∵反比例函数y＝（k≠0）图象过点A（8，4），∴4＝，得k＝32，∴反比例函数的解析式为y＝；（2）设BP＝b，则AP＝b+2，∵点A（8，4），AB⊥x轴于点B，∴AB＝4，∠ABP＝90°，∴b2+42＝（b+2）2，解得，b＝3，∴OP＝8﹣3＝5，即线段OP的长是5；（3）设点D的坐标为（d， d），∵点A（8，4），点B（8，0），点P（5，0），S△ODP＝S△ABO，∴，解得，d＝，∴d＝，∴点D的坐标为（，）．15．阅读理解：如图（1），在平面直角坐标系xOy中，已知点A的坐标是（1，2），点B的坐标是（3，4），过点A、点B作平行于x轴、y轴的直线相交于点C，得到Rt△ABC，由勾股定理可得，线段AB＝＝．得出结论：（1）若A点的坐标为（x1，y1），B点的坐标为（x2，y2）请你直接用A、B两点的坐标表示A、B两点间的距离；应用结论：（2）若点P在y轴上运动，试求当PA＝PB时，点P的坐标．（3）如图（2）若双曲线L1：y＝（x＞0）经过A（1，2）点，将线段OA绕点O旋转，使点A恰好落在双曲线L2：y＝﹣（x＞0）上的点D处，试求A、D两点间的距离．解：（1）∵A点的坐标为（x1，y1），B点的坐标为（x2，y2），∴根据两点间的距离公式得，AB＝；（2）设点P（0，a），∵A的坐标是（1，2），点B的坐标是（3，4），∵PA＝，PB＝，∵PA＝PB，∴＝，∴a＝5，∴P（0，5）；（3）∵双曲线L1：y＝（x＞0）经过A（1，2）点，∴OA＝，k＝1×2＝2，∴双曲线L1：y＝（x＞0），双曲线L2：y＝﹣（x＞0），设点D坐标为（m，﹣）（m＞0），∴OD＝，由旋转知，OA＝OD，∴＝，∴m＝±1或m＝±2，∵m＞0，∴m＝1或m＝2，∴D（1，﹣2）或（2，﹣1）．∵A（1，2），∴AD＝4或．。
2020-2021中考数学反比例函数-经典压轴题含答案
2020-2021中考数学反比例函数-经典压轴题含答案经典压轴题含答案 一、反比例函数 1．如图．一次函数y=x+b 的图象经过点B （﹣1，0），且与反比例函数），且与反比例函数 （k 为不等于0的常数）的图象在第一象限交于点A （1，n ）．求：（1）一次函数和反比例函数的解析式；（2）当1≤x≤6时，反比例函数y 的取值范围．【答案】（1）解：把点B （﹣1，0）代入一次函数y=x+b 得： 0=﹣1+b ，∴b=1， ∴一次函数解析式为：y=x+1，∵点A （1，n ）在一次函数y=x+b 的图象上，∴n=1+1，∴n=2，∴点A 的坐标是（1，2）．∵反比例函数反比例函数的图象过点A （1，2）． ∴k=1×2=2，∴反比例函数关系式是：y=（2）解：反比例函数y=，当x ＞0时，y 随x 的增大而减少，的增大而减少， 而当x=1时，y=2，当x=6时，y= ，∴当1≤x≤6时，反比例函数y 的值：的值：≤y≤2 【解析】【分析】（1）根据题意首先把点B （﹣1，0）代入一次函数y=x+b 求出一次函数解析式，又点A （1，n ）在一次函数y=x+b 的图象上，再利用一次函数解析式求出点A 的坐标，然后利用代入系数法求出反比例函数解析式，（2）根据反比例函数的性质分别求出当x=1，x=6时的y 值，即可得到答案．2．心理学家研究发现，一般情况下，一节课40分钟中，学生的注意力随教师讲课的变化而变化．开始上课时，学生的注意力逐步增强，中间有一段时间学生的注意力保持较为理想的稳定状态，随后学生的注意力开始分散．经过实验分析可知，学生的注意力指标数y 随时间x（分钟）的变化规律如下图所示（其中AB、BC分别为线段，CD为双曲线的一部分）：（1）开始上课后第五分钟时与第三十分钟时相比较，何时学生的注意力更集中？（2）一道数学竞赛题，需要讲19分钟，为了效果较好，要求学生的注意力指标数最低达到36，那么经过适当安排，老师能否在学生注意力达到所需的状态下讲解完这道题目？ 【答案】（1）解：设线段AB所在的直线的解析式为y1=k1x+20，把B（10，40）代入得，k1=2，∴y1=2x+20．设C、D所在双曲线的解析式为y2= ，把C（25，40）代入得，k2=1000，∴当x1=5时，y1=2×5+20=30，当 ，∴y1＜y2∴第30分钟注意力更集中．（2）解：令y1=36，∴36=2x+20，∴x1=8令y2=36，∴ ，∴∵27.8﹣8=19.8＞19，∴经过适当安排，老师能在学生注意力达到所需的状态下讲解完这道题目．【解析】【分析】（1）根据一次函数和反比例函数的应用，用待定系数法求出线段AB所时和 进行比较得到在的直线的解析式，和C、D所在双曲线的解析式；把x1=5时和y1＜y2 ， 得出第30分钟注意力更集中；（2）当y1=36时，得到x1=8，当y2=36，得到，得到 ， 由27.8﹣8=19.8＞19，所以经过适当安排，老师能在学生注意力达到所需的状态下讲解完这道题目.3．抛物线y= +x+m的顶点在直线y=x+3上，过点F（﹣2，2）的直线交该抛物线于点M、N两点（点M在点N的左边），MA⊥x轴于点A，NB⊥x轴于点B．（1）先通过配方求抛物线的顶点坐标（坐标可用含m的代数式表示），再求m的值； （2）设点N的横坐标为a，试用含a的代数式表示点N的纵坐标，并说明NF=NB；（3）若射线NM交x轴于点P，且PA•PB= ，求点M的坐标．【答案】（1）解：y= x2+x+m= （x+2）2+（m﹣1）∴顶点坐标为（﹣2，m﹣1）∵顶点在直线y=x+3上，∴﹣2+3=m﹣1，得m=2；（2）解：过点F作FC⊥NB于点C，∵点N在抛物线上，的纵坐标为： a2+a+2，∴点N的纵坐标为：即点N（a， a2+a+2）在Rt△FCN中，FC=a+2，NC=NB﹣CB= a2+a，∴NF2=NC2+FC2=（ a2+a）2+（a+2）2，=（ a2+a）2+（a2+4a）+4，而NB2=（ a2+a+2）2，=（ a2+a）2+（a2+4a）+4∴NF2=NB2，NF=NB（3）解：连接AF、BF，由NF=NB，得∠NFB=∠NBF，由（2）的思路知，MF=MA，∴∠MAF=∠MFA，∵MA⊥x轴，NB⊥x轴，∴MA∥NB，∴∠AMF+∠BNF=180°∵△MAF和△NFB的内角总和为360°，∴2∠MAF+2∠NBF=180°，∠MAF+∠NBF=90°，∵∠MAB+∠NBA=180°，∴∠FBA+∠FAB=90°，又∵∠FAB+∠MAF=90°，∴∠FBA=∠MAF=∠MFA，又∵∠FPA=∠BPF，∴△PFA∽△PBF，∴ = ，PF2=PA×PB= ，过点F作FG⊥x轴于点G，在Rt△PFG中，PG= = ，∴PO=PG+GO= ，（﹣ ，0）∴P（﹣，0）代入y=kx+b， 设直线PF：y=kx+b，把点F（﹣2，2）、点P（﹣（﹣解得k= ，b= ，∴直线PF ：y= x+， 解方程解方程 x 2+x+2= x+ ， 得x=﹣3或x=2（不合题意，舍去）， 当x=﹣3时，y= ，∴M （﹣3，）． 【解析】【分析】（1）利用配方法将二次函数化成顶点式，写出顶点坐标，由顶点再直线y=x+3上，建立方程求出m 的值。
2021中考数学热点题型专练反比例函数含解析
热点08 反比例函数【命题趋势】1．反比例函数解析式的确定；2．反比例函数中k的几何意义；3．反比例函数与一次函数结合,根据图象解答相关问题．【满分技巧】一、反比例函数的图象及性质利用图象解决问题,从图上获取有用的信息,是解题的关键所在．已知点在图象上,那么点一定满足这个函数解析式,反过来如果这点满足函数的解析式,那么这个点也一定在函数图象上．还能利用图象直接比较函数值或是自变量的大小．将数形结合在一起,是分析解决问题的一种好方法．二、反比例函数的图象与几何图形的关系1．常见的有：（1）双曲线与三角形的关系；（2）双曲线与四边形的关系；（3）双曲线与圆的关系；（4）两条双曲线之间的关系．2．在平面直角坐标系中与几何图形相联系时,通常要构造一个三角形,以坐标轴上的边为底,相对顶点的横坐标（或纵坐标）的绝对值为高；如果没有坐标轴上的边,则用坐标轴将其分割后求解．【限时检测】（建议用时：30分钟）一、选择题1．在反比例函数y=﹣6x图象上的点是A．（﹣2,3）B．（4,﹣2）C．（6,1）D．（2,3）【答案】A【解析】A．把x=﹣2代入y=﹣6x得：y=﹣62-=3,即A项正确,B．把x=4代入y=﹣6x得：y=﹣6342=-≠﹣2,即B项错误,C．把x=6代入y=﹣6x得：y=﹣66=﹣1≠1,即C项错误,D．把x=2代入y=﹣6x得：y=﹣62=﹣3≠3,即D项错误,故选A．2．对于反比例函数6y x=-,当10x -<时,y 的取值范围是A ．6yB ．60y -≤<C ．06y <D ．6y <-【答案】A 【解析】∵k =–6<0, ∴6y x=-的图象在第二象限上,y 随x 的增大而增大, ∴10x -<时,∴6y ．故选A ．3．若点A （﹣1,y 1）,B （2,y 2）,C （3,y 3）在反比例函数y =的图象上,则y 1,y 2,y 3的大小关系是 A ．y 3<y 2<y 1 B ．y 2<y 1<y 3 C ．y 1<y 3<y 2 D ．y 1<y 2<y 3【答案】C【解析】∵点A （﹣1,y 1）,B （2,y 2）,C （3,y 3）在反比例函数y =的图象上,∴y 1==﹣6,y 2==3,y 3==2,又∵﹣6<2<3,∴y 1<y 3<y 2．故选C ． 4．已知反比例函数8y x=-,下列结论错误的是 A ．y 随x 的增大而减小 B ．图象位于二、四象限内 C ．图象必过点()2,4- D ．当10x -<<时,>8y【答案】A【解析】在反比例函数y =–8x-中, ∵k =–8<0,∴在每个象限内,y 随x 的增大而增大,故选项A 错误； ∵k =–8<0,∴图象在二,四象限内,故B 选项正确； ∵–2×4=–8,∴图象必经过（–2,4）,故C 选项正确； ∵k =–8<0,每一象限内,y 随x 的增大而增大,当–1<x <0时,y >8,故D 选项正确, 故选A ． 5．若反比例函数y =2kx-的图象位于第一、第三象限,则k 的取值范围是 6x6x 61-6263A ．k <2B ．k >﹣2C ．k <﹣2D ．k >2【答案】A 【解析】∵y =2kx-的图象位于第一、第三象限, ∴2﹣k >0,k <2． 故选A ．6．如图,一次函数y 1=k 1x +b 1与反比例函数22k y x=的图象交于点A （1,3）,B （3,1）两点,若y 1<y 2,则x 的取值范围是A ．x <1B ．x <3C ．0<x <3D ．x >3或0<x <1【答案】D【解析】一次函数图象位于反比例函数图象的下方, 由图象可得当x >3或0<x <1时,y 1<y 2,故选D ． 7．如图,已知双曲线y =2x经过Rt △OAB 的直角边AB 的中点P ,则△AOP 的面积为A ．12B ．1C ．2D ．4【答案】B【解析】∵双曲线y =2x经过P ,∴S △ABP =2k 丨丨=1, ∵P 为AB 边上的中点, ∴S △AOP =S △ABP =1, 故选B ．8．如图,矩形ABCD 的边AB 在x 轴上,反比例函数(0)ky k x=≠的图象过D 点和边BC 的中点E ,连接DE ,若△CDE 的面积是1,则k 的值是A ．3B ．4C ．D ．6【答案】B【解析】设E 的坐标是m n k mn =（，），，, 则C 的坐标是（m ,2n ）, 在mny x =中,令2y n =,解得：2m x =, ∵1CDE S =△,∴1122m n m -=,即1122m n ⨯=, ∴4mn =, ∴4k =, 故选B ． 二、填空题10．已知反比例函数kyx=（k为常数,0k≠）的图象位于第二、第四象限,写出一个符合条件的k的值为__________．【答案】–1（答案不唯一）【解析】∵比例函数kyx=（k为常数,k0≠）的图象位于第二、第四象限,∴k<0,∴k可以为–1,故答案为：–1（答案不唯一）．11．已知反比例函数y=6kx-的图象在每一象限内y随x的增大而增大,则k的取值范围是__________．【答案】k<6【解析】∵反比例数6kyx-=的图象在每一象限内y随x的增大而增大,∴k﹣6<0,解得k<6．故答案为：k<6．12．如图,已知直线y=2x﹣2与x轴、y轴分别交于A、B两点,与反比例函数y=kx（x>0）的图象交于点C,过点C作CD⊥x轴于点D,若OA=AD,则k的值为__________．【答案】4【解析】∵直线y1=2x﹣2与坐标轴交于A、B两点,∴A （1,0）,B （0,﹣2）, ∴OA =1,OB =2,在△OBA 和△DCA 中,90OAB DAC AOB ADC OA AD ∠=∠⎧⎪∠=∠=︒⎨⎪=⎩,∴△OBA ≌△DCA , ∴AD =OA =1,CD =OB =2, ∴C （2,2）, ∵点C 在y =kx上, ∴k =4． 故答案为：4． 13．如图,A 、B 两点在双曲线y =5x上,分别经过A 、B 两点向坐标轴作垂线段,已知S 阴影=2,则S 1+S 2=__________．【答案】6【解析】根据题意得S 1+S 阴影=S 2+S 阴影=5, 而S 阴影=2,所以S 1=S 2=3, 所以S 1+S 2=6．故答案为：6． 三、解答题14．已知反比例函数3y mx=-和一次函数y =kx ﹣1的图象都经过点P （m ,﹣3m ）． （1）求点P 的坐标和这个一次函数的解析式；（2）若点M （a ,y 1）和点N （a +1,y 2）都在这个一次函数的图象上．试通过计算或利用一次函数的性质,说明y 1大于y 2．【解析】（1）将点P （m ,﹣3m ）代入反比例函数解析式可得：﹣3m =﹣3, 即m =1,故P 的坐标（1,﹣3）,将点P （1,﹣3）代入一次函数解析式可得：﹣3=k ﹣1,故k =﹣2,故一次函数的解析式为y=﹣2x﹣1．（2）∵M、N都在y=﹣2x﹣1上,∴y1=﹣2a﹣1,y2=﹣2（a+1）﹣1=﹣2a﹣3,∴y1﹣y2=﹣2a﹣1﹣（﹣2a﹣3）=﹣1+3=2>0, ∴y1>y2．15．如图直线y1=–x+4,y2=34x+b都与双曲线y=kx交于点A（1,m）,这两条直线分别与x轴交于B,C两点．（1）求k的值；（2）直接写出当x>0时,不等式34x+b>kx的解集；（3）若点P在x轴上,连接AP,且AP把△ABC的面积分成1∶2两部分,求此时点P的坐标．【解析】（1）把A（1,m）代入y1=–x+4,可得m=–1+4=3,∴A（1,3）,把A（1,3）代入双曲线y=kx,可得k=1×3=3．（2）∵A（1,3）,∴当x>0时,不等式34x+b>kx的解集为：x>1．（3）y1=–x+4,令y=0,则x=4, ∴点B的坐标为（4,0）,把A（1,3）代入y2=34x+b,可得3=34×1+b,∴b=94,∴y2=34x+94,令y=0,则x=–3,即C（–3,0）,∴BC=7,∵AP把△ABC的面积分成1：2两部分,∴CP=13BC=73,或BP=13BC=73,∴OP=3–73=23,或OP=4–73=53,∴P（–23,0）或（53,0）．16．如图,一次函数y1=kx+b（k,b为常数,k≠0）的图象与反比例函数y2=mx（m为常数,m≠0）的图象相交于点M（1,4）和点N（4,n）．（1）反比例函数与一次函数的解析式．（2）函数y2=mx的图象（x>0）上有一个动点C,若先将直线MN平移使它过点C,再绕点C旋转得到直线PQ,PQ交x轴于点A,交y轴点B,若BC=2CA,求OA·OB的值．【解析】（1）将点M（1,4）代入y2=mx（m为常数,m≠0）,∴m=1×4=4,∴反比例函数的解析式为y=4 x ,将N（4,n）代入y=4x,∴n=1,∴N（4,1）,将M（1,4）,N（4,1）代入y1=kx+b,得到441k bk b+=⎧⎨+=⎩,∴15kb=-⎧⎨=⎩,∴一次函数的解析式为y=﹣x+5．（2）设点C（a,b）,则ab=4,过C点作CH⊥OA于点H．①当点B在y轴的负半轴时,如图1,∵BC=2CA,∴AB=CA．∵∠AOB=∠AHC=90°,∠OAB=∠CAH, ∴△ACH∽△ABO．∴OB=CH=b,OA=AH=12 a,∴OA•OB=12ab=2．②当点B在y轴的正半轴时,如图2,当点A在x轴的正半轴时,∵BC=2CA,∴13 CA AB=∵CH∥OB,∴△ACH∽△ABO．∴13 CH AH CAOB OA AB===,∴OB=3b,OA=3 2 a,∴9182OA OB ab⋅==；③当点A在x轴的负半轴时,BC=2CA不可能．综上所述,OA•OB的值为18或2．17．如图,直线l：y=x+1与y轴交于点A,与双曲线kyx=（x>0）交于点B（2,a）．（1）求a,k的值．（2）点P是直线l上方的双曲线上一点,过点P作平行于y轴的直线,交直线l于点C,过点A作平行于x 轴的直线,交直线PC于点D,设点P的横坐标为m．①若m=32,试判断线段CP与CD的数量关系,并说明理由；②若CP>CD,请结合函数图象,直接写出m的取值范围．【解析】（1）∵直线l：y=x+1经过点B（2,a）, ∴a=2+1=3,∴B（2,3）,∵点B（2,3）在双曲线kyx=（x>0）上,∴k=2×3=6．（2）①∵点P的横坐标为32,把x=32代入y=6x得,y=632=4,代入y=x+1得,y=32+1=52,∴P（32,4）,C（32,52）,∵直线l：y=x+1与y轴交于点A, ∴A（0,1）,∴D（32,1）,∴CP=4﹣52=32,CD=52﹣1=32,∴CP=CD；②由图象结合①的结论可知,若CP>CD,m的取值范围为0<m<32．18．模具厂计划生产面积为4,周长为m的矩形模具．对于m的取值范围,小亮已经能用“代数”的方法解决,现在他又尝试从“图形”的角度进行探究,过程如下：m。
2021年中考数学专题复习：反比例函数压轴题 试题精选汇编(含答案)
2021年中考数学专题复习：反比例函数压轴题 试题精选汇编1．已知：如图，一次函数的图象与反比例函数的图象交于A ，B 两点，与y 轴正半轴交于点C ，与x 轴负半轴交于点D ，OB ＝，tan ∠DOB ＝．（1）求反比例函数的解析式； （2）当S △ACO ＝S △OCD 时，求点C 的坐标．2．如图1，矩形OABC 的顶点A 、C 分别在x 、y 轴的正半轴上，点B 在反比例函数y ＝（k＞0）的第一象限内的图象上，OA ＝4，OC ＝3，动点P 在y 轴的右侧，且满足S △PCO ＝S 矩形OABC ．（1）若点P 在这个反比例函数的图象上，求点P 的坐标；（2）连接PO 、PC ，求PO +PC 的最小值；（3）若点Q 是平面内一点，使得以B 、C 、P 、Q 为顶点的四边形是菱形，请你直接写出满足条件的所有点Q 的坐标．3．教师办公室有一种可以自动加热的饮水机，该饮水机的工作程序是：放满水后接通电源，则自动开始加热，每分钟水温上升10℃，待加热到100℃，饮水机自动停止加热，水温开始下降．水温y（℃）和通电时间x（min）成反比例函数关系，直至水温降至室温，饮水机再次自动加热，重复上述过程．设某天水温和室温均为20℃，接通电源后，水温y（℃）和通电时间x（min）之间的关系如图所示，回答下列问题：（1）分别求出当0≤x≤8和8＜x≤a时，y和x之间的函数关系式；（2）求出图中a的值；（3）李老师这天早上7：30将饮水机电源打开，若他想在8：10上课前喝到不低于40℃的开水，则他需要在什么时间段内接水？4．如图，在平面直角坐标系中，正六边形ABCDEF的对称中心P在反比例函数y＝（k＞0，x＞0）的图象上，边CD在x轴上，点B在y轴上，已知CD＝2．（1）点A是否在该反比例函数的图象上？请说明理由；（2）若该反比例函数图象与DE交于点Q，求点Q的横坐标；（3）平移正六边形ABCDEF，使其一边的两个端点恰好都落在该反比例函数的图象上，试描述平移过程．5．工匠制作某种金属工具要进行材料煅烧和锻造两个工序，即需要将材料烧到800℃，然后停止煅烧进行锻造操作，经过8min时，材料温度降为600℃．如图，煅烧时温度y（℃）与时间x（min）成一次函数关系；锻造时，温度y（℃）与时间x（min）成反比例函数关系．已知该材料初始温度是32℃．（1）分别求出材料煅烧和锻造时y与x的函数关系式，并且写出自变量x的取值范围；（2）根据工艺要求，当材料温度低于400℃时，须停止操作．那么锻造的操作时间最多有多长？（3）如果加工每个零件需要锻造12分钟，并且当材料温度低于400℃时，需要重新煅烧．通过计算说明加工第一个零件，一共需要多少分钟．6．如图，在平面直角坐标系中，已知等腰直角三角形ABC，∠BAC＝90°，点A（0，），B（1，0），点C在反比例函数y＝（k＞0）上．（1）求反比例函数的解析式．（2）将点B向上平移后落在反比例函数图象上的点记为点D，连结DA，DC，求△ACD的面积．7．如图，在直角坐标系中，直线y1＝ax+b与双曲线y2＝（k≠0）分别相交于第二、四象。
2020-2021中考数学与反比例函数有关的压轴题含答案
2020-2021中考数学与反比例函数有关的压轴题含答案一、反比例函数1．如图，在平面直角坐标系中，一次函数y1=ax+b（a≠0）的图象与y轴相交于点A，与反比例函数y2= （c≠0）的图象相交于点B（3，2）、C（﹣1，n）．（1）求一次函数和反比例函数的解析式；（2）根据图象，直接写出y1＞y2时x的取值范围；（3）在y轴上是否存在点P，使△PAB为直角三角形？如果存在，请求点P的坐标；若不存在，请说明理由．【答案】（1）解：把B（3，2）代入得：k=6∴反比例函数解析式为：把C（﹣1，n）代入，得：n=﹣6∴C（﹣1，﹣6）把B（3，2）、C（﹣1，﹣6）分别代入y1=ax+b，得：，解得：所以一次函数解析式为y1=2x﹣4（2）解：由图可知，当写出y1＞y2时x的取值范围是﹣1＜x＜0或者x＞3．（3）解：y轴上存在点P，使△PAB为直角三角形如图，过B作BP1⊥y轴于P1，∠B P1 A=0，△P1AB为直角三角形此时，P1（0，2）过B作BP2⊥AB交y轴于P2∠P2BA=90，△P2AB为直角三角形在Rt△P1AB中，在Rt△P1 AB和Rt△P2 AB∴∴P2（0，）综上所述，P1（0，2）、P2（0，）．【解析】【分析】（1）利用待定系数法求出反比例函数解析式，进而求出点C坐标，最后用再用待定系数法求出一次函数解析式；（2）利用图象直接得出结论；（3）分三种情况，利用勾股定理或锐角三角函数的定义建立方程求解即可得出结论．2．如图，点P（x，y1）与Q（x，y2）分别是两个函数图象C1与C2上的任一点．当a≤x≤b 时，有﹣1≤y1﹣y2≤1成立，则称这两个函数在a≤x≤b上是“相邻函数”，否则称它们在a≤x≤b 上是“非相邻函数”．例如，点P（x，y1）与Q （x，y2）分别是两个函数y=3x+1与y=2x﹣1图象上的任一点，当﹣3≤x≤﹣1时，y1﹣y2=（3x+1）﹣（2x﹣1）=x+2，通过构造函数y=x+2并研究它在﹣3≤x≤﹣1上的性质，得到该函数值的范围是﹣1≤y≤1，所以﹣1≤y1﹣y2≤1成立，因此这两个函数在﹣3≤x≤﹣1上是“相邻函数”．（1）判断函数y=3x+2与y=2x+1在﹣2≤x≤0上是否为“相邻函数”，并说明理由；（2）若函数y=x2﹣x与y=x﹣a在0≤x≤2上是“相邻函数”，求a的取值范围；（3）若函数y= 与y=﹣2x+4在1≤x≤2上是“相邻函数”，直接写出a的最大值与最小值．【答案】（1）解：是“相邻函数”，理由如下：y1﹣y2=（3x+2）﹣（2x+1）=x+1，构造函数y=x+1，∵y=x+1在﹣2≤x≤0，是随着x的增大而增大，∴当x=0时，函数有最大值1，当x=﹣2时，函数有最小值﹣1，即﹣1≤y≤1，∴﹣1≤y1﹣y2≤1，即函数y=3x+2与y=2x+1在﹣2≤x≤0上是“相邻函数”（2）解：y1﹣y2=（x2﹣x）﹣（x﹣a）=x2﹣2x+a，构造函数y=x2﹣2x+a，∵y=x2﹣2x+a=（x﹣1）2+（a﹣1），∴顶点坐标为：（1，a﹣1），又∵抛物线y=x2﹣2x+a的开口向上，∴当x=1时，函数有最小值a﹣1，当x=0或x=2时，函数有最大值a，即a﹣1≤y≤a，∵函数y=x2﹣x与y=x﹣a在0≤x≤2上是“相邻函数”，∴﹣1≤y1﹣y2≤1，即，∴0≤a≤1（3）解：y1﹣y2= ﹣（﹣2x+4）= +2x﹣4，构造函数y= +2x﹣4，∵y= +2x﹣4∴当x=1时，函数有最小值a﹣2，当x=2时，函数有最大值，即a﹣2≤y≤ ，∵函数y= 与y=﹣2x+4在1≤x≤2上是“相邻函数”，∴﹣1≤y1﹣y2≤1，即，∴1≤a≤2；∴a的最大值是2，a的最小值1【解析】【分析】（1）y1﹣y2=（3x+2）﹣（2x+1）=x+1，构造函数y=x+1，因为y=x+1在﹣2≤x≤0，是随着x的增大而增大，所以当x=0时，函数有最大值1，当x=﹣2时，函数有最小值﹣1，即﹣1≤y≤1，所以﹣1≤y1﹣y2≤1，即函数y=3x+2与y=2x+1在﹣2≤x≤0上是“相邻函数”；（2）y1﹣y2=（x2﹣x）﹣（x﹣a）=x2﹣2x+a，构造函数y=x2﹣2x+a，因为y=x2﹣2x+a=（x﹣1）2+（a﹣1），所以顶点坐标为：（1，a﹣1），又抛物线y=x2﹣2x+a的开口向上，所以当x=1时，函数有最小值a﹣1，当x=0或x=2时，函数有最大值a，即a﹣1≤y≤a，因为函数y=x2﹣x与y=x﹣a在0≤x≤2上是“相邻函数”，所以﹣1≤y1﹣y2≤1，即0≤a≤1；（3）当x=1时，函数有最小值a﹣2，当x=2时，函数有最大值，因为函数y=与y=﹣2x+4在1≤x≤2上是“相邻函数”，﹣1≤y1﹣y2≤1，即1≤a≤2，所以a的最大值是2，a 的最小值1.3．给出如下规定：两个图形G1和G2，点P为G1上任一点，点Q为G2上任一点，如果线段PQ的长度存在最小值，就称该最小值为两个图形G1和G2之间的距离．在平面直角坐标系xOy中，O为坐标原点．（1）点A的坐标为A（1，0），则点B（2，3）和射线OA之间的距离为________，点C （﹣2，3）和射线OA之间的距离为________；（2）如果直线y=x+1和双曲线y= 之间的距离为，那么k=________；（可在图1中进行研究）（3）点E的坐标为（1，），将射线OE绕原点O顺时针旋转120°，得到射线OF，在坐标平面内所有和射线OE，OF之间的距离相等的点所组成的图形记为图形M．①请在图2中画出图形M，并描述图形M的组成部分；（若涉及平面中某个区域时可以用阴影表示）．②将射线OE，OF组成的图形记为图形W，直线y=﹣2x﹣4与图形M的公共部分记为图形N，请求出图形W和图形N之间的距离．【答案】（1）3；（2）﹣4（3）解：①如图，x轴正半轴，∠GOH的边及其内部的所有点（OH、OG分别与OE、OF 垂直），；②由①知OH所在直线解析式为y=﹣ x，OG所在直线解析式为y= x，由得，即点M（﹣，），由得：，即点N（﹣，），则﹣≤x≤﹣，图形N（即线段MN）上点的坐标可设为（x，﹣2x﹣4），即图形W与图形N之间的距离为d，d===∴当x=﹣时，d的最小值为 = ，即图形W和图形N之间的距离．【解析】【解答】解：（1）点（2，3）和射线OA之间的距离为3，点（﹣2，3）和射线OA之间的距离为 = ，故答案分别为：3，；（2）直线y=x+1和双曲线y= k x 之间的距离为，∴k＜0（否则直线y=x+1和双曲线y= 相交，它们之间的距离为0）．过点O作直线y=x+1的垂线y=﹣x，与双曲线y= 交于点E、F，过点E作EG⊥x轴，如图1，由得，即点F（﹣，），则OF= = ，∴OE=OF+EF=2 ，在Rt△OEG中，∠EOG=∠OEG=45°，OE=2 ，则有OG=EG= OE=2，∴点E的坐标为（﹣2，2），∴k=﹣2×2=﹣4，故答案为：﹣4；【分析】（1）由题意可得出点B（2，3）到射线OA之间的距离为B点纵坐标，根据新定义得点C（﹣2，3）和射线OA之间的距离；（2）根据题意即可得k＜0（否则直线y=x+1和双曲线y= k x 相交，它们之间的距离为0）．过点O作直线y=x+1的垂线y=﹣x，与双曲线y= k x 交于点E、F，过点E作EG⊥x 轴，如图1，将其联立即可得点F坐标，根据两点间距离公式可得OF长，再由OE=OF+EF 求出OE长，在Rt△OEG中，根据等腰直角三角形的性质可得点E的坐标为（﹣2，2），将E点代入反比例函数解析式即可得出k值.（3）①如图，x轴正半轴，∠GOH的边及其内部的所有点（OH、OG分别与OE、OF垂直）；②由①知OH所在直线解析式为y=﹣ x，OG所在直线解析式为y= x，分别联立即可得出点M、N坐标，从而得出x取值范围，根据题意图形N（即线段MN）上点的坐标可设为（x，﹣2x﹣4），从而求出图形W与图形N之间的距离为d，由二次函数性质知d 最小值.4．如图，四边形OP1A1B1、A1P2A2B2、A2P3A3B3、…、A n﹣1P n A n B n都是正方形，对角线OA1、A1A2、A2A3、…、A n﹣1A n都在y轴上（n≥1的整数），点P1（x1，y1），点P2（x2，y2），…，P n（x n， y n）在反比例函数y= （x＞0）的图象上，并已知B1（﹣1，1）．（1）求反比例函数y= 的解析式；（2）求点P2和点P3的坐标；（3）由（1）、（2）的结果或规律试猜想并直接写出：△P n B n O的面积为 ________ ，点P n的坐标为________ （用含n的式子表示）．【答案】（1）解：在正方形OP1A1B1中，OA1是对角线，则B1与P1关于y轴对称，∵B1（﹣1，1），∴P1（1，1）．则k=1×1=1，即反比例函数解析式为y=（2）解：连接P2B2、P3B3，分别交y轴于点E、F，又点P1的坐标为（1，1），∴OA1=2，设点P2的坐标为（a，a+2），代入y=得a=-1，故点P2的坐标为（-1，+1），则A1E=A2E=2-2，OA2=OA1+A1A2=2，设点P3的坐标为（b，b+2），代入y=（>0）可得b=-，故点P3的坐标为（-，+）（3）1；（-，+）【解析】【解答】解：（3）∵=2=2×=1，=2=2×=1，…∴△P n B n O的面积为1，由P1（1，1）、P2（﹣1， +1）、P3（﹣，+ ）知点P n的坐标为（﹣，+ ），故答案为：1、（﹣， +）．【分析】（1）由四边形OP1A1B1为正方形且OA1是对角线知B1与P1关于y轴对称，得出点P1（1，1），然后利用待定系数法求解即可；（2）连接P2B2、P3B3，分别交y轴于点E、F，由点P1坐标及正方形的性质知OA1=2，设P2的坐标为（a，a+2），代入解析式求得a的值即可，同理可得点P3的坐标；（3）先分别求得S△P1B1O、S△P2B2O的值，然后找出其中的规律，最后依据规律进行计算即可.5．如图1，已知一次函数y=ax+2与x轴、y轴分别交于点A，B，反比例函数y= 经过点M．（1）若M是线段AB上的一个动点（不与点A、B重合）．当a=﹣3时，设点M的横坐标为m，求k与m之间的函数关系式．（2）当一次函数y=ax+2的图象与反比例函数y= 的图象有唯一公共点M，且OM= ，求a的值．（3）当a=﹣2时，将Rt△AOB在第一象限内沿直线y=x平移个单位长度得到Rt△A′O′B′，如图2，M是Rt△A′O′B′斜边上的一个动点，求k的取值范围．【答案】（1）解：当a=﹣3时，y=﹣3x+2，当y=0时，﹣3x+2=0，x= ，∵点M的横坐标为m，且M是线段AB上的一个动点（不与点A、B重合），∴0＜m＜，，DANG则，﹣3x+2= ，当x=m时，﹣3m+2= ，∴k=﹣3m2+2m（0＜m＜）（2）解：由题意得：，ax+2= ，ax2+2x﹣k=0，∵直线y=ax+2（a≠0）与双曲线y= 有唯一公共点M时，∴△=4+4ak=0，ak=﹣1，∴k=﹣，则，解得：，∵OM= ，∴12+（﹣）2=（）2，a=±（3）解：当a=﹣2时，y=﹣2x+2，∴点A的坐标为（1，0），点B的坐标为（0，2），∵将Rt△AOB在第一象限内沿直线y=x平移个单位得到Rt△A′O′B′，∴A′（2，1），B′（1，3），点M是Rt△A′O′B′斜边上一动点，当点M′与A′重合时，k=2，当点M′与B′重合时，k=3，∴k的取值范围是2≤k≤3【解析】【分析】（1）当a=﹣3时，直线解析式为y=﹣3x+2，求出A点的横坐标，由于点M的横坐标为m，且M是线段AB上的一个动点（不与点A、B重合）从而得到m的取值范围，由﹣3x+2= ,由X=m得k=﹣3m2+2m（0＜m＜）；（2）由ax+2= 得ax2+2x﹣k=0，直线y=ax+2（a≠0）与双曲线y= 有唯一公共点M时，△=4+4ak=0，ak=﹣1，由勾股定理即可；（3）当a=﹣2时，y=﹣2x+2，从而求出A、B两点的坐标，由平移的知识知A′，B′点的坐标，从而得到k的取值范围。
(2021年整理)反比例函数压轴题集含答案
反比例函数压轴题集含答案编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（反比例函数压轴题集含答案）的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。
本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为反比例函数压轴题集含答案的全部内容。
反比例函数压轴题集含答案一．选择题1．如图转动一长为4cm，宽为3cm的长方形木板,在桌面上作无滑动的翻滚（顺时针方向），木板上的点A位置变化为A→A1→A2，其中第二次翻滚时被桌面上另一小木块挡住，且使木板与桌面成30°角,则A翻滚到A2时，共经过的路径长为（）cm．A．3.5π B．4。
5πC．5πD．10π二．填空题2．如图，正△ABO的边长为2，O为坐标原点，A在x轴上，B在第二象限,△ABO沿x轴正方向作无滑动的翻滚，经一次翻滚后得到△A1B1O,则翻滚3次后点B的对应点的坐标是，翻滚2017次后AB中点M经过的路径长为．3．如图，在平面直角坐标系中，矩形AOBD的两边在坐标轴上,点A为(0，6）,点B为（6，0），E、F分别为OB、BD边上的中点，以BE，BF为边作矩形BEGF．将矩形BEGF绕点B顺时针旋转，在旋转过程中OE、DF所在的直线交于点M．（1)当将矩形BEGF绕点B顺时针旋转30°时，∠OMD= ．(2）当将矩形BEGF绕点B转一周时，则点M所经过的路径长为．4．如图,边长为1的正方形ABCD 放置在平面直角坐标系中，顶点A与坐标原点O 重合，点B在x轴上．将正方形ABCD沿x轴正方向作无滑动滚动，当点D第一次落在x轴上时，D点的坐标是,D点经过的路径的总长度是；当点D第2014次落在x轴上时，D点经过的路径的总长度是．5．如图,菱形ABCD中,AB=2,∠C=60°，我们把菱形ABCD的对称中心称作菱形的中心．菱形ABCD在直线l上向右作无滑动的翻滚，每绕着一个顶点旋转60°叫一次操作，则经过1次这样的操作菱形中心O所经过的路径长为；经过18次这样的操作菱形中心O所经过的路径总长为；经过3n（n为正整数)次这样的操作菱形中心O所经过的路径总长为．（结果都保留π）三．解答题6．如图,在平面直角坐标系xOy中，动点A（a，0）在x轴的正半轴上,定点B（m，n）在第一象限内（m＜2≤a），在△OAB外作正方形ABCD和正方形OBEF，连接FD，点M为线段FD的中点,作BB1⊥x轴于点B1，作FF1⊥x轴于点F1．（1）填空：由≌△,及B(m，n）可得点F的坐标为,同理可得点D的坐标为；(说明：点F，点D的坐标用含m，n,a的式子表示）（2）直接利用（1）的结论解决下列问题：①当点A在x轴的正半轴上指定范围内运动时,点M总落在一个函数图象上，求该函数的解析式（不必写出自变量x的取值范围）；②当点A在x轴的正半轴上运动且满足2≤a≤8时，求点M所经过的路径的长．7．如图,在平面直角坐标系中，点A在x轴上，△ABO是直角三角形，∠ABO=90°，点B的坐标为（﹣1，2)，将△ABO绕原点O顺时针旋转90°得到△A1B1O．（1）在旋转过程中，点B所经过的路径长是多少?（2）分别求出点A1,B1的坐标；(3）连接BB1交A1O于点M，求M的坐标．8．如图，在平面直角坐标系中,菱形OABC的顶点A在x轴的正半轴上，反比例函数y=的图象经过点C（3,m)．(1）m= ，点B的坐标为（）；（2）将这个菱形沿y轴负半轴方向平移，当顶点B落在反比例函数图象上时，求菱形平移的距离．9．矩形ABCD的边AB=8，AD=6，现将矩形ABCD放在直线L上，且沿着L向右作无滑动翻滚,当它翻滚类似于开始的位置A4B4C4D4时（如图所示)，得A2B2C2D2、A3B3C3D3①标注好点A所对应的点A2，A3的位置及把相应的字母填在直线L上的两括号内．②求顶点A所经过的路线长．10．如图,边长为2的正六边ABCDEF在直线l上按顺时针方向作无滑动的翻滚．(1)当正六边形绕点F顺时针旋转度时，A落在点A1位置；(2）当点A翻滚到点A2的位置时，求点A所经过的路径长．11．如图,在平面直角坐标系中，A（，0），B（,2）．把矩形OABC逆时针旋转30°得到矩形OA1B1C1,(1)求B1点的坐标；（2)求过点（2，0）且平分矩形OA1B1C1面积的直线l方程；（3）设（2）中直线l交y轴于点P，直接写出△PC1O与△PB1A1的面积和的值及△POA1与△PB1C1的面积差的值．12．如图，在△ABC中，已知AB=AC=5，BC=6，且△ABC≌△DEF，将△DEF与△ABC 重合在一起，△ABC不动，△DEF运动，并满足：点E在边BC上沿B到C的方向运动，且DE、始终经过点A,EF与AC交于M点．（1）求证:△ABE∽△ECM；（2)探究：在△DEF运动过程中，重叠部分能否构成等腰三角形？若能,求出BE的长；若不能，请说明理由;（3）当线段AM最短时，求重叠部分的面积．13.如图，已知动点A在函数的图象上，AB⊥x轴于点B，AC⊥y轴于点C,延长CA至点D，使AD=AB，延长BA至点E,使AE=AC．直线DE分别交x,y轴分别于点P，Q．当QE：DP=4：9时，图中阴影部分的面积等于．14.如图，已知直线l：y=﹣2x+2与x轴、y轴交于A、B两点，平移直线l交y=于C、D两点，且CD=2AB,若AC=5，求D点坐标及k的值．15．如图,直线l：y=﹣2x﹣2,与x轴y轴交于A，B两点,平移直线l交双曲线y=（x ＞0）于C，D两点，且CD=2AB,连接AC，交y轴于E点，S△ABC=3S△ABE，求k的值．反比例函数压轴题集含答案参考答案一．选择题(共2小题）1．A；二．填空题（共5小题）2．(5，）；（+896）π；3．90°；6π;4．（3，0）；π;（1007+）π；5．;;；三．解答题（共31小题)6．△FOF1；OBB1；(﹣n,m)；(a+n，a﹣m）；7．；8．4；8，4；9．；10．60；11．；12．；13．;14．;15．；16．；17．；18．；19．；20．；21．；22．；23．；24．15：7:14．；25．；26．；27．；。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
2021年中考数学压轴题专项训练《反比例函数》1．如图，反比例函数y1＝和一次函数y2＝mx+n相交于点A（1，3），B（﹣3，a），（1）求一次函数和反比例函数解析式；（2）连接OA，试问在x轴上是否存在点P，使得△OAP为以OA为腰的等腰三角形，若存在，直接写出满足题意的点P的坐标；若不存在，说明理由．解：（1）∵点A（1，3）在反比例函数y1＝的图象上，∴k＝1×3＝3，∴反比例函数的解析式为y1＝，∵点B（﹣3，a）在反比例函数y1＝的图象上，∴﹣3a＝3，∴a＝﹣1，∴B（﹣3，﹣1），∵点A（1，3），B（﹣3，﹣1）在一次函数y2＝mx+n的图象上，∴，∴，∴一次函数的解析式为y2＝x+2；（2）如图，∵△OAP为以OA为腰的等腰三角形，∴①当OA＝OP时，∵A（1，3），∴OA＝，∵OP＝，∵点P在x轴上，∴P（﹣，0）或（，0），②当OA＝AP时，则点A是线段OP的垂直平分线上，∵A（1，3），∴P（2，0），即：在x轴上存在点P，使得△OAP为以OA为腰的等腰三角形，此时，点P的坐标为（﹣，0）或（2，0）或（，0）．2．在平面直角坐标系xOy中，函数y＝（x＞0）的图象G经过点A（3，2），直线l：y＝kx﹣1（k≠0）与y轴交于点B，与图象G交于点C．（1）求m的值；（2）横、纵坐标都是整数的点叫做整点．记图象G在点A，C之间的部分与线段BA，BC 围成的区域（不含边界）为W．①当直线l过点（2，0）时，直接写出区域W内的整点个数；②若区域W内的整点不少于4个，结合函数图象，求k的取值范围．解：（1）把A（3，2）代入y＝得m＝3×2＝6，（2）①当直线l过点（2，0）时，直线解析式为y＝x﹣1，解方程＝x﹣1得x1＝1﹣（舍去），x2＝1+，则C（1+，），而B（0，﹣1），如图1所示，区域W内的整点有（3，1）一个；②如图2，直线l在AB的下方时，直线l：y＝kx﹣1过（6，1）时，1＝6k﹣1，解得k＝，当直线在OA的上方时，直线经过（1，4）时，4＝k﹣1，解得k＝5，观察图象可知：当k≤或k≥5时，区域W内的整点不少于4个．3．如图，在平面直角坐标系中，四边形OABC的顶点坐标分别为O（0，0），A（6，0），B（4，3），C（0，3）．动点P从点O出发，以每秒个单位长度的速度沿边OA向终点A运动；动点Q从点B同时出发，以每秒1个单位长度的速度沿边BC向终点C运动，设运动的时间为t秒，PQ2＝y．（1）直接写出y关于t的函数解析式及t的取值范围：；（2）当PQ＝时，求t的值；（3）连接OB交PQ于点D，若双曲线y＝经过点D，问k的值是否变化？若不变化，请求出k的值；若变化，请说明理由．解：（1）过点P作PE⊥BC于点E，如图1所示．当运动时间为t秒时（0≤t≤4）时，点P的坐标为（t，0），点Q的坐标为（4﹣t，3），∴PE＝3，EQ＝|4﹣t﹣t|＝|4﹣t|，∴PQ2＝PE2+EQ2＝32+|4﹣t|2＝t2﹣20t+25，∴y关于t的函数解析式及t的取值范围：；故答案为：．（2）当时，整理，得5t2﹣16t+12＝0，解得：t1＝2，．（3）经过点D的双曲线的k值不变．连接OB，交PQ于点D，过点D作DF⊥OA于点F，如图2所示．∵OC＝3，BC＝4，∴．∵BQ∥OP，∴△BDQ∽△ODP，∴，∴OD＝3．∵CB∥OA，∴∠DOF＝∠OBC．在Rt△OBC中，，，∴，，∴点D的坐标为，∴经过点D的双曲线的k值为．4．如图，一次函数y＝kx+b的图象与反比例函数y＝的图象交于点A（﹣3，m+8），B（n，﹣6）两点．（1）求一次函数与反比例函数的解析式；（2）求△AOB的面积；（3）若P（x1，y1），Q（x2，y2）是该反比例函数图象上的两点，且当x1＜x2时，y1＞y2，指出点P、Q各位于哪个象限？解：（1）将A（﹣3，m+8）代入反比例函数y＝得﹣3（m+8）＝m，解得m＝﹣6，∴点A的坐标为（﹣3，2），反比例函数解析式为y＝﹣，将点B（n，﹣6）代入y＝﹣得﹣6n＝﹣6，解得n＝1，∴点B的坐标为（1，﹣6），将点A（﹣3，2），B（1，﹣6）代入y＝kx+b得，解得，∴一次函数解析式为y＝﹣2x﹣4；（2）设AB与x轴相交于点C，如图，当﹣2x﹣4＝0，解得x＝﹣2，则点C的坐标为（﹣2，0），∴S△AOB＝S△AOC+S△BOC，＝×2×2+×2×6，＝2+6，＝8；（3）∵当x1＜x2时，y1＞y2，∴点P和点Q不在同一象限，∴P在第二象限，Q在第四象限．5．如图，平面直角坐标系中，一次函数y＝x﹣1的图象与x轴，y轴分别交于点A，B，与反比例函数y＝的图象交于点C，D，CE⊥x轴于点E，＝．（1）求反比例函数的表达式与点D的坐标；（2）以CE为边作▱ECMN，点M在一次函数y＝x﹣1的图象上，设点M的横坐标为a，当边MN与反比例函数y＝的图象有公共点时，求a的取值范围．解：（1）由题意A（1，0），B（0，﹣1），∴OA＝OB＝1，∴∠OAB＝∠CAE＝45°∵AE＝3OA，∴AE＝3，∵EC⊥x轴，∴∠AEC＝90°，∴∠EAC＝∠ACE＝45°，∴EC＝AE＝3，∴C（4，3），∵反比例函数y＝经过点C（4，3），∴k＝12，由，解得或，∴D（﹣3，﹣4）．（2）如图，设M（a，a﹣1）．当点N在反比例函数的图象上时，N（a，），∵四边形ECMN是平行四边形，∴MN＝EC＝3，∴|a﹣1﹣|＝3，解得a＝6或﹣2或﹣1±（舍弃），∴M（6，5）或（﹣2，﹣3），观察图象可知：当边MN与反比例函数y＝的图象有公共点时4＜a≤6或﹣3≤a≤﹣2．6．如图，一次函数y＝kx+2的图象与y轴交于点A，正方形ABCD的顶点B在x轴上，点D 在直线y＝kx+2上，且AO＝OB，反比例函数y＝（x＞0）经过点C．（1）求一次函数和反比例函数的解析式；（2）点P是x轴上一动点，当△PCD的周长最小时，求出P点的坐标；（3）在（2）的条件下，以点C、D、P为顶点作平行四边形，直接写出第四个顶点M的坐标．解：（1）设一次函数y＝kx+2的图象与x轴交于点E，连接BD，如图1所示．当x＝0时，y＝kx+2＝2，∴OA＝2．∵四边形ABCD为正方形，OA＝OB，∴∠BAE＝90°，∠OAB＝∠OBA＝45°，∴∠OAE＝∠OEA＝45°，∴OE＝2，点E的坐标为（﹣2，0）．将E（﹣2，0）代入y＝kx+2，得：﹣2k+2＝0，解得：k＝1，∴一次函数的解析式为y＝x+2．∵∠OBD＝∠ABD+∠OBA＝90°，∴BD∥OA．∵OE＝OB＝2，∴BD＝2OA＝4，∴点D的坐标为（2，4）．∵四边形ABCD为正方形，∴点C的坐标为（2+2﹣0，0+4﹣2），即（4，2）．∵反比例函数y＝（x＞0）经过点C，∴n＝4×2＝8，∴反比例函数解析式为y＝．（2）作点D关于x轴的对称点D′，连接CD′交x轴于点P，此时△PCD的周长取最小值，如图2所示．∵点D的坐标为（2，4），∴点D′的坐标为（2，﹣4）．设直线CD′的解析式为y＝ax+b（a≠0），将C（4，2），D′（2，﹣4）代入y＝ax+b，得：，解得：，∴直线CD′的解析式为y＝3x﹣10．当y＝0时，3x﹣10＝0，解得：x＝，∴当△PCD的周长最小时，P点的坐标为（，0）．（3）设点M的坐标为（x，y），分三种情况考虑，如图3所示．①当DP为对角线时，，解得：，∴点M1的坐标为（，2）；②当CD为对角线时，，解得：，∴点M2的坐标为（，6）；③当CP为对角线时，，解得：，∴点M3的坐标为（，﹣2）．综上所述：以点C、D、P为顶点作平行四边形，第四个顶点M的坐标为（，2），（，6）或（，﹣2）．7．如图在平面直角坐标系中，一次函数y＝﹣2x﹣4的图象与反比例函数y＝的图象交于点A（1，n），B（m，2）（1）求反比例函数关系式及m的值；（2）若x轴正半轴上有一点M满足△MAB的面积为16，求点M的坐标；（3）根据函数图象直接写出关于x的不等式在＜﹣2x﹣4的解集解：（1）∵一次函数y＝﹣2x﹣4的图象过点A（1，n），B（m，2）∴n＝﹣2﹣4，2＝﹣2m﹣4∴n＝﹣6，m＝﹣3，∴A（1，﹣6）把A（1，﹣6）代入y＝得，k＝﹣6，∴反比例函数关系式为y＝﹣；（2）设直线AB与x轴交于N点，则N（﹣2，0），设M（m，0），m＞0，∵S△MAB＝S△BMN+S△AMN，△MAB的面积为16，∴|m+2|×（2+6）＝16，解得m＝2或﹣6（不合题意舍去），∴M（2，0）；（3）由图象可知：不等式在＜﹣2x﹣4的解集是x＜﹣3或0＜x＜1．8．如图，在平面直角坐标系中，点A（3，5）与点C关于原点O对称，分别过点A、C作y 轴的平行线，与反比例函数的图象交于点B、D，连结AD、BC，AD与x 轴交于点E（﹣2，0）．（1）求直线AD对应的函数关系式；（2）求k的值；（3）直接写出阴影部分图形的面积之和．解：（1）设直线AD对应的函数关系式为y＝ax+b．∵直线AD过点A（3，5），E（﹣2，0），∴解得∴直线AD的解析式为y＝x+2．（2）∵点A（3，5）关于原点O的对称点为点C，∴点C的坐标为（﹣3，﹣5），∵CD∥y轴，∴设点D的坐标为（﹣3，a），∴a＝﹣3+2＝﹣1，∴点D的坐标为（﹣3，﹣1），∵反比例函数y＝的图象经过点D，∴k＝﹣3×（﹣1）＝3；（3）如图：∵点A和点C关于原点对称，∴阴影部分的面积等于平行四边形CDGF的面积，∴S阴影＝4×3＝12．9．如图，一次函数y＝kx+b的图象分别与反比例函数y＝的图象在第一象限交于点A（4，3），与y轴的负半轴交于点B，且OA＝OB．（1）求函数y＝kx+b和y＝的表达式；（2）已知点C（0，8），试在该一次函数图象上确定一点M，使得MB＝MC，求此时点M 的坐标．解：（1）把点A（4，3）代入函数得：a＝3×4＝12，∴y＝，OA＝5，∵OA＝OB，∴OB＝5，∴点B的坐标为（0，﹣5），把B（0，﹣5），A（4，3）代入y＝kx+b得：∴y＝2x﹣5；（2）作MD⊥y轴．∵点M在一次函数y＝2x﹣5上，∴设点M的坐标为（x，2x﹣5）．∵MB＝MC，∴CD＝BD，∴x2+（8﹣2x+5）2＝x2+（﹣5﹣2x+5）2∴8﹣（2x﹣5）＝2x﹣5+5解得：x＝∴2x﹣5＝，∴点M的坐标为（，）．10．如图，矩形OABC的顶点A、C分别在x、y轴的正半轴上，点B在反比例函数y＝（k ≠0）的第一象限内的图象上，OA＝3，OC＝5，动点P在x轴的上方，且满足S△PAO＝S．矩形OABC（1）若点P在这个反比例函数的图象上，求点P的坐标；（2）连接PO、PA，求PO+PA的最小值；（3）若点Q是平面内一点，使得以A、B、P、Q为顶点的四边形是菱形，则请你直接写出满足条件的所有点Q的坐标．解：（1）由题意，可知：点B的坐标为（3，5）．∵点B在反比例函数y＝（k≠0）的第一象限内的图象上，∴k＝3×5＝15，∴反比例函数的解析式为y＝．∵S△PAO＝S矩形OABC，∴×3×y P＝×3×5，∴y P＝3．当y＝3时，＝3，解得：x＝5，∴当点P在这个反比例函数的图象上时，点P的坐标为（5，3）．（2）由（1）可知：点P在直线y＝3上，作点O关于直线y＝3的对称点O′，连接AO′交直线y＝3于点P，此时PO+PA取得最小值，如图1所示．∵点O的坐标为（0，0），∴点O′的坐标为（0，6）．∵点A的坐标为（3，0），∴AO′＝＝3，∴PO+PA的最小值为3．（3）∵AB∥y轴，AB＝5，点P的纵坐标为3，∴AB不能为对角线，只能为边．设点P的坐标为（m，3），分两种情况考虑，如图2所示：①当点Q在点P的上方时，AP＝AB＝5，即（m﹣3）2+（3﹣0）2＝25，解得：m1＝﹣1，m2＝7，∴点P1的坐标为（﹣1，3），点P2的坐标为（7，3）．又∵PQ＝5，且PQ∥AB∥y轴，∴点Q1的坐标为（﹣1，8），点Q2的坐标为（7，8）；②当点Q在点P的下方时，BP＝AB＝5，即（m﹣3）2+（3﹣5）2＝25，解得：m3＝3﹣，m4＝3+，同理，可得出：点Q3的坐标为（3﹣，﹣2），点Q4的坐标为（3+，﹣2）．综上所述：当以A、B、P、Q为顶点的四边形是菱形时，点Q的坐标为（﹣1，8），（7，8），（3﹣，﹣2）或（3+，﹣2）．11．如图，已知C，D是反比例函数y＝图象在第一象限内的分支上的两点，直线CD分别交x轴、y轴于A，B两点，设C，D的坐标分别是（x1，y1）、（x2，y2），且x1＜x2，连接OC、OD．（1）若x1+y1＝x2+y2，求证：OC＝OD；（2）tan∠BOC＝，OC＝，求点C的坐标；（3）在（2）的条件下，若∠BOC＝∠AOD，求直线CD的解析式．（1）证明：∵C，D是反比例函数y＝图象在第一象限内的分支上的两点，∴y1＝，y2＝．∵x1+y1＝x2+y2，即x1+＝x2+，∴x1﹣x2＝．又∵x1＜x2，∴＝1，∴＝x2＝y1，＝x1＝y2．∴OC＝＝，OD＝＝，∴OC＝OD．（2）解：∵tan∠BOC＝，∴＝．又∵OC＝，∴+＝10，∴x1＝1，y1＝3或x1＝﹣1，y1＝﹣3．∵点C在第一象限，∴点C的坐标为（1，3）．（3）解：∵∠BOC＝∠AOD，∴tan∠AOD＝，∴＝．∵点C（1，3）在反比例函数y＝的图象上，∴m＝1×3＝3，∴x2•y2＝3，∴x2＝3，y2＝1或x2＝﹣3，y2＝﹣1．∵点D在第一象限，∴点D的坐标为（3，1）．设直线CD的解析式为y＝kx+b（k≠0），将C（1，3），D（3，1）代入y＝kx+b，得：，解得：，∴直线CD的解析式为y＝﹣x+4．12．如图，在平面直角坐标系中，矩形OABC的两边分别在x轴、y轴上，D是对角线的交点，若反比例函数y＝的图象经过点D，且与矩形OABC的两边AB，BC分别交于点E，F．（1）若D的坐标为（4，2）①则OA的长是8 ，AB的长是 4 ；②请判断EF是否与AC平行，井说明理由；③在x轴上是否存在一点P．使PD+PE的值最小，若存在，请求出点P的坐标及此时PD+PE的长；若不存在．请说明理由．（2）若点D的坐标为（m，n），且m＞0，n＞0，求的值．解：（1）①∵点D的坐标为（4，2），∴点B的坐标为（8，4），∴OA＝8，AB＝4．故答案为：8；4．②EF∥AC，理由如下：∵反比例函数y＝的图象经过点D（4，2），∴k＝4×2＝8．∵点B的坐标为（8，4），BC∥x轴，AB∥y轴，∴点F的坐标为（2，4），点E的坐标为（8，1），∴BF＝6，BE＝3，∴＝，＝，∴＝．∵∠ABC＝∠EBF，∴△ABC∽△EBF，∴∠BCA＝∠BFE，∴EF∥AC．③作点E关于x轴对称的点E′，连接DE′交x轴于点P，此时PD+PE的值最小，如图所示．∵点E的坐标为（8，1），∴点E′的坐标为（8，﹣1），∴DE′＝＝5．设直线DE′的解析式为y＝ax+b（a≠0），将D（4，2），E′（8，﹣1）代入y＝ax+b，得：，解得：，∴直线DE′的解析式为y＝﹣x+5．当y＝0时，﹣x+5＝0，解得：x＝，∴当点P的坐标为（，0）时，PD+PE的值最小，最小值为5．（2）∵点D的坐标为（m，n），∴点B的坐标为（2m，2n）．∵反比例函数y＝的图象经过点D（m，n），∴k＝mn，∴点F的坐标为（m，2n），点E的坐标为（2m， n），∴BF＝m，BE＝n，∴＝，＝，∴＝．又∵∠ABC＝∠EBF，∴△ABC∽△EBF，∴＝＝．13．如图，一次函数y＝kx+b（k≠0）的图象与反比例函数y＝（m≠0）的图象交于A（﹣3，1），B（1，n）两点．（1）求反比例函数和一次函数解析式；（2）结合图象直接写出不等式﹣kx﹣b＞0的解．解：（1）∵点A（﹣3，1）在反比例函数y＝（m≠0）的图象上，∴m＝（﹣3）×1＝﹣3，∴反比例函数的表达式为y＝﹣，∵点B（1，n）也在反比例函数y＝﹣的图象上，∴n＝﹣＝﹣3，即B（1，﹣3），把点A（﹣3，1），点B（1，﹣3）代入一次函数y＝kx+b中，得，解得，∴一次函数的表达式为y＝﹣x﹣2；（2）如图所示，当＞kx+b时，x的取值范围是﹣3＜x＜0或x＞1，所以不等式﹣kx﹣b＞0的解是：﹣3＜x＜0或x＞1．14．如图，在平面直角坐标系xOy内，函数y＝的图象与反比例函数y＝（k≠0）图象有公共点A，点A的坐标为（8，a），AB⊥x轴，垂足为点B．（1）求反比例函数的解析式；（2）点P在线段OB上，若AP＝BP+2，求线段OP的长；（3）点D为射线OA上一点，在（2）的条件下，若S△ODP＝S△ABO，求点D的坐标．解：（1）∵函数y＝的图象过点A（8，a），∴a＝×8＝4，∴点A的坐标为（8，4），∵反比例函数y＝（k≠0）图象过点A（8，4），∴4＝，得k＝32，∴反比例函数的解析式为y＝；（2）设BP＝b，则AP＝b+2，∵点A（8，4），AB⊥x轴于点B，∴AB＝4，∠ABP＝90°，∴b2+42＝（b+2）2，解得，b＝3，∴OP＝8﹣3＝5，即线段OP的长是5；（3）设点D的坐标为（d， d），∵点A（8，4），点B（8，0），点P（5，0），S△ODP＝S△ABO，∴，解得，d＝，∴d＝，∴点D的坐标为（，）．15．阅读理解：如图（1），在平面直角坐标系xOy中，已知点A的坐标是（1，2），点B的坐标是（3，4），过点A、点B作平行于x轴、y轴的直线相交于点C，得到Rt△ABC，由勾股定理可得，线段AB＝＝．得出结论：（1）若A点的坐标为（x1，y1），B点的坐标为（x2，y2）请你直接用A、B两点的坐标表示A、B两点间的距离；应用结论：（2）若点P在y轴上运动，试求当PA＝PB时，点P的坐标．（3）如图（2）若双曲线L1：y＝（x＞0）经过A（1，2）点，将线段OA绕点O旋转，使点A恰好落在双曲线L2：y＝﹣（x＞0）上的点D处，试求A、D两点间的距离．解：（1）∵A点的坐标为（x1，y1），B点的坐标为（x2，y2），∴根据两点间的距离公式得，AB＝；（2）设点P（0，a），∵A的坐标是（1，2），点B的坐标是（3，4），∵PA＝，PB＝，∵PA＝PB，∴＝，∴a＝5，∴P（0，5）；（3）∵双曲线L1：y＝（x＞0）经过A（1，2）点，∴OA＝，k＝1×2＝2，∴双曲线L1：y＝（x＞0），双曲线L2：y＝﹣（x＞0），设点D坐标为（m，﹣）（m＞0），∴OD＝，由旋转知，OA＝OD，∴＝，∴m＝±1或m＝±2，∵m＞0，∴m＝1或m＝2，∴D（1，﹣2）或（2，﹣1）．∵A（1，2），∴AD＝4或．。