模糊集合及其运算讲解
模糊集合及其运算讲解

1、模糊子集
定义:设U是论域,称映射
A : U [0,1],
U
~
x A( x) [0,1]
A
~
~
确定了一个U上的模糊子集 A 。映射 A 称为 A 隶属函
~
~
~
数,A( x)
~
称为 x
对
A 的隶属程度,简称隶属度。
~
模糊子集 A 由隶属函数 A 唯一确定,故认为二者
~
~
是等同的。为简单见,通常用A来表示
模糊集合及其运算
确定性
—— 经典数学
量
随机性 —— 随机数学
不确定性
模糊性 —— 模糊数学
随机性:事件本身的状态是清楚的,但是否发生
不确定 。 (事件是否发生不确定)
明天有雨,掷一枚骰子出现6点
模糊性:事件本身的状态不很分明,不在于事件
发生与否。(事件本身的状态不确定)
青年人,高个子
模糊数学也是由于实践的需要而产生的,模糊概念 (或现象)处处存在。 有时使用模糊性比使用精确性还要好 。 例如,“大胡子高个子长头发戴宽边黑色眼镜的中年 男人” 模糊数学决不是把数学变成模模糊糊的东西,它也 具有数学的共性:条理分明、一丝不苟。即使描述模 糊概念(或现象),也会描述得清清楚楚。 一般来说,随机性是一种外在因果的不确定性,
模糊矩阵的幂 A2 A A
例:
设A 0.4 0.1
0.5 0.2
0.6 , 0.3
B
0.1 0.3 0.5
0.2 0.4
, 则
0.6
A B 0.5 0.6 0.3 0.3
0.1 0.2 0.2 B A 0.3 0.3 0.3
二、模糊计算

§2.3 模糊集合的运算 2.3.1 模糊集合的基本运算 一、模糊集合并、交、补运算定义2.3.1 模糊集合的包含、相等设A ~、B ~为论域X 上的两个模糊集合,对于X 中每一个元素x ,都有)()(~~x x BAμμ≥,则称A ~包含B ~,记作B A ~~⊇。
如果B A ~~⊇,且A B ~~⊇,则说A ~与B ~相等,记作B A ~~=。
由于模糊集合是通过隶属函数来表征的,模糊集合相等也可用隶属函数来定义。
若对于X 上的所有元素x ,都有)()(~~x x BAμμ=,模糊集合A ~与B ~相等。
定义2.3.2 模糊空集设A ~为论域X 上的模糊集合,对于X 中每一个元素x ,都有0)(~=x Aμ,则称A ~为模糊空集,记作φ=A ~。
定义2.3.3 模糊集合并、交、补基本运算设A ~、B ~为论域X 上的两个模糊集合,令B A ~~ 、B A ~~ 、C A ~分别表示模糊集合A ~与B ~的并集、交集、补集,对应的隶属函数分别为B A~~ μ、B A ~~ μ、C A~μ,对于X 的任一元素x ,定义: )(V )()(B ~A ~B ~A~x x x μμμ∆ (2.3.1) )()()(B ~A~B ~A~x x x μμμΛ∆ (2.3.2)补算子 (2.3.3) 式中“V ”表示取大运算,“Λ”表示取小运算,称其为Zadeh 算子。
在此定义下,两个模糊集合的并、交实质是在做下面的运算①)](,)(max[B ~A ~B ~A~x x μμμ= 并算子 (2.3.4) )](,)(min[B ~A~B ~A~x x μμμ= 交算子 (2.3.5) 为了加深对模糊集合并、交、补基本运算的理解,现在给出模糊集合A ~和B ~,见图2.3.1(a)。
其中A ~为高斯分布,B ~为三角分布,二者的并、交运算结果如图2.3.1(b)的图2.3.1(c)所示,当然模糊集合的并、交运算可以推广到任意个模糊集合。
模糊集合及其运算(教材)
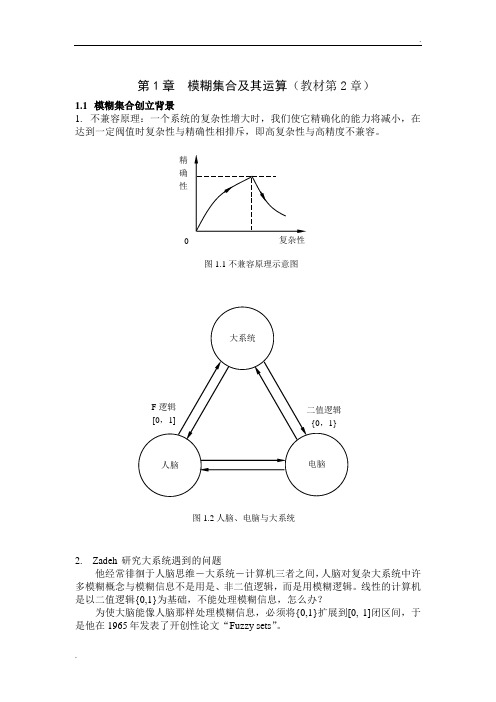
第1章 模糊集合及其运算(教材第2章)1.1 模糊集合创立背景1. 不兼容原理:一个系统的复杂性增大时,我们使它精确化的能力将减小,在达到一定阀值时复杂性与精确性相排斥,即高复杂性与高精度不兼容。
2. Zadeh 研究大系统遇到的问题他经常徘徊于人脑思维-大系统-计算机三者之间,人脑对复杂大系统中许多模糊概念与模糊信息不是用是、非二值逻辑,而是用模糊逻辑。
线性的计算机是以二值逻辑{0,1}为基础,不能处理模糊信息,怎么办?为使大脑能像人脑那样处理模糊信息,必须将{0,1}扩展到[0, 1]闭区间,于是他在1965年发表了开创性论文“Fuzzy sets ”。
0 复杂性 精 确 性图1.1不兼容原理示意图图1.2人脑、电脑与大系统举例解释模糊性与随机性两个概念的差异。
1.2 经典集合及其运算 1. 复习经典集合理论定义: 基于某种属性的、确定的、彼此可区别的事物全体。
论域: 研究对象的全体称为论域(全域、全集、空间、话题) 元素与集合之间的关系: 属于与不属于 集合之间关系: 包含与相等集合的基本运算: 并、交、补运算 集合的三种基本形式如下:定义式:A B {x |x A x B }∈∈U @或(只用符合字母)描述式:(只用文字)由属于一个集合或另一个集合的元素构成的集合称为这两个集合的并文氏图:(只用图)集合的直积(叉积,笛卡尔积):两个集合A,B 的直积:A B {(x,)|x A y B }y ∆⨯=∈∈且注意几点:(1) 序偶不能颠倒顺序(x, y )≠ (y, x), 因此A ×B ≠ B ×A ; (2) 直积可推广到n 个集合; (3) 当R 为实数集,即R={x|-∞<x < +∞},R×R={(x, y)| -∞<x<+∞,-∞<y<+∞}称R×R=R 2为二维欧氏空间。
2. 映射与关系(1) 映射f :x→y ; (2) 关系:集合X×Y 直积的一个子集R 称为X 到Y 的二元关系,简称关系; (3) 映射是关系的特例,因为f :x→y 显然{(x, y)|y=f(x)}⊂X×Y 。
模糊集合论及其应用

模糊集合论及其应用模糊集合论是一种重要的数学工具,它能够处理现实世界中的模糊、不确定和不精确的信息,具有广泛的应用前景。
本文首先介绍模糊集合论的基本概念和运算,然后探讨其在决策分析、控制理论、人工智能等领域的应用,并最后展望其未来发展方向。
一、模糊集合论的基本概念和运算1.1 模糊集合的定义在传统的集合论中,一个元素只能属于集合或不属于集合,不存在中间状态。
而在模糊集合论中,一个元素可以同时属于多个集合,并且对于不同的元素,其属于集合的程度也不同。
因此,模糊集合论将集合的概念进行了扩展,使其能够更好地描述现实世界中的不确定性和模糊性。
设X为一个非空的集合,称为全集,一个模糊集A是一个从X到[0,1]的函数,即:$$A(x):Xrightarrow[0,1]$$其中,A(x)表示元素x属于模糊集A的隶属度,取值范围为[0,1]。
当A(x)=1时,表示x完全属于A;当A(x)=0时,表示x完全不属于A;当0<A(x)<1时,表示x部分属于A。
1.2 模糊集合的运算模糊集合的运算包括模糊集合的交、并、补和乘积等。
模糊集合的交:对于两个模糊集合A和B,其交集为:$$(Acap B)(x)=min{A(x),B(x)}$$模糊集合的并:对于两个模糊集合A和B,其并集为:$$(Acup B)(x)=max{A(x),B(x)}$$模糊集合的补:对于一个模糊集合A,其补集为:$$(eg A)(x)=1-A(x)$$模糊集合的乘积:对于两个模糊集合A和B,其乘积为:$$(Atimes B)(x,y)=min{A(x),B(y)}$$其中,(A×B)(x,y)表示元素(x,y)属于模糊集合A×B的隶属度。
1.3 模糊关系和模糊逻辑在模糊集合论中,还有两个重要的概念,即模糊关系和模糊逻辑。
模糊关系是指一个元素对另一个元素的隶属度,可以用矩阵表示。
例如,设A和B是两个模糊集合,它们之间的模糊关系R可以表示为: $$R=begin{bmatrix} R_{11} & R_{12} R_{21} & R_{22}end{bmatrix}$$其中,Rij表示元素i与元素j之间的隶属度。
模糊集合之运算

0 ≤ A c ( x) ≤ 1
(4.2)
認 Fuzzy
一般常用的模糊集合之補集定義除 (4.1a) 外尚有: (1) 門檻式:
1, 當 z ≤ l c( z ) = 0, 當 z > l
(4.3)
其中 z ∈[0, 1] 及 l ∈[0, 1) , l 稱為門檻 (Threshold)
c(z) 1
(4.1b) 只是 t-基準之一種。其它之 t-基準運算定義仍有許 多。在此用 t ( p, q ) 代表 p 與 q 之 t-基準或 p ∩ q,其中 p
及 q 為某個模糊集合之歸屬函 (如 A(x),B(x) ),因此
0 ≤ p, q ≤ 1 是必然的。
10
認 Fuzzy
常用的模糊交集運算定義: 標準交集 (Standard Intersection):
p, 當 q = 1 t ( p , q ) = q , 當 p = 1 0, 其 他
(4.10)
其中 (4.7)~(4.10) 之大小關係:
( 4.10) ≤ ( 4.9) ≤ ( 4.8) ≤ ( 4.7)
其他學者提出的交集公式 page 4-7 and 4.3.
12
認 Fuzzy
4.4 模糊集 (t-反基,s-norms 或 t-conorms)
認 Fuzzy
第 四 章
模 糊 集 合 之 運 算
1
認 Fuzzy
4.1 模糊集合運算之種
三種模糊集合運算:集 (Union)、補集 (Complement)、 及交集 (Intersection)。 標準運算: A ( x ) = 1 A( x )
( A ∩ B )( x ) = min( A( x ), B ( x ))
模糊集合运算法则

模糊集合运算法则模糊集合运算法则是一种建立在模糊集合理论基础上的数学模型,它允许从集合中提取成员元素,以及使用模糊函数对多个集合之间进行运算,而且能够考虑运算结果的不确定性。
模糊集合运算法则也是一种测量数据归纳和推理的重要手段。
它的应用在很大程度上可以用于解决实际问题。
本文将介绍模糊集合运算法则的定义,以及它的几种应用。
一、模糊集合运算法则的定义模糊集合运算法则是一种建立在模糊集合理论基础上的数学模型。
它研究的是具有特定元素的及其概率的模糊集合,以及它们之间的运算关系。
模糊集合运算法则是用来描述微妙的数学关系,给出了一种以概率定义的一组模糊集合的方法,并根据这组模糊集合的特征,构造一组运算关系,以便可以进行复杂的数学运算。
模糊集合运算法则的基本思想是:在模糊集合中,不同的元素有可能出现同一概率的元素,而不同的概率可以由不同的运算关系来表示,比如可以使用集合交、并、补和差运算表示。
使用模糊集合运算法则,就可以形成概率模型,以实现集合之间的运算,其中最重要的是模糊函数。
二、模糊集合运算法则的应用(1)多属性决策分析多属性决策分析是指利用多个指标分析决策问题。
使用模糊集合运算法则可以在模糊环境下进行多属性决策分析。
利用模糊函数可以得出多个指标之间的关系,以此来帮助做出合理的决策。
(2)模糊推理模糊推理是一种以概率推断的知识表示形式,是从特定假设及概率模型中推断出结论的过程。
模糊集合运算法则可以帮助计算各种概率,并利用模糊函数计算不同概率的结果,来帮助做出合理的推断。
(3)数据归纳模糊集合运算法则还可以用于数据归纳,即通过对模糊集合中的元素进行运算,来推断出新的信息。
这种方法可以用于统计抽样,计算概率等方面,可以很好地帮助收集和分析数据,以便更好地确定最优策略。
综上所以,模糊集合运算法则是一种有效的处理模糊环境下数据的工具,可以有效地解决实际问题。
模糊集合运算法则通过模糊函数来描述和处理模糊环境,分析数据归纳和推理,以及多属性决策分析等。
模糊集合的运算以及合成

模糊集合的运算以及合成标题:模糊集合的运算与合成概述:模糊集合是一种用于处理不确定性和模糊性问题的数学工具。
它能够更好地描述现实世界中的不确定性和模糊性情况。
本文将讨论模糊集合的运算及其合成方法,并通过人类视角的叙述,使读者更好地理解和感受这一概念。
引言:在现实生活中,我们常常遇到一些模糊的问题,比如说“这个人高吗?”、“这个饭菜辣吗?”等等。
这些问题往往没有一个确定的答案,而是具有一定的不确定性。
为了更好地处理这种不确定性,人们提出了模糊集合的概念。
1. 模糊集合的运算模糊集合的运算包括交集、并集和补集。
通过这些运算,我们可以对模糊集合进行综合和分析。
1.1 交集运算交集运算是指将两个模糊集合的元素逐个比较,取其中相对较小的隶属度作为交集结果的隶属度。
例如,对于模糊集合A和B,其交集记为A∩B,其隶属度的计算公式为:μ(A∩B) = min{μA(x), μB(x)}1.2 并集运算并集运算是指将两个模糊集合的元素逐个比较,取其中相对较大的隶属度作为并集结果的隶属度。
例如,对于模糊集合A和B,其并集记为A∪B,其隶属度的计算公式为:μ(A∪B) = max{μA(x), μB(x)}1.3 补集运算补集运算是指将一个模糊集合的元素的隶属度取反,得到其补集。
例如,对于模糊集合A,其补集记为A',其隶属度的计算公式为:μ(A') = 1 - μA(x)2. 模糊集合的合成模糊集合的合成是指将多个模糊集合综合起来,得到一个新的模糊集合。
合成方法包括合取、析取和修正。
2.1 合取合成合取合成是指将多个模糊集合的隶属度进行逐个相乘,得到新的模糊集合。
例如,对于模糊集合A和B,其合取合成记为A⊗B,其隶属度的计算公式为:μ(A⊗B) = μA(x)* μB(x)2.2 析取合成析取合成是指将多个模糊集合的隶属度进行逐个相加,得到新的模糊集合。
例如,对于模糊集合A和B,其析取合成记为A⊕B,其隶属度的计算公式为:μ(A⊕B) = μA(x) + μB(x) - μA(x) * μB(x)2.3 修正合成修正合成是指将一个模糊集合的隶属度与另一个模糊集合的隶属度进行修正,得到新的模糊集合。
模糊数学第二讲 模糊集合及其运算

实际生活中有些概念并非清晰概念, 例如鲜美的食品、美丽 的景色、魁梧的身材、漂亮的服装、高个子…等等.对于这些 概念,普通集合就无能为力.
7
2014-8-15
定义1 :设U为论域,U在闭区间[0,1]上的任一映射A[0,1]称 为U上的隶属函数。 对于任意的xU,隶属函数值A(x)称为x对A的隶属度。A为论 域U上的模糊集合。
( A B) C ( A C ) ( B C )
论域:被讨论对象的全体组成的集合称为论域。
包含: AB :对于任意xA ,必有yB. 空集:若对于任意集合A,都有A,则称是任意集合A的空集.
幂集:设U是论域,U的所有子集所组成的集合称为U的幂集, 记为P(U). 例如,U={a,b,c},则
P(U)={,{a}, {b}, {c}, {a,b}, {b,c}, {a,c}, {a,b,c}}
2014-8-15
两个模糊子集的交并运算还可以推广到任意多个 模糊集合的情形。
定义3 设At F (U ), t T , T 是指标集.u U , 规定 ( ( 称
tT tT tT
At )(u ) At (u ) sup At (u );
tT tT tT
At )(u ) At (u ) inf At (u ).
A U U , A U A,
A AC A B) c Ac B c ,
2014-8-15
( A B) c Ac B c
5
特征函数
特征函数CA(u) 表示论域U中的元素u是否属于U的子集A. 若uA, 则CA(u) =1;若 uA ,则CA(u) =0. 显然,特征函数是论域U到{0,1}的一 个映射. 例如,设U自然数组成的集合,A={1,2,3},则A的特征函数为
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1、模糊子集
定义:设U是论域,称映射
A : U [0,1],
U
~
x A( x) [0,1]
A
~
~
确定了一个U上的模糊子集 A 。映射 A 称为 A 隶属函
~
~
~
数,A( x)
~
称为 x
对
A 的隶属程度,简称隶一确定,故认为二者
~
~
是等同的。为简单见,通常用A来表示
表示取大; 表示取小。
余: Ac ( x) 1 A( x),x U
例 设论域U = {x1, x2, x3, x4, x5}(商品集),在U 上定义两个模糊集: A =“商品质量好” B =“商 品质量坏”,并设
A = (0.8, 0.55, 0, 0.3, 1). B = (0.1, 0.21, 0.86, 0.6, 0). 则Ac=“商品质量不好”, Bc=“商品质量不坏”.
(4)有界和、取小算子 (,)
a b 1 (a b),a b min{a,b}
(5)有界和、乘积算子 (,)
a b 1 (a b),a b ab
(6)Einstain算子 ( , )
a b
ab
,a b
ab
1 ab
A : U {0,1} u A(u),
其中
A (u)
1, 0,
u A u A
函数 A 称为集合A的特征函数。
二、模糊集合及其运算
美国控制论专家Zadeh教授正视了经典集合描述的 “非此即彼”的清晰现象,提示了现实生活中的绝大多数 概念并非都是“非此即彼”那么简单,而概念的差异常以 中介过渡的形式出现,表现为“亦此亦彼”的模糊现象。 基于此,1965年, Zadeh教授在《Information and Control》杂志上发表了一篇开创性论文“Fuzzy Sets”, 标志着模糊数学的诞生。
A A( x) xU x
2、模糊集的运算
定义:设A,B是论域U的两个模糊子集,定义
相等: A B A( x) B( x),x U
包含: A B A( x) B( x),x U
并: ( A B)(x) A( x) B( x),x U 交: ( A B)(x) A( x) B( x),x U
1 (1 a)(1 b)
3、模糊矩阵 定义:设 R (rij )mn ,0 rij 1,称R为模糊矩阵。
当 rij 只取0或1时,称R为布尔(Boole)矩阵。 当模糊方阵 R (rij )nn的对角线上的元素 rii 都为1时, 称R为模糊自反矩阵。
(1)模糊矩阵间的关系及运算 定义:设 A (aij )mn , B (bij )mn 都是模糊矩阵,定义 相等:A B aij bij 包含:A B aij bij
A
~
和
A
~
。
“高个子”——1.80高个子,1.79可以略低于1 (99%)的程度属于高个.
模糊子集通常简称模糊集,其表示方法有: (1)Zadeh表示法
A A( x1) A( x2 ) A( xn )
x1
x2
xn
这里
A( xi xi
)
表示
xi
对模糊集A的隶属度是
A(
xi
)。
如
Ac= (0.2, 0.45, 1, 0.7, 0). Bc= (0.9, 0.79, 0.14, 0.4, 1). 可见Ac B, Bc A. 商品质量不好商品质量坏 又 A∪Ac = (0.8, 0.55, 1, 0.7, 1) U,
A∩Ac = (0.2, 0.45, 0, 0.3, 0) .
A 1 0.8 0.2 0 12 34
(2)序偶表示法 A {( x1, A( x1)),( x2, A( x2 )),,( xn , A( xn ))}
(3)向量表示法 A ( A( x1), A( x2 ),, A( xn ))
若论域U为无限集,其上的模糊集表示为:
模糊性是一种内在结构的不确定性。
一、经典集合与特征函数
集合:具有某种特定属性的对象集体。
通常用大写字母A、B、C等表示。
论域:对局限于一定范围内进行讨论的对象的全体。
通常用大写字母U、V、X、Y等表示。
论域U中的每个对象u称为U的元素。
在论域U中任意给定一个元素u及任意给定一个
经典集合A,则必有 u A或者u A ,用函数表示为:
模糊集合及其运算
确定性
—— 经典数学
量
随机性 —— 随机数学
不确定性
模糊性 —— 模糊数学
随机性:事件本身的状态是清楚的,但是否发生
不确定 。 (事件是否发生不确定)
明天有雨,掷一枚骰子出现6点
模糊性:事件本身的状态不很分明,不在于事件
发生与否。(事件本身的状态不确定)
青年人,高个子
模糊数学也是由于实践的需要而产生的,模糊概念 (或现象)处处存在。 有时使用模糊性比使用精确性还要好 。 例如,“大胡子高个子长头发戴宽边黑色眼镜的中年 男人” 模糊数学决不是把数学变成模模糊糊的东西,它也 具有数学的共性:条理分明、一丝不苟。即使描述模 糊概念(或现象),也会描述得清清楚楚。 一般来说,随机性是一种外在因果的不确定性,
模糊集合的截集
定义:设 AF ( X ) , [0,1],记 (A) ={ xX | A(x) },
称 (A) 为 A 的 截集,简记为 A 。
例取 则有
A 1 0.8 0.6 0.5 0.2 0
x1 x2
x3
x4
x5
x6
A1 {x1}, A0.8 {x1, x2}, A0.7 {x1, x2}, A0.6 {x1, x2 , x3}, A0.4 {x1, x2 , x3 , x4}, A0.2 {x1, x2 , x3 , x4 , x5} A0 X。
几个常用的算子:
(1)Zadeh算子 (,) a b max{a,b},a b min{a,b}
(2)取大、乘积算子 (,) a b max{a,b},a b ab
(3)环和、乘积算子 (ˆ ,) a ˆ b a b ab,a b ab
