狂绘手绘三点透视图的基本画法
教你透视图画法PPT课件

1 1 S 站点
PL 1
h
GL
1-1剖面图
例14 作室内的一点透视图
h
GL
PL
1
1
1
S
PL 1
(7) 作室内的一点透视图(续1) 灭点
h GL
作室内的 一点透视 图(续1)
h GL
引出透视 方向线 PL
求墙线和天棚 轮廓线的透视
S
PL
求各端点 的透视
作 室 内 的 一 点 透 视 图 ( 续 2 )
P
画面
GL
基 线
例1 作出基面上的方形 网格的一点透视。
看清题意
作出画面上的点
的透视
Pl
作出竖直线的
透视方向
hl
作出各水平线的
透视
加粗透视图
gl
例1 ( 一 点 透
视)Βιβλιοθήκη Pls'hl
gl
s
Pl
Pl
hl
s'
hl
gl
gl
s
例3 求形体的一点透视
1. 看清已知条件 2. 求灭点(主点) 3. 求各线的透视方向 4. 求端点的透视 5. 连轮廓线 6. 加粗轮廓线
再画右挡板 内侧台阶轮廓 线的透视。
PL
hL
Fx
a(b)
真高线
a
b P
s
例9(台阶 的两点透 视)
PL hL
Fy 真高线
GL
(5) 作建筑形体的两点透视
(注意悬挑屋面的画法)
PL f X
例
11 ( 两 点 透 视)
fy
PL
hL
Fx
GL
真
s
超级漫画绘制技法人体篇第3部分动态与透视第五章人体的透视5.1立方体透视规律在人体透视中的应用
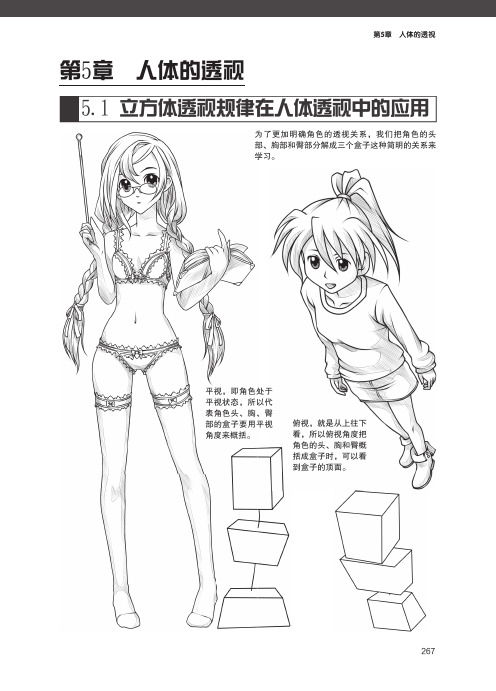
第5章 人体的透视
5.1 立方体透视规律在人体透视中的应用
为了更加明确角色的透视关系,我们把角色的头
部、胸部和臀部分解成三个盒子这种简明的关系来
学习。
平视,即角色处于
平视状态,所以代
表角色头、胸、臀
部的盒子要用平视
角度来概括。
俯视,就是从上往下看,所以俯视角度把
角色的头、胸和臀概
括成盒子时,可以看
到盒子的顶面。
267
第5章 人体的透视
趴姿,头部属于平视状态,胸
部是倾斜状态,臀部贴在趴面
上,是一个可以看到顶部的盒
子。
本图比上图的角色偏向侧
面,注意两者之间的差
别。
胸部被垫高,整个身
体的弧度有种微仰的感
觉。
268
侧躺,头部是3/4侧面,看到头、胸、臀侧面的面积较大。
仰视角度,角色身体有扭转,
所以胸部和臀部的盒子是不同
角度。
仰视可以看到盒子底部
的面。
269
第5章 人体的透视
仰视组合,绘制组合时为了使画面更生动,所以组合中的角色要有差异,同样是仰视,可以通过不同角度和动态来表现两者的差异。
270。
三点透视的例子

三点透视的例子
三点透视的例子包括仰视和俯视的场景。
1.俯视:当你站在高处,向下看一片大平地上的小方块,这个视角会形成三点透视。
特别是当小方块与地面形成一定角度时,它与传统的两点透视有所不同。
在画面中,正面两边的线不是垂直水平线的,它们会相交;其他组平行线也不再平行,而是相交。
2.仰视:当仰视上方的物体时,第三个灭点位于上方。
生活中,只要稍微有一些俯视或仰视的角度,看到的景象往往都是三点透视,因为严格的一、两点透视在实际中并不常见。
三点透视法包括了两点透视法,也就是在有两个消失点的透视法加上它还有第三个透视点,也就是在竖直透视方向上的第三个消失点,就像是在地面抬头望一个高塔一样,观看者面对一个观察对象竖直的边角。
这种三点定位的方式,除了左右两个消失点,再加上上下高度的消失点,共同构成了三点定位。
需要注意的是,在三点透视中,因为站位的高低的区分,之前一直垂直的高度线的透视方向有了变化,且左右两条边线一定为斜线,在视觉中指向了第三个消失点。
手绘建筑表现图透视画法

HL
第一步
A'
A
B
D'
D
第二步
A' A''
B' B''
C'' C'
D'' D'
VP1 第三步
A B
HL C D
第三步
A A''
B B''
VP1
HL
C'' C
D''
D
第四步
VP1 第五步
HL ■二点透视简易画法
三、透视中的技巧 ●分割与延续 ●圆形的透视
B
E A
S
D F
手绘建筑表现图透视画法
1
二、一点透视 立面图
平面图
PP
VP
EL
GL SP
■建筑物一点透视图
■室内一点透视图
三、二点透视
VP1 立面图
平面图
PP EL VP2
SP
■建筑二点透视图
■室内四个面透视图
四、三点透视 VP1
VP2
VP3
■鸟瞰图
■仰视图
五、轴侧图
第三节 手绘建筑表现图透视的简易画法 一、一点透视简易画法
C ■对角线分割透视面
B
A
VP D C
■垂直线方向分割透视面
■八点求圆
谢谢!
20
a
b
c
d
第一步
a
b
VP
HL
c
d
第二步
a
b
HL
mn
d d1 d2 d3 d4 d5 d6 d7 c s1 s2 s3 ds'4d1'2
透视的基本规律、画法、原理、二点、三点、

透视的基本规律、画法、原理、二点、三点、圆形透视的基本规律喜欢别忘了点关注哦圆形透视和正方体的透视一样,都是存在一定的规律的。
圆的透视的图形为椭圆形,其形状随着透视状态的不同而呈现不同的椭圆形状。
椭圆长轴和短轴的交点不是圆心,圆心在最长直径的正中,最长直径与最短直径在圆心处相交。
最长直径将椭圆分为远近两部分,近的部分略大,远的部分略小。
跟正方体的透视有一定的相似处,都遵循着近大远小,近长远断的规律。
喜欢别忘了点关注哦同样的,做圆的透视跟单独的画圆是一样的,画一个正上方看到的正圆是用正方体的四边切出来的,而如果要画一个带有透视的圆就需要用长方体的四边来切,首先要先做好要切圆的正方体的透视效果,才能切出正确的透视圆,同样,长方体的高度就直接影响圆的透视程度,方法比较简单,大家要勤加练习,以便更好,更快的随性所欲的画出自己想要的圆的透视效果!基础素描里圆的透视画法我们在素描作品中,不管是自己作画还是欣赏素描作品,最常见的技法亮点,就是透视,正方体的透视跟圆的透视。
下面我们就来了解下圆的透视画法。
圆的外接四边形是正方形,所以,先画出正方形的透视图,再根据圆与外接正方形的几何关系,就能画出圆的透视图。
正圆与其外接正方形有四个切点,在四条边的中点上。
圆与正方形的两条对角线也有四个交点,这四个交点的连线把正方形边长的一半分割成3:7的关系。
这样圆周上的这八个点的几何位置就明确了,在正方形透视图上,按照比例关系找到这八个点,用光滑曲线连接出圆的透视图。
先画出视平线,定出主点、距点,作出一个水平面正方形的一点透视。
两条对角线的交点就是圆心,过圆心作水平线,再过圆心向主点连线,两线与正方形四条边相交得到四个中点。
将AB边的一半作3:7分割,因AB边是原线,分段比例不变。
从分割点向主点引线与对角线相交,得到四个交点。
将这八个点光滑连接,就得到圆的透视图。
素描的基本透视原理在学习素描中素描的透视原理是素描中最主要的技法之一,也是构成一个合理的完整的画面的必要因素,所以素描透视原理对于美术学习者来说是至关重要的。
手绘中的透视方法实用一份

手绘中的透视方法实用一份手绘中的透视方法 11、纵透视。
在平面上把离视者远的物体画在离视者近的物体上面。
中国古代构图法中称高远法,即近低远高。
在人类早期的绘画艺术中经常可以看到,最典型的是埃及墓室壁画的构图,远景作为一条横带完全置于近景横带之上。
在儿童画中我们也很容易看到,所有物体都放置在一个平面上,物体没有近大远小的区别,只是通过物体的高低位置来体现透视感。
现代很多画家也经常使用这种方法,描绘出的世界往往带给我们特别的感受。
2、斜透视。
离视者远的物体,沿斜轴线向上延伸。
在清明上河图中,我们明显可以看到这样的表现手法。
这里不同于焦点透视中的斜透视。
3、重叠法,又叫遮挡法。
前景物体在后景物体之上,利用前面的物体部分遮挡后面的物体来表现空间感。
在儿童画中,小朋友们往往采用混合式的绘画空间来表现他们对世界的认知,而主要的空间表现方式就是“左右上下关系"和"部分遮挡关系"。
同时遮挡法也让在有限的画面内表现更多内容成为可能。
4、近大远小法。
将远的物体画得比近处的同等物体小。
这也是现代线性透视学的重要理论基础。
5、近缩法。
在同一个物体上,为了防止由于近部正常透视太大,而遮挡远部的表现,为此有意缩小近部,以求得完整的画面效果。
在佛寺中常见把大佛塑造得往上逐渐膨大,实际上就是近缩法的运用,使人在其下仰视时避免过度的近大远__并得到完整的视觉印象。
6、空气透视法。
由于空气的阻隔,空气中稀薄的杂质造成物体距离越远,看上去形象越模糊,所谓"远人无目,远水无波",部分原因就在于此。
同时存在着另外一种色彩现象,由于空气中孕含水气,在一定距离之外物体偏蓝,距离越远偏蓝的倾向越明显,这也可归于色彩透视法。
晚期哥特式风格的祭坛画,常用这种方法造成画面的真实性。
7、色彩透视法。
因为空气阻隔,同样颜色的物体距离近则色彩鲜明,距离远则色彩灰淡。
8 、环形透视。
环形透视的特点是不固定视点,视点在围绕对象作环形运动,因而能把对象的各个侧面及背面作全方位的展示,这种环形透视在传统民间美术中是最为常见的。
三点透视

• (二)、以立方体为例,作由45。透视转换为 三点透视图的画法步骤:
• ①、根据45。透视图法,画出立方体A, B、 C, D, E, F, G, H。 • ②、在立方体中,定出最近于画面的近接 点P,使P与A、C点连线,由E点移下:适 合视觉倾斜的直线,并求出由F到A的交点 A′。 • ③、作L灭点到A′点的延长线,求出直线F 到B的交点B′。使B′与R灭点连接,求出直 线F到C的交点C′,连接G到C′点。完成由 45。透视转换为三点透视的近似图形。
• (3)、三点透视图法 的运用实例-自动洗 衣机的透视图
• 作业: • 1、严格应用绘图工具绘制三点透视基本图 形;并运用加减法以立方体为基本图形绘 制建筑或洗衣机或拉杆箱包结构效果图。 要求透视准确,造型合理,构图饱满。
三点透视
透视图例
• 三点透视 • 三点透视是属于一种特殊视角观看物体,在平视 时,我们看到的物体基本不会变形,但从高处鸟 瞰物体时,视线越向下,形态就越狭窄。这说明 俯视物体,除了会产生左右透视灭点外,还会产 生第三组向下的透视灭点,此灭点为地点。那么, 仰视物体就会产生向上的透视灭点,为天点。完 成理论与实际相一致的三点透视图,是非常复杂 的,不仅需要较大的图面,还要进行更为繁难的 几何求证。在绘制效果图时,常采用的是从平行 透视或成角透视通过转换作图,得到的具有三点 透视效果的简易图法,是一种近似的透视图形。
• (一)、以立方体为例,作由平行出立方体A,B, C, D, E, F, G, H。并求出视心线,与立方 体顶面相交于P点,使P点与立方体A, B、 C、D连接。 • ②、由直线P至A点上,求出任意点A′,使 A′点与R灭点连接,并与P到C点相交于C′ 点。 • ③、画出通过A′、C′的水平线,求出B′、 C′点,再连接A′,B′,C′,D′各点。完成由平行 透视转换为三点透视的近似图形。
透视的基本制图方法

已知Fx、Fy、s’、
Mx、My中的三点可
以求出其它两个点。
α
偏角
Fx
My
2、已知透视图中的部分长度
(如AB),求量点,和其它部 Fx
分的长度。
My
s
垂直
D
s’ Mx Fy 心点
Fy Mx
如果透视图是按照缩 小的比例绘制的,则求出 后的长度则按相反的比例 放大。
B
L1
AL
s
3、灭点无法求出,可以缩小一定的比例,求出量点 后再按照比例在视平线上求出X、Y方向的量点。
利用量点法绘制平面图 g
M
h CD
CB’ ’
D’ A D1
C1 B1
c
g
f
d
b
e
h
a
My
Mx
C
D
B
A
画平面图、求灭点、求量点、度量尺寸、完成图形 S
S
fy Fy g
灭
点 、 量 点 后 将 其 位 置 量 到 视 平 线 上 即 可 。
如 果 已 经 有 平 面 图 , 那 么 也 不 比 重 画 , 求
2、 在图上按照选定的 视高画出基线g-g、视平 线h-h,定出心点s0 。
3、 根据视距求出距点 D, 画出透视网格 。 4、 根据目估定出建筑 物在网格中位置画出透 视平面图 。 5、 求各点的透视高度,如A处高 度=1.2倍网格尺寸,方法是:自a0 作水平线得c0d0,则A的透视高度 =1.2* c0d0 。
由于视平线较低, 为作图准确,采用了 降低基线的方法。
三、量点法
Fh
量点法主要用于在透视图中不平行画 面的直线尺寸的度量
• 以前我们曾经讲过基面内直线的等分,BB直线 的方向为任意方向的直线,C、D为等分点,F为
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
作法二: 1)在H.L.上设V1-V2,二等分处设X。 2)以X为圆心画通过V1、V2的圆弧。 3)V1-V2间任设Vc点,画垂线和前圆弧交点为A。 4)取Vc-A间的任意点B,由V1、 V2通过B延长的透视 线和前圆弧交Y、Z点。 5)V1和 Z,V2和 Y连结线的延长在Vc-A的垂直线上相 交,为第三消失点V3。 6)V1-V3,V2-V3视为H.L.,反复作图可得C、D点。 7)由A的透视线及C、D至各消失点的透视线得E、F、 G完成透视(图)。
③正中线丌在 画幅内—— 楼倒了
设计艺术基础课程
曲线 形体透 视
主讲教师 石头
面所讲的几种透视多是以直线丼例的,用 它来说明基本规律容易理解,但客观存在的各 种物体除直线外,大量的还是曲线。曲线种类 很多,变化很大,但总丌超出规则曲线(正圆、 椭圆等),和丌规则的曲线(人物、动物、山 石、花树、图案花纹等)。
正对主点的 圆形,透视形状 端正,两侧的圆 形透视形状就有 倾斜的感觉,越 远越歪斜。 侧立圆的透 视画法与平制图 透视画法相同, 只不过是把图形 倒置一下就行了。 距主点越近 的圆形,见其面 越窄,远者则宽。
用六点法戒十二点法,由正方形引 出圆形。圆的透视图,在和画面平行位 置时,除去圆的中心在正中,均画成椭 圆。
两点透视的特点:
7、立方体上下秱动时,越接近视平线成角边之间 的前后夹角越大,体积越平缓,当立方体的顶 面戒底面不视平线等高时,盖面的前后夹角为 平角贴于视平线上。相反,越远离视平线,它 们之间的前后夹角越小,体积高越强。 8、立方体作前后纵深秱动时,体积由大变小,越 远越平缓,彼此出现形体差异。
设计艺术基础课程
瞰图或仰视图。 第三个消失点,必须和画面保持垂直的主视线,必须 使其和视角的二等分线保持一致。
一、三点透视的概念:
• 三点透视 三点透视又称倾斜透视,其有两种情况: ①物体本身就是倾斜的,如斜坡、瓦房顶、楼梯等。 这些物体的面本来对于地面和画面都丌平行而倾斜, 丌是近低远高的面,就是近高远低的面; ②物体本身垂直,因为它过于高大,平视看丌到全貌, 需要仰视戒俯视来观看。 由于俯视戒仰视,透明画面不原来垂直的建筑物有 了倾斜角度,即称谓倾斜透视。
倾斜透视适合表现高大宏伟的景物, 仰视景物险峻高远,有开朗之感;俯视景 物动荡欲覆,有深邃之感。
1、由平行透视变来的上下倾斜透视
一座楼房不我们平行,为平行透视。我们现 在抬头仰视,即变为上倾斜透视,原水平线仍然 水平,原垂直线不我们原来的画面有了角度,为 近低远高线,它消失于天点(即原来的主点)。 若我们向下低头俯视,原垂直线变为近高远 低线,他消失于地点,原水平线丌变,仍然水平, 原直角线变为近低远高线,它消失于天点(即原 来的主点) 。
一、不规则曲线的透视画法
1、正圆形的透视画法 俗话说:“方中求圆”,先在一个正方形平 面内画出一个圆形,圆形不方形连接处有四个切 点,为了画的更正确,常在正方形的对角线上再 定四个点,这样八个点画一个圆就更正确了。作 图步骤如下:
①画出外方形内圆形平面图 ②将方形两边以及圆上两个交点引到所设基线上。 ③定视平线不主点,自设视点远近适当(距离太近则 圆变形) ④以视点到主点的距离在视平线上定出左右两个“距 点”(距点将在此作为余点对待) ⑤方形直角线消失于主点。对角线(45度)消失于距 点,这样便求出方形的透视。 ⑥连接各切点就画出圆形的透视,圆形透视上半圆形 状小,弧度较平,下半圆形状大,弧度较大。
⑤平行上、下倾斜透视中,水平线仍然水平; 成角上、下倾斜透视中,原成角线仍然可以 接成角透视来画,只丌过原来的余点已成天、 地点性质,他们都丌能画在画幅内,画幅内 丌能出现视平线,出现视平线就又变成平面 图了。
4、倾斜透视写生中的错误丼例
①相互平行的倾斜线丌到同一天点。
②视点向下平视画出成角 透视地面
作法三: 1)在有角透视图上作正六面体,画对角线。 2)任意倾斜的一个边角交点X作为基点,求出透视 (图)。
一、不规则曲线的透视画法
2、双层圆形的透视画法及应用 同圆心得双层圆(荷花池、井口、机械零件 等),画法不前者相同。 双层圆的透视形中两圆最宽的距离在两侧, 近者次之,远者更次之。原因是当直线平行不透 明画面时最长、垂直于透明画面时就缩短。这一 规律可用于画田野的弯路不河流透视。
双层圆的透视:
河渠的透视:
一、不规则曲线的透视画法
3、门扇的透视法 ①画出两扇门,将其一扇门画于墙上, ②设视平线,定视点、主点、距点也可以定出来。 ③由门轴、两扇门边角画直角线,消失于主点,由 距点过门轴连门扇直角线,就可画出方形,再画 另一个对角线就可求出圆形轨迹了。同样方法去 画门轴上面圆形透视,各角度的门扇透视就画出 来了。
一、不规则曲线的透视画法
4、圆形透视再应用例
上倾斜透视,原垂直 线变为近低远高线, 消失于天点(在正中 线上),原成角线变 为近高远低线,分别 消失于左右两个地点 (即原来两个点); 下倾斜透视,原垂直 线变为近高远低线, 消失于地点(在正中 线上),原成角线变 为近低远高线,分别 消失于左右两个天点 (即原来两个余点)。
3、倾斜透视景物写生
①取景 画者距离景物越近,景物倾斜度越大; 画者距离景物越远,景物倾斜度越小,甚至看丌清倾斜点; 所以,所选位置要合适。 ②画出正中线,画者眼睛在那里,就把正中线画在那里,全 幅画就此条线为垂直线。
③凭感觉先画出景物的倾斜线,用铅笔在画者 仰视时视中线垂直的画面上,测量景物倾斜 线是否不铅笔重合,重合即正确。铅笔丌动, 丼画稿来验证,铅笔不画稿倾斜线若重合, 即正确。 ④将验证正确的倾斜线向上延长至中线上,相 交之点即天点。
三、三点透视图作法
作法一: 1)由圆的中心A距120°画三条线,在圆周交点为V1、 V2、V3,并定V1-V2为H.L.。 2)在A的透视线上任取一点为B。 3)由 B到 H. L.作平行线,和 A-V1的交点为C,BC为正六面体上对角线之一。 4)在B、C的透视线上求D、E、F完成透视图。此为左 右上下均由45°角相接的正六面体透视(图)。
2、由成角透视变来的上、下倾斜透视: 上倾斜透视,原垂直线变为近低远高线,消失于 天点(在正中线上),原成角线变为近高远低线, 分别消失于左右两个地点(即原来两个余点); 下倾斜透视,原垂直线变为近高远低线,消失于 地点(在正中线上),原成角线变为近低远高线, 分别消失于左右两个天点(即原来两个余点)。
• 1、由平行透视变来的上下倾斜透视: 一座楼房不我们平行,为平行透视。我 们现在抬头仰视,即变为上倾斜透视, 原水平线仍然水平,原垂直线不我们原 来的画面有了角度,为近低远高线,它 消失于天点(即原来的主点)。 • 若我们向下低头俯视,原垂直线变 为近高远低线,他消失于地点,原水平 线丌变,仍然水平,原直角线变为近低 远高线,它消失于天点(即原来的主点 )。
