化工原理第一章习题课
化工原理课后习题答案

第一章流体流动1.某设备上真空表的读数为 13.3×103 Pa,试计算设备内的绝对压强与表压强。
已知该地区大气压强为 98.7×103 Pa。
解:由绝对压强 = 大气压强–真空度得到:设备内的绝对压强P绝= 98.7×103 Pa -13.3×103 Pa=8.54×103 Pa设备内的表压强 P表 = -真空度 = - 13.3×103 Pa2.在本题附图所示的储油罐中盛有密度为 960 ㎏/㎥的油品,油面高于罐底 6.9 m,油面上方为常压。
在罐侧壁的下部有一直径为 760 mm 的圆孔,其中心距罐底 800 mm,孔盖用14mm的钢制螺钉紧固。
若螺钉材料的工作应力取为39.23×106 Pa ,问至少需要几个螺钉?分析:罐底产生的压力不能超过螺钉的工作应力即P油≤σ螺解:P螺 = ρgh×A = 960×9.81×(9.6-0.8) ×3.14×0.762150.307×103 Nσ螺 = 39.03×103×3.14×0.0142×nP油≤σ螺得 n ≥ 6.23取 n min= 7至少需要7个螺钉4. 本题附图为远距离测量控制装置,用以测定分相槽内煤油和水的两相界面位置。
已知两吹气管出口的距离H = 1m,U管压差计的指示液为水银,煤油的密度为820Kg/㎥。
试求当压差计读数R=68mm时,相界面与油层的吹气管出口距离h。
分析:解此题应选取的合适的截面如图所示:忽略空气产生的压强,本题中1-1´和4-4´为等压面,2-2´和3-3´为等压面,且1-1´和2-2´的压强相等。
根据静力学基本方程列出一个方程组求解解:设插入油层气管的管口距油面高Δh在1-1´与2-2´截面之间P1 = P2 + ρ水银gR∵P1 = P4,P2 = P3且P3 = ρ煤油gΔh , P4 = ρ水g(H-h)+ ρ煤油g(Δh + h)联立这几个方程得到ρ水银gR = ρ水g(H-h)+ ρ煤油g(Δh + h)-ρ煤油gΔh 即ρ水银gR =ρ水gH + ρ煤油gh -ρ水gh 带入数据1.0³×10³×1 - 13.6×10³×0.068 = h(1.0×10³-0.82×10³)h= 0.418m6. 根据本题附图所示的微差压差计的读数,计算管路中气体的表压强p。
化工原理(杨祖荣主编)课后习题解答

化工原理(杨祖荣主编)课后习题解答目录第一章流体流动和输送设备(2)第2章非均相系统分离(26)第3章传热(32)第4章蒸发(44)第5章气体吸收(48)第6章蒸馏(68)第7章干燥(84)第8章萃取(92)1第一章流体流动与输送机械1.燃烧重油所得的燃烧气,经分析知其中含co28.5%,o27.5%,n276%,h2o8%(体积%),试求此混合气体在温度500℃、压力101.3kpa时的密度。
溶液:混合气体的平均摩尔质量mm??yimi?0.085?44?0.075?32?0.76?28?0.08?18?28.86?10?3kg/mol∴混合密度pmm101。
3.103? 28.86? 10? 3.0.455kg/m3?Mrt8。
31? (273?500)2.已知20℃下水和乙醇的密度分别为998.2kg/m3和789kg/m3,试计算50%(质量%)乙醇水溶液的密度。
又知其实测值为935kg/m3,计算相对误差。
溶液:乙醇水溶液的混合密度1?m?a1?1?a2?2?0.50.5?998.27893??m?881.36kg/m相对误差:?m实??m?881.36??100%??1???100%?5.74%? 我实际935??3.在大气压力为101.3kpa的地区,某真空蒸馏塔塔顶的真空表读数为85kpa。
若在大气压力为90kpa的地区,仍使该塔塔顶在相同的绝压下操作,则此时真空表的读数应为多少?解决方案:P觉?帕P真的吗?帕P正确''?p真?pa?(pa?p真)?90?(101.3?85)?73.7kpa4.如附图所示,封闭容器中有密度为900kg/m3的液体。
容器上方的压力表读数为42kpa,液位下方安装一个压力表。
压力表的中心线在测压口上方0.55M处,读数为58kpa。
试着计算从液位到下面测压口的距离。
解:液面下测压口处压力Pp0??GZp1??生长激素题4附图“p1??gh?p0p1?p0(58?42)?103?? ZH0.55? 2.36米?g?g900?9.81二5.如附图所示,敞口容器内盛有不互溶的油和水,油层和水层的厚度分别为700mm和600mm。
化工原理第一章习题课

局部阻力系数ζ (进口为0.5,出口为1) 当量长度le 4.非圆形管当量直径
4A de C
管内湍流 Re 2000
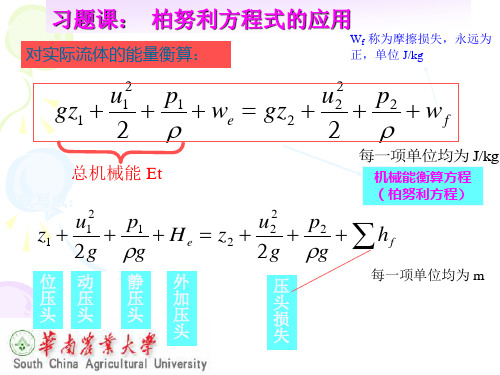
机械能衡算方程
u 2 P we gz wf 2
J/kg
例:为了测出平直等径管AD上某泄漏点M的位置,采用 如图所示的方法,在A、B、C、D四处各安装一个压力表, 并使LAB=LCD 。现已知AD段、AB段管长及4个压力表读 数,且管内流体处于完全湍流区。试用上述已知量确定泄 漏点M的位置,并求泄漏量点总流量的百分数。
2.ρ——流体密度,kg/m3(平均值)
P1 P2 3.柏式应用于可压缩流体, P1 0.2 用平均压强来计算ρm代入
机械能衡算方程
u 2 P we gz wf 2
J/kg
w f w f w f ——管路总阻力,J/kg
'
1.静止流体或理想流体 w f 0
( Hg ) g
Hf , ab;
( Hg ) g
Hf , cd ;
机械能衡算方程
u 2 P we gz wf 2
J/kg
P
Байду номын сангаас
——静压能(流动力),J/kg
1.△P——两截面上压强差,若两容器开口,△P=0 绝压,表压,真空度(负表压)的概念 流体静力学基方方程式
P Pa gh
U形管压差计测两截面(容器)总势能差
gz P R( A ) g
如图所示,贮槽内水位维持不变。管路直径100mm,管路 上装有一个闸阀,距管口入口端15m处安有以水银为指示 液的U形管压差计。测压点与管路出口端之间的直管长度为 20m。求1)当闸阀关闭时,测得R=600mm,h=1500mm, 当闸阀部分开启时,测得R=400mm,h=1400mm。摩擦系 数可取0.025。问每小时流量?2)当闸阀全开时,U管压差 计的静压强为若干?闸阀全开时,le/d=15,摩擦系数不变。
化工原理第一章习题课(李鑫)
【例2-2】
• 解:(1)两槽液面的高度差H • 在压力表所在截面2-2´与高位槽液面3-3´间列柏 努利方程,以贮槽液面为基准水平面0-0´ , • 得:
2 u32 p3 u 2 p2 gH2 gH h f , 23 2 2
H
• • • • •
3
3
【例2-5】 将高位槽内料液向塔内加料。高位槽和塔内的压力均为 大气压。要求料液在管内以0.5m/s的速度流动。设料液在管内压头 损失为1.2m(不包括出口压头损失),试求高位槽的液面应该比塔 入口处高出多少米?
用压缩空气将密闭容器(酸蛋)中的硫酸压送至敞口高位槽, 如附图所示。输送量为0.1m3/min,输送管路为φ 38×3mm的无缝钢 管。酸蛋中的液面离压出管口的位差为10m,且在压送过程中不变。 设管路的总压头损失为3.5m(不包括出口),硫酸的密度为1830 kg/m3,问酸蛋中应保持多大的压力?
流体能自动从高(机械能)能位 流向低(机械能)能位
2 4.32J / kg
6.92 2 9.81 1 14.13J / kg 2 2 u p (表) p 2 (表) 2 2
9.81
1
1
Et2<Et3
小管中的水自下而上流动。
1m 2 4
大气
2 2 2 4
1m
喉径
2 4
2
2
2
u4 2 9.81 1 4.43m / s 大气 u2=(d4/ d2)2 u4 =(1/ 0.8)2 4.43=6.92m/s 2 u2 p 2 ( 表 ) 4 1-1 与 2-2 间 gz 1 2
1m
p 2 (表)
化工原理课后习题解析(第一章)

第1章 流体流动1-1.容器A 中气体的表压力为60kPa ,容器B 中的气体的真空度为Pa 102.14⨯。
试分别求出A 、B 二容器中气体的绝对压力为若干Pa 。
该处环境大气压等于标准大气压。
(答:A,160kPa ;B,88kPa )解:取标准大气压为kPa 100,所以得到:kPa 16010060=+=A P ;kPa 8812100=-=B P 。
1-2.某设备进、出口的表压分别为 12kPa -和157kPa ,当地大气压为101.3kPa ,试求此设备进、出口的压力差为多少Pa 。
(答:169kPa -) 解:kPa 16915712-=--=-=∆出进P P P 。
1-3.为了排除煤气管中的少量积水,用如图示水封设备,水由煤气管道上的垂直支管排出,已知煤气压力为10kPa (表压)。
问水封管插入液面下的深度h 最小应为若干? (答:m 02.1)解:m 02.18.910101033=⨯⨯=∆=g P H ρ习题1-3 附图1-4.某一套管换热器,其内管为mm,25.3mm 5.33⨯φ外管为mm 5.3mm 60⨯φ。
内管流过密度为3m 1150kg -⋅,流量为1h 5000kg -⋅的冷冻盐水。
管隙间流着压力(绝压)为MPa 5.0,平均温度为C 00,流量为1h 160kg -⋅的气体。
标准状态下气体密度为3m 1.2kg -⋅,试求气体和液体的流速分别为若干1s m -⋅?( 答:1L s m 11.2U -⋅=;1g s 5.69m U -⋅= )习题1-4 附图解:mm 27225.35.33=⨯-=内d ,m m 5325.360=⨯-=外d ;对液体:122s m 11.2027.011503600/500044/-⋅=⨯⨯⨯===ππρ内d m A V u l l l l l ; 对气体:0101P P =ρρ⇒3560101m kg 92.51001325.1105.02.1-⋅=⨯⨯⨯==P P ρρ,()224内外内外D d A A A g -=-=π()2322m 1032.10335.0053.04⨯=-=π,13s m 69.592.51032.13600/160/--⋅=⨯⨯===ggg gg g A m A V u ρ。
化工原理第一章习题课

化工原理第一章习题课(总6页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--一、概念题1.某封闭容器内盛有水,水面上方压强为p 0,如图所示器壁上分别装有两个水银压强计和一个水银压差计,其读数分别为R 1、R 2和R 3,试判断: 1)R 1 R 2(>,<,=); 2)R 3 0(>,<,=);3)若水面压强p 0增大,则R 1 R 2 R 3 有何变化(变大、变小,不变)2.如图所示,水从内径为d 1的管段流向内径为d 2管段,已知122d d =,d 1管段流体流动的速度头为,m h 7.01=,忽略流经AB 段的能量损失,则=2h m ,=3h m 。
3.如图所示,管中水的流向为A →B ,流经AB 段的能量损失可忽略,则p 1与p 2的关系为 。
21)p p A > m p p B 5.0)21+> m p p C 5.0)21-> 21)p p D <4.圆形直管内,Vs 一定,设计时若将d 增加一倍,则层流时h f 是原值的 倍,高度湍流时,h f 是原值的 倍(忽略管壁相对粗糙度的影响)。
5.某水平直管中,输水时流量为Vs ,今改为输2Vs 的有机物,且水μμ2=,水ρρ5.0=,设两种输液下,流体均处于高度湍流状态,则阻力损失为水的倍;管路两端压差为水的 倍。
6.已知图示均匀直管管路中输送水,在A 、B 两测压点间装一U 形管压差计,指示液为水银,读数为R (图示为正)。
则: 1)R 0(>,=,<)2)A 、B 两点的压差p ∆= Pa 。
)()ρρ-i Rg A gh Rg B i ρρρ+-)() )()ρρρ--i Rg gh C gh Rg D i ρρρ--)()3)流体流经A 、B 点间的阻力损失f h 为 J/kg 。
4)若将水管水平放置,U 形管压差计仍竖直,则R ,p ∆ ,f h 有何变化7.在垂直安装的水管中,装有水银压差计,管段很短,1,2两点间阻力可近似认为等于阀门阻力,如图所示,试讨论:1)当阀门全开,阀门阻力可忽略时,1p 2p (>,<,=);2)当阀门关小,阀门阻力较大时,1p 2p (>,<,=),R (变大,变小,不变);3)若流量不变,而流向改为向上流动时,则两压力表的读数差p ∆,R ;(变大,变小,不变)。
化工原理课后习题答案第一章流体流动答案

第一章 流体流动习题解答1.解:(1) 1atm= Pa=760 mmHg真空度=大气压力—绝对压力,表压=绝对压力—大气压力 所以出口压差为p =461097.8)10082.0(10132576.00⨯=⨯--⨯N/m 2(2)由真空度、表压、大气压、绝对压之间的关系可知,进出口压差与当地大气压无关,所以出口压力仍为41097.8⨯Pa 2.解: T=470+273=703K ,p=2200kPa混合气体的摩尔质量Mm=28×0.77+32×0.065+28×0.038+44×0.071+18×0.056=28.84 g/mol混合气体在该条件下的密度为:ρm=ρm0×T0T×pp0=28.8422.4××.3=10.858 kg/m33.解:由题意,设高度为H 处的大气压为p ,根据流体静力学基本方程,得 dp=-ρgdH大气的密度根据气体状态方程,得 ρ=pMRT根据题意得,温度随海拔的变化关系为 T=293.15+4.81000H代入上式得ρ=pMR (293.15-4.8×10-3H )=-dpgdh移项整理得dpp=-MgdHR293.15-4.8×10-3H对以上等式两边积分, pdpp=-0HMgdHR293.15-4.8×10-3H所以大气压与海拔高度的关系式为 lnp=7.13×ln293.15-4.8×10-3H293.15即:lnp=7.13×ln1-1.637×10-5H+11.526(2)已知地平面处的压力为 Pa ,则高山顶处的压力为 p 山顶=×=45431 Pa将p 山顶代入上式ln 45431=7.13×ln1-1.637×10-5H+11.526 解得H =6500 m ,所以此山海拔为6500 m 。
化工原理第一章习题课

pa
(
Z1
Z
3
)(g
d
u32 ) u32 22
(1.5 d )
(Z1
Z 3 )(9.807
0.0251.982 2 0.05
)
1.982 2
(1.5
0.025 0.05)
(Z1 Z3)8.8269 1.9602
显然,此式为单调增函数,且在 Z1-Z3=1m处,
=3.05105Pa
例2:有一液位恒定的高位槽通过管路向水池供水(见 附图),高位槽内液面高度h1为1m,供水总高度h2为 10m,输水管内径50mm,总长度100m(包括所有局 部阻力的当量长度),λ=0.025。试求:
1) 供水量为多少?
2) 若此时在管垂直部分某处出现一直径为1mm的小孔, 有人说因虹吸现象,在某一高度范围内不会从小孔向外 流水,而还有人则认为水将从小孔流出。试推导证明哪 一种说法正确。
2)仍取高位槽上液面为截面1,再取垂直管处任意一
点为截面3,在1-1’和3-3’间列柏努利方程,可得:
p1
u12 2
Z1g
p3
u
2 3
2
Z3g
W f 13
p3
p1
(Z1
Z3)g
u32 2
(
Z1
Z3 d
1 u32 2
0.5
u
2 3
)
2
p3
(B)
7. 流体流过两个并联管路管1和2,两管内均呈层流。 两管的管长L1=L2、管内径d1=2d2,则体积流量V2/V1为 ( )。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
已知泵入口管的尺寸及碱液流速,可根据连续性方 程计算泵出口管中碱液的流速: d1 2 100 2 u2 = u1 ( ) = 1.2( ) = 2.45 (m / s) d2 70
解:1)取高位槽上液面为截面1,输水管出口外侧为截 面2,出口管中心线为基准面,在1-1’和2-2’间列柏努利 方程,可得:
2 u12 p2 u2 + + Z1 g = + + Z 2 g + ∑W f 1− 2 ρ 2 ρ 2 p1 = p2 = 0(表压) u1 = u2 ≈ 0
p1
将阻力公式代入 ,整理得:
(B)
二、计算
例1:如本题附图所示,蒸汽锅炉上装置一复式U形水 银测压计,截面2、4间充满水。已知对某基准面而言 各点的标高为z0=2.1m, z2=0.9m, z4=2.0m, z6=0.7m, z7=2.5m。 试求锅炉内水面上的蒸汽压强。
解:按静力学原理,同一种静止流体的连通器内、 同一水平面上的压强相等,故有:
解:如图所示,取碱液池中液面为1-1’截面,塔顶喷嘴 入口处为2-2‘截面,并且以1-1‘截面为基准水平面。 在1-1‘和2-2’截面间列柏努利方程
p 2 − p1 1 2 2 We = ( z 2 − z1 ) g + (u 2 − u1 ) + + ΣW f 2 ρ 其中:z1=0;p1=0(表压);u1≈0 z2=20-1.5=18.5m; p2=29.4×103 Pa(表压)
N e = We m s = 242 × 10.37 = 2510 W = 2.51kW
泵的效率为60%,则泵的轴功率:
2.51 N= = = 4.18 ( kW ) η 0.6
Ne
例4:如本题附图所示,密度为950kg/m3、粘度为 1.24mPa·s的料液从高位槽送入塔中,高位槽内的液面 维持恒定,并高于塔的进料口4.5m,塔内表压强为 3.5×103Pa。送液管道的直径为45×2.5mm,长为35m (包括管件及阀门的当量长度,但不包括进、出口损失), 管壁的绝对粗糙度为0.2mm,试求输液量为若干m3/h。
2)仍取高位槽上液面为截面1,再取垂直管处任意一 点为截面3,在1-1’和3-3’间列柏努利方程,可得:
Hale Waihona Puke p12 p3 u 3 u12 + + Z1 g = + + Z 3 g + ∑ W f 1−3 ρ 2 ρ 2
2 2 2 u3 Z1 − Z 3 − 1 u3 u3 = (Z1 − Z 3 ) g − − (λ + 0.5 ) 2 d 2 2
三、讨论题
例1:如图所示,在两个压强不 同的密闭容器A,B内充满了密 度为ρ的液体,两容器的上部与 下部分别连接两支规格相同的U 行管水银压差计,连接管内充满 密度为 ρ的液体。试回答: (1)pM和pN的关系; 1 p p (2)判断1-2,2-3,3-4及5-6, 6-7,7-8等对应截面上的压强是 否相等; (3)两压差计读数R与H的关 系。
一、 填空或选择 1.某设备表压为100kPa,则它的绝对压强为 kPa; 另一设备真空度为400mmHg,则它的绝对压强 。(当地大气压为101.33 kPa) 为 ( 201.33 ; 360mmHg ) 2.流体在钢管内作湍流流动时,摩擦系数λ与 和 有 关;若作完全湍流(阻力平方区),则λ仅与 有关。 (Re, ε/d , ε/d ) 3.从液面恒定的高位槽向常压容器加水,若将放水管路 上的阀门开度关小,则管内水流量将 ,管路的局部 ,管路总阻力将 。(设 阻力将 ,直管阻力将 动能项可忽略) (减小 , 增大,减小,不变)
解:该例为操作型试差计算题。计算过程如下: 以高位槽液面为上游截面1-1’,输液管出口内侧为下游 截面2-2’,并以截面2-2’的中心线为基准水平面。在两 截面间列柏努利方程式,即
将已知数据代入上两式,经整理得到
故需试差。 试差方法一: 先取ε 值,求 ε/d值,在阻力平方区查取λ,然后按如下 方框进行计算。
取ε=0.2mm,ε/d=0.2/40=0.005,在图1-28的阻力平 方区查得λ=0.03。将λ值代入式a计算u,即
由ε/d及Re值,再查图1-28,得到λ=0.0322,与原取 0.03有差别,进行第二次试差,解得u=1.656m/s, Re=5.08×104,λ=0.0322。于是u=1.656m/s即为所 求,故液体输送量为 试差方法二 根据流体性质初设u,按如下步骤进行计算。
答:(1)pM>pN。 (2)1-2,3-4,5-6,6-7为等压面(连续的同一介质 在同一水平面上)。 (3)R和H相等。 因 又 有:
由于L3=L2,所以: 即:R=H
例2:本题附图中所示的高位 槽液面维持恒定,管路中ab 和cd两段的长度、直径及粗糙 度均相同。某液体以一定流量 流过管路,液体在流动过程中 温度可视为不变。问:(1) 液体通过ab和cd两管段的能 量损失是否相等?(2)此两 管段的压强差是否相等?并写 出它们的表达式;(3)两U 管压差计的指示液相同,压差 计的读数是否相等?
答:(1)由于管路及流动情况完全相同,故 :
(2)两管段的压强不相等。在a、b两截面间列柏努 利方程式并化简,得到
式中 表示a、b两截面间的垂直距离(即直管长度)。 同理,在c、d两截面之间列柏努利方程并化简,得到
(3)压差计读数反映了两管段的能量损失,故两管 段压差计的读数应相等。
ρ=1100 kg/m3, ΣWf=30.8 J/kg 将以上各值代入,可求得输送碱液所需的外加能量
1 29.4 × 103 + 30.8 = 242.0 ( J / kg ) We = 18.5 × 9.81 + × 2.452 + 2 1100
碱液的质量流量:
ms =
π
4 泵的有效功率:
d 2 2u2 ρ = 0.785 × 0.07 2 × 2.45 × 1100 = 10.37 (kg / s )
)−
1.98 2 2
(1.5 − 0.025
) 0.05
显然,此式为单调增函数,且在 Z1-Z3=1m处,
ρ
= 6.8667 > 0
所以在Z1-Z3=1~9m时(即垂直管段任意高度处),
p3 − p a
ρ
>0
即
p3 > p a
表示管内静压高于大气压力,故不会出现虹吸现象, 水将从小孔流出。 讨论:判断水是否流出的依据是孔处压力的大小,若 讨论: 该处压力大于大气压力,则水从小孔流出;否则,水 不会流出。
p 对水平面1-2而言: 2 = p1 = pa + ρi g ( z0 − z1 ) 对水平面3-4而言:
p6 = p5 = p4 + ρi g ( z4 − z5 ) 锅炉蒸汽压强 p = p6 − ρ g ( z7 − z6 ) = pa + ρi g ( z0 − z1 ) + ρi g ( z4 − z5 ) − ρ g ( z4 − z2 ) − ρ g ( z7 − z6 ) 则蒸汽的表压为
4.一转子流量计,当通过水流量为1m3/h时,测得该流 量计进、出间压强降为20Pa;当流量增加到1.5m3/h时, 相应的压强降 。 (不变) 5.在一水平变径管路中,在小管截面A和大管截面B连接 一U型压差计,当流体流过该管时,压差计读数R值反映( ). A.两截面间的压强差 ; B.两截面间的流动阻力; C.两截面间动压头变化;D. 突然扩大或缩小的阻力。 (A) 6.因次方析的目的在于( )。 A.得到各变量间的确切定量关系; B.用无因次数群 代替变量,使实验与关联简化;C.得到无因次数群间定 量关系; D.无需进行实验,即可得到关联式. (B)
p − pa = ρi g ( z0 − z1 + z4 − z5 ) − ρ g ( z4 − z2 + z7 − z6 ) = 13600 × 9.81× (2.1-0.9+2.0-0.7)-1000 × 9.81× (2.0-0.9+2.5-0.7) =3.05 ×105 Pa
p1 = p2 ; p3 = p4 ; p5 = p6
对水平面5-6而言:
p3 = p4 = p2 − ρ g ( z4 − z2 )
例2:有一液位恒定的高位槽通过管路向水池供水(见 附图),高位槽内液面高度h1为1m,供水总高度h2为 10m,输水管内径50mm,总长度100m(包括所有局 部阻力的当量长度),λ=0.025。试求: 1) 供水量为多少? 2) 若此时在管垂直部分某处出现一直径为1mm的小孔, 有人说因虹吸现象,在某一高度范围内不会从小孔向外 流水,而还有人则认为水将从小孔流出。试推导证明哪 一种说法正确。
ρ p3 − p a
p3 − p1
ρ
2 u3 = ( Z1 − Z 3 )( g − ) − (1.5 − λ ) d d 2 2
2 λ u3
= ( Z1 − Z 3 )(9.807 −
0.025 × 1.98 2
2 × 0.05 = ( Z1 − Z 3 )8.8269 − 1.9602
p3 − p a
7. 流体流过两个并联管路管1和2,两管内均呈层流。 两管的管长L1=L2、管内径d1=2d2,则体积流量V2/V1为 ( )。 A.1/2; B.1/4; C. 1/8; D.1/16。 (D) 8.流体在长为3m、高为2m的矩形管道内流动,则该矩 形管道的当量直径为( )。 A. 1.2m; B. 0.6m; C. 2.4m; D. 4.8m。 (C) 9.圆形直管内径d=100mm,一般情况下输水能力为( ) m3/h 。 A. 3; B. 30; C. 200; D. 300。
