高中数学反比例与三角函数
高中数学概念公式大全

高中数学概念公式大全1.代数与函数:- 一次函数的方程:y = kx + b- 二次函数的方程:y = ax² + bx + c- 三次函数的方程:y = ax³ + bx² + cx + d-指数函数的方程:y=a^x- 对数函数的方程:y = logₐ(x)-幂函数的方程:y=x^a-绝对值函数的方程:y=,x- 正弦函数的方程:y = A sin(Bx + C) + D- 余弦函数的方程:y = A cos(Bx + C) + D-反比例函数的方程:y=k/x2.平面解析几何:-直线的一般式方程:Ax+By+C=0- 直线的斜截式方程:y = kx + b-直线的点斜式方程:y-y₁=k(x-x₁)-直线的两点式方程:(y-y₁)/(y₂-y₁)=(x-x₁)/(x₂-x₁) -圆的标准方程:(x-h)²+(y-k)²=r²-椭圆的标准方程:(x-h)²/a²+(y-k)²/b²=1-双曲线的标准方程:(x-h)²/a²-(y-k)²/b²=1- 抛物线的标准方程:y = ax² + bx + c-平行线的判定:两直线的斜率相等-垂直线的判定:两直线的斜率的乘积为-13.空间解析几何:- 空间直线的参数方程:x = x₁ + at, y = y₁ + bt, z = z₁ + ct -空间直线的对称式方程:(x-x₁)/a=(y-y₁)/b=(z-z₁)/c-空间平面的一般式方程:Ax+By+Cz+D=0-空间平面的点法式方程:(x-x₀)/A=(y-y₀)/B=(z-z₀)/C-两直线的位置关系:平行、异面、交于一点-直线与平面的位置关系:相交、平行、共面、垂直-两平面的位置关系:平行、重合、相交4.三角函数与解三角形:- 任意角的辅助角公式:sin(π - θ) = sinθ, cos(π - θ) = -cosθ, tan(π - θ) = -tanθ-任意角的和差公式:sin(θ₁ ± θ₂) = sinθ₁cosθ₂ ± cosθ₁sinθ₂cos(θ₁ ± θ₂) = cosθ₁cosθ₂∓ sinθ₁sinθ₂tan(θ₁ ± θ₂) = (tanθ₁ ± tanθ₂)/(1 ∓ tanθ₁tanθ₂)-二倍角公式:sin2θ = 2sinθcosθcos2θ = cos²θ - sin²θtan2θ = (2tanθ)/(1 - tan²θ)-三角函数的诱导公式:sin(π ± θ) = ±sinθ, cos(π ± θ) = -cosθ, tan(π ± θ) = ±tanθ-等腰三角形的性质:两底角相等,底边平分顶角,底边上的高相等- 直角三角形的性质:勾股定理(a² + b² = c²),正弦定理(sinθ = a/c),余弦定理(cosθ = b/c),正切定理(tanθ = a/b)。
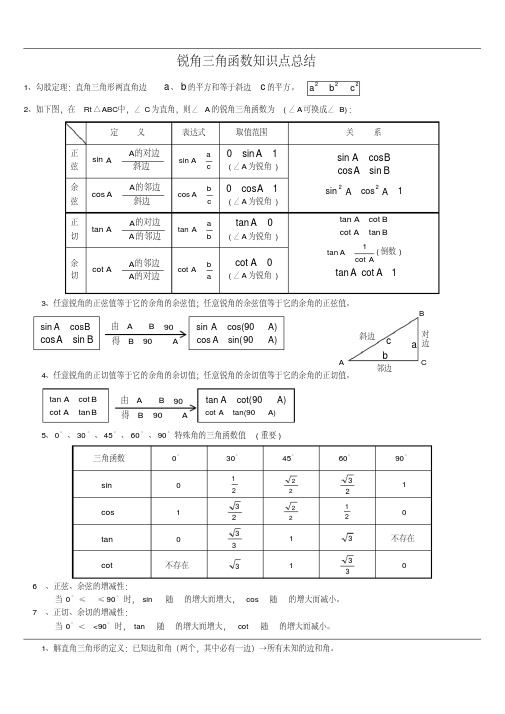
中考数学总复习---三角函数与反比例函数知识点总结大全
1: m 的形式,如
l
把坡面与水平面的夹角记作
(叫做 坡角 ),那么 i h tan 。 l
3、从某点的指北方向按顺时针转到目标方向的水平角,叫做方位角。如图
3, OA 、 OB、 OC、 OD 的方向角分
别是: 45°、 135°、 225°。
4、指北或指南方向线与目标方向
线所成的小于 90° 的水平角,叫做方向角。如图
(1) y x (2) y 3
2 (3) xy = 21( 4) y
5 ( 5) y
x
x2
例 2.当 m 取什么值时,函数 y (m 2) x3 m2 是反比例函数?
3 ( 6) y 1 3 ( 7)y= x- 4
2x
x
例 3.若函数 y (2m 1)x m2 2 是反比例函数,且它的图像在第二、四象限,则
A的对边 斜边
A的邻边 斜边
A的对边 A 的邻边
sin A a c
0 sin A 1
( ∠ A 为锐角 )
b 0 cosA 1
cos A c ( ∠ A 为锐角 )
a tan A
b
tan A 0
( ∠ A 为锐角 )
余 cot A
切
A的邻边 A的对边
cot A b a
cot A 0
( ∠ A 为锐角 )
m 的值是 ___________
例 4.已知函数 y= y1+y2, y1 与 x 成正比例, y 2 与 x 成反比例,且当 (1)求 y 与 x 的函数关系式 (2)当 x=- 2 时,求函数 y 的值
x= 1 时, y= 4;当 x= 2 时, y= 5
2.反比例函数图像上的点的坐标满足: xy k
反比例+三角函数
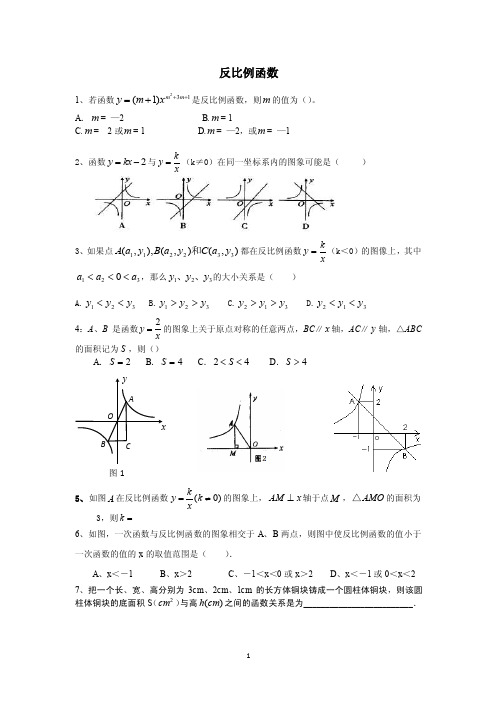
反比例函数1、若函数132)1(+++=m mx m y 是反比例函数,则m 的值为()。
A .m = —2 B.m = 1C.m = 2或m = 1D.m = —2,或m = —12、函数2y kx =-与ky x=(k ≠0)在同一坐标系内的图象可能是( )3、如果点),(),(),,(332211y a C y a B y a A 和都在反比例函数xky =(k <0)的图像上,其中 3210a a a <<<,那么321y y y 、、的大小关系是( )A.321y y y <<B.321y y y >>C.312y y y >>D.312y y y << 4:A 、B 是函数2y x=的图象上关于原点对称的任意两点,BC ∥x 轴,AC ∥y 轴,△ABC 的面积记为S ,则()A .2S =B .4S =C .24S <<D .4S >5、如图A 在反比例函数(0)ky k x=≠的图象上,AM x ⊥轴于点M ,AMO △的面积为3,则k =6、如图,一次函数与反比例函数的图象相交于A 、B 两点,则图中使反比例函数的值小于一次函数的值的x 的取值范围是( ).A 、x <-1B 、x >2C 、-1<x <0或x >2D 、x <-1或0<x <2 7、把一个长、宽、高分别为3cm 、2cm 、1cm 的长方体铜块铸成一个圆柱体铜块,则该圆柱体铜块的底面积S (2cm )与高)(cm h 之间的函数关系是为_________________________.图18、如图,一次函数b x y +=和反比例函数)0k (xky ≠=交于点A (2,1). (1)求反比例函数和一次函数的解析式; (2)求△AOB 的面积;(3)根据图像写出一次函数的值大于反比例函数的值的x 的取值范围;三角函数1. 如图1,在Rt △ABC 中,ACB ∠90=,CD ⊥AB 于D ,若3BC =,4AC =,则tan BCD ∠的值为( )A .34B .43C .35D .452、3、(坡度)若某人沿坡度i =3:4的斜坡前进10米,则他所在的位置比原来的位置升高_______米3-1、某人沿着山坡前进60m ,这人所在位置升高了330,则这个山坡的坡度是C图1().45cos 260sin 330tan 630002--4、如图,点A是一个半径为300米的圆形森林公园的中心,在森林公园附近有B、C两个村庄,现要在B、C两村庄之间修一条长为1000米的笔直公路将两村连通,经测得∠ABC=45o,∠ACB=30o,问此公路是否会穿过该森林公园?请通过计算进行说明。
三角函数的反函数与反比例关系

三角函数的反函数与反比例关系三角函数是数学中重要的一类函数,包括正弦函数、余弦函数和正切函数等。
而三角函数的反函数则是将其输入与输出进行对换,即将自变量作为函数的因变量,从而得到与原函数互为反函数的函数。
与此同时,三角函数还存在着与反函数相关的反比例关系,即两两三角函数的值互为倒数。
本文将会探讨三角函数的反函数与反比例关系。
一、正弦函数与反正弦函数正弦函数是三角函数中的一种,可以表示为sin(x),其中x为自变量。
而反正弦函数则是将正弦函数的自变量与因变量进行对换,表示为arcsin(x)或sin^(-1)(x)。
反正弦函数的定义域为[-1, 1],值域为[-π/2,π/2]。
利用反正弦函数,我们可以得到一个角度的正弦值。
例如,当sin(x) = 0.5时,可以通过反正弦函数得到x = arcsin(0.5) = 30°。
反正弦函数的结果是一个角度值,表示正弦函数的自变量取得相应值时的角度。
二、余弦函数与反余弦函数余弦函数是三角函数中的另一种,可以表示为cos(x),其中x为自变量。
反余弦函数则是将余弦函数的自变量与因变量进行对换,表示为arccos(x)或cos^(-1)(x)。
反余弦函数的定义域为[-1, 1],值域为[0, π]。
利用反余弦函数,我们可以得到一个角度的余弦值。
例如,当cos(x) = 0.5时,可以通过反余弦函数得到x = arccos(0.5) = 60°。
反余弦函数的结果同样是一个角度值,表示余弦函数的自变量取得相应值时的角度。
三、正切函数与反正切函数正切函数是三角函数中的另一种,可以表示为tan(x),其中x为自变量。
反正切函数则是将正切函数的自变量与因变量进行对换,表示为arctan(x)或tan^(-1)(x)。
反正切函数的定义域为(-∞, ∞),值域为(-π/2, π/2)。
利用反正切函数,我们可以得到一个角度的正切值。
例如,当tan(x) = 1时,可以通过反正切函数得到x = arctan(1) = π/4。
反比例、三角、二次函数精讲

专题:反比例函数、二次函数、三角函数一. 【重点、难点】这三部分涉及的知识非常灵活,学生掌握起来特别困难。
在这里建议大家在复习中注意以下几点: 1. 深入理解概念。
反比例函数和二次函数都有自己的一般形式。
它们都有较灵活的变形。
如反比例函数y k x=可写成y =kx -1的形式,二次函数除了一般形式外,还可有顶点式、交点式,在具体的题目中,应用起来也很方便。
研究三角函数的前提是在直角三角形中,正弦、余弦、正切的概念必须记牢,才能在计算中灵活应用。
2. 注意数形结合,函数之所以被大部分同学认为较难,是函数可以从“数”和“形”两个方面进行研究,有的题目给出的“数”的形式,让你找到“形”的变化。
当然,有的题目反之,如果同学们不能使“数”和“形”两方面顺利地相互转化,自然驾驭不了知识。
【二次函数的知识点】1、解析式:(1)一般式: ____________________(2)顶点式:____________________,此时二次函数的顶点坐标为__________(3)交点式:y=a (x-x 1)(x-x 2)其中x 1、x 2是二次函数与___轴的两个交点的___坐标,此时二次函数的对称轴为直线______________;2、二次函数的图象与性质:3、 ①二次函数y=ax 2+bx+c (a ≠0)与X 轴只有一个交点或顶点在X 轴上,则 ___________;②二次函数y=ax 2+bx+c (a ≠0)的顶点在Y 轴上或图象关于Y 轴对称,则_________; ③二次函数y=ax 2+bx+c (a ≠0)经过原点,则_________;【反比例函数的知识点】1、反比例函数x k y =(k≠0)的图象称为_________,既是轴对称图形,也是中心对称图形.2、反比例函数的图像与性质:3、k 的几何意义二、【例题分析】 例1. 如图,O 为坐标原点,二次函数y=ax 2+bx+c 的图象与x 轴相交于点A 、B ,与y 轴交于点C ,点A 的坐标是(-1,0)点C 的坐标为(0,-3),且BO =CO(1)求出B 点坐标和这个二次函数的解析式; (2)求△ABC 的面积。
反比例,三角函数

17.(8分)(2012•成都)如图,在一次测量活动中,小华站在离旗杆底部(B处)6米的D处,仰望旗杆顶端A,测得仰角为60°,眼睛离地面的距离ED为1.5米.试帮助小华求出旗杆AB的高度.(结果精确到0.1米,)18.(8分)(2012•成都)如图,一次函数y=﹣2x+b(b为常数)的图象与反比例函数(k为常数,且k≠0)的图象交于A,B两点,且点A的坐标为(﹣1,4).(1)分别求出反比例函数及一次函数的表达式;(2)求点B的坐标.24.(4分)(2012•成都)如图,在平面直角坐标系xOy中,直线AB与x轴、y轴分别交于点A,B,与反比例函数(k为常数,且k>0)在第一象限的图象交于点E,F.过点E作EM⊥y轴于M,过点F 作FN⊥x轴于N,直线EM与FN交于点C.若(m为大于l的常数).记△CEF的面积为S1,△OEF 的面积为S2,则=_________.(用含m的代数式表示)16、(2011•成都)如图,在亚丁湾一海域执行护航任务的我海军某军舰由东向西行驶.在航行到B处时,发现灯塔A在我军舰的正北方向500米处;当该军舰从B处向正西方向行驶至达C处时,发现灯塔A在我军舰的北偏东60°的方向.求该军舰行驶的路程.(计算过程和结果均不取近似值)19、(2011•成都)如图,已知反比例函数错误!未找到引用源。
的图象经过点(错误!未找到引用源。
,8),直线y=﹣x+b经过该反比例函数图象上的点Q(4,m).(1)求上述反比例函数和直线的函数表达式;(2)设该直线与x轴、y轴分别相交于A、B两点,与反比例函数图象的另一个交点为P,连接0P、OQ,求△OPQ的面积.21、(2011•成都)在平面直角坐标系xOy中,点P(2,a)在正比例函数错误!未找到引用源。
的图象上,则点Q(a,3a﹣5)位于第象限.ABC D25、(2011•成都)在平面直角坐标系xOy 中,已知反比例函数错误!未找到引用源。
高中六个特殊函数图像

高中六个特殊函数图像高中函数的学习是一项重要而又令人兴奋的任务,它可以帮助学生理解和操作数学,并使其能够应用于实际的问题。
函数的图形是有关函数的重要性的可视化表示,它们可以帮助学生更好地理解和应用函数。
在本文中,我们将关注高中函数的六个特殊函数图像--正弦函数、余弦函数、指数函数、对数函数、幂函数和反比例函数。
正弦函数是一种经常用于描述物理系统周期性变化的函数。
它是由三角函数和 Trilogy组合构成的,表达式是 y=asin(bx+c)。
它的图像表示为一条由纵轴和横轴(即x轴)上的点组成的曲线,每个点的位置可以通过x的变换而不断变化。
图像的形状取决于a,b,c参数的取值。
正弦函数的图像可以用来描述物体的阻力,从而更好地了解某些不可预知的系统物理现象。
余弦函数也是一种经常用于描述物理系统变化的函数,表达式为y=acos(bx+c)。
它的图像表示为由点组成的曲线,和正弦函数类似,控制参数由a,b,c决定图像的形状。
余弦函数的图像可以用来描述惯性力,反应物体在不同重力中的运动变化,从而更好地了解物理过程。
指数函数是一种常用的数学函数,表达式为 y=aebx,其中e是自然对数的基数。
指数函数的图像表示为由点组成的抛物线,参数由a和b决定图形的形状,它表示了数与数之间关系的可视化描述。
熟悉指数函数的图像有助于学生更好地使用它们来解决日常问题,比如财务问题等。
对数函数也是一种常用的数学函数,它由三角函数和日志函数组成,表达式为 y=alogbx。
它的图形表示为一条由点组成的折线,参数由a和logb决定图形的形状。
学习对数函数的图像有助于帮助学生理解数学关系,并从中推导出更多的结果。
幂函数既是数学函数,也是物理函数,表达式为 y=axb。
它的图形表示为一条由点组成的抛物线,参数由a和b决定图形的形状。
幂函数图形经常用于描述各种自然现象,如质量、衰减等。
学习幂函数的图形有助于学生更好地理解它们的用途以及它们在解决实际问题时的作用。
《高中数学课件:几种常见函数的图像和性质》

探索几种常见函数的图像和性质,包括一次函数、二次函数、反比例函数、 幂函数、指数函数、对数函数、三角函数和常函数。
一次函数
一次函数是指具有形式y = kx + b的函数,图像为一条直线,斜率k决定了直 线的倾斜程度,纵截距b决定了直线与y轴的交点。
二次函数
Step 3
根据底数a的不同,求解指数函 数的通式。
推导对数函数的通式
1
Step 2
2
代入任意一点的坐标和底数a到对数函数
的通式y = log_a(x)中。
3
Step 1
通过两个点的坐标(x1, y1)和(x2, y2)计算 底数a:a = 10^((y1 - y2) / (x1 - x2))。
Step 3
推导反比例函数的通式
1 Step 1
2 Step 2
通过两个点的坐标(x1, y1)和(x2, y2)计算比例 系数k:k = y1 * x1 = y2 * x2。
代入一个点的坐标(x, y)和比例系数k到反比例 函数的通式y = k/x中,得到反比例函数的通 式。
推导幂函数的通式
Step 1
取幂函数的对数y = log_a(x), 其中a为底数。
二次函数是指具有形式y = ax^2 + bx + c的函数,图像为一条开口向上或向下 的曲线,顶点坐标为(-b/2a, c-b^2/4a)。
反比例函数
反比例函数是指具有形式y = k/x的函数,图像为一条曲线,呈现出一个反比 例的关系,x越大,y越小。
幂函数
幂函数是指具有形式y = kx^n的函数,图像的形态取决于指数n的值,n为正 偶数时,图像在原点右侧上升,n为正奇数时,则图像在全范围上升。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
反比例函数与三角函数试题
一、选择题
1.如图,在Rt ABC
△中,ACB
∠=900,1
BC=,2
AB=,则下列结论正确的是()
A.
3
sin
2
A= B.
1
tan
2
A= C.
3
cos
2
B= D.tan3
B=
所示,则tanα的值是2.如图三角形在方格纸中的位置如图
()A.
3
4
B.
4
3
C.
3
5
D.
4
5
3.将宽为2cm的长方形纸条折叠成如图所示的形状,那么折痕PQ的长是()
A.
2
3
3
cm B.
4
3
3
cm C.5cm D.2cm
4.在△ABC中,∠A、∠B都是锐角,且sinA=
1
2
,cosB=
3
2
,则△ABC的形状是()
A.直角三角形 B.钝角三角形C.锐角三角形 D.不能确定
5.如图Rt△ABC中,∠ACB=90°,CD⊥AB于D,BC=3,AC=4,设∠BCD=a,则tanA•的值为().
A.
3
4 B.
4
3 C.
3
5 D.
4
5
6.在△ABC中,三边之比为a:b:c=1:
3
:2,则sinA+tanA等于().
A.
32313331
.3..
6222
B C D
++
+
7.若( 3 tanA-3)2+│2cosB- 3 │=0,则△ABC().
A.是直角三角形 B.是等边三角形 C.是含有60°的任意三角形 D.是顶角为钝角的等腰三角形8.已知30°<α<60°,下列各式正确的是()
A. B. C. D.
9.如图2,沿AC方向开山修路,为了加快施工进度,要在小山的另一边同时施工.从AC上的一点B,取∠ABD=145°,BD=500米,∠D=55°,要使A,C,E成一直线,那么开挖点E离点D的距离是()
A.500sin55°米 B. 500cos55°米 C.500tan55°米 D.500tan35°米
10.函数()9
2
2
2-
-
+
=m
m
x
m
y是反比例函数,则m的值是()
A. 2
4-
=
=m
m或 B.4
=
m C. 2
-
=
m D. 1
-
=
m
11、反比例函数
x
k
y=的图象如图所示,点M是该函数图象上一点,MN垂直于x轴,垂足是点N,如果S△MON=2,则k的值为() A 2 B -2 C 4 D -4
12、如图,一次函数y
1
=x-1与反比例函数y
2
=
x
2
的图像交于点A(2,1), B(-1,-2),则使y1>y2的x的取值范
围是( )
题号 1 2 3 4 5 6 7 8 9 10 11 12 答案
1. 已知反比例函数的图象经过点(m ,2)和(-2,3)则m 的值为__________.
2. Rt △ABC 中,∠C=90°,若sinA=
4
5
,AB=10,则BC=_______. 3. 如图,点A 在双曲线1y x =上,点B 在双曲线3
y x
=上,且AB ∥x 轴,C 、D 在x 轴上,若四边形ABCD
的面积为矩形,则它的面积为 .
4.如图,在坡度为1:2 的山坡上种树,要求株距(相邻两树间的水平距离)是6米,斜坡上相邻两树间的坡面距离是 米。
5.在直角坐标系中,有如图所示的t ,R ABO AB x ∆⊥轴于点B ,斜边3
105
AO AOB =∠=,sin ,反比例函数(0)k
y x x
=
>的图像经过AO 的中点C ,且与AB 交于点D ,则点D 的坐标为 . 三、计算题
(1 )1
01|32|20093tan 303-⎛⎫
-+--+ ⎪⎝⎭
°
(2) 0
2009
12sin 603tan 30(1)3⎛⎫
-++- ⎪⎝⎭°°
(3)104cos30sin 60(2)(20092008)-︒︒+---
(4)0
0000030cos 30sin 45cos 45sin 60cos 60sin -+
四、解答题
1、根据下列条件, ∠C=90°解直角三角形
(1)BC=8,∠B=60°. (2)AC=2,AB=2.
2、如图, 已知反比例函数y =
x
k
的图象与一次函数
y =a x +b 的图象交于M (2,m )和N (-1,-4)两点.(1)求这两个函数的解析式;(2)求△MON 的面积;
(3)请判断点P (4,1)是否在这个反比例函数的图象上,并说明理由. (4)根据图象写出使反比例函数的值大于一次函数的值的x 的取值范围
3、如图,放置在水平桌面上的台灯的灯臂AB 长为40cm ,灯罩BC 长为30cm ,灯臂与底座构成的∠BAD=60°. 使用发现,光线最佳时灯罩BC 与水平线所成的角为30°,此时灯罩顶端C 到桌面的高度CD 是多少cm ?(忽略底座高度,结果精确到0.1cm ,参考数据:3≈1.732)
4.某汽车的功率P 为一定值,汽车行驶时的速度v (米/秒)与它所受的牵引力F (牛)之间的函数关系如下图所示:
(1)这辆汽车的功率是多少?请写出这一函数的表达式;
(2)当它所受牵引力为1200牛时,汽车的速度为多少千米/时?
5.某校教学楼上悬挂着宣传条幅DC ,小丽同学在点A 处,测得条幅顶端D 的仰角为30°,再向条幅方向前进10米后, 又在点B 处测得条幅顶端D 的仰角为45°,已知测点A 、B 和C 离地面高度都为1.44米,求条幅顶端D 点距离地面的高度.
E 60°30°A
B
C
D。
