计算机图形学实验z-buffer算法
计算机图形学——隐藏线和隐藏面的消除(消隐算法)

计算机图形学——隐藏线和隐藏⾯的消除(消隐算法)⼀、概述由于投影变换失去了深度信息,往往导致图形的⼆义性。
要消除⼆义性,就必须在绘制时消除被遮挡的不可见的线或⾯,习惯上称作消除隐藏线和隐藏⾯(或可见线判定、可见⾯判定),或简称为消隐。
经过消隐得到的投影图称为物体的真实感图形。
下⾯这个图就很好体现了这种⼆义性。
消隐后的效果图:消隐算法的分类所有隐藏⾯消隐算法必须确定:在沿透视投影的投影中⼼或沿平⾏投影的投影⽅向看过去哪些边或⾯是可见的两种基本算法1、以构成图像的每⼀个像素为处理单元,对场景中的所有表⾯,确定相对于观察点是可见的表⾯,⽤该表⾯的颜⾊填充该像素.适于⾯消隐。
算法步骤:a.在和投影点到像素连线相交的表⾯中,找到离观察点最近的表⾯;b.⽤该表⾯上交点处的颜⾊填充该像素;2、以三维场景中的物体对象为处理单元,在所有对象之间进⾏⽐较,除去完全不可见的物体和物体上不可见的部分.适于⾯消隐也适于线消隐。
算法步骤:a.判定场景中的所有可见表⾯;b.⽤可见表⾯的颜⾊填充相应的像素以构成图形;提醒注意1.假定构成物体的⾯不能相互贯穿,也不能有循环遮挡的情况。
2.假定投影平⾯是oxy平⾯,投影⽅向为z轴的负⽅向。
如果构成物体的⾯不满⾜该假定,可以把它们剖分成互不贯穿和不循环遮挡的情况。
例如,⽤图b中的虚线便可把原来循环遮挡的三个平⾯,分割成不存在循环遮挡的四个⾯。
⼆、可见⾯判断的有效技术1、边界盒指能够包含该物体的⼀个⼏何形状(如矩形/圆/长⽅体等),该形状有较简单的边界。
边界盒技术⽤于判断两条直线是否相交。
进⼀步简化判断2、后向⾯消除(Back-face Removal)思路:把显然不可见的⾯去掉,减少消隐过程中的直线求交数⽬如何判断:根据定义寻找外(或内)法向,若外法向背离观察者,或内法向指向观察者,则该⾯为后向⾯。
注意:如果多边形是凸的,则可只取⼀个三⾓形计算有向⾯积sp。
如果多边形不是凸的,只取⼀个三⾓形计算有向⾯积sp可能会出现错误,即F所在的⾯为前向⾯也可能出现sp≥0的情况,因此,需按上式计算多边形F的有向⾯积。
计算机图形学第五次实验报告

《计算机图形学》实验报告实验十一真实感图形一、实验教学目标与基本要求初步实现真实感图形, 并实践图形的造型与变换等。
二、理论基础运用几何造型, 几何、投影及透视变换、真实感图形效果(消隐、纹理、光照等)有关知识实现。
1.用给定地形高程数据绘制出地形图;2.绘制一(套)房间,参数自定。
三. 算法设计与分析真实感图形绘制过程中, 由于投影变换失去了深度信息, 往往导致图形的二义性。
要消除这类二义性, 就必须在绘制时消除被遮挡的不可见的线或面, 习惯上称之为消除隐藏线和隐藏面, 或简称为消隐, 经过消隐得到的投影图称为物体的真实图形。
消隐处理是计算机绘图中一个引人注目的问题, 目前已提出多种算法, 基本上可以分为两大类:即物体空间方法和图象空间方法。
物体空间方法是通过比较物体和物体的相对关系来决定可见与不可见的;而图象空间方法则是根据在图象象素点上各投影点之间的关系来确定可见与否的。
用这两类方法就可以消除凸型模型、凹形模型和多个模型同时存在时的隐藏面。
1).消隐算法的实现1.物体空间的消隐算法物体空间法是在三维坐标系中, 通过分析物体模型间的几何关系, 如物体的几何位置、与观察点的相对位置等, 来进行隐藏面判断的消隐算法。
世界坐标系是描述物体的原始坐标系, 物体的世界坐标描述了物体的基本形状。
为了更好地观察和描述物体, 经常需要对其世界坐标进行平移和旋转, 而得到物体的观察坐标。
物体的观察坐标能得到描述物体的更好视角, 所以物体空间法通常都是在观察坐标系中进行的。
观察坐标系的原点一般即是观察点。
物体空间法消隐包括两个基本步骤, 即三维坐标变换和选取适当的隐藏面判断算法。
选择合适的观察坐标系不但可以更好地描述物体, 而且可以大大简化和降低消隐算法的运算。
因此, 利用物体空间法进行消隐的第一步往往是将物体所处的坐标系转换为适当的观察坐标系。
这需要对物体进行三维旋转和平移变换。
常用的物体空间消隐算法包括平面公式法、径向预排序法、径向排序法、隔离平面法、深度排序法、光线投射法和区域子分法。
融合SGM与Z—Buffer的真正射影像遮挡检测算法

A Dr .2 Ol 7
2 O 1 7年 4月
融合 S GM 与 Z — B u f f e r 的 真 正 射 影 像 遮 挡 检 测 算 法
化 雪 诚 , 吴 军 , 彭智 勇
( 1 . 桂 林 电子 科 技 大 学 电 子 工 程 与 自动 化 学 院 , 广 西 桂 林 5 4 1 0 0 4 ; 2 . 桂 林 电 子 科 技 大学 广 西 自动检 测技 术 与 仪 器 重 点 实验 室 , 广 西 桂 林 5 4 1 0 0 4 3 . 桂 林 电子 科 技 大 学 广 西 信 息 科 学 实验 中 心 , 广 西 桂 林 5 4 1 0 0 4 )
A t r u e o r t h o p ho t o o c c l u s i o n d e t e c t i o n a l g o r i t hm b a s e d o n S GM a n d Z— Bu f f e r
HUA Xu e c h e n g ,W U J u n ,P ENG Z h i y o nFra bibliotekg ’ ’ 。
摘 要 : 针对 真 正 射 影 像 制 作 过 程 中 因相 机 倾 斜 和 高 大 建 筑 物 产 生 的 遮 挡 问 题 , 提 出了一种 融合 S G M与 Z — B u f f e r的 真 正 射 影 像 遮 挡 检 测 算 法 。该 算 法 利 用 S GM 密 集 匹 配 检 测 到 的 遮 挡 信 息 作 为 遮 挡 判 断 的 条 件 , 井与传统 Z B u f f e r 算 法 的 遮 挡 判断准则相结合 , 作 为 真 正 射 影 像 制作 过 程 中 遮 挡 检 测 的判 断 准则 , 通过判 断准则的接连判 断 , 实 现遮挡 区域 的准确检 测 。 实 验 对 航 空 立 体 影 像 使 用 该 算 法 并 与 传 统 方 法 进 行 对 比实 验 , 结果 表明 , 该算 法在遮 挡 区域检 测的准 确性 更高 , 且 在 一 定
《计算机图形学》题集

《计算机图形学》题集一、选择题(每题2分,共20分)1.计算机图形学主要研究的是:A. 计算机硬件的设计B. 计算机软件的开发C. 图像的生成、处理与显示D. 计算机网络技术2.下列哪个不是计算机图形学的应用领域?A. 游戏开发B. 医学影像处理C. 文字编辑D. 三维动画制作3.在计算机图形学中,像素(Pixel)是:A. 图像的最小单位B. 显示器的大小C. 图像的分辨率D. 图像的颜色深度4.下列哪个是光栅图形显示器的特点?A. 直接使用矢量数据表示图像B. 图像由像素阵列组成C. 分辨率固定不变D. 不适用于动态图像显示5.在三维图形变换中,平移变换不会改变物体的:A. 形状B. 大小C. 方向D. 位置6.下列哪个算法常用于三维图形的消隐处理?A. 光线追踪算法B. Z-Buffer算法C. 纹理映射算法D. 反走样算法7.在计算机图形学中,下列哪个术语用于描述物体表面的明暗程度?A. 色彩B. 光照模型C. 纹理D. 透明度8.下列哪个不是计算机图形学中的基本图形生成算法?A. 中点画线算法B. Bresenham画圆算法C. 扫描线填充算法D. Cohen-Sutherland线段裁剪算法9.在计算机图形学中,下列哪个概念用于描述物体的三维形状?A. 像素B. 几何模型C. 色彩模型D. 光照模型10.下列哪个不是真实感图形生成的基本步骤?A. 几何建模B. 光照模型计算C. 纹理映射D. 数据压缩二、填空题(每题2分,共14分)1.计算机图形学中的“图形”主要分为两大类:和。
2.在三维图形变换中,旋转变换可以使用______矩阵来实现。
3.在计算机图形学中,______是指使用数学方法来模拟真实世界中光线与物体表面的相互作用。
4.在进行三维图形的消隐处理时,______算法是一种常用的方法,它通过维护一个深度缓冲区来实现。
5.在计算机图形学中,______是一种常用的图像滤波技术,可以用于图像的平滑处理。
计算机图形学作业及答案

计算机图形学作业及答案1、计算机图形系统的组成包括哪些?答:计算机图形系统由硬件和软件两部分组成,硬件包括:主计算机、图形显示器以及I/O 交互工具和存储设备;软件包括操作系统、高级语言、图形软件和应用软件。
现代计算机图形系统与一般计算机系统最主要的差别是具有图形的输入、输出设备以及必要的交互工具,在速度和存储容量上具有较高的要求。
另外,人也是这个系统的组成部分。
2、简述光栅扫描式显示器的性能指标?答:⑴分辨率:指显示器在屏幕水平(垂直)方向可显示多少像素,分辨率以象素点为基本单位。
表示方法为320×200、640×480等。
显示分辨率与显卡上的缓冲存储器的容量有关,容量越大,显示分辨率越高。
分辨率越高,显示的字符或图像越清晰。
⑵ 亮度等级数目和色彩:指单种颜色亮度可变化的数目,亮度等级范围的提升可使图像看 上去更柔和自然色彩包括可选择显示颜色的数目以及一帧画面可同时显示的颜色数。
⑶ 显示速度:指显示字符、图形,特别是动态图像的速度,可用最大带宽表示:水平像素 数*垂直像素数*最大刷新率。
3、具有相同分辨率的彩色光栅显示器与黑白光栅在结构上有何区别? 答:彩色:对于红、绿、蓝的三个原色有三个位面的帧缓存和三个电子枪,每个位面的帧缓冲对应一个电子枪即对应一种颜色;对每个颜色的电子枪可以通过增加帧缓存位面来提高颜色种类和灰度级,通过三种原色的组合可以产生不同种类的颜色。
彩色光栅显示器主要是有红、绿、蓝的三个原色所组成,每种原色电子枪有8个位面的帧缓存和8位的数模转换器,每种原色有256种亮度,三种原色组合可为16771216种颜色,也可以通过颜色查找表查找,故帧缓存位数至少24位。
黑白:黑白光栅显示器的帧缓存是一块连续的计算机存储器,每个像素需1位存储器,每个存储器只有0或1两个状态。
因此一个位面的帧缓存只能产生黑白图形。
可以增加象素点的位面数,通过多个位面显示出多种灰度级。
常用的消隐算法及总结

常用的消隐算法及总结数学092邹继瑶 090064摘要:用计算机生成三维物体的真实图形是计算机图形学研究的重要内容。
真实图形在仿真模拟、几何造型、广告影视、指挥控制和科学计算的可视化等许多领域都有广泛应用。
经过消隐得到的投影图称为物体的真实图形。
较常用的消隐算法有画家算法、Z-Buffer算法及其它一些改进算法。
消隐算法从算法基本思想、算法描述和算法步骤等方面对画家算法、Z-Buffer算法和其它改进算法进行了分析,并得出了它们相关的特点。
关键词:计算机图形学消隐景物空间消隐图像空间消隐算法引言:近年来,产生真实的虚拟环境是计算机图形学孜孜以求的目标。
在虚拟对象或场景的创建中要用到许多综合处理过程,每一种都非常令人感兴趣也非常重要。
计算机辅助设计、科学可视化、模拟训练、医疗成像、娱乐、广告等等,所有的这些,都要依赖于当今最前沿的计算机图形技术。
伴随着计算机硬件、软件的飞速发展,计算机图形学技术也得到了质的飞跃。
特别是面向对象技术和多媒体技术取得的成功,使得图形学成为计算机软件业中一个重要的分支。
而程序设计方法、数据库系统和人工智能等新技术渗入到计算机图形学领域,又为计算机图形学提供了更加宽阔的发展空间和强劲动力。
计算机图形学是研究通过计算机将数据转换成图形,并在专用显示设备上显示的原理、方法和技术的学科。
主要介绍了计算机图形系统的基本知识,图形生成与显示的算法,图形的表示与图形的数据结构,图形的几何变换与投影变换,图形的裁剪技术,图形消隐处理,真实感图形的生成等内容。
面消隐作为图形学中一个分支是本文的一个重要的研究内容。
一.消隐的基本概念由于屏幕上的一些图元被另一些图元挡住所造成的。
例如,当需要描绘一个由多边形面组成的三维物体时,那么它的一部分必然要被挡住,要在屏幕上显示的必须是可见的东西。
打个比方,对于一个立方体,无论从哪个方向进行透视处理,最多只能看到其中的三个面。
这样,就要想出一种方法来决定哪些面是所能看到的。
浅谈HiZ-buffer
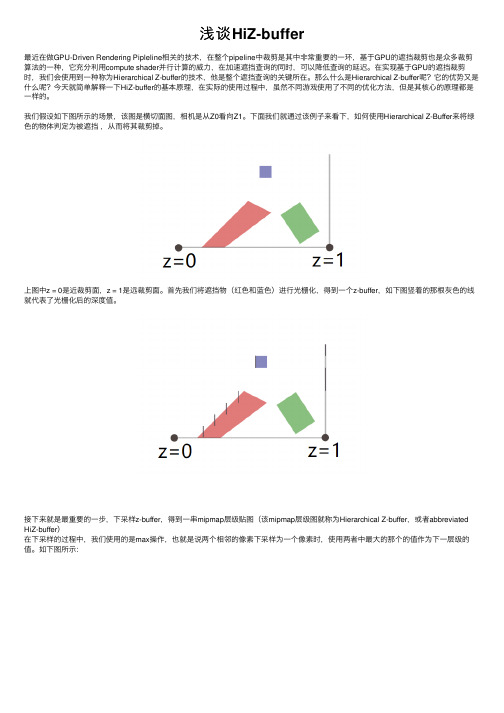
浅谈HiZ-buffer最近在做GPU-Driven Rendering Pipleline相关的技术,在整个pipeline中裁剪是其中⾮常重要的⼀环,基于GPU的遮挡裁剪也是众多裁剪算法的⼀种,它充分利⽤compute shader并⾏计算的威⼒,在加速遮挡查询的同时,可以降低查询的延迟。
在实现基于GPU的遮挡裁剪时,我们会使⽤到⼀种称为Hierarchical Z-buffer的技术,他是整个遮挡查询的关键所在。
那么什么是Hierarchical Z-buffer呢?它的优势⼜是什么呢?今天就简单解释⼀下HiZ-buffer的基本原理,在实际的使⽤过程中,虽然不同游戏使⽤了不同的优化⽅法,但是其核⼼的原理都是⼀样的。
我们假设如下图所⽰的场景,该图是横切⾯图,相机是从Z0看向Z1。
下⾯我们就通过该例⼦来看下,如何使⽤Hierarchical Z-Buffer来将绿⾊的物体判定为被遮挡,从⽽将其裁剪掉。
上图中z = 0是近裁剪⾯,z = 1是远裁剪⾯。
⾸先我们将遮挡物(红⾊和蓝⾊)进⾏光栅化,得到⼀个z-buffer,如下图竖着的那根灰⾊的线就代表了光栅化后的深度值。
接下来就是最重要的⼀步,下采样z-buffer,得到⼀串mipmap层级贴图(该mipmap层级图就称为Hierarchical Z-buffer,或者abbreviated HiZ-buffer)在下采样的过程中,我们使⽤的是max操作,也就是说两个相邻的像素下采样为⼀个像素时,使⽤两者中最⼤的那个的值作为下⼀层级的值。
如下图所⽰:由上图可以看出,每⼀次下采样,都是对上⼀层级的保守估计,到了第4级就只剩下⼀个深度值了。
由于下采样的时候⽤的是max操作,所以如果⼀个物体在level 2中深度值判定为被遮挡,那么它肯定在level 1中也是被遮挡的。
得到HiZ-buffer之后,我们就可以基于它来进⾏遮挡裁剪了:计算得到绿⾊物体的AABB包围盒,该包围盒的x-max/min和y-max/min⽤来决定采样哪⼀层级的HiZ-buffer(也就是看哪⼀层级的尺⼨能够涵盖包围盒的所有像素),在本例中该AABB包围盒符合level 2,所以我们选择采样level2,从⽽得到⼀个z-buffer的保守估计。
3D图像生成算法原理

3D图像生成算法原理一、建齐次坐标二、着色模型三、Z缓存四、纹理映射在这些步骤中,显示部分(GPU)只负责完成第三、四步,而前两个步骤主要就是依靠CPU 来完成。
而且,这还仅仅只就是3D图象的生成,还没有包括游戏中复杂的AI运算。
场景切换运算等等……无疑,这些元素还需要CPU去完成,这就就是为什么在运行大型3D的时候,当场景切换时再强劲的显卡都会出现停顿的现象。
3D芯片的处理对象就是多边形表示的物体。
用多边形表示物体有两个优点:首先就是直接(尽管繁琐),多边形表示的物体其表面的分段线性特征除轮廓外可以通过明暗处理(shading)技术消除;其次就是仅存储多边形顶点的几何信息,多边形内部每个象素的明暗颜色计算所需的信息由这些顶点信息插值而来,这正就是易于用图形硬件支持的快速明暗处理技术。
支持多边形绘制的图形硬件同样也可以绘制由双三次曲面片表示的物体,通过对这种物体的表面进行三角剖分,用逼近的三角形网格代替原物体的曲面表示就可以做到这一点。
当然,用多边形表示物体也有其缺点,如增加了纹理映射与阴影生成的难度,当需要详细表示复杂物体时所需的三角形数量将变得非常庞大。
将多边形表示的物体显示到计算机屏幕上,这一过程涉及物体在计算机内部的表示方式即物体的数据结构,由物体组成的场景的组织结构,物体从场景到屏幕空间要经过的一系列变换,以及产生最终屏幕图象要经过的一系列光栅化处理。
这些方面都涉及到特定的处理算法,相应的算法又有许多不同的变种。
下面仅就3D芯片涉及的图形处理过程及相关算法做一简单分析介绍,这些就是理解3D图形处理及图形硬件的基础。
一、3D物体的表示法具有复杂外形的物体其表面可以由多边形面片来近似表示。
以图1的圆柱为例,其柱面可以由2N个三角形近似,其两端可以由两个N边形来近似。
多边形模型在其轮廓上的分段线性特征就是这一表示法主要的视觉缺陷,改进的唯一途径就是增加多边形的分辨率。
对于一个复杂形体来说,为了充分表示其细节,常常要用到十万个以上的多边形。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验六 9-7一、实验题目z-buffer 算法的代表性案例是绘制三个相互交叉的红绿蓝条,如图9-85所示,请使用MFC 编程实现。
二、实验思想Z-Buffer 算法建立两个缓冲器:深度缓冲器,用以存储图像空间中每一像素相应的深度值,初始化为最大深度值(z s 坐标)。
帧缓冲器,用以存储图像空间中的每个像素的颜色,初始化为屏幕的背景色。
① 帧缓冲器初始值置为背景色。
② 确定深度缓冲器的宽度、高度和初始深度。
一般将初始深度置为最大深度值。
③ 对于多边形表面中的每一像素(x s ,y s ),计算其深度值z s (x s ,y s )。
④ 将z s (x s ,y s )与存储在z 缓冲器中该位置的深度值zBuffer (x s ,y s )进行比较。
⑤ 如果z s (x s ,y s )≤zBuffer (x s ,y s ),则将此像素的颜色写入帧缓冲器,且用z (x s ,y s )重置zbuffer (x s ,y s )。
三、实验代码CZBuffer::~CZBuffer(){delete []P;}void CZBuffer::SetPoint(CPi3 p[],int m){P=new CPi3[m];for(int i=0;i<m;i++){P[i]=p[i];}PNum=m;}void CZBuffer::CreateBucket()//创建桶表{int yMin,yMax;yMin=yMax=P[0].y;for(int i=0;i<PNum;i++)//查找多边形所覆盖的最小和最大扫描线{if(P[i].y<yMin){yMin=P[i].y;//扫描线的最小值}if(P[i].y>yMax){yMax=P[i].y;//扫描线的最大值}}for(int y=yMin;y<=yMax;y++){if(yMin==y)//建立桶头结点{HeadB=new CBucket;//建立桶的头结点CurrentB=HeadB;//CurrentB为CBucket当前结点指针CurrentB->ScanLine=yMin;CurrentB->pET=NULL;//没有连接边链表CurrentB->next=NULL;}else//建立桶的其它结点{CurrentB->next=new CBucket;CurrentB=CurrentB->next;CurrentB->ScanLine=y;CurrentB->pET=NULL;CurrentB->next=NULL;}}}void CZBuffer::CreateEdge()//创建边表{for(int i=0;i<PNum;i++){CurrentB=HeadB;int j=(i+1)%PNum;//边的第二个顶点,P[i]和P[j]构成边if(P[i].y<P[j].y)//边的终点比起点高{Edge=new CAET;Edge->x=P[i].x;//计算ET表的值Edge->yMax=P[j].y;Edge->k=(P[j].x-P[i].x)/(P[j].y-P[i].y);//代表1/kEdge->pb=P[i];//绑定顶点和颜色Edge->pe=P[j];Edge->next=NULL;while(CurrentB->ScanLine!=P[i].y)//在桶内寻找该边的yMin{CurrentB=CurrentB->next;//移到yMin所在的桶结点}}if(P[j].y<P[i].y)//边的终点比起点低{Edge=new CAET;Edge->x=P[j].x;Edge->yMax=P[i].y;Edge->k=(P[i].x-P[j].x)/(P[i].y-P[j].y);Edge->pb=P[i];Edge->pe=P[j];Edge->next=NULL;while(CurrentB->ScanLine!=P[j].y){CurrentB=CurrentB->next;}}if(int(P[j].y)!=P[i].y){CurrentE=CurrentB->pET;if(CurrentE==NULL){CurrentE=Edge;CurrentB->pET=CurrentE;}else{while(CurrentE->next!=NULL){CurrentE=CurrentE->next;}CurrentE->next=Edge;}}}}void CZBuffer::Gouraud(CDC *pDC)//填充多边形{double CurDeep=0.0;//当前扫描线的深度double DeepStep=0.0;//当前扫描线随着x增长的深度步长double A,B,C,D;//平面方程Ax+By+Cz+D=0的系数CVector V21(P[1],P[2]),V10(P[0],P[1]);CVector VN=V21*V10;A=VN.X();B=VN.Y();C=VN.Z();D=-A*P[1].x-B*P[1].y-C*P[1].z;DeepStep=-A/C;//计算直线deep增量步长CAET *T1,*T2;HeadE=NULL;for(CurrentB=HeadB;CurrentB!=NULL;CurrentB=CurrentB->next){for(CurrentE=CurrentB->pET;CurrentE!=NULL;CurrentE=CurrentE->next) {Edge=new CAET;Edge->x=CurrentE->x;Edge->yMax=CurrentE->yMax;Edge->k=CurrentE->k;Edge->pb=CurrentE->pb;Edge->pe=CurrentE->pe;Edge->next=NULL;AddEt(Edge);}EtOrder();T1=HeadE;if(T1==NULL){return;}while(CurrentB->ScanLine>=T1->yMax)//下闭上开{T1=T1->next;HeadE=T1;if(HeadE==NULL)return;}if(T1->next!=NULL){T2=T1;T1=T2->next;}while(T1!=NULL){if(CurrentB->ScanLine>=T1->yMax)//下闭上开{T2->next=T1->next;T1=T2->next;}else{T2=T1;T1=T2->next;}}CRGB Ca,Cb,Cf;//Ca、Cb代边上任意点的颜色,Cf代表面上任意点的颜色Ca=Interpolation(CurrentB->ScanLine,HeadE->pb.y,HeadE->pe.y,HeadE->pb.c,He adE->pe.c);Cb=Interpolation(CurrentB->ScanLine,HeadE->next->pb.y,HeadE->next->pe.y,He adE->next->pb.c,HeadE->next->pe.c);BOOL Flag=FALSE;double xb,xe;//扫描线的起点和终点坐标for(T1=HeadE;T1!=NULL;T1=T1->next){if(Flag==FALSE){xb=T1->x;CurDeep=-(xb*A+CurrentB->ScanLine*B+D)/C;//z=-(Ax+By-D)/CFlag=TRUE;}else{xe=T1->x;for(double x=xb;x<xe;x++)//左闭右开{Cf=Interpolation(x,xb,xe,Ca,Cb);if(CurDeep>=ZB[ROUND(x)+Width/2][CurrentB->ScanLine+Height/2])//如果新采样点的深度大于原采样点的深度{ZB[ROUND(x)+Width/2][CurrentB->ScanLine+Height/2]=CurDeep;//xy坐标与数组下标保持一致pDC->SetPixel(ROUND(x),CurrentB->ScanLine,RGB(Cf.red*255,Cf.green*255,Cf.b lue*255));}CurDeep+=DeepStep;}Flag=FALSE;}}for(T1=HeadE;T1!=NULL;T1=T1->next)//边的连续性{T1->x=T1->x+T1->k;}}delete HeadB;delete HeadE;delete CurrentE;delete CurrentB;delete Edge;}void CZBuffer::AddEt(CAET *NewEdge)//合并ET表{CAET *CE;CE=HeadE;if(CE==NULL){HeadE=NewEdge;CE=HeadE;}else{while(CE->next!=NULL){CE=CE->next;}CE->next=NewEdge;}}void CZBuffer::EtOrder()//边表的冒泡排序算法{CAET *T1,*T2;int Count=1;T1=HeadE;if(T1==NULL){return;}if(T1->next==NULL)//如果该ET表没有再连ET表{return;//桶结点只有一条边,不需要排序}while(T1->next!=NULL)//统计结点的个数{Count++;T1=T1->next;}for(int i=1;i<Count;i++)//冒泡排序{T1=HeadE;if(T1->x>T1->next->x)//按x由小到大排序{T2=T1->next;T1->next=T1->next->next;T2->next=T1;HeadE=T2;}else{if(T1->x==T1->next->x){if(T1->k>T1->next->k)//按斜率由小到大排序{T2=T1->next;T1->next=T1->next->next;T2->next=T1;HeadE=T2;}}}T1=HeadE;while(T1->next->next!=NULL){T2=T1;T1=T1->next;if(T1->x>T1->next->x)//按x由小到大排序{T2->next=T1->next;T1->next=T1->next->next;T2->next->next=T1;T1=T2->next;}else{if(T1->x==T1->next->x){if(T1->k>T1->next->k)//按斜率由小到大排序{T2->next=T1->next;T1->next=T1->next->next;T2->next->next=T1;T1=T2->next;}}}}}}CRGB CZBuffer::Interpolation(double t,double t1,double t2,CRGB c1,CRGB c2)//线性插值{CRGB c;c=(t-t2)/(t1-t2)*c1+(t-t1)/(t2-t1)*c2;return c;}void CZBuffer::InitDeepBuffer(int width,int height,double depth)//初始化深度缓冲{Width=width,Height=height;ZB=new double *[Width];for(int i=0;i<Width;i++)ZB[i]=new double[Height];for(i=0;i<Width;i++)//初始化深度缓冲for(int j=0;j<Height;j++)ZB[i][j]=double(depth);}四、程序结果截图。
