第四章题解
近世代数第四章 环与域题解讲解

第四章环与域§1 环的定义一、主要内容1.环与子环的定义和例子。
在例子中,持别重要的是效域上的多项式环、n阶全阵环和线性变换环,以及集M的幂集环.2.环中元素的运算规则和环的非空子集S作成子环的充要条件:二、释疑解难1.设R是一个关于代数运算十,·作成的环.应注意两个代数运算的地位是不平等的,是要讲究次序的.所以有时把这个环记为(R,十,·)(或者就直接说“R对十,·作成一个环”).但不能记为R,·,十).因为这涉及对两个代数运算所要求满足条件的不同.我们知道,环的代数运算符号只是一种记号.如果集合只有二代数运算记为 ,⊕,又R对 作成一个交换群,对⊕满足结合律且⊕对 满足左、右分配律,即就是说,在环的定义里要留意两个代数运算的顺序.2.设R对二代数运算十,·作成一个环.那么,R对“十”作成一个加群,这个加群记为(R,十);又R对“·”作成一个半群,这个乍群记为(R,·).再用左、右分配律把二者联系起来就得环(R,十.·).三、习题4.1解答1.2.3.4.5.6.7.8.证明:循环环必是交换环,并且其子环也是循环环.§4.2 环的零因子和特征一、主要内容1.环的左、右零因子和特征的定义与例子.2.若环R 无零因子且阶大于1,则R 中所有非零元素对加法有相同的阶.而且这个相同的阶不是无限就是一个素数.这就是说,阶大于l 且无零因子的环的特征不是无限就是一个素数. 有单位元的环的特征就是单位元在加群中的阶.3.整环(无零因子的交换环)的定义和例子. 二、释疑解难1.由教材关于零因子定义直接可知,如果环有左零因子,则R 也必然有右零因子.反之亦然.但是应注意,环中一个元素如果是一个左零因子,则它不一定是一个右零因子.例如,教材例l 中的元素⎪⎪⎭⎫⎝⎛0001就是一个例子.反之,一个右零因子也不一定是一个左零因子.例如,设置为由一切方阵),(00Q y x y x ∈∀⎪⎪⎭⎫ ⎝⎛对方阵普通加法与乘法作成的环.则易知⎪⎪⎭⎫⎝⎛0001是R 的一个右零因子,但它却不是R 的左零因子.2.关于零因子的定义.关于零因子的定义,不同的书往往稍有差异,关键在于是否把环中的零元也算作零因子.本教材不把零元算作零因子,而有的书也把零元算作零因子.但把非牢的零因子称做真零因子.这种不算太大的差异,读者看参考书时请留意.3.关于整环的定义.整环的定义在不同的书中也常有差异.大致有以下4种定义方法: 定义1 无零因子的交换环称为整环(这是本教材的定义方法). 定义2 阶大于l 且无零因子的交换环,称为整环. 定义3 有单位元且无零因子的交换环,称为整环.定义4 阶大于1、有单位元且无零因子的交换环,称为整环.以上4种定义中,要求整环无零因子、交换是共同的,区别就在于是否要求有单位元和阶大于1.不同的定义方法各有利弊,不宜绝对肯定哪种定义方法好或不好.这种情况也许到某个时期会得到统一.但无论如何现在看不同参考书时应留意这种差异.本教材采用定义1的方法也有很多原因,现举一例。
马克思第四章课后习题解答

第四章1、如何理解“资本来到世间,从头到脚,每个毛孔都滴着血和肮脏的东西”?答:资本主义的发展史,就是资本剥削劳动、列强掠夺弱国的历史,这种剥夺的历史是用血和火的文字载入人类编年史的。
在自由竞争时代,西方列强用坚船利炮在世界范围开辟殖民地,贩卖奴隶,贩卖鸦片,依靠殖民战争和殖民地贸易进行资本积累和扩张。
发展到垄断阶段后,统一的、无所不包的世界市场和世界资本主义经济体系逐步形成,资本家垄断同盟为瓜分世界而引发了两次世界大战,给人类带来巨大浩劫。
二战后,由于社会主义的胜利和民族解放运动的兴起,西方列强被迫放弃了旧的殖民主义政策,转而利用赢得独立和解放的广大发展中国家大规模工业化的机会,扩大资本的世界市场,深化资本的国际大循环,通过不平等交换、资本输出、技术垄断以及债务盘剥等,更加巧妙地剥削和掠夺发展中国家的资源和财富。
在当今经济全球化进程中,西方发达国家通过它们控制的国际经济、金融等组织,通过它们制定的国际“游戏规则”,推行以所谓新自由主义为旗号的经济全球化战略,继续主导国际经济秩序,保持和发展它们在经济结构和贸易、科技、金融等领域的全球优势地位,攫取着经济全球化的最大好处。
资本惟利是图的本性、资本主义生产无限扩大的趋势和整个社会生产的无政府状态,还造成日益严重的资源、环境问题,威胁着人类的可持续发展和生存。
我们今天看到的西方发达资本主义国家的繁荣稳定,是依靠不平等、不合理的国际分工和交换体系,依靠发展中国家提供的广大市场、廉价资源和廉价劳动力,通过向发展中国家转嫁经济社会危机和难题、转移高耗能高污染产业等方式实现的。
资本主义没有也不可能给世界带来普遍繁荣和共同富裕。
2、如何理解商品二因素的矛盾来自劳动二重性的矛盾?答:商品二因素是由生产商品的劳动二重性决定的。
生产商品的劳动,一方面是具体劳动,另一方面又是抽象劳动。
具体劳动创造商品的使用价值,抽象劳动形成商品的价值。
具体劳动反映人与自然的关系,而抽象劳动反映的则是社会生产关系,是一个历史范畴。
第04章 集成运算放大电路题解

第四章集成运算放大电路自测题一、选择合适答案填入空内。
(1)集成运放电路采用直接耦合方式是因为。
A.可获得很大的放大倍数B. 可使温漂小C.集成工艺难于制造大容量电容(2)通用型集成运放适用于放大。
A.高频信号B.低频信号C.任何频率信号(3)集成运放制造工艺使得同类半导体管的。
A.指标参数准确B.参数不受温度影响C.参数一致性好(4)集成运放的输入级采用差分放大电路是因为可以。
A.减小温漂B. 增大放大倍数C. 提高输入电阻(5)为增大电压放大倍数,集成运放的中间级多采用。
A.共射放大电路B.共集放大电路C.共基放大电路解:(1)C (2)B (3)C (4)A (5)A二、判断下列说法是否正确,用“√”或“×”表示判断结果填入括号内。
(1)运放的输入失调电压U I O 是两输入端电位之差。
( ) (2)运放的输入失调电流I I O 是两端电流之差。
( ) (3)运放的共模抑制比cdCMR A A K =( ) (4)有源负载可以增大放大电路的输出电流。
( )(5)在输入信号作用时,偏置电路改变了各放大管的动态电流。
( ) 解:(1)× (2)√ (3)√ (4)√ (5)× 三、电路如图T4.3所示,已知β1=β2=β3=100。
各管的U B E 均为0.7V ,试求I C 2的值。
图T4.3解:分析估算如下: 100BE1BE2CC =--=RU U V I R μ AβCC B1C0B2C0E1E2CC1C0I I I I I I I I I I I I R +=+=+====1001C =≈⋅+=R R I I I ββμA四、电路如图T4.4所示。
图T4.4(1)说明电路是几级放大电路,各级分别是哪种形式的放大电路(共射、共集、差放……);(2)分别说明各级采用了哪些措施来改善其性能指标(如增大放大倍数、输入电阻……)。
解:(1)三级放大电路,第一级为共集-共基双端输入单端输出差分放大电路,第二级是共射放大电路,第三级是互补输出级。
《理论力学》第四章-力系平衡试题及答案
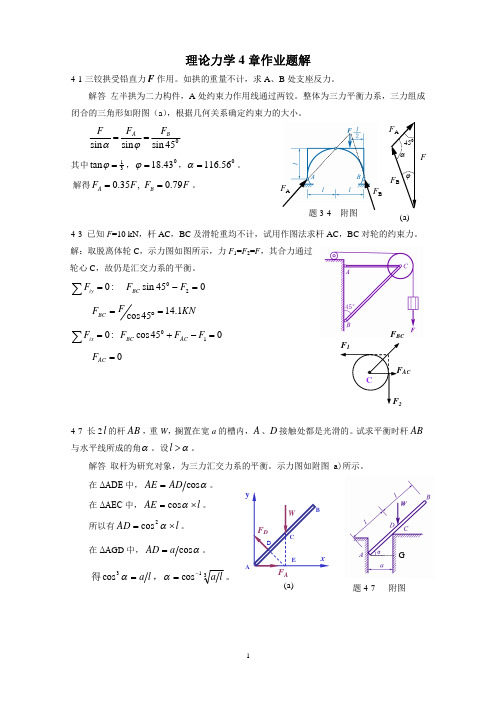
理论力学4章作业题解4-1三铰拱受铅直力F 作用。
如拱的重量不计,求A 、B 处支座反力。
解答 左半拱为二力构件,A 处约束力作用线通过两铰。
整体为三力平衡力系,三力组成闭合的三角形如附图(a ),根据几何关系确定约束力的大小。
45sin sin sin B A F F F ==j a其中31tan =j ,043.18=j ,056.116=a 。
解得F F F F B A 79.0 ,35.0==。
4-3 已知F =10 kN ,杆AC ,BC 及滑轮重均不计,试用作图法求杆AC ,BC 对轮的约束力。
解:取脱离体轮C ,示力图如图所示,力F 1=F 2=F ,其合力通过轮心C ,故仍是汇交力系的平衡。
:0=åiyF 045sin 20=-F F BCKN FF BC 1.1445cos =°=045cos :010=-+=åF F F FAC BC ix0=AC F4-7 长2l 的杆AB ,重W ,搁置在宽a 的槽内,A 、D 接触处都是光滑的。
试求平衡时杆AB 与水平线所成的角a 。
设a >l 。
解答 取杆为研究对象,为三力汇交力系的平衡。
示力图如附图(a)所示。
在ΔADE 中,a cos AD AE =。
在ΔAEC 中,l AE ´=a cos 。
所以有l AD ´=a 2cos 。
在ΔA GD 中,a cos a AD =。
得a =a 3cos ,31cosl a -=a 。
F BCAC题3-4 附图F BF AF BF AFa45j(a)A (a)题4-7 附图G4-9 AB ,AC ,AD 三连杆支撑一重物,如图所示。
已知W=10kN ,AB =4m ,AC =3 m ,且ABEC 在同一水平面内,试求三连杆所受的力。
解:取铰A 研究,示力图如图示,为汇交力系的平衡。
0=åix F : 05430sin =´°+AD AB F F 0=åiy F : 05330sin =´°+AD AC F F 0=åiZF: 030cos =-°W F AD联立求解KNF KNF KN F AD AC AB 5.115.36.4=-=-=4-8 图示结构上作用一水平力F 。
第四章 习题解答

1 第四章 习题解答3/150、试用实验方法鉴别晶体SiO 2、SiO 2 玻璃、硅胶和SiO 2 熔体。
它们的结构有什么不同?解答:利用X-射线粉末衍射检测。
晶体SiO 2——质点在三维空间做有规律的排列,各向异性。
SiO 2 熔体——内部结构为架状,近程有序,远程无序。
SiO 2 玻璃——各向同性。
硅胶——疏松多孔。
7/151、SiO 2 熔体的粘度在1000℃时为1014 Pa·s ,在1400℃时为107 Pa·s 。
SiO 2 玻璃粘滞流动的活化能是多少?上述数据为恒压下取得,若在恒容下获得,你认为活化能会改变吗?为什么?解答:(1)根据公式:)exp(0RTE ∆=ηη 1000℃时,η=1014 Pa·s ,T=1000+273=1273K , )1273314.8exp(10014⨯∆=E η (1) 1400℃时,η=107 Pa·s ,T =1400+273=1673K ,)1673314.8exp(1007⨯∆=E η (2) 联立(1)和(2)式解得:η0 = 5.27×10-16 Pa·s ,△E = 713.5 kJ/mol(2)若在在恒容下获得,活化能不会改变。
因为活化能是液体质点作直线运动所必需的能量。
它与熔体组成和熔体[SiO 4]聚合程度有关。
212/151、一种用于密封照明灯的硼硅酸盐玻璃,它的退火点是544℃,软化点是780℃。
求:(1)这种玻璃粘性流动的活化能;(2)它的工作范围;(3)它的熔融范围。
解答:(1)根据公式:)exp(0RTE ∆=ηη 退火点544℃, η=1012Pa·s ,T=544+273=817K , )817314.8exp(10012⨯∆=E η (1) 软化点为780℃,η=4.5×106 Pa·s ,T=780+273=1053K ,)1053314.8exp(104.506⨯∆=⨯E η (2)联立(1)和(2)式解得:η0 = 1.39×10-12 Pa·s ,△E = 373.13 kJ/mol 。
第4章 习题解答
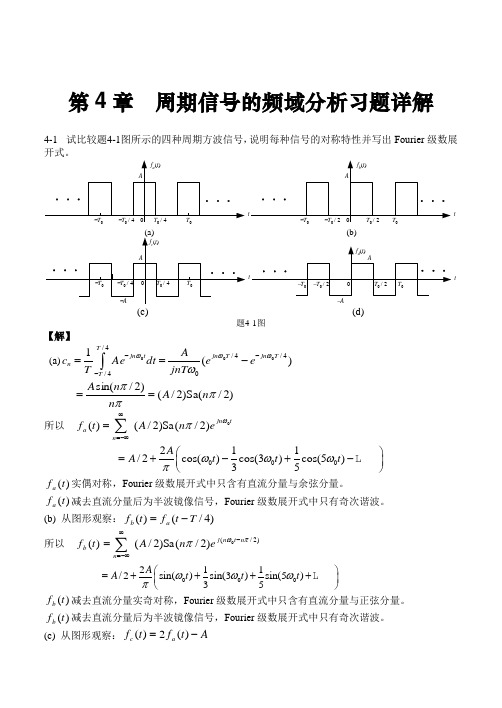
第4章 周期信号的频域分析习题详解4-1 试比较题4-1图所示的四种周期方波信号,说明每种信号的对称特性并写出Fourier 级数展开式。
tt(b)tt-A(c) (d)题4-1图【解】 (a))(14/4/04/4/000T jn T jn tjn T T n eejnT A dt AeTc ωωωω----==⎰)2/(Sa )2/()2/sin(πππn A n n A ==所以 tjn n a e n A t f 0)2/(Sa )2/()(ωπ∑∞-∞==000211/2cos()cos(3)cos(5)35A A t t t ωωωπ⎛⎫=+-+- ⎪⎝⎭)(t f a 实偶对称,Fourier 级数展开式中只含有直流分量与余弦分量。
)(t f a 减去直流分量后为半波镜像信号,Fourier 级数展开式中只有奇次谐波。
(b) 从图形观察:)4/()(T t f t f a b -=所以 )(t f b )2/(0)2/(Sa )2/(πωπn t n j n en A -∞-∞=∑=000211/2sin()sin(3)sin(5)35A A t t t ωωωπ⎛⎫=++++ ⎪⎝⎭)(t f b 减去直流分量实奇对称,Fourier 级数展开式中只含有直流分量与正弦分量。
)(t f b 减去直流分量后为半波镜像信号,Fourier 级数展开式中只有奇次谐波。
(c) 从图形观察:A t f t f a c -=)(2)(第4章 周期信号的频域分析 83所以 tjn n n c en A t f 0)2/(Sa )(0,ωπ∑∞≠-∞==000411c o s ()c o s (3)c o s (5)35A t t t ωωωπ⎛⎫=-+- ⎪⎝⎭)(t f c 实偶对称,且是半波镜像信号,Fourier 级数展开式中只含有奇次谐波的余弦分量。
(d) 从图形观察:)4/()(T t f t f c d -=所以 )2/(0,0)2/(Sa )(πωπn t n j n n d en A t f -∞≠-∞=∑=000411sin()sin(3)sin(5)35A t t t ωωωπ⎛⎫=++- ⎪⎝⎭)(t f d 实奇对称,且是半波镜像信号,Fourier 级数展开式中只含有奇次谐波的正弦分量。
计算机系统结构 第四章(习题解答)
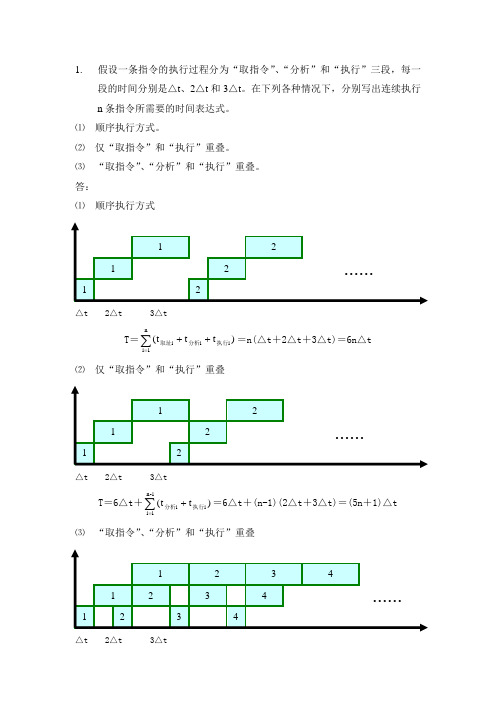
1. 假设一条指令的执行过程分为“取指令”、“分析”和“执行”三段,每一段的时间分别是△t 、2△t 和3△t 。
在下列各种情况下,分别写出连续执行n 条指令所需要的时间表达式。
⑴ 顺序执行方式。
⑵ 仅“取指令”和“执行”重叠。
⑶ “取指令”、“分析”和“执行”重叠。
答:⑴ 顺序执行方式12 ......1 2 12T =∑=++n1i i i i )t t t (执行分析取址=n(△t +2△t +3△t)=6n △t⑵ 仅“取指令”和“执行”重叠12 ......1 212T =6△t +∑=+1-n 1i i i )t t (执行分析=6△t +(n-1)(2△t +3△t)=(5n +1)△t⑶ “取指令”、“分析”和“执行”重叠12 34 ......1 2 3 41234△t2△t3△t△t2△t3△t△t2△t3△tT =6△t +∑=1-n 1i i )t (执行=6△t +(n-1)(3△t)=(3n +3)△t2. 一条线性流水线有4个功能段组成,每个功能段的延迟时间都相等,都为△t 。
开始5个任务,每间隔一个△t 向流水线输入一个任务,然后停顿2个△t ,如此重复。
求流水线的实际吞吐率、加速比和效率。
答:1 2 3 4 5 6 7 8 9 10 11 12 13 14 15...1 2 3 4 5 6 7 8 9 10 11 12 13 14 151 2 3 4 5 6 7 8 9 10 11 12 13 14 15 1 2 3 4 56 7 8 9 10 11 12 13 14 151 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23我们可以看出,在(7n+1)Δt 的时间内,可以输出5n 个结果,如果指令的序列足够长(n →∞),并且指令间不存在相关,那么,吞吐率可以认为满足:)n (t75t )n /17(5t )1n 7(n 5TP ∞→∆=∆+=∆+=加速比为:)n (720n /17201n 7n 20t )1n 7(t 4n 5S ∞→=+=+=∆+∆⨯=从上面的时空图很容易看出,效率为:)n (75n /1751n 7n 5t )1n 7(4t 4n 5E ∞→=+=+=∆+⨯∆⨯=3. 用一条5个功能段的浮点加法器流水线计算∑==101i i A F 。
《概率论与数理统计》第04章习题解答

第四章 正态分布1、解:(0,1)ZN(1){ 1.24}(1.24)0.8925P Z ∴≤=Φ={1.24 2.37}(2.37)(1.24)0.99110.89250.0986P Z <≤=Φ-Φ==-= {2.37 1.24}( 1.24)( 2.37)(1.24)(2.37)0.89250.99110.0986P Z -<≤-=Φ--Φ-=-Φ+Φ=-+=(2){}0.9147()0.9147 1.37{}0.05261()0.0526()0.9474 1.62P Z a a a P Z b b b b ≤=∴Φ==≥=-Φ=Φ==,,得,,,得2、解:(3,16)XN8343{48}()()(1.25)(0.25)0.89440.59870.295744P X --∴<≤=Φ-Φ=Φ-Φ=-= 5303{05}()()(0.5)(0.75)44(0.5)1(0.75)0.691510.77340.4649P X --<≤=Φ-Φ=Φ-Φ-=Φ-+Φ=-+= 31(25,36){25}0.95442(3,4){}0.95X N C P X C X N C P X C -≤=>≥、()设,试确定,使;()设,试确定,使解:(1)(25,36){25}0.9544X N P X C -≤=,{2525}0.9544P C X C ∴-≤≤+=25252525()()0.954466()()2()10.9544666()0.9772,21266C C C C CC CC +---Φ-Φ=-Φ-Φ=Φ-=Φ=∴==即, (2)(3,4){}0.95XN P X C >≥,331()0.95()0.952231.6450.292C CCC ---Φ≥Φ≥-≥≤-即,,4、解:(1)2(3315,575)XN4390.2533152584.753315{2584.754390.25}()()575575(1.87)( 1.27)(1.87)1(1.27)0.969310.89800.8673P X --∴≤≤=Φ-Φ=Φ-Φ-=Φ-+Φ=-+= (2)27193315{2719}()( 1.04)1(1.04)10.85080.1492575P X -≤=Φ=Φ-=-Φ=-=(25,0.1492)YB ∴4440{4}(0.1492)(10.1492)0.6664ii i i P Y C -=∴≤=-=∑5、解:(6.4,2.3)X N{}{}1()81(1.055)10.85540.14462.3(85}0.17615 6.451(0.923)(0.923)0.82121()2.3P X P X X P X -Φ>-Φ-∴>>======->-Φ-Φ-Φ6、解:(1)2(11.9,(0.2))XN12.311.911.711.9{11.712.3}()()(2)(1)(2)1(1)0.20.20.977210.84130.8185P X --∴<<=Φ-Φ=Φ-Φ-=Φ-+Φ=-+= 设A ={两只电阻器的电阻值都在欧和欧之间} 则2()(0.8185)0.6699P A ==(2)设X , Y 分别是两只电阻器的电阻值,则22(11.9,(0.2))(11.9,(0.2))X N Y N ,,且X , Y 相互独立[]22212.411.9{(12.4)(12.4)}1{12.4}{12.4)}1()0.21(2.5)1(0.9938)0.0124P X Y P X P Y -⎡⎤∴>>=-≤⋅≤=-Φ⎢⎥⎣⎦=-Φ=-=7、一工厂生产的某种元件的寿命X (以小时计)服从均值160μ=,均方差为的正态分布,若要求{120200}0.80P X <<≥,允许最大为多少解:因为2(160,)XN σ由2001601201600.80{120200}()()P X σσ--≤<<=Φ-Φ从而 40402()10.80()0.9σσΦ-≥Φ≥,即,查表得401.282σ≥,故σ≤8、解:(1)2(90,(0.5))XN8990{89}()(2)1(2)10.97720.02280.5P X -∴<=Φ=Φ-=-Φ=-= (2)设2(,(0.5))X N d由808080{80}0.991()0.99()0.99 2.330.50.50.5d d d P X ---≥≥∴-Φ≥Φ≥≥,,,即 从而d ≥ 9、解:22~(150,3),~(100,4)X Y X N Y N 与相互独立,且则(1)2221~(150(100,3)4)(250,5)W X Y N N =+++=()222222~2150100,(2)314(200,52)W X Y N N =+-⨯+-⨯+⨯=-22325~(125,)(125,(2.5))22X Y W N N +== (2)242.6250{242.6}()( 1.48)1(1.48)10.93060.06945P X Y -+<=Φ=Φ-=-Φ=-= 12551255125522212551251255125()1()(2)1(2)2.5 2.522(2)220.97720.0456X Y X Y X Y P P P ⎧+⎫++⎧⎫⎧⎫->=<-+>+⎨⎬⎨⎬⎨⎬⎩⎭⎩⎭⎩⎭--+-=Φ+-Φ=Φ-+-Φ=-Φ=-⨯=10、解:(1)22~(10,(0.2)),~(10.5,(0.2))X N Y N X Y ,且与相互独立22~(0.5,2(0.2))(0.5,(0.282))X Y N N ∴--⨯=-0(0.5){0}()(1.77)0.96160.282P X Y ---<=Φ=Φ=(2)22~(10,(0.2)),~(10.5,)X N Y N X Y σ设,且与相互独立222~(0.5,2(0.2))(0.5,(0.2))X Y N N σ∴--⨯=-+0.90{0}P X Y ≤-<=Φ=Φ由1.28≥,故σ≤11、设某地区女子的身高(以m 计)2(1.63,(0.025))WN ,男子身高(以m 计)2(1.73,(0.05))MN ,设各人身高相互独立。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
4-1 在定态操作反应器的进口物料中脉冲注入示踪物料。
出口处示踪物浓度随时间变化的情况如下。
假设在该过程中物料的密度不发生变化,试求物料的平均停留时间与])(2)(4[3109753864210c c c c c c c c c c tdt c i +++++++++∆=⎰∞]0)5.20.1025.1(2)0.10.55.125.6(40[32++++++++==100min)/1(100)()(0tii c dtc t c t E ==⎰∞})(])()()()([2])()()()([4)({31010997755338866442211_t E t t E t t E t t E t t E t t E t t E t t E t t E t t E t tt +++++++++∆=]0)03.08.05.0(2)14.05.075.013.0(40[32+++++++++=min 187.6=⎰∞=-=-=02222971.8187.625.47)(t dt t E t tσmin 24-2 无量纲方差表达式的推导 (1)推导无量纲方差222/ttσσθ=;(2)推导CSTR 的22tt=σ。
1. τθt=2. ττtet E -=1)(证明:222)(i i i ittt t E t -∆=∑∞σ⎰∞--=221tdt e t t ττ22)()()()(ττθθττθ--=⎰∞-d t E()]1)1([022--=⎰∞θθθτd E22θστ= 222/τσσθt=∴ 220222)(1)(--∞-=-=⎰⎰t dt e tt dt t E t ttττσ222ττ-=2τ=22τσ=t4-3 设()θF 及()θE 分别为闭式流动反应器的停留时间分布函数及停留时间分布密度函数,θ为对此停留时间。
(1)若该反应器为平推流反应器,试求①F(1); ②E(1);③F(0.8);④E(0.8);⑤F(1.2) (2)若该反应器为全混流反应器,试求①F(1); ②E(1);③F(0.8);④E(0.8);⑤F(1.2) (3)若该反应器为非理想流动反应器,试求 ①F(∞); ②F(0);③E(∞);④E(0);⑤⎰∞0)(θθd E ;⑥⎰∞)(θθθd E解1平推流模型0)(=θF )(t t 〈 0)(=θE )(t t ≠1)(=θF )(t t≥ ∞=)(θE )(t t =)()(τθtF F =⎪⎩⎪⎨⎧===2.1,18.0,01,1θθθ⎩⎨⎧=====8.0,01,1)()(θθτθt E E2 全混流θθ-=e E )( , θθ--=e F 1)(==)()(τθt f F ⎪⎭⎪⎬⎫=-=-=----699.01551.01632.012.18.01e e e ⎪⎩⎪⎨⎧===2.18.01θθθ ==)()(τθtE E ⎪⎭⎪⎬⎫==--449.0368.08.01e e ⎩⎨⎧==8.01θθ3非理想流动模型a 多釜串联θθθN N N e N N E ---=1)!1()(, 0)(C C F N =θ()()1]!11)(!21)(!111[1)(12=-++++-=∞--N N N N N N e F θθθθ()()0]!11)(!21)(!111[1)0(12=-++++-=--N N N N N N eF θθθθ()()()0!11=-=∞--θθN N Ne N N E()()1,00!1001≠=-=-N e N N E N N()()1!1!1)(01010=-=-=⎰⎰⎰∞--∞--∞θθθθθθθθd e N N d e N N d E N N NN N N ()1!1)(0=-=⎰⎰∞-∞θθθθθθd e N N d E N N N4-4 C(t)t/min4-18图用阶跃法测定某一闭式流动反应器的停留时间分布,得到离开反应器的示踪剂浓度与时间的关系,如图4-18所示。
⎪⎩⎪⎨⎧-=120)(t t c 3322〉≤≤≤t t t试求 (1)该反应器的停留时间分布函数)(θF 及分布密度函数)(θE ;(2)数学期望θ 及方差2θσ;(3)若用多釜串联模型来模拟该反应器,则模型参数是多少?(4)若用轴向扩散模型来模拟该反应器,则模型参数是多少?(5)若在此反应器内进行1级不可逆反应,反应速率常数1min 1-=k ,且无副反应,试求反应器出口转化率。
解(1).()()θF c t c t F ==0)(⎪⎩⎪⎨⎧-=120)(t t c 3322〉≤≤≤t t t()⎪⎩⎪⎨⎧-==∴120)(0t c t c t F 3322〉≤≤≤t t t ,()θF t F =)(⎪⎩⎪⎨⎧=∆∆=010)(0t c c t E3322〉≤≤≤t t t ,()t t E E =)(θ()⎰⎰⎰⎰==⋅++⋅==∞∞2233225232100t dt t tdt dt t dt t tE t()⎪⎪⎩⎪⎪⎨⎧=0250θE 3322〉≤≤≤t t t(2). 1==-ttθ()751]425[254425]010[25432232322202222222=-=-+⨯+=-==⎰⎰⎰⎰⎰∞-∞-dt t dt t dt t dt t tt dt t E t tt σσθ(3). 多釜串联模型75122222====θσσστt t t N ()()()θθθθθ75175751!17575!1-----=-=e e N N E N N N()()]!11)(!21)(!111[1)(12---++++-=N N N N N N e F θθθθθ ()()]75!1751)75(!21)75(!111[1)(175275---++++-=θθθθθ e F(4). 轴向扩散模型()0133.075112222==--=-Pee Pe Pe θσ 试差 Pe=0.001(5).()⎰⎰⎰⎰∞---∞-++==-332200101dte dt e dt e dt t E e x kt ktktktA0855.023=-=-te%45.91=A x4-5. 为了测定某一闭式流动反应器的停留时间分布,采用脉冲输入法,反应(1)反应物料在该反应器中的平均停留时间t 及方差2θσ(2)停留时间小于4.0min 的物料所占的分率。
解(1).])(2)(4[3109753864210c c c c c c c c c c tdt c i +++++++++∆=⎰∞()()025.46321365040[31++++++++++=33.30=33.30)()(0tiic dt c t c t E ==⎰∞ min 1 })(])()()()([2])()()()([4)({31111997755338866442211_t E t t E t t E t t E t t E t t E t t E t t E t t E t t E t tt +++++++++∆=()088.4]0528.089.0792.0196.02297.0686.099.0492.0040[31=+⎪⎪⎭⎫⎝⎛+++++++++=⎰∞=-=-=0222253.10088.4244.27)(t dt t E t tσ63.0222==tt σσθ(2). ()()()()()()24]321[2014E E E E E dt t E ++++⨯=⎰361.0=4-6将一定量的示踪剂从一管式流动反应器的进口处注入,并在该反应器的出口处连续检测示踪剂的浓度()t c ,得到如下数据:(1)试根据上述实验数据计算平均停留时间;(2)如果在该管式反应器中进行一级不可逆反应RA k −→−1,11min 045.0-=k 试计算反应物A 的平均转化率;(3)试根据理想平推流模型计算平均转化率并与(2)结果进行比较;(4)若按照多级CSTR 模型处理,求模型参数N 和停留时间分布函数F(t)。
(1). 应用辛普森法则()800=⎰∞dt t c , ()()80t c t E i =1/min})(])()()([2])()()()([4)({3997755338866442211_t E t t E t t E t t E t t E t t E t t E t t E t t E t tt ++++++++∆= min 73.11=()8.360222=-=⎰∞t dt t E t ii tσ (2).R A k −→−111min 045.0-=k()6.0415.010=⨯==-⎰∞-dt t E e x ktA , %40=A x(3).平推流%7.99997.01173.11045.0==-=-=⨯--e e x kt A,返混造成了实际转化率下降了50多。
(4)多级CSTR 串联模型47.38.3673.11222≈===-t t N σ ()324332841[1θθθθθ+++-=-eF , -=tt θ()()θF t F =4-7. 用阶跃法测定某一闭式流动反应器的停留时间分布,得到离开反应器的示(1)试求该反应器的停留时间分布函数及平均停留时间;(2)若在该反应器内的物料为微观流体,且进行1级不可逆反应,反应速率常数105.0-=s k,预计反应器出口出的转化率;(3)若在该反应器内的物料为宏观流体,其他条件不变,试问反应器出口处的转化率是多少?解. (1) ()()0c t c t F = , ()()t t F t E ∆∆=()()∑⎰∞∞∆==i iitt E t dt t tE t()S 2.620151069010107751010136510101955101052451010133510107251510415033333333=+⨯⨯⨯+⨯⨯⨯+⨯⨯⨯+⨯⨯⨯+⨯⨯⨯+⨯⨯⨯+⨯⨯⨯+⨯⨯⨯+=--------(2). 微观()()∑⎰∆≈=--∞-nii kt kt A t t E e dt t E e x i 01%4.86,136.0100136.0=-=⨯=A x(3). 宏观,对于一级反应宏观流体与微观流体转化率一样%4.86=Ax4-8.已知一等温闭式流动反应器的停留时间分布密度函数()t te t E 416-=min-1试求:(1)平均停留时间;(2)空时;(3)空速;(4)停留时间小于1min 的物料所占得分率;(5)停留时间大于1min 的物料所占的分率;(6)若用CSTR 串联模型来模拟反应器,则模型参数(N )为多少? 解. (1) ()t te t E416-=()21281604040420=====⎰⎰⎰⎰∞-∞-∞-∞dt e tdedt e t dt t tE t tttmin(2). 空时21==-t τmin(3). 空速 21==τSmin-1(4). ()4441141101416-----=-===⎰⎰⎰e edt e dt tedt t E tt t9817.0=(5). ()0183.0110=-⎰dt t E(6). CSTR 串联模型参数为:()8323612160404042430222=====-=⎰⎰⎰⎰⎰∞-∞-∞-∞-∞-dt e dtt e det dt e t t dt t E t t t tttσ328321,1222222=⎪⎭⎫⎝⎛====--t t t N N tσσσθ4-9 在一个全混釜中,等温下进行零级反应A →B ,反应速率为()L mol r A ∙=min /9,进料浓度L mol c A /100=,流体在反应器内的平均停留时间min 1=t,请按下列情况分别计算反应器出口转化率:(1)若反应物料为微观流体; (2)若反应物料为宏观流体; 解. A →B L mol r A∙=min /9, L mol c A /100= min 1=t(1).微观流体91010AfAfAfA c r c c t -=⇒-=, L mol c Af/1=%90=Afx(2)宏观流体,零级反应,反应速率与浓度无关,kt c c A A =-0()Lmol t k C dt t E kt C dt t E c c A A A A /1910)()(000--=-=-==-∞∞⎰⎰ 90.0=Ax ,与微观流体转化效果相同4-10 在具有如下停留时间分布的反应器,等温进行一级不可逆反应A →P ,反应速率常数为1min2-。
