3.3刚体定轴转动中的功与能
刚体绕定轴转动的动能定理

刚体绕定轴转动的动能定理1. 引言刚体是指其内部各点之间的相对位置关系在运动过程中不会发生改变的物体。
刚体绕定轴转动是指刚体在固定轴线上做圆周运动的情况。
动能定理是物理学中的一条重要定理,描述了物体运动过程中动能的变化与外力做功之间的关系。
本文将对刚体绕定轴转动的动能定理进行全面详细、完整且深入的阐述。
2. 刚体绕定轴转动在刚体绕定轴转动的情况下,我们需要考虑刚体的转动惯量和角速度等因素。
转动惯量是描述刚体对转动运动抵抗程度的物理量,通常用符号I表示。
角速度是描述刚体旋转快慢程度的物理量,通常用符号ω表示。
根据牛顿第二定律和角动量守恒定律,我们可以得到刚体绕定轴转动时的基本方程:τ=Iα其中,τ表示作用于刚体上产生转矩(力矩)大小,α表示角加速度。
刚体绕定轴转动的运动规律与作用在刚体上的转矩和转动惯量有关。
3. 动能定理的推导根据刚体绕定轴转动的基本方程,我们可以推导出刚体绕定轴转动的动能定理。
我们来考虑刚体上某一质点的动能T。
由于刚体上各质点都在绕着同一个轴旋转,因此它们具有相同的角速度ω。
设某一质点到轴心的距离为r,则该质点具有的线速度v为v=rω。
该质点的动能T′可以表示为:T′=12mv2=12m(rω)2=12mr2ω2其中,m表示质点的质量。
由于刚体是由众多质点组成的,因此整个刚体的动能T 可以表示为所有质点动能之和:T=∑Tni=1′i其中,n表示刚体上质点的总数。
根据牛顿第二定律和角动量守恒定律,我们知道刚体绕定轴转动时转动惯量I和角加速度α之间存在关系τ=Iα。
将该关系代入动能的表达式中,得到:T=12Iω2其中,ω表示整个刚体的角速度。
刚体绕定轴转动的动能可以表示为12Iω2。
这就是刚体绕定轴转动的动能定理。
4. 动能定理的物理意义刚体绕定轴转动的动能定理描述了刚体在转动过程中动能的变化与外力做功之间的关系。
根据动能定理,我们可以得出以下物理结论:1.外力对刚体做功会改变刚体的动能。
大学物理 3.3刚体定轴转动中的功与能

冲头做的功。
解:以 1和 2 分别表示冲孔前后的飞轮的角速度
2n 1
8rad s1
1 60
1 0.2 0.8
2
1
1
由转动动能定理 A 1 J 2 1 J 2 1 J 2 0.82 1
2
2 2
1
2
1
又 J 1 mr2 2
A 5.45103 J
1.绕定轴转动刚体的动能
Δm ,Δm ,,Δm ,,Δm
1
2
i
N
r, r, , r , r
1
2
i,
N
v,v ,,v,,v
1
2
i
N
v r
i
i
E 1 Δmv 2
i2
ii
刚体的总动能
E 1 Δm v 2 1 Δm r 2 2
例3-7半径R质量M的圆盘滑轮可绕通过盘心的水平轴转 动,滑轮上绕有轻绳,绳的一端悬挂质量为m的物体。 当物体从静止下降距离h时,物体速度是多少?
解:以滑轮、物体和地球组成系统为研究对 象。由于只有保守力做功,故机械能守恒。
设终态时重力势能为零
R M
初态:动能为零,重力势能为
v
末态:动能包括滑轮转动动能和物体平动动能
2
合外力矩对刚体所做的功等于刚体转动动能的增量。 这就是刚体定轴转动的动能定理
例3-6 某一冲床利用飞轮的转动动能通过曲柄连杆机构 的传动,带动冲头在铁板上穿孔。已知飞轮为均匀圆盘, 其半径为r=0.4m,质量为m=600kg,飞轮的正常转速 是 n 240r min,1 冲一次孔转速降低20%。求冲一次孔
刚体的能量定轴转动的动能定理
三、转动动能
刚体绕定轴以角速度旋转 刚体的动能应为各质元动能之 和为此将刚体分割成很多很小的
r i vi mi
M
质元 m1, m2 mi mn
r 任取一质元 mi 距转轴 i ,则该质元动能:
mivi2 / 2 mi (ri)2 / 2 miri22 / 2
故刚体的转动动能:
n
Ek Ek
在一微小过程中 力矩作的功
dA Md (1)
在一微小过程中
XX 力1矩O1作的2功2 M M
dA Md (1)
在考虑一个有限过程,设
在力矩作用下,刚体的角
位置由 功
1
2
则力矩的
A dA 2 Md (2) 1
力矩的功反映力矩对空间的积累作用,力矩越 大,在空间转过的角度越大,作的功就越大。 这种力矩对空间的积累作用的规律是什么呢?
/2 mg L cosd
0
2
mgL / 2
N
YZ
XO
r
mg
依动能定理
A力矩
1 2
J2
1 2
J02
A力矩
mg
L 2
mg
L 2
1 2
J
2
0
mgL J
mgL 1 mL2
3g L
3
XX
1
1 O
2
2
2 1
Md
1 2
J
2 2
1 2
J12
M
M
例)设一细杆的质量为m,长为L,一端支以
枢轴而能自由旋转,设此杆自水平静止释放。
求: 当杆过铅直位置时的角速度:
N
YZ
XO
r
mg
定轴转动的动能定理

例题2 一根质量为m、长为 l 的均匀细棒OA (如图),可绕通过其一
端的光滑轴O在竖直平面内转动,今使棒从水平位置开始自由下摆,求细棒
摆到竖直位置时其中点C和端点A的速度。
C
解 先对细棒OA 所受的力作一分析;重力G O
作用在棒的中心点C,方向竖直下;轴和棒之间没
A
有摩擦力,轴对棒作用的支承力 N 垂直于棒和 轴
的接触 面且通过O点,在棒的下摆过程中,此力
的方向和大小是随时改变的。
A
在棒的下摆过程中,对转轴O而言,支撑力N通
G
过O点,所以支撑力N的力矩等于零,重力G的力矩则
是变力矩,大小等于mg(l /2) cos ,棒转过一极小的角位移d 时,重力
矩所作的元功是
dW mg l cosd
2
在使棒从水平位置下摆到竖直位置过程中,重力矩所作的功是
度ω0=0,转动动能为0,重力势能为 mg(2l 选下摆到竖直位置hc=0),下摆到竖
直位置时角速度ω=ω,转动动能为
1 2
J重2 力势能为0。
mg l 1 J 2
22
由此得
3g l
mgl
J
所以细棒在竖直位置时,端点A和中心点C的速度分别为
vA l 3gl
vC
l
2
1 2
3gl
J2
2
1 2
J12
刚体定轴转动的动能定理:总外力矩对刚体所做的功等于刚体转动动能
的增量。
注:
1. 刚体的转动动能
刚体的转动动能应该是组成刚体的各个质点的动能之和。
设刚体中第i个质点的质量为 mi ,速度为 vi
刚体做定轴转动时,各质点的角速度相同。
,则该质点的动能为
3.2 定轴转动中的功能关系

A= ∫
θ2
2.恒力 矩的功
M与ω 方向相同 A > 0 M与ω 方向相反 A < 0
A = M∆θ
P = Mω
θ1
内容 Mdθ 小结
3.力矩的功率 3.力矩的功率
作者 杨 鑫
3.2 定轴转动中的功能关系
20 第3章 刚体的定轴转动 20
二、转动动能
三、动能定理
1 2 1 2 1 2 Ek = Iω A = Iω2 − Iω1 2 2 2 四、机械能守恒定律 c m hc 1.刚体重力势能 1.刚体重力势能 EP = mgh c
作者 杨 鑫
内容 回顾
① 各质点都绕转轴 作 圆 周 运 动 ②运 动 的 角 量 (∆θ, ω, β)都一样
O
ω
定轴
3.2 定轴转动中的功能关系
第3章 刚体的定轴转动
33
4.刚体定轴转动的角量描述 4.刚体定轴转动的角量描述 (1)角 (1)角 量 ①角位置
转动平面
ωO 。 θ = θ (t ) A θ ②角位移 ∆θ = θ −θ 2 1 x ③角速度 ω = d θ dt ω
作者 杨 鑫
I = mr
2
dm = λdx dm = σds 2 dI = r dm dm = ρdV
I = I1 + I2 +⋯+ In
I = ∫ r dm
2 m
I =∑ ∆m r
2 i i
3.2 定轴转动中的功能关系
11 第3章 刚体的定轴转动 11
2 . 物 理 意 义 量度刚体转动惯性的物理量 3 . 决定转动 ①与物体的总质量有关 惯 量 的 ②与转轴的位置有关 三 个 因 素 ③与物体的质量分布有关 4 . 平 行 轴 刚体对任意轴的转动惯量等 定 理 于刚体对通过质心轴的转动 惯量加上 加上刚体的质量与两平 惯量加上刚体的质量与两平 m 行轴之间距离平方的乘积 Od C
刚体定轴转动的功和能

《大学物理》练习题 刚体定轴转动的功和能班级 ___________ 学号 __________ 姓名 _________ 成绩 ________基本要求:(1) 掌握力矩的功、转动动能、动能定理、含刚体的机械能守恒定律及应用内容提要: 1. 力矩的功:⎰=θMd A2 转动动能:刚体的转动惯量与角速度平方乘积的一半。
221ωJ E k =3 刚体定轴转动的动能定理:合外力矩对定轴转动刚体所做的功等于刚体转动动能的增量21222121ωωJ J A -=若在刚体转动过程中,只有重力做功,其他非保守内力不做功,则刚体在重力场中机械能守恒.常量=+=C mgh J E 221ω一、选择题1. 如图所示, 一匀质细杆可绕通过其一端的水平光滑轴在竖直平面内自由转动. 杆长 l = (5/3)m,今使杆从与竖直方向成60°角的位置由静止释放(g 取10m/s 2), 则杆的最大角速度为 [ ] (A) 3rad/s.(B) rad/s (C) 9 rad/s.60° 图(D)3rad/s.2.一人站在旋转平台的中央,两臂侧平举,整个系统以2rad/s 的角速度旋转,转动惯量为.如果将双臂收回则系统的转动惯量变为.此时系统的转动动能与原来的转动动能之比E k / E k0为[ ] (A)2.(B) 2. (C) 3. (D) 3.3.如图所示,一匀质细杆可绕通过上端与杆垂直的水平光滑固定轴旋转,初始状态为静止悬挂。
现有一个小球自左方水平打击细杆.设小球与细杆之间为非弹性碰撞,则在碰撞过程中对细杆与小球这一系统 [ ] (A) 只有机械能守恒.(B) 只有动量守恒.(C) 只有对转轴O 的角动量守恒. (D) 机械能、动量角和动量均守恒. 二.填空题1.一匀质细杆AB,长为l ,质量为m . A 端挂在一光滑的固定水平轴上, 细杆可以在竖直平面内自由摆动.杆从水平位置由静止释放开始下摆,当下摆 时,杆的角速度为 .2.将一质量为m 的小球, 系于轻绳的一端, 绳的另一端穿过光滑水平桌面上的小孔用手拉住, 先使小球以角速度1在桌面上做半径为r 1的园周运动, 然后缓慢将绳下拉, 使半径缩小为r 2, 在此过程中小球的动能增量是 .○· O 图三.计算题1.有一质量为m 1、长为l 的均匀细棒,静止平放在滑动摩擦系数为的水平桌面上,它可绕通过其端点O 且与桌面垂直的固定光滑轴转动. 另有一水平运动的质量为m 2的小滑块,从侧面垂直于棒与棒的另一端A 相撞,设碰撞时间极短,已知小滑块在碰撞前后的速度分别为v 1和v 2,如图所示. 求碰撞后从细棒开始转动到停止转动的过程所需的时间 (以知棒绕O 点的转动惯量J=m 1l 2/3).2.一长l=0.4m 的均匀木棒,质量M=1.0kg ,可绕水平轴O 在竖直内转动,开始时棒自然地竖直悬垂,今有质量m=8g 的子弹以s m v 200 地速率从A 点射入棒中,假定A 点与O 点的距离为43l ,求:(1)、棒开始运动时的角速度; (2)、棒的最大偏转角。
刚体的能量,定轴转动的动能定理

yi
MgyC
M
g
mi
三、转动动能
刚体绕定轴以角速度旋转 刚体的动能应为各质元动能之 和为此将刚体分割成很多很小的 质元 m , m m m
1 2 i
2 i i 2
ri M
vi m
i
1 2 2 2 E mi ri J /2 k E k i 1 2 n 1 2 2 1 Ek lim mi ri ( r 2 dm) 2 m 0 2 2 mghC mvC J 2 2
四、力矩的功、定轴转动的动能定理 设有一外力 F 作用在 + d ds 刚体上,绕 O轴作定轴 转动( F 在垂直于轴 O 的平面内)。 M M 在时间 内刚体角位移为 dt d 力 F 作的功:
F
r
ds rd dA F ds F sin rd Md
故刚体的转动动能:
n
i
m v / 2 mi (ri ) / 2 mi ri / 2
2 2
任取一质元 mi 距转轴 ri ,则该质元动能:
n
对既有平动又有转动的刚体的动能、机械能又 如何呢?
势能零点
1 2 2 Ek 1 mvC J m、J C 2 2 C vC
其平动动能应为各质元动能和。
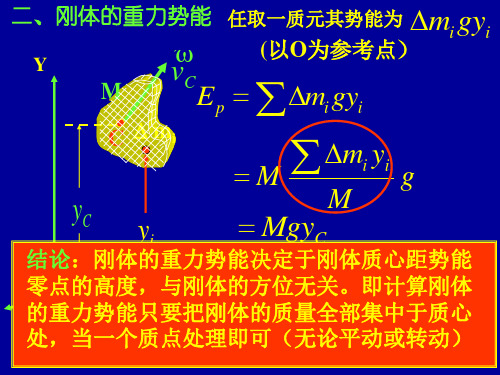
二、刚体的重力势能 任取一质元其势能为 m gy i i (以O为参考点)
Y
M
vC
C mi
E p mi gyi
m y M
i
i
yC
结论:刚体的重力势能决定于刚体质心距势能 X 零点的高度,与刚体的方位无关。即计算刚体 O 的重力势能只要把刚体的质量全部集中于质心 处,当一个质点处理即可(无论平动或转动)
第三章刚体的定轴转动

§3.1 刚体定轴转动的动能定理和转动定律
二、刚体定轴转动的动能定理 B、对于定轴转动刚体,所有内力的功总和在任何过程中均为零。(内力成对,大小相等方向相反,
一对内力矩的代数和为零;∴内力矩的功总和为零。另一角度,内力的功相对位移为零 .)
3、功率:
d A F 2d r
pdAMdM
dt dt
当 与 M 同方向, 和 为正 当 与 M 反方向, 和 为负
§3.1 刚体定轴转动的动能定理和转动定律
1 2 其中(:1 3M h 2 1 m l2l(12) ca 2o M s) 1( 3g )m h 2g(h 2 ) h 2 a (1 co )s(4 )
由(2)(3)(4)式求得:
2Mg(1lcos)/22mg(1acos)
M2l/3m a2
(Ml 2ma)g(1cos)
2
25
整理,得:
1 10 gh,
b7
vcb
10 gh 7
§3.2 定轴转动的动量矩定理和动量矩守恒定律
(2)小球到达A点不脱离轨道,要求小球在A点的速 度vA 和角速度A满足:
m v a A 2 m g v A 2 a,gA 2 v b A 2 2 a b 2 g (4 )
由机械能守恒:
b<<a
飞轮作变加速转动
§3.1 刚体定轴转动的动能定理和转动定律 例题3-1-2:一长为 l ,重为W的均匀梯子,靠墙放置,如图。墙光滑,地面粗糙, 当梯子与地面成角 时,处于平衡状态,求梯子与地面的摩擦力。
解:刚体平衡同时要满足两个条件:
Fi 0
Mi 0
列出分量方程:
O
水平方向:
f1N2 0
竖直方向:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
解:以 ω 和 ω 分别表示冲孔前后的飞轮的角速度
1 2
ω = (1 − 0 .2 )ω = 0.8ω
2 1
2
2
2πn ω = = 8πrad ⋅ s 60
1 1
−1
1
1 1 1 由转动动能定理 A = Jω − Jω = Jω (0 .8 − 1) 2 2 2 1 又 J = mr A = −5 .45 × 10 J 2
课后习题 3-8
θ1
θ2
二、刚体的转动动能和重力势能
1.绕定轴转动刚体的动能 绕定轴转动刚体的动能 绕定轴转动刚体的
∆ ,∆ ,⋅⋅⋅,∆ ,⋅⋅⋅,∆ m m m m r r r r r, r ,⋅⋅⋅, r ⋅⋅⋅, r r r r r v ,v ,⋅⋅⋅,v ,⋅⋅⋅,v
1 2 i
1 2 i, N
N
Q = rω v 1 E= ∆ v m 2
2 2 2
1 1
2
3
质量M的圆盘滑轮可绕通过盘心的水平轴转 例3-7半径R质量 的圆盘滑轮可绕通过盘心的水平轴转 半径 质量 滑轮上绕有轻绳,绳的一端悬挂质量为m的物体 的物体。 动,滑轮上绕有轻绳,绳的一端悬挂质量为 的物体。 当物体从静止下降距离h时 物体速度是多少? 当物体从静止下降距离 时,物体速度是多少? 以滑轮、 解:以滑轮、物体和地球组成系统为研究对 由于只有保守力做功,故机械能守恒。 象。由于只有保守力做功,故机械能守恒。 设终态时重力势能为零 初态:动能为零,重力势能为mgh 初态:动能为零,重力势能为 末态: 末态:动能包括滑轮转动动能和物体平动动能 由机械能守恒
i i
i i i
2
1
2
i
N
刚体的总动能
1 1 E = ∑ ∆ v = (∑∆ r )ω m m 2 2
2 2 k i i i i
2
m ∑∆ r正是刚体对转轴的转动惯量
i i
2
1 E = Jω 2
k
2
刚体的转动动能
2. 定轴转动刚体的势能
刚体受到保守力作用,可引入势能概念。重 刚体受到保守力作用,可引入势能概念。 力场中刚体就具有一定重力势能 重力势能。 力场中刚体就具有一定重力势能。
ω
R M
r v
m
h
1 1 mgh = Jω + mv 2 2
2
2
QJ =
1 MR , v = R ω 2
2
mgh v=2 M + 2m
的均匀细直棒, 例3.8 一根长为 l ,质量为 m 的均匀细直棒,可绕轴 O 在竖直平 面内转动,初始时它在水平位置, 面内转动,初始时它在水平位置,求它由此下摆 θ 角时的 ω
dt
dA= M θ d
对于一有限过程
dω )d = Jω ω θ d dA= M θ = (J d dt
ω2 ω 1
A= ∫ dA= ∫ Jω ω d
1 1 2 2 A = Jω2 − Jω 1 2 2
合外力矩对刚体所做的功等于刚体转动动能的增量。 合外力矩对刚体所做的功等于刚体转动动能的增量。 这就是刚体定轴转动的动能定理
3.3 刚体定轴转动中的功和能
一、力矩做功
v 力F 所做元功表示为
dθ
O
β
• P
r dA= Fcosβ dr = Fcosβ ⋅ rdθ
r v dr F
dA= M θ d
r r
外力对转动刚体所做的元功等于相应的力矩和角位移 的乘积 对于有限角位移, 对于有限角位移,外力做功用积分表示
A= ∫ M θ d
1 解:重力矩为 M= m cosθ gl 2
由动能定理
θ θ
O
•
m
l
x
θ
•C
m g l A= ∫ M θ = ∫ m cosθdθ d g 0 0 2 1 2 lm g 1 2 J= m l = sinθ −0 = Jω −0 3 2 2 3gsinθ 1/ 2 3gsinθ 2 ω =( ) ω = l l
例3-6 某一冲床利用飞轮的转动动能通过曲柄连杆机构 的传动,带动冲头在铁板上穿孔。已知飞轮为均匀圆盘, 的传动,带动冲头在铁板上穿孔。已知飞轮为均匀圆盘, 其半径为r=0.4m,质量为 其半径为 ,质量为m=600kg,飞轮的正常转速 , 是 n = 240 r ⋅ min 冲一次孔转速降低 ,冲一次孔转速降低20%。求冲一次孔 。 冲头做的功。 冲头做的功。
E = ∑∆mgh = g∑∆mh
p i i i i
根据质心定义, 根据质心定义,该刚体质心高度为
h=
c
m ∑∆ h
i i
m
重力势能可以表示为
E = mgh
p c
三、定轴转动的动能定理
设作用于刚体的合外力矩为M,刚体转过角位 移dθ时,合外力矩的功为 由转动定律: 由转动定律:M = Jβ = J dω
