四年级奥数 第8讲 有趣的数阵图
(完整word版)四年级奥数第八章有趣的数阵图练习教案
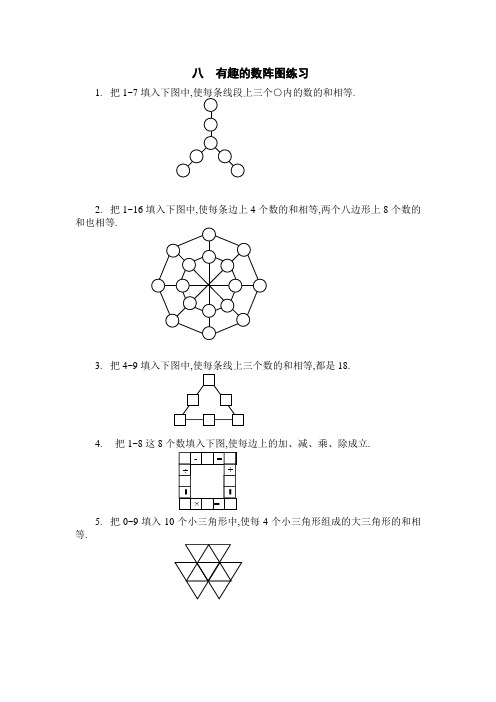
八 有趣的数阵图练习
1. 把1~7
.
2. 把
1~16填入下图中,使每条边上4个数的和相等,两个八边形上8个数的和也相等.
3. 把4~9填入下图中,使每条线上三个数的和相等,都是18.
4. 把1~8这8个数填入下图,使每边上的加、减、乘、除成立.
5. 把0~9
填入10个小三角形中,使每4个小三角形组成的大三角形的和相等.
6. 把1~11填入图中,使每条线上三个数的和相等.
7. 把1~8,填入图中,使每条线及正方形四个顶点上的数的和相等.
8. 把1~9,填入下图中,使每条线段三个数和及四个顶点的和也相等.
9. 把17,23,25,31,46,53,58,66,72,88,94,100十二个数填入下图,使任意三个相邻的数相加的和除以7的余数相等.。
【精编】中小学精品课件四年级数学趣的数阵图课件.ppt

1
5
2
4
6
3
猴博士送你一句数学家名言:
有趣的数阵图
四年级上学期 《数学探究 我快乐》第51页~54页
让猴博士告诉你
将一些数按照一定的规律排列而成的图 形,通常叫做数阵图。
例1 在下面的三角形数阵图的 里,填入 适当的数,使三边上3个 里的数的和是12。
5
1
3
6
2
4
猴博士考考你
在正方形数阵图中的 里填入适当的数,使 每条线上的3个数的和等于21。
4
11
6975 Nhomakorabea8
3 10
例2 在下面图中的 里,填上适当的数,使 每条线上3个 里的数的和等于13。
8
1
4
3 6
2 7
猴博士考考你
把10到20这11个数填在图中的 条线段上的3个数的和等于45。
里,使每
20
16 14
10
19
11
15
13
12
17
18
例3、把1、2、3、4、5这5个自然数填入到图 中的 里,使每条线段上的3个数的和相等。
1
猴博士考考你
把3到7这5个数分别填入到“T”和“十”字形 的方格内,使横、竖两行的3个数的和相等。
3 3
和猴博士一起玩个数学游戏好吗?
第一关 把1、2、3、4、5、6、7这7个数字填入图中
的 里,使每条线上的 里的3个数的和相等。
6
1
7 32
4
5
第二关 将1、2、3、4、5、6填入到下面的小圆圈里,
小学奥数基础教程之数阵图
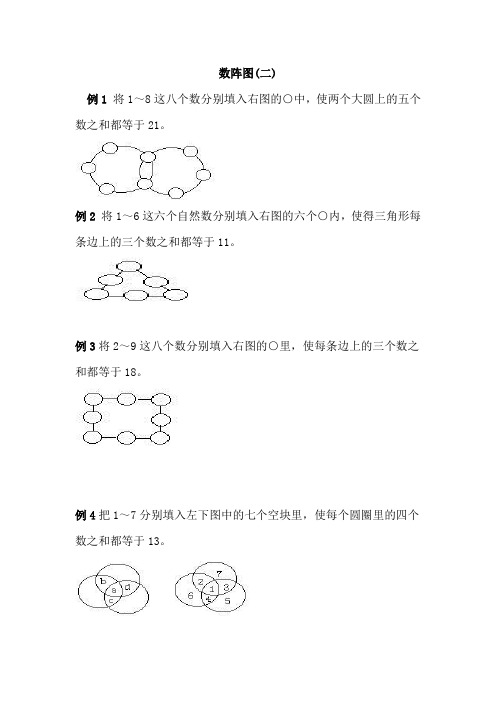
数阵图(二)
例1将1~8这八个数分别填入右图的○中,使两个大圆上的五个数之和都等于21。
例2将1~6这六个自然数分别填入右图的六个○内,使得三角形每条边上的三个数之和都等于11。
例3将2~9这八个数分别填入右图的○里,使每条边上的三个数之和都等于18。
例4把1~7分别填入左下图中的七个空块里,使每个圆圈里的四个数之和都等于13。
1.把1~8填入下页左上图的八个○里,使每个圆圈上的五个数之和都等于20。
2.把1~6这六个数填入右上图的○里,使每个圆圈上的四个数之和都相等。
3.将1~8填入左下图的八个○中,使得每条边上的三个数之和都等于15。
4.将1~8填入右上图的八个○中,使得每条直线上的四个数之和与每个圆周上的四个数之和都相等。
5.将1~7填入右图的七个○,使得每条直线上的各数之和都相等。
6.把1,3,5,7,9,11,13分别填入左图中的七个空块中,使得每个圆内的四个数之和都等于34。
四年级数学趣的数阵图课件

1
猴博士考考你
把3到7这5个数分别填入到“T”和“十” 字形的方格内,使横、竖两行的3个数的和 相等。
3 3
和猴博士一起玩个数学游戏好吗?
第一关 把1、2、3、4、5、6、7这7个数字填入图中 的 里,使每条线上的 里的3个数的和相等。
6 1 3 7 2
4
5
第二关 将1、2、3、4、5、6填入到下面的小圆圈里, 使每个大圆圈上4个数的和都是16,你能办到吗?
有趣的数阵图
四年级上学期 《数学探究 我快乐》第51页~54页
金坛市金城镇中心小学
丁国新
让猴博士告诉你
将一些数按照一定的规律排列而成的图 形,通常叫做数阵图。
例1 在下面的三角形数阵图的 里, 填入适当的数,使三边上3个 里的数的和 是12。
5
1
3 2
4
6
猴博士考考你
在正方形数阵图中的 里填入适当的 数,使每条线上的3个数的和等于21。
1
5
2
4
6
3
猴博士送你一句数学家名言:
数学好玩!
陈省身
谢谢各位!
; /kxiantu/ k线理论
ath18cwb
蹭过来,谁知 吩咐的是:“我身子如此,不得向诸长辈和姐妹们问安,你且替我去请安、问好、道声惭愧。”请安问好,是露脸的事啊, 光明正大可去菊花会上了,还不用偷溜的!乐韵喜出望外,当即答应下来——话说回来了,表 一向身子太弱,几乎所有的亲族活动都不参 加,也不屑得跟人面子上交代交代,今儿怎么开窍了?乐韵有些疑惑。“对了,替我给诸长辈与姐妹们带些礼物去罢!”宝音道,“你看 带些什么去好?”带点见面礼,哪怕是一朵花一根草呢,接受方出于情面,就要对乐韵有所赏赐了!带个见面礼是好的!乐韵果然拼命动 脑袋的想,临急临忙拿些什么去呢?自家人原不用太贵重,表 屋里也没什么好东西,每个人都送过来太难办……对了!重阳菊花会,就送 花儿罢!乐韵嘻嘻笑道:“ 屋后那两株芙蓉开得倒好,不如乐韵剪一篮子,送去给奶奶姑娘们添妆如何?”芙蓉?宝音微微一怔,想起来, 应该说的是表 屋后木芙蓉树,算起来,现在倒正在着花时候,攒上一篮子没问题,统总拎过去,谁爱拿就拿,做个整团儿人情,可不比给 每人准备礼物来得便当。乐韵在这方面,果然有急智。她点头道:“便是这样罢!”洛月注目宝音,分明想问,那两株木芙蓉,是 心爱之 物,平常都舍不得让人接近的,今儿怎么舍得让人剪了去?真要是韩玉笙在,听了乐韵建议,准气得咳血,不准动花儿分毫,宝音却想花 开无非要谢的,竟不如往合适的地方去,因此轻轻易易便准了。乐韵只怕宝音反悔,忙着道:“那姑娘快休息要紧!乐韵自会照料得。” 兴冲冲往门外去,宝音冷不丁又丢出来一句:“午前必要回还!”乐韵想想,她的午饭按例还在表 屋里开,菊花会那边有头有脸的人都在, 要蹭也不太好蹭,可不要回来吃饭么?这条却使得的,便应了,去掇个竹匾,寻个花剪,挎个三腿小圆凳往后头去。且喜两棵树都生得不 高,踩上凳子,就够到了下头的枝干,咔嚓咔嚓剪起来。这树一株大红、一株粉白。洛月剪完了一色,又去剪另一色,猛抬头看见邱妈妈 拢着手、虎着脸瞪着自己。乐韵一时头皮有些发麻,叫了声“邱妈妈”,辩解道:“这次可是姑娘叫我剪的,您也看见了!”邱妈妈哼了 一声,走开。临走丢下一句话:“仔细摔断你的腿!”乐韵呆了会儿,恨恨举手,“咔叭”又剪下去。这一篮子鲜洁丰丽芙蓉花朵挎去菊 花宴上,众人们反应多半是:“哟,今儿笙妹妹怎么想着我们?”各各拣了几朵,就席面上多多少少也给了乐韵一些儿赏,乐韵勾留至近 午,一向相熟的丫头筱筱过来问她:“你留在这儿吃么?听说今儿中午有九品羹,还有芋大嫂拿手的鲜虾蛋卷,连我们下头人都有份!” 乐韵还未回答,筱筱又“哦”了一声:“不过我是跟着我们四姑娘,才有
四年级奥数讲义:有趣的数阵图(一)

四年级奥数讲义:有趣的数阵图(一)大家都知道了历史悠久的三阶幻方.再推广一些,结合某些几何图形,把一些数字填入图形的某种位置上,并使数字满足一定的约束条件,这类问题,习惯上称为“数阵图”.幻方是特殊的数阵图,幻方发展较快,因为它后来与试验方案设计及一些高深数学分支有关,成为数阵图中最重要课题.本讲主要介绍一般数阵图及解此类题的推理思考方法,由于它既有数字之间运算,又要结合图形,对开发学生综合思考和形象思维很有益.先看例题.例 1 下面图形包括六个加法算式,要在圆圈里填上不同的自然数,使六个算式都成立,那么最右边圆圈中的数最少是几?分析为便于说理,各圆圈内欲填的数依次用字母A、B、C、D、E、F、G、H、I代替(上右图).经观察,I=A+B+C+D.题目要I尽可能小,最极端的想法,希望A、B、C、D只占用1、2、3、4.但这会产生矛盾.因为1总要和2、3、4中的某两个实施加法,但1+2给予G、H、E、F中某值为3与A、B、C、D中已有的3冲突;同样1+3给于G、H、E、F中某值为4又与A、B、C、D中已有的4冲突;所以A、B、C、D不能是1、2、3、4.那么退而求之,不妨先设A=1.如先考虑B,B尽可能小,最好,B=2,从而决定了E=3,C≠3,D≠3.这样一来,C,D只能取4和5.但如C=4导致G=5和D=5冲突,而C=5,D=4,又导致G=A+C=6和H=B+D=2+4=6冲突.在碰了钉子后,回看在A=1设定后,不应随随便便先填B的值.从结构上看,因为B,C地位对称,不妨先考虑D.D尽可能小,最好设D=2,B、C至少取3、5,若如此,由B+D或C+D产生的5会与B、C中已有的5矛盾.所以,B、C可能取3、6.从而形成了:A=1、D=2、B、C取3、6(B,C地位对称).这样一来其他字母所代表的值就立即推出,不妨设B=3,C=6,A+B=E=4,C+D=6+2=8=F;A+C=1+6=7=G,B+D=3+2=5=H,恰好满足E+F=4+8=12=I;G+H=7+5=12=I;综上所述:A=1,D=2,B=3,C=6决定了其他值,且决定了I=12.是一个较小的I的值,自然要问I 值还可能比12小吗?分析I的值有三种不同的获得方式:I=A+B+C+D=E+F=G+H.3I=A+B+C+D+E+F+G+H,而8个字母最少是代表1、2、…、7、8的情况.3I≥(1+2+…+7+8)=36,I≥12.现已推出了使I=12的一种填法,所以是最佳方案了.例2 如右图,五圆相连,每个位置的数字都是按一定规律填写的,请找出规律,并求出x所代表的数.分析经观察,图中所填数的规律为两个圆相交部分的数等于与它相邻两部分里的数的和的一半.比如:(26+18)÷2=22.(30+26)÷2=28.(24+30)÷2=27.解: x+18=17×2x=16.经检验,16和24相加除以2,也恰好等于20.例3 在下图中的各题中,将从1开始的连续自然数填入各题的圆圈中,要使每边上的数字之和都相等,中心处各有几种填法?(每小题请给出一个解)分析1 图(A)中的中心圆填入的数设为x,x参与3条线的连加,设每条线数字和都为S.由题意:1+2+3+…+7+2x=3S即28+2x=3S或28+2x≡0(mod 3)借用同余工具,是在两个未知数的不定方程中先缩小x应该取值的范围.在mod3情况下,只要试探x≡0,1,2三个值,很轻松地解出:x≡1(mod3),回复到x取值范围为1,2,…,7.有x1=1,x2=4,x3=7,得到:x1=1,S1=10;x2=4,S2=12;x3=7,S3=14;由此看出关键在求S(公共和)及x(参与相加次数最多的圆中值).此方法对下面解(B)、(C)、(D).都适用.注意:每条线上的数字之和随着中心数的变化而变化.分析2 我们分析图(B),首先应该考虑中心数,(B)题共10个数,由于中心数比其他数多使用了二次(总共使用三次).如果中心数用x表示,三条边的数码总和应为:1+2+3+4+5+6+7+8+9+10+2x=55+2x同理,因为是3条边,所以55+2x应是3的倍数55+2x≡0(mod 3),把x≡0、1、2代入试验,得x≡1(mod 3),即x=1、4、7、10.四种解.①当x=1时,55+2x=57,57÷3=19②当x=4时,55+2x=63,63÷3=21③当x=7时,55+2x=69,69÷3=23④当x=10时,55+2x=75,75÷3=25读者可按照上面相似的规律自己去分析一下图中(C)、(D)两题.解:(A)图:中心数可以为1、4、7,有三种填法,请读者补充其他两种解法.(B)图:中心数可以为1、4、7、10.有四种填法,请你补充其他三种填法.(C)图:中心数可以为1、5、9.有三种填法,请你补充其他两种填法.(D)图:中心数可以为1、6、11.有3种填法,请你补充其他两种填法.例 4 在下左图的七个圆圈内各填上一个数,要求每条线上的三个数中,当中的数是两边两个数的平均数,现在已填好两个数,求x是多少?分析为了便于说明问题,我们用字母表示各个圆圈内所表示的数,如上右图所示:根据题意,我们观察:因为每一条直线上的三个数中,当中的数是两边的两个数的平均数.所以可以得出:D=(13+17)÷2=15.还可以得出以下三式:C=(B+15)÷2 (1)A=(13+B)÷2 (2)C=(A+17)÷2 (3)将上述三个算式进行变形,成下面三个算式:2C=B+15 (4)2A=13+B (5)2C=A+17 (6)用(4)式减去(5)式得出:2C-2A=2C-A=1C=A+1将C=A+1代入(6)式得到:2(A+1)=A+17,A=15.x=19.即:解:(略)例5 如下左图有5个圆,它们相交后相互分成几个区域,现在两个区域里已分别填上数字10、6,请在另外七个区域里分别填进2、3、4、5、6、7、9七个数字,使每个圈内的数的和都是15.分析为了便于说明,我们用字母表示其他的7个区域.如上右图.根据题意可以得出:A=5、G=9,九个区域中数的总和为:(2+3+4+5+6+7+9)+10+6=52,而每个圆圈内数的和是15,五个圆圈内数的总和为:15×5=75,又75-52=23,由此得出重叠的部分的四个数A、C、E、G的和是23.由于A=5和G=9已经填好,因此,余下的两个部分C+E的和是:23-5-9=9,此时9只有两种分解的可能:2+7=9、3+6=9.在E、F、G这个圆圈内,∵G=9,∴E不能填6、7.也不能填3(否则F也等于3),只能填2,这样,E=2,C=7.解:例6 如下左图所示4个小三角形的顶点处共有6个圆圈.如果在这些圆圈中分别填上6个质数,它们的和是20,而且每个小三角形三顶点上的数之和相等,问这6个质数的积是多少?分析为了叙述方便,我们用字母表示图中圆圈里的数.如上右图所示.通过观察,我们不难发现,小三角形A1B2C2和小三角形A2B2C2有两个共同的顶点B2,C2,而这两个小三角形顶点上数字的和相等.因此A1=A2.同理有B1=B2,C1=C2,所以,此图只能填A、B、C三个质数(两个A、两个B、两个C.以下:A1=A2记为A,B1=B2记为B,C1=C2记为C)∵6个圆圈中的6个质数之和为20,即:2×(A+B+C)=20A+B+C=10.∴10分成三个质数之和只能是10=2+3+5.这样,A、B、C分别是2、3、5.这时所填6个数的积是:2×2×3×3×5×5=900.解:例7 能否将自然数1~10填入五角星各交点的“○”内使每条直线上的4个数字之和都相等?分析与解答不能,用反证法.假设可以填成数阵图,观察发现:十个点中的每一个点恰好是两条直线的公共点.因而全部直线(共5条)上数字总和,应该等于全部点上数字总和的2倍.记每条直线上数字和为S,则有5S=(1+2+3+…+10)×2,从而解出S=22.10和1必同在某一直线上.不然,如含有10的两条直线都不含有1,这样,这两条线上8个数字(10自然被计上两次)之和(本应为2S)大于等于2×10+2+3+4+5+6+7=47>44=2S.形成矛盾.所以10、1必处同一直线.此外,有三个数字与10不同线,不妨记为x、y、z.显然x+y+z={10数总和}-{其余七个数和}而这{其余七个数和}恰好为2S-10.所以x+y+z=55-2×22+10=21.已推出10,1共线.进一步看出,1无论在什么位置都与x、y、z三数中的两个共线.设1与x、y共线,此线上另一数设为v.则有1+x+y+v=22,从而x+y+v=21.前已证x+y+z=21,因而导致v=z的矛盾.其他情况推证类似,所以没有题设的填法.习题九1.将1~9这九个数字分别填入右图中的九个圆圈中,使各条边上的四个圆圈内的数的和相等.2.将0.01、0.02、…、0.09这九个数分别填入右图九个圆圈内,使每条边上的四个圆圈内的数之和都等于0.2.(此题与题1共用一图)3.在右图的空白的区域内分别填上1、2、4、6四个数,使每个圆中的四个数的和都是15.。
四年级下数学奥数-有趣的数阵图 全国通用( 17 张)

4
6
B3
5
C1
2~9填入左下图的八个○中,使得每条边上的三个数之和都等 于18。
4 A
5
9 B
四条边数字总和: 4×18=72
2-9九数之和:
6
2 2+3+4+5+6+7+8+9=44
A+B+C+D=72-44=28
C
3
D 故只能选,
8
7
4+9+8+7=28
将1~8这八个数分别填入右图的○里,使每条边上的三个数之 和都等于15。
6 31 5 4 72
将1-6这六个数字填入下图的圆圈中,使每个大 圆圈上4个数字之和为14。
3
1
2
4
6
5
把2~7这六个数填入右上图的○里,使每个圆 圈上的四个数之和都等于18。
将1、2、3、4、5、6填在下图中,使每条边上三个数之和等于9。
A:(48-45)÷3=1
练 1-9一数练之:和将:11~+27+入3+下4图+5的+6○+7内=,28使得每条边上的三个数字之6和都等于12。 4
横行、竖行五数和:24+24=48
7
8
9
四条线数之和: 12×4=48 1-9数之和:
1+2+3+4+5+6+7+8+9=45 A:(48-45)÷3=1 剩下的数字平均分成四组, 每组数字之和12-1=11 所以应为: 2+9、3+8、4+7、5+6。
将2-10这九个数填入下图圆圈内,使每条线上三个数字相加之和为 22.
四年级奥数讲义:有趣的数阵图(一)

四年级奥数讲义:有趣的数阵图(一)大家都知道了历史悠久的三阶幻方.再推广一些,结合某些几何图形,把一些数字填入图形的某种位置上,并使数字满足一定的约束条件,这类问题,习惯上称为“数阵图”.幻方是特殊的数阵图,幻方发展较快,因为它后来与试验方案设计及一些高深数学分支有关,成为数阵图中最重要课题.本讲主要介绍一般数阵图及解此类题的推理思考方法,由于它既有数字之间运算,又要结合图形,对开发学生综合思考和形象思维很有益.先看例题.例 1 下面图形包括六个加法算式,要在圆圈里填上不同的自然数,使六个算式都成立,那么最右边圆圈中的数最少是几?分析为便于说理,各圆圈内欲填的数依次用字母A、B、C、D、E、F、G、H、I代替(上右图).经观察,I=A+B+C+D.题目要I尽可能小,最极端的想法,希望A、B、C、D只占用1、2、3、4.但这会产生矛盾.因为1总要和2、3、4中的某两个实施加法,但1+2给予G、H、E、F 中某值为3与A、B、C、D中已有的3冲突;同样1+3给于G、H、E、F中某值为4又与A、B、C、D中已有的4冲突;所以A、B、C、D不能是1、2、3、4.那么退而求之,不妨先设A=1.如先考虑B,B尽可能小,最好,B=2,从而决定了E=3,C≠3,D≠3.这样一来,C,D只能取4和5.但如C=4导致G=5和D=5冲突,而C=5,D=4,又导致G=A+C=6和H=B+D=2+4=6冲突.在碰了钉子后,回看在A=1设定后,不应随随便便先填B的值.从结构上看,因为B,C 地位对称,不妨先考虑D.D尽可能小,最好设D=2,B、C至少取3、5,若如此,由B+D或C+D产生的5会与B、C中已有的5矛盾.所以,B、C可能取3、6.从而形成了:A=1、D=2、B、C取3、6(B,C地位对称).这样一来其他字母所代表的值就立即推出,不妨设B=3,C=6,A+B=E=4,C+D=6+2=8=F;A+C=1+6=7=G,B+D=3+2=5=H,恰好满足E+F=4+8=12=I;G+H=7+5=12=I;综上所述:A=1,D=2,B=3,C=6决定了其他值,且决定了I=12.是一个较小的I的值,自然要问I值还可能比12小吗?分析I的值有三种不同的获得方式:I=A+B+C+D=E+F=G+H.3I=A+B+C+D+E+F+G+H,而8个字母最少是代表1、2、…、7、8的情况.3I≥(1+2+…+7+8)=36,I≥12.现已推出了使I=12的一种填法,所以是最佳方案了.例2 如右图,五圆相连,每个位置的数字都是按一定规律填写的,请找出规律,并求出x所代表的数.分析经观察,图中所填数的规律为两个圆相交部分的数等于与它相邻两部分里的数的和的一半.比如:(26+18)÷2=22.(30+26)÷2=28.(24+30)÷2=27.解: x+18=17×2x=16.经检验,16和24相加除以2,也恰好等于20.例3 在下图中的各题中,将从1开始的连续自然数填入各题的圆圈中,要使每边上的数字之和都相等,中心处各有几种填法?(每小题请给出一个解)分析1 图(A)中的中心圆填入的数设为x,x参与3条线的连加,设每条线数字和都为S.由题意:1+2+3+…+7+2x=3S即28+2x=3S或28+2x≡0(mod 3)借用同余工具,是在两个未知数的不定方程中先缩小x应该取值的范围.在mod3情况下,只要试探x≡0,1,2三个值,很轻松地解出:x≡1(mod3),回复到x取值范围为1,2,…,7.有x1=1,x2=4,x3=7,得到:x1=1,S1=10;x2=4,S2=12;x3=7,S3=14;由此看出关键在求S(公共和)及x(参与相加次数最多的圆中值).此方法对下面解(B)、(C)、(D).都适用.注意:每条线上的数字之和随着中心数的变化而变化.分析2 我们分析图(B),首先应该考虑中心数,(B)题共10个数,由于中心数比其他数多使用了二次(总共使用三次).如果中心数用x表示,三条边的数码总和应为:1+2+3+4+5+6+7+8+9+10+2x=55+2x同理,因为是3条边,所以55+2x应是3的倍数55+2x≡0(mod 3),把x≡0、1、2代入试验,得x≡1(mod 3),即x=1、4、7、10.四种解.①当x=1时,55+2x=57,57÷3=19②当x=4时,55+2x=63,63÷3=21③当x=7时,55+2x=69,69÷3=23④当x=10时,55+2x=75,75÷3=25读者可按照上面相似的规律自己去分析一下图中(C)、(D)两题.解:(A)图:中心数可以为1、4、7,有三种填法,请读者补充其他两种解法.(B)图:中心数可以为1、4、7、10.有四种填法,请你补充其他三种填法.(C)图:中心数可以为1、5、9.有三种填法,请你补充其他两种填法.(D)图:中心数可以为1、6、11.有3种填法,请你补充其他两种填法.例 4 在下左图的七个圆圈内各填上一个数,要求每条线上的三个数中,当中的数是两边两个数的平均数,现在已填好两个数,求x是多少?分析为了便于说明问题,我们用字母表示各个圆圈内所表示的数,如上右图所示:根据题意,我们观察:因为每一条直线上的三个数中,当中的数是两边的两个数的平均数.所以可以得出:D=(13+17)÷2=15.还可以得出以下三式:C=(B+15)÷2 (1)A=(13+B)÷2 (2)C=(A+17)÷2 (3)将上述三个算式进行变形,成下面三个算式:2C=B+15 (4)2A=13+B (5)2C=A+17 (6)用(4)式减去(5)式得出:2C-2A=2C-A=1C=A+1将C=A+1代入(6)式得到:2(A+1)=A+17,A=15.x=19.即:解:(略)例5 如下左图有5个圆,它们相交后相互分成几个区域,现在两个区域里已分别填上数字10、6,请在另外七个区域里分别填进2、3、4、5、6、7、9七个数字,使每个圈内的数的和都是15.分析为了便于说明,我们用字母表示其他的7个区域.如上右图.根据题意可以得出:A=5、G=9,九个区域中数的总和为:(2+3+4+5+6+7+9)+10+6=52,而每个圆圈内数的和是15,五个圆圈内数的总和为:15×5=75,又75-52=23,由此得出重叠的部分的四个数A、C、E、G的和是23.由于A=5和G=9已经填好,因此,余下的两个部分C+E 的和是:23-5-9=9,此时9只有两种分解的可能:2+7=9、3+6=9.在E、F、G这个圆圈内,∵G=9,∴E不能填6、7.也不能填3(否则F也等于3),只能填2,这样,E=2,C=7.解:例6 如下左图所示4个小三角形的顶点处共有6个圆圈.如果在这些圆圈中分别填上6个质数,它们的和是20,而且每个小三角形三顶点上的数之和相等,问这6个质数的积是多少?分析为了叙述方便,我们用字母表示图中圆圈里的数.如上右图所示.通过观察,我们不难发现,小三角形A1B2C2和小三角形A2B2C2有两个共同的顶点B2,C2,而这两个小三角形顶点上数字的和相等.因此A1=A2.同理有B1=B2,C1=C2,所以,此图只能填A、B、C三个质数(两个A、两个B、两个C.以下:A1=A2记为A,B1=B2记为B,C1=C2记为C)∵6个圆圈中的6个质数之和为20,即:2×(A+B+C)=20A+B+C=10.∴10分成三个质数之和只能是10=2+3+5.这样,A、B、C分别是2、3、5.这时所填6个数的积是:2×2×3×3×5×5=900.解:例7 能否将自然数1~10填入五角星各交点的“○”内使每条直线上的4个数字之和都相等?分析与解答不能,用反证法.假设可以填成数阵图,观察发现:十个点中的每一个点恰好是两条直线的公共点.因而全部直线(共5条)上数字总和,应该等于全部点上数字总和的2倍.记每条直线上数字和为S,则有5S=(1+2+3+…+10)×2,从而解出S=22.10和1必同在某一直线上.不然,如含有10的两条直线都不含有1,这样,这两条线上8个数字(10自然被计上两次)之和(本应为2S)大于等于2×10+2+3+4+5+6+7=47>44=2S.形成矛盾.所以10、1必处同一直线.此外,有三个数字与10不同线,不妨记为x、y、z.显然x+y+z={10数总和}-{其余七个数和}而这{其余七个数和}恰好为2S-10.所以x+y+z=55-2×22+10=21.已推出10,1共线.进一步看出,1无论在什么位置都与x、y、z三数中的两个共线.设1与x、y共线,此线上另一数设为v.则有1+x+y+v=22,从而x+y+v=21.前已证x+y+z=21,因而导致v=z的矛盾.其他情况推证类似,所以没有题设的填法.习题九1.将1~9这九个数字分别填入右图中的九个圆圈中,使各条边上的四个圆圈内的数的和相等.2.将0.01、0.02、…、0.09这九个数分别填入右图九个圆圈内,使每条边上的四个圆圈内的数之和都等于0.2.(此题与题1共用一图)3.在右图的空白的区域内分别填上1、2、4、6四个数,使每个圆中的四个数的和都是15.。
一起学奥数--有趣的数阵图

擦掉1、5、9(留意这三个数的位置),剩下的数首尾相加,
和相等。
4
8
2
随便挑选一组,填到左图圆圈内。
分析例4、5,图形特征与数字特征相同的情况下,填数的方式雷同。
例6、把1~11这十一个数分别填入下图中的各个○内,使每条线段上 三个○内的数的和都等于22。
1
10 5 6 11 9 2
78
4
3
【分析】图形特征:这是中心辐射型,中间圆圈重复使用五次。 数字特征:1-11为11个连续自然数,呈等差数列。与
4组数列分别填在三个顶角,构建成的直线的和不同,所以基本解有4个。而每组三个数在 三个顶点的位置又有6种方式。所以合计填法为: 4×6=24种。
本题可以通过确定直线最小值和最大值,计算出公共点的和,再 分类讨论,剔除不合适的组。方法相对原始,但不容易漏掉。
例3、把1~12这十二个数,分别填在下图中正方形四条边上的十二个 ○内,使每条边上四个○内数的和都等于22,试求出一个基本解。
因为1-12是一个等差数列,确定1-4为四个顶角,且按逆时针方向排列后,可以把剩下 的分成5-8,9-12两组,分别填在直线上对应的位置。
最后一步的规律必须让学生领会。可以把和都为22的条件去掉做讲解
例4、把1~7这七个数分别填入下图中的各个圆圈内,使每条线段上三个 ○内的数的和相等。
7
2
1
4 5
例:将1~16分别填入下图中圆圈内,要求每个扇形上四个数之和及中 间正方形的四个数之和都是34,图中已填好八个数,请将其余的数填完。
9 15 5
10
【分析】图形特征:左图中有16个圆圈,要填的数字为16个,且16 个圆圈可以在大圆上组成4个扇形,4个扇形上的数字之和都为34
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第8讲.有趣的数阵图
数阵图,就是把一些数按照一定的规则,填在某一特定图形的规定位置上,这种图形,我们称它为数阵图。
数阵图的种类繁多、绚丽多彩,这里我们将主要介绍两种数阵图,即封闭型数阵图和开放型数阵图。
解答这类问题时,常用以下知识:
1.等差数列的求和公式:
总和=(首项+末项)x项数/2
2.计算中的奇偶问题:
奇数+奇数=偶数
偶数+偶数=偶数
奇数+偶数=奇数
3.10以内数字有如下关系:
(1)1+9=2+8=3+7=4+6
(2)1+8=2+7=3+6=4+5
(3)2+9=3+8=4+7=5+6
在解答这类问题时,要善于确定所求的和与关键数字间的关系式,用试验的方法,找到相等的和与关键数字;要会对基本解中的数进行适当调整,得到其他的解,从而培养自己的观察能力、思维的灵活性和严密性。
例1.把1,2,3,4,5,6这六个数填在如下图的6个圆圈中,使每条边上的三个数之和都等于9.
例2.把1,2,3,4,5,6填在如下图的6个圆圈中,使每条边上的三个数之和相等,有几个基本解?
随堂练习1
(1)将1~4这四个数分别填入图中内数的和相等。
(1) (2)
(2)把数字1,3,4,5,6分别填在上图三角形3条边上的5个圆圈内,使每条边上3个圆圈内数的和等于9。
例3.把1~12这十二个数,分别填在如右图中正方形四条边上的十二个圆圈内,使每条边上四个圆圈内数的和都等于22,试求出一个基本解。
随堂练习2
将数字1,2,3,4,5,6填入图中的小圆圈内,使每个大圆上4个数字的和都是16.
例4.把1~7这七个数分别填入如图中的各个圆圈内,使每条线段上三个圆圈内的数的和相等。
例5 .将1~9这九个数,分别填入如图中的各个圆圈内,使每条线段上三个圆圈内的和相等。
例6.把1~11这十一个数分别填入如图中的各个圆圈内,使每条线段上三个圆圈内的数的和都等于22.
随堂练习3.
(1)将1~5这五个数分别填入如果中的圆圈内,使每条线段上三个圆圈内的和相等。
(1) (2)
(2)将6~10这五个数分别填入如图中的圆圈内,使每条线段上三个圆圈内的数的和相等。
