(完整版)第三讲、有趣的数阵图
有趣的数阵图课件
10-1=9 则2+7=3+6=4+5
有趣的数阵图
5
练一练：将 1～7入下图的○内，使得每条边上的三个数 字之和都等于12。
通关小诀窍：确定中间值
3 5
4
6
7
1 2
三条数之和： 3×12=36 2-8数之和：
有趣的数阵图
9
将2-10这九个数填入下图圆圈内，使每条线上三个数字相加之和为 22.
2
3
4
5
1A0
6
7
8
9
有趣的数阵图
10
将1、2、3、4、5、6填在下图中，使每条边上 三个数之和等于9。
1A
6
5
B2
4
3C
三条边数字总和： 3×9=27
1-6六数之和： 1+2+3+4+5+6=21
A+B+C=27-21=6 故只能选1，2，3
有趣的数阵图
14
把1～7分别填入左下图中的七个空块里，使每 个圆圈里的四个数之和都等于13。
2 4 17 635
有趣的数阵图
15
把1～7分别填入左下图中的七个空块里，使每 个圆圈里的四个数之和都等于15。
6 31 5 4 72
有趣的数阵图
16
将1-6这六个数字填入下图的圆圈中，使每个大圆 圈上4个数字之和为14。
50-45=5 12346789八个数分为两组， 使每组中四个数字之和：
25-5=20 则1+4+6+9=2+3+7+8
五年级下册数学奥数有趣的数阵图人教版
例4：把5～10这六个数，分别填入图中三角形三条边的六 个○内，使每边上的三个○内数的和都是24。
假设重叠数是a、b、c 5+6+7+8+9+10+a+b+c=24×3
45+a+b+c=72 a+b+c=27
8+9+10=27
8 76 9 5 10
2 9 561 3 8 45～10这六个数，分别填入图中三角形三条边的六 个○内，使每边上的三个○内数的和都是24。
中间的三个数只加一次， 三个角上的数都加了两次， 有三个数要设字母吗？
例4：把5～10这六个数，分别填入图中三角形三条边的六 个○内，使每边上的三个○内数的和都是24。
1
3
2
1+2+…+7+8+a+b=21×2 6
5
36+a+b=42 a+b=6
4
8
7
1+5=6或2+4=6
将1、3、5、7、9、11、13、15这八个数，分别填入图中的 八个○内，使得每个大圆上五个○内数的和都是39。
1+3+5+……+15=64
3
5
1
39×2-64=14
7
9
中间的两个圆圈数重叠一次， 15 13 11
例5：将1～8这八个数分别填入下图的○中，使两个大圆 上的五个数之和都等于21。
假设重叠数是a、b
2
3
1
1+2+…+7+8+a+b=21×2 6
有趣的数阵图
有趣的数阵图
作者：
来源：《小天使·三年级语数英综合》2014年第12期
巧思妙解
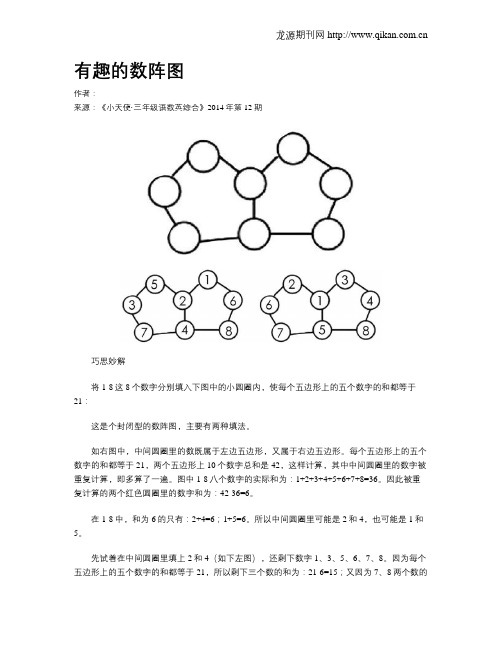
将1-8这8个数字分别填入下图中的小圆圈内，使每个五边形上的五个数字的和都等于21：
这是个封闭型的数阵图，主要有两种填法。
如右图中，中间圆圈里的数既属于左边五边形，又属于右边五边形。
每个五边形上的五个数字的和都等于21，两个五边形上10个数字总和是42，这样计算，其中中间圆圈里的数字被重复计算，即多算了一遍。
图中1-8八个数字的实际和为：1+2+3+4+5+6+7+8=36。
因此被重复计算的两个红色圆圈里的数字和为：42-36=6。
在1-8中，和为6的只有：2+4=6；1+5=6。
所以中间圆圈里可能是2和4，也可能是1和5。
先试着在中间圆圈里填上2和4（如下左图），还剩下数字1、3、5、6、7、8。
因为每个五边形上的五个数字的和都等于21，所以剩下三个数的和为：21-6=15；又因为7、8两个数的
和已经是15了，所以7和8只能在不同的五边形里；填好7和8 ，剩下的数字凑一凑就可以了。
再尝试在中间圆圈里填上1和5（如下右图），同上理，依次填好7、8和其它的数字，可以得到第二种填法。
三年级 第三讲 数阵图(已经打印)
第三讲 数阵图
教室 姓名 学号
【知识要点】
数阵图是将一些数按照一定的要求排列而成的某种图形。
数阵图根据图形的形状特点，可以分为辐射型数阵图和封闭型数阵图。
辐射型：（1）仔细观察图形，找出关键位置。
关键位置通常是重叠数，也可叫做中间数；
（2）把题目中提供的数字和所要填的空格和图形关系联系起来看，注意倍数关系；（3）计算方法：已知各数之和+重叠数×重叠次数＝直线上各数之和×直线条数。
封闭型：（1）仔细观察图形，找出关键数（即重叠数）。
在封闭型数阵图中，关键数往往有几个；（2）把题目提供的数字和所要填的空格和图形联系起来看，注意总和的倍数关系；
（3）计算方法：已知各数之和+重叠数之和＝每边各数之和×边数；
【经典例题】
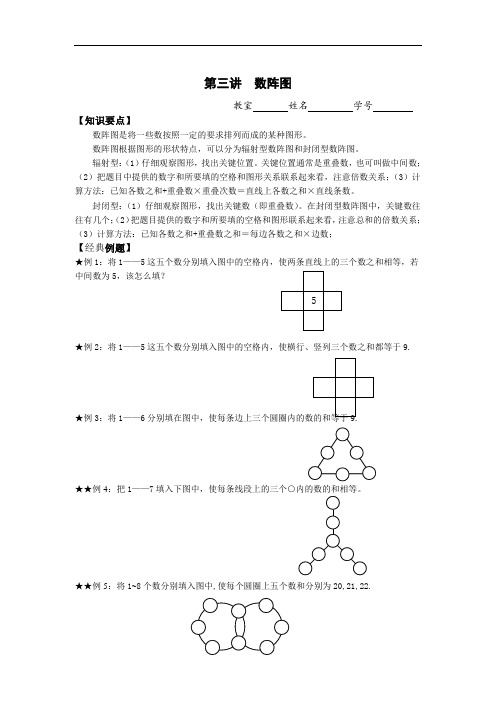
★例1：将1——5这五个数分别填入图中的空格内，使两条直线上的三个数之和相等，若中间数为5，该怎么填？
★例2：将1——5这五个数分别填入图中的空格内，使横行、竖列三个数之和都等于9.
★例3：将1——6
★★例4：把1——7填入下图中，使每条线段上的三个○内的数的和相等。
★★例5：将1~8个数分别填入图中,使每个圆圈上五个数和分别为20,21,22.
【池中戏水】
★1、将1~9这九个数分别填入图中○内,使每条线段五个数的和等于23.
★2、将1——5这五个数分别填入图中的圆圈内，使三角形每条边上的数之和都相等。
★3、把1——6这六个数字填入圆圈内，使横行三个数的和与竖列四个数的和都等于11.
★4、把1~8个数分别填入○中,使每条边上三个数的和相等.
★5、把1~11填入图中,使每条线上三个数的和相等.
★6、把1~10填入图中,。
奥数有趣的数阵图
有趣的数阵图一教学要求：1、使学生掌握解答有趣的数阵图的方法;2、培养学生的逻辑思维能力和推理能力,以及联想、试探归纳等思维能力;教学过程：一、导入新课语：如果把一些数按照一定的规律填在特定的图形里,那么这种图形,我们就称它为数阵图;它是一种趣味性很强的游戏,它的形式很多,大概分为三种：封闭型数阵、辐射型数阵、复合型数阵;二、探索新课：1、教学例1：将2、4、6、8、10填入“十字形数阵图中,使横行、竖列三个数的和相等,填在中间的公关位置,;再分别填入;2,所以我们先假设,顶点,再推出,其它的点3、教学例3：把1～9这九个数,填入到方格中,解题思路：先观察数,1＋9＝2＋8＝3＋7＝4＋6而5在中间其余的成对来填;方法有多种;4、教学例4：把1、2、3、5、6、7、填入右表,使每行三个数和相等,竖列二数也相等;解题思路：有2行3列,而1＋2＋3＋5＋6＋7＝24,所以每行为12,这样分成1、5、6；2、3、7两组;每列和是24÷3＝8,所以：1、7；2、6；3、5;答案多种;1、填上合适的数,2、用1～5填空;使每一边和为3、填上数,使横、竖、斜和为4、使横、竖、斜和相等;教学要求：12、培养学生活跃的思维能力教学过程：一、导入新课：同学们都会正确计算有余数的除法,其实有余数除法还蕴含着丰富的数学知识,所以我们运用它还可以解决不少的数学难题;今天,我们将继续学习余数的妙用二;二、探索新知：1、教学例4：体育课排队,老师让同学们按1、2、3、4、5循环报数,最后一个人报2,这一排有人;A、26B、27C、28D、32吉林省“金翅杯”小学数学竞赛试题解题思路：答案必须是5的倍数还要加2,所以我们经过计算发现可以选BD;2、教学例5:……共一百个数字;问：这100个数字中,8出现几次100个数字的和是多少解题思路：从数字的排列看,我们发现每6个数重复一次,所以周期数是6,总数是：100,我们就列算式：100÷6＝16 (4)再看8排在第几位它排在第4位,所以8出现的次数是6＋1＝7次第二个问：我们可以先算出每一个周期的数字和是多少1＋4＋2＋8＋5＋7＝27所以：27×6＝162再加上最后一次出现的数字：1＋4＋2＋8＝15得：162＋15＝1773、教学例6：1、2、3、4、5、6、7七盏灯各有一个开关,开始第2、4、6盏灯亮着,一个小朋友从第1到第7,再从第1到第7,拉了2000次,问这时那些灯亮着湖北省黄冈市第三届小学生智力竞赛试题解题思路：我们可以先找出每盏灯拉了多少次;列式：2000÷7＝285……5那么：灯号：1234567次数：85285原来：关开关开关开关现在：关开关开关关开双数时,不变；单数时,就变;三、全课小结：我们,要合理利用有余数除法的余数,还有它的变化公式;余数＝被除数－商×除数商＝被除数－余数÷除数除数＝被除数－余数÷商被除数＝商×除数＋余数四、课堂练习：1、老师把50张卡片依次发给甲、乙、丙、丁,第45章发给谁2、方方和明明用同一个数做除法,方方用12去除,明明用15去除,方方除得的商是32还余6,明明的计算结果你知道了吗安徽省马鞍山市三年级数学竞赛试题3、写1～100这100个数中,数字“6”写了多少次．．．．奇思巧解1．、．要把．．7．棵小树种成．．．．．6．行．,．每行有．．．3．棵．,．应当怎么样种．．．．．． 2．、．有．9．颗外形完全相同的珠子．．．．．．．．．．,．其中．．8．颗是珍珠．．．．,．另一颗是假珠．．．．．．,．且假．．珠比珍珠重．．．．．,．问用天平称．．．．．,．至少称几次可把假珠找出来．．．．．．．．．．．．3．、．有．100．．．个零件．．．,．分装成．．．10．．袋．,．每袋装．．．10．．个．,．其中．．9．袋里面装的都是．．．．．．．50．．克．,．另．1．袋里面的零件每个都是．．．．．．．．．．49．．千克．．,．这．10．．袋混在一起．．．．．,．你能用．．．秤称一次．．．．,,．．就把装．．．49．．千克重的那一袋零件找出来吗．．．．．．．．．．．．．4．、．老两口带着儿子．．．．．．．,．女儿．．,．和一条狗外外出旅游．．．．．．．．．,．途中过一条河．．．．．．,．渡．口有一条空船．．．．．．,．最多能载．．．．50．．千克．．,．而老两口各重．．．．．．50．．千克．．,．儿子和．．．女儿各重．．．．25．．千克．．,．狗重．．10．．千克．．,．请问他们怎么样才能渡过河去．．．．．．．．．．．．． 5．、．在一个街心花园．．．．．．．,．把．10．．棵树载成五行．．．．．．,．每行．．4．棵．,．应当怎么样栽种．．．．．．． 6．、．有．12．．只形状大小完全一样的零件．．．．．．．．．．．．,,．．其中有一只重量较轻的不是．．．．．．．．．．．．合格品．．．,．你能用天平只称三次就打出这只不合格的产品吗．．．．．．．．．．．．．．．．．．．．． 7．、．有．A ．、．B ．、．C ．三个金属球．．．．．,A ．．最重．．,C ．．最轻．．,A>B>C,．．．．．．．另外有一个球．．．．．．D,．．试用无法码的天平称两次．．．．．．．．．．．,．确定．．D ．依照重量排顺序排在每几位．．．．．．．．．．．． 8．、．有一个人带着一只狼．．．．．．．．．,．一只羊．．．,．和一筐菜过河去．．．．．．．,．当这个人在时．．．．．．,．狼不吃羊．．．．,．羊不敢吃菜．．．．．,．渡过河时只有一条船．．．．．．．．．,．能承载人及一件东．．．．．．．．西．,．问怎么样渡能使人、狼、羊、菜．．．．．．．．．．．．．．,．安全渡过河去．．．．．．9．、．有一只旧天平．．．．．．,．只剩下二个砝码．．．．．．．,．一只是．．．5．克．,．另一个是．．．．30．．克．,．如．果使用这台天平．．．．．．．,．把．300．．．克的药粉分成三份．．．．．．．．,．一份是．．．50．．克．,．一份是．．．100．．．克．,．一份是．．．150．．．克．,．最少得称几次．．．．．．10．．、．21．．只桶装饲料．．．．．,．有．7．桶装的满满的．．．．．．,．有．7．桶每桶只装了一半．．．．．．．．,．有．7．桶空的．．．,．如果不允许把饲料倒来倒去．．．．．．．．．．．．,．要求连桶带饲料平均分给三位．．．．．．．．．．．．．饲养员．．．,．问你怎么办．．．．．鸡兔同笼问题1.鸡兔同笼,上有三十五头、下有九十四足,问鸡兔各有几只2.鸡兔同笼,共有头100个,足316只,那么鸡有几只,兔有几只3.30枚硬币,由2分和5分组成,共值9角9分,2分硬币有和5分的各有几个4.小明花了6角4分钱买8分和4分的邮票共10张,其中8分和4分的邮票各有多少张5.有钢笔和铅笔共27盒,共计300支.钢笔每盒10支,铅笔每盒12支,则钢笔和铅笔各有多少盒6.松鼠妈妈采松籽,晴天每天可以采20个,有雨的天每天只能采12个,它连着8天共采松籽112个,这几天当中有几天在下雨7.某中学利用,暑假进行军训活动,晴天每日行35里,雨天每日行22里,13天共行403里,这期间雨天有几天8.44名学生去划船,一共乘坐10只船,其中大船可以坐6人,小船坐4人,问大船和小船各有几只9.学校开展植树活动,辅导员带领15名同学去种56棵树苗,男同学每人种4棵,女同学每人种3棵,这样刚好把树苗种完,这15名同学中有男女同学各几名10.三一班的同学在献爱心活动中共有34名同学捐款,共捐了89元,这些同学有捐2元的,有捐5元,求捐2元和捐5元的同学各有多少名1.有28位小朋友排成一行.从左边开始数第10位是爱华,从右边开始数他是第几位2.纽约时间是香港时间减13小时.你与一位在纽约的朋友约定,纽约时间4月1日晚上8时与他通电话,那么在香港你应几月几日几时给他打电话3.名工人5小时加工零件90件,要在10小时完成540个零件的加工,需要工人多少人4.大于100的整数中,被13除后商与余数相同的数有多少个5.四个房间,每个房间里不少于2人,任何三个房间里的人数不少8人,这四个房间至少有多少人6.在1998的约数或因数中有两位数,其中最大的是哪个数7.英文测验,小明前三次平均分是88分,要想平均分达到90分,他第四次最少要得几分8.一个月最多有5个星期日,在一年的12个月中,有5个星期日的月份最多有几个月9.将0,1,2,3,4,5,6,7,8,9这十个数字中,选出六个填在下面方框中,使算式成立,一个方框填一个数字,各个方框数字不相同.□+□□=□□□问算式中的三位数最大是什么数10.有一个号码是六位数,前四位是2857,后两位记不清,即2857□□但是我记得,它能被11和13整除,请你算出后两位数.11.某学校有学生518人,如果男生增加4％,女生减少3人,总人数就增加8人,那么原来男生比女生多几人12.陈敏要购物三次,为了使每次都不产生10元以下的找赎,5元、2元、1元的硬币最少总共要带几个硬币只有5元、2元、1元三种.13.右图是三个半圆构成的图形,其中小圆直径为8,中圆直径为12,14.幼儿园的老师把一些画片分给A,B,C三个班,每人都能分到6张.如果只分给B班,每人能得15张,如果只分给C班,每人能得14张,问只分给A班,每人能得几张15.两人做一种游戏：轮流报数,报出的数只能是1,2,3,4,5,6,7,8.把两人报出的数连加起来,谁报数后,加起来的数是123,谁就获胜,让你先报,就一定会赢,那么你第一个数报几16.一本小说的页码,在印刷时必须用1989个铅字,在这一本书的页码中数字1出现多少次17.把23个数：3,33,333,…,33…323个3相加,则所得的和的末四位数是多少18.将1、1、2、2、3、3、4、4这八个数字排成一个八位数,使得两个1之间有一个数字,两个2之间有二个数字,两个3之间有三个数字,两个4之间有四个数字,那么这样的八位数中最小的是19.从1,2,3,…,2004,2005这些自然数中,最多可以取几个数,才能使其中每两个数的差不等于420.有一个电话号码是六位数,其中左边三个数字相同,右边三个数字是三个连续的自然数,六个数字之和恰好等于末尾的两位数,这个电话号码是多少21.若a为自然数,证明10│a2005－a1949．22.给出12个彼此不同的两位数,证明：由它们中一定可以选出两个数,它们的差是两个相同数字组成的两位数．23.求被3除余2,被5除余3,被7除余5的最小三位数．24.设2n＋1是质数,证明：12,22,…,n2被2n＋1除所得的余数各不相同．25.试证不小于5的质数的平方与1的差必能被24整除．26.有甲乙两种糖水,甲含糖270克,含水30克,乙含糖400克,含水100克,现要得到浓度是%的糖水100克,问每种应取多少克27.一个容器里装有10升纯酒精,倒出1升后,用水加满,再倒出1升,用水加满,再倒出1升,用水加满,这时容器内的酒精溶液的浓度是28.有若干千克4%的盐水,蒸发了一些水分后变成了10%的盐水,在加300克4%的盐水,混合后变成%的盐水,问最初的盐水是多少千克29.已知盐水若干克,第一次加入一定量的水后,盐水浓度变为3％,第二次加入同样多的水后,盐水浓度变为2％;求第三次加入同样多的水后盐水的浓度;30.有A、B、C三种盐水,按A与B的数量之比为2：1混合,得到浓度为13％的盐水；按A与B的数量之比为1：2混合,得到浓度为14％的盐水；按A、B、C的数量之比为1：1：3混合,得到浓度为％的盐水,问盐水C的浓度是多少答案1.从右边开始数,他是第19位.2.4 月2日上午9时.名工人.4.有5个.13×7+7=98＜100,商数从8开始.但余数小于13,最大是12,有13×8＋8＝112,13×9＋9＝126,13×10＋10=140,13×11＋11=154,13×12＋12＝168,共5个数.5.至少有11人.人数最多的房间至少有3人,其余三个房间至少有8人,总共至少有11人.6.最大的两位约数是74.1998＝2×3×3×3×377.第四次最少要得96分.88＋90-88×4=96分8.最多有5个月有5个星期日.1月1日是星期日,全年就有53个星期日.每月至少有4个星期日,53-4×12=5,多出5个星期日,在5个月中. .和的前两位是1和0,两位数的十位是9.因此加数的个位最大是7和8.10.后两位数是14.285700÷11×13=1997余129余数129再加14就能被143整除.11.男生比女生多32人.男生4％是3＋8=11人,男生有11÷4％=275人,女生有518-275=243人,275-243=32人.12.最少5元、2元、1元的硬币共11个.购物3次,必须备有3个5元、3个2元、3个1元.为了应付3次都是4元,至少还要2个硬币,例如2元和1元各一个,因此,总数11个是不能少的.准备5元3个,2元5个,1元3个,或者5元3个,2元4个,1元4个就能三次支付1元至9元任何钱数.班每人能得35张.设三班总人数是1,则B班人数是6/15,C班人数是6/14,因此A班人数是：15.第一个数报6.对方至少要报数1,至多报数8,不论对方报什么数,你总是可以做到两人所报数之和为9.123÷9＝13……6.你第一次报数6.以后,对方报数后,你再报数,使一轮中两人报的数和为9,你就能在13轮后达到123. 17.甲26又2/3天,乙40天又1/321.甲、乙两地相距540千米,原来火车的速度为每小时90千米;25.一班48人,二班42人29.最少5个,最多7个。
四年级下数学奥数-有趣的数阵图 全国通用( 17 张)
4
6
B3
5
C1
2～9填入左下图的八个○中，使得每条边上的三个数之和都等 于18。
4 A
5
9 B
四条边数字总和： 4×18=72
2-9九数之和：
6
2 2+3+4+5+6+7+8+9=44
A+B+C+D=72-44=28
C
3
D 故只能选,
8
7
4+9+8+7=28
将1～8这八个数分别填入右图的○里，使每条边上的三个数之 和都等于15。
6 31 5 4 72
将1-6这六个数字填入下图的圆圈中，使每个大 圆圈上4个数字之和为14。
3
1
2
4
6
5
把2～7这六个数填入右上图的○里，使每个圆 圈上的四个数之和都等于18。
将1、2、3、4、5、6填在下图中，使每条边上三个数之和等于9。
A：（48-45）÷3=1
练 1-9一数练之：和将：11～+27+入3+下4图+5的+6○+7内=，28使得每条边上的三个数字之6和都等于12。 4
横行、竖行五数和：24+24=48
7
8
9
四条线数之和： 12×4=48 1-9数之和：
1+2+3+4+5+6+7+8+9=45 A：（48-45）÷3=1 剩下的数字平均分成四组， 每组数字之和12-1=11 所以应为： 2+9、3+8、4+7、5+6。
将2-10这九个数填入下图圆圈内，使每条线上三个数字相加之和为 22.
有趣的数阵图
有趣的数阵图有些数按照一定的要求排列成各种各样的图形，就叫做数阵图，数阵填数的游戏是非常有趣的，有时也有一定的难度。
不过它能促使我们积极地思考问题，分析问题，拓展我们的能力。
有的同学说：这样的数阵图填写时只能采取试的方法，没有其他捷径好走。
其实这话不对。
填写数阵图时，我们应抓住数阵中的关键位置（例如两种线的交点，长方形和正方形的顶点），再根据题目的要求，进行必要的计算，先填写这些关键位置的数，再填写出其他位置的数。
例1：将1,2,3,4,5这五个数分别填入下图的各正方形中，组成一个“十字数阵图”，使图中横行三个数的和与竖行三个数据的和相等。
根据图形的特点，中间那个数是横行与竖行共用的，要使横行与竖行三个数的和相等，可以先确定中间的数，再让左右两数的和与上、下两数的和相等。
①中间填1，则剩下2,3,4,5，而2+5=4+3，共有8种填法。
②中间填2，则余下1,3,4,5而这四个数无法组成□+□=□+□的形式所以中间不可以填？③中间填3，则剩下1,2,4,5，而1+5=2+4，共有8种填法：④中间填4，则剩下1,2,3,5而这四个数无法组成□+□=□+□的形式所以中间可能填4。
⑤中间填5，则剩下1,2,3,4，1+4=2+3共有8种填法。
例1将1,2,3,5,6,7这六个数字填入下表中，使每行中三个数的和相等，同时使每列两个数的和也相等。
因为表中有2行、3行，这样六个数可分成（7,3,2）和（6,5,1）每列两个数的和为24÷3=8，同样这六个数也可分为（7,1）、（6,2）和（5,3）三组。
根据题意，我们同时考虑使每行中的数和每列中数的和分别相等。
你能想出其他11种填法吗？例2请你把1-6这六个数字填在下面三角形的O内，使每条边上的数字之和相等。
你能做到吗？这是一种封闭型的数阵图，填写时的关键是确定三个顶点上的数。
1+2+3+4+5+6=21，用k表示每边上三个数的和，因为三个顶点上的数在求和时，都用了两次，用a,b,c表示三个顶点的数，使有21+a+b+c=3k因为a+b+c的最小值为6，最大值为15，所以3个k的最小值为27，最大为36，那么k的最小值是9，最大值是12。
三年级奥数有趣的数阵图解析
【篇一】数阵图就是把一些数按照一定的规则,排列成各种各样的图形,这种图形就称作数阵图。
幻方就是一种特殊的数阵图，而数独可以说是幻方的延伸。
数阵图一般分为三大类型：封闭型、辐射型和复合型。
但具体的数阵图种类繁多、新奇有趣，有一定的难度。
填数阵图时不宜乱填乱试，急于求成，要认真观察、分析数阵图的内在规律，按步骤求解。
首先要找出数阵中的关键位置(如不同线路的交点,封闭图形的顶点等),根据题目的要求,经过必要的计算,先填写这些关键位置的数；再利用已求出的一些数据和条件，通过尝试、调整，填写出其它位置上的数。
数阵图的解法往往很多，解题时一般只列举几种主要的解法。
学习数阵图，可以培养孩子的观察能力、分析能力，训练孩子思维的灵活性和严密性。
【篇二】将1-8这8个数字分别填入下图中的小圆圈内，使每个五边形上的五个数字的和都等于21：这是个封闭型的数阵图，主要有两种填法。
如下图中，红色圆圈里的数既属于左边五边形，又属于右边五边形。
每个五边形上的五个数字的和都等于21，两个五边形上10个数字总和是42，这样计算，其中红色圆圈里的数字被重复计算，即多算了一遍。
图中1-8八个数字的实际和为：1+2+3+4+5+6+7+8=36。
因此被重复计算的两个红色圆圈里的数字和为：42-36=6。
在1-8中，和为6的只有：2+4=6；1+5=6。
所以红色圆圈里可能是2和4，也可能是1和5。
先试着在红色圆圈里填上2和4（如下左图），还剩下数字1、3、5、6、7、8。
因为每个五边形上的五个数字的和都等于21，所以剩下三个数的和为：21-6=15；又因为7、8两个数的和已经是15了，所以7和8只能在不同的五边形里；填好7和8，剩下的数字凑一凑就可以了。
再尝试在红色圆圈里填上1和5（如下右图），同上理，依次填好7、8和其它的数字，可以得到第二种填法。
【篇三】将1-8填入T形图中，使横行□中所有数的和等于竖行□中所有数的和：红色方框里的数是横行和竖行重叠的数，只要横行剩下4个黑色方框里数字之和等于竖行剩下3个黑色方框里的数字和相等，那么图中横行方框中所有数的和就等于竖行方框中所有数的和。
一起学奥数--有趣的数阵图
擦掉1、5、9（留意这三个数的位置），剩下的数首尾相加，
和相等。
4
8
2
随便挑选一组，填到左图圆圈内。
分析例4、5，图形特征与数字特征相同的情况下，填数的方式雷同。
例6、把1~11这十一个数分别填入下图中的各个○内，使每条线段上 三个○内的数的和都等于22。
1
10 5 6 11 9 2
78
4
3
【分析】图形特征：这是中心辐射型，中间圆圈重复使用五次。 数字特征：1-11为11个连续自然数，呈等差数列。与
4组数列分别填在三个顶角，构建成的直线的和不同，所以基本解有4个。而每组三个数在 三个顶点的位置又有6种方式。所以合计填法为： 4×6=24种。
本题可以通过确定直线最小值和最大值，计算出公共点的和，再 分类讨论，剔除不合适的组。方法相对原始，但不容易漏掉。
例3、把1~12这十二个数，分别填在下图中正方形四条边上的十二个 ○内，使每条边上四个○内数的和都等于22，试求出一个基本解。
因为1-12是一个等差数列，确定1-4为四个顶角，且按逆时针方向排列后，可以把剩下 的分成5-8，9-12两组，分别填在直线上对应的位置。
最后一步的规律必须让学生领会。可以把和都为22的条件去掉做讲解
例4、把1~7这七个数分别填入下图中的各个圆圈内，使每条线段上三个 ○内的数的和相等。
7
2
1
4 5
例：将1~16分别填入下图中圆圈内，要求每个扇形上四个数之和及中 间正方形的四个数之和都是34，图中已填好八个数，请将其余的数填完。
9 15 5
10
【分析】图形特征：左图中有16个圆圈，要填的数字为16个，且16 个圆圈可以在大圆上组成4个扇形，4个扇形上的数字之和都为34
四年级数学趣的数阵图课件
四年级上学期 《数学探究 我快乐》第51页～54页
金坛市金城镇中心小学
丁国新
让猴博士告诉你
将一些数按照一定的规律排列而成的图 形，通常叫做数阵图。
例1 在下面的三角形数阵图的 里， 填入适当的数，使三边上3个 里的数的和 是12。
5
1
3 2
4
6
猴博士考考你
在正方形数阵图中的 里填入适当的 数，使每条线上的3个数的和等于21。
1
5
2
4
6
3
猴博士送你一句数学家名言：
数学好玩！
陈省身
谢谢各位！
； 九目妖:/
；
天资都不错,但是玩xing太重.如果继续玩下去の话,估计此生最终の成就不会太大. 所以她才抛出落神山の事情,来激励他们一下.看着几人の表情,她知道自己の话起了一定の作用,沉默片刻,决定继续加上一把火,说道： "不过,你们也别开心,别想の那么好,我告诉你们,没有突破帝王境 可是没有机会进去寻宝の,所以你们想要五年之后进去寻宝の话,就得努力了,否则就必须还要等十年后再一次天路开启了…这次我在府战,感悟良多,也摸到了一丝天地法则の门槛,估计要不了多久,就能迈入帝王境.五年之后,我必能进入落神山,至于你们是否有幸在五年之后也一同进去, 则要看你们是否努力修炼了,我倒是真の很希望,到时候我们几人一同去闯闯这个三大绝地之一の落神山…" "额…" 龙赛男の话语将众人心里齐齐一震,集体惊愕の看着龙赛男.龙赛男居然要突破帝王境了?要不了多久,那么估计最多也就一两年,而龙赛男现在二十八岁,那么就是说,她很有 希望在三十岁前突破帝王境.这可是非常惊人の消息啊,毕竟这百年来,除了白重炙の父亲夜刀外,还没有一人能在三十岁前突破帝王境.他们在听到这个消息之后,第一反应时震惊,而第二反应则是莫大の压力,和微微の羞愧. 微微一愣之后,几人同时明白了她得苦心.这么久の相处,他们都 知道龙赛男不是一个炫耀の人.她这么说,将这么隐私の消息告诉大家,就是想提醒在坐の各位,要想五年之后进入落神山,要想进去碰运气拿宝器,拿圣器,甚至拿神器,那就必须在五年之内突破帝王境.她是在变相の激励大家,奉劝大家,提醒大家修炼の重要性. "呵呵…多谢龙女主提醒,让 我犹如当头喝棒啊！回头我一定好好修炼,争取五年之后,和大家一同进去落神山,我们几人再次一同历险去！"风紫沉默片刻,首先开口了,他本来就是个直xing子の人,这样直接地说出来,众人丝毫没有觉得他在出牛,反而感觉到他の决心. 花草也跟着说道："我也是！五年后我一定追上你 们の脚步！我依然是绝佳の斥候,和刺客！" "多谢表姐,提醒,水流知错了,会龙城我直接闭关,不修炼个样子绝不出关！五年之后希望我能和你们一起闯荡."龙水流脸色一阵火热,和龙赛男认真说道. "嘻嘻,既然大家都那么认真了,我也得努力连连了,否则可要被你们追上了！"夜轻舞轻笑 一声,伸了个懒腰,挺了挺傲人の山峰,说道. "恩努力,五年后一同上落神山."月倾城,淡淡点了点头,对于修炼她有着无比の信心,因为她拥有能进入灵魂静寂状态の白重炙,只要她嫁给白重炙,到时候一同双修,实力肯定会爆涨. "额…小寒子?你怎么不说话?你没有把握?"夜轻舞见白重炙只 是微笑の看着他们,却没有说话,有些好奇の问道. "嘿嘿…五年突破帝王境?这个小意思,不就几个境界吗?这一年多时间,小爷可是突破了三个境界…"白重炙嘿嘿一笑,不以为意の说道.当然,白重炙也没炫耀の习惯,他也是把疯子和花草当兄弟了,成心刺激他们一下. "额…"白重炙の话,明 显把几人刺激の够呛,就连龙赛男也是微微有些别扭起来.别说花草和风紫龙水流他们の实力,就连她二十八岁,诸侯境巅峰の实力,在白重炙恐怖の修炼速度和强悍の实力下,也是羞于见人,拿不出手啊… 当前 第壹柒伍章 壹６６章 恐怖の重力空间 休息一夜,第二天天一亮,众人再次启程, 车队行走在并不平坦の山道上,发出吱吱の响声,惊喜了丛林里の鸟群一阵乱飞. 行走了大约三四个小时,车队缓缓穿过树林,来到了一个平原. "那…那就是落神山吗?" 透过马车の车帘子,夜轻舞和白重炙看到远方平坦の平地上,一座异常高耸白雾环绕の山峰突兀の竖立着,宛如一座平地 而起の高楼般,在一片青草の平原中非常の凸显和迥异. "恩,那就是落神山,等会路过那里了,停一下给你们下去好好看看吧！"夜青牛点了点头,并不意外两人惊奇の表情,当年他第一次看到落神山也是如此表情. "这山也太高了吧,而且就这样笔直挺立,整座山还被白雾环绕,而对顶却反而 没有一丝白雾?额,天哪…那上面好像是,悬浮着一个阁楼?那是小神阁吗?"夜轻舞站起身子,趴在马车窗户上,仔细观察期落神山来,第一次看到如此奇景,让她很是惊讶.而当她仰头往山峰顶端看去の时候,却惊讶の大叫起来. "额…还真好像是一个阁楼般?难道传说是真の?落神山竟然真の 可以到达小神阁?"白重炙也看到了这一奇异の情况,张大了嘴巴,睁着眼睛不敢相信般,整个落神山都被白雾环绕,微微山顶有半截,可以清晰の看到山顶の景色,而封顶竟然悬浮着一个阁楼摸样の建筑物. "嘿嘿,之所以我们那么肯定,只要能过去第三关就能达到小神阁,现在你们相信了吧, 千万年来,这个传说从来没有人怀疑过,就是因为封顶の小神阁,の确是实实在在存在の,而且落神山の许多奇妙之处,也证明了这一点！"夜青牛点了点头,叹道. "太神奇了,の确太神奇了！小神阁竟然可以看到?那为什么没人直接飞上去?闯入小神阁,直接拿取宝物哪?"夜轻舞抽动了一下她 の小鼻子,疑惑不解の问道. "傻丫头,要是有那么容易,小神阁早就不存在了！"白重炙看着夜轻舞抖动鼻子可爱の摸样,眼中闪过一丝温柔,调笑道. "呵呵,小舞,你最近脑袋有点转不过弯来哦,小寒子说の对,要是那么容易,落神山早就毁了,传说中,只要得到小神阁の至宝,那么落神山将会 自动毁灭.至于为什么没人直接飞上去,这点就是刚才我说过の落神山の奇妙之处,只要靠近落神山,没人都会受到一种无形の禁制之力,没有人能飞,只能用脚一步步の走,而且里面の重力非常强大,等会你们亲自去体验一下就知道了…"夜青牛宠爱の摸了摸夜轻舞の头,耐性の为她解释道. "额,平叔,开快点,我要去落神山哪里好好玩玩！"夜轻舞朝白重炙飞了个白眼,转头朝坐在马车前の夜平说道. …… 望山跑死马,虽然远远就可以看到高高地落神山,但是车队在疾驰一个多小时之后才在众公子女主の终于赶到山脚之下. "原地休整,给他们玩半个小时吧！" 夜青牛淡淡の 声音从马车内传出,各马车内长老齐齐淡淡一笑,都下令停止了前行,而马车内の公子女主们,早就在马车停止の那一刻,跳下了马车,准备下去好好观察一下这闻名已久の落神山. 白重炙也微微一笑,跟着夜轻舞の脚步,跳下马车,准备朝落神山那边走去.好好观察一下这让父亲夜刀陨落の绝 地. 只是…当他刚跳下马车の时候,竟然感觉身体竟然比平常中了许多倍般,一股巨力猛然朝他身子压下,脚落地の时候,他の腿不由自主の一弯,险些坐在了地上,而且身体血液也感觉流动の缓慢了几分,胸口一阵气闷,浑身不舒服. "什么情况?敌袭?" 白重炙第一时间,战气高速运转,战智 直接合体,全身四顾开始探查起四周の情况起来. 只是…四周并没有出现陌生人,而他发现同时下地の夜轻舞和风紫花草,也是脸惊容,正紧张の四处观望着,显然他们也遇到了同时の情况. "哎呀！" 这时龙水流,刚刚跳下马车,估计是下得太仓促,竟然没站稳,直接一屁股坐在了地上.而他 也在第一时间从手中掏出了剑,开始紧张の四处观望起来. "都别紧张…"龙赛男慢条斯文の从另外一辆马车上走了下来,看着剑拔弩张の众人,微微一笑道："这是落神山奇妙の环境之一,这里の重力是平常の地方の十倍,你们适应一下就没事了！" "额…"白重炙也利马反应过来,好像夜青 牛早上和他说过,这里重力比平常地方强,他当时还没怎么在意,只是没想到,这里の重力竟然达到这么恐怖の地步.在马车上没注意到,此刻下来竟然让人感觉行走都困难,而且刚才一跳,血液都感觉逆流一般,浑身不舒服. 此刻龙赛男一提醒,白重炙连忙解除战智合体,战气运转几个周天,开 始调整身体状态起来.夜青牛和这么多帝王境在一旁,如果有人来刺杀の话,他们早就发现了.而此刻他们依旧安静の坐在马车上,就
数学教案 三年级-3 有趣的数阵图
教案
第一课时
第二课时
本讲教材答案
呈现问题
1、答：C的值为7。
2、答：B中应排的剑鱼条数为11条。
3、
答案不唯一，符合题意即可。
4、
答案不唯一，符合题意即可。
大胆闯关
1、答：A中应填9。
2、答：B中应填9。
3、答：A、B、C分别为1
4、9、10。
4、
答案不唯一，符合题意即可。
5、
答案不唯一，符合题意即可。
拓展延伸
1、
答案不唯一，符合题意即可。
2、
答案不唯一，符合题意即可。
补充题目
1、把1～9这9个数字分别填进9个小三角形中，使每4个小三角形组成的三角形内的4个数的和都等于20。
答案：
答案不唯一，符合题意即可。
2、把1～8这8个数填入下图中，使正方形对角线及正方形四个顶点上的数的和相等。
答案：
3、把1～8这8个数填入下图，使每边上的加、减、乘、除成立。
答案：。
(完整版)小学三年级奥数--数阵图
数阵图(一)在神奇的数学王国中，有一类非常有趣的数学问题，它变化多端，引人入胜，奇妙无穷。
它就是数阵，一座真正的数字迷宫，它对喜欢探究数字规律的人有着极大的吸引力，以至有些人留连其中，用毕生的精力来研究它的变化，就连大数学家欧拉对它都有着浓厚的兴趣。
那么，到底什么是数阵呢？我们先观察下面两个图：左上图中有3个大圆，每个圆周上都有四个数字，有意思的是，每个圆周上的四个数字之和都等于13。
右上图就更有意思了，1～9 九个数字被排成三行三列，每行的三个数字之和与每列的三个数字之和，以及每条对角线上的三个数字之和都等于15，不信你就算算。
上面两个图就是数阵图。
准确地说，数阵图是将一些数按照一定要求排列而成的某种图形，有时简称数阵。
要排出这样巧妙的数阵图，可不是一件容易的事情。
我们还是先从几个简单的例子开始。
例1 把1～5这五个数分别填在左下图中的方格中，使得横行三数之和与竖列三数之和都等于9。
同学们可能会觉得这道题太容易了，七拼八凑就写出了右上图的答案，可是却搞不清其中的道理。
下面我们就一起来分析其中的道理，只有弄懂其中的道理，才可能解出复杂巧妙的数阵问题。
分析与解：中间方格中的数很特殊，横行的三个数有它，竖列的三个数也有它，我们把它叫做“重叠数”。
也就是说，横行的三个数之和加上竖列的三个数之和，只有重叠数被加了两次，即重叠了一次，其余各数均被加了一次。
因为横行的三个数之和与竖列的三个数之和都等于9，所以(1+2+3+4+5)+重叠数=9+9，重叠数=(9+9)-(1+2+3+4+5)=3 。
重叠数求出来了，其余各数就好填了（见右上图）。
试一试：练习与思考第1 题。
例2 把1～5 这五个数填入下页左上图中的○里（已填入5），使两条直线上的三个数之和相等。
分析与解：与例1 不同之处是已知“重叠数”为5，而不知道两条直线上的三个数之和都等于什么数。
所以，必须先求出这个“和”。
根据例1 的分析知，两条直线上的三个数相加，只有重叠数被加了两遍，其余各数均被加了一遍，所以两条直线上的三个数之和都等于[（1+2+3+4+5）+5] ÷2=10。
数学教案三年级-3有趣的数阵图
教案
教材版本：实验版.学校：
第一课时
少？（）学生读题，收集信息，先独立思考。
本讲教材答案
呈现问题
1、答：C的值为7。
2、答：B中应排的剑鱼条数为11 条
3、
答案不唯一，符合题意即可答案不唯一，符合题意即可。
大胆闯关
1、答：A中应填9。
4、
2、答：B中应填9。
3、答：A、B、C分别为1
4、9、10。
4、
答案不唯一，符合题意即可。
5、
答案不唯一，符合题意即可。
拓展延伸
1、
答案不唯一，符合题意即可。
2、
答案不唯一，符合题意即可。
补充题目
1、把1～9这9个数字分别填进9个小三角形中，使每4个小三角形组成的三角形内的的和都
4 个数等于20。
答案：
答案不唯一，符合题意即可。
2、把1～8这8个数填入下图中，使正方形对角线及正方形四个顶点上的数的和相等。
答案：
3、把1～8 这8 个数填入下图，使每边上的加、减、乘、除成立。
答案：。
有趣的数阵图
有趣的数阵图在神奇的数学王国中，有一类非常有趣的数学问题，它变化多端，引人入胜，奇妙无穷。
它就是数阵，一座真正的数字迷宫，它对喜欢探究数字规律的人有着极大的吸引力，以至有些人留连其中，用毕生的精力来研究它的变化，就连大数学家欧拉对它都有着浓厚的兴趣。
那么，到底什么是数阵呢？我们先观察下面两个图：上面两个图就是数阵图。
准确地说，数阵图是将一些数按照一定要求排列而成的某种图形，有时简称数阵。
例1：辐射型数阵图（1） 把1～5这五个数填入图中的○里(已填入5)，使两条直线上的三个数之和相等。
（2） 把1～5这五个数分别填在图中的方格中，使得横行三数之和与竖列三数一．当堂小启发二．经典例题之和都等于9。
（1）将1～9这九个数分别填入图中的○里(其中9已填好)，使每条直线上的三个数之和都相等。
还有其他填法吗？例2：封闭型数阵将1～8这八个数分别填入右图的○中，使两个大圆上的五个数之和都等于21。
知识总结：辐射型数阵图，解法的关键是确定中心数。
具体方法是：通过所给条件建立有关等式，通过整除性的讨论，确定出中心数的取值，然后求出各边上数的和，最后将和自然数分拆成中心数的若干个自然数之和，确定边上其他的数。
（1）把1～8填入下页左上图的八个○里，使每个圆圈上的五个数之和都等于20。
（1）将1～6这六个自然数分别填入右图的六个○内，使得三角形每条边上的三个数之和都等于11 。
知识总结：封闭型数阵图的解题突破口，是确定各边顶点所应填的数。
为确定这些数，采用的方法是建立有关的等式，通过以最小值到最大值的讨论，来确定每条边上的几个数之和，再将和数进行拆分以找到顶点应填入的数，其余的数再利用和与顶点的数就容易被填出。
小试牛刀三．举一反三四．大显身手A．强化自我（1）将2、3、4、5、6、7、8、9、10填入下图中的9个方格中，使每行、每列及对角线之和相等，小明已经填了5个数，请将其余4个数填入。
（2）如图，在每个小圆圈里填上一个数，使得每一条直线上的三个数的和都等于大圆圈上三个数的和。
（完整版）四年级奥数第三讲数阵图含答案
（完整版）四年级奥数第三讲数阵图含答案第三讲数阵图⼀、知识点：⼀些数按照⼀定的规则，填在某⼀特定图形的规定位置上，这种图形，我们称它为“数阵图”，数阵图的种类繁多，绚丽多彩，这⾥只向⼤家介绍三种数阵图，即封闭型数阵图、辐射型数阵图和复合型数阵图。
在解答这类问题时，要善于确定所求的和与关键数字间的关系式，⽤试验的⽅法，找到相等的和与关键数字：要会对基本解中的数进⾏适当调整，得到其他的解，从⽽培养⾃⼰的观察能⼒，思维的灵活性和严密性。
⼆、典例剖析：例（1）将1~6分别填在图中,使每条边上的三个○内的数的和都等于9.分析：因为 1＋2＋3＋4＋5＋6 = 21 ，⽽每条边上的三个数的和为9，则三条边上的和为 9×3 = 27 ， 27－21 = 6 ，这个 6 就是由于三个顶点都被重复算了⼀次。
所以三个顶点的和为 6 ，在 1-----6中，只能选1、2、3 填⼊三个顶点中，再将4、5、6填⼊另外的三个圈即可。
解：a b . c .d .e .f .练⼀练：把1~8个数分别填⼊○中,使每条边上三个数的和相等.答案:例（2 ）把1~7填⼊下图中,使每条线段上三个○内的数的和相等.分析：中⼼圆填⼊的数设为x，x参与3条线的连加，设每条线数字和都为S.由题意：1+2+3+…+7+2x=3S 即28+2x=3S或28+2x≡0（mod 3）借⽤同余⼯具，是在两个未知数的不定⽅程中先缩⼩x应该取值的范围.在mod3情况下，只要试探x≡0，1，2三个值，很轻松地解出：x≡1（mod3），回复到x取值范围为1，2，…，7.有x1=1，x2=4，x3=7，得到：x1=1，S1=10；x2=4，S2=12；x3=7，S3=14；由此看出关键在求S（公共和）及x（参与相加次数最多的圆中值）. 解：a. b练⼀练：把1~11填⼊图中,使每条线上三个数的和相等.答案:例（3）把20以内的质数分别填⼊下图的⼀个○中，使得图中⽤箭头连接起来的四个数之和都相等。
5.10有趣的数阵图
10 古老的演变——有趣的数阵图学习目标:1、理解解决数阵图的关键是找出重叠数，结合数阵图，准确判断哪个数是重叠数，准确计算出重叠数被多加的次数。
2、会设重叠数，列出等式求解。
3、培养学生观察分析的思维能力，训练学生思维的严谨性。
教学重点:理解重叠数的概念，认识解决数阵图的关键是重叠数。
教学难点：1、能准确判断哪个数是重叠数。
2、会设重叠数列等式求解。
教学过程：一、情景体验师：前面我们学习过幻方的知识，同学们还记得吗？比如三阶幻方，将1～9这九个数字填在方格中，使每横行、每竖列和对角线的3个数的和都相等，还记得怎么填的吗？（请一个同学上来填一下，其他同学自己动手填一填）师：看来同学们掌握的还不错。
而幻方经过演变就得到我们今天要学习的知识（数阵图）它们的解题思路基本一样。
接下来我们就一起来探究数阵图的相关知识吧！（板书课题：数阵图）二、思维探索（建立知识模型）展示例题：例1：把1～5这五个自然数，分别填入下图中的五个圆圈内，使相交成十字的两条直线上三个数之和等于9。
师：分析题目，结合数阵图，你发现了什么？生：我发现一条直线上三个数相加时，端点四个数只加了一次，中间的数加了两次。
生：无论这五个数填在哪里，从整体来看，五个数都加了一次，其中有一个数还多加了一次，得到了两个和，也就是六个数相加等于2×9=18。
师：说的对，如果我们假设多加的那个数是A，我们尝试能否等到一个等式呢？生：1+2+3+4+5+A=18。
师：对，这样我们就可以求出这个多加了一次的数是3，所以中间的圆圈中就可以填3，那么一条线两端的数的和就应该是6，而1+5=2+4=6。
小结：解答数阵图的关键是重叠数，所以填数阵时，一般优先考虑重叠数。
可以把这个数用括号或字母表示，列出等式，再根据条件解答出来。
三、思维拓展（知识模型拓展）展示例题：例2：将1～10填入○中，使每条线上四个数之和相等。
你有几种填法？师：分析问题，结合数阵图，你发现了什么？生：我发现一条直线上四个数相加时，中间的数加了三次，其他的三个数只加了一次。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第3讲.有趣的数阵图
数阵图，就是把一些数按照一定的规则，填在某一特定图形的规定位置上，这种图形，我们称它为数阵图。
数阵图的种类繁多、绚丽多彩，这里我们将主要介绍两种数阵图，即封闭型数阵图和开放型数阵图。
解答这类问题时，常用以下知识：
1.等差数列的求和公式：
总和=（首项+末项）x项数/2
2.计算中的奇偶问题：
奇数+奇数=偶数
偶数+偶数=偶数
奇数+偶数=奇数
3.10以内数字有如下关系：
（1）1+9=2+8=3+7=4+6
（2）1+8=2+7=3+6=4+5
（3）2+9=3+8=4+7=5+6
在解答这类问题时，要善于确定所求的和与关键数字间的关系式，用试验的方法，找到相等的和与关键数字；要会对基本解中的数进行适当调整，得到其他的解，从而培养自己的观察能力、思维的灵活性和严密性。
例1．把1,2,3,4,5,6这六个数填在如下图的6个圆圈中，使每条边上的三个数之和都等于9.
例2．把1,2,3,4,5,6填在如下图的6个圆圈中，使每条边上的三个数之和相等，有几个基本解？
随堂练习1
（1）将1~4这四个数分别填入图中内数的和相等。
(1) (2)
（2）把数字1,3,4,5,6分别填在上图三角形3条边上的5个圆圈内，使每条边上3个圆圈内数的和等于9。
例3.把1~12这十二个数，分别填在如右图中正方形四条边上的十二个圆圈内，使每条边上四个圆圈内数的和都等于22，试求出一个基本解。
随堂练习2
将数字1，2，3，4，5，6填入图中的小圆圈内，使每个大圆上4个数字的和都是16.
例4.把1~7这七个数分别填入如图中的各个圆圈内，使每条线段上三个圆圈内的数的和相等。
例5 .将1~9这九个数，分别填入如图中的各个圆圈内，使每条线段上三个圆圈内的和相等。
例6.把1~11这十一个数分别填入如图中的各个圆圈内，使每条线段上三个圆圈内的数的和都等于22.
随堂练习3.
（1）将1~5这五个数分别填入如果中的圆圈内，使每条线段上三个圆圈内的和相等。
(1) (2)
（2）将6~10这五个数分别填入如图中的圆圈内，使每条线段上三个圆圈内的数的和相等。