简单六方格子-坐标纸-方便绘图
上册微专题七网格坐标系中的旋转作图及旋转证明人教版九年级数学全一册精品系列PPT

上册 微专题七 网格(坐标系)中的旋转作图及旋转 证明-20 20秋人 教版九 年级数 学全一 册课件 (共27 张PPT)
变形3答图
上册 微专题七 网格(坐标系)中的旋转作图及旋转 证明-20 20秋人 教版九 年级数 学全一 册课件 (共27 张PPT)
微专题七 网格(坐标系)中的旋转作图及旋转证明
一 二
一 网格(坐标系)中的旋转作图 (教材 P62 习题 23.1 第 4 题) 如图 1,分别画出△ABC 绕点 O 逆时针旋转 90°和 180°后的图形.
图1
解:如答图,△A1B1C1 是△ABC 绕点 O 逆时针旋转 90°后的图形;△A2B2C2 是 旋转 180°后的图形.
上册 微专题七 网格(坐标系)中的旋转作图及旋转 证明-20 20秋人 教版九 年级数 学全一 册课件 (共27 张PPT)
上册 微专题七 网格(坐标系)中的旋转作图及旋转 证明-20 20秋人 教版九 年级数 学全一 册课件 (共27 张PPT)
二 旋转证明 (教材 P63 习题 23.1 第 10 题) 如图 5,△ABD,△AEC 都是等边三角形.BE 与 DC 有什么关系?你能用旋转 的性质说明上述关系成立的理由吗?
图人 教版九 年级数 学全一 册课件 (共27 张PPT)
顶点与原点重合,直角顶点 C 在第二象限,将 Rt△OCB 绕原点顺时针旋转 120°后得
到△OC′B′,则 B 点的对应点 B′的坐标是( A )
A.( 3,-1)
B.(1,- 3)
C.(2,0)
D.( 3,0)
上册 微专题七 网格(坐标系)中的旋转作图及旋转 证明-20 20秋人 教版九 年级数 学全一 册课件 (共27 张PPT)
六年级数学上册教学设计-数形结合-人教版

六年级数学上册教学设计数形结合人教版教学内容本节课将引导学生深入理解数学中“数形结合”的概念,通过直观的图形来理解和解决数学问题。
课程内容主要围绕人教版六年级数学上册中关于“数形结合”的相关章节,包括但不限于:坐标平面、函数图像、几何图形的量化分析等。
教学目标1. 知识与技能:使学生能够正确理解数形结合的基本概念,掌握坐标平面上的点与二元组的关系,能够绘制简单的函数图像,并利用图形解决实际问题。
2. 过程与方法:通过观察、操作、分析等实践活动,培养学生运用数形结合思想解决问题的能力,增强学生的空间想象力和逻辑思维能力。
3. 情感态度与价值观:激发学生对数学学习的兴趣,培养学生合作交流、探索创新的意识,让学生体验到数学与实际生活的紧密联系。
教学难点1. 概念理解:学生对“数形结合”这一抽象概念的理解和内化。
2. 图形与数值转换:学生将具体图形中的信息转换为数值计算,或将数值计算结果通过图形表现出来的能力。
3. 问题解决策略:如何引导学生运用数形结合思想,找到解决数学问题的有效策略。
教具学具准备教师准备:多媒体教学设备、PPT课件、坐标纸、绘图工具。
学生准备:坐标纸、直尺、圆规、彩笔等绘图工具。
教学过程1. 导入新课:通过展示生活中的数形结合实例,如温度变化图、股票走势图等,引起学生的兴趣,导入新课。
2. 探究新知:引导学生观察坐标平面,探讨坐标点与二元组的对应关系。
通过绘制简单的函数图像,让学生直观感受数与形的结合。
3. 实践操作:学生分组进行图形绘制和数据分析,合作完成数形结合的实践任务。
5. 巩固练习:布置相关的练习题,让学生独立完成,巩固所学知识。
6. 课堂小结:回顾本节课的学习内容,强调数形结合的重要性。
板书设计板书将简洁明了地呈现本节课的主要内容和关键知识点,包括数形结合的定义、坐标平面的介绍、函数图像的绘制方法等。
同时,通过图表和示例,直观展示数形结合在解决实际问题中的应用。
作业设计作业将包括基础题、提高题和拓展题三个层次,旨在巩固学生对数形结合概念的理解,提高学生运用数形结合解决问题的能力。
十四种空间格子

同学们,再见!
的平行六面体的体积力求最小。
十四种空间格子
空间格子的划分
划分7种平行六面体
对应于7个晶系
形状及参数?
4mm
十四种空间格子
十四种空间格子
2.平行六面体中结点的分布
1)原始格子( primitive, P):结点分布于平行六面体的八个角顶。 2)底心格子( end-centered, C、A、B):结点分布于平行六面体 的角顶及某一对面的中心。 3)体心格子( body-centered, I):结点分布于平行六面体的角顶和 体中心。
4)面心格子( face-centered, F):结点分布于平行六面体的角顶和
三对面的中心。
十四种空间格子
以下两个平面点阵图案,画出其空间格子:
mm2(L22P) 4mm(L44P)
十四种空间格子
4mm
十四种空间格子
mm2 引出问题:空间格子可以有带心的格子; 另外请思考:如果上面的图案对称为3m,该怎么画?
十四种空间格子
总结: 在四种格子类型当中,其中底心、
体心、面心格子称带心的格子,这是因为有 些晶体结构在符合其对称的前提下不能画出 原始格子,只能画出带心的格子。
十四种空间格子
七个晶系—七套晶体常数—七种平行六面体种形状。 每种形状有四种类型,那么就有7×4=28种空间格子?
但在这28种中,某些类型的格子彼此重复并可转换,还有
一些不符合某晶系的对称特点而不能在该晶系中存在,因 此,只有14种空间格子,也叫14种布拉维格子。(A.Bravis
于1848年最先推导出来的)
结构化学第七章课件

Laue方程的推导
a (cos -cos0 )= h h为整数 即在入射角为0 时,在方向产
生衍射。
直线点阵上衍射圆锥的形成
Laue 方程组: 对于空间点阵,应同时满足以下三式,
h、k、l为整数(但并不都是互质整数)--衍射指标。
Laue 方程把衍射方向和晶胞参数联系在一起。
Laue方程组决定了衍射方向的分立性,因为空间点阵的 衍射方向是以三个互不平行的直线点阵为轴的的三组圆 锥面的共交线,所以只有某些特定方向上才会出现衍射。
h k l=nh* nk* nl* 才能产生反射。 如果某一晶面(h*k*l*)产生n级衍射,则可把其看作是晶 面(nh*nk*nl*)的一级衍射。晶面(h*k*l*)的面间距为d, 则晶面(nh*nk*nl*)的面间距就是d/n,于是Bragg方程可 写成:
2 (dh*k*l*)/n sinn = 即:2 dhkl sin =
d hkl
a h2 k2 l2
正交晶系
dh*k*l*
1 ( h* )2 ( k )2 (l )2
abc
六方晶系
dh*k*l*
1
4( h*2
hk 3a2
k
2
)
l 2 c2
Bragg方程表明,晶面指标为(h*k*l*)的晶面只对某些
角的入射线产生反射。可以证明,对于这些晶面,只有 衍射方向hkl和晶面指标(h*k*l*)满足:
1. 宏观对称元素和对称操作 晶体的理想外形在宏观表现出来的对称性
对称元素 旋转轴 (n或n) 反映面 (m) 对称中心 (i)
反轴 ( n )
对称操作
旋转 L() =2/n
反映 M 反演 I
旋转反演L()I
AutoCAD快速入门

AutoCAD快速入门AutoCAD快速入门(一):界面布局:点击查看AutoCAD快速入门(二):图形窗口:点击查看AutoCAD快速入门(三):捕捉栅格绘制直线:点击查看AutoCAD快速入门(四):使用坐标绘图:点击查看AutoCAD快速入门(五):对象捕捉:点击查看AutoCAD快速入门(六):绘制圆:点击查看AutoCAD快速入门(七):打开、新建和保存文件:点击查看AutoCAD快速入门(八):选择对象:点击查看AutoCAD快速入门(九):绘制多段线:点击查看AutoCAD快速入门(十):移动、旋转和复制:点击查看AutoCAD快速入门(十一):删除、修剪和延伸:点击查看AutoCAD快速入门(十二):偏移:点击查看AutoCAD快速入门(十三):倒角和圆角:点击查看AutoCAD快速入门(十四):夹点编辑:点击查看AutoCAD快速入门(十五):图层基础操作:点击查看AutoCAD快速入门(十六):修改颜色、线型和线宽:点击查看AutoCAD快速入门(十七):利用图层控制对象属性:点击查看AutoCAD快速入门(十八):填充:点击查看AutoCAD快速入门(十九):添加文字:点击查看AutoCAD快速入门(二十):文字样式:点击查看AutoCAD快速入门(二十一):修改文字:点击查看AutoCAD快速入门(二十二):添加标注:点击查看AutoCAD快速入门(二十三):标注样式:点击查看AutoCAD快速入门(二十四):修改标注:点击查看AutoCAD快速入门(二十五):图块:点击查看AutoCAD快速入门(二十六):图像:点击查看AutoCAD快速入门(二十七):外部参照:点击查看AutoCAD快速入门(二十八):布局:点击查看AutoCAD快速入门(二十九):视口:点击查看AutoCAD快速入门(三十):打印:点击查看一界面布局对于CAD初学者来说,了解操作界面的布局至关重要,因为只有了解软件的界面布局,才能方便地与他人交流,才有可以正确领会各种教程和技巧,才能在操作时迅速地找到目标功能,提高学习的兴趣和效率。
第六章 空间点阵
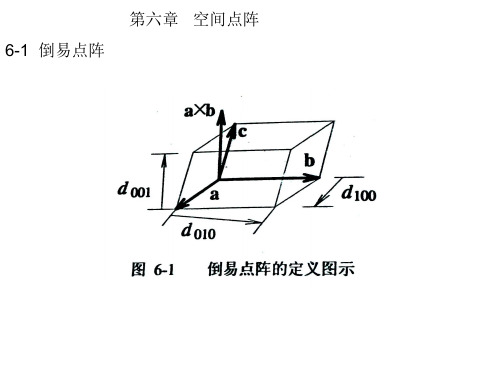
3
4 正点阵空间的位矢 R uvw u a v b w c 长度表示为 a u u 2 R uvw R uvw R uvw u , v , w b a b c v u , v , w G v w w c 5 h1 k 1l1 与 h 2 k 2 l 2 两平面夹角为两倒易矢 rh1 k 1 l1 * 与 rh 2 k 2 l 2 * 间
7
实际晶体中出现几率大
的是 Miller 指数小的晶面。
定义 2:一族晶面中离原点最 近的平面点阵在轴 a , b , c 上的 1 1 1 截距分别为 a , b , c 的 , , ,整数数组即为该晶面 的 Miller 指数。 h k l 定义 3:设一族点阵平面分别 将基矢 a , b , c 分为 h 段 , k 段 , l 段,则 该晶面的 Miller 指数为 hkl 。
a x a y a z a x a y a z ax ay az ax ay az 2 v a b c a b c bx by bz bx b y bz bx b y bz bx b y bz c c c c c c cx cy cz cx cy cz x y z x y z a a a b a c 2 1 b a b b b c det G 同理 v * det G * det G c a c b c c
Fourier
( x ua , y vb , z wc ) F hkl e
hkl
hkl
六角图的画法

六⾓图的画法所谓六⾓图就是利⽤功率表测量电流相位的⼀种⽅法,它是⼀种简单有效的相位检测⽅法。
利⽤六⾓图能正确的判断出:1)同⼀组电流互感器三相电流之间的相位是否正确。
2)功率⽅向继电器接线是否正确。
3)差动保护中不同组别电流互感器的电流相位是否正确。
4)电流互感器变⽐是否正确。
因此,向量六⾓图在实际应⽤中具有相当⼴泛的⽤途。
六⾓图的原理在⼀定坐标系统中,任何相量都可以⽤它在任何两个相交轴上的垂直投影来表⽰。
根据这⼀原理,我们采⽤的坐标系统是互成120’的三相对称电压系统。
由于线电压不受零序电压的⼲扰,所以采⽤三相线电压作为测量三相电流相位的基准量。
在相量图中,被测电流在⼀个电压相量上的投影,可以确定该电流相量端点的轨迹;在两个电压相量上的投影,可以确定被测电流相量端点的位置(即电流的相位和⼤⼩);⽤此⽅法得出不同⽅向的电流数值,进⾏⽮量计算,即可检验结果的准确性。
六⾓图实验将被测电流Ia按规定极性接⼊功率表的电流端⼦,再将同⼀系统的电压Uab、U bc、Uca按规定极性依次接⼊同⼀功率表的电压端⼦,分别读取Uab、Ubc、Uca 电压下的功率表的读数(其读数有正、负),再依次将Ib、Ic接⼊功率表重复上述试验。
⼀、绘制差动相量六⾓图,我们⼀般⽤的试验⼯具是钳形电流相位表,这个表可以测量电流、电压幅值,和电压与电流之间的夹⾓,两个电流之间的夹⾓。
要绘制六⾓图,我们只需要测量电流的幅值,与电流和电压(固定选取⼀相电压,如Uan)的夹⾓。
钳形电流表可取U1,I2,这样电压超前电流30度。
取U2, I1这样电压滞后电流30度。
在保护屏后边测量差动电流的幅值,以及电流和选定的电压的夹⾓,然后以选⽤的电压为基准(设为0度)画出测量所得的电流量,就绘制出了差动相量六⾓图。
⼆、在继电保护回路中,对有相位要求的电流回路,⼀般⽤电流相量六⾓图来判断电流回路接线是否正确。
从电流相量六⾓图可以直观反映出:同⼀组电流互感器三相电流IA、IB、Ic之间的关系;差动保护中不同组别电流互感器的电流之间的关系;阻抗或⽅向元件的电流和电压之间的相位关系。
chap8-晶体结构的几何理论

4mm(L44P)
mm2(L22P)
4mm
mm2
引出: 引出:空间格子可以有带心的格子
平行六面体中结点的分布
1)原始格子(P):结点分布于平行六面体的八个角顶。 )原始格子( ) 结点分布于平行六面体的八个角顶。 2)底心格子( C、A、B):结点分布于平行六面体的角 )底心格子( ) 顶及某一对面的中心。 顶及某一对面的中心。 3)体心格子(I ):结点分布于平行六面体的角顶和体中心。 )体心格子 :结点分布于平行六面体的角顶和体中心。 4)面心格子(F):结点分布于平行六面体的角顶和三对 )面心格子( ) 面的中心。 面的中心。
第八章 晶体结构的几何理论
主要教学内容
• • • • • • • 十四种空间格子* 十四种空间格子 空间格子中点的坐标、行列及面网符号* 空间格子中点的坐标、行列及面网符号 晶胞* 晶胞 晶体内部结构的对称要素* 晶体内部结构的对称要素 空间群(符号 符号)* 空间群 符号 等效点系 晶格缺陷
思考题: 思考题:
8.1 十四种空间格子 十四种空间格子(space lattice)
回顾: 回顾: • 空间格子是表示晶体结构中质点重复规 律的立体几何图形。 律的立体几何图形。 • 空间格子要素包括结点、行列、面网、 空间格子要素包括结点、行列、面网、 单位平行六面体。 单位平行六面体。
1.平行六面体的选择
平行六面体是空间格子中最小重复单位 对于每一种晶体结构而言,其结点的分布是客观存在的, 对于每一种晶体结构而言,其结ቤተ መጻሕፍቲ ባይዱ的分布是客观存在的, 但平行六面体的选择是人为的。 但平行六面体的选择是人为的。 空间格子是无限图形。在一个空间格子中可以划分出无数 空间格子是无限图形。 种不同形状和大小的平行六面体。如何划分? 种不同形状和大小的平行六面体。如何划分?
