图形的旋转测试题

合集下载

旋转单元测试试题及答案

答案：Ｂ．
第13题.如图，已知四边形，是关于点成中心对称图形，试判定四边形的形状．并说明理由．
答案：解：是平行四边形，理由如下：
四边形是关于点成中心对称图形．
．
四边形是平行四边形．
第14题. 在等边三角形、平行四边形、矩形和圆这四个图形中，即是轴对称图形，又是中心对称图形的有（）
Ａ．1个Ｂ．2个Ｃ．3个Ｄ．4个
Ａ．矩形、菱形、正方形都是中心对称图形，对角线的交点是对称中心
Ｂ．中心对称的对称中心只有一个，而轴对称图形的对称轴可能不只一条
Ｃ．中心对称图形一定是轴对称图形
Ｄ．正方形有4条对称轴，一个对称中心
答案：Ｃ．
第20题.把图中的各三角形绕边中点，旋转，画出得到的图形，并说明拼成了一个什么图形？分析它的对称性．
答案：Ｂ．
第32题. 下列文字中属于中心对称图形的有（）
Ａ．干Ｂ．中Ｃ．我Ｄ．甲
答案：Ｂ．
第33题. 下图中是中心对称图形的是（）
Ａ．Ａ和ＢＢ．Ｂ和ＣＣ．Ｃ和ＤＤ．都是
答案：Ｂ．
第34题.如图与关于点成中心对称．则 _______ ， ______， ________．
答案：＝，，．
第35题.已知四边形和点，作四边形使四边形和四边形交于点成中心对称．
Ａ．只能作一个Ｂ．能作三个Ｃ．能作无数个Ｄ．不存在
答案：Ａ．
第24题. 已知及边上一点，画出以点为对称中心的对称图形．
答案：略．
第25题. 等边三角形、正方形、菱形和等腰梯形这四个图形中，是中心对称图形的有（）
Ａ．1个Ｂ．2个Ｃ．3个Ｄ．4个
答案：Ｂ．
第26题. 下列各图中，不是中心对称图形的是（）

旋转单元测试题及答案

旋转单元测试题及答案一、选择题1. 旋转的定义是什么？A. 绕某一点转动B. 沿直线平移C. 缩放D. 反射2. 旋转变换不改变图形的哪些性质？A. 形状B. 大小C. 面积D. 所有选项3. 旋转对称图形在旋转多少度后能与自身重合？A. 90度B. 180度C. 360度D. 任意角度二、填空题4. 一个图形绕着某一点旋转____度后，与原图形重合，这个点称为图形的______。

5. 在平面直角坐标系中，若将点P(x, y)绕原点O(0, 0)逆时针旋转θ度，旋转后的坐标为______。

三、简答题6. 请简述旋转的性质，并给出一个生活中的例子。

7. 解释什么是旋转对称图形，并给出一个例子。

四、计算题8. 在平面直角坐标系中，点A(3, 4)绕原点O(0, 0)顺时针旋转90度，求旋转后点A的新坐标。

9. 若一个图形在旋转对称变换下，其旋转中心为点P(1, 2)，旋转角度为120度，请画出旋转后的图形。

五、论述题10. 论述旋转在几何证明中的应用，并给出一个具体的几何证明例子。

答案：一、1. A2. D3. C二、4. 180，旋转中心5. (-y, x)三、6. 旋转的性质包括保持图形的形状和大小不变，旋转中心到图形上任意两点的距离相等。

生活中的例子包括门的开关，地球的自转等。

7. 旋转对称图形是指在旋转一定角度后能与自身重合的图形，例如等边三角形。

四、8. 点A的新坐标为(4, -3)。

9. 根据旋转对称图形的定义，旋转后的图形与原图形形状相同，位置不同，具体图形需根据题目要求绘制。

五、10. 旋转在几何证明中常用于证明图形的全等或相似，例如利用旋转证明两个三角形全等。

具体例子需根据题目要求给出。

小学旋转测试题及答案

小学旋转测试题及答案一、选择题（每题2分，共10分）1. 一个正方形旋转90度后，它的形状会改变吗？A. 会B. 不会C. 不确定答案：B2. 一个圆在平面内旋转360度后，它的位置会改变吗？A. 会B. 不会C. 不确定答案：B3. 一个等边三角形绕着它的一个顶点旋转120度后，它的位置会改变吗？A. 会B. 不会C. 不确定答案：B4. 一个矩形绕着它的中心点旋转180度后，它的形状和位置会改变吗？A. 形状和位置都会改变B. 形状不会改变，位置会改变C. 形状和位置都不会改变答案：C5. 如果一个图形绕着一个点旋转了360度，那么这个图形的位置会回到原来的位置吗？A. 会B. 不会C. 不确定答案：A二、填空题（每题2分，共10分）1. 一个图形绕着一个点旋转____度后，会回到原来的位置。

答案：3602. 一个图形旋转后，它的形状____改变。

答案：不会3. 一个图形绕着它的中心点旋转，它的形状和位置____改变。

答案：不会4. 一个图形旋转180度后，它的位置____改变。

答案：会5. 一个图形绕着一个点旋转90度后，它的位置____改变。

答案：会三、判断题（每题2分，共10分）1. 一个正方形旋转180度后，它的形状和位置都会改变。

（）答案：×2. 一个圆在平面内旋转任意角度后，它的形状都不会改变。

（）答案：√3. 一个矩形绕着它的一个顶点旋转90度后，它的形状不会改变。

（）答案：√4. 一个等边三角形绕着它的中心点旋转120度后，它的位置不会改变。

（）答案：√5. 一个图形旋转360度后，它的位置一定会回到原来的位置。

（）答案：√四、简答题（每题5分，共20分）1. 请简述旋转对称图形的特点。

答案：旋转对称图形是指一个图形绕着一个点旋转一定角度后，能够与自身重合的图形。

这样的图形在旋转过程中，其形状和大小不会发生改变，只是位置发生了变化。

2. 为什么一个圆在平面内旋转任意角度后，它的形状不会改变？答案：一个圆在平面内旋转任意角度后，它的形状不会改变，因为圆是所有点到圆心距离相等的点的集合，无论旋转多少角度，这些点到圆心的距离都保持不变，因此圆的形状不会发生改变。

中考数学专题训练之图形的旋转测试题(1)

中考数学专题训练之图形的旋转测试题（1）一．选择题（共10小题）1．如图，在平面直角坐标系中，点A（3，0），点B（0，1），连接AB，将线段AB绕点A 顺时针旋转90°得到线段AC，连接OC，则线段OC的长度为（）A．4B．3√2C．2√5D．52．如图，在平面直角坐标系xOy中，等边△ABC绕点O顺时针旋转90°得到△DEF，点B，C在x轴上．下面判断不正确的是（）A．△ABC≌△DEF B．∠AED＝120°C．OA=√3OF D．DE＝OB+AE 3．如图，在Rt△ABC中，∠ABC＝90°，AB＝BC=√2，将△ABC绕点C逆时针旋转60°，得到△MNC，连接BM，则BM的长是（）A．√3+1B．2√3C．√3+2D．√2+14．如图，将△ABC绕直角顶点C逆时针旋转，使得点B落在斜边AB上的B′处得△A'B'C，若∠A＝35°，则∠ACB′的度数为（）A．70°B．55°C．35°D．20°5．若自行车的车轮形如正方形，使车轮能平稳行驶，则地面形状大致为（）A．B．C．D．6．如图，△ABC和△AED均为等腰直角三角形，∠BAC＝∠EAD＝90°，AB＝AC，AD＝AE，点B在线段ED上，已知AD=4√2，BD＝2，则tan∠BCD的值为（）A．13B．3√1010C．√1010D．37．在平面直角坐标系中，点（3，5）关于原点对称点的坐标是（）A．（3，5）B．（﹣3，5）C．（﹣3，﹣5）D．（3，﹣5）8．如图，在△ABC中，∠CAB＝m°，在同一平面内，将△ABC绕点A旋转到△AB'C'的位置，使CC'∥AB，则∠BAB'＝（）A．3m﹣120B．180﹣2m C．3m﹣180D．m﹣309．如图，将△ABC绕点A顺时针旋转90°到△ADE，若∠DAE＝50°，则∠CAD＝（）A．30°B．40°C．50°D．90°10．已知点A（1，a）、点B（b，2）关于原点对称，则a+b的值为（）A．3B．﹣3C．﹣1D．1二．填空题（共10小题）11．如图，将△OAB绕点O顺时针旋转40°得到△ODC，点D恰好落在AB上，若∠AOC ＝108°，则∠B的度数是．12．如图，在△ABC中，AB＝AC，∠BAC＝120°，O为BC的中点，将△ABC绕点O顺时针旋转得到△DEF，当点D，E分别在边AC和CA的延长线上，连接CF，若AD＝4，则△OFC的面积是．13．如图所示的图形绕其中心至少旋转度就可以与原图形完全重合．14．如图，将Rt△AOB置于直角坐标系中，边OB，OA分别在x轴，y轴上，将△AOB绕点A旋转，点D落在边AB上．若∠OAB＝60°，OA＝1，则点C的坐标为．15．如图，E 是正方形ABCD 内一点，将△ABE 绕点B 顺时针旋转与△CBF 重合，若BE =√2，则EF ＝．16．如图，在△ABC 中，BC ＝1，AB ＝3，以AC 为边向上作等边△ACD ，连接DB ，当∠ABC ＝时，BD 最大，最大值为．17．平面直角坐标示中，点（2，﹣4）关于原点O 的对称点是．18．如图，将面积为7的正方形OABC 和面积为9的正方形ODEF 分别绕原点O 顺时针旋转，使OA ，OD 落在数轴上，点A ，D 在数轴上对应的数字分别为a 、b ，则b ﹣a ＝．19．如图，在△ABC 中，AB ＝AC ，∠BAC ＝90°，点D 是CB 延长线上一点，BD BC =12，连接AD ，将线段AD 绕点A 逆时针旋转45°交线段BC 于点E ，若BD ＝m ，用含m 的式子表示线段AE 的长为．20．如图，将△AOB 绕点O 按逆时针方向旋转55°后得到△COD ，若∠AOB ＝15°，则∠AOD ＝．三．解答题（共5小题）21．如图，在△ABC 中，∠A ＝30°，∠C ＝90°，BC ＝1，将△ABC 绕点B 旋转180°，点A 落在点A ′处，求AA ′的长度．22．如图，平面直角坐标系中，△ABC的三个顶点分别是A（﹣3，2），B（﹣1，4），C（0，2）．（1）请画出△ABC关于原点对称的△A1B1C1，并求出C1点的坐标；（2）将△ABC以点A为旋转中心顺时针旋转90°，画出旋转后的△AB2C2，并求出C2点的坐标．23．综合与探究已知四边形ABCD是菱形，AB＝4，∠ABC＝60°，∠MAN的两边分别与射线CB，DC 相交于点E，F，且∠MAN＝60°．【初步感知】（1）当E是线段CB的中点时（如图1），AE与EF的数量关系为．【深入探究】（2）如图2，将图1中的∠MAN绕点A顺时针旋转α（0°＜α＜30°），（1）中的结论还成立吗？说明理由．【拓展应用】（3）如图3，将图2中的∠MAN绕点A继续顺时针旋转，当α＝45°时，求点F到BC 的距离．24．如图是由小正方形组成的7×6的网格，每个小正方形的顶点叫做格点，△ABC的三个顶点都是格点，D也是格点，仅用无刻度的直尺在给定网格中完成画图，画图过程用虚线表示．（1）先在边AB上画点E，使DE∥BC，再在边AC上画点F，使∠DF A＝∠BFC；（2）先将△ABC绕点D逆时针方向旋转90°得△A1B1C1，画出△A1B1C1，再画点A关于直线∁l C的对称点A′．25．在△ABC中，BD是AC边上的高，AD＝3，CD＝2，BD＝3，点M在AD上，且AM＝2，动点P从点A出发向B运动，速度为每秒1个单位长度．连接PM，作点A关于直线PM的对称点A′，设点P的运动时间为t秒（t＞0）．（1）连接CP，当CP⊥AB时，求△BCP的面积．（2）当点A在△ABC内部（不包括边缘）时，直接写出t的取值范围：．（3）若动点P从点A出发，沿折线AB﹣BD以每秒1个单位长度的速度运动，当MA′∥AB时，求t的值．。

(完整版)图形的旋转测试题(含答案)

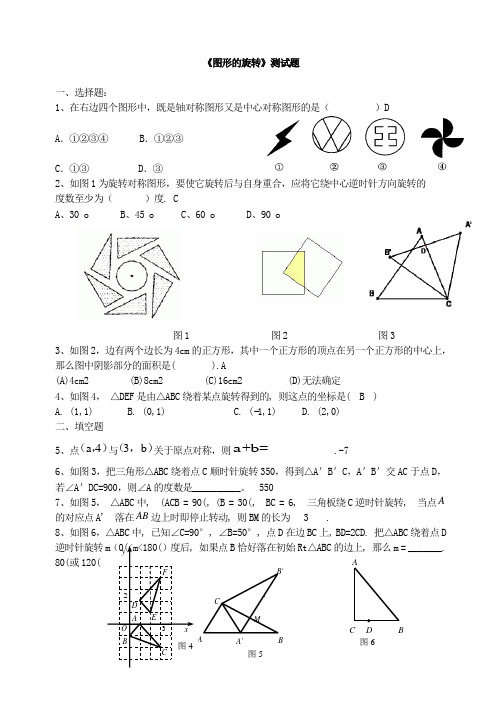
MB' A'C A B 图5 图4 《图形的旋转》测试题一、选择题：1、在右边四个图形中，既是轴对称图形又是中心对称图形的是（）DA ．①②③④B ．①②③C ．①③D ．③2、如图1为旋转对称图形，要使它旋转后与自身重合，应将它绕中心逆时针方向旋转的度数至少为（）度. CA 、30 oB 、45 oC 、60 oD 、90 o图1 图2 图33、如图2，边有两个边长为4cm 的正方形，其中一个正方形的顶点在另一个正方形的中心上，那么图中阴影部分的面积是( ).A(A)4cm2 (B)8cm2 (C)16cm2 (D)无法确定4、如图4， △DEF 是由△ABC 绕着某点旋转得到的, 则这点的坐标是( B )A. (1,1)B. (0,1)C. (−1,1)D. (2,0)二、填空题5、点a 4（，）与3b （，）关于原点对称，则a b += .-76、如图3，把三角形△ABC 绕着点C 顺时针旋转350，得到△A ＇B ＇C ，A ＇B ＇交AC 于点D ，若∠A ＇DC=900，则∠A 的度数是__________。

5507、如图5， △ABC 中, (ACB = 90(, (B = 30(, BC = 6, 三角板绕C 逆时针旋转, 当点A的对应点A' 落在AB 边上时即停止转动, 则BM 的长为 3 .8、如图6，△ABC 中, 已知∠C=90°, ∠B=50°, 点D 在边BC 上, BD=2CD. 把△ABC 绕着点D逆时针旋转m （0(<m<180(）度后, 如果点B 恰好落在初始Rt △ABC 的边上, 那么m = _______. 80(或.O A B C D E F x y2 3图6 A C BD三、解答题9、作图题（1）如图7，画出△ABC 绕点O 顺时针旋转60°所得到的图形．图7 图8（2）如图8,在直角坐标系中,点P 的坐标为(3,4),将OP 绕原点O 逆时针旋转90°得到线段OP ′,(1)在图中画出线段OP ′;(2)P ′的坐标为 ______. (-4,3)1、如图，在△ABC 中，∠B=900，∠C=300，AB=1，将△ABC 绕顶点 A 旋转1800，点C 落在C1处，则C C1的长为（）A ．24B ．4C ．32D ．522、如图，△ABC 中，∠ACB=1200，将它绕着点C 旋转300 后得到△DCE ，则∠ACE=∠A+∠E=3、如图，在Rt △ABC 中，∠ACB=90°，∠A=35°，以直角顶点C•为旋转中心，将△ABC 旋转到△A ′B ′C 的位置，其中A ′、B ′分别是A 、B 的对应点，且点B 在斜边A ′B ′上，直角边CA ′交AB 于D ，求∠BDC 的度数．E DC BA B A C O ABC B C4，如图，正方形ABCD 中，E 在BC 上，F 在AB 上且∠FDE=45°，•△DEC 按顺时针方向转动一个角度后成为△DGA ．（1）图中哪一个点是旋转中心？（2）旋转了多少度？（3）指出图中的对应点，对应线段和对应角；（4）求∠GDF 的度数．5、已知如图，正方形ABCD 中，E 为CD 边上一点，F 为BC 边上一点，CE=CF:(1)EBC FDC ∠∠与相等吗？（2）△DCF 能与△BCE 重合吗？（3）试判断BE 与DF 的位置关系并说明理由,6．如图所示，四边形ABCD 中，∠BAD=∠C=90°，AB=AD ，AE ⊥BC 于E ，△BEA 旋转后能与△DFA 重合．（1）旋转中心是哪一点？（2）旋转了多少度？（3）若AE=5cm ，求四边形ABCD 的面积．7，如图，K 是正方形ABCD 内一点，以AK 为一边作正方形AKLM ，使L ，M ，D 在AK 的同旁，连结BK 和DM ，试用旋转的思想说明线段BK 与DM 的关系． C FEDB A,8，.如图所示，等边△ABC中，D是AB边上的动点(不与A、B重合)，以CD为一边，向上作等边△EDC。

数学旋转测试题附答案

第3题图ED C BA 第4题图O D CBA 第5题AB 旋转测试题一、选择题：1.一个图形经过旋转变化后，发生改变的是 .A.旋转中心B.旋转角度C.图形的形状D.图形的位置 2.下列图形中绕某个旋转180°后能与自身重合的有 .①正方形； ②长方形； ③等边三角形； ④线段； ⑤角； ⑥平行四边形 A. 5个 B. 2个 C. 3个 D. 4个3.如图所示，△ABC 中，AC ＝5，中线AD ＝7，△EDC 是由△ADB 旋转180°所得，则AB 边的取值范围是 .A. 1＜AB ＜29B. 4＜AB ＜24C. 5＜AB ＜19D. 9＜AB ＜194.如图，已知△OAB 绕点O 沿逆时针方向旋转80°到△OCD 的位置，且∠A ＝110°，∠D ＝40°，则∠AOD 的度数为 .A. 30°B. 40°C. 50°D. 60°5.将方格纸中的图形（如图所示）绕点O 沿顺时针方向旋转90°后，得到的图形是6.下列图形中，是中心对称图形而不是轴对称图形的是 . A.等边三角形 B.矩形 C.平行四边形 D.菱形7.点A （－3，2）关于x 轴的对称点为点B ，点B 关于原点的对称点为C ，则点C 的坐标是 .A.（3，2）B.（－3，2）C.（3，－2）D.（－2，3） 8.已知点A 的坐标为（a ，b ），O 为原点，连结OA ，将线段OA 绕点O 按逆时针方向旋转90°得OA 1，则点A 1的坐标为 .A.（－a ，b ）B.（a ，－b ）C.（－b ，a ）D.（b ，－a ） 9.如图，△ABC 为等腰三角形，AB ＝AC ，∠A ＝38°，现将△ABC 绕点旋转，使BC 的对应边落在AC 上，则其旋转角为 .A. 38°B. 52°C. 71°D. 81°10.如图所示，在直角三角形ABC 中，∠C ＝90°，AC ＝6，BC ＝8，将△ABC 绕点B 旋第9题图EDCB A 第10题图CB A 第16题图C /B /()A /C B A 第17题图B /A /C B A转90°，得到关于点A 的对称点D ，则AD 的长是 .A. 20B. 10√2C. 10D. 20√211.平面直角坐标系中有一图案，如果将图案中各点的横、纵坐标都乘以－1，所得图案与原图案相比 .A.向下平移了一个单位长度B.向左平移了一个单位长度C.关于坐标轴成轴对称D.关于坐标原点成中心对称12.在正方形ABCD 中，E 是CD 上一点，F 是BC 上一点，且EF ＝BF ＋DE ，则∠EAF 的度数是 .A. 30°B. 60°C. 45°D. 小于60° 二、填空题：13.线段的对称中心是，平行四边形的对称中心是，圆的对称中心是 .14.已知A 、B 、O 三点不在同一直线上，A 、A /关于点O 对称，B 、B /关于点O 对称，那么线段AB 与A /B /的关系是 .16.如图在Rt △ABC 中，∠C ＝90°，∠A ＝60°，AC ＝3cm ，将△ABC 绕B 点旋转到 △A /B /C /的位置且使A 、B 、C /三点在同一直线上，则A 点经过的最短路线长是 cm.17.如图，将Rt △ABC 绕C 点逆时针旋转得到△A /B /，若∠A /CB ＝160°，则此图形旋转角是度.18.若矩形ABCD 的对称中心恰为原点O ，且点B 坐标为（－2，－3），则点D 坐标为 .19.点（1，－3）绕原点顺时针旋转90°得到的点的坐标是；直线y ＝－3x 绕原点顺时针旋转90°得到的直线的解析式为 . 20.阅读课题学习：“如果一个图形绕着某点O 旋转α后所得的图形与原图形重合，则称此图形关于点O 有角α的旋转对称。

初三旋转测试题卷子及答案

初三旋转测试题卷子及答案一、选择题（每题3分，共15分）1. 一个点绕原点旋转90度后，其坐标变为原来的什么？A. 相反数B. 倒数C. 两倍D. 四倍2. 一个图形绕某点旋转180度后，与原图形的关系是？A. 完全重合B. 完全相反C. 部分重合D. 没有关系3. 一个图形绕某点旋转60度后，其面积和周长会如何变化？A. 面积不变，周长不变B. 面积变小，周长变小C. 面积不变，周长变长D. 面积变小，周长变大4. 一个图形绕其对称轴旋转180度后，图形的位置会如何变化？A. 完全重合B. 完全相反C. 部分重合D. 没有变化5. 如果一个图形绕某点旋转了θ度，那么它的旋转矩阵是什么？A. [cosθ -sinθ; sinθ cosθ]B. [cosθ sinθ; -sinθ cosθ]C. [sinθ cosθ; cosθ -sinθ]D. [sinθ -sinθ; cosθ cosθ]二、填空题（每题2分，共10分）6. 一个点P(x, y)绕原点旋转θ度后，其新坐标为_________。

7. 若一个图形绕点(a, b)旋转θ度，其旋转后的图形与原图形的对应点坐标变化关系为_________。

8. 一个正方形绕其中心点旋转45度后，其四个顶点的坐标变化情况是_________。

9. 一个圆绕其圆心旋转任意角度，其形状和大小_________。

10. 旋转矩阵可以表示为_________，其中θ为旋转角度。

三、解答题（每题5分，共20分）11. 给定一个点P(1, 2)，求该点绕原点旋转120度后的坐标。

12. 一个矩形ABCD，其中A(-1, 1)，B(1, 1)，C(1, -1)，D(-1, -1)，求该矩形绕点A旋转90度后的顶点坐标。

13. 描述一个正方形绕其对称轴旋转90度后，四个顶点的坐标变化情况。

14. 解释旋转矩阵在图形旋转变换中的作用。

四、综合题（每题5分，共10分）15. 一个正六边形绕其中心点旋转60度后，求其顶点坐标的变化。

图形旋转测试题

C A B
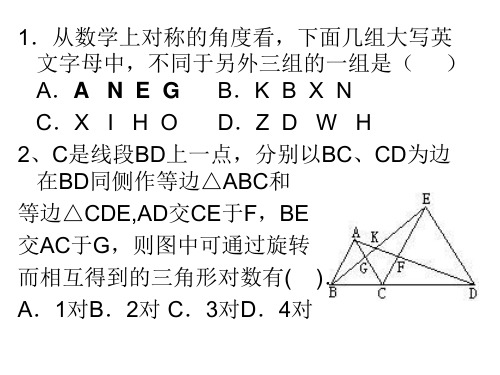
30°
C
30°
B （12题）
A
• 1．如果两个图形可通过旋转而相互得到，则下列说法中正确的有( )． • ①对应点连线的中垂线必经过旋转中心． • ②这两个图形大小、形状不变． • ③对应线段一定相等且平行． • ④将一个图形绕旋转中心旋转某个定角后必与另一个图形重合． • A．1个 B．2个 C．3个 D．4个
1、图中的一个矩形是另一个矩形顺时针方向旋转90°后形成的个数是（） A．l个 B．2个 C．3个 D．4个 • 5．下列图形中，是中心对称的图形有（） • ①正方形；②长方形；③等边三角形； • ④线段； ⑤角； ⑥平行四边形。 • A．5个 B．2个 C．3个 D．4个
A 如图，在梯形 A B C D 中， D ∥ B C ， A D 2， B C △ 点M是AD的中点， M B C 是等边三角形．（1）求证：梯形 A B C D 是等腰梯形；（2）动点P、Q分别在线段BC和MC上运动，且∠ M P Q 6 0 保持不变．设 P C x， M Q y，求Y与X的函数关系式；（3）在（2）中：①当动点P、 Q运动到何处时，以点P、M和点A、B、C、D中的两个点为顶点的四边形是平行四边形？并指出符合条件的平行四边形的个数； ②当Y取最小值时，判断 △ P Q C 的形状，并说明理由．
• • • • • • •
1．下列正确描述旋转特征的说法是（） A．旋转后得到的图形与原图形形状与大小都发生变化． B．旋转后得到的图形与原图形形状不变，大小发生变化． C．旋转后得到的图形与原图形形状发生变化，大小不变． D．旋转后得到的图形与原图形形状与大小都没有变化． 2．下列描述中心对称的特征的语句中，其中正确的是（） A．成中心对称的两个图形中，连接对称点的线段不一定经过对称中心 • B．成中心对称的两个图形中，对称中心不一定平分连接对称点的线段 • C．成中心对称的两个图形中，对称点的连线一定经过对称中心，但不一定被对称中心平分 • D．成中心对称的两个图形中，对称点的连线一定经过对称中心，且被对称中心平分

中考数学真题《图形的旋转》专项测试卷(附答案)

中考数学真题《图形的旋转》专项测试卷(附答案)学校:___________班级：___________姓名：___________考号：___________（30题）一、单选题1．（2023·江苏无锡·统考中考真题）如图，ABC 中 55BAC ∠=︒ 将ABC 逆时针旋转(055),αα︒<<︒得到ADE DE 交AC 于F ．当40α=︒时点D 恰好落在BC 上此时AFE ∠等于（）A ．80︒B ．85︒C ．90︒D ．95︒2．（2023·天津·统考中考真题）如图，把ABC 以点A 为中心逆时针旋转得到ADE 点B C 的对应点分别是点D E 且点E 在BC 的延长线上连接BD 则，下列结论一定正确的是（）A ．CAE BED ∠=∠B ．AB AE =C ．ACE ADE ∠=∠D ．CE BD =3．（2023·四川宜宾·统考中考真题）如图，ABC 和ADE 是以点A 为直角顶点的等腰直角三角形把ADE 以A 为中心顺时针旋转点M 为射线BD CE 的交点．若3AB 1AD =．以下结论： ①BD CE = ①BD CE ⊥ ①当点E 在BA 的延长线上时 33MC -=①在旋转过程中当线段MB 最短时 MBC 的面积为12．其中正确结论有（）A ．1个B ．2个C ．3个D ．4个4．（2023·山东聊城·统考中考真题）如图，已知等腰直角ABC 90ACB ∠=︒ 2AB = 点C 是矩形ECGF 与ABC 的公共顶点且1CE = 3CG = 点D 是CB 延长线上一点且2CD =．连接BG DF 在矩形ECGF 绕点C 按顺时针方向旋转一周的过程中当线段BG 达到最长和最短时线段DF 对应的长度分别为m 和n 则，mn的值为（）A ．2B ．3C 10D 13二填空题5．（2023·江苏连云港·统考中考真题）以正五边形ABCDE 的顶点C 为旋转中心按顺时针方向旋转使得新五边形A B CD E ''''的顶点D 落在直线BC 上则，正五边ABCDE 旋转的度数至少为______°．6．（2023·湖南张家界·统考中考真题）如图，AO 为BAC ∠的平分线且50BAC ∠=︒ 将四边形ABOC 绕点A 逆时针方向旋转后得到四边形AB O C ''' 且100OAC '∠=︒则，四边形ABOC 旋转的角度是______．7．（2023·湖南常德·统考中考真题）如图1 在Rt ABC △中 90ABC ∠=︒ 8AB = 6BC = D 是AB 上一点且2AD = 过点D 作DE BC ∥交AC 于E 将ADE 绕A 点顺时针旋转到图2的位置．则图2中BDCE的值为__________．8．（2023·江苏无锡·统考中考真题）已知曲线12C C 、分别是函数2(0),(0,0)ky x y k x x x=-<=>>的图像边长为6的正ABC 的顶点A 在y 轴正半轴上顶点B C 在x 轴上（B 在C 的左侧）现将ABC 绕原点O 顺时针旋转当点B 在曲线1C 上时点A 恰好在曲线2C 上则，k 的值为__________．9．（2023·辽宁·统考中考真题）如图，线段8AB = 点C 是线段AB 上的动点将线段BC 绕点B 顺时针旋转120°得到线段BD 连接CD 在AB 的上方作Rt DCE ∆ 使90,30DCE E ∠=∠= 点F 为DE 的中点连接AF 当AF 最小时 BCD ∆的面积为___________．10．（2023·江西·统考中考真题）如图，在ABCD 中 602B BC AB ∠=︒=，将AB 绕点A 逆时针旋转角α（0360α︒<<︒）得到AP 连接PC PD ．当PCD 为直角三角形时旋转角α的度数为_______．11．（2023·上海·统考中考真题）如图，在ABC 中 35C ∠=︒ 将ABC 绕着点A 旋转(0180)αα︒<<︒ 旋转后的点B 落在BC 上点B 的对应点为D 连接AD AD ，是BAC ∠的角平分线则，α=________．12．（2023·湖南郴州·统考中考真题）如图，在Rt ABC △中 90BAC ∠=︒ 3cm AB = =60B ∠︒．将ABC 绕点A 逆时针旋转得到AB C ''△ 若点B 的对应点B '恰好落在线段BC 上则，点C 的运动路径长．．．．．是___________cm （结果用含π的式子表示）．13．（2023·内蒙古·统考中考真题）如图，在Rt ABC △中 90,3,1ACB AC BC ∠=︒== 将ABC 绕点A 逆时针方向旋转90︒ 得到AB C ''△．连接BB ' 交AC 于点D 则，ADDC的值为________．14．（2023·黑龙江绥化·统考中考真题）已知等腰ABC 120A ∠=︒ 2AB =．现将ABC 以点B 为旋转中心旋转45︒ 得到A BC ''△ 延长C A ''交直线BC 于点D ．则A D '的长度为_______． 15．（2023·浙江嘉兴·统考中考真题）一副三角板ABC 和DEF 中90304512C D B E BC EF ∠=∠=︒∠=︒∠=︒==，，，．将它们叠合在一起边BC 与EF 重合 CD 与AB 相交于点G （如图1）此时线段CG 的长是___________ 现将DEF 绕点()C F 按顺时针方向旋转（如图2）边EF 与AB 相交于点H 连结DH 在旋转0︒到60︒的过程中线段DH 扫过的面积是___________．三解答题16．（2023·北京·统考中考真题）在ABC 中 ()045B C αα∠=∠=︒<<︒ AM BC ⊥于点M D 是线段MC 上的动点（不与点M C 重合）将线段DM 绕点D 顺时针旋转2α得到线段DE ．(1)如图1 当点E 在线段AC 上时求证：D 是MC 的中点(2)如图2 若在线段BM 上存在点F （不与点B M 重合）满足DF DC = 连接AE EF 直接写出AEF ∠的大小并证明．17．（2023·四川自贡·统考中考真题）如图1 一大一小两个等腰直角三角形叠放在一起 M N 分别是斜边DE AB 的中点 2,4DE AB ==．(1)将CDE 绕顶点C 旋转一周请直接写出点M N 距离的最大值和最小值(2)将CDE 绕顶点C 逆时针旋转120︒（如图2）求MN 的长．18．（2023·四川达州·统考中考真题）如图，网格中每个小正方形的边长均为1 ABC 的顶点均在小正方形的格点上．(1)将ABC 向下平移3个单位长度得到111A B C △ 画出111A B C △ (2)将ABC 绕点C 顺时针旋转90度得到222A B C △ 画出222A B C △ (3)在（2）的运动过程中请计算出ABC 扫过的面积．19．（2023·辽宁·统考中考真题）在Rt ABC ∆中 90°ACB ∠= CA CB = 点O 为AB 的中点点D 在直线AB 上（不与点,A B 重合）连接CD 线段CD 绕点C 逆时针旋转90° 得到线段CE 过点B 作直线l BC ⊥ 过点E 作EF l ⊥ 垂足为点F 直线EF 交直线OC 于点G ．(1)如图，当点D 与点O 重合时请直接写出线段AD 与线段EF 的数量关系 (2)如图，当点D 在线段AB 上时求证：2CG BD BC +=(3)连接DE CDE 的面积记为1S ABC 的面积记为2S 当:1:3EF BC =时请直接写出12S S 的值．20．（2023·四川乐山·统考中考真题）在学习完《图形的旋转》后刘老师带领学生开展了一次数学探究活动【问题情境】刘老师先引导学生回顾了华东师大版教材七年级下册第121页“探索”部分内容：如图，将一个三角形纸板ABC 绕点A 逆时针旋转θ到达AB C ''△的位置那么可以得到：AB AB '=AC AC '= BC B C ''= BAC B AC ''∠=∠ ABC AB C ''∠=∠ ACB AC B ''∠=∠（）刘老师进一步谈到：图形的旋转蕴含于自然界的运动变化规律中即“变”中蕴含着“不变” 这是我们解决图形旋转的关键故数学就是一门哲学．【问题解决】（1）上述问题情境中“（）”处应填理由：____________________（2）如图，小王将一个半径为4cm 圆心角为60︒的扇形纸板ABC 绕点O 逆时针旋转90︒到达扇形纸板A B C '''的位置．①请在图中作出点O①如果=6cm BB '则，在旋转过程中点B 经过的路径长为__________ 【问题拓展】小李突发奇想将与（2）中完全相同的两个扇形纸板重叠一个固定在墙上使得一边位于水平位置另一个在弧的中点处固定然后放开纸板使其摆动到竖直位置时静止此时两个纸板重叠部分的面积是多少呢？如图所示请你帮助小李解决这个问题．21．（2023·浙江绍兴·统考中考真题）在平行四边形ABCD 中（顶点,,,A B C D 按逆时针方向排列） 12,10,AB AD B ==∠为锐角且4sin 5B =．(1)如图1 求AB 边上的高CH 的长．(2)P 是边AB 上的一动点点,C D 同时绕点P 按逆时针方向旋转90︒得点,C D ''． ①如图2 当点C '落在射线CA 上时求BP 的长． ①当AC D ''△是直角三角形时求BP 的长．22．（2023·四川南充·统考中考真题）如图，正方形ABCD 中点M 在边BC 上点E 是AM 的中点连接EDEC ．(1)求证：ED EC =(2)将BE 绕点E 逆时针旋转使点B 的对应点B '落在AC 上连接MB '．当点M 在边BC 上运动时（点M 不与B C 重合）判断CMB '的形状并说明理由．(3)在（2）的条件下已知1AB = 当45DEB ∠'=︒时求BM 的长．23．（2023·江苏扬州·统考中考真题）【问题情境】在综合实践活动课上李老师让同桌两位同学用相同的两块含30︒的三角板开展数学探究活动两块三角板分别记作ADB 和,90,30A D C ADB A D C B C ∠=∠=︒∠''''=∠=︒△ 设2AB =．【操作探究】如图1 先将ADB 和A D C ''的边AD A D ''重合再将A D C ''绕着点A 按顺时针．．．方向旋转旋转角为()0360αα︒≤≤︒ 旋转过程中ADB 保持不动连接BC ．(1)当60α=︒时 BC =________ 当22BC = α=________︒ (2)当90α=︒时画出图形并求两块三角板重叠部分图形的面积(3)如图2 取BC 的中点F 将A D C ''绕着点A 旋转一周点F 的运动路径长为________． 24．（2023·湖南·统考中考真题）（1）[问题探究]如图1 在正方形ABCD 中对角线AC BD 、相交于点O ．在线段AO 上任取一点P （端点除外）连接PD PB 、．①求证：PD PB =①将线段DP 绕点P 逆时针旋转使点D 落在BA 的延长线上的点Q 处．当点P 在线段AO 上的位置发生变化时 DPQ ∠的大小是否发生变化？请说明理由 ①探究AQ 与OP 的数量关系并说明理由．（2）[迁移探究]如图2 将正方形ABCD 换成菱形ABCD 且60ABC ∠=︒ 其他条件不变．试探究AQ 与CP 的数量关系并说明理由．25．（2023·湖北随州·统考中考真题）1643年法国数学家费马曾提出一个著名的几何问题：给定不在同一条直线上的三个点A B C 求平面上到这三个点的距离之和最小的点的位置意大利数学家和物理学家托里拆利给出了分析和证明该点也被称为“费马点”或“托里拆利点” 该问题也被称为“将军巡营”问题． (1)下面是该问题的一种常见的解决方法请补充以下推理过程：（其中①处从“直角”和“等边”中选择填空 ①处从“两点之间线段最短”和“三角形两边之和大于第三边”中选择填空 ①处填写角度数 ①处填写该三角形的某个顶点）当ABC 的三个内角均小于120︒时如图1 将APC △绕点C 顺时针旋转60︒得到A P C '' 连接PP '由60PC P C PCP ''=∠=︒，可知PCP '△为 ① 三角形故PP PC '= 又P A PA ''= 故PA PB PC PA PB PP A B '''++=++≥由 ① 可知当B P P ' A 在同一条直线上时 PA PB PC ++取最小值如图2 最小值为A B ' 此时的P 点为该三角形的“费马点” 且有APC BPC APB ∠=∠=∠= ①已知当ABC 有一个内角大于或等于120︒时 “费马点”为该三角形的某个顶点．如图3 若120BAC ∠≥︒则，该三角形的“费马点”为 ① 点．(2)如图4 在ABC 中三个内角均小于120︒ 且3430AC BC ACB ==∠=︒，，已知点P 为ABC 的“费马点” 求PA PB PC ++的值(3)如图5 设村庄A B C 的连线构成一个三角形且已知4km 23km 60AC BC ACB ==∠=︒，，．现欲建一中转站P 沿直线向A B C 三个村庄铺设电缆已知由中转站P 到村庄A B C 的铺设成本分别为a 元/km a 元/km 2a 元/km 选取合适的P 的位置可以使总的铺设成本最低为___________元．（结果用含a 的式子表示）26．（2023·四川·统考中考真题）如图1 已知线段AB AC 线段AC 绕点A 在直线AB 上方旋转连接BC 以BC 为边在BC 上方作Rt BDC 且30DBC ∠=︒．(1)若=90BDC ∠︒ 以AB 为边在AB 上方作Rt BAE △ 且90AEB ∠=︒ 30EBA ∠=︒ 连接DE 用等式表示线段AC 与DE 的数量关系是(2)如图2 在(1)的条件下若DE AB ⊥ 4AB = 2AC = 求BC 的长(3)如图3 若90BCD ∠=︒ 4AB = 2AC = 当AD 的值最大时求此时tan CBA ∠的值．27．（2023·湖北黄冈·统考中考真题）【问题呈现】CAB △和CDE 都是直角三角形 90,,ACB DCE CB mCA CE mCD ∠=∠=︒== 连接AD BE 探究ADBE 的位置关系．(1)如图1 当1m =时直接写出AD BE 的位置关系：____________(2)如图2 当1m ≠时（1）中的结论是否成立？若成立给出证明若不成立说明理由．【拓展应用】(3)当3,7,4m AB DE ===时将CDE 绕点C 旋转使,,A D E 三点恰好在同一直线上求BE 的长．28．（2023·内蒙古赤峰·统考中考真题）数学兴趣小组探究了以下几何图形．如图① 把一个含有45︒角的三角尺放在正方形ABCD 中使45︒角的顶点始终与正方形的顶点C 重合绕点C 旋转三角尺时 45︒角的两边CM CN 始终与正方形的边AD AB 所在直线分别相交于点M N 连接MN 可得CMN ．【探究一】如图① 把CDM 绕点C 逆时针旋转90︒得到CBH 同时得到点H 在直线AB 上．求证：CNM CNH ∠=∠【探究二】在图①中连接BD 分别交CM CN 于点E F ．求证：CEF CNM △∽△【探究三】把三角尺旋转到如图①所示位置直线BD 与三角尺45︒角两边CM CN 分别交于点E F ．连接AC 交BD 于点O 求EFNM的值．29．（2023·湖南·统考中考真题）问题情境：小红同学在学习了正方形的知识后进一步进行以下探究活动：在正方形ABCD 的边BC 上任意取一点G 以BG 为边长向外作正方形BEFG 将正方形BEFG 绕点B 顺时针旋转．特例感知：（1）当BG 在BC 上时连接DF AC ，相交于点P 小红发现点P 恰为DF 的中点如图①．针对小红发现的结论请给出证明（2）小红继续连接EG 并延长与DF 相交发现交点恰好也是DF 中点P 如图① 根据小红发现的结论请判断APE 的形状并说明理由规律探究：（3）如图① 将正方形BEFG 绕点B 顺时针旋转α 连接DF 点P 是DF 中点连接AP EP AEAPE 的形状是否发生改变？请说明理由．30．（2023·贵州·统考中考真题）如图① 小红在学习了三角形相关知识后对等腰直角三角形进行了探究在等腰直角三角形ABC 中 ,90CA CB C =∠=︒ 过点B 作射线BD AB ⊥ 垂足为B 点P 在CB 上．(1)【动手操作】如图① 若点P 在线段CB 上画出射线PA 并将射线PA 绕点P 逆时针旋转90︒与BD 交于点E 根据题意在图中画出图形图中PBE ∠的度数为_______度 (2)【问题探究】根据（1）所画图形探究线段PA 与PE 的数量关系并说明理由 (3)【拓展延伸】如图① 若点P 在射线CB 上移动将射线PA 绕点P 逆时针旋转90︒与BD 交于点E 探究线段,,BA BP BE 之间的数量关系并说明理由．参考答案一单选题1．（2023·江苏无锡·统考中考真题）如图，ABC 中 55BAC ∠=︒ 将ABC 逆时针旋转(055),αα︒<<︒得到ADE DE 交AC 于F ．当40α=︒时点D 恰好落在BC 上此时AFE ∠等于（）A ．80︒B ．85︒C ．90︒D ．95︒【答案】B【分析】根据旋转可得B ADB ADE ∠=∠=∠ 再结合旋转角40α=︒即可求解．【详解】解：由旋转性质可得：55BAC DAE ∠=∠=︒ AB AD = ①40α=︒①15DAF ∠=︒ 70B ADB ADE ∠=∠=∠=︒ ①85AFE DAF ADE ∠=∠+∠=︒故选：B ．【点睛】本题考查了几何—旋转问题掌握旋转的性质是关键．2．（2023·天津·统考中考真题）如图，把ABC 以点A 为中心逆时针旋转得到ADE 点B C 的对应点分别是点D E 且点E 在BC 的延长线上连接BD 则，下列结论一定正确的是（）A ．CAE BED ∠=∠B ．AB AE =C ．ACE ADE ∠=∠D ．CE BD = 【答案】A【分析】根据旋转的性质即可解答．【详解】根据题意由旋转的性质可得AB AD = AC AE = BC DE = 故B 选项和D 选项不符合题意=ABC ADE ∠∠=ACE ABCBAC∴=ACE ADEBAC 故C 选项不符合题意=ACB AED =ACB CAECEA=AED CEA BED∴=CAE BED 故A 选项符合题意故选：A ．【点睛】本题考查了旋转的性质熟练掌握旋转的性质和三角形外角运用是解题的关键．3．（2023·四川宜宾·统考中考真题）如图，ABC 和ADE 是以点A 为直角顶点的等腰直角三角形把ADE 以A 为中心顺时针旋转点M 为射线BD CE 的交点．若3AB 1AD =．以下结论： ①BD CE = ①BD CE ⊥ ①当点E 在BA 的延长线上时 33MC -=①在旋转过程中当线段MB 最短时 MBC 的面积为12．其中正确结论有（）A ．1个B ．2个C ．3个D ．4个【答案】D【分析】证明BAD CAE ≌即可判断① 根据三角形的外角的性质得出① 证明DCM ECA ∠∠∽得出313-= 即可判断① 以A 为圆心 AD 为半径画圆当CE 在A 的下方与A 相切时 MB 的值最小可得四边形AEMD 是正方形在Rt MBC 中22MC BC MB -21 然后根据三角形的面积公式即可判断①．【详解】解：①ABC 和ADE 是以点A 为直角顶点的等腰直角三角形 ①,,90BA CA DA EA BAC DAE ==∠=∠=︒ ①BAD CAE ∠=∠ ①BAD CAE ≌①ABD ACE ∠=∠ BD CE = 故①正确设ABD ACE α∠=∠= ①45DBC α∠=︒-,①454590EMB DBC BCM DBC BCA ACE αα∠=∠+∠=∠+∠+∠=︒-+︒+=︒ ①BD CE ⊥ 故①正确当点E 在BA 的延长线上时如图所示①DCM ECA ∠=∠ 90DMC EAC ∠=∠=︒ ①DCM ECA ∠∠∽①MC CDAC EC= ①3AB = 1AD =．①31CD AC AD =-= 222CE AE AC =+= 313-=①33MC -=故①正确 ①如图所示以A 为圆心 AD 为半径画圆①90BMC ∠=︒ ①当CE 在A 的下方与A 相切时 MB 的值最小 90ADM DAE AEM ∠=∠=∠=︒①四边形AEMD 是矩形又AE AD =①四边形AEMD 是正方形 ①1MD AE ==①222BD EC AC AE =- ①21MB BD MD =-= 在Rt MBC 中 22MC BC MB -①PB 取得最小值时 222MC AB AC MB +-()2332121+--①)()1112121222BMCSMB MC =⨯==故①正确故选：D ．【点睛】本题考查了旋转的性质相似三角形的性质勾股定理切线的性质垂线段最短全等三角形的性质与判定正方形的性质熟练掌握以上知识是解题的关键．4．（2023·山东聊城·统考中考真题）如图，已知等腰直角ABC 90ACB ∠=︒ 2AB = 点C 是矩形ECGF与ABC 的公共顶点且1CE = 3CG = 点D 是CB 延长线上一点且2CD =．连接BG DF 在矩形ECGF 绕点C 按顺时针方向旋转一周的过程中当线段BG 达到最长和最短时线段DF 对应的长度分别为m 和n 则，mn的值为（）A ．2B ．3C 10D 13【答案】D【分析】根据锐角三角函数可求得1AC BC == 当线段BG 达到最长时此时点G 在点C 的下方且BC G 三点共线求得4BG = 5DG = 根据勾股定理求得26DF = 即26m = 当线段BG 达到最短时此时点G 在点C 的上方且B C G 三点共线则，2BG = 1DG = 根据勾股定理求得2DF 即2n = 即可求得13mn【详解】①ABC 为等腰直角三角形 2AB = ①2sin 4521AC BC AB ==⋅︒== 当线段BG 达到最长时此时点G 在点C 的下方且B C G 三点共线如图：则4BG BC CG =+= 5DG DB BG =+=在Rt DGF △中 22225126DF DG GF =++ 即26m =当线段BG 达到最短时此时点G 在点C 的上方且B C G 三点共线如图：则2BG CG BC =-= 1DG BG DB =-=在Rt DGF △中 2222112DF DG GF =++ 即2n = 故26132m n == 故选：D ．【点睛】本题考查了锐角三角函数勾股定理等根据旋转推出线段BG 最长和最短时的位置是解题的关键．二填空题5．（2023·江苏连云港·统考中考真题）以正五边形ABCDE 的顶点C 为旋转中心按顺时针方向旋转使得新五边形A B CD E ''''的顶点D 落在直线BC 上则，正五边ABCDE 旋转的度数至少为______°．【答案】72【分析】依据正五边形的外角性质即可得到DCF ∠的度数进而得出旋转的角度．【详解】解：①五边形ABCDE 是正五边形①530726DCF ∠÷=︒=︒①新五边形A B CD E ''''的顶点D 落在直线BC 上则，旋转的最小角度是72︒故答案为：72．【点睛】本题主要考查了正多边形旋转性质关键是掌握正多边形的外角和公式的运用．6．（2023·湖南张家界·统考中考真题）如图，AO 为BAC ∠的平分线且50BAC ∠=︒ 将四边形ABOC 绕点A 逆时针方向旋转后得到四边形AB O C ''' 且100OAC '∠=︒则，四边形ABOC 旋转的角度是______．【答案】75︒【分析】根据角平分线的性质可得25BAO OAC ==︒∠∠ 根据旋转的性质可得50BAC B AC ''∠=∠=︒ 25B AO O AC ''''==︒∠∠ 求得75OAO '∠=︒ 即可求得旋转的角度．【详解】①AO 为BAC ∠的平分线 50BAC ∠=︒①25BAO OAC ==︒∠∠①将四边形ABOC 绕点A 逆时针方向旋转后得到四边形AB O C '''①50BAC B AC ''∠=∠=︒ 25B AO O AC ''''==︒∠∠①1002575OAO OAC O AC ''''∠=∠-∠=︒-︒=︒故答案为：75︒．【点睛】本题考查了角平分线的性质旋转的性质熟练掌握以上性质是解题的关键．7．（2023·湖南常德·统考中考真题）如图1 在Rt ABC △中 90ABC ∠=︒ 8AB = 6BC = D 是AB 上一点且2AD = 过点D 作DE BC ∥交AC 于E 将ADE 绕A 点顺时针旋转到图2的位置．则图2中BDCE的值为__________．【答案】45【分析】首先根据勾股定理得到2210AC AB BC += 然后证明出ADE ABC △△∽ 得到AD AEAB AC= 进而得到ADABAE AC = 然后证明出ABD ACE ∽ 利用相似三角形的性质求解即可．【详解】①在Rt ABC △中 90ABC ∠=︒ 8AB = 6BC = ①2210AC AB BC +①DE BC ∥①90ADE ABC ∠=∠=︒ AED ACB ∠=∠①ADE ABC △△∽ ①ADAEAB AC = ①ADABAE AC =①BAC DAE ∠=∠①BAC CAD DAE CAD ∠+∠=∠+∠①BAD CAE ∠=∠①ABD ACE ∽ ①84105BD AB CD AC ===．故答案为：45．【点睛】此题考查了相似三角形的性质和判定解题的关键是熟练掌握相似三角形的性质和判定定理．8．（2023·江苏无锡·统考中考真题）已知曲线12C C 、分别是函数2(0),(0,0)k y x y k x x x=-<=>>的图像边长为6的正ABC 的顶点A 在y 轴正半轴上顶点B C 在x 轴上（B 在C 的左侧）现将ABC 绕原点O 顺时针旋转当点B 在曲线1C 上时点A 恰好在曲线2C 上则，k 的值为__________．【答案】6【分析】画出变换后的图像即可（画AOB 即可）当点A 在y 轴上点B C 在x 轴上时根据ABC 为等边三角形且AO BC ⊥ 可得3OB OA = 过点A B 分别作x 轴垂线构造相似则，BFO OEA ∽ 根据相似三角形的性质得出3AOE S =△ 进而根据反比例函数k 的几何意义即可求解．【详解】当点A 在y 轴上点B C 在x 轴上时连接AOABC 为等边三角形且AO BC ⊥则，30BAO ∠=︒∴tan tan30BAO ∠=︒=3OB OA = 如图所示过点,A B 分别作x 轴的垂线交x 轴分别于点,E FAO BO ⊥ 90BFO AEO AOB ∠=∠=∠=︒∴90BOF AOE EAO ∠=︒-∠=∠∴BFO OEA ∽ ∴213BFO AOE S OB SOA ⎛⎫== ⎪⎝⎭ ∴212BFO S -==∴3AOE S =△∴6k =．【点睛】本题考查了反比例函数的性质 k 的几何意义相似三角形的性质与判定正确作出辅助线构造相似三角形是解题关键．9．（2023·辽宁·统考中考真题）如图，线段8AB = 点C 是线段AB 上的动点将线段BC 绕点B 顺时针旋转120°得到线段BD 连接CD 在AB 的上方作Rt DCE ∆ 使90,30DCE E ∠=∠= 点F 为DE 的中点连接AF 当AF 最小时 BCD ∆的面积为___________．3【分析】连接CF BF ， BF ，CD 交于点P 由直角三角形的性质及等腰三角形的性质可得BF 垂直平分CF 60ABF ∠=︒为定角可得点F 在射线BF 上运动当AF BF ⊥时 AF 最小由含30度角直角三角形的性质即可求解．【详解】解：连接CF BF ， BF ，CD 交于点P 如图，①90DCE ∠= 点F 为DE 的中点①FC FD =①30E ∠=①60FDC ∠=︒,①FCD 是等边三角形①60DFC FCD ∠=∠=︒①线段BC 绕点B 顺时针旋转120°得到线段BD①BC BD =①FC FD =①BF 垂直平分CF 60ABF ∠=︒①点F 在射线BF 上运动①当AF BF ⊥时 AF 最小此时9030FAB ABF ∠=︒-∠=︒ ①142BF AB == ①1302BFC DFC ∠=∠=︒ ①90FCB BFC ABF ∠=∠+∠=︒①122BC BF == ①112PB BC == ①由勾股定理得223PC BC PB - ①223CD PC == ①11231322BCD S CD PB =⋅=⨯△3【点睛】本题考查了等腰三角形性质含30度直角三角形的性质斜边中线性质勾股定理线段垂直平分线的判定勾股定理旋转的性质确定点F 的运动路径是关键与难点．10．（2023·江西·统考中考真题）如图，在ABCD 中 602B BC AB ∠=︒=，将AB 绕点A 逆时针旋转角α（0360α︒<<︒）得到AP 连接PC PD ．当PCD 为直角三角形时旋转角α的度数为_______．【答案】90︒或270︒或180︒【分析】连接AC 根据已知条件可得90BAC ∠=︒ 进而分类讨论即可求解．【详解】解：连接AC 取BC 的中点E 连接AE 如图所示①在ABCD 中 602B BC AB ∠=︒=， ①12BE CE BC AB ===①ABE 是等边三角形①60BAE AEB ∠=∠=︒ AE BE =①AE EC = ①1302EAC ECA AEB ∠=∠=∠=︒ ①90BAC ∠=︒①AC CD ⊥如图所示当点P 在AC 上时此时90BAP BAC ∠=∠=︒则，旋转角α的度数为90︒当点P 在CA 的延长线上时如图所示则，36090270α=︒-︒=︒当P 在BA 的延长线上时则，旋转角α的度数为180︒ 如图所示①PA PB CD == PB CD ∥①四边形PACD 是平行四边形①AC AB ⊥①四边形PACD 是矩形①90PDC ∠=︒即PDC △是直角三角形综上所述旋转角α的度数为90︒或270︒或180︒故答案为：90︒或270︒或180︒．【点睛】本题考查了平行四边形的性质与判定等边三角形的性质与判定矩形的性质与判定旋转的性质熟练掌握旋转的性质是解题的关键．11．（2023·上海·统考中考真题）如图，在ABC 中 35C ∠=︒ 将ABC 绕着点A 旋转(0180)αα︒<<︒ 旋转后的点B 落在BC 上点B 的对应点为D 连接AD AD ，是BAC ∠的角平分线则，α=________．【答案】1103⎛⎫︒ ⎪⎝⎭【分析】如图，AB AD = BAD ∠=α 根据角平分线的定义可得CAD BAD α∠=∠= 根据三角形的外角性质可得35ADB α∠=︒+ 即得35B ADB α∠=∠=︒+ 然后根据三角形的内角和定理求解即可．【详解】解：如图，根据题意可得：AB AD = BAD ∠=α①AD 是BAC ∠的角平分线①CAD BAD α∠=∠=①35ADB C CAD α∠=∠+∠=︒+ AB AD =①35B ADB α∠=∠=︒+则在ABC 中 ①180C CAB B ∠+∠+∠=︒①35235180αα︒++︒+=︒ 解得：1103α⎛⎫=︒ ⎪⎝⎭故答案为：1103⎛⎫︒ ⎪⎝⎭【点睛】本题考查了旋转的性质等腰三角形的性质三角形的外角性质以及三角形的内角和等知识熟练掌握相关图形的性质是解题的关键．12．（2023·湖南郴州·统考中考真题）如图，在Rt ABC △中 90BAC ∠=︒ 3cm AB = =60B ∠︒．将ABC 绕点A 逆时针旋转得到AB C ''△ 若点B 的对应点B '恰好落在线段BC 上则，点C 的运动路径长．．．．．是___________cm （结果用含π的式子表示）．3π【分析】由于AC 旋转到AC ' 故C 的运动路径长是CC '的圆弧长度根据弧长公式求解即可．【详解】以A 为圆心作圆弧CC ' 如图所示．在直角ABC 中 =60B ∠︒则，30C ∠=︒则()2236cm BC AB ==⨯=． ①)22226333cm AC BC AB =--．由旋转性质可知 AB AB '= 又=60B ∠︒①ABB '是等边三角形．①60BAB '∠=︒．由旋转性质知 60CAC '∠=︒．故弧CC '的长度为：()602333cm 3603AC πππ⨯⨯⨯=⨯ 3π【点睛】本题考查了含30︒角直角三角形的性质勾股定理旋转的性质弧长公式等知识点解题的关键是明确C 点的运动轨迹．13．（2023·内蒙古·统考中考真题）如图，在Rt ABC △中 90,3,1ACB AC BC ∠=︒== 将ABC 绕点A 逆时针方向旋转90︒ 得到AB C ''△．连接BB ' 交AC 于点D 则，AD DC 的值为________．【答案】5【分析】过点D 作DF AB ⊥于点F 利用勾股定理求得10AB根据旋转的性质可证ABB ' DFB △是等腰直角三角形可得DF BF = 再由1122ADB SBC AD DF AB =⨯⨯=⨯⨯ 得=10AD DF 证明AFD ACB 可得DF AF BC AC = 即3AF DF = 再由=10AF DF 求得10=DF 从而求得52AD = 12CD = 即可求解．【详解】解：过点D 作DF AB ⊥于点F①90ACB ∠=︒ 3AC = 1BC = ①223110AB +①将ABC 绕点A 逆时针方向旋转90︒得到AB C ''△ ①==10AB AB ' 90BAB '∠=︒①ABB '是等腰直角三角形①45ABB '∠=︒又①DF AB ⊥①45FDB ∠=︒①DFB △是等腰直角三角形①DF BF = ①1122ADB S BC AD DF AB =⨯⨯=⨯⨯ 即=10AD DF ① 90C AFD ∠=∠=︒ CAB FAD ∠=∠①AFD ACB ①DF AF BC AC= 即3AF DF = 又①=10AF DF ①10=DF ①105=10=2AD 51=3=22CD - ①52==512AD CD 故答案为：5．【点睛】本题考查旋转的性质等腰三角形的判定与性质相似三角形的判定与性质三角形的面积熟练掌握相关知识是解题的关键．14．（2023·黑龙江绥化·统考中考真题）已知等腰ABC 120A ∠=︒ 2AB =．现将ABC 以点B 为旋转中心旋转45︒ 得到A BC ''△ 延长C A ''交直线BC 于点D ．则A D '的长度为_______．【答案】423423+-或【分析】根据题意先求得23BC = 当ABC 以点B 为旋转中心逆时针旋转45︒ 过点B 作BE A B '⊥交A D '于点E 当ABC 以点B 为旋转中心顺时针旋转45︒ 过点D 作DF BC '⊥交BC '于点F 分别画出图形根据勾股定理以及旋转的性质即可求解．【详解】解：如图所示过点A 作AM BC ⊥于点M①等腰ABC 120BAC ∠=︒ 2AB =． ①30ABC ACB ∠=∠=︒ ①112AM AB == 223BM CM AB AM =- ①23BC =如图所示当ABC 以点B 为旋转中心逆时针旋转45︒ 过点B 作BE A B '⊥交A D '于点E①120BAC ∠=︒①60DA B '∠=︒ 30A EB '∠=︒在Rt A BE '中 24A E A B ''== 2223BE A E A B ''-= ①等腰ABC 120BAC ∠=︒ 2AB =． ①30ABC ACB ∠=∠=︒①ABC 以点B 为旋转中心逆时针旋转45︒ ①45ABA '∠=︒①180********DBE ∠=︒-︒-︒-︒=︒ 1804530105A BD '∠=︒-︒-︒=︒ 在A BD '中 1801806010515D DA B A BD ∠=︒-∠-∠=︒-︒-︒=''︒, ①D EBD ∠=∠ ①23EB ED ==①423A D A E DE ''=+=+如图所示当ABC 以点B 为旋转中心顺时针旋转45︒ 过点D 作DF BC '⊥交BC '于点F在BFD △中 45BDF CBC ∠'=∠=︒ ①DF BF =在Rt DC F '中 30C '∠=︒ ①3'DF ①33BC BF BF ==①33DF BF ==①2623DC DF '==-①6232423A D C D A C ''''=-=-=- 综上所述 A D '的长度为423-423+ 故答案为：43-43+【点睛】本题考查了旋转的性质勾股定理含30度角的直角三角形的性质熟练掌握旋转的性质分类讨论是解题的关键．15．（2023·浙江嘉兴·统考中考真题）一副三角板ABC 和DEF 中90304512C D B E BC EF ∠=∠=︒∠=︒∠=︒==，，，．将它们叠合在一起边BC 与EF 重合 CD 与AB 相交于点G （如图1）此时线段CG 的长是___________ 现将DEF 绕点()C F 按顺时针方向旋转（如图2）边EF 与AB 相交于点H 连结DH 在旋转0︒到60︒的过程中线段DH 扫过的面积是___________．【答案】6662 1218318π-【分析】如图1 过点G 作GH BC ⊥于H 根据含30︒直角三角形的性质和等腰直角三角形的性质得出3BH GH = GH CH = 然后由12BC =可求出GH 的长进而可得线段CG 的长如图2 将DEF 绕点C 顺时针旋转60︒得到11D E F 1FE 与AB 交于1G 连接1D D 1AD 22D E F 是DEF 旋转0︒到60︒的过程中任意位置作1DN CD ⊥于N 过点B 作1BM D D ⊥交1D D 的延长线于M 首先证明1CDD 是等边三角形点1D 在直线AB 上然后可得线段DH 扫过的面积是弓形12D D D 的面积加上1D DB 的面积求出DN 和BM 然后根据线段DH 扫过的面积111121D DBCD DD DBD D D CD D S SS SS=+=-+弓形扇形列式计算即可．【详解】解：如图1 过点G 作GH BC ⊥于H①3045ABC DEF DFE ∠=︒∠=∠=︒， 90GHB GHC ∠=∠=︒ ①3BH GH = GH CH = ①312BC BH CH GH GH =+=+= ①36GH =①()226366662CG GH ===如图2 将DEF 绕点C 顺时针旋转60︒得到11D E F 1FE 与AB 交于1G 连接1D D 由旋转的性质得：1160E CB DCD ∠=∠=︒ 1CD CD = ①1CDD 是等边三角形①30ABC ∠=︒ ①190CG B ∠=︒ ①112CG BC =①1CE BC =①1112CG CE = 即AB 垂直平分1CE①11CD E 是等腰直角三角形 ①点1D 在直线AB 上连接1AD 22D E F 是DEF 旋转0︒到60︒的过程中任意位置则线段DH 扫过的面积是弓形12D D D 的面积加上1D DB 的面积 ①12BC EF == ①22DC DB === ①1162DC D D == 作1DN CD ⊥于N 则，132ND NC == ①()()222211623236DN D D ND =-=-过点B 作1BM D D ⊥交1D D 的延长线于M 则，90M ∠=︒ ①160D DC ∠=︒ 90CDB ∠=︒①118030BDM D DC CDB ∠=︒-∠-∠=︒ ①1322BM BD == ①线段DH 扫过的面积112D DBD D D S S =+弓形111CD DD DBCD D S S S=-+扇形(260621123623236022π⋅=-⨯⨯ 1218318π=-故答案为：6662 1218318π-．【点睛】本题主要考查了旋转的性质含30︒直角三角形的性质二次根式的运算解直角三角形等边三角形的判定和性质勾股定理扇形的面积计算等知识作出图形证明点1D 在直线AB 上是本题的突破点灵活运用各知识点是解题的关键．三解答题16．（2023·北京·统考中考真题）在ABC 中 ()045B C αα∠=∠=︒<<︒ AM BC ⊥于点M D 是线段MC 上的动点（不与点M C 重合）将线段DM 绕点D 顺时针旋转2α得到线段DE ．(1)如图1 当点E 在线段AC 上时求证：D 是MC 的中点(2)如图2 若在线段BM 上存在点F （不与点B M 重合）满足DF DC = 连接AE EF 直接写出AEF ∠的大小并证明．【答案】(1)见解析 (2)90AEF ∠=︒ 证明见解析【分析】（1）由旋转的性质得DM DE = 2MDE α∠= 利用三角形外角的性质求出C DEC α∠=∠= 可得DE DC = 等量代换得到DM DC =即可（2）延长FE 到H 使FE EH = 连接CH AH 可得DE 是FCH 的中位线然后求出B ACH ∠∠= 设DM DE m == CD n = 求出2BF m CH == 证明()SAS ABF ACH ≅ 得到AF AH = 再根据等腰三角形三线合一证明AE FH ⊥即可．。

图形旋转测试题及答案

图形旋转测试题及答案一、选择题1. 一个图形绕某点旋转了90°，下列说法正确的是：A. 图形的大小不变B. 图形的形状不变C. 图形的位置不变D. 以上说法都不正确答案：A、B2. 下列哪个图形旋转180°后与原图形完全重合？A. 正方形B. 圆形C. 长方形D. 三角形答案：B二、填空题3. 若一个图形绕中心点O旋转____度，可以得到与原图形关于点O对称的图形。

答案：1804. 一个等腰三角形绕底边的中点旋转____度，可以得到与原图形完全重合的图形。

答案：180三、简答题5. 描述一个正方形绕其一个顶点旋转90°后，图形的位置变化情况。

答案：正方形绕其一个顶点旋转90°后，其四个顶点的位置将分别移动到原来对角线的顶点位置。

具体来说，如果原正方形的顶点分别为A、B、C、D，且A为旋转中心，则旋转后，A点位置不变，B点移动到C点位置，C点移动到D点位置，D点移动到B点位置。

四、计算题6. 已知一个正六边形绕其中心点O旋转60°后，求旋转后顶点的新位置。

答案：正六边形的每个顶点绕中心点O旋转60°后，每个顶点的新位置将沿着正六边形的外接圆的圆周上移动，每个顶点相对于原来的位置旋转了60°的弧度。

五、论述题7. 论述图形旋转的性质及其在几何学中的应用。

答案：图形旋转是一种几何变换，它保持图形的大小和形状不变，只改变图形的位置。

旋转的性质包括旋转角度的可加性，即连续旋转两个角度相当于旋转这两个角度的和。

在几何学中，图形旋转常用于证明图形的对称性，解决几何构造问题，以及在变换几何中研究图形的不变性质等。

小升初图形旋转试题及答案

小升初图形旋转试题及答案一、选择题1. 下列哪个图形在旋转180度后与原图形相同？A. 正方形B. 对角线相等的菱形C. 等边三角形D. 圆答案：D2. 如果一个图形绕着它的中心点旋转90度，那么这个图形必须具有哪种对称性？A. 反射对称B. 旋转对称C. 对称中心D. 平移对称答案：B3. 在平面直角坐标系中，将一个点 (x, y) 绕原点旋转90度，新的坐标是多少？A. (y, x)B. (-x, -y)C. (-y, x)D. (y, -x)答案：C二、填空题4. 一个图形绕着一个点旋转____度可以得到它的中心对称图形。

答案：1805. 在平面上，如果一个图形绕某一点旋转____度后与自身重合，那么这个点称为这个图形的旋转中心。

答案：360三、解答题6. 如图所示，一个正方形ABCD的边长为4厘米，E是AD的中点，F是CD上的一点，且DF=1厘米。

现在将三角形ADE绕着点E旋转，使得A点落在F点的位置。

请问，点D旋转后落在了哪个位置？答案：首先，由于E是AD的中点，AE=ED=2厘米。

旋转后，A点落在F点的位置，因此旋转角度为60度（因为ADE是一个等边三角形，旋转60度A点会落在F点）。

由于旋转是中心对称，点D将落在旋转后三角形AFE的对角线上，且DE=DF=1厘米，所以点D的新位置是距离E点2厘米，与F点相隔1厘米的点。

7. 在一个平面直角坐标系中，点P的坐标为(3, 4)。

现在将点P绕原点O旋转180度，求旋转后点P'的坐标。

答案：旋转180度相当于将点关于原点对称，因此P'的坐标是(-3, -4)。

四、综合题8. 给定一个正五边形ABCDE，其中E是顶点，并且已知EB=EC=2厘米。

现在将正五边形绕点E旋转60度，求旋转后点A落在的新位置。

答案：正五边形的内角是108度。

旋转60度后，点A将沿着五边形的外接圆移动到与点E相隔108+60=168度的位置。

由于正五边形的对称性，这个位置将是五边形的另一个顶点或其对边的延长线上。

旋转测试题及答案

旋转测试题及答案一、选择题1. 一个物体绕着一个固定点旋转，这个固定点被称为什么？A. 旋转中心B. 旋转轴C. 旋转半径D. 旋转角答案：A2. 如果一个物体绕着一个点旋转了180度，这个物体的状态是：A. 完全翻转B. 回到原位C. 位置不变D. 无法确定答案：B3. 在平面几何中，一个点绕原点旋转90度后，其坐标的变化是：A. 坐标不变B. 坐标变为原来的相反数C. 横坐标变为纵坐标，纵坐标变为横坐标的相反数D. 横坐标变为纵坐标的相反数，纵坐标变为横坐标答案：C二、填空题4. 旋转对称图形在旋转一定角度后，图形的______不变。

答案：形状和大小5. 一个物体在平面上绕一点旋转，如果旋转角度为360度，物体将______。

答案：回到原位三、简答题6. 描述一个物体绕着一个点旋转的过程，并说明旋转的性质。

答案：一个物体绕着一个点旋转的过程是物体的每一个点都以旋转点为中心，按照相同的旋转角度进行移动。

旋转的性质包括旋转的方向（顺时针或逆时针）、旋转的角度以及旋转的中心点。

旋转后，物体上各点到旋转中心的距离保持不变，形状和大小也保持不变。

四、计算题7. 如果一个点P(x, y)绕原点(0, 0)顺时针旋转90度，求旋转后点P 的新坐标。

答案：旋转后点P的新坐标为(-y, x)。

五、论述题8. 论述旋转在日常生活中的应用，并给出至少两个例子。

答案：旋转在日常生活中有广泛的应用。

例如：- 门的开关：门围绕门轴的旋转使得我们可以打开或关闭门。

- 风力发电机：风力发电机的叶片围绕中心轴旋转，将风能转换为电能。

六、绘图题9. 给定一个正方形ABCD，点A位于(0, 0)，点B位于(1, 0)，点C位于(1, 1)，点D位于(0, 1)。

请画出正方形绕点A顺时针旋转45度后的图形。

答案：[绘图题，答案需要根据旋转的几何规则进行作图，此处不提供具体图形，考生需自行绘制]。

初三旋转测试题及答案

初三旋转测试题及答案一、选择题（每题3分，共30分）1. 旋转对称图形是指绕某一点旋转一定角度后能够与自身重合的图形。

下列选项中，哪一个不是旋转对称图形？A. 正方形B. 正三角形C. 五边形D. 圆2. 一个图形绕某点旋转180°后与原图形重合，这个点称为图形的：A. 旋转中心B. 对称轴C. 旋转角D. 旋转对称中心3. 一个图形绕一点旋转90°后与自身重合，这个图形是：A. 正方形B. 正三角形C. 正五边形D. 正六边形4. 一个图形绕某点旋转180°后与自身重合，这个点是图形的：A. 对称轴B. 旋转中心C. 旋转对称中心D. 旋转角5. 一个图形绕某点旋转120°后与自身重合，这个图形是：B. 正三角形C. 正五边形D. 正六边形6. 一个图形绕某点旋转360°后与自身重合，这个点是图形的：A. 对称轴B. 旋转中心C. 旋转对称中心D. 旋转角7. 一个图形绕某点旋转60°后与自身重合，这个图形是：A. 正方形B. 正三角形C. 正六边形D. 正八边形8. 一个图形绕某点旋转45°后与自身重合，这个图形是：A. 正方形B. 正三角形C. 正五边形D. 正八边形9. 一个图形绕某点旋转30°后与自身重合，这个图形是：A. 正方形B. 正三角形C. 正六边形D. 正十二边形10. 一个图形绕某点旋转72°后与自身重合，这个图形是：A. 正方形C. 正六边形D. 正十边形二、填空题（每题4分，共20分）1. 一个图形绕某点旋转______度后与自身重合，这个点是图形的旋转中心。

2. 一个图形绕某点旋转______度后与自身重合，这个图形是正六边形。

3. 一个图形绕某点旋转______度后与自身重合，这个图形是正五边形。

4. 一个图形绕某点旋转______度后与自身重合，这个图形是正三角形。

5. 一个图形绕某点旋转______度后与自身重合，这个图形是正方形。

旋转测试题及答案人教版

旋转测试题及答案人教版一、选择题1. 一个图形绕某一点旋转180°后，下列说法正确的是（）A. 形状不变，大小不变，位置变化B. 形状不变，大小不变，位置不变C. 形状变化，大小不变，位置变化D. 形状变化，大小变化，位置不变答案：A2. 如果一个图形绕着一个点旋转了90°，那么这个图形（）A. 形状不变，大小不变，位置变化B. 形状变化，大小不变，位置变化C. 形状不变，大小变化，位置不变D. 形状变化，大小变化，位置不变答案：A二、填空题3. 一个正方形绕其中心点旋转90°后，得到的图形仍然是一个______。

答案：正方形4. 一个等边三角形绕着它的一个顶点旋转120°后，得到的图形仍然是一个______。

答案：等边三角形三、解答题5. 描述一个图形绕某一点旋转的过程，并说明旋转后图形的位置和形状的变化。

答案：一个图形绕某一点旋转的过程包括确定旋转中心、旋转角度和旋转方向。

旋转后，图形的位置会发生变化，但形状和大小保持不变。

例如，一个矩形绕其中心点旋转90°后，其位置会改变，但仍然是一个矩形，且边长和角度不变。

6. 如果一个图形绕着一个点旋转了180°，描述旋转后图形与原图形的关系。

答案：当一个图形绕着一个点旋转180°后，旋转后的图形与原图形关于旋转中心对称。

这意味着如果将旋转后的图形与原图形重叠，它们会完全重合，只是方向相反。

结束语：通过以上题目的练习，可以加深对旋转变换的理解，掌握旋转的性质和特点。

希望同学们能够熟练运用这些知识，解决实际问题。

图形的旋转测试题

18. 如图，在 △ ABC 中， AB=AC，点 P 是 △ABC 内一点，且∠ APB=∠ APC．求证： BP = CP．
图1 图2
20. 已知，点 P 是正方形 ABCD 内的一点，连 PA、 PB、 PC. （ 1）将 △ PAB 绕点 B 顺时针旋转 90°到 △ P′CB 的位置（如图 1） . ①设 AB 的长为 a， PB 的长为 b（b<a），求 △ PAB 旋转到 △ P′CB 的过程中边
内
不订
A
B
C
D
要
3. 有下列四个说法，其中正确说法的个数是 ( )．
答 ①图形旋转时，位置保持不变的点只有旋转中心；
题
②图形旋转时，图形上的每一个点都绕着旋转中心旋转了相同的角度；
)
③图形旋转时，对应点与旋转中心的距离相等；
④图形旋转时，对应线段相等，对应角相等，图形的形状和大小都没有发生变化．
线
A． 1 个 B． 2 个 C． 3 个 D． 4 个
度的整倍数之后能和自己重合 .
10. 如图， △ ABC 绕点 A 顺时针旋转 45°得到 △ A′B′C′，若∠ BAC=90 °，AB=AC= 2 ，则
图中阴影部分的面积等于
_________ ．
13．如图，直角梯形 ABCD 中， AD ∥ BC， AB⊥BC， AD=2 ，将腰 CD 以 D 为中心逆时针旋转 90°至 ED ，连接 AE、 DE ，△ ADE 的面积为 3，则 BC 的长为 _________．
D. 5 个 ()
A．①② B．②③ C．③④ D．①④
7. 如图，若将△ ABC 绕点 O 顺时针旋转 180°后得到△ A B C ，则 A 点的对应点 A 点

第23章《旋转》全章测试含答案

4月初三数学第23章《旋转》全章测试测试时间45分钟，满分100分一.选择题1. 下列图形中，既是轴对称图形又是中心对称图形的是( )A B C D2. 平面直角坐标系内一点P（－2,3）关于原点对称点的坐标是（）A、（3，－2）B、（2,3）C、（－2，－3）D、（2，－3）3.如图，将Rt△ABC绕点A按顺时针旋转一定角度得到Rt△ADE，点B的对应点D恰好落在BC边上．若AC=3，∠B=60°，则CD的长为（）A. 0.5 B．1.5 C．2 D. 14.如图，把菱形ABOC绕点O顺时针旋转得到菱形DFOE，则下列角中不是旋转角的为( )．A．∠BOF B．∠AODC．∠COE D．∠COF5. 如图所示,已知△ABC与△CDA关于点O对称,过O任作直线EF分别交AD,BC于点E,F,下面的结论:(1)点E和点F,点B和点D是关于中心O的对称点.(2)直线BD必经过点O.(3)四边形DEOC与四边形BFOA的面积必相等.(4)△AOE与△COF成中心对称,其中正确的个数为( )A.1B.2C.3D.46. 在如图4×4的正方形网格中,△MNP绕某点旋转一定的角度,得到△M1N1P1,则其旋转中心可能是( )A.点AB.点BC.点CD.点D二、填空题7.在平面直角坐标系中，将点A（4，2）绕原点逆时针方向旋转90°后，其对应点A′的坐标为．8.如图所示,将△ABC绕点A按逆时针旋转30°后,得到△ADC′,则∠ABD的度数是.9.如图，把边长为1的正方形ABCD绕顶点A逆时针旋转30°到正方形A′B′C′D′，则它们的公共部分的面积等于______．10.如图，在平面直角坐标系中，将△ABO绕点A顺时针旋转到△AB1C1的位置，点B、O分别落在点B1、C1处，点B1在x轴上，再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置，点C2在x轴上，将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置，点A2在x轴上，依次进行下去…．若点A（，0），B（0，4），则点B 的横坐标为．三、解答题11.在下列网格图中，每个小正方形的边长均为1个单位．在Rt△ABC中，∠C=90°，AC=3，BC=4．（1）试在图中做出△ABC以A为旋转中心，沿顺时针方向旋转90°后的图形△AB1C1；（2）若点B的坐标为（﹣3，5），试在图中画出直角坐标系，并标出A、C两点的坐标；（3）根据（2）的坐标系作出与△ABC关于原点对称的图形△A2B2C2，并标出B2、C2两点的坐标．12.如图，在Rt△ABC中，∠ACB=90°，∠B=30°，将△ABC绕点C按顺时针方向旋转n度后，得到△DEC，点D刚好落在AB边上．（1）求n的值；（2）若F是DE的中点，判断四边形ACFD的形状，并说明理由．13. 已知：如图，P为等边△ABC内一点，∠APB=113°，∠APC=123°，试说明：以AP、BP、CP为边长可以构成一个三角形，并确定所构成三角形的各内角的度数．14.（1）如图，正方形ABCD中，点E，F分别在边BC，CD上，∠EAF=45°，延长CD到点G，使DG=BE，连结EF，AG．求证：EF=FG．（2）如图，等腰直角三角形ABC中，∠BAC=90°，AB=AC，点M，N在边BC上，且∠MAN=45°，若BM=1，CN=3，求MN的长．参考答案1.C2.D3.D4.D5.D6.B(7.)4,2758.039.310. 10070．11. （1）△AB1C1如图所示；（2）如图所示，A（0，1），C（﹣3，1）；（3）△A2B2C2如图所示，B2（3，﹣5），C2（3，﹣1）．12. （1）∵在Rt△ABC中，∠ACB=90°，∠B=30°，将△ABC绕点C按顺时针方向旋转n 度后，得到△DEC，∴AC=DC，∠A=60°，∴△ADC是等边三角形，∴∠ACD=60°，∴n的值是60；（2）四边形ACFD是菱形；理由：∵∠DCE=∠ACB=90°，F是DE的中点，∴FC=DF=FE，∵∠CDF=∠A=60°，∴△DFC是等边三角形，∴DF=DC=FC，∵△ADC是等边三角形，∴AD=AC=DC，∴AD=AC=FC=DF，∴四边形ACFD是菱形．13. ∠PBD＝53°，∠BPD＝64°，∠PDB＝63°．14. （1）证明：在正方形ABCD中，∴∠ABE=∠ADG，AD=AB，在△ABE和△ADG中，∴△ABE≌△ADG（SAS），∴∠BAE=∠DAG，AE=AG，∴∠EAG=90°，在△FAE和△GAF中，，∴△FAE≌△GAF（SAS），∴EF=FG（2）解：如图2，过点C作CE⊥BC，垂足为点C，截取CE，使CE=BM．连接AE、EN．∵AB=AC，∠BAC=90°，∴∠B=∠C=45°．∵CE⊥BC，∴∠ACE=∠B=45°．在△ABM和△ACE中，∴△ABM≌△ACE（SAS）．∴AM=AE，∠BAM=∠CAE．∵∠BAC=90°，∠MAN=45°，∴∠BAM+∠CAN=45°．于是，由∠BAM=∠CAE，得∠MAN=∠EAN=45°．在△MAN和△EAN中，∴△MAN≌△EAN（SAS）．∴MN=EN．在Rt△ENC中，由勾股定理，得EN2=EC2+NC2．∴MN2=BM2+NC2．∵BM=1，CN=3，∴MN2=12+32，∴MN=。

小学旋转测试题目及答案

小学旋转测试题目及答案一、选择题1. 一个正方形旋转180度后，其形状和大小会如何变化？A. 形状和大小都不变B. 形状不变，大小变小C. 形状改变，大小不变D. 形状和大小都改变答案：A2. 一个圆形在平面上旋转任意角度，其形状和大小会如何变化？A. 形状和大小都不变B. 形状不变，大小变小C. 形状改变，大小不变D. 形状和大小都改变答案：A3. 一个等腰直角三角形绕着其直角边旋转180度，其形状和大小会如何变化？A. 形状和大小都不变B. 形状不变，大小变小C. 形状改变，大小不变D. 形状和大小都改变答案：A二、填空题1. 当一个物体绕着一个点旋转360度后，其位置和方向将______。

答案：保持不变2. 如果一个物体绕着一个点旋转90度，那么它的位置将______。

答案：改变三、判断题1. 一个物体绕着一个轴旋转180度后，它将回到原始位置。

（）答案：正确2. 一个物体绕着一个轴旋转360度后，它的位置和方向将发生变化。

（）答案：错误四、简答题1. 描述一个物体绕着一个点旋转90度后，它的位置和方向的变化。

答案：物体绕着一个点旋转90度后，它的位置相对于旋转点将顺时针或逆时针移动到新的位置，方向也会相应地顺时针或逆时针旋转90度。

2. 解释为什么一个圆形在平面上旋转任意角度，其形状和大小都不会改变。

答案：圆形是一个对称图形，无论旋转到哪个角度，其所有点到中心点的距离都是相等的，因此形状和大小都不会因为旋转而发生变化。

初中数学：《图形的旋转》测试题及答案

初中数学：《图形的旋转》测试题及答案一、选择题1．在图形旋转中,下列说法错误的是（）A．图形上的每一点到旋转中心的距离相等B．图形上的每一点转动的角度相同C．图形上可能存在不动点D．图形上任意两点的连线与其对应两点的连线相等2．下面的四个图案中,既包含图形的旋转,又包含图形的轴对称的是（）A．B． C．D．3．如图所示的图案绕旋转中心旋转后能够与自身重合,那么它的旋转角可能是（）A．60°B．90°C．72°D．120°4．如图,摆放有五杂梅花,下列说法错误的是（以中心梅花为初始位置）（）A．左上角的梅花只需沿对角线平移即可B．右上角的梅花需先沿对角线平移后,再顺时针旋转45°C．右下角的梅花需先沿对角线平移后,再顺时针旋转180D．左下角的梅花需先沿对角线平移后,再顺时针旋转90°5．△ABC绕着A点旋转后得到△AB′C′,若∠BAC′=130°,∠BAC=80°,则旋转角等于（）A．50°B．210°C．50°或210°D．130°二、填空题6．在图形的平移、旋转、轴对称变换中,其相同的性质是______．7．如图,△ABC和△ADE均是顶角为42°的等腰三角形,BC、DE分别是底边,图中的△ABD绕A旋转42°后得到的图形是______,它们之间的关系是______,其中BD=______．8．如图,将△OAB绕点O按逆时针方面旋转至△0A′B′,使点B恰好落在边A′B′上．已知AB=4cm,BB′=1cm,则A′B长是______cm．9．如图,在平面直角坐标系中,点A的坐标为（1,4）,将线段OA绕点O顺时针旋转90°得到线段OA′,则点A′的坐标是______．10．如图,自正方形ABCD的顶点A引两条射线分别交BC、CD于E、F,∠EAF=45°,在保持∠EAF=45°的前提下,当点E、F分别在边BC、CD上移动时,BE+DF与EF 的关系是______．11．如图,在直角坐标系中,已知点A（﹣3,0）,B（0,4）,对△OAB连续作旋转变换,依次得到三角形①,②,③,④…,则三角形⑩的直角顶点的坐标为______．三、综合提高题12．观察下列图形,它可以看作是什么“基本图形”通过怎样的旋转而得到的？13．如图：若∠AOD=∠BOC=60°,A、O、C三点在同一条线上,△AOB与△COD是能够重合的图形．求：（1）旋转中心；（2）旋转角度数；（3）图中经过旋转后能重合的三角形共有几对？若A、O、C三点不共线,结论还成立吗？为什么？（4）求当△BOC为等腰直角三角形时的旋转角度；（5）若∠A=15°,则求当A、C、B在同一条线上时的旋转角度．14．作图：（1）如图甲,以点O为中心,把点P顺时针旋转45°．（2）如图乙,以点O为中心,把线段AB逆时针旋转90°．（3）如图丙,以点O为中心,把△ABC顺时针旋转120°．（4）如图丁,以点B为中心,把△ABC旋转180°．15．如图,K是正方形ABCD内一点,以AK为一边作正方形AKLM,使L,M,D在AK的同旁,连接BK和DM,试用旋转的思想说明线段BK与DM的关系．16．如图,已知A、B是线段MN上的两点,MN=4,MA=1,MB＞1．以A为中心顺时针旋转点M,以B为中心逆时针旋转点N,使M、N两点重合成一点C,构成△ABC,设AB=x．（1）求x的取值范围；（2）若△ABC为直角三角形,求x的值．17．如图在Rt△OAB中,∠OAB=90°,OA=AB=6．（1）请你画出将△OAB绕点O沿逆时针方向旋转90°,得到的△OA1B1；（2）线段OA1的长度是______,∠AOB1的度数是______；（3）连接AA1,求证：四边形OAA1B1是平行四边形．《图形的旋转》参考答案与试题解析一、选择题1．在图形旋转中,下列说法错误的是（）A．图形上的每一点到旋转中心的距离相等B．图形上的每一点转动的角度相同C．图形上可能存在不动点D．图形上任意两点的连线与其对应两点的连线相等【解答】解：A、在图形旋转中,根据旋转的性质,图形上对应点到旋转中心的距离相等,故本选项错误；B、图形上的每一点转动的角度都等于旋转角,正确；C、以图形上一点为旋转中心,则这个点不动,正确；D、旋转前后两个图形全等,则图形上任意两点的连线与其对应两点的连线相等,正确．故选A．2．下面的四个图案中,既包含图形的旋转,又包含图形的轴对称的是（）A．B． C．D．【解答】解：A、只包含图形的旋转,不符合题意；B、只是轴对称图形,不符合题意；C、只是轴对称图形,不符合题意；D、既包含图形的旋转,又包含图形的轴对称,符合题意．故选：D．3．如图所示的图案绕旋转中心旋转后能够与自身重合,那么它的旋转角可能是（）A．60°B．90°C．72°D．120°【解答】解：该图形被平分成五部分,因而每部分被分成的圆心角是72°,并且圆具有旋转不变性,因而旋转72度的整数倍,就可以与自身重合．故选C．4．如图,摆放有五杂梅花,下列说法错误的是（以中心梅花为初始位置）（）A．左上角的梅花只需沿对角线平移即可B．右上角的梅花需先沿对角线平移后,再顺时针旋转45°C．右下角的梅花需先沿对角线平移后,再顺时针旋转180D．左下角的梅花需先沿对角线平移后,再顺时针旋转90°【解答】解：由平移和旋转可得,D选项中左下角的梅花需先沿对角线平移后,再逆时针旋转90°,所以D选项错误．故选：B．5．△ABC绕着A点旋转后得到△AB′C′,若∠BAC′=130°,∠BAC=80°,则旋转角等于（）A．50°B．210°C．50°或210°D．130°【解答】解：∵∠BAC′=130°,∠BAC=80°,∴如图1,∠CAC′=∠BAC′﹣∠BAC=50°,如图2,∠CAC′=∠BAC′+∠BAC=210°．∴旋转角等于50°或210°．故选C．二、填空题6．在图形的平移、旋转、轴对称变换中,其相同的性质是图形的形状、大小不变,只改变图形的位置．【解答】解：在图形的平移、旋转、轴对称变换中,其相同的性质是图形的形状、大小不变,只改变图形的位置．7．如图,△ABC和△ADE均是顶角为42°的等腰三角形,BC、DE分别是底边,图中的△ABD绕A旋转42°后得到的图形是△ACE ,它们之间的关系是全等,其中BD= CE ．【解答】解：△ABD绕点A逆时针旋转42°得到△ACE,它们之间的关系是全等,其中BD=CE．8．如图,将△OAB绕点O按逆时针方面旋转至△0A′B′,使点B恰好落在边A′B′上．已知AB=4cm,BB′=1cm,则A′B长是 3 cm．【解答】解：根据旋转的性质,得：A′B′=AB=4cm．∴A′B=A′B′﹣BB′=4﹣1=3（cm）．9．如图,在平面直角坐标系中,点A的坐标为（1,4）,将线段OA绕点O顺时针旋转90°得到线段OA′,则点A′的坐标是（4,﹣1）．【解答】解：由图知A点的坐标为（1,4）,根据旋转中心O,旋转方向顺时针,旋转角度90°,画图,从而得A′点坐标为（4,﹣1）．故答案为：（4,﹣1）．10．如图,自正方形ABCD的顶点A引两条射线分别交BC、CD于E、F,∠EAF=45°,在保持∠EAF=45°的前提下,当点E、F分别在边BC、CD上移动时,BE+DF与EF 的关系是BE+DF=EF ．【解答】解：如图,延长CD到M,使DM=BE,连接AM、EF；∵四边形ABCD为正方形,∴∠B=∠ADC=90°,AB=AD；在△ABE与△ADM中,,∴△ABE≌△ADM（SAS）,∴∠BAE=∠DAM,AE=AM；∴∠BAE+DAF=∠DAM+∠DAF=∠MAF；∵∠EAF=45°,∴∠BAE+DAF=90°﹣45°=45°,∴∠EAF=∠MAF=45°；在△EAF与△MAF中,,∴△EAF≌△MAF（SAS）,∴MF=EF,而MF=MD+DF=BE+DF,∴BE+DF=EF,故答案为BE+DF=EF．11．如图,在直角坐标系中,已知点A（﹣3,0）,B（0,4）,对△OAB连续作旋转变换,依次得到三角形①,②,③,④…,则三角形⑩的直角顶点的坐标为（36,0）．【解答】解：由原图到图③,相当于向右平移了12个单位长度,象这样平移三次直角顶点是（36,0）,再旋转一次到三角形⑩,直角顶点仍然是（36,0）,则三角形⑩的直角顶点的坐标为（36,0）．故答案为：（36,0）．三、综合提高题12．观察下列图形,它可以看作是什么“基本图形”通过怎样的旋转而得到的？【解答】解：图形（1）是通过一条线段绕点O旋转360°而得到的；图形（2）可以看作是“一个Rt△ABC”绕线段AC旋转360°而得到的；图形（3）将矩形ABCD绕AD旋转一周而得到的．13．如图：若∠AOD=∠BOC=60°,A、O、C三点在同一条线上,△AOB与△COD是能够重合的图形．求：（1）旋转中心；（2）旋转角度数；（3）图中经过旋转后能重合的三角形共有几对？若A、O、C三点不共线,结论还成立吗？为什么？（4）求当△BOC为等腰直角三角形时的旋转角度；（5）若∠A=15°,则求当A、C、B在同一条线上时的旋转角度．【解答】解：（1）∵△AOB与△COD是能够重合的图形,∴旋转中心是点O；（2）根据题意得：旋转角是∠AOD或∠BOC,∴旋转角度数是60°,（3）经过旋转后能重合的三角形有△AOB与△DOC,△AOE与△DOF,△BOE与△COF 共三对,若A、O、C三点不共线,△AOE与△DOF,△BOE与△COF不一定重合,结论不一定成立,∵若A、O、C三点不共线,∠DOB≠60°,∴∠AOD=∠BOC=60°≠∠DOB,∴△BOE与△COF不一定重合,结论不一定成立；（4）∵△BOC为等腰直角三角形,∴∠BOC=∠AOD=90°,∴旋转角度为：90°,（5）∵180°﹣∠BOC=180°﹣60°=120°,∴旋转角度为120°．14．作图：（1）如图甲,以点O为中心,把点P顺时针旋转45°．（2）如图乙,以点O为中心,把线段AB逆时针旋转90°．（3）如图丙,以点O为中心,把△ABC顺时针旋转120°．（4）如图丁,以点B为中心,把△ABC旋转180°．【解答】解：（1）如图甲,点P′为所求；（2）如图乙,线段A′B′为所求；（3）如图丙,△A′B′C′为所求；（4）如图丁,△A′BC′为所求．15．如图,K是正方形ABCD内一点,以AK为一边作正方形AKLM,使L,M,D在AK的同旁,连接BK和DM,试用旋转的思想说明线段BK与DM的关系．【解答】解：BK与DM的关系是互相垂直且相等．∵四边形ABCD和四边形AKLM都是正方形,∴AB=AD,AK=AM,∠BAK=90°﹣∠DAK,∠DAM=90°﹣∠DAK,∴∠BAK=∠DAM,∴△ABK≌△ADM（SAS）．把△ABK绕A逆时针旋转90°后与△ADM重合,∴BK=DM且BK⊥DM．16．如图,已知A、B是线段MN上的两点,MN=4,MA=1,MB＞1．以A为中心顺时针旋转点M,以B为中心逆时针旋转点N,使M、N两点重合成一点C,构成△ABC,设AB=x．（1）求x的取值范围；（2）若△ABC为直角三角形,求x的值．【解答】解：（1）在△ABC中,∵AC=1,AB=x,BC=3﹣x．∴,解得1＜x＜2．（4分）（2）①若AC为斜边,则1=x2+（3﹣x）2,即x2﹣3x+4=0,无解．②若AB为斜边,则x2=（3﹣x）2+1,解得,满足1＜x＜2．③若BC为斜边,则（3﹣x）2=1+x2,解得,满足1＜x＜2．∴或．17．如图在Rt△OAB中,∠OAB=90°,OA=AB=6．（1）请你画出将△OAB绕点O沿逆时针方向旋转90°,得到的△OA1B1；（2）线段OA1的长度是 6 ,∠AOB1的度数是135°；（3）连接AA1,求证：四边形OAA1B1是平行四边形．【解答】（1）解：△OA1B1如图所示．（2）解：根据旋转的性质知,OA1=OA=6．∵将△OAB绕点O沿逆时针方向旋转90°,得到的△OA1B1 ,∴∠BOB1=90°．∵在Rt△OAB中,∠OAB=90°,OA=AB=6, ∴∠BOA=∠OBA=45°,∴∠AOB1=∠BOB1+∠BOA=90°+45°=135°,即∠AOB1的度数是135°．故答案是：6,135°；（3）证明：根据旋转的性质知,△OA1B1≌△OAB,则∠OA1B1=∠OAB=90°,A1B1=AB,∵将△OAB绕点O沿逆时针方向旋转90°,得到的△OA1B1 ,∴∠A1OA=90°,∴∠OA1B1=∠A1OA,∴A1B1∥OA．又∵OA=AB,∴A1B1=OA,∴四边形OAA1B1是平行四边形．。