八年级数学全等三角形拔高练习(竞赛班)
(完整)全等三角形证明之能力拔高(经典题目)

全等三角形能力拔高题姓名:一、角度转化问题1.已知:如图,AB⊥AE,AD⊥AC,∠E=∠B,DE=CB.求证:AD=AC.2.已知:如图,AD=AE,AB=AC,∠DAE=∠BAC.求证:BD=CE.3.已知:如图,在△MPN中,H是高MQ和NR的交点,且MQ=NQ.求证:HN=PM.4.如图,在△ABC中,∠ACB=90°,AC=BC,直线l经过顶点C,过A、B两点分别作l 的垂线AE、BF,E、F为垂足.当直线l不与底边AB相交时,求证:EF=AE+BF.5.已知:如图,AE⊥AB,BC⊥AB,AE=AB,ED=AC.求证:ED⊥AC.二、二次全等问题1.已知:如图,线段AC、BD交于O,∠AOB为钝角,AB=CD,BF⊥AC于F,DE⊥AC于E,AE=CF.求证:BO=DO.2.已知:如图,AC与BD交于O点,AB∥DC,AB=DC.若过O点作直线l,分别交AB、DC于E、F两点,求证:OE=OF.3.如图,E在AB上,∠1=∠2,∠3=∠4,那么AC等于AD吗?为什么?4.已知:如图,DE⊥AC,BF⊥AC,AD=BC,DE=BF.求证:AB∥DC.MF E CBA5、已知:如图,AD 平分∠BAC ,DE ⊥AB 于E ,DF ⊥AC 于F ,DB=DC , 求证:EB=FC【练习】1、已知∠B=∠E=90°,CE=CB ,AB ∥CD. 求证:△ADC 是等腰三角形。
2、如图:AB=AC ,ME ⊥AB ,MF ⊥AC ,垂足分别为E 、F ,ME=MF 。
求证:MB=MCG FEDC BA3、已知,△ABC 和△ECD 都是等边三角形,且点B ,C ,D 在一条直线上求证:BE=AD4、如图:在△ABC 中,∠C =90°,AD 平分∠ BAC ,DE ⊥AB 交AB 于E ,BC=30, BD :CD=3:2,则DE= 。
5、如图,已知,EG ∥AF ,请你从下面三个条件中,再选出两个作为已知条件,另一个作为结论,推出一个正确的命题。
八年级数学全等三角形证明拔高集训(经典)

八年级数学全等三角形证明拔高集训(经典)1.如图所示,△ABC和△BDE都是等腰直角三角形,其中∠ABC=∠BDE=90,且AB=CB,BD=ED,连接AD并交BE于F,且AF=DF,AD=AB。
证明BE=2CD。
2.在Rt△ABC中,∠BAC=90,且AB=AC。
点D和E 分别位于AC和CA的延长线上,且CD=AE。
连接BD,过点A作AM⊥BD于M交BC于N,连接EN并延长交BD于F。
证明DF=EF。
3.如图所示,△ABC中,∠ACB=90,点D在BC上,且AC=DC。
连接AD,过点C作CE⊥___于E,点F在CE 的延长线上,连接DF。
若∠F=45,证明AE=EF。
4.如图所示,△ABC和△DAF都是等腰直角三角形,其中∠BAC=∠DAF=90,且AB=AC,AD=AF。
DF的延长线交BC于E,且∠AFC=90.证明BE=CE。
5.在Rt△ABC中,∠BAC=90,且AB=AC。
点E为AC 上一点,连接BE,过点A作AE⊥BE于H交BC于D。
点F也为AC上一点,且AE=CF。
连接DF交BE于G,连接AG。
若AG平分∠CAD,证明AH=AC。
6.如图所示,∠ACB=∠CDE=90,且AC=BC,AB=2CD=2ED。
连接BD交CE于G,且GD=GB。
F是AB的中点。
证明___。
7.在Rt△ABC中,∠ACB=90°,且AC=BC。
AD、BE分别垂直于过点C的直线于D、E,延长BE至F。
连接CF,以CF为腰作等腰直角三角形GCF,使∠GCF=90°,连接AG 交过点C的直线于H。
证明BF=2CH。
8.在△ABC中,AD⊥BC于D,点E在BC上,且AB=BE=CD。
点F是AE的中点,连接CF并延长交AB于G。
若AD=BD,证明BG=BD。
9.在Rt△ABC中,∠ABC=90,且AB=CB。
点E、O分别为BC、AC的中点,连接AE。
过点B作BG⊥AE于G交AC于M,过点A作AH⊥GO交其延长线于H。
全等三角形拔高题目附带答案

全等三角形提高练习1. 如下图,△≌△,的延长线过点E ,∠∠105°,∠10°,∠50°,求∠的度数。
2. 如图,△中,∠30°,将△绕点O 顺时针旋转52°,得到△A ′′,边A ′B ′与边交于点C 〔A ′不在上〕,那么∠A3. 如下图,在△中,∠90°,D 、E么∠C 的度数是多少?AB'C4. 如下图,把△绕点C 顺时针旋转35°,得到△A ′B ′C ,A ′假设∠A ′90°,那么∠5. ,如下图,,⊥于D ,且50,而40,那么是多少?6. 如图,△中,∠90°,,分别过点B 、C 作过点A 的垂线、,垂足分别为D 、E ,假设3,2,那么7. 如图,是△的角平分线,⊥,⊥,垂足分别是E 、F 垂直吗?证明你的结论。
A B8.如下图,在△中,为∠的角平分线,⊥于E,⊥于F,△的面积是28220,8,求的长。
9.,如图:,∠∠E,∠∠,∠∠,求证:⊥10.如图,,⊥于D,⊥于E,与相交于点HC B11. 如下图,,为△的高,E 为上一点,交于F ,且有,,求证:⊥12.△、△均是等边三角形,、分别与、交于点M 、N〔3〕△为等边三角形 〔4〕∥ 13.:如图1,点C 为线段上一点,△、△都是等边三角形,交于点E ,交于点F (1) 求证:BAB(2)求证:△为等边三角形14.∠60°;⑤△是等边三角形;⑥∥,其中正确的有〔A.3个 B. 4个 C. 5个 D. 6个15.:、是△的高,点F在上,,点G在的延长线上,16.如图:在△中,、分别是、两边上的高,在上截取,在的延长线上截取,连结、求证:〔1〕〔2〕与的位置关系如何AB B17.如图,E 是正方形的边的中点,点F 在上,且∠∠ 求证:18.如下图,△中,,D 是延长线上一点,∠60°,E 是上一点,且,求证:19.如下图,在△中,∠90°,平分∠,⊥,垂足为F ,,求证:D20.如图:,直线、相交于C ,∠∠180°,∥,交于F21.如图,是∠的平分线,P 是上一点,⊥于D ,⊥于E ,F 是上一点,连接和,求证:22.:如图,⊥于点F ,⊥于点E ,且,求证:〔1〕△≌△ 〔2〕 点D 在∠A 的平分线上B23.如图,∥,O 是∠与∠的平分线的交点,⊥于E距离是多少?24.如图,过线段的两个端点作射线、画∠、∠的平分线交于E 〔1〕∠是什么角?〔2〕过点E 作一直线交于D ,交于C ,观察线段、,你有何发现? 〔3〕无论的两端点在、如何移动,只要经过点E ,①;②谁成立?并说明理由。
全等三角形竞赛试题(含答案)

全等三角形提升练习1. 如下图,△ ABC ≌△ ADE ,BC 的延伸线过点E ,∠ ACB=∠ AED=105°,∠ CAD=10°,∠ B=50°,求∠ DEF 的度数。
EDFCAB2. 如图,△ AOB 中,∠ B=30°,将△ AOB 绕点 O 顺时针旋转 52°,获得△ A ′ OB ′,边 A ′ B ′与边 OB交于点 C (A ′不在 OB 上),则∠ A ′ CO 的度数为多少BA'CB'AO3.如下图,在△ ABC 中,∠ A=90°, D 、 E 分别是 AC 、 BC 上的点,若△ ADB ≌△ EDB ≌△ EDC ,则∠ CA的度数是多少DB CE4.如下图, 把△ ABC 绕点 C 顺时针旋转 35°,获得△ A ′B ′ C ,A ′ B ′交 AC 于点 D ,若∠ A ′ DC=90°,则∠ A=A'ADB'B C5. 已知,如下图, AB=AC , AD ⊥BC 于 D ,且 AB+AC+BC=50cm,而6.如图, Rt △ ABC 中,∠ BAC=90°, AB=AC ,分别过点 B 、C 作过点若 BD=3, CE=2,则 DE=AB+BD+AD=40cm ,则 AD 是多少CADBA 的垂线 BC 、CE ,垂足分别为 D 、E ,BCD AE7. 如图, AD 是△ ABC 的角均分线, DE ⊥AB , DF ⊥ AC ,垂足分别是E 、F ,连结 EF ,交 AD 于G , AD 与EF 垂直吗证明你的结论。
AEGFBDC8. 如下图,在△ ABC 中, AD 为∠ BAC 的角均分线, DE ⊥ AB 于 E , DF ⊥ AC 于 F ,△ ABC 的面积是28cm 2 ,AB=20cm , AC=8cm ,求 DE 的长。
全等三角形截长补短拔高练习(含答案)

八年级数学全等三角形辅助线添加之截长补短(全等三角形)拔高练习试卷简介:本讲测试题共两个大题,第一题是证明题,共7个小题,每小题10分;第二题解答题,2个小题,每小题15分。
学习建议:本讲内容是三角形全等的判定——辅助线添加之截长补短,其中通过截长补短来添加辅助线是重点,也是难点。
希望同学们能学会熟练通过截长补短来做辅助线,进而构造出全等的三角形。
一、解答题(共1道,每道20分)1.AD+AB).答案:中∴DF=BE,在△CFD和△CEB中所以△CFD≌△CEB(SAS),∴∠2=∠FDC,又∠1+∠FDC=180°,∴∠1+∠2=180°。
解题思路:见到角平分线就要想到作垂直,找到全等关系是解决此类问题的关键易错点:找到三角形全等的所有条件试题难度:四颗星知识点:三角形二、证明题(共8道,每道10分)1.如图,已知△ABC中,∠A=90°,AB=AC,BE平分∠ABC,CE⊥BD于E,求证:CE=BD.延长ABC BE CE CE=EH=CH又2+1=CE=BDCE=BDCH=BD2.如图,已知正方形ABCD中,E为BC边上任意一点,AF平分∠DAE.求证:AE-BE=DF.答案:证明:延长CB到M使BM=DF,连结AM.在△ADF和△ABM中∴△ADF≌△ABM(SAS)∴∠1=∠3,∠M=∠4,由于AB∥DC,AF平分∠EAD,所以∠BAF=∠4,∠1=∠2,∴∠2=∠3,从而∠MAE=∠BAF=∠4=∠M,∴AE=ME=BM+BE=DF+BE,∴AE-BE=DF.将DF是关键。
3.恰好平分答案:在BA上截取BF=BC,∵BE恰好平分ABC∴CBE=FBE又BC=BF,BE=BE∴△BCE≌△BFE∴C=BFE又AD∥BC∴C+D=180°而BFE+AFE=180°∴AFE= D又∵AE=AE,EAF=EAD∴△AEF≌△AED∴AF=AD∴AD+BC=AF+BF=AB解题思路:要证明两条线段和等于一条线段,最常想到的是截长补短法.截长:在BA上截取BF=BC 或者在AB上截取AF=AD;补短:延长BC至G,使BG=BA易错点:不会利用截长补短方法解题试题难度:四颗星知识点:全等三角形的判定与性质4.如图,在△ABC中,AB>AC,1=2,P为AD上任意一点.求证:AB-AC>PB-PC.试题难度:三颗星知识点:三角形三边关系5.如图所示:在△ABC中,∠1=∠2,∠B=2∠C,求证:AC=AB+BD.在边又6.的大小关答案:判断:AC=AE+CD证明:令AD与CE的交点为G,在AC上截取AF=AE,在△AEG和△AFG中AD、;于是中分别证明7.EG∥AB 交CB答案:判断:CF=GB证明:过点F作FH⊥AB于点H,由于AF平分∠CAB,则在△ACF与△AHF中∴△ACF≌△AHF,则CF=FH,而FH⊥AB,CD⊥AB,∴FH∥CD,从而∠4=∠5,∴∠3=∠4,∴CF=CE,从而CE=FH,又EG∥AB,所以∠6=∠B∠CEG=∠CDB=90°;则△CEG≌△FHB,∴CG=FB,故CF=BG解题思路:找到全等关系是证明的关键易错点:想到将线段转移,想不到全等。
八年级数学全等三角形拔高练习-(竞赛班)

八年级数学全等三角形拔高题(竞赛班)一、选择题.1. 如图,已知AB ∥CD,AD ∥BC ,AC 与BD 交于O ,AE ⊥BD 于E ,CF ⊥BD 于F ,那么图中全等的三角形有【 】A.5对B.6对C.7对D.8对O F EDCBA2. 下面四个命题:①两个三角形有两边及一角对应相等,则这两个三角形全等;② 两个三角形有两角及一边对应相等,则这两个三角形全等; ③两个三角形的三条边分别对应相等,则这两个三角形全等;④ 两个三角形的三个角分别对应相等,则这两个三角形全等.其中真命题是【 】A. ② ③B. ① ③C. ③ ④D. ② ④3. 已知三角形的每条边长是整数,且小于等于4,这样的互不全等的三角形有【 】A.10个B.12个C.13个D.14个4. 如图,在等边△ABC 中,AD =BE =CF,D 、E 、F 不是中点,连结AE 、BF 、CD,构成一些三角形.如果三个全等的三角形组成一组,那么图中全等的三角形的组数是【 】A.3个B.4个C.5个D.6个C 'B 'A 'FEDCBA5.若在ABC ∆中,∠ABC 的平分线交AC 于D,AC =AB +BD,∠C =300,则∠B 的度数为【 】A.450B.600C.750D.9006.将长度为20的铁丝为成三边长均为整数的三角形,那么不全等的三角形的个数是【 】A.5B.6C.8D.10 7.如图等边△ABC 中,∠BFC=1200,那么 【 】A 、AD >CEB 、AD <CEC 、AD=CED 、不确定8.如图△ABC 中,AD 是△ABC 中线,E ,F 分别是在AB ,AC 上,且DE ⊥DF ,则【 】A 、BE+CF >EFB 、BE+CF=EFC 、BE+CF < EFD 、BE+CF 与EF 大小不定9.如图,△ABC中∠B=600,AD 与CE 是角平分线且相交于点O ,则 【 】 A 、AE+CD > AC B 、AE+CD < AC C 、AE+CD= AC D 、AE+CD 与 AC 大小不定10.正三角形ABD 和正三角形CBD 的边长均为,现把它们拼合起来如图,E 是AD 上异于A ,D 两点的一动点,F 是CD 上一动点,满足AE+CF=AB ,当E ,F 移动时,三角形BEF 的形状为 【 】 A 、不等边三角形 B 、等腰直角三角形 C 、等腰三角形非正三角形 D 、正三角形 11、在直角梯形ABCD 中,AD BC ∥,90ABC AB BC E ∠==°,,为AB 边上一点,15BCE ∠=°,且AE AD =.连接DE 交对角线AC 于H ,连接BH .下列结论:①ACD ACE △≌△; ②CDE △为等边三角形; ③2EH BE=;④EDC EHC S AHS CH=△△. 其中结论正确的是【 】 A .只有①②B .只有①②④C .只有③④D .①②③④12、图(三)、图(四)、图(五)分别表示甲、乙、丙三人由A 地到B 地的路线图。
(最新最全)全等三角形练习题综合拔高题_共6页
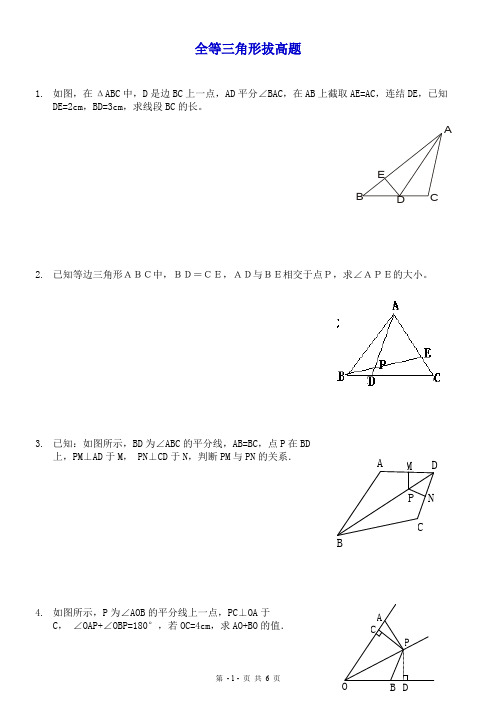
全等三角形拔高题1.如图,在ΔABC 中,D 是边BC 上一点,AD 平分∠BAC,在AB 上截取AE=AC ,连结DE ,已知DE=2cm ,BD=3cm ,求线段BC 的长。
2.已知等边三角形ABC中,BD=CE,AD与BE相交于点P,求∠APE的大小。
3.已知:如图所示,BD 为∠ABC 的平分线,AB=BC ,点P 在BD上,PM⊥AD 于M , PN⊥CD 于N ,判断PM 与PN 的关系.4.如图所示,P 为∠AOB 的平分线上一点,PC⊥OA 于C , ∠OAP+∠OBP=180°,若OC=4cm ,求AO+BO 的值.ABCDE P D ACBM NPA C5.如图所示,A,E,F,C在一条直线上,AE=CF,过E,F分别作DE ⊥AC,BF⊥AC,若AB=CD,可以得到BD平分EF,为什么?若将△DEC的边EC沿AC方向移动,变为如图所示时,其余条件不变,上述结论是否成立?请说明理由.6.如图,△ABC中,D是BC的中点,过D点的直线GF交AC于F,交AC的平行线BG于G点,DE⊥DF,交AB于点E,连结EG、EF.(1)求证:BG=CF;(2)请你判断BE+CF与EF的大小关系,并说明理由。
7.已知:如图E在△ABC的边AC上,且∠AEB=∠ABC。
(1)求证:∠ABE=∠C;(2)若∠BAE的平分线AF交BE于F,FD∥BC交AC于D,设AB=5,AC=8,求DC的长。
GDFACBEGD FACBEFED CBAG8.如图,在△ABC 和△DCB 中,AB = DC ,AC = DB ,AC 与DB 交于点M .(1)求证:△ABC ≌△DCB ;(2)过点C 作CN ∥BD ,过点B 作BN ∥AC ,CN 与BN 交于点N ,试判断线段BN 与CN 的数量关系,并证明你的结论.9.已知:如图,DC ∥AB ,且DC =AE ,E 为AB 的中点,(1)求证:△AED ≌△EBC .(2)观看图前,在不添辅助线的情况下,除△EBC 外,请再写出两个与△AED 的面积相等的三角形.(直接写出结果,不要求证明):10.如图①,E 、F 分别为线段AC 上的两个动点,且DE ⊥AC 于E ,BF ⊥AC 于F ,若AB =CD ,AF =CE ,BD 交AC 于点M .(1)求证:MB =MD ,ME =MF(2)当E 、F 两点移动到如图②的位置时,其余条件不变,上述结论能否成立?若成立请给予证明;若不成立请说明理由.BCADMOEDCBA11.如图,已知在△ABC 中,∠BAC 为直角,AB=AC ,D 为AC 上一点,CE⊥BD 于E .(1)若BD 平分∠ABC,求证CE=BD ;12(2)若D 为AC 上一动点,∠AED 如何变化,若变化,求它的变化范围;若不变,求出它的度数,并说明理由。
人教版八年级数学上册《三角形全等的判定》拔高练习
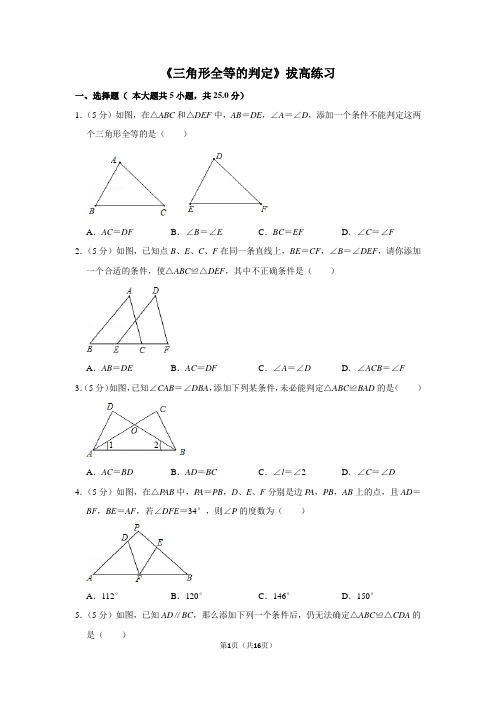
《三角形全等的判定》拔高练习一、选择题(本大题共5小题,共25.0分)1.(5分)如图,在△ABC和△DEF中,AB=DE,∠A=∠D,添加一个条件不能判定这两个三角形全等的是()A.AC=DF B.∠B=∠E C.BC=EF D.∠C=∠F 2.(5分)如图,已知点B、E、C、F在同一条直线上,BE=CF,∠B=∠DEF,请你添加一个合适的条件,使△ABC≌△DEF,其中不正确条件是()A.AB=DE B.AC=DF C.∠A=∠D D.∠ACB=∠F 3.(5分)如图,已知∠CAB=∠DBA,添加下列某条件,未必能判定△ABC≌BAD的是()A.AC=BD B.AD=BC C.∠l=∠2D.∠C=∠D 4.(5分)如图,在△P AB中,P A=PB,D、E、F分别是边P A,PB,AB上的点,且AD=BF,BE=AF,若∠DFE=34°,则∠P的度数为()A.112°B.120°C.146°D.150°5.(5分)如图,已知AD∥BC,那么添加下列一个条件后,仍无法确定△ABC≌△CDA的是()A.∠B=∠D B.AB∥DC C.AB=CD D.BC=AD二、填空题(本大题共5小题,共25.0分)6.(5分)如图,已知AB=CB,要使△ABD≌△CBD,则可以添加的一个条件是.7.(5分)如图,AB=AC,点D在AB上,点E在AC上,DC,EB交于点F,请添加一个条件.使△ADC≌△AEB(填一个即可)8.(5分)如图,已知AE=AD,要直接利用AAS证明△ABE≌△ACD,应添加的条件是.9.(5分)根据下列条件:①AB=3,AC=4,AC=8;②∠A=60°,∠B=45°,AB=4;③AB=5,BC=3,∠A=30°;④AB=3,BC=4,AC=5,其中能画出唯一三角形是(填序号).10.(5分)两组邻边相等的四边形叫做“筝形”,如图,四边形ABCD是一个筝形,其中AB=CB,AD=CD,詹姆斯在探究筝形的性质时,得到如下结论:①AC⊥BD;②△ABD ≌△CBD;③AO=CO=AC;④四边形ABCD的面积=AC×BD,其中,正确的结论有.三、解答题(本大题共5小题,共50.0分)11.(10分)如图,点D在线段BC上,∠B=∠ADB,∠BAD=∠CAE,∠C=∠E.求证:AC=AE.12.(10分)如图,AF=BE,AC∥BD,CE∥DF,求证:CE=DF.13.(10分)如图,已知点B,E,C,F在一条直线上,BE=CF,AC∥DE,∠A=∠D.(1)求证:△ABC≌△DFE;(2)若BF=14,EC=4,求BC的长.14.(10分)如图,点E、A、C在同一直线上,AB∥CD,∠B=∠E,AC=CD 求证:(1)∠BAC=∠ECD;(2)BC=ED.15.(10分)(1)如图1,四边形ABCD中,∠A=∠B=90°,∠ADC,∠BCD的角平分线交于AB边上的点E,求证:①CD=AD+BC;②E是AB的中点;(2)如图2,(1)中的条件“∠A=∠B=90°”改为“条件AD∥BC”,其他条件不变,(1)中的结论是否都依然成立?请什么理由.《三角形全等的判定》拔高练习参考答案与试题解析一、选择题(本大题共5小题,共25.0分)1.(5分)如图,在△ABC和△DEF中,AB=DE,∠A=∠D,添加一个条件不能判定这两个三角形全等的是()A.AC=DF B.∠B=∠E C.BC=EF D.∠C=∠F【分析】根据全等三角形的判定定理,结合各选项的条件进行判断即可.【解答】解:A、添加AC=DF,满足SAS,可以判定两三角形全等;B、添加∠B=∠E,满足ASA,可以判定两三角形全等;C、添加BC=EF,不能判定这两个三角形全等;D、添加∠C=∠F,满足AAS,可以判定两三角形全等;故选:C.【点评】本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.2.(5分)如图,已知点B、E、C、F在同一条直线上,BE=CF,∠B=∠DEF,请你添加一个合适的条件,使△ABC≌△DEF,其中不正确条件是()A.AB=DE B.AC=DF C.∠A=∠D D.∠ACB=∠F 【分析】根据全等三角形的判定方法逐项判断即可.【解答】解:∵BE=CF,∴BE+EC=EC+CF,即BC=EF,且∠ABC=∠DEF,∴当AC=DF时,满足SSA,无法判定△ABC≌△DEF,故B不能;当AB=DE时,满足SAS,可以判定△ABC≌△DEF,故B可以;当∠ACB=∠F时,满足ASA,可以判定△ABC≌△DEF,故C可以;当∠A=∠D时,满足AAS,可以判定△ABC≌△DEF,故D可以;故选:B.【点评】本题主要考查全等三角形的判定方法,掌握全等三角形的判定方法是解题的关键,即SSS、SAS、ASA、AAS和HL.3.(5分)如图,已知∠CAB=∠DBA,添加下列某条件,未必能判定△ABC≌BAD的是()A.AC=BD B.AD=BC C.∠l=∠2D.∠C=∠D【分析】根据全等三角形的判定定理(SAS,ASA,AAS,SSS)判断即可.【解答】解:A、∵AC=BD,∠CAB=∠DBA,AB=AB,∴根据SAS能推出△ABC≌△BAD,故本选项错误;B、根据AD=BC和已知不能推出△ABC≌△BAD,故本选项正确;C、∵∠CAB=∠DBA,AB=AB,∠1=∠2,∴根据ASA能推出△ABC≌△BAD,故本选项错误;D、∵∠C=∠D,∠CAB=∠DBA,AB=AB,∴根据AAS能推出△ABC≌△BAD,故本选项错误;故选:B.【点评】本题考查了对全等三角形的判定定理的应用,注意:全等三角形的判定定理有SAS,ASA,AAS,SSS.4.(5分)如图,在△P AB中,P A=PB,D、E、F分别是边P A,PB,AB上的点,且AD=BF,BE=AF,若∠DFE=34°,则∠P的度数为()A.112°B.120°C.146°D.150°【分析】根据等腰三角形的性质得到∠A=∠B,证明△ADF≌△BFE,得到∠ADF=∠BFE,根据三角形的外角的性质求出∠A=∠DFE=42°,根据三角形内角和定理计算即可.【解答】解:∵P A=PB,∴∠A=∠B,在△ADF和△BFE中,,∴△ADF≌△BFE(SAS),∴∠ADF=∠BFE,∵∠DFB=∠DFE+∠EFB=∠A+∠ADF,∴∠A=∠DFE=34°,∴∠P=180°﹣∠A﹣∠B=112°,故选:A.【点评】本题考查的是等腰三角形的性质、全等三角形的判定和性质、三角形的外角的性质,掌握等边对等角、全等三角形的判定定理和性质定理、三角形的外角的性质是解题的关键.5.(5分)如图,已知AD∥BC,那么添加下列一个条件后,仍无法确定△ABC≌△CDA的是()A.∠B=∠D B.AB∥DC C.AB=CD D.BC=AD【分析】根据全等三角形的判定的方法进行解答即可.【解答】解:A、∵AD∥BC,∴∠DAC=∠BCA,由得出△ABC≌△CDA,不符合题意;B、∵AD∥BC,∴∠DAC=∠BCA,∵AB∥DC,∴∠BAC=∠DCA,由得出△ABC≌△CDA,不符合题意;C、由AB=CD,AC=CA,∠DAC=∠BCA无法得出△ABC≌△CDA,符合题意;D、∵AD∥BC,∴∠DAC=∠BCA,由得出△ABC≌△CDA,不符合题意;故选:C.【点评】此题主要考查了全等三角形的判定,关键是由已知得到两个已知条件,再根据全等三角形的判定找出能使△ABC≌△CDA的另一个条件.二、填空题(本大题共5小题,共25.0分)6.(5分)如图,已知AB=CB,要使△ABD≌△CBD,则可以添加的一个条件是∠ABD =∠CBD或AD=CD.【分析】判定全等三角形时需要添加什么条件,取决于题目中的已知条件,若已知两边对应相等,则找它们的夹角或第三边.【解答】解:①添加∠ABD=∠CBD.在△ABD和△CBD中,∵,∴△ABD≌△CBD(SAS);②添加AD=CD.在△ABD和△CBD中,∵,∴△ABD≌△CBD(SSS).故答案为:∠ABD=∠CBD或AD=CD.(答案不唯一)【点评】本题主要考查了全等三角形的判定定理,能灵活运用判定进行证明是解此题的关键.7.(5分)如图,AB=AC,点D在AB上,点E在AC上,DC,EB交于点F,请添加一个条件AD=AE.使△ADC≌△AEB(填一个即可)【分析】△ADC和△AEB中,已知的条件有AB=AC,∠A=∠A;要判定两三角形全等只需条件一组对应角相等或AD=AE即可.【解答】解:添加条件:AD=AE,在△ABE和△ACD中,,∴△ADC≌△AEB(SAS),故答案为:AD=AE.【点评】本题考查三角形全等的判定方法;判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.添加时注意:AAA、SSA不能判定两个三角形全等,不能添加,根据已知结合图形及判定方法选择条件是正确解答本题的关键.8.(5分)如图,已知AE=AD,要直接利用AAS证明△ABE≌△ACD,应添加的条件是∠B=∠C.【分析】根据AAS证明△ABE≌△ACD即可.【解答】解:添加的条件是∠B=∠C,在△ABE与△ACD中,∴△ABE≌△ACD(AAS),故答案为:∠B=∠C.【点评】本题考查全等三角形的判定,解题的关键是正确找出条件证明全等三角形,本题属于基础题型.9.(5分)根据下列条件:①AB=3,AC=4,AC=8;②∠A=60°,∠B=45°,AB=4;③AB=5,BC=3,∠A=30°;④AB=3,BC=4,AC=5,其中能画出唯一三角形是②④(填序号).【分析】根据三角形的三边关系定理,先看看能否组成三角形,再根据全等三角形的判定定理判断即可.【解答】解:①∵3+4<8,∴根据AB=3,BC=4,AB=8不能画出三角形,故本选项错误;②根据∠A=60°,∠B=30°,AB=4,符合全等三角形的判定定理ASA,即能画出唯一三角形,故本选项正确;③根据AB=5,BC=3,∠A=30°不能画出唯一三角形,故本选项错误;④根据AB=3,BC=4,AC=5,符合全等三角形的判定定理SSS,即能画出唯一三角形,故本选项正确;故答案为:②④.【点评】本题考查了三角形的三边关系定理和全等三角形的判定定理,注意:全等三角形的判定定理有SAS,ASA,AAS,SSS.10.(5分)两组邻边相等的四边形叫做“筝形”,如图,四边形ABCD是一个筝形,其中AB=CB,AD=CD,詹姆斯在探究筝形的性质时,得到如下结论:①AC⊥BD;②△ABD ≌△CBD;③AO=CO=AC;④四边形ABCD的面积=AC×BD,其中,正确的结论有①②③④.【分析】由题意可得BD是AC的垂直平分线,可得AO=CO=AC,AC⊥BC,根据“SSS”可证△ABD≌△CBD,由三角形的面积公式可得S四边形ABCD=2××AO×BD=×AC ×BD.【解答】解:∵AB=CB,AD=CD,∴BD是AC的垂直平分线,∴AO=CO=AC,AC⊥BC,故①③正确,∵AB=BC,AD=CD,BD=BD∴△ABD≌△CBD(SAS)故②正确∵S四边形ABCD=2S△ABD,∴S四边形ABCD=2××AO×BD=×AC×BD故④正确故答案为:①②③④【点评】本题考查了全等三角形的判定与性质,线段垂直平分线的性质,熟练运用全等三角形的性质解决问题是本题的关键.三、解答题(本大题共5小题,共50.0分)11.(10分)如图,点D在线段BC上,∠B=∠ADB,∠BAD=∠CAE,∠C=∠E.求证:AC=AE.【分析】欲证明AC=AE,只要证明△ABC≌△ADE(AAS)即可.【解答】证明:∵∠B=∠ADB,∴AB=AD,∵∠BAD=∠CAE,∴∠BAD+∠CAD=∠CAE+∠CAD,∴∠BAC=∠DAE,在△ABC和△ADE中,∴△ABC≌△ADE(AAS),∴AC=AE.【点评】本题考查全等三角形的判定和性质,解题的关键是正确寻找全等三角形全等的条件,属于中考常考题型.12.(10分)如图,AF=BE,AC∥BD,CE∥DF,求证:CE=DF.【分析】只要证明△AEC≌△BFD(ASA)即可解决问题.【解答】证明:∵AC∥BD,CE∥DF,∴∠A=∠B,∠CEA=∠DFB,∵AF=BE,∴AF+EF=BE+EF,∴AE=BF.在△AEC和△BFD中,∴△AEC≌△BFD(ASA),∴CE=DF.【点评】本题考查全等三角形的判定和性质,平行线的性质等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.13.(10分)如图,已知点B,E,C,F在一条直线上,BE=CF,AC∥DE,∠A=∠D.(1)求证:△ABC≌△DFE;(2)若BF=14,EC=4,求BC的长.【分析】(1)根据AAS证明△ABC≌△DFE即可解决问题.(2)求出BE的长即可解决问题.【解答】(1)证明:∵AC∥DE,∴∠ACB=∠DEF,∵BE=CF,∴BC=EF,在△ABC和△DFE中,,∴△ABC≌△DFE(AAS).(2)解:∵BF=14,EC=4,∴BE+CF=14﹣4=10,∵BE=CF,∴BE=CF=5,∴BC=BE+EC=5+4=9.【点评】本题考查全等三角形的判定和性质,平行线的性质等知识,解题的关键是正确寻找全等三角形解决问题,属于中考常考题型.14.(10分)如图,点E、A、C在同一直线上,AB∥CD,∠B=∠E,AC=CD 求证:(1)∠BAC=∠ECD;(2)BC=ED.【分析】(1)利用平行线的性质即可证明.(2)证明△BAC≌△ECD(AAS)即可解决问题.【解答】证明:(1)∵AB∥CD,∴∠BAC=∠ECD,(2)在△BAC和△ECD中,,∴△BAC≌△ECD(AAS),∴BC=DE.【点评】本题考查全等三角形的判定和性质,平行线的性质等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.15.(10分)(1)如图1,四边形ABCD中,∠A=∠B=90°,∠ADC,∠BCD的角平分线交于AB边上的点E,求证:①CD=AD+BC;②E是AB的中点;(2)如图2,(1)中的条件“∠A=∠B=90°”改为“条件AD∥BC”,其他条件不变,(1)中的结论是否都依然成立?请什么理由.【分析】(1)如图1﹣1中,过点E作EF⊥CD于点F.利用角平分线的性质定理可得AE=EB.利用全等三角形的性质证明AAD=DF,CB=CF即可.(2)结论仍然成立.如图2中,在CD上截取DF=DA,连接EF,利用全等三角形的性质证明即可.【解答】(1)证明:如图1﹣1中,过点E作EF⊥CD于点F.∵ED,EC分别平分∠ADC,∠BCD,且∠A=∠B=90°,∴EF=AE=BE,即E是AB中点,在Rt△AED和Rt△FED中,,∴Rt△AED≌Rt△FED(HL),∴AD=FD,同法可得:BC=CF,∴CD=DF+CF=AD+BC.(2)解:结论仍然成立.理由如下:如图2中,在CD上截取DF=DA,连接EF,在△EAD和△EFD中,,∴△EAD≌△EFD(SAS),∴EA=EF,∠DAE=∠DFE,∵AD∥BC,∴∠DAB+∠ABC=180°,∴∠EBC=∠EFC,在△EBC和△EFC中,,∴△EBC≌△EFC(ASA),∴EB=EF,BC=FC,∴CD=DF+FC=AD+BC.【点评】本题考查角平分线的性质定理,全等三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
八年级数学全等三角形拔高题(竞赛班)一、选择题.1. 如图,已知∥∥,与交于O ,⊥于E ,⊥于F ,那么图中全等的三角形有【 】 A.5对 B.6对 C.7对 D.8对O F EDCBA2. 下面四个命题:①两个三角形有两边及一角对应相等,则这两个三角形全等;② 两个三角形有两角及一边对应相等,则这两个三角形全等; ③两个三角形的三条边分别对应相等,则这两个三角形全等;④ 两个三角形的三个角分别对应相等,则这两个三角形全等.其中真命题是【 】A. ② ③B. ① ③C. ③ ④D. ② ④3. 已知三角形的每条边长是整数,且小于等于4,这样的互不全等的三角形有【 】A.10个B.12个C.13个D.14个 4. 如图,在等边△中==、E 、F 不是中点,连结、、,构成一些三角形.如果三个全等的三角形组成一组,那么图中全等的三角形的组数是【 】A.3个B.4个C.5个D.6个C 'B 'A 'FEDCBA5.若在ABC ∆中,∠的平分线交于=+,∠C =300,则∠B 的度数为【 】 A.450 B.600 C.750 D.9006.将长度为20的铁丝为成三边长均为整数的三角形,那么不全等的三角形的个数是【 】A.5B.6C.8D.10 7.如图等边△中,∠1200,那么 【 】A 、>B 、<C 、D 、不确定8.如图△中,是△中线,E ,F 分别是在,上,且⊥,则【 】 A 、> B 、C 、 <D 、与大小不定9.如图,△中∠600,与是角平分线且相交于点O ,则 【 】 A 、> B 、<C 、D 、与 大小不定10.正三角形和正三角形的边长均为,现把它们拼合起来如图,E 是上异于A ,D 两点的一动点,F 是上一动点,满足,当E ,F 移动时,三角形的形状为 【 】 A 、不等边三角形 B 、等腰直角三角形 C 、等腰三角形非正三角形 D 、正三角形11、在直角梯形ABCD 中,AD BC ∥,90ABC AB BC E ∠==°,,为AB 边上一点,15BCE ∠=°,且AE AD =.连接DE 交对角线AC 于H ,连接BH .下列结论:①ACD ACE △≌△; ②CDE △为等边三角形; ③2EHBE=; ④EDC EHC S AHS CH=△△. 其中结论正确的是【 】A .只有①②B .只有①②④C .只有③④D .①②③④12、图(三)、图(四)、图(五)分别表示甲、乙、丙三人由A 地到B 地的路线图。
已知:甲的路线为:A →C →B 。
乙的路线为:A →D →E →F →B ,其中E 为AB 的中点。
丙的路线为:A →I →J →K →B ,其中J 在AB 上,且AJ >JB 。
若符号「→」表示「直线前进」,则根据图(三)、图(四)、图(五)的数据,判断三人行进路线长度的大小关系为何?【 】(A) 甲=乙=丙 (B) 甲<乙<丙 (C) 乙<丙<甲 (D )丙<乙<甲 。
13.在△和A B C '''∆中, AB A B ''=,B B '∠=∠,补充条件后仍不一定能保证ABC ∆≌A B C '''∆,则补充的条件是【 】A.BC B C ''=B.A A '∠=∠C.AC A C ''=D.C C '∠=∠ 14.若在ABC ∆中,∠的平分线交于,∠300,则∠B 的度数为【 】A.450B.600C.750D.900 15.下面四个命题(1)有两条边与一个角对应相等的两个三角形全等;(2)有两个角与一条边对应相等的两个三角形全等; (3)周长与面积分别相等的两个三角形全等;(4)边和角中,有五个元素分别相等的两个三角形全等.其中正确命题的个数是【 】 A.1个 B.2个 C. 3个 D.4个 二、填空题.1.在不等边△中,,⊥,⊥,.①,②∥,③△≌△,其中正确的代号是2. 如图,如果正方形中=,∠=350,那么∠的度数是 .NM A EDCB3.已知:4,2,D 是中点,是整数,则 .4.如图,△和△是△分别沿着、边翻折180°形成的,若∠150°,则∠的度数为. 5.已知△中,∠45°,4,H 是高和的交点,则线段的长度为.ADBCDC BE AHFEDCB AFEDCBAOEDCBAFEDC BA 70707070506070CPN MBA6.如图是△的边上一点交于点E,给出3个论断:①;②;③∥. 以其中一个论断为结论,其余两个论断为条件,可作出3个命题.其中正确的命题个数是 .AFED C B9.如图,四边形中平分∠⊥于E,()12AE AD AB =+,则∠∠的大小为 .DE CBA10.如图,△的三边、、长分别是20、30、40,其三条角平分线将△分为三个三角形,则S △:S △:S △ . 三、解答题.1. (北京中考题)已知ABC ∆中,60A ∠=,BD 、CE 分别平分ABC ∠和.ACB ∠,BD 、CE 交于点O ,试判断BE 、CD 、BC 的数量关系,并加以证明.DOECB A2.如图,点M 为正三角形ABD 的边AB 所在直线上的任意一点(点B 除外),作60DMN ∠=︒,射线MN 与DBA ∠外角的平分线交于点N ,DM 与MN 有怎样的数量关系?NEB M A D3.如图,点M 为正方形ABCD 的边AB 上任意一点,MN DM ⊥且与ABC ∠外角 的平分线交于点N ,MD 与MN 有怎样的数量关系?NCDEBM A4.已知:如图,是正方形,∠∠. 求证:.FEDCBA5.以ABC ∆的AB 、AC 为边向三角形外作等边ABD ∆、ACE ∆,连结CD 、BE 相交于点O .求证:OA 平分DOE ∠.6、 如图所示,ABC ∆是边长为1的正三角形,BDC ∆是顶角为120︒的等腰三角 形,以D 为顶点作一个60︒的MDN ∠,点M 、N 分别在AB 、AC 上,求AMN ∆的周长.NMDCBA7、如图,在ABC ∆中,60BAC ∠=︒,AD 是BAC ∠的平分线,且AC AB BD =+,求ABC ∠的度数.8.如图所示,在ABC ∆中,44BAC BCA ︒∠=∠=,M 为ABC ∆内一点,使得30MCA ︒∠=,16MAC ︒∠=,求BMC ∠的度数.9、如图,在△ 中,,延长到D ,使,取的中点E ,连接和. 求证:2.HEBDAC题图第5题图第 4 C O10、 如图,已知C 为线段上的一点,∆和∆都是等边三角形,和相交于F 点,和交于E 点。
求证:∆是等边三角形。
ABCMNE F1211. 如图,在等腰△中,∠C =90°,D 是斜边上上任一点,⊥于E ,⊥交的延长线于F ,⊥于H 点,交于G . 求证:=.12.在△中,为边上的中线.求证:<() .13.已知:D 是中点,∠90°,求证:12CD AB =.14.已知:∠1=∠2,,,求证:15.如图,已知∥,、分别平分∠和∠,过点E ,则与相等吗?请说明理由16.如图所示,已知∠1=∠2,⊥于P ,交延长线于M , 求证:2∠(∠∠B )21PFMD BA C E17. 如图,点O 是等边ABC △内一点,110AOB BOC α∠=∠=,.将BOC△绕点C 按顺时针方向旋转60得ADC △,连接OD .(1)求证:COD △是等边三角形;(2)当150α=时,试判断AOD △的形状,并说明理由; (3)探究:当α为多少度时,AOD △是等腰三角形?ABCDO110α18 .已知:如图,ABC △是等边三角形,过AB 边上的点D 作DG BC ∥,交AC 于点G ,在GD 的延长线上取点E ,使DE DB =,连接AE CD ,. (1)求证:AGE DAC △≌△;(2)过点E 作EF DC ∥,交BC 于点F ,请你连接AF ,并判断AEF △是怎BACDF2 1 EDABCEDFC B ACDCBAF E DC B A 样的三角形,试证明你的结论.CGAEDBF19、如图,△中,E 、F 分别在、上,⊥,D 是中点,试比较与的大小.20、如图,△中,,E 是的中点,求证:平分∠.E D CBA21、如图,ABC ∆中,2,平分BAC ∠,且,求证:⊥22、如图,已知在ABC 内,060BAC ∠=,040C ∠=,P ,Q 分别在,上,并且,分别是BAC ∠,ABC ∠23、如图,在四边形中,>=,平分ABC ∠,求证: 0180=∠+∠C A24、如图,已知在△中,∠60°,△的角平分线相交于点O ,求证:25、如图,△中,平分∠,⊥且平分,⊥于E ,⊥于F.(1)说明的理由; (2)如果a ,b ,求、的长.26 、正方形中,E 为上的一点,F 为上的一点,,求∠的度数.27、 已知:如图,四边形中,平分∠,⊥ 于E ,且∠∠180︒,求证:ABDCE 12CE DGFC BA。
