人教版数学七年级上《41几何图形》同步练习(有答案)MnMMKM

合集下载

人教版数学七年级上《4.1几何图形》同步练习（含答案）

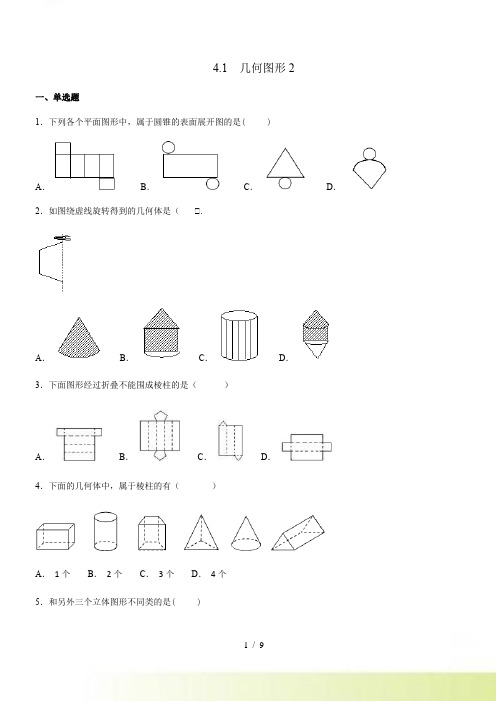
4.1 几何图形2一、单选题1．下列各个平面图形中，属于圆锥的表面展开图的是( )A．B．C．D．2．如图绕虚线旋转得到的几何体是（）.A．B．C．D．3．下面图形经过折叠不能围成棱柱的是（）A．B．C．D．4．下面的几何体中，属于棱柱的有（）A．1个B．2个C．3个D．4个5．和另外三个立体图形不同类的是( )A．B．C．D．6．下列说法错误的是（）A．若直棱柱的底面边长都相等，则它的各个侧面面积相等B．n棱柱有n个面，n个顶点C．长方体，正方体都是四棱柱D．三棱柱的底面是三角形7．将图1围成图2的正方体，则图1中的红心“”标志所在的正方形是正方体中的（）A、面CDHEB、面BCEFC、面ABFGD、面ADHG8．小明为了鼓励芦山地震灾区的学生早日走出阴影，好好学习，制作了一个正方体礼盒（如图）．礼盒每个面上各有一个字，连起来组成“芦山学子加油”，其中“芦”的对面是“学”，“加”的对面是“油”，则它的平面展开图可能是（）A．B．C．D．9．如图是一无盖长方体盒子的展开图（重叠部分不计），则该无盖长方体的容积为（）A．4 B．3 C．8 D．1210．将“创建文明城市”六个字分别写在一个正方体的六个面上，这个正方体的平面展开图如图所示，那么在这个正方体中，与“创”字相对的字是（）A.文B.明C.城D.市二、填空题11．如图是一个棱长为2 cm的立方体，若要把它截成八个棱长1 cm的小立方体，至少需截____次．12．将一个圆分割成三个扇形，使它们圆心角度数比为2）3）4，则这3个圆心角中度数最大的为________）13．下列请写出下列几何体，并将其分类．（只填写编号）如果按“柱”“锥”“球”来分，柱体有_____，椎体有_____，球有_____）如果按“有无曲面”来分，有曲面的有_____，无曲面的有_____）14．如图所示，截去正方体一角变成一个多面体，这个多面体有______个面，有______条棱，有______个顶点．15．如图所示，一个长方体的长为4cm，宽为3cm，高为5cm．则长方体所有棱长的和为_______________；长方体的表面积为_______________ ）16．如图是一个正方体的表面展开图，若正方体中相对的面上的数互为相反数，则2x）y的值为_________）三、解答题17．在一个长方形中，长和宽分别为4cm）3cm，若该长方形绕着它的一边旋转一周，则形成的几何体的体积是多少？（结果用π表示）18.如图所示是长方体的平面展开图，设AB=x，若AD=4x）AN=3x））1）求长方形DEFG的周长与长方形ABMN的周长（用字母x进行表示）；）2）若长方形DEFG的周长比长方形ABMN的周长少8，求x的值；）3）在第（2）问的条件下，求原长方体的容积．19．如图是一个三棱柱，观察这个三棱柱，请回答下列问题：）1）这个三棱柱共有多少个面？）2）这个三棱柱一共有多少条棱？）3）这个三棱柱共有多少顶点？）4）通过对棱柱的观察，请你说出n棱柱的面数、顶点数及棱的条数．20．学习了“展开与折叠”后，同学们了解了一些简单几何体的展开图，小明在家用剪刀剪一个如图（1）的长方体纸盒，但不小心多剪开了一条棱，得到图（2）中的纸片①和②，请解答下列问题：（1）小明共剪开条棱；（2）现在小明想将剪断的纸片②拼接到纸片①上，构成该长方体纸盒的展开图，请你在①中画出纸片②的一种位置；（3）请从A，B两题中任选一题作答．A．若长方体纸盒的长，宽，高分别为m，m，n（单位：cm，m＞n），求（2）中展开图的周长．B．若长方体纸盒的长，宽，高分别是a，b，c（单位：cm，a＞b＞c），如图（3），画出它的展开图中周长最大时的展开图，并求出周长（用含a，b，c的式子表示）21．用5个相同的正方体搭出如图所示的组合体．(1)分别画出从正面、左面、上面看这个组合体时看到的图形；(2)如果在这个组合体中，再添加一个相同的正方体组成一个新组合体，从正面、左面看这个新组合体时，看到的图形与原来相同．你认为这个设想能实现吗？若能，画出添加正方体后，从上面看这个组合体时看到的图形；若不能，说明理由．参考答案1．D 2．D 3．D 4．C 5．B 6．B 7．A 8．D 9．C 10．B 11．3 12．160°13．）1））2））6））3））4））5））2））3））5））1））4））6）14．7 12 715．48cm 94cm216．-317．形成的几何体的体积是36πcm3或48πcm3）18．）1）6x,8x））2）x=4））3）384）【详解】（1）∵AB=x，若AD=4x，AN=3x，∴长方形DEFG的周长为2（x+2x）=6x，长方形ABMN的周长为2（x+3x）=8x；（2）依题意，8x-6x=8，解得：x=4；（3）原长方体的容积为x•2x•3x=6x3，将x=4代入，可得容积6x3=384．19．）1）5））2）9；（3）6；（4）（n+2）、2n，3n）【解析】分析：观察棱柱得出规律，求解即可.详解：（1）这个三棱柱共有5个面；（2）这个三棱柱一共有9条棱；（3）这个三棱柱共有6顶点（4）n棱柱的面数（n+2）、顶点数是2n，棱的条数是3n．20．（1）8（2）四种情况（3）.A、①③的周长为6m+8n；②④的周长为8m+6n;B 、画图见解析，周长为2c+4b+8a.【解析】试题分析：（1）根据平面图形得出剪开棱的条数；（2）根据长方体的展开图的情况可知有四种情况；（3）A、观察（2）中的展开图分别进行计算即可得；B、展开平面图求周长的公式与展开的方式无关所以无论怎么展开我们通过实践都可以得出以下结论：假设长，宽，高分别为x，y，z(x，y，为任意值)周长c＝2x＋4y＋8z，这个平面图的周长最大也就是当x最小，z最大.即c＝2c＋4b＋8a，这个平面图的周长最小也就是当x最大，z最小.即c＝2a＋4b＋8c.试题解析：（1）小明共剪了8条棱，故答案为：8；（2）如图，四种情况．，，；（3）A、①、③的周长为6m+8n；②、④的周长为8m+6n；B、展开图如图所示，周长为：2c＋4b＋8a.21．）1）见解析；（2）能实现）添加正方体后从上面看到的图形见解析.【解析】试题分析：（1）由已知条件可知，主视图有3列，每列小正方数形数目分别为2，1，1；左视图有2列，每列小正方形数目分别为2，1；俯视图有3列，每列小正方形数目分别为2，1，1．据此可画出图形．（2）根据再添加一个小正方体，使得它的主视图和左视图不变，则可以在从左起第一行第2列或第3列添加一个立方体即可得出答案．试题解析：(1)画出的图形如图①所示．(2)能实现．添加正方体后从上面看到的图形如图②所示，有两种情况．。

人教版七年级上册 4.1 几何图形同步练习(带答案)

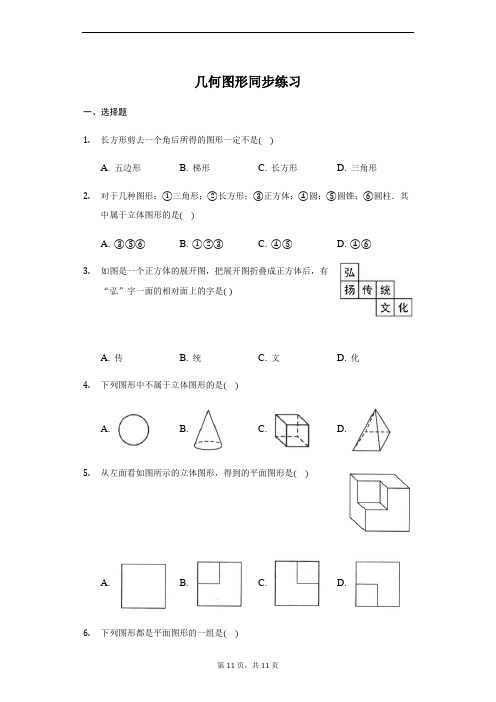
几何图形同步练习一、选择题1.长方形剪去一个角后所得的图形一定不是()A. 五边形B. 梯形C. 长方形D. 三角形2.对于几种图形：①三角形；②长方形；③正方体；④圆；⑤圆锥；⑥圆柱．其中属于立体图形的是()A. ③⑤⑥B. ①②③C. ④⑤D. ④⑥3.如图是一个正方体的展开图，把展开图折叠成正方体后，有“弘”字一面的相对面上的字是()A. 传B. 统C. 文D. 化4.下列图形中不属于立体图形的是()A. B. C. D.5.从左面看如图所示的立体图形，得到的平面图形是()A. B. C. D.6.下列图形都是平面图形的一组是()A. 三角形、正方形，球、圆锥B. 点、线、面，体C. 角、线段，平行四边形、圆D. 点、等腰三角形，射线、圆柱7.如下图所示的立体图形，从正面看得到的平面图形是()A. B.C. D.8.如图，将长方形ABCD绕CD边旋转一周，得到的几何体是()A. 棱柱B. 圆锥C. 圆柱D. 棱锥9.如图是交通禁止驶入标志，组成这个标志的几何图形有()A. 圆、长方形B. 圆、直线C. 球、长方形D. 球、线段10.在一个不透明的布袋中，装有一个简单几何体模型，甲乙两人在摸后各说出了它的一个特征，甲：它有曲面；乙：它有顶点．该几何体模型可能是()A. 球B. 三棱锥C. 圆锥D. 圆柱11.下列几何体中，含有曲面的有()A. 1个B. 2个C. 3个D. 4个12.如图，一个立方体的六个面上标着连续的正整数，若相对两个面上所标之数的和相等，则这六个数的和为()A. 75B. 76C. 78D. 81二、填空题13.在如图所示的图形中，柱体有________，锥体有________，球体有________．①②③④⑤⑥⑦⑧14.如图，小明一家四口人坐在桌子周围，桌上正中央有一把水壶，请从选项中选择他们分别看到的是水壶的哪个面：小明，爸爸，妈妈，妹妹.(填字母代号)15.如图的几何体由个曲面和个平面组成，面与面相交成的线中有条是直线，条是曲线，有个顶点．16.已知棱柱共有12个面，则该棱柱共有______个顶点，共有______条棱．17.将一根长4米的圆柱体木料锯成2段(2段都是圆柱体)，表面积增加60平方分米，这根木料的体积是______立方分米．三、解答题18.分别指出下图中的几何图形可看作由哪些简单的图形组成?机器猫邮封会笑的人19.图形世界是多姿多彩的，请写出几个常见的几何图形(不少于5种)．20.如图四个几何体分别是三棱柱，四棱柱，五棱柱和六棱柱，三棱柱有5个面，9条棱，6个顶点，观察图形，填写下面的空．(1)四棱柱有______个面，______条棱，______个顶点；(2)六棱柱有______个面，______条棱，______个顶点；(3)由此猜想n棱柱有______个面，______条棱，______个顶点．21.将一个长方形绕它的一边所在的直线旋转一周，得到的几何体是圆柱，现在有一个长为4cm，宽为3cm的长方形，分别绕它的长、宽所在直线旋转一周，得到不同的圆柱体，它们的表面积分别是多大？(结果保留π)22.如图所示，木工师傅把一个长为1.6米的长方体木料锯成3段后，表面积比原来增加了80cm2，那么这根木料本来的体积是多少？答案和解析1.【答案】C【解答】解：当截线为经过正方形对角2个顶点的直线时，剩余图形为三角形(如图1)；当截线如图2所示，剩余图形是梯形(如图2)；当截线为只经过正方形一组邻边的一条直线时，剩余图形是五边形(如图3)．故不可能是长方形．故选C．2.【答案】A【解析】解：①②④属于平面图形，③⑤⑥属于立体图形．3.【答案】C【解答】解：这是一个正方体的平面展开图，共有六个面，其中面“扬”与面“统”相对，面“弘”与面“文”相对，面“传”与面“化”相对．故选C．4.【答案】A【解答】解：A.圆属于平面图形，故A符合题意；B.圆锥属于立体图形，故B不符合题意；C.属于立体图形，故C不符合题意；D.属于立体图形，故D不符合题意，故选A．5.【答案】C【解答】解：缺少的部分从正面看，在立体图形的左上角，从左面看应在立体图形的右上角．故选C．6.【答案】C【解答】解：A.球和圆锥不是平面图形，故不符合题意；B.“体”不属于平面图形，故不符合题意；C.都属于平面图形，故符合题意；D.圆柱不属于平面图形，故不符合题意．故选C．7.【答案】D【解答】解：根据几何体的特征，从正面看到的平面图形应是D选项图形．故选D．8.【答案】C【解答】解：将长方形ABCD绕CD边旋转一周，得到的几何体是圆柱．故选C．9.【答案】A【解答】解：根据图形可得组成这个标志的几何图形有长方形、圆．故选A．10.【答案】C【解答】解：A、球有曲面，但是没有顶点，故这个选项不符合题意；B、三棱锥有顶点，但是没有曲面，故这个选项不符合题意；C、圆锥既有曲面，又有顶点，故这个选项符合题意；D、圆柱有曲面，但是没有顶点，故这个选项不符合题意．故选：C．11.【答案】B【解答】解：含有曲面的有球，圆柱，共2个，故选：B．12.【答案】A【解析】解：∵六个面上标着连续的正整数，∴六个数可能是10，11，12，13，14，15或9，10，11，12，13，14，若六个数为9，10，11，12，13，14，则10与13处于相对面，与实际图形不符；若六个数为10，11，12，13，14，15，则符合题意，这六个数的和为3×(10+15)=75，故选：A．依据六个面上标着连续的正整数，即可得到六个数可能是10，11，12，13，14，15或9，10，11，12，13，14，再根据实际图形，即可得到六个数为10，11，12，13，14，15，进而得出这六个数的和．本题主要考查了正方体相对两个面上的文字，从实物出发，结合具体的问题，辨析几何体的展开图，通过结合立体图形与平面图形的转化，建立空间观念，是解决此类问题的关键．13.【答案】①②③⑦；⑤⑥；④【解答】解：①②③⑦是柱体；⑤⑥是锥体；④是球体．故答案为①②③⑦；⑤⑥；④．14.【答案】D；B；C；A【解答】解：小明从左看物体，得到的平面图形是D；爸爸从后面看物体，得到的平面图形是B；妈妈从右面看物体，得到的平面图形是C；妹妹从正面看物体，得到的平面图形是A．故答案为D；B；C；A．15.【答案】1；4；7；2；6【解答】解：根据图形可得：如图的几何体由1个曲面和4个平面组成，面与面相交成的线中有7条是直线2条是曲线，有6个顶点．16.【答案】20 30【解析】解：∵棱柱共有12个面，∴此棱柱为10棱柱，故则该棱柱共有20个顶点，共有30条棱．17.【答案】1200【解答】解：4米=40分米，60÷2=30(平方分米)，30×40=1200(立方分米)，所以这根木料的体积是1200立方分米．故答案为：1200．18.【答案】解：机器猫由两个三角形、两个圆、两条线段组成；邮封由一个长方形、两个三角形、两个圆组成；会笑的人由两个圆、两个三角形、两条线段组成．19.【答案】解：如：三角形、四边形、球、圆柱、圆锥、圆等．【解析】本题考查了认识常见的平面图形和立体图形，熟悉生活中常见的平面图形和立体图形是解题的关键，本题属于结论开放型问题，答案不唯一，常见的几何图形如：三角形、四边形、球、圆柱、圆锥、圆等．20.【答案】(1)6；12；8；(2)8；18；12；(3)(n+2)；3n；2n【解答】解：(1)四棱柱有6个面，12条棱，8个顶点；(2)六棱柱有8个面，18条棱，12个顶点；(3)由此猜想n棱柱有(n+2)个面，3n条棱，2n个顶点．故答案为：(1)6，12，8；(2)8，18，12；(3)(n+2)，3n，2n．21.【答案】解：情况①：π×3×2×4+π×32×2=24π+18π=42π(cm2)；情况②：π×4×2×3+π×42×2=24π+32π=56π(cm2).答：它们的表面积分别是42πcm2或56πcm2．22.【答案】解：∵把长方体木料锯成3段后，其表面积增加了四个截面，因此每个截面的面积为20cm2，∴这根木料本来的体积是：1.6×100×20=3200(cm3)第11页，共11页。

人教版七年级上册4.1 几何图形同步测试(有答案)

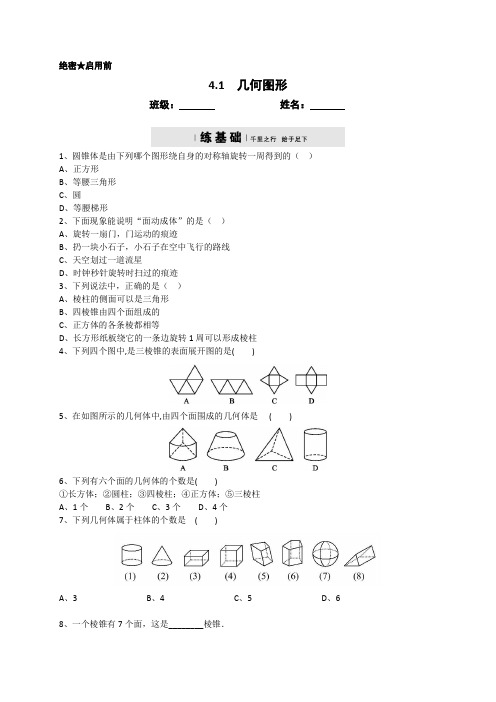
绝密★启用前4.1 几何图形班级：姓名：1、圆锥体是由下列哪个图形绕自身的对称轴旋转一周得到的（）A、正方形B、等腰三角形C、圆D、等腰梯形2、下面现象能说明“面动成体”的是（）A、旋转一扇门，门运动的痕迹B、扔一块小石子，小石子在空中飞行的路线C、天空划过一道流星D、时钟秒针旋转时扫过的痕迹3、下列说法中，正确的是（）A、棱柱的侧面可以是三角形B、四棱锥由四个面组成的C、正方体的各条棱都相等D、长方形纸板绕它的一条边旋转1周可以形成棱柱4、下列四个图中,是三棱锥的表面展开图的是()5、在如图所示的几何体中,由四个面围成的几何体是()6、下列有六个面的几何体的个数是()①长方体；②圆柱；③四棱柱；④正方体；⑤三棱柱A、1个B、2个C、3个D、4个7、下列几何体属于柱体的个数是()A、3B、4C、5D、68、一个棱锥有7个面，这是________棱锥．9、如果一个棱柱共有15条棱，那么它的底面一定是________边形．10、长方体是一个立体图形，它有________个面，________条棱，________个顶点．11、六棱柱有________个顶点，________个面，________条棱．12、如图,5×5方格中,已有5个阴影小正方形,请再选取一个小正方形,使所选的小正方形和阴影部分组合后能折叠成一个正方体.把所有可能的选择都标记出来,直接在图中把所选的小正方形标上序号①②③….13、将如图所示的图形剪去一个小正方形,使余下的部分恰好能折成一个正方体,下列编号为1,2,3,6的小正方形中不能剪去的是(填编号).1、将右面正方体的平面展开图重新折成正方体后,“共”字对面的字是()A.阖B.家C.幸D.福2、骰子是一种特殊的数字立方体(如图),它符合规则:相对两面的点数之和总是7,下面四幅图中可以折成符合规则的骰子的是()3、下列图形中,属于立体图形的是( )4、下列图形中,不可以作为一个正方体的展开图的是( )5、如图是一个正方体的表面展开图,则原正方体中与“你”字所在面相对的面上标的字是( )A、遇B、见C、未D、来6、如图，从一个多边形的某一条边上的一点（不与端点重合）出发，分别连接这个点与其他所有顶点，可以把这个多边形分割成若干个三角形，由三角形、四边形、五边形为例，你能总结出什么规律？n边形呢？7、已知长方形的长为4cm．宽为3cm，将其绕它的一边所在的直线旋转一周，得到一个几何体，(1)求此几何体的体积；(2)求此几何体的表面积．（结果保留π）1、（2019·山西）某正方体的每个面上都有一个汉字，如图是它的的一个展开图，那么在原正方体中，与“点”字所在的面相对的面上的汉字是（）2、（2019·四川）如图是由一些小立方体与圆锥组合成的立体图形，它的主视图是（）3、（2019·贵州）由下面正方体的平面展开图可知，原正方体“中”字所在面的对面的汉字是（）4、（2019·江苏）一个几何体的侧面展开图如图所示，则该几何体的地面是（）参考答案1-7、BACBCCD8、六9、五10、6；12；811、12；8；1812、如图所示.13、31-5、CCCCD6、解：由图中可以看出三角形被分为2个三角形；四边形被分为3个三角形，五边形被分为4个三角形，那么n边形被分为（n﹣1）个三角形．7、（1）解：长方形绕一边旋转一周，得圆柱．情况①：π×32×4=36π（cm3）；情况②：π×42×3=48π（cm3）（2）解：情况①：π×3×2×4+π×32×2=24π+18π=42π（cm2）；情况②：π×4×2×3+π×42×2=24π+32π=56π（cm2）．1-4、BCBB。

人教版七年级数学上册同步练习4.1.1 几何图形(含答案)-精品.doc

第四章图形认识初步
4.1.1 几何图形
基础检测 1.把下列几何图形与对应的名称用线连起来.
圆柱圆锥正方体长方体棱柱球
2.分别画
出下列平面图形: 长方形正方形三角形圆
3.从上向下看图(1),应是如图(2)中所示的( )
C D
B A
(2)
4.如图,是一个正方体盒子(6个面)的侧面展开图的一部分,请将它补充完整.
5.如图(1),一本书上放着一个粉笔盒,指出图(2)中的三个平面图形各是从哪个方向看图(1)所看到的.
( )( )
( )1()(2)
6.如图,四种图形各是哪种立体图形的表面展开所形成的画出相应的四种立体图形.
拓展提高
7.如图,四个图形分别是四个公司的标志,请用线将它们联系起来:
中国联合通信有限公司
摩托罗拉(中国)电子有限公司
方正数码有限公司
w w w .x k b 1.c o m
中国电信集团公司
8.如图,上面是一些具体的物体,下面是一些立体图形,试找出与下面立体图形相类似的实物(用线连接).
9.你能只用一笔画出下列图形吗
4.1.1 几何图形答案:
3.D
5.从左面,从上向下,从正面.。

人教版数学七年级上同步训练：4.1《几何图形》(1)【含答案】

七年级数学（人教版上）同步练习第四章第一节几何图形（一）【典型例题】例 1：填空：（ 1）长方体、正方体都有个面，长方体的 6 个面可能都是形，也有可能都有 2 个面是形，它的面达成同样。

答： 6 个面，长方形，正方形，对（ 2）正方体的 6 个面都是形，6个面的面积是。

答：正方形，相等（ 3）圆柱的上、下底面是；（4）圆锥的底面是答：圆，圆例 2：填空：（ 1）三棱柱的上、下底面是；侧面是。

答：三角形，四边形（ 2）四棱柱的上、下底面是；侧面是。

答：四边形四边形例 3：一个三棱柱的底面边长为acm，侧棱长为bcm。

（ 1）这个三棱柱共有几个面?它们分别是什么形状?哪些面的形状、面积完整同样? （ 2）这个三棱柱共有多少条棱，它们的长度分别是多少？答：（ 1） 5 个面，此中 3 个侧面是长方形，两个底面是三角形，两个底面形状完整相同，三个侧面形状完整同样。

（ 2）共有 9 条棱，此中侧棱长均为bcm，底面棱长均为acm．例 4：图中的两个图形经过折叠可否围成棱柱?先想想，再试一试。

答：都能够，第一个能够围成六棱柱；第二个能够围成三棱柱例 5：将一个正方体的表面沿某些棱剪开，展成一个平面图形，把你睁开后的不一样平面图形都画出来，看看有几种。

答：1）2）3）例 6：两位同学用图形画出的小动物中，哪个图形是用立体图形构成的？用了哪些立体图形？哪个图形是用平面图形构成的？用了哪些平面图形？答：第一个图形是由圆柱体、长方体、球体、正方体构成；第二个图形是由三角形、长方形、五边形、六边形、圆构成。

【模拟试题】（答题时间： 40 分钟）1. 判断正误（ 1）圆柱的上下两个面同样大（）（ 2）圆柱、圆锥的底面都是圆（）（ 3）棱柱的底面是四边形（）（ 4）棱锥的侧面都是三角形（）（ 5）棱柱的侧面可能是三角形（）（ 6）圆柱的侧面是长方形（）（ 7）球体不是多面体（）（ 8）圆锥是多面体（）（ 9）棱柱、棱锥都是多面体（）（ 10）柱体都是多面体（）2.一个四棱柱被一刀切去一部分，试举例说明剩下的部分能否可能仍是四棱柱。

人教版数学七年级上册第4章4.1几何图形同步练习(解析版)

人教版数学七年级上册第4章 4.1几何图形同步练习一、单选题（共10题；共20分）1、一个几何体的边面全部展开后铺在平面上，不可能是（）A、一个三角形B、一个圆C、三个正方形D、一个小圆和半个大圆2、下列图形中，是棱锥展开图的是（）A、B、C、D、3、下列图形是四棱柱的侧面展开图的是（）A、B、C、D、4、将选项中的四个正方体分别展开后，所得的平面展开图与如图不同的是（）A、B、C、D、5、如图是一个正方体的表面展开图，这个正方体可能是（）A、B、C、D、6、一个几何体的展开图如图所示，这个几何体是（）A、棱柱B、棱锥C、圆锥D、圆柱7、将一个正方体的表面沿某些棱剪开，展成一个平面图形，至少要剪开（）条棱．A、3B、5C、7D、98、在下面的图形中，不可能是正方体的表面展开图的是（）A、B、C、D、9、如图所示的正方体，如果把它展开，可以得到（）A、B、C、D、10、下列四个图形中是如图展形图的立体图的是（）A、B、C、D、二、填空题（共3题；共4分）11、一个棱锥的棱数是24，则这个棱锥的面数是________．12、如图中的几何体有________个面，面面相交成________线．13、如图是棱长为2cm的正方体，过相邻三条棱的中点截取一个小正方体，则剩下部分的表面积为________cm2．三、计算题（共4题；共20分）14、一个长方形的两边分别是2cm、3cm，若将这个长方形绕一边所在直线旋转一周后是一个什么几何体？请求出这个几何体的底面积和侧面积．15、已知有一个长为5cm，宽为3cm的长方形，若以这个长方形的一边所在的直线为轴，将它旋转一周，你能求出所得的几何体的表面积吗？16、有一个长方形绕它的一边所在的直线旋转一周，得到的几何体是圆柱．现在有一个长为6cm，宽为5cm的长方形，分别绕它的长、宽所在直线旋转一周，得到不同的圆柱，它们的体积分别是多大？17、我们知道，将一个长方形绕它的一边旋转一周得到的几何体是圆柱，现有一个长是5cm，宽是3cm的长方形，分别绕它的长和宽所在的直线旋转一周，得到不同的圆柱几何体，分别求出它们的体积．四、解答题（共3题；共15分）18、请你用式子表示如图所示的长方体形无盖纸盒的容积（纸盒厚度忽略不计）和表面积．这些式子是整式吗？如果是，请你分别指出它们是单项式，还是多项式．19、将一个长方形绕它的一边所在的直线旋转一周，得到的几何体是圆柱，现在有一个长为4厘米，宽为3厘米的长方形，分别绕它的长、宽所在的直线旋转一周，得到不同的圆柱体，它们的体积分别是多大？20、如图所示为一个正方体截去两个角后的立体图形，如果照这样截取正方体的八个角，则新的几何体的棱有多少条？请说明你的理由．答案解析部分一、单选题1、【答案】B【考点】几何体的展开图【解析】【解答】解：正四面体展开是个3角形；顶角为90度，底角为45度的两个正三棱锥对起来的那个6面体展开可以是3个正方形；一个圆锥展开可以是一个小圆+半个大圆．故选B．【分析】由平面图形的折叠及立体图形的表面展开图的特点解题．2、【答案】C【考点】几何体的展开图【解析】【解答】解：A、是三棱柱的展开图，故此选项错误；B、是一个平面图形，故此选项错误；C、是棱锥的展开图，故此选项正确；D、是圆柱的展开图，故此选项错误．故选：C．【分析】根据图形结合所学的几何体的形状得出即可．3、【答案】A【考点】几何体的展开图【解析】【解答】解：由分析知：四棱柱的侧面展开图是四个矩形组成的图形．故选：A．【分析】根据四棱柱的侧面展开图是矩形图进行解答即可．4、【答案】B【考点】几何体的展开图【解析】【解答】解：观察图形可知，将选项中的四个正方体分别展开后，所得的平面展开图与如图不同的选项B．故选：B．【分析】立体图形的侧面展开图，体现了平面图形与立体图形的联系．立体图形问题可以转化为平面图形问题解决．5、【答案】B【考点】几何体的展开图【解析】【解答】解：由题意，得四个小正方形组合成一个正方体的面，是阴影，是空白，故选：B．【分析】根据展开图折叠成几何体，四个小正方形组合成一个正方体的面，可得答案．6、【答案】B【考点】几何体的展开图【解析】【解答】解：圆锥的侧面展开图是扇形，底面是圆，故选：B．【分析】根据圆锥的展开图，可得答案．7、【答案】C【考点】几何体的展开图【解析】【解答】解：∵正方体有6个表面，12条棱，要展成一个平面图形必须5条棱连接，∴至少要剪开12﹣5=7条棱，故选：C．【分析】根据正方体的棱的条数以及展开后平面之间应有棱连着，即可得出答案．8、【答案】B【考点】几何体的展开图【解析】【解答】解：由四棱柱四个侧面和上下两个底面的特征可知，A，C，D选项可以拼成一个正方体，而B选项，上底面不可能有两个，故不是正方体的展开图．故选：B．【分析】由平面图形的折叠及正方体的展开图解题．9、【答案】D【考点】几何体的展开图【解析】【解答】解：如图所示的正方体，如果把它展开，可以得到．故选：D．【分析】根据题干，3个黑色图形经过1个顶点，由此可以判断选项D是这个正方体的展开图．10、【答案】A【考点】几何体的展开图【解析】【解答】解：因为含小黑正方形的面不能与含大黑正方形的面相邻，两个小黑正方形不能在同一行，所以B，C不是左边展形图的立体图；两个小黑正方形在大黑正方形的对面”，那么A图中，正好是大黑正方形在上面，那么小黑正方形就在底面，A符合；故选：A．【分析】因为含小黑正方形的面不能与含大黑正方形的面相邻，两个小黑正方形不能在同一行，据此判断．二、填空题11、【答案】13【考点】认识立体图形【解析】【解答】解：由题意，得侧棱=底棱=12，棱锥是十二棱锥，十二棱锥有十二个侧面，一个底面，故答案为：13．【分析】根据棱锥的侧棱与底棱相等，可得棱锥，根据棱锥的特征，可得答案．12、【答案】3；曲【考点】认识立体图形【解析】【解答】解：图中的几何体叫做圆台，它是由3个面围成的，面与面相交所成的线是曲线．故答案为：3, 曲．【分析】由圆台的概念和特征即可解．图中的几何体叫做圆台，它是由3个面围成的，面与面相交所成的线是曲线．13、【答案】24【考点】几何体的表面积，截一个几何体【解析】【解答】解：过相邻三条棱的中点截取一个小正方体，则剩下部分的表面积为2×2×6=24cm2．故答案为：24．【分析】由于是在正方体的顶点上截取一个小正方体，去掉小正方形的三个面的面积，同时又多出小正方形的三个面的面积，表面积没变，由此求得答案即可．三、计算题14、【答案】解：这个长方形绕一边所在直线旋转一周后是圆柱．当2cm是底面半径时，圆柱的底面积是πr2=22π=4π（cm2），圆柱的侧面积是2πrh=2π×2×3=12π（cm2）；当3cm是底面半径时，圆柱的底面积是πr2=32π=9π（cm2），圆柱的侧面积是2πrh=2π×3×2=12π（cm2）．【考点】点、线、面、体，有理数的乘法【解析】【分析】根据长方形绕一边旋转一周，可得圆柱．分类讨论：2cm是底面半径，3cm是底面半径，根据圆的面积公式，可得圆柱的底面积，根据圆柱的侧面积公式，可得答案．15、【答案】几何体的表面积为48πcm2或80πcm2．【考点】认识立体图形，点、线、面、体，几何体的表面积【解析】【解答】当以5cm的边为轴旋转一周时，圆柱的表面积=2×π×32+2π×3×5=18π+30π=48πcm2；当以3cm的边为轴旋转一周时，圆柱的表面积=2×π×52+2π×5×3=50π+30π=80πcm2．所以答案为：几何体的表面积为48πcm2或80πcm2．【分析】以5cm的边为轴旋转一周得到的是一个底面半径为3cm，高为5cm的圆柱；以3cm边为轴旋转一周得到的是一个底面半径为5cm，高为3cm的圆柱．16、【答案】解：绕长所在的直线旋转一周得到圆柱体积为：π×52×6=150π（cm3）；绕宽所在的直线旋转一周得到圆柱体积为：π×62×5=180π（cm3）．答：它们的体积分别是150π（cm3）和180π（cm3）．【考点】点、线、面、体，有理数的乘方【解析】【分析】根据圆柱体的体积=底面积×高求解，注意底面半径和高互换得圆柱体的两种情况．17、【答案】【解答】解：分两种情况：①绕长所在的直线旋转一周得到圆柱体积为：π×32×5=45π（cm3）；②绕宽所在的直线旋转一周得到圆柱体积为：π×52×3=75π（cm3）．故它们的体积分别为45πcm3或75πcm3．【考点】点、线、面、体【解析】【分析】根据圆柱体的体积=底面积×高求解，注意底面半径和高互换得圆柱体的两种情况．四、解答题18、【答案】解：根据题意得：长方体的体积为abc；表面积为ab+2（ac+bc），体积结果为单项式；表面积结果为多项式【考点】单项式，多项式，几何体的表面积【解析】【分析】根据长方体的体积=长×宽×高，表面积等于2（长×宽+长×高+宽×高），列出关系式即可做出判断．19、【答案】解：绕长所在的直线旋转一周得到圆柱体积为：π×32×4=36πcm3．绕宽所在的直线旋转一周得到圆柱体积：π×42×3=48πcm3【考点】点、线、面、体【解析】【分析】圆柱体的体积=底面积×高，注意底面半径和高互换得圆柱体的两种情况．20、【答案】解：∵一个正方体有12条棱，一个角上裁出3条棱，即8个角共3×8条棱，∴12+3×8=36条．故新的几何体的棱有36条【考点】截一个几何体【解析】【分析】一个正方体有12条棱，一个角上裁出3条棱，即8个角共3×8条棱，相加即可．。

人教版初中数学七年级上册《4.1 几何图形》同步练习卷

人教新版七年级上学期《4.1 几何图形》同步练习卷一．填空题（共32小题）1．已知圆柱的底面积为60cm2，高为4cm，则这个圆柱体积为cm3．2．马小虎准备制作一个封闭的正方体盒子，他先用5个大小一样的正方形制成如图所示的拼接图形（实线部分），经折叠后发现还少一个面，请你在图中的拼接图形上再接一个正方形，使新拼接成的图形经过折叠后能成为一个封闭的正方体盒子（添加所有符合要求的正方形，添加的正方形用阴影表示）．3．如果圆柱的侧面展开图是相邻两边长分别为6，16π的长方形，那么这个圆柱的体积等于．4．如图所示，1条直线将平面分成2个部分，2条直线最多可将平面分成4个部分，3条直线最多可将平面分成7个部分，4条直线最多可将平面分成11个部分．现有n条直线最多可将平面分成56个部分，则n的值为．5．用一个平面去截一个几何体，截面形状为三角形，则这个几何体可能为：①正方体；②圆柱；③圆锥；④正三棱柱（写出所有正确结果的序号）．6．如图，将一张边长为6cm的正方形纸片按虚线裁剪后，恰好围成底面是正六边形的棱柱，则这个六棱柱的侧面积为cm2．7．如图，在一次数学活动课上，张明用17个边长为1的小正方体搭成了一个几何体，然后他请王亮用其他同样的小正方体在旁边再搭一个几何体，使王亮所搭几何体恰好可以和张明所搭几何体拼成一个无缝隙的大长方体（不改变张明所搭几何体的形状），那么王亮至少还需要个小立方体，王亮所搭几何体的表面积为．8．一个圆柱的底面直径为6cm，高为10cm，则这个圆柱的侧面积是cm2（结果保留π）．9．在右边的展开图中，分别填上数字1，2，3，4，5，6，使得折叠成正方体后，相对面上的数字之和相等，则a＝，b＝，c＝．10．以下三组图形都是由四个等边三角形组成．能折成多面体的选项序号是．11．从棱长为2的正方体毛坯的一角，挖去一个棱长为1的小正方体，得到一个如图所示的零件，则这个零件的表面积为．12．如图，立方体的六个面上标着连续的整数，若相对的两个面上所标之数的和相等．则这六个数的和为．13．一个矩形绕着它的一边旋转一周，所得到的立体图形是．14．若将棱长为2的正方体切成8个棱长为1的小正方体，则所有小正方体表面积的和是原正方体表面积的倍；若将棱长为3的正方体切成27个棱长为1的小正方体，则所有小正方体表面积的和是原正方体表面积的倍；若将棱长为n（n＞1，n为整数）的正方体切成n3个棱长为1的小正方体，则所有小正方体表面积的和是原正方体表面积的倍．15．观察下列图形的排列规律（其中△是三角形，□是正方形，〇是圆），〇△□□〇△□〇△□□〇△□……若第一个图形是圆，则第2008个图形是（填图形名称）．16．立方体木块的六个面分别标有数字1、2、3、4、5、6，如图，是从不同方向观察这个立方体木块看到的数字情况，数字1和5对面的数字的和是．17．用一张面积为36π2cm2的正方形纸片围成圆柱的侧面积，则圆柱的底面半径＝cm．18．如图，正方体（图1）的展开图如图2所示，在图1中M、N分别是FG、GH的中点，CM、CN、MN是三条线段；请在图2中画出CM、CN、MN这三条线段．19．将一个棱长为8、各个面上均涂有颜色的正方体，锯成64个同样大小的小正方体，其中所有恰有2面涂有颜色的小正方体表面积之和为．20．观察下列A，B，C三个图形，从A到B，从B到C的变化都具有某种规律，按照这种规律填出D图21．如图是一个正方体的展开图，标注了字母a的面是正方体的正面．如果正方体相对两个面上的式子的值相等，求（y﹣x）2015的值．22．建设节约型社会就是使每一位公民养成节约意识，形成人人节约的良好习惯．节约与否不仅是个生活习惯、生活小节问题，更是个思想道德境界的问题．我们拥有的一切物质财富，无一不是劳动的结晶，每一滴水，每一度电，每一张纸，都凝结着劳动者的心血与汗水，所以，我们应该节约．假如你送给好朋友们的一个棱长为1的正方体礼物，需要用一张正方形彩纸包装，若不把纸撕开，那么所需纸的最小边长为．23．填空：（1）在圆周上有7个点A，B，C，D，E，F和G，连接每两个点的线段共可作出条．（2）已知5条线段的长分别是3，5，7，9，11，若每次以其中3条线段为边组成三角形，则最多可构成互不全等的三角形个．（3）三角形的三边长都是正整数，其中有一边长为4，但它不是最短边，这样不同的三角形共有个．（4）以正七边形的7个顶点中的任意3个为顶点的三角形中，锐角三角形的个数是．（5）平面上10条直线最多能把平面分成个部分．（6）平面上10个圆最多能把平面分成个区域．24．如图，这是一个由三个大小不同的正方体所组成的装饰物，现在要对它的表面涂油漆、假设三个正方体的边长分别为a，b，c，其中a＜b＜c．那么该装饰物涂漆面积最少（当该装饰物水平放置在桌面上的时候，不能从外观上看见装饰物的任何裸露）是．25．如图，MN是圆柱底面的直径，NO是圆柱的高，在圆柱的侧面上，过点M，P．有一条绕了四周的路径最短的金属丝，现将圆柱侧面沿NO剪开，所得的侧面展开图可以是：（填序号）．26．用一个平面去截一个长方体，裁面是一个多边形，这个多边形的边数最多有条．27．一个正方体物体，被切一刀后，它的切面不可能是（写出所有的答案）28．在二行三列的方格棋盘上沿骰子的某条棱翻动骰子（相对面上分别标有1点和6点，2点和5点，3点和4点），在每一种翻动方式中，骰子不能后退．开始时骰子如图（1）那样摆放，朝上的点数是2；最后翻动到如图（2）所示的位置，此时骰子朝上的点数不可能的数是．29．如图，是正方形的表面展形图，如果相对两个面数字之和相等，且A+B+C＝14，则6A ﹣2B+3C＝．30．有一个正方体，A，B，C的对面分别是x，y，z三个字母，如图所示，将这个正方体从现有位置依此翻到第1，2，…，12格，这时顶上的字母是．31．很多同学都知道空间多面体有一个欧拉公式：顶点数+面数﹣棱数＝2，如长方体有8个顶点、6个面与12条棱，满足8+6﹣12＝2．现在请你观察如下的平面图形，图1是一个三角形，它将整个平面分成了内部与外部两个区域；图2是由平面上5个点组成的两个不重叠的三角形，任意3点都不在一条直线上；图3是由平面上7个点组成的3个互不重叠的三角形，任意3点都不在一条直线上．我们还可以画出由平面上更多的点组成的具有相同特征的三角形组合图形，试猜想它们的点数a、边数b与区域数c满足的一个等式是．32．如图，AB平行MN平行FG平行DC，AD平行CE，BC平行DE，则图中三角形的个数比梯形的个数少个．人教新版七年级上学期《4.1 几何图形》2019年同步练习卷参考答案与试题解析一．填空题（共32小题）1．已知圆柱的底面积为60cm2，高为4cm，则这个圆柱体积为240cm3．【分析】根据圆柱体积＝底面积×高，即可求出结论．【解答】解：V＝S•h＝60×4＝240（cm3）．故答案为：240．【点评】本题考查了认识立体图形，牢记圆柱的体积公式是解题的关键．2．马小虎准备制作一个封闭的正方体盒子，他先用5个大小一样的正方形制成如图所示的拼接图形（实线部分），经折叠后发现还少一个面，请你在图中的拼接图形上再接一个正方形，使新拼接成的图形经过折叠后能成为一个封闭的正方体盒子（添加所有符合要求的正方形，添加的正方形用阴影表示）．【分析】由平面图形的折叠及正方体的展开图解题．【解答】解：，故答案为：．【点评】本题通过考查正方体的侧面展开图，展示了这样一个教学导向，教学中要让学生确实经历活动过程，而不要将活动层次停留于记忆水平．我们有些老师在教学“展开与折叠”时，不是去引导学生动手操作，而是给出几种结论，这样教出的学生肯定遇到动手操作题型时就束手无策了．3．如果圆柱的侧面展开图是相邻两边长分别为6，16π的长方形，那么这个圆柱的体积等于144或384π．【分析】分两种情况：①底面周长为6高为16π；②底面周长为16π高为6；先根据底面周长得到底面半径，再根据圆柱的体积公式计算即可求解．【解答】解：①底面周长为6高为16π，π×（）2×16π＝π××16π＝144；②底面周长为16π高为6，π×（）2×6＝π×64×6＝384π．答：这个圆柱的体积可以是144或384π．故答案为：144或384π．【点评】本题考查了展开图折叠成几何体，本题关键是熟练掌握圆柱的体积公式，注意分类思想的运用．4．如图所示，1条直线将平面分成2个部分，2条直线最多可将平面分成4个部分，3条直线最多可将平面分成7个部分，4条直线最多可将平面分成11个部分．现有n条直线最多可将平面分成56个部分，则n的值为10．【分析】n条直线最多可将平面分成S＝1+1+2+3…+n＝n（n+1）+1，依此可得等量关系：n条直线最多可将平面分成56个部分，列出方程求解即可．【解答】解：依题意有n（n+1）+1＝56，解得n1＝﹣11（不合题意舍去），n2＝10．答：n的值为10．故答案为：10．【点评】考查了点、线、面、体，规律性问题及一元二次方程的应用；得到分成的最多平面数的规律是解决本题的难点．5．用一个平面去截一个几何体，截面形状为三角形，则这个几何体可能为：①正方体；②圆柱；③圆锥；④正三棱柱①③④（写出所有正确结果的序号）．【分析】当截面的角度和方向不同时，圆柱体的截面无论什么方向截取圆柱都不会截得三角形．【解答】解：①正方体能截出三角形；②圆柱不能截出三角形；③圆锥沿着母线截几何体可以截出三角形；④正三棱柱能截出三角形．故截面可能是三角形的有3个．故答案为：①③④．【点评】本题考查几何体的截面，截面的形状既与被截的几何体有关，还与截面的角度和方向有关．6．如图，将一张边长为6cm的正方形纸片按虚线裁剪后，恰好围成底面是正六边形的棱柱，则这个六棱柱的侧面积为36﹣12cm2．【分析】这个棱柱的侧面展开正好是一个长方形，长为6，宽为6减去两个六边形的高，再用长方形的面积公式计算即可求得答案．【解答】解：∵将一张边长为6的正方形纸片按虚线裁剪后，恰好围成一个底面是正六边形的棱柱，∴这个正六边形的底面边长为1，高为，∴侧面积为长为6，宽为6﹣2的长方形，∴面积为：6×（6﹣2）＝36﹣12．故答案为：36﹣12．【点评】此题主要考查了正方形的性质、矩形的性质以及剪纸问题的应用．此题难度不大，注意动手操作拼出图形，并能正确进行计算是解答本题的关键．7．如图，在一次数学活动课上，张明用17个边长为1的小正方体搭成了一个几何体，然后他请王亮用其他同样的小正方体在旁边再搭一个几何体，使王亮所搭几何体恰好可以和张明所搭几何体拼成一个无缝隙的大长方体（不改变张明所搭几何体的形状），那么王亮至少还需要19个小立方体，王亮所搭几何体的表面积为48．【分析】首先确定张明所搭几何体所需的正方体的个数，然后确定两人共搭建几何体所需小立方体的数量，求差即可．【解答】解：∵王亮所搭几何体恰好可以和张明所搭几何体拼成一个无缝隙的大长方体，∴该长方体需要小立方体4×32＝36个，∵张明用17个边长为1的小正方体搭成了一个几何体，∴王亮至少还需36﹣17＝19个小立方体，表面积为：2×（9+7+8）＝48，故答案为19，48．【点评】本题考查了立体图形的相关知识，能够确定两人所搭几何体的形状是解答本题的关键，难度不大．8．一个圆柱的底面直径为6cm，高为10cm，则这个圆柱的侧面积是60πcm2（结果保留π）．【分析】直接利用圆柱体侧面积公式求出即可．【解答】解：∵一个圆柱的底面直径为6cm，高为10cm，∴这个圆柱的侧面积是：πd×10＝60π（cm2）．故答案为：60π．【点评】此题主要考查了圆柱体侧面积求法，正确根据圆柱体侧面积公式是解题关键．9．在右边的展开图中，分别填上数字1，2，3，4，5，6，使得折叠成正方体后，相对面上的数字之和相等，则a＝6，b＝2，c＝4．【分析】根据正方体的展开图的特点，找到向对面，再由相对面上的数字之和相等，可得出a、b、c的值．【解答】解：1与a相对，5与b相对，3与c相对，∵1+a＝5+b＝3+c，六个面上的数字为分别1，2，3，4，5，6∴a＝6，b＝2，c＝4；故答案为：6，2，4．【点评】本题考查了正方体的展开图，注意正方体的空间图形，从相对面入手，分析及解答问题．10．以下三组图形都是由四个等边三角形组成．能折成多面体的选项序号是（1）（3）．【分析】由平面图形的折叠及三棱锥的展开图解题．【解答】解：只有图（1）、图（3）能够折叠围成一个三棱锥．故答案为：（1）（3）．【点评】本题考查了展开图折叠成几何体的知识，属于基础题型．11．从棱长为2的正方体毛坯的一角，挖去一个棱长为1的小正方体，得到一个如图所示的零件，则这个零件的表面积为24．【分析】根据几何体表面积的计算公式，从正方体毛坯一角挖去一个小正方体得到的零件的表面积等于原正方体表面积，即可得出答案．【解答】解：挖去一个棱长为1的小正方体，得到的图形与原图形表面积相等，则表面积是2×2×6＝24．故答案为：24．【点评】此题考查了几何体的表面积，本题有多种解法，一种是把每个面的面积计算出来然后相加，这样比较麻烦，另一种算法就是解答中的这种，这种方法的关键是能想象出得到的图形与原图形表面积相等．12．如图，立方体的六个面上标着连续的整数，若相对的两个面上所标之数的和相等．则这六个数的和为39．【分析】由题意“六个连续的整数”“两个相对面上的数字和相等”，则由4，5，7三个数字看出可能是2，3，4，5，6，7或3，4，5，6，7，8或4，5，6，7，8，9，因为相对面上的数字和相等，所以第一种情况必须是4，5相对，第二种情况必须是4，7相对，故这六个数字只能是4，5，6，7，8，9，再求出这六个数的和即可．【解答】解：从4，5，7三个数字看出可能是2，3，4，5，6，7或3，4，5，6，7，8或4，5，6，7，8，9，因为相对面上的数字和相等，所以第一种情况必须是4，5处于对面，第二种情况必须是4，7处于对面，故这六个数字只能是4，5，6，7，8，9，所以这六个数的和为4+5+6+7+8+9＝39．故答案为：39．【点评】本题考查灵活运用正方体的相对面解答问题，立意新颖，是一道不错的题．13．一个矩形绕着它的一边旋转一周，所得到的立体图形是圆柱体．【分析】本题是一个矩形绕着它的一边旋转一周，根据面动成体的原理即可解．【解答】解：以矩形的一边所在直线为旋转轴，形成的旋转体叫做圆柱体．故答案为圆柱体．【点评】根据圆柱体的形成可作出判断．本题主要考查圆柱的定义．14．若将棱长为2的正方体切成8个棱长为1的小正方体，则所有小正方体表面积的和是原正方体表面积的2倍；若将棱长为3的正方体切成27个棱长为1的小正方体，则所有小正方体表面积的和是原正方体表面积的3倍；若将棱长为n（n＞1，n为整数）的正方体切成n3个棱长为1的小正方体，则所有小正方体表面积的和是原正方体表面积的n倍．【分析】根据正方体的概念和特性以及表面积的计算公式即可解．【解答】解：棱长为n（n＞1，n为整数）的正方体的表面积是6n2，把它切成n3个棱长为1的小正方体，则每个小正方体的表面积是6，则所有小正方体表面积的和是6n3．故答案为：2，3，n．【点评】本题主要考查正方体的表面积的计算方法，是一个基本的题目．15．观察下列图形的排列规律（其中△是三角形，□是正方形，〇是圆），〇△□□〇△□〇△□□〇△□……若第一个图形是圆，则第2008个图形是三角形（填图形名称）．【分析】解此类题首先要仔细观察图形找出其中的规律进行解答．【解答】解：观察图形的排列规律知，7个图形循环一次，2008÷7＝286…6，又由第一个图形是圆形，则第2008个图形是三角形．故答案为：三角形．【点评】本题属于总结规律的问题，注意观察所给出的图形的排列特点，主要看它的循环规律．16．立方体木块的六个面分别标有数字1、2、3、4、5、6，如图，是从不同方向观察这个立方体木块看到的数字情况，数字1和5对面的数字的和是7．【分析】从3个图形看，和1相邻的有2，4，5，6，那么和1相对的就是3．则和2相邻的有1，3，4，5，那么和2相对的就是6．则和5相对的就是4．再将数字1和5对面的数字相加即可．【解答】解：根据三个图形的数字，可推断出来，1对面是3；2对面是6；5对面是4．∴3+4＝7．则数字1和5对面的数字的和是7．故答案为：7．【点评】本题主要考查学生的空间想象能力和推理能力，也可动手制作一个正方体，根据题意在各个面上标上数字，再确定对面上的数字，可以培养动手操作能力和空间想象能力．17．用一张面积为36π2cm2的正方形纸片围成圆柱的侧面积，则圆柱的底面半径＝3cm．【分析】先求出正方形的边长，即圆柱的底面周长，再根据圆柱的底面半径＝底面周长÷π÷2计算求解．【解答】解：这个圆柱的底面周长就是正方形的边长，面积为36π2cm2的正方形，边长即为6π，所以半径＝6π÷π÷2＝3cm．答：圆柱的底面半径为3cm．故答案为：3．【点评】此题的关键是理解柱的底面周长就是正方形的边长，然后利用周长公式求半径．18．如图，正方体（图1）的展开图如图2所示，在图1中M、N分别是FG、GH的中点，CM、CN、MN是三条线段；请在图2中画出CM、CN、MN这三条线段．【分析】先分别找到M、N、C在正方体的展开图中的对应点，再在展开图中连接即可．【解答】解：作图如下：故答案为：．【点评】本题考查了正方体的展开图，熟练掌握正方体平面展开图的特征是解决此类问题的关键．注意找准M、N、C在正方体的展开图中的对应点．19．将一个棱长为8、各个面上均涂有颜色的正方体，锯成64个同样大小的小正方体，其中所有恰有2面涂有颜色的小正方体表面积之和为576．【分析】将一个棱长为8、各个面上均涂有颜色的正方体，锯成64个同样大小的小正方体，则小正方体的棱长是2，表面积是2×2×6＝24，并且恰有2面涂有颜色的小正方体共有24个，则这样的小正方体表面积的和是24×24＝576．【解答】解：根据以上分析：小正方体的棱长是2，表面积是2×2×6＝24，恰有2面涂有颜色的小正方体共有24个．则这样的小正方体表面积的和是24×24＝576．故答案为576．【点评】解决本题的关键是能够分析出恰有2面涂有颜色的小正方体的个数，本题主要训练了空间想象能力．20．观察下列A，B，C三个图形，从A到B，从B到C的变化都具有某种规律，按照这种规律填出D图【分析】根据图示可知图案是按逆时针旋转的．【解答】解：根据以上分析D图是．【点评】本题要注意图片中不同形状对应的不同的位置，然后根据其变化的规律作答．21．如图是一个正方体的展开图，标注了字母a的面是正方体的正面．如果正方体相对两个面上的式子的值相等，求（y﹣x）2015的值．【分析】根据正方体相对两个面上的式子的值相等列出方程组，从而可求得x、y的值，然后再进行计算即可．【解答】解：根据题意可知：．解得：．∴（y﹣x）2015＝（1﹣3）2015＝（﹣2）2015＝﹣22015．【点评】本题主要考查的是正方体相对两个面上的文字，根据题意列出关于x、y的方程组是解题的关键．22．建设节约型社会就是使每一位公民养成节约意识，形成人人节约的良好习惯．节约与否不仅是个生活习惯、生活小节问题，更是个思想道德境界的问题．我们拥有的一切物质财富，无一不是劳动的结晶，每一滴水，每一度电，每一张纸，都凝结着劳动者的心血与汗水，所以，我们应该节约．假如你送给好朋友们的一个棱长为1的正方体礼物，需要用一张正方形彩纸包装，若不把纸撕开，那么所需纸的最小边长为．【分析】作出草图，考虑沿正方形彩纸对角线折叠，最后再把彩纸的四个角的直角三角形折起盖住上表面．【解答】解：把正方形如图划分，CB＝2AB＝2CD，用标②的面作为底面，标③、④、⑤、⑥的作为侧面，四个标①的部分正好盖住立方体的上表面，由正方体的棱长为1，∴BC＝＝，AB＝CD＝，∴AD＝BC+CD＝+2×＝2．故答案为：2．【点评】本题考查了几何体的表面积，考虑正方体的一个面用四部分覆盖是解题的关键，作出图形更形象直观．23．填空：（1）在圆周上有7个点A，B，C，D，E，F和G，连接每两个点的线段共可作出21条．（2）已知5条线段的长分别是3，5，7，9，11，若每次以其中3条线段为边组成三角形，则最多可构成互不全等的三角形7个．（3）三角形的三边长都是正整数，其中有一边长为4，但它不是最短边，这样不同的三角形共有8个．（4）以正七边形的7个顶点中的任意3个为顶点的三角形中，锐角三角形的个数是14．（5）平面上10条直线最多能把平面分成56个部分．（6）平面上10个圆最多能把平面分成92个区域．【分析】我们可以对每道题进行分析，找出其中的规律，从而得到所求的结果．比如（4）通过分析每两个顶点边线为边的三角形各种可能的角的大小进行，以正七边形的边为三角形一边的所有三角形均为钝角三角形，满足条件的三角形的三顶点两两之间至少有正七边的一个顶点隔开，这样的三角形以正七边形各顶点来看，每个顶点都存在两个满足条件的三角形，一共是14个．【解答】解：（1）由分析知：在圆周上有7个点A，B，C，D，E，F和G，连接每两个点的线段共可作出21条；（2）已知5条线段的长分别是3，5，7，9，11，若每次以其中3条线段为边组成三角形，则最多可构成互不全等的三角形7个；（3）三角形的三边长都是正整数，其中有一边长为4，但它不是最短边，这样不同的三角形共有5个；（4）通过分析每两个顶点边线为边的三角形各种可能的角的大小进行，以正七边形的边为三角形一边的所有三角形均为钝角三角形，满足条件的三角形的三顶点两两之间至少有正七边的一个顶点隔开，这样的三角形以正七边形各顶点来看，每个顶点都存在两个满足条件的三角形，一共是14个；（5）1条直线分平面为2个部分，再加1条，将2这两部分又都隔开，于是又多2个部分．再画第3条，要想将平面分成最多块，那么这条直线需与两条直线都相交，且与之前的交点不重复，这样就会多出3个部分．依此类推，每画第N条直线，要想将平面分成最多块，就会比之前多出N个部分．于是10条直线能将平面分成2+2+3+4+…+10＝56个部分；（6）1个圆：22个圆：2+23个圆：2+2+44个圆：2+2+4+6…10个圆2+2+4+…+（10×2﹣2）＝92原因：增加一个圆，这个圆（最多）可与前面各个圆相交，且只能有两个交点（以1个圆考虑，与另一圆相交，增加两个交点，便多分出2个部分）n个圆也适用，第n个与前n﹣1个交，n﹣1个每个都会多两个交点，即多分出2个部分增加n×2﹣2个．【点评】本题主要考查认识平面图形，关键是找到蕴含的规律．24．如图，这是一个由三个大小不同的正方体所组成的装饰物，现在要对它的表面涂油漆、假设三个正方体的边长分别为a，b，c，其中a＜b＜c．那么该装饰物涂漆面积最少（当该装饰物水平放置在桌面上的时候，不能从外观上看见装饰物的任何裸露）是4a2+4b2+5c2．【分析】解此类题首先要计算表面积，即从上面看到的面积+四个侧面看到的面积+下面看到的面积．【解答】解：根据分析其表面积＝a2+b2+c2+c2+2（a2+b2+c2）+a2+b2+c2＝5a2+4b2+4c2，即涂上颜色的面积最少为4a2+4b2+5c2．故答案为：4a2+4b2+5c2．【点评】主要考查了立体图形的视图问题．解题的关键是能把从不同的方向上看到的图形面积抽象出来（即利用视图的原理），从而求得总面积．25．如图，MN是圆柱底面的直径，NO是圆柱的高，在圆柱的侧面上，过点M，P．有一条绕了四周的路径最短的金属丝，现将圆柱侧面沿NO剪开，所得的侧面展开图可以是：②（填序号）．【分析】根据两点之间线段最短，剪开后所得的侧面展开图中的金属丝是线段，即可选择．注意P点在展开图中长边的中点处【解答】解：圆柱侧面沿NO剪开，根据两点之间线段最短，剪开后所得的侧面是长方形，P点在展开图中长边的中点处，金属丝是线段，且从P点开始到M点为止．故选②．【点评】本题着重考查学生对立体图形与平面展开图形之间的转换能力，与课程标准中。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

4.1 几何图形2
一、单选题
1．下列各个平面图形中，属于圆锥的表面展开图的是( )
A．B．C．D．2．如图绕虚线旋转得到的几何体是（）.
A．B．C．D．
3．下面图形经过折叠不能围成棱柱的是（）
A．B．C．D．
4．下面的几何体中，属于棱柱的有（）
A．1个B．2个C．3个D．4个
5．和另外三个立体图形不同类的是( )
A．B．C．D．6．下列说法错误的是（）
A．若直棱柱的底面边长都相等，则它的各个侧面面积相等
B．n棱柱有n个面，n个顶点
C．长方体，正方体都是四棱柱
D．三棱柱的底面是三角形
7．将图1围成图2的正方体，则图1中的红心“”标志所在的正方形是正方体中的（）
A、面CDHE
B、面BCEF
C、面ABFG
D、面ADHG
8．小明为了鼓励芦山地震灾区的学生早日走出阴影，好好学习，制作了一个正方体礼盒（如图）．礼盒每个面上各有一个字，连起来组成“芦山学子加油”，其中“芦”的对面是“学”，“加”的对面是“油”，则它的平面展开图可能是（）
A．B．C．D．
9．如图是一无盖长方体盒子的展开图（重叠部分不计），则该无盖长方体的容积为（）
A．4 B．3 C．8 D．12
10．将“创建文明城市”六个字分别写在一个正方体的六个面上，这个正方体的平面展开图如图所示，那么在这个正方体中，与“创”字相对的字是（）
A.文
B.明
C.城
D.市
二、填空题
11．如图是一个棱长为2 cm的立方体，若要把它截成八个棱长1 cm的小立方体，至少需截____次．
12．将一个圆分割成三个扇形，使它们圆心角度数比为2：3：4，则这3个圆心角中度数最大的为 ________．
13．下列请写出下列几何体，并将其分类．（只填写编号）
如果按“柱”“锥”“球”来分，柱体有_____，椎体有_____，球有_____；
如果按“有无曲面”来分，有曲面的有_____，无曲面的有_____．
14．如图所示，截去正方体一角变成一个多面体，这个多面体有______个面，有______条棱，有______个顶点．
15．如图所示，一个长方体的长为4cm，宽为3cm，高为5cm．则长方体所有棱长的和为_______________；长方体的表面积为_______________ ．
16．如图是一个正方体的表面展开图，若正方体中相对的面上的数互为相反数，则2x－y的值为_________．
三、解答题
17．在一个长方形中，长和宽分别为4cm、3cm，若该长方形绕着它的一边旋转一周，则形成的几何体的体积是多少？（结果用π表示）
18.如图所示是长方体的平面展开图，设AB=x，若AD=4x，AN=3x．
（1）求长方形DEFG的周长与长方形ABMN的周长（用字母x进行表示）；
（2）若长方形DEFG的周长比长方形ABMN的周长少8，求x的值；
（3）在第（2）问的条件下，求原长方体的容积．
19．如图是一个三棱柱，观察这个三棱柱，请回答下列问题：
（1）这个三棱柱共有多少个面？
（2）这个三棱柱一共有多少条棱？
（3）这个三棱柱共有多少顶点？
（4）通过对棱柱的观察，请你说出n棱柱的面数、顶点数及棱的条数．
20．学习了“展开与折叠”后，同学们了解了一些简单几何体的展开图，小明在家用剪刀剪一个如图（1）的长方体纸盒，但不小心多剪开了一条棱，得到图（2）中的纸片①和②，请解答下列问题：
（1）小明共剪开条棱；
（2）现在小明想将剪断的纸片②拼接到纸片①上，构成该长方体纸盒的展开图，请你在①中画出纸片②的一种位置；
（3）请从A，B两题中任选一题作答．
A．若长方体纸盒的长，宽，高分别为m，m，n（单位：cm，m＞n），求（2）中展开图的周长．
B．若长方体纸盒的长，宽，高分别是a，b，c（单位：cm，a＞b＞c），如图（3），画出它的展开图中周长最大时的展开图，并求出周长（用含a，b，c的式子表示）
21．用5个相同的正方体搭出如图所示的组合体．
(1)分别画出从正面、左面、上面看这个组合体时看到的图形；
(2)如果在这个组合体中，再添加一个相同的正方体组成一个新组合体，从正面、左面看这个新组合体时，看到的图形与原来相同．你认为这个设想能实现吗？若能，画出添加正方体后，从上面看这个组合体时看到的图形；若不能，说明理由．
参考答案
1．D2．D3．D4．C5．B6．B7．A8．D9．C10．B11．3
12．160°
13．（1）（2）（6）（3）（4）（5）（2）（3）（5）（1）（4）（6）
14．7127
15．48cm94cm2
16．-3
17．形成的几何体的体积是36πcm3或48πcm3．
18．（1）6x,8x；（2）x=4；（3）384．
【详解】
（1）∵AB=x，若AD=4x，AN=3x，
∴长方形DEFG的周长为2（x+2x）=6x，
长方形ABMN的周长为2（x+3x）=8x；
（2）依题意，8x-6x=8，
解得：x=4；
（3）原长方体的容积为x•2x•3x=6x3，
将x=4代入，可得容积6x3=384．
19．（1）5；（2）9；（3）6；（4）（n+2）、2n，3n．
【解析】分析：观察棱柱得出规律，求解即可.
详解：（1）这个三棱柱共有5个面；（2）这个三棱柱一共有9条棱；（3）这个三棱柱共有6顶点（4）n 棱柱的面数（n+2）、顶点数是2n，棱的条数是3n．
20．（1）8（2）四种情况（3）.A、①③的周长为6m+8n；②④的周长为8m+6n;B 、画图见解析，周长为2c+4b+8a.
【解析】试题分析：（1）根据平面图形得出剪开棱的条数；
（2）根据长方体的展开图的情况可知有四种情况；
（3）A、观察（2）中的展开图分别进行计算即可得；
B、展开平面图求周长的公式与展开的方式无关所以无论怎么展开我们通过实践都可以得出以下结论：假设长，宽，高分别为x，y，z(x，y，为任意值)周长c＝2x＋4y＋8z，
这个平面图的周长最大也就是当x最小，z最大.即c＝2c＋4b＋8a，
这个平面图的周长最小也就是当x最大，z最小.即c＝2a＋4b＋8c.
试题解析：（1）小明共剪了8条棱，
故答案为：8；
（2）如图，四种情况．
，，；
（3）A、①、③的周长为6m+8n；②、④的周长为8m+6n；
B、展开图如图所示，
周长为：2c＋4b＋8a.
21．（1）见解析；（2）能实现，添加正方体后从上面看到的图形见解析.
【解析】试题分析：（1）由已知条件可知，主视图有3列，每列小正方数形数目分别为2，1，1；左视图有2列，每列小正方形数目分别为2，1；俯视图有3列，每列小正方形数目分别为2，1，1．据此可画出图形．
（2）根据再添加一个小正方体，使得它的主视图和左视图不变，则可以在从左起第一行第2列或第3列添加一个立方体即可得出答案．
试题解析：(1)画出的图形如图①所示．
(2)能实现．添加正方体后从上面看到的图形如图②所示，有两种情况．。