轴心受力构件局稳定计算
轴心受压构件的稳定系数
1
2
3
4
5
6
7
8
9
0
10
20
30
40
50
60
70
80
90
100
110
120
130
140
150
160
170
180
190
200
1.000
0.984
0.937
0.848
0.766
0.690
0.618
0.552
0.493
0.439
0.394
0.359
0.328
0.299
0.272
0.248
0.227
0.208
0.322
0.288
0.259
0.234
0.212
0.193
0.176
0.162
0.149
0.137
0.127
0.996
0.978
0.946
0.910
0.870
0.823
0.769
0.707
0.641
0.575
0.511
0.453
0.402
0.357
0.318
0.285
0.256
0.232
0.210
0.202
0.184
0.169
0.155
0.143
0.132
1.000
0.989
0.963
0.929
0.891
0.847
0.797
0.739
0.675
0.608
0.542
0.481
0.426
钢结构强度稳定性计算书

钢结构强度稳定性计算书计算依据:1、《钢结构设计规范》GB50017-2003一、构件受力类别:轴心受压构件。
二、强度验算:1、轴心受压构件的强度,可按下式计算:σ = N/A n≤ f式中N──轴心压力,取N= 10 kN;A n──净截面面积,取A n= 298 mm2;轴心受压构件的强度σ= N / A n = 10×103 / 298 = 33.557 N/mm2;f──钢材的抗压强度设计值,取f= 205 N/mm2;由于轴心受压构件强度σ= 33.557 N/mm2≤承载力设计值f=205 N/mm2,故满足要求!2、摩擦型高强螺栓连接处的强度,按下面两式计算,取最大值:σ = (1-0.5n1/n)N/A n≤ f式中N──轴心压力,取N= 10 kN;A n──净截面面积,取A n= 298 mm2;f──钢材的抗压强度设计值,取f= 205 N/mm2;n──在节点或拼接处,构件一端连接的高强螺栓数目,取n = 4;n1──所计算截面(最外列螺栓处)上高强螺栓数目;取n1 = 2;σ= (1-0.5×n1/n)×N/A n=(1-0.5×2/4)×10×103/298=25.168 N/mm2;σ = N/A ≤ f式中N──轴心压力,取N= 10 kN;A──构件的毛截面面积,取A= 354 mm2;σ=N/A=10×103/354=28.249 N/mm2;由于计算的最大强度σmax = 28.249 N/mm2≤承载力设计值=205 N/mm2,故满足要求!3、轴心受压构件的稳定性按下式计算:N/φA n≤ f式中N──轴心压力,取N= 10 kN;l──构件的计算长度,取l=5000 mm;i──构件的回转半径,取i=23.4 mm;λ──构件的长细比, λ= l/i= 5000/23.4 = 213.675;[λ]──构件的允许长细比,取[λ]=250 ;构件的长细比λ= 213.675 ≤[λ] = 250,满足要求;φ──轴心受压构件的稳定系数, λ=l/i计算得到的构件柔度系数作为参数查表得φ=0.165;A n──净截面面积,取A n= 298 mm2;f──钢材的抗压强度设计值,取f= 205 N/mm2;N/(φA n)=10×103/(0.165×298)=203.376 N/mm2;由于σ= 203.376 N/mm2≤承载力设计值f=205 N/mm2,故满足要求!。
C82-格构式轴心受压构件分肢稳定性及分肢局部稳定性

稳 定计算。
x
分肢采用热轧型钢时,其翼缘和腹板一般
都能满足局部稳定要求,不必验算。
y
y
x
当分肢采用焊接组合截面时,其翼缘和腹
板宽厚比应满足局部稳定要求。 将分肢当一 y 实腹式轴压构件来验算其局部
x y
稳定性即可。
x
3、格构式轴心受压构件分肢稳定性及分肢局部稳定性
▪ 分肢既是组成整体截面的一部分,在缀材节点
之间又是一个单独的实腹式受压构件。故应验 柱
算分肢强度、刚度、稳定性,保证各分肢失稳 肢 θ l1
不先于格构式构件整体失稳。
缀
条
▪ 当分肢长细比满足下列条件时可不必验算分肢
的强度、刚度、稳定性。
缀条柱的分肢长细ax
max ,
max
ox
y
柱 肢
缀
l01
板
t
缀板柱的分肢长细比:
l i 40 且 0 .5
1
01
1
max
max , 当 <50 时,取 50
max
ox y
max
max
a
1
x
1
x
格构式轴心受压构件的分肢承受压力,应进行板件的局部
B94-实际轴心受压构件整体稳定计算公式

x
x
x
x
格构式
y
x
y
x
y
x
x
x
x 焊接,翼缘为 轧制或剪切边
b类
c类
y
y
y
y
焊接,翼缘为轧
y 焊接,板件
x
制或剪切边 x
宽厚比≤20
c类
c类
轴心受压构件截面分类(板厚t≥40mm)
截面形式
对x轴
b x
y
h
轧制工字形 或H形截面
t<80mm
b类
t≥80mm
c类
y
x
x
y
焊接工字 形形截面
翼缘为焰切边
b类
y
边
轧制等 边角钢
对x轴
y x
y
xx
x
y
x
x
y
y
y
y
y
b类
y 轧制、焊接
x
x
轧制或 焊接
x
板件宽厚比
大于20
y x
y
x 轧制截面和翼 缘为焰切边的 焊接截面
y
x
y
x 焊接,板件 边缘焰切
对y轴 b类
轴心受压构件截面分类(板厚t<40mm)
截面形式
对x轴 对y轴
y
y
y
y
y
x
x
x
x
x
焊接
y
y
y
y
b类 b类
计算 l0
i
据
截面类型
查表
得到
代入公 式验算
N f
A
如何提高轴心受压构件整体稳定性 ?
由公式 N f 及 l0
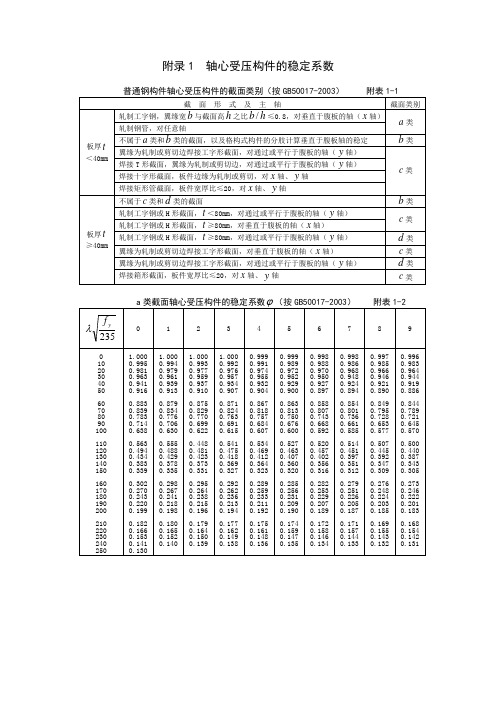
附录1轴心受压构件的稳定系数

附录1轴⼼受压构件的稳定系数附录1 轴⼼受压构件的稳定系数普通钢构件轴⼼受压构件的截⾯类别(按GB50017-2003)附表1-1截⾯形式及主轴截⾯类别板厚t <40mm轧制⼯字钢,翼缘宽b 与截⾯⾼h 之⽐h b /≤0.8,对垂直于腹板的轴(x 轴) a 类轧制钢管,对任意轴不属于a 类和b 类的截⾯,以及格构式构件的分肢计算垂直于腹板轴的稳定b 类翼缘为轧制或剪切边焊接⼯字形截⾯,对通过或平⾏于腹板的轴(y 轴) c 类焊接T 形截⾯,翼缘为轧制或剪切边,对通过或平⾏于腹板的轴(y 轴)焊接⼗字形截⾯,板件边缘为轧制或剪切,对x 轴、y 轴焊接矩形管截⾯,板件宽厚⽐≤20,对x 轴、y 轴板厚t ≥40mm不属于c 类和d 类的截⾯b 类轧制⼯字钢或H 形截⾯,t <80mm ,对通过或平⾏于腹板的轴(y 轴) c 类轧制⼯字钢或H 形截⾯,t ≥80mm ,对垂直于腹板的轴(x 轴)轧制⼯字钢或H 形截⾯,t ≥80mm ,对通过或平⾏于腹板的轴(y 轴) d 类翼缘为轧制或剪切边焊接⼯字形截⾯,对垂直于腹板的轴(x 轴)c 类翼缘为轧制或剪切边焊接⼯字形截⾯,对通过或平⾏于腹板的轴(y 轴)d 类焊接箱形截⾯,板件宽厚⽐≤20,对x 轴、y 轴c 类a 类截⾯轴⼼受压构件的稳定系数?(按GB50017-2003)附表1-2235yf λ0 1 2 3 4 5 6 7 8 9 0 10 20 30 40 50 60 70 80 90 100 110 120 130 140 150 160 170 180 190 200 210 220 230 240 2501.000 0.995 0.981 0.963 0.941 0.916 0.883 0.839 0.783 0.714 0.638 0.563 0.494 0.434 0.383 0.339 0.302 0.270 0.243 0.220 0.199 0.182 0.1660.153 0.141 0.1301.000 0.994 0.979 0.961 0.939 0.913 0.879 0.834 0.776 0.706 0.630 0.555 0.488 0.429 0.378 0.335 0.298 0.267 0.241 0.218 0.198 0.180 0.1650.152 0.1401.000 0.993 0.977 0.959 0.937 0.910 0.875 0.829 0.770 0.699 0.622 0.448 0.481 0.423 0.373 0.331 0.295 0.264 0.238 0.215 0.196 0.179 0.1640.150 0.1391.000 0.992 0.976 0.957 0.934 0.907 0.871 0.824 0.763 0.691 0.615 0.541 0.475 0.418 0.369 0.327 0.292 0.262 0.236 0.213 0.194 0.177 0.162 0.149 0.1380.999 0.991 0.974 0.955 0.932 0.904 0.867 0.818 0.757 0.684 0.607 0.534 0.469 0.412 0.3640.323 0.289 0.259 0.233 0.211 0.192 0.175 0.161 0.148 0.1360.999 0.989 0.972 0.952 0.929 0.900 0.863 0.813 0.750 0.676 0.600 0.527 0.463 0.407 0.360 0.320 0.285 0.256 0.231 0.209 0.190 0.174 0.159 0.147 0.1350.998 0.988 0.970 0.950 0.927 0.897 0.858 0.807 0.743 0.668 0.592 0.520 0.457 0.402 0.356 0.316 0.282 0.253 0.229 0.207 0.189 0.172 0.158 0.146 0.1340.998 0.986 0.968 0.948 0.924 0.894 0.854 0.801 0.736 0.661 0.585 0.514 0.451 0.397 0.351 0.312 0.279 0.251 0.226 0.205 0.187 0.171 0.157 0.144 0.1330.142 0.131235y f λ0 1 2 3 4 5 6 7 8 9 0 10 20 30 40 50 60 70 80 90 100 110 120 130 140 150 160 170 180 190 200 210 220 230 240 2501.000 0.992 0.970 0.936 0.899 0.8560.807 0.751 0.688 0.6210.5550.493 0.437 0.387 0.345 0.3080.276 0.249 0.225 0.204 0.1860.170 0.156 0.144 0.133 0.1231.000 0.991 0.967 0.932 0.895 0.8520.802 0.745 0.681 0.614 0.5490.487 0.432 0.383 0.341 0.3040.273 0.246 0.223 0.202 0.1840.169 0.155 0.143 0.1321.000 0.989 0.963 0.929 0.891 0.8470.797 0.739 0.675 0.608 0.5420.481 0.426 0.378 0.337 0.3010.270 0.244 0.220 0.200 0.1830.167 0.154 0.142 0.1310.999 0.987 0.960 0.925 0.887 0.8420.791 0.732 0.668 0.601 0.5360.475 0.421 0.374 0.333 0.2980.267 0.241 0.218 0.198 0.1810.166 0.153 0.141 0.1300.999 0.985 0.957 0.922 0.882 0.8380.786 0.726 0.661 0.594 0.5290.470 0.416 0.370 0.329 0.2950.265 0.239 0.216 0.197 0.1800.165 0.151 0.140 0.1290.998 0.983 0.953 0.918 0.878 0.8330.780 0.720 0.655 0.588 0.5230.464 0.411 0.365 0.326 0.2910.262 0.236 0.214 0.195 0.1780.163 0.150 0.138 0.1280.997 0.981 0.950 0.914 0.874 0.8280.774 0.714 0.648 0.581 0.5170.458 0.406 0.361 0.322 0.2880.259 0.234 0.212 0.193 0.1760.162 0.149 0.137 0.1270.256 0.232 0.210 0.191 0.1750.160 0.148 0.136 0.1260.995 0.976 0.943 0.906 0.865 0.8180.763 0.701 0.635 0.568 0.5050.447 0.397 0.353 0.315 0.2820.254 0.229 0.208 0.190 0.1730.159 0.146 0.135 0.1250.994 0.973 0.939 0.903 0.861 0.8130.757 0.694 0.628 0.561 0.4990.442 0.392 0.349 0.311 0.2790.251 0.227 0.206 0.188 0.1720.158 0.145 0.134 0.124c 类截⾯轴⼼受压构件的稳定系数?(按GB50017-2003)附表1-4235y f λ0 1 2 3 4 5 6 7 8 9 0 10 20 30 40 50 60 70 80 90 100 110 120 130 140 150 160 170 180 190 200 210 220 230 240 2501.000 0.992 0.966 0.902 0.8390.775 0.709 0.648 0.578 0.517 0.463 0.419 0.379 0.342 0.309 0.280 0.254 0.230 0.210 0.192 0.176 0.162 0.1500.138 0.128 0.1191.000 0.990 0.959 0.896 0.833 0.768 0.702 0.636 0.572 0.511 0.458 0.415 0.375 0.339 0.306 0.277 0.251 0.228 0.208 0.190 0.175 0.161 0.1480.137 0.1271.000 0.988 0.953 0.890 0.826 0.762 0.695 0.629 0.566 0.505 0.454 0.411 0.371 0.335 0.303 0.274 0.249 0.226 0.206 0.189 0.173 0.159 0.147 0.136 0.1260.999 0.986 0.947 0.884 0.820 0.755 0.689 0.623 0.559 0.500 0.449 0.407 0.367 0.332 0.300 0.271 0.246 0.224 0.205 0.187 0.172 0.1580.1460.135 0.1250.999 0.983 0.940 0.877 0.814 0.748 0.682 0.616 0.553 0.494 0.445 0.403 0.364 0.328 0.297 0.269 0.244 0.222 0.203 0.186 0.170 0.157 0.145 0.134 0.124 0.998 0.981 0.934 0.871 0.807 0.742 0.676 0.610 0.547 0.488 0.441 0.399 0.360 0.325 0.294 0.266 0.242 0.220 0.201 0.184 0.169 0.156 0.144 0.133 0.1240.997 0.978 0.928 0.865 0.801 0.735 0.669 0.604 0.541 0.483 0.436 0.395 0.356 0.322 0.291 0.264 0.239 0.218 0.199 0.182 0.168 0.154 0.143 0.132 0.1230.996 0.976 0.921 0.858 0.794 0.729 0.662 0.597 0.535 0.477 0.432 0.391 0.353 0.319 0.288 0.261 0.237 0.216 0.197 0.181 0.166 0.153 0.142 0.131 0.1220.995 0.973 0.915 0.852 0.788 0.722 0.656 0.591 0.529 0.472 0.428 0.387 0.349 0.315 0.285 0.258 0.235 0.214 0.196 0.179 0.165 0.152 0.140 0.130 0.1210.993 0.970 0.909 0.846 0.781 0.715 0.649 0.584 0.523 0.467 0.423 0.383 0.346 0.312 0.282 0.256 0.233 0.212 0.194 0.178 0.163 0.151 0.139 0.129 0.120235y f λ0 1 2 3 4 5 6 7 8 90 10 20 30 40 50 60 70 80 90 100 110 120 130 140 150 160 170 180 190 2001.000 0.984 0.937 0.848 0.766 0.690 0.618 0.552 0.493 0.439 0.394 0.359 0.328 0.299 0.272 0.248 0.227 0.208 0.191 0.176 0.1621.000 0.981 0.927 0.840 0.759 0.683 0.612 0.546 0.487 0.434 0.390 0.356 0.325 0.296 0.270 0.246 0.225 0.206 0.189 0.1740.999 0.978 0.918 0.831 0.751 0.675 0.605 0.540 0.481 0.429 0.387 0.353 0.322 0.293 0.267 0.244 0.223 0.204 0.188 0.1730.999 0.974 0.909 0.823 0.743 0.668 0.598 0.534 0.476 0.424 0.383 0.350 0.319 0.290 0.265 0.242 0.221 0.203 0.186 0.1710.998 0.969 0.900 0.815 0.735 0.661 0.591 0.528 0.470 0.419 0.380 0.346 0.316 0.288 0.262 0.240 0.219 0.201 0.184 0.170 0.996 0.965 0.8910.990 0.949 0.865 0.782 0.705 0.632 0.565 0.504 0.449 0.401 0.366 0.334 0.304 0.277 0.253 0.231 0.212 0.194 0.178 0.1640.987 0.944 0.857 0.774 0.697 0.625 0.559 0.498 0.444 0.397 0.363 0.331 0.301 0.275 0.251 0.229 0.210 0.192 0.177 0.163Q235钢冷弯薄壁型钢轴⼼受压构件的稳定系数?(按50018-2002)附表1-6λ0 1 2 3 4 5 6 7 8 90 10 20 30 40 50 60 70 80 90 100 110 120 130 140 150 160 170 180 190 200 210 220 230 240 250 1.000 0.974 0.947 0.918 0.886 0.852 0.818 0.775 0.722 0.661 0.588 0.516 0.452 0.396 0.349 0.308 0.274 0.245 0.220 0.199 0.180 0.164 0.150 0.138 0.127 0.117 0.997 0.971 0.944 0.915 0.882 0.849 0.814 0.770 0.716 0.654 0.580 0.509 0.446 0.391 0.344 0.305 0.271 0.213 0.218 0.197 0.179 0.163 0.149 0.137 0.126 0.995 0.968 0.941 0.912 0.879 0.846 0.810 0.765 0.710 0.648 0.573 0.502 0.440 0.386 0.340 0.301 0.268 0.240 0.216 0.195 0.177 0.161 0.148 0.136 0.125 0.992 0.966 0.938 0.909 0.875 0.843 0.806 0.760 0.704 0.641 0.566 0.496 0.434 0.381 0.336 0.298 0.265 0.237 0.214 0.193 0.175 0.160 0.146 0.135 0.124 0.989 0.963 0.936 0.906 0.872 0.839 0.802 0.755 0.698 0.634 0.558 0.489 0.428 0.376 0.332 0.294 0.262 0.235 0.211 0.191 0.174 0.159 0.145 0.133 0.123 0.987 0.960 0.933 0.903 0.868 0.836 0.797 0.750 0.692 0.626 0.551 0.483 0.423 0.371 0.328 0.291 0.259 0.232 0.209 0.189 0.172 0.157 0.144 0.132 0.122 0.984 0.958 0.930 0.899 0.864 0.832 0.793 0.744 0.686 0.618 0.544 0.476 0.417 0.367 0.324 0.287 0.256 0.230 0.207 0.188 0.171 0.156 0.143 0.131 0.121 0.981 0.955 0.927 0.896 0.861 0.829 0.789 0.739 0.680 0.611 0.537 0.470 0.412 0.362 0.320 0.284 0.253 0.227 0.205 0.186 0.169 0.154 0.141 0.130 0.120 0.979 0.952 0.924 0.893 0.858 0.825 0.784 0.733 0.673 0.603 0.530 0.464 0.406 0.357 0.316 0.281 0.251 0.225 0.203 0.184 0.167 0.153 0.140 0.129 0.119 0.976 0.949 0.921 0.889 0.855 0.822 0.779 0.728 0.667 0.595 0.523 0.458 0.401 0.353 0.312 0.277 0.248 0.223 0.201 0.182 0.166 0.152 0.139 0.128 0.118λ0 1 2 3 4 5 6 7 8 90 10 20 30 40 5060 70 80 90 100110 120 130 140 150160 170 180 190 200 210 220 230 240 250 1.0000.9710.9400.9060.8670.8290.7770.7100.6320.5500.4750.4050.3470.3000.2610.2290.2030.1810.1620.1460.1320.1200.1090.902 0.864 0.824 0.771 0.703 0.623 0.542 0.467 0.398 0.342 0.296 0.258 0.227 0.201 0.179 0.160 0.144 0.130 0.119 0.108 0.099 0.091 0.994 0.965 0.934 0.898 0.860 0.819 0.765 0.695 0.615 0.535 0.460 0.392 0.337 0.2920.129 0.118 0.107 0.098 0.091 0.991 0.962 0.930 0.894 0.857 0.815 0.759 0.688 0.607 0.527 0.452 0.386 0.332 0.288 0.251 0.221 0.196 0.175 0.157 0.141 0.128 0.116 0.106 0.098 0.090 0.988 0.959 0.927 0.890 0.853 0.8100.327 0.284 0.248 0.218 0.194 0.173 0.155 0.140 0.127 0.115 0.106 0.097 0.089 0.985 0.956 0.924 0.886 0.849 0.805 0.746 0.672 0.591 0.512 0.438 0.375 0.322 0.280 0.245 0.216 0.191 0.171 0.153 0.138 0.126 0.114 0.1050.845 0.800 0.739 0.664 0.583 0.504 0.431 0.369 0.318 0.276 0.242 0.213 0.189 0.169 0.152 0.137 0.124 0.113 0.104 0.095 0.088 0.979 0.949 0.917 0.878 0.841 0.794 0.732 0.656 0.574 0.497 0.424 0.363 0.313 0.272 0.2380.112 0.103 0.094 0.087 0.976 0.946 0.913 0.874 0.837 0.789 0.725 0.648 0.566 0.489 0.418 0.358 0.309 0.269 0.235 0.208 0.185 0.165 0.149 0.134 0.122 0.111 0.102 0.094 0.086 0.973 0.943 0.909 0.870 0.833 0.783 0.7180.2650.2320.2050.1830.1630.1470.1330.1210.1100.1010.0930.086附录2 普通受弯钢构件稳定系数⼀、焊接⼯字形和轧制H 型钢等截⾯简⽀梁焊接⼯字形和轧制H 型钢等截⾯简⽀梁的整体稳定系数应按下式计算:y b y x y b b f h t W Ah 2354.414320212+???? ??+?=ηλλβ? (附2-1)式中 b β——梁整体稳定等效弯矩系数,根据荷载的形式和作⽤位置按附表2-1选⽤;y λ——梁的侧向长细⽐,y y i l /1=λ;1l ——梁的侧向计算长度,取受压翼缘侧向⽀承点间的距离;y i ——梁⽑截⾯对y 轴的回转半径; A ——梁的⽑截⾯⾯积; h ——梁的截⾯⾼度;x W ——梁受压翼缘边缘纤维的⽑截⾯抵抗矩;y f ——钢材的屈服强度;b η——截⾯不对称影响系数:双轴对称焊接⼯字形截⾯(附图2-1a 、d )的b η=0;单轴对称焊接⼯字形截⾯:加强受压翼缘(附图2-1b ))12(8.0-=b b αη,加强受拉翼缘(附图2-1c )的12-=b b αη;b α——受压翼缘与全截⾯侧向惯性矩⽐值,yb I II I I 1211=+=α;1I 、2I ——受压翼缘和受拉翼缘对y 轴的惯性矩。
受压构件的稳定(结构稳定原理)

127第2章 受压构件的稳定2.1 轴心受压构件的稳定轴心压杆就其自身的截面形状和尺寸而言,有较长细的杆,也有较中短的杆,这可用长细比i l /0=λ来表达。
对于长细比大的长细压杆,可以认为是在弹性范围内失稳;对于长细比小的中短杆件,则可能是在弹塑性范围内失稳。
因此,应该分别按弹性范围和弹塑性范围来分析理想轴心压杆的临界荷载。
2.1.1 理想轴心压杆的弹性稳定用理想轴心压杆的欧拉荷载E P 除以杆件的截面积A ,可得轴心压杆欧拉临界应力22202)/(λππσE i l E A P E cr===,式中i 为回转半径,AIi =。
由此可计算出应力值为材料比例极限p σ时的长细比p λ,并以此作为长细杆和中短杆的分界;压杆的长细比大于p λ时称为长细杆或大柔度杆,长细比小于p λ时称为中短杆或小柔度杆。
对于理想轴心压杆来说,长细杆是在弹性范围内工作的,所以压杆的稳定分析为弹性稳定问题。
通过弹性压杆的静力平衡条件,可以建立理想轴心压杆的平衡微分方程式,解平衡微分方程则可求得轴心压杆的临界荷载。
下面来看几个边界条件不同的理想轴心压杆的弹性稳定分析。
1)一端固定一端铰接的压杆 (1)用静力法求解如图2-1所示一端固定一端铰接的等截面轴心受压弹性直杆,设其已处于新的曲线平衡形式,则取任意截面的弯矩为)(x l Q Py M -+-=式中Q 为上端支座反力。
由y EI M ''-=,压杆挠曲线的平衡微分方程为:)(x l Q Py y EI -+-='' 图2-1一端固定一端铰接压杆128即 )(x l EIQ y EI P y -=+'' (2.1) 令EIPk =2,则有 )(22x l PQk y k y -=+'' (2.2) 此微分方程的通解为)(sin cos x l PQkx B kx A y -++= (2.3) 式中A 、B 为积分常数,Q /P 也是未知的。
轴心受压构件的整体稳定性

2、缀条设计 内力: V1:分配到一个缀材面的剪力。当每根柱子都有两个缀材面时,此时V1为V/2; n 承受剪力V1的斜缀条数,单缀条体系,n =1;双缀条超静定体系,通常简单地认为每根缀条负担剪力V2之半,取n =2; 缀条夹角,在30~60之间采用。 斜缀条常采用单角钢。由于角钢只有一个边和构件的肢件连接,考虑到受力时的偏心作用,计算时可将材料强度设计值乘以折减系数r =0.85。
横缀条主要用于减小肢件的计算长度,其截面尺寸与斜缀条相同,也可按容许长细比确定,取较小的截面。
3、缀板设计
缀板用角焊缝与肢件相连接,搭接的长度一般为20~30 mm。角焊缝承受剪力T和弯矩M的共同作用。
剪力: 弯矩(与肢件连接处):
算例6 P136 例4-5 算例7 P138 例4-6
算例4 P124 例4-3 算例5 P124 例4-4
第五节 格构式轴心受压构件设计
格构式截面
肢件:槽钢、工字钢、角钢
缀件:缀条、缀板
一、 格构式轴心受压构件长细比计算
1、绕实轴长细比计算:同实腹式;
2、绕虚轴长细比计算:考虑剪切变形,采用换算长细比;
换算长细比
式中 y 整个构件对虚轴的长细比; A 整个构件的横截面的毛面积; A1y 构件截面中垂直于y轴各斜缀条的毛截面面积之和; 为防止单肢件失稳先于整体失稳,规范规定: 缀条构件:单肢长细比不大于两方向长细比较大值0.7倍;
轴心受压构件的截面分类(板厚t40mm)
1、轴心受压构件稳定系数表达式 1)当 2)当
1)钢材品种(即fy和E);2)长细比;3)截面分类;
稳定系数影响因素:
式中 N 轴心受压构件的压力设计值; A 构件的毛截面面积; 轴心受压构件的稳定系数,取两主轴稳定系数较小者; f 钢材的抗压强度设计值。
钢结构基础第六章 轴心受力构件-稳定

第六章 轴心受力构件
局部失稳产生的背景:
1.3 1.2 1.1 Isolated Local Mode
kL
PL ( EI )
PE PL
Brown Dede Tomblin Trovillion Zureick Euler Local Column Eq. 1
2 z 2 0
第六章 轴心受力构件
2. 弯扭屈曲
单轴对称截面
第六章 轴心受力构件
开口截面的弯扭屈曲临界力Nxz ,可由下式计算:
i0 N Ex N xz N z N xz N xz e0 0
2 2 2
NEx为关于对称轴x的欧拉临界力。 引进弯扭屈曲换算长细比xz:
2 xz
1 2
2 x
2 z
1 22 x2 2 z
2 e0 41 2 i0
2 2 x z
第六章 轴心受力构件
6.5 杆端约束对轴心受压构件整体稳定性的影响
实际压杆并非全部铰接,对于任意支承情况的压杆,其临 界力为:
N cr
EI
2
1. 轴心受压柱的实际承载力
压杆的压力挠度曲线
第六章 轴心受力构件
轴心受压柱按下式计算整体稳定:
N f
A
cr
fy
式中 N 轴心受压构件的压力设计值; A 构件的毛截面面积;
f 轴心受压构件的稳定系数 ; N
cr
fy
f 钢材的抗压强度设计值 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1、某焊接组合工字形截面轴心受压柱,轴心压力设计值kN N 1500=,柱的计算长度m l x 80=,m l y 40=。
钢材用Q235,翼缘板为焰切边,截面无削弱。
验算:实腹柱腹板和翼缘的局部稳定。
2、某钢屋架中的轴心受压上弦杆,承受的轴心压力设计值为kN N 1000=, 计算长度m l x 5.10=,m l y 30=。
节点板厚mm 14,钢材用Q235,采用双角钢组合T 形截面,选用121001602⨯⨯L ,短边相连。
如图所示。
验算:此截面的局部稳定。
3、某梯形钢屋架轴心受压腹杆AB 如图所示。
截面为单角钢,规格8125⨯L ,与节点板单面连接,轴压力设计值为kN N 200=,
杆件几何长度为m l 8.1=,截面无削弱。
验算:此杆的强度和稳定。
4、某轴心受压构件截面如图所示,其承受的轴心压力设计值kN N 4000=(包括自重),计算长度m l x 5.30=,m l y 70=。
翼缘板为剪切边,每块翼缘板上设有两个直径mm d 240=,的螺栓孔,钢材用Q235。
验算:此柱截面。
5、如图所示,AB 杆的几何长度为mm 20392⨯,选用单角钢890⨯L ,
kN N 9.241=(压力),kN N 9.272=(压力)。
验算:AB 杆的承载力。
